随着工业生产技术水平的不断发展,基于数据驱动的故障检测技术受到学术界的广泛关注,以主元分析(principal component analysis, PCA)为代表的多元统计分析方法迅速发展,衍生出多种新的故障检测方法[1-7]。
近年来,随着化工生产过程的日趋复杂,越来越体现出其非高斯、多工况的特点。因此如何有效地提取化工生产过程中的有效信息,实现对非高斯、多模态过程的故障检测受到越来越多的关注。传统线性检测方法在非线性过程中检测效果不理想,为解决这一问题,SCHÖLKOPF等[8]提出核主元分析(kernel principal component analysis,KPCA)的故障检测方法,其基本思想是通过非线性映射将输入空间的过程数据映射到高维特征空间,但是KPCA算法在解决多模态问题方面存在局限性,同时KPCA算法容易受核参数的影响。目前为止,选择合适的核参数仍是一个难题。为了提高KPCA检测性能,王亚君等[9]提出了一种多动态核主元分析的检测方法,该方法构造了适合批量生产过程的多模型、非线性和动态的建模方法。为了提高非高斯化工过程的多工况性能监测,PENG等[10]提出基于即时学习和极端学习机的非高斯化工过程在线性能监控方法。为了提高多模态过程中的故障诊断率,YANG等[11]提出了一种基于变分模态分解(variational modal decomposition, VMD)的故障诊断方法,将即时学习改进的模糊c均值聚类(improved fuzzy c-means clustering for just in time learning, IJITL)和递归最小二乘支持向量机(recursive least squares support vector machine, RLSSVM)相结合,提高多模态过程故障诊断率。为了消除数据间的多模态特性,MA等[12]提出一种局部近邻标准化的数据预处理方法(local neighborhood standardization,LNS),利用每个样本局部近邻的均值和标准差标准化该样本,使数据标准化后尽可能的服从单峰高斯分布,但该方法近邻数k的选取对检测结果影响较大,而且该方法根据经验选取的近邻数k需要以各个模态过程知识为依托,具有一定的局限性。GUO等[13-14]提出差分局部保持投影(differential locality preserving projections,DIFLPP)算法,运用差分方法对数据进行预处理,消除原始数据的非线性和多模态特征。GUO等[15]又提出加权差分算法对数据进行预处理,通过使用加权差分方法对离散程度差异不大的多模态数据进行预处理,能够剔除原始数据的多模态特征和非线性特征,从而提高故障检测率,但该方法对模态间离散程度有一定的要求。ZHONG等[16-18]提出利用局部熵(local entropy,LE)提取数据特征来对数据进行预处理的方法,该方法可以有效地消除数据间的多模态特性,但是提取的局部熵数据不完全服从高斯分布。为了解决这一问题,本文提出一种新的基于改进局部熵PCA (improved local entropy principal component analysis,ILEPCA)故障检测方法。其基本思想是运用改进局部熵的方法对原始数据进行预处理,消除数据的多模态和非高斯特性,在此基础上运用PCA进行故障检测。
2 基于改进局部熵PCA的故障检测 2.1 基于改进局部熵PCA算法为了解决多模态问题,ZHONG等[17]引入熵(entropy)的概念。在故障检测过程中,熵越大,系统越混乱,不确定性越大。当异常值偏离正常值后,其不确定性必然改变。因此可以用熵作为统计指标来衡量系统过程状态是否正常。
对于一个随机变量x,其样本集表示为x= [x1, x2, ..., xn],其中n是样本号,香农熵定义为:
| $ \mathit{\boldsymbol{H}} = - \sum\nolimits_{i = 1}^n {p\left( {{\mathit{\boldsymbol{x}}_i}} \right)\log p\left( {{\mathit{\boldsymbol{x}}_i}} \right)} $ | (1) |
其中,p(xi)为xi处的概率密度。由于实际的概率密度是未知的,因此通常情况下使用其概率密度估计。核密度估计[19-20]是概率密度估计中最常见的,定义如下:
| $ \hat p\left( {{\mathit{\boldsymbol{x}}_i}} \right) = \frac{1}{{nh}}\sum\nolimits_{i = 1}^n {K\left\{ {\frac{{\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_i}}}{h}} \right\}} $ | (2) |
其中K(•)为核函数,h为预先给定的正数,通常称为窗口宽度或光滑参数,n为观测器的个数。本文采用高斯函数作为核函数。核密度估计p(xi)的准确度不仅与核函数的选取有关,还与窗宽h密切相关,一般选择拇指法则来计算最佳窗宽h [21]为:
| $ h = 1.06S{n^{ - 1/5}} $ | (3) |
其中S是样本标准差,n为样本总数。
工业过程中存在多个运行模态,这意味着来自不同模态的数据拥有不同的概率密度和分布特性,为了消除多模态的影响,ZHONG等[17]将kNN思想引入到核密度估计当中,建立局部概率密度(local probability density, LPD)估计函数如下:
| $ \hat p\left( {{\mathit{\boldsymbol{x}}_i}} \right) = \frac{1}{{kh}}\sum\nolimits_{{\mathit{\boldsymbol{x}}_j} \in {\rm{kNN}}\left( {{\mathit{\boldsymbol{x}}_i}} \right)} {K\left\{ {\frac{{{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_j}}}{h}} \right\}} $ | (4) |
其中kNN(xi)为样本xi的k近邻域,i为采样时刻。式(5)列出了邻域kNN(xi)内所包含的所有样本,xik表示xi的第k个最近邻,近邻顺序是依据与xi之间的欧式距离大小来排列的,即:
| $ {\rm{kNN}}\left( {{\mathit{\boldsymbol{x}}_i}} \right) = \left\{ {\mathit{\boldsymbol{x}}_i^1, \mathit{\boldsymbol{x}}_i^2, \ldots , \mathit{\boldsymbol{x}}_i^k} \right\} $ | (5) |
由式(4)所得的概率密度将使得原始数据集由全体训练样本缩短到k个样本,通过对k个样本进行密度估计来提取数据的局部密度信息。在多模态过程中,局部概率密度比全局概率密度更加接近模态的真实值,但是方差的变化会导致窗宽h的变化,不同模态下的密度估计值主要源于h的变化,为消除h的影响,ZHONG等[17]做了进一步的改进,如下:
| $ \hat p\left( {{\mathit{\boldsymbol{x}}_i}} \right) = \frac{1}{k}\sum\nolimits_{{\mathit{\boldsymbol{x}}_j} \in {\rm{kNN}}\left( {{\mathit{\boldsymbol{x}}_i}} \right)} {K\left\{ {\frac{{d\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}} \right)}}{{d\left( {{\mathit{\boldsymbol{x}}_j}, \mathit{\boldsymbol{x}}_j^k} \right)}}} \right\}} $ | (6) |
根据式(6)计算每个样本局部概率密度的估计值,通过使用d(xj, xjk)作为局部化标准,将h的主要影响抵消掉,从而解决由窗宽导致的影响问题。
通过上述分析将式(4)中的概率密度估计,应用式(6)给出的局部概率密度更加合理,而由局部概率密度得到的信息熵可以理解为样本的局部熵。鉴于信息熵的累加和形式,将移动窗口技术应用到熵变化过程中。假设观测数据X的局部概率密度估计矩阵为P= Rm*n,其中n为样本,m为变量。L是移动窗口的宽度,则t时刻的移动窗口Pt为:
| $ {\mathit{\boldsymbol{P}}_{\rm{t}}} = \left[ {\begin{array}{*{20}{c}} {{{\hat p}_1}\left( {t - L + 1} \right)}&{{{\hat p}_1}\left( {t - L + 1} \right)}& \cdots &{{{\hat p}_1}\left( {t - L + 1} \right)}\\ {{{\hat p}_1}\left( {t - L + 2} \right)}&{{{\hat p}_2}\left( {t - L + 2} \right)}& \cdots &{{{\hat p}_2}\left( {t - L + 2} \right)}\\ \vdots & \vdots & \ddots & \vdots \\ {{{\hat p}_m}\left( t \right)}&{{{\hat p}_m}\left( t \right)}& \cdots &{{{\hat p}_m}\left( t \right)} \end{array}} \right] $ | (7) |
则t时刻的局部熵向量ht为:
| $ {\mathit{\boldsymbol{h}}_{\rm{t}}} = {\left[ {\begin{array}{*{20}{c}} {{h_1}\left( t \right)}&{{h_2}\left( t \right)}& \cdots &{{h_m}\left( t \right)} \end{array}} \right]^{\rm{T}}} $ | (8) |
| $ {h_i}\left( t \right) = - \sum\nolimits_{j = t - L + 1}^t {{{\hat p}_i}\left( j \right)\log {{\hat p}_i}\left( j \right)} \;\;\;\;\;\;\;i = 1, \ldots , m $ | (9) |
局部熵变换将原始观测数据矩阵X转换为局部熵矩阵,从而实现了从原始数据空间到局部熵变量空间的转换过程。利用局部熵对数据进行预处理虽然能够消除数据的多模态特性,但是不能使数据服从高斯分布。现通过数值例子加以说明。假设有两个不同模态的数据,其中每个模态有200个样本。每个样本有2个变量,在每个模态中是独立的。模态1中,变量x1是服从[8, 0.52]的正态分布,变量x2是服从[8, 10]的均匀分布。在模态2中,变量x1是服从[11, 13]的均匀分布,变量x2是服从[14, 0.42]的正态分布。所有训练样本的散点图如图 1(a)所示,“星号”代表第一模态训练样本,“圆圈”代表第二模态训练样本。所有训练样本的序列图如图 1(b)所示。从图 1(a)和(b)可以看出原始数据存在两个模态。现在通过Kolmogorov-Smirnov方法检验原始数据是否服从高斯分布,结果如表 1所示。H0表示测试结果,P0为是否接受高斯分布的概率值。对于变量xt (t = 1, 2),如果H0 = 0且P0在5%显著性水平上,则xt服从高斯分布。相反,如果H0 = 1且P0在5%显著性水平下,则xt不服从高斯分布。从表 1可以看出原始数据服从非高斯分布。

|
图 1 训练数据散点图和序列图 Fig.1 Scatter and sequence plots of training data |
|
|
表 1 原始数据的Kolmogorov-Smirnov检验结果 Table 1 Results of Kolmogorov-Smirnov test for original data |
现利用局部熵对两个模态的训练数据进行预处理,预处理后的散点图如图 2(a)所示,“星号”代表第一模态训练数据,“圆圈”代表第二模态训练数据,lei表示变量xi的局部熵。训练数据中每个变量预处理后的局部熵序列图如图 2(b)所示,从图 2可以看出,两个模态的数据重合在一起,将原始多模态数据转换为单模态数据。现在利用Kolmogorov-Smirnov方法检验基于局部熵预处理后的数据是否服从高斯分布,结果如表 2所示。从表 2可以看出局部熵数据服从非高斯分布。

|
图 2 局部熵数据散点图和序列图 Fig.2 Scatter and sequence plots of local entropy data |
|
|
表 2 局部熵数据的Kolmogorov-Smirnov检验结果 Table 2 Results of Kolmogorov-Smirnov test for local entropy data |
为了解决以上问题,本文提出一种新的改进的局部熵(improved local entropy,ILE)方法处理多模态和非高斯数据。通过引入k近邻的均值来代替前一个局部化标准,提出改进的局部概率密度估计(improved local probability density, ILPD)为:
| $ {\hat p_{\rm{I}}}\left( {{\mathit{\boldsymbol{x}}_i}} \right) = \frac{1}{k}\sum\nolimits_{{\mathit{\boldsymbol{x}}_j} \in {\rm{kNN}}\left( {{\mathit{\boldsymbol{x}}_i}} \right)} {K\left\{ {\frac{{d\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}} \right)}}{{d{m_j}}}} \right\}} $ | (10) |
其中xi是X的样本,kNN(xi)是xi的第k近邻样本,dmj表示如下:
| $ d{m_j} = \frac{1}{{{k_j}}}\sum\nolimits_{s = 1}^{{k_j}} {d\left( {{\mathit{\boldsymbol{x}}_j}, \mathit{\boldsymbol{x}}_j^s} \right)} $ | (11) |
其中d(xj, xjs)代表xj与xjs之间的欧式距离。xjs是xj的第s近邻样本,近邻顺序kj是依据与xj之间的欧式距离大小来排列的,即:
| $ d\left( {{\mathit{\boldsymbol{x}}_j}, \mathit{\boldsymbol{x}}_j^1} \right) \le d\left( {{\mathit{\boldsymbol{x}}_j}, \mathit{\boldsymbol{x}}_j^2} \right) \le \ldots d\left( {{\mathit{\boldsymbol{x}}_j}, \mathit{\boldsymbol{x}}_j^k} \right) $ | (12) |
基于改进的局部概率密度,运用式(1)计算改进的局部熵,改进局部熵方法不仅可以更好地消除多模态特征,还可以使预处理的数据服从高斯分布。利用改进局部熵对以上数值例子进行数据预处理得到的数据散点图如图 3(a)所示。“星号”代表第一模态训练数据,“圆圈”代表第二模态训练数据,Ilei表示变量xi的改进的局部熵。基于改进的局部熵序列图如图 3(b)所示,从图 3可以看出,改进的局部熵可以消除原始数据的多模态特性。利用Kolmogorov-Smirnov方法检验基于改进局部熵预处理后的数据是否服从高斯分布,结果如表 3所示。从表 3可以看出,变量x1和变量x2均服从高斯分布。

|
图 3 改进局部熵数据散点图和序列图 Fig.3 Scatter and sequence plots of improved local entropy data |
|
|
表 3 改进局部熵数据的Kolmogorov-Smirnov检验结果 Table 3 Results of Kolmogorov-Smirnov test for improved local entropy data |
为了说明改进局部熵方法能够消除数据的多模态和非高斯特性,以变量x1为例,原始数据、局部熵数据和改进局部熵数据的变量分布图分别如图 4所示。从图 4(a)可以看出,原始数据分布在两个模态,不服从高斯分布。从图 4(b)可以看出,局部熵数据是单模态,但不服从高斯分布。由此可见,局部熵方法可以剔除数据的多模态特性,但是不能剔除数据的非高斯特性。从图 4(c)可以看出,数据属于一个模态并且近似服从高斯分布,说明改进局部熵方法可以有效地剔除数据的多模态和非高斯特性,验证了该方法的有效性。

|
图 4 变量x1的分布图 Fig.4 Distribution plots of variable x1 |
对改进局部熵数据H建立PCA模型,对H进行标准化,使H的各列方差为1,均值为0。然后计算H的协方差矩阵如下:
| $ \mathit{\boldsymbol{S}} = {\mathop{\rm cov}} \left( x \right) \approx \frac{1}{{n - 1}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}} $ | (13) |
其中n是样本个数。对协方差矩阵S进行特征值分解,计算出特征值和特征向量。根据式(15)求主元个数l。
| $ \frac{{\sum\nolimits_{i = 1}^l {{\lambda _i}} }}{{\sum\nolimits_{i = 1}^n {{\lambda _i}} }} \ge 85\% $ | (14) |
式中λi为协方差矩阵的特征根,其中由前l个特征向量构成的矩阵就是负载矩阵Pl。根据下式计算Q和T2统计量。
| $ \mathit{\boldsymbol{Q}} = \mathit{\boldsymbol{e}}{\mathit{\boldsymbol{e}}^{\rm{T}}} = \mathit{\boldsymbol{H}}\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{P}}_l}\mathit{\boldsymbol{P}}_l^{\rm{T}}} \right){\mathit{\boldsymbol{H}}^{\rm{T}}} $ | (15) |
| $ {\mathit{\boldsymbol{T}}^2} = \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{P}}_l}{\Lambda ^{ - 1}}\mathit{\boldsymbol{P}}_l^{\rm{T}}{\mathit{\boldsymbol{H}}^{\rm{T}}} $ | (16) |
式中Λ = diag{λ1, λ2, ..., λl}。本文根据核密度估计[22-23] (kernel density estimation,KDE)确定SPE和T 2控制限。核密度估计是一种非参数估计方法,其不需要知道过程数据的先验知识,不要求数据服从某种特定的分布,已广泛应用于过程监视领域控制限的确定。核密度估计定义如下:
| $ f\left( {\mathit{\boldsymbol{x}}, h} \right) = \frac{1}{{nh}}\sum\limits_{j = 1}^n {K\left\{ {\frac{{\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_i}}}{h}} \right\}} , \;\;\;K\left( \mathit{\boldsymbol{x}} \right) > 0\;\;\;{\rm{and}}\;\;\;\int {K\left( \mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}} = 1} $ | (17) |
其中K是高斯核函数,h是窗口宽度。则置信水平为α = 0.05的95%控制限Cα可以通过下式计算:
| $ \int_{ - \infty }^{{C_{\rm{ \mathsf{ α} }}}} {f\left( {\mathit{\boldsymbol{x}}, h} \right){\rm{d}}\mathit{\boldsymbol{x}} = 1 - \alpha } $ | (18) |
使用改进的局部熵对数据进行预处理后,然后运用PCA进行监视,满足PCA对单一模态数据以及高斯分布特性的前提假设,从而使检测结果达到预期效果。
2.2 基于改进局部熵PCA的工业过程故障检测改进局部熵PCA算法可以对多模态非高斯过程工业数据进行故障检测,该检测过程分为两步:离线建模和故障检测。基于改进局部熵PCA算法的故障检测流程图如图 5所示。

|
图 5 基于ILEPCA方法的故障检测流程图 Fig.5 Flow chart of fault detection based on ILEPCA |
(1) 建模过程
1) 收集正常操作时的历史数据集X。
2) 利用改进局部熵算法对X进行预处理得到H,剔除原始数据的多模态和非高斯特征;
3) 对H进行标准化处理,使其各列均值为0、方差为1;
4) 建立PCA模型,获得负载矩阵Pl;
5) 计算SPE和T2统计量,并根据核密度估计分别计算SPE的控制限SPEα和T2的控制限Tα2。
(2) 故障检测
1) 新来一个时刻数据xnew,利用改进局部熵算法对xnew进行预处理得到hnew,再利用建模数据的均值和方差将hnew标准化得到hnew1;
2) 将hnew1投影到PCA模型上,并计算统计量SPEnew和Tnew2;
3) 将统计量SPEnew和T new2与控制限SPEα和Tα2进行比较。若统计量大于控制限,则该反应时刻的数据样本是故障的;否则是正常的。
3 仿真结果与分析 3.1 数值仿真以GE和SONG设计的数值例子为例[24]。该例子中包含5个变量,由以下模型产生:
| $ \begin{array}{l} {\mathit{\boldsymbol{x}}_1} = 0.576\;8{s_1} + 0.376\;6{s_2} + {e_1}\\ {\mathit{\boldsymbol{x}}_2} = 0.738\;2s_1^2 + 0.056\;6{s_2} + {e_2}\\ {\mathit{\boldsymbol{x}}_3} = 0.829\;1{s_1} + 0.400\;9s_2^2 + {e_3}\\ {\mathit{\boldsymbol{x}}_4} = 0.651\;9{s_1}{s_2} + 0.207\;0{s_2} + {e_4}\\ {\mathit{\boldsymbol{x}}_5} = 0.397\;2{s_1} + 0.804\;5{s_2} + {e_5} \end{array} $ | (19) |
其中e1,e2,e3,e4和e5是服从[0,0.01]的白噪声。数据源s1和s2的变化可以改变操作条件,因此,通过改变数据源构造两种不同的操作模态。模态1:s1服从[-10, -7]的均匀分布,s2服从[-15, 12]的正态分布。模态2:s1服从[2, 5]的均匀分布,s2服从[7, 12]的正态分布。每个模态产生100个样本,组成具有200个样本的多模态训练数据集。另外每个模态产生100个样本,组成具有200个样本的校验数据集。在模态1运行时,对变量x1增加一幅值为0.01*(i-400)的故障,产生100个故障样本组成测试数据集。图 6是训练样本、校验样本、故障样本的数据分布散点图。“星号”代表训练数据,“圆圈”代表校验数据,“方块”代表故障数据。横轴和纵轴分别表示变量1和变量2。从图 6可以看出,该数值例子是多模态实例。应用Kolmogorov-Smirnov方法检验原始数据是否服从高斯分布,结果如表 4所示。从表 4可以看出,变量x1、x2、x3、x4和x5均服从非高斯分布。

|
图 6 数据散点图 Fig.6 Scatter plot of data |
|
|
表 4 数值例子的Kolmogorov-Smirnov检验结果 Table 4 Results of Kolmogorov-Smirnov test for the numerical example |
对多模态、非高斯数值例子运用PCA、KPCA、局部熵PCA(local entropy PCA, LEPCA)和ILEPCA方法进行故障检测,检测结果如图 7所示。为了得到更好的检测结果,四种方法的主元个数通过累计贡献率确定;在LEPCA中,近邻数k = 5;在ILEPCA中,选取近邻样本k = 13,选取近邻样本均值的近邻数s = 9。图中虚线代表 95%控制限,“星号”代表训练数据,“圆圈”代表校验数据,“方块”代表故障数据。从图 7可以看出,PCA算法的SPE统计量检测出17个故障数据,13个样本出现误报;T 2统计量检测出13个故障样本,22个样本出现误报。KPCA算法的SPE统计量检测出13个故障数据,19个样本出现误报;T 2统计量检测出16个故障样本,22个样本出现误报。LEPCA算法的SPE统计量检测出全部故障数据,但是有19个样本出现误报;T 2统计量检测出77个故障样本,14个样本出现误报。ILEPCA算法的SPE统计量检测出全部故障数据,4个样本出现误报;T 2统计量检测出99个故障样本,8个样本出现误报。与PCA、KPCA和LEPCA方法相比,ILEPCA检测出的故障样本最多,误报样本最少,从而验证ILEPCA算法的有效性。

|
图 7 4种方法对数值例子的检测结果 Fig.7 Detection results of four methods for the numerical example |
表 5是4种算法对数值例子的检测结果。由表 5可以看出,ILEPCA算法的检测效果要明显优于PCA和KPCA。因为PCA和KPCA需要数据满足高斯分布和单一模态的前提假设,对非高斯分布和多模态数据检测效果不理想。LEPCA算法虽然故障检测率较高,但是误报率也明显较高,这是由于经过局部熵预处理后的数据服从非高斯分布。综上所述,与其它3种算法对比,ILEPCA算法的误报率最低,故障检测率最高,验证了该算法的有效性和优越性。
|
|
表 5 3种算法对数值例子的检测结果对比 Table 5 Comparison of detection results of four algorithms for the numerical example |
半导体生产过程作为一个完善的工业过程仿真平台,在基于数据驱动的故障检测研究领域得到了广泛的应用。本文应用半导体工业实例— A1堆腐蚀过程[25-26]比较不同故障检测方法的性能。半导体数据是来源于美国德州仪器公司的半导体生产过程实际数据,是一个典型的非线性、时变、多阶段和多工况的复杂多模态间歇过程。该数据是由3个模态的107个正常批次和20个故障批次组成,其中1~34批次为第一模态,35~70批次为第二模态,71~107批次为第三模态。每个模态分别选取32个批次用于建模,剩下的正常批次作为校验批次用来验证模型的准确性,因此建模批次为96个,校验批次为11个,故障批次为20个。从21个测量变量中选取17个变量作为检测变量,如表 6所示。
|
|
表 6 半导体生产过程所用的检测变量 Table 6 Variables used in the semiconductor manufacturing process |
每个批次是不等长的,持续时间在95~112 s之间变化。本文运用最短长度法获得等长批次。为了消除传感器中初始的波动影响,去除开始的5个样本,保留85个样本以适应最短的批次。将三维建模数据X(96×85×17)沿批次方向展开成二维矩阵X(96×1445)。对校验数据和故障数据也进行同样的处理。
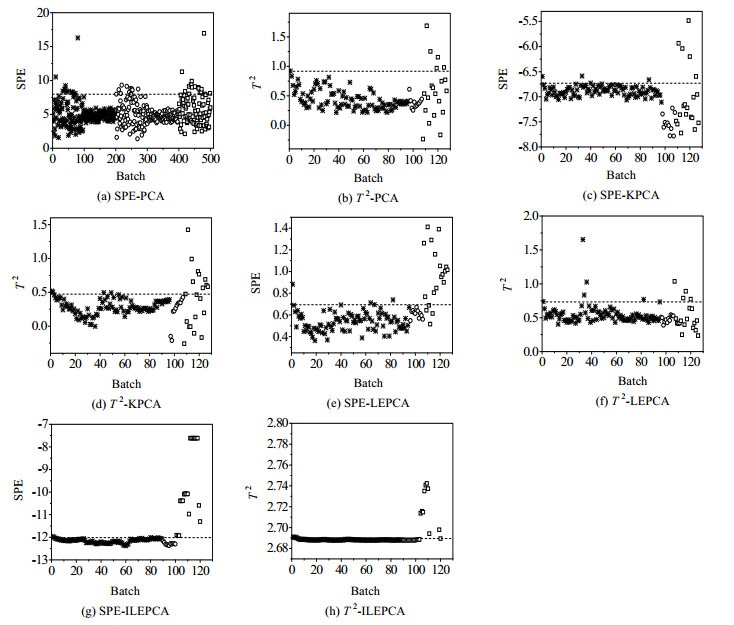
对二维数据矩阵分别运用PCA、KPCA、LEPCA和ILEPCA方法进行建模,并对11个校验批次和20个故障批次数据进行故障检测。四种方法的主元个数由累计贡献率决定。在LEPCA中,近邻数k = 3;在ILEPCA中,近邻数k = 9,近邻数s = 7。4种方法的检测结果如图 8所示。在ILEPCA算法的T 2统计量检测中,由于故障7~10和故障12~18较大,在图中没有显示出来。图中虚线代表 95%控制限,“星号”代表训练数据,“圆圈”代表校验数据,“方块”代表故障数据。从图 8可以看出PCA的SPE统计量检测出17个故障数据,5个校验数据出现误报;T 2统计量没有出现误报,而故障数据仅检测出5个。KPCA的SPE统计量检测出5个故障数据,没有误报;T 2统计量检测出9个故障数据,没有误报。LEPCA的SPE统计量检测出16个故障数据,没有误报;T 2统计量检测出4个故障数据,没有误报。ILEPCA的SPE统计量检测出全部故障数据,没有误报;T 2统计量检测出16个故障数据,没有误报。与PCA、KPCA和LEPCA算法相比,ILEPCA算法的检测效果最好,验证了基于改进局部熵PCA算法在工业过程故障检测中的有效性。
|
图 8 4种方法对半导体数据的故障检测图 Fig.8 Detection results of four methods for semiconductor data |
表 7是4种算法对半导体数据的检测结果对比。由表 7可以看出,PCA算法的T 2检测指标没有误报,但其故障检测率较低,SPE检测指标故障检测率较高,但是其误报率也相对较高,效果不如ILEPCA算法。KPCA算法的SPE检测指标和T 2检测指标均没有误报,但是KPCA算法的故障检测率要低于ILEPCA算法。LEPCA算法的SPE检测指标和T 2检测指标虽然没有误报率,但是故障检测率低于ILEPCA算法。综上所述,与其它3种算法对比,ILEPCA算法在没有误报的情况下,故障检测率最高,说明该方法对多模态非高斯数据的故障检测非常有效,验证了该算法的有效性和优越性。
|
|
表 7 4种算法对半导体数据的检测结果对比 Table 7 Comparison of detection results of four algorithms for semiconductor data |
本文提出一种基于改进局部熵PCA的多模态非高斯过程故障检测方法。引入k近邻的均值对局部概率密度函数进行改进,消除窗口h对核密度估计准确性的影响。利用改进的局部概率密度构造数据的局部熵,消除多模态和非高斯特性。在此基础上运用PCA进行故障检测,从而提高故障检测率。将本文的方法应用到数值例子和实际的半导体工业数据中,仿真结果表明,与传统的故障检测算法相比,本文算法提高故障检测率,降低误报率,验证了该方法的有效性。
符号说明:
| d(xi, xik) | —样本xi和其第k个近邻样本xik之间的欧氏距离 | n | —样本数 |
| d(xi, xi*) | —数据点xi到xi的第i个最近邻点的欧式距离 | n(xi) | —样本xi点的局部邻域 |
| dij2 | —第i个样本与它的第j个近邻的欧式距离的平 | P | —局部概率密度估计矩阵 |
| 方和 | Pl | —负载矩阵 | |
| dmj | — k近邻的均值 | s | —近邻样本均值的近邻数 |
| h | —窗口宽度 | S | —样本标准差 |
| H | —改进局部熵矩阵 | t | —时刻 |
| hnew | —新来时刻改进局部熵数据 | X | —数据集 |
| ht | —局部熵向量 | x1, x2 | —模态1和模态2内数据变量 |
| k | — xi的所选近邻样本个数 | xi | —矩阵X中的第i个样本 |
| kNN(xi) | —样本xi点的k近邻域 | xj | —邻域kNN(xi)的样本 |
| l | —主元个数 | —样本点xi的第k个近邻样本 | |
| L | —移动窗口宽度 | xnew | —新来时刻数据 |
| m | —变量数 | λi | —协方差矩阵的特征根 |
| [1] |
周东华, 李钢, 李元. 数据驱动的工业过程故障检测与诊断技术[M]. 北京: 科学出版社, 2011: 1-76. ZHOU D H, LI G, LI Y. Fault detection and diagnosis technology of industrial process based on data driven[M]. Beijing: Science Press, 2011: 1-76. |
| [2] |
张汉元, 田学民. 基于异步PCA的故障识别方法[J]. 高校化学工程学报, 2016, 30(3): 680-685. ZHANG H Y, TIAN X M. A fault identification method based on asynchronous PCA[J]. Journal of Chemical Engineering of Chinese Universities, 2016, 30(3): 680-685. DOI:10.3969/j.issn.1003-9015.2016.03.026 |
| [3] |
GUEDDI I, NASRI O, BENOTHMAN K, et al. Fault Detection and Isolation of spacecraft thrusters using an extended principal component analysis to interval data[J]. International Journal of Control Automation & Systems, 2017, 15(2): 1-14. |
| [4] |
HAMADACHE M, LEE D. Principal component analysis based signal-to-noise ratio improvement for inchoate faulty signals:Application to ball bearing fault detection[J]. International Journal of Control Automation & Systems, 2017, 15(2): 1-12. |
| [5] |
JAFFEL I, TAOUALI O, HARKAT M F, et al. Kernel principal component analysis with reduced complexity for nonlinear dynamic process monitoring[J]. International Journal of Advanced Manufacturing Technology, 2016, 88(9-12): 1-15. |
| [6] |
ADEDIGBA S A, KHAN F, YANG M. Dynamic failure analysis of process systems using principal component analysis and Bayesian network[J]. Industrial & Engineering Chemistry Research, 2017, 56(8): 2094-2106. |
| [7] |
GE Z Q, YANG C J, SONG Z H. Improved kernel PCA-based monitoring approach for nonlinear processes[J]. Chemical Engineering Science, 2009, 64(9): 2245-2255. DOI:10.1016/j.ces.2009.01.050 |
| [8] |
SCHÖLKOPF B, SMOLA A, MÜLLER K. Nonlinear component analysis as a kernel eigenvalue problem[J]. Neural Computation, 1998, 10(5): 1299-1319. DOI:10.1162/089976698300017467 |
| [9] |
王亚君, 周岐. 基于多动态核PCA的统计过程监测策略研究[J]. 辽宁工业大学学报, 2012, 32(5): 295-298. WANG Y J, ZHOU Q. Research on statistical process monitoring strategy based on multi-dynamic kernel PCA[J]. Journal of Liaoning University of Technology, 2012, 32(5): 295-298. DOI:10.3969/j.issn.1674-3261.2012.05.005 |
| [10] |
PENG X, TANG Y, DU W L, et al. An online performance monitoring and modeling paradigm based on just-in-time learning and extreme learning machine for non-Gaussian chemical process[J]. Industrial & Engineering Chemistry Research, 2017, 56(23): 6671-6684. |
| [11] |
YANG Q, BA C, LI C, et al. An ensemble fault diagnosis approach of multimode process based[C]//International Conference on signal proceessing, communications and computing. Xiamen: IEEE, 2017.
|
| [12] |
MA H H, HU Y, SHI H B. A novel local neighborhood standardization strategy and its application in fault detection of multimode processes[J]. Chemometrics and Intelligent Laboratory Systems, 2012, 118(7): 287-300. |
| [13] |
郭金玉, 仲璐璐, 李元. 基于差分局部保持投影的非线性过程故障检测[J]. 信息与控制, 2018, 47(2): 200-205. GUO J Y, ZHONG L L, LI Y. Fault detection of nonlinear process based on differential locality preserving projections[J]. Information and Control, 2018, 47(2): 200-205. |
| [14] |
郭金玉, 仲璐璐, 李元. 基于统计差分LPP的多模态间歇过程故障检测[J]. 计算机应用研究, 2019, 36(1): 123-126. GUO J Y, ZHONG L L, LI Y. Fault detection of multi-mode batch process based on statistics difference LPP[J]. Application Research of Computers, 2019, 36(1): 123-126. |
| [15] |
郭金玉, 王鑫, 李元. 基于加权差分主元分析的化工过程故障检测[J]. 高校化学工程学报, 2018, 32(1): 183-192. GUO J Y, WANG X, LI Y. Fault detection in chemical processes using weighted differential principal component analysis[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(1): 183-192. DOI:10.3969/j.issn.1003-9015.2018.01.025 |
| [16] |
钟娜, 邓晓刚, 徐莹. 基于LECA的多工况过程故障检测方法[J]. 化工学报, 2015, 66(12): 4929-4940. ZHONG N, DENG X G, XU Y. Fault detection method based on LECA for multimode process[J]. CIESC Journal, 2015, 66(12): 4929-4940. |
| [17] |
ZHONG N, DENG X G. Multimode non-Gaussian process monitoring based on local entropy independent component analysis[J]. The Canadian Journal of Chemical Engineering, 2017, 95(2): 319-330. DOI:10.1002/cjce.22651 |
| [18] |
DENG X G, ZHONG N, WANG L. Nonlinear multimode industrial process fault detection using modified kernel principal component analysis[J]. IEEE Access, 2017, 5(99): 23121-23132. |
| [19] |
ROSENBLATT M. Curve estimates[J]. Annals of Mathematical Statistics, 1971, 42(6): 1815-1842. DOI:10.1214/aoms/1177693050 |
| [20] |
PARZEN E. On estimation of a probability density function and mode[J]. Annals of Mathematical Statistics, 1962, 33(3): 1065-1076. DOI:10.1214/aoms/1177704472 |
| [21] |
SILVERMAN B W. Using kernel density estimates to investigate multimodality[J]. Journal of the Royal Statistical Society, 1981, 43(1): 97-99. |
| [22] |
ODIOWEI P P, CAO Y. Nonlinear dynamic process monitoring using canonical variate analysis and kernel density estimations[J]. Computer Aided Chemical Engineering, 2009, 27(1): 1557-1562. |
| [23] |
MORI J, YU J. Quality relevant nonlinear batch process performance monitoring using a kernel based multiway non-Gaussian latent subspace projection approach[J]. Journal of Process Control, 2014, 24(1): 57-71. DOI:10.1016/j.jprocont.2013.10.017 |
| [24] |
GE Z Q, SONG Z H. Multimode process monitoring based on Bayesian method[J]. Journal of Chemometrics, 2009, 23(12): 636-650. |
| [25] |
LEE S P, CHAO A K, TSUNG F, et al. Monitoring batch processes with multiple on-off steps in semiconductor manufacturing[J]. Journal of Quality Technology, 2011, 43(2): 142-157. |
| [26] |
YU J. Fault detection using principal components based Gaussian mixture model for semiconductor manufacturing processes[J]. Semiconductor Manufacturing, 2011, 24(3): 432-444. DOI:10.1109/TSM.2011.2154850 |




