由于开环式的控制策略遵循相似的轨迹模式,随着间歇反应过程[1]多批次的运行,虽然数据量会不断增加,但有效信息量并不随批次的增加呈线性增长,因此间歇反应过程往往是在有限信息量的基础上进行建模和参数估计[2]。针对多批次数据,传统参数估计方法如极大似然法(maximum likelihood estimation,MLE)[3-4]、最大期望法(expectation maximization,EM) [5]等联立所有数据进行参数估计会导致问题的规模十分庞大,并且随着批次数据逐渐增加,采用传统优化方法求解基于多批次数据的参数估计问题会在求解能力和计算效率上存在一定的问题。基于扩展卡尔曼滤波(extended kalman filter,EKF)[6]的估计方法是有效的,但在非线性很强的情况下参数估计是有偏的;马尔可夫链蒙特卡尔方法(markov chain monte carlo,MCMC)[7]通过抽取样本数值逼近概率密度函数进行参数估计,但对于具有多状态多参数模型,它的计算代价是非常昂贵的。针对此类问题通过引入随机梯度下降算法(stochastic gradient descent,SGD)[8]对模型中的反应动力学参数进行估计。SGD源于1951年Robbins和Monro[9]提出的随机逼近,主要用于求解大规模系统优化问题以及处理机器学习任务[10-14]。随着对随机优化算法的深入研究,衍生了不同版本的变体算法[15-18],为了充分利用历史梯度信息,随机平均梯度算法(stochastic average gradient,SAG)[19]和加速随机平均梯度(stochastic average gradient accelerated,SAGA)等[20]通过新梯度替代旧梯度的方式,充分考虑历史梯度信息的同时减少了梯度计算量。但以上随机梯度下降算法大部分以黑箱优化器的形式使用,针对多批次数据集的反应机理模型,Bae等[21]提出广义化的拉普拉斯近似极大似然估计(generalization of laplace approximation maximum likelihood estimation,gLAMLE)算法,基于扩展目标函数,利用多批次数据进行迭代估计,并在迭代更新中引入学习率,减小由于参数变化过快导致的数值震荡,但结果仍然无法保证被估参数的收敛性,甚至可能会减缓收敛速度。本研究引用扩展目标函数的思想,提出基于扩展目标函数的随机梯度下降算法,在联立求解的框架下进行参数估计,减小了单次估计的计算量,提升单次估计速度的同时保证了被估参数的收敛性。
2 基于多批次数据的参数估计问题 2.1 问题描述假定间歇反应过程中每一次反应操作都是相同的,本研究考虑实际工况中进料时存在随机扰动的影响,导致构建系统模型时状态初值会受随机变量的影响而发生一定的变化,由于状态初值发生随机性改变,导致每次工况产生的批次数据存在一定的差异性。随着反应操作的不断进行,会生成大规模多批次的数据量,基于多批次数据进行反应动力学参数估计会使得求解优化问题的规模十分庞大。针对此类问题考虑如下微分代数模型:
| $ \frac{{{\text{d}}{{\boldsymbol{z}}^{(n)}}{{(}}t{{)}}}}{{{\text{d}}t}} = f{{(}}{{\boldsymbol{z}}^{(n)}}{{(}}t{{),}}{{\mathit{\pmb{ θ}} }}{{)}} $ | (1a) |
| $ \boldsymbol{y}_{\text{p}} ^{({{n}})}({{t}}) = g({{\boldsymbol{z}}^{({{n}})}}({{t}}),{{\mathit{\pmb{ θ}} }}) $ | (1b) |
| $ \boldsymbol{y}_{\text{m}} ^{({{n}})}({{t}}) = \boldsymbol{y}_{\text{p}} ^{({{n}})}({{t}}) + {{\mathit{\pmb{ ε}} }} $ | (1c) |
| $ {{\boldsymbol{z}}^{(n)}}({t_0}) = {{\boldsymbol{z}}_0} + {{\mathit{\pmb{ η}} }}{{ }} $ | (1d) |
式中:z(n)(t)属于Rnz,表示第n批次数据集对应的微分代数模型中的状态向量,Rnz表示nz维实数集;yp(n)(t)和ym(n)(t)同时属于Rny,分别为第n批次数据集对应的输出预测向量和输出测量向量,Rny表示ny维实数集;ε属于Rny,为输出测量噪声向量,其中噪声向量中每个元素服从均值为0、方差为δ2的正态分布;η属于Rnz,表示进料向量上的随机扰动,其中扰动向量中每个元素服从均值为0、方差为δ2的正态分布;θ属于Rnp,表示模型中的参数向量,Rnp表示np维实数集,且f : Rnz+np →Rnz,g : Rnz+np →Rny属于可微函数;t表示时间,t0表示初始时刻,z0表示t0时刻对应的状态初值,上标n=1, …, N,N为数据总批次大小。
2.2 联立配置点法针对公式(1)中的模型,采用联立配置点法进行求解,微分状态变量使用有限元的多项式来近似,其中有限元[ti-1, ti],i=1, …, nfe,满足t0 < t1 < … < tnfe=tf,nfe表示时间轴上有限元的个数,tnfe表示第nfe个有限元对应的时间点,tf表示终止时间,在有限元上使用Gauss-Legendre点或者Radau点的拉格朗日插值多项式如下:
| $ {\boldsymbol{z}}_k^{(n)}(t) = \sum\limits_{k = 0}^K {{l_k}(\tau ){\boldsymbol{z}}_{ik}^{(n)}} $ | (2) |
| $ t={t}_{i-1}+({t}_{i}-{t}_{i-1})\tau {,}\tau \in [0,1] $ | (3) |
| $ {l_k}(\tau ) = \prod\limits_{j = 0, \ne k}^K {\frac{{\tau - {\tau _j}}}{{({\tau _k} - {\tau _j})}}} $ | (4) |
式中:τ表示相对时间,K为配置点的个数,zk(n)(t)表示第n批次中使用k个配置点描述的状态向量,
| $ \boldsymbol{y}_{\text{p}} ^{({{n}},{{s}})} = g({\boldsymbol{z}}_{}^{({{n}})}({{{t}}_{{s}}}),{{\mathit{\pmb{ θ}} }}) $ | (5) |
式中:yp(n, s)表示第n批次数据中ts时刻的预测向量。第n批次数据中ts时刻的测量向量可以表示为ym(n, s),其中s=1, …, M,假设有N批次数据并且每批次含有M个时间采样点,利用多批次测量数据,可以得到以下优化问题用于估计模型参数:
| $ {\text{min }}J{{ = }}\frac{1}{2}\sum\limits_{n = 1}^N {\sum\limits_{s = 1}^M {[{\boldsymbol{y}}_{\text{m}}^{(n,s)}} } - {\boldsymbol{y}}_{\text{p}}^{(n,s)}{]^{text{T}}}{\boldsymbol{V}}_n^{ - 1}[{\boldsymbol{y}}_{\text{m}}^{(n,s)} - {\boldsymbol{y}}_{\text{p}}^{(n,s)}] $ | (6a) |
| $ {\text{s}}{\text{.t}}{{.}}\;\;\;\sum\limits_{j = 0}^K {{{l'}_j}({\tau _k}){\boldsymbol{z}}_{_{ij}}^{(n)} - ({t_i} - {t_{i - 1}})f({\boldsymbol{z}}_{_{ik}}^{(n)},{{\mathit{\pmb{ θ}} }}} ) = 0 $ | (6b) |
| $ {\boldsymbol{z}}_{i + 1,0}^{(n)} = \sum\limits_{j = 0}^K {{l_j}(1){\boldsymbol{z}}_{_{ij}}^{(n)}{,_{}}i = 1, \cdots ,{\text{nfe}} - 1} {,_{}}j = 1, \cdots ,K $ | (6c) |
| $ \boldsymbol{y}_{\text{p}} ^{({{n}},{{s}})} = g({\boldsymbol{z}}_{}^{({{n}})}({{{t}}_{{s}}}),{{\mathit{\pmb{ θ}} }}){,_{}}{{\boldsymbol{z}}_{1,0}} = {\boldsymbol{z}}({{{t}}_0}) $ | (6d) |
式中:Vn表示对角方差矩阵,其对角线上第p个元素对应第p个输出的方差;Vn−1表示Vn矩阵的逆矩阵,
采用多批次数据进行参数估计时,若在噪声扰动下每次只基于单批次数据进行参数估计,则参数估计的精度不够理想。Bae等[21]利用gLAMLE算法进行参数估计时,通过设定采样率β来决定Nm大小,将整个数据集放入缓冲区,遍历每一批次数据时,再从余下所有批次数据中随机选取Nm批次数据集构成扩展目标函数达到抵消噪声扰动的作用,同时基于Nm+1批次数据的全部样本对参数进行优化更新。本研究借助gLAMLE算法中扩展目标函数的思想,结合随机梯度下降设计了近似随机梯度下降算法。
对于每一批次数据设计如下目标函数:
| $ {{{J}}^{({{n,s}})}} = \frac{1}{2}{\left[ {\boldsymbol{y}_{\text{m}} ^{({{n}},{{s}})} - g({{\boldsymbol{z}}^{({{n}})}}({{{t}}_{{s}}}),{{\mathit{\pmb{ θ}} }})} \right]^\text{T}}{\boldsymbol{V}}_{{n}}^{ - 1}\left[ {\boldsymbol{y}_{\text{m}} ^{({{n}},{{s}})} - g({{\boldsymbol{z}}^{({{n}})}}({{{t}}_s}),{{\mathit{\pmb{ θ}} }})} \right] $ | (7) |
类似于gLAMLE算法,采用如下随机扩展目标函数:
| $ J_{\text{e}}^{(n,s)} = {J^{(n,s)}} + \sum\limits_{j \in {S_{\text{e}}}^{(n)},j \ne n} {{J^{(j,s)}}} $ | (8) |
式中:
随机梯度下降算法是机器学习、深度学习领域中比较流行的优化算法,在随机平均梯度下降算法的基础上,通过引入3.1中随机扩展目标函数的概念,抵消部分由于随机干扰引起的估计误差,命名为随机扩展目标平均梯度下降法(stochastic extended objective average gradient descent,SEOAG)。
假定模型预测函数为
| $ \boldsymbol{y}_{\text{p}} ^{({{n,s}})} = g({\boldsymbol{z}}_{}^{({{n}})}({{{t}}_{{s}}}),{{\mathit{\pmb{ θ}} }}) $ | (9) |
随机扩展目标函数为
| $ J_{\text{e}}^{(n,s)} = J_{}^{(n,s)} + \sum\limits_{j \in {S_{\text{e}}}^{(n)},j \ne n} {{J^{(j,s)}}}, \text{其中} {{{J}}^{({{n,s}})}} = \frac{1}{2}{\left[ {\boldsymbol{y}_{\text{m}} ^{({{n,s}})} - \boldsymbol{y}_{\text{p}} ^{({{n,s}})}} \right]^\text{T}}{\boldsymbol{V}}_{{n}}^{ - 1}\left[ {\boldsymbol{y}_{\text{m}} ^{({{n,s}})} - \boldsymbol{y}_{\text{p}} ^{({{n,s}})}} \right] $ | (10) |
SEOAG算法流程如下所示:
1) 初始化参数,修正梯度向量设为av,且令初始时刻的av=0,迭代停止精度e*,第0次梯度信息设为d0=0,参数初值θ0=(θ1, …, θnp),迭代次数r=0,迭代终止次数Number,学习率为α;随机扩展批次为Nm;
2) 根据初值θ0得到的初始灵敏度信息和预测数据,将灵敏度数据和预测数据映射到[−1, 1],得到标度化矩阵C、D,利用C和D对模型进行标度化处理;
While(r < Number):
for n=1, …, N do
3) 随机从Se(n)数据集中选择Nm个数据集,设为Se(n);
4) 通过公式(10)构建扩展目标函数;
5) 将第n批次的样本列表中M个样本随机打乱;
for s=1, …, M do
6) 计算r时刻参数的灵敏度矩阵和预测数据,并求出梯度
7) 计算梯度修正公式:
8) 判断av的二范数是否小于e*,若成立跳出程序,不成立继续执行下一步;
9) 将第r时刻的梯度信息保存为:
10) 计算更新公式:
end
end
end
11) 输出参数θ。
SEOAG算法在每一次迭代更新项中不仅包含新梯度信息,并且包含旧梯度信息。每次迭代更新前将样本数据进行随机打乱处理,进行顺序遍历确保充分利用了所有数据,然后通过引入随机扩展目标函数的概念,增加随机数据量达到抵消随机扰动的效果,此算法在保留SAG算法优点的同时,抵消了一部分噪声扰动的影响,减小了参数变化引起的数值震荡。
3.3 灵敏度计算3.2节中梯度信息的计算涉及状态变量对参数的灵敏度信息,而式(1)中约束模型整体属于常微分方程组,因此可以采用微分方程法求解待估计参数的灵敏度信息矩阵:
对式(1a)中等式两边的参数进行求导得到
| $ {\text{d}}\frac{{{\text{d}}{{\boldsymbol{z}}^{(n)}}(t)/{\text{d}}t}}{{{\text{d}}{{\mathit{\pmb{ θ}} }}}} = {\text{d}}\frac{{{\text{d}}{{\boldsymbol{z}}^{(n)}}(t)/{\text{d}}{{\mathit{\pmb{ θ}} }}}}{{{\text{d}}t}} = \frac{{{\text{d}}f({{\boldsymbol{z}}^{(n)}}(t),{{\mathit{\pmb{ θ}} }})}}{{{\text{d}}{{\mathit{\pmb{ θ}} }}}} $ | (11a) |
| $ \frac{{{\text{d}}{{\boldsymbol{z}}^{(n)}}(0)}}{{{\text{d}}{{\mathit{\pmb{ θ}} }}}} = 0 $ | (11b) |
| $ \frac{{{\text{d}}\boldsymbol{y}_{{p}}^{(n)}(t)}}{{{\text{d}}{{\mathit{\pmb{ θ}} }}}} = \frac{{\partial g({{\boldsymbol{z}}^{(n)}}(t),{{\mathit{\pmb{ θ}} }})}}{{\partial {{\boldsymbol{z}}^{(n)}}(t)}}\frac{{{\text{d}}{{\boldsymbol{z}}^{(n)}}(t)}}{{{\text{d}}{{\mathit{\pmb{ θ}} }}}} + \frac{{\partial g({{\boldsymbol{z}}^{(n)}}(t),{{\mathit{\pmb{ θ}} }})}}{{\partial {{\mathit{\pmb{ θ}} }}}} $ | (11c) |
运用联立配置法将式(2)、(3)、(4)代入式(11),配置点方程可以写成:
| $ \sum\limits_{j = 0}^k {{{l'}_j}({\tau _k})\frac{{{\text{d}}{\boldsymbol{z}}_{_{ij}}^{(n)}}}{{{\text{d}}{{\mathit{\pmb{ θ}} }}}} - ({t_i} - {t_{i - 1}})f(\frac{{{\text{d}}{\boldsymbol{z}}_{_{ik}}^{(n)}}}{{{\text{d}}{{\mathit{\pmb{ θ}} }}}},{{\mathit{\pmb{ θ}} }}) = 0} $ | (12a) |
| $ \frac{{{\text{d}}{\boldsymbol{z}}_{_{i + 1,0}}^{(n)}}}{{{\text{d}}{{\mathit{\pmb{ θ}} }}}} - \;\;\;\sum\limits_{j = 0}^k {{l_j}(} 1)\frac{{{\text{d}}{\boldsymbol{z}}_{_{i + 1,0}}^{(n)}}}{{{\text{d}}{{\mathit{\pmb{ θ}} }}}} = 0{{ , }}\frac{{{\text{d}}{\boldsymbol{z}}_{_{1,0}}^{(n)}}}{{{\text{d}}{{\mathit{\pmb{ θ}} }}}} = 0 $ | (12b) |
| $ \frac{{\text{d}\boldsymbol{y}_p^{({{n}})}({{{t}}_{{{i}} - 1}} + ({{{t}}_{{i}}} - {{{t}}_{{{i}} - 1}}){\tau _{{j}}})}}{{\text{d}{{\mathit{\pmb{ θ}} }}}} = \frac{{\partial g({\boldsymbol{z}}_{{{ij}}}^{({{n}})},{{\mathit{\pmb{ θ}} }})}}{{\partial {\boldsymbol{z}}_{{{ij}}}^{({{n}})}}}\frac{{\text{d}{\boldsymbol{z}}_{{{ij}}}^{({{n}})}}}{{\text{d}{{\mathit{\pmb{ θ}} }}}} + \frac{{\partial g({\boldsymbol{z}}_{{{ij}}}^{({{n}})},{{\mathit{\pmb{ θ}} }})}}{{\partial {{\mathit{\pmb{ θ}} }}}} $ | (12c) |
联立求解方程组(6b~6d)和(12a~12c), 即可得到待估计参数的灵敏度信息矩阵。
3.4 标度化处理机器学习中不同样本的特征数据存在量纲的差异,由于数据间的差别可能很大,会直接影响学习的结果,因此必须对输入和输出数据按照一定比例进行缩放,使之落在特定的区域内,便于进行结果分析,其中主要有归一化和标准化等预处理方式。而基于随机优化算法对反应机理模型进行参数估计时,不同状态变量对不同参数也存在量纲的差异,由于这种差异会导致模型对不同参数的影响程度不同,基于此类问题,本研究借鉴标准化预处理思想对模型进行标度化处理。整个参数估计过程可以看成[yp, 1(n, 1)…yp, ny(n, 1)…yp, 1(n, M)…yp, ny(n, M)]T=Γ×θ的形式,其中输入量Γ为灵敏度矩阵,输出量为[yp, 1(n, 1)…yp, ny(n, 1)…yp, 1 (n, M)…yp, ny (n, M)]T,基于初始时刻θ0的灵敏度矩阵和第一批次的测量数据得到标度化矩阵,利用标度化矩阵对模型的输入变量和输出变量同时进行标度化处理后将数据映射到[−1, 1],具体标度过程如下所示:
第1批次的ny个输出变量的所有测量数据为
将转换后的θtr和yptr(n, s)分别代入式(6)和式(12)中对模型进行标度化处理后转换为
| $ \min {{ J = }}\frac{1}{2}\sum\limits_{{{n}} = 1}^{{N}} {\sum\limits_{{{s}} = 1}^{{M}} {{{[\boldsymbol{y}_{\text{m}} ^{({{n,s}})} - {{\boldsymbol{D}}^{ - 1}} \times \boldsymbol{y}_{\text{p}} ^{{tr} ({{n}},{{s}})}]}^\text{T}}V_{{n}}^{ - 1}[\boldsymbol{y}_{\text{m}} ^{({{n}},s)} - {{\boldsymbol{D}}^{ - 1}} \times \boldsymbol{y}_{\text{p}} ^{{tr} ({{n}},{{s}})}]} } $ | (13a) |
| $ \text { s.t. } \sum\limits_{j=0}^{k} l_{j}^{\prime}\left(\tau_{k}\right) \boldsymbol{D}^{-1} \boldsymbol{y}_{i j}^{\mathrm{tr}(n)}-\left(t_{i}-t_{i-1}\right) f\left(\boldsymbol{D}^{-1} \times \boldsymbol{y}_{i k}^{\mathrm{tr}(n)}, \boldsymbol{C} \times \boldsymbol{\theta}^{\mathrm{tr}}\right)=0$ | (13b) |
| $ \sum\limits_{j=0}^{k} l_{j}^{\prime}\left(\tau_{k}\right) \frac{\mathrm{d}\left(\boldsymbol{D}^{-1} \times \boldsymbol{z}_{i j}^{(n)}\right)}{\mathrm{d}\left(\boldsymbol{C} \times \boldsymbol{\theta}^{\mathrm{tr}}\right)}-\left(t_{i}-t_{i-1}\right) f\left(\frac{\mathrm{d}\left(\boldsymbol{D}^{-1} \times \boldsymbol{z}_{i k}^{(n)}\right)}{\mathrm{d}\left(\boldsymbol{C} \times \boldsymbol{\theta}^{\mathrm{tr}}\right)}, \boldsymbol{C} \times \boldsymbol{\theta}^{\mathrm{tr}}\right)=0 $ | (13c) |
| $ {\boldsymbol{z}}_{i + 1,0}^{(n)} = \sum\limits_{j = 0}^k {{l_j}(1){{\boldsymbol{D}}^{ - 1}}{\boldsymbol{z}}_{_{ij}}^{(n)}{,_{}}i = 1, \cdots ,{\text{nfe}} - 1} $ | (13d) |
| $ \boldsymbol{y}_{\mathrm{p}}^{(n, s)}=g\left(\boldsymbol{D}^{-1} \times \boldsymbol{y}^{\mathrm{tr}(n)}\left(t_{s}\right), \boldsymbol{C} \times \boldsymbol{\theta}^{\mathrm{tr}}\right), \boldsymbol{z}_{1,0}=\boldsymbol{z}\left(t_{0}\right) $ | (13e) |
| $ \sum\limits_{j=0}^{k} l_{j}^{\prime}\left(\tau_{k}\right) \frac{\mathrm{d}\left(\boldsymbol{D}^{-1} \times \boldsymbol{z}_{i j}^{(n)}\right)}{\mathrm{d}\left(\boldsymbol{C} \times \boldsymbol{\theta}^{\mathrm{tr}}\right)}-\left(t_{i}-t_{i-1}\right) f\left(\frac{\mathrm{d}\left(\boldsymbol{D}^{-1} \times \boldsymbol{z}_{i k}^{(n)}\right)}{\mathrm{d}\left(\boldsymbol{C} \times \boldsymbol{\theta}^{\mathrm{tr}}\right)}, \boldsymbol{C} \times \boldsymbol{\theta}^{\mathrm{tr}}\right)=0 $ | (13f) |
假设式(8)中任意批次的目标函数J(n, s)都是可微的,并且对应的每一个梯度都是Lipschitz连续的,即对于参数区间内任意的θ1,θ2 (属于Rnp),满足不等式
| $ {{||}}\nabla {J^{(n,s)}}({{{\mathit{\pmb{ θ}} }}_1}) - \nabla {J^{(n,s)}}({{{\mathit{\pmb{ θ}} }}_2})|| \leqslant {L_n}||{{{\mathit{\pmb{ θ}} }}_1} - {{{\mathit{\pmb{ θ}} }}_2}|| $ | (14) |
式中:Ln为Lipschitz常数,假设任意批次的目标函数J(n, s)都满足强凸性,由于SEOAG目标函数中随机扩展了Nm个J(j, s),其中j∈Se(n),j≠n,因此Je(n, s)等于Nm个强凸函数之和,即Je(n, s) (θ) = J(v_1, s)(θ)+ J(v_2, s)(θ)+… + J(v_Nm, s)(θ),其中v_1, …, v_Nm表示从1, …, N中(除n以外)随机选取的Nm个数,根据不等式(14)可知对于任意的θ1、θ2满足
| $ \begin{gathered} \,\parallel \nabla {J^{({\text{v}}\_1,s)}}({{{\mathit{\pmb{ θ}} }}_1}) - \nabla {J^{({\text{v}}\_1,s)}}({{{\mathit{\pmb{ θ}} }}_2})\parallel \leqslant {L_{{\text{v}}\_1}}\parallel {{{\mathit{\pmb{ θ}} }}_1} - {{{\mathit{\pmb{ θ}} }}_2}\parallel \hfill \\ \,\parallel \nabla {J^{({\text{v}}\_2,s)}}({{{\mathit{\pmb{ θ}} }}_1}) - \nabla {J^{({\text{v}}\_2,s)}}({{{\mathit{\pmb{ θ}} }}_2})\parallel \leqslant {L_{{\text{v}}\_2}}\parallel {{{\mathit{\pmb{ θ}} }}_1} - {{{\mathit{\pmb{ θ}} }}_2}\parallel \hfill \\ {{ }} \vdots \hfill \\ \;\;\;\;\;\;\parallel \nabla {J^{({\text{v}}\_{N_{\text{m}}},s)}}({{{\mathit{\pmb{ θ}} }}_1}) - \nabla {J^{({\text{v}}\_{N_{\text{m}}},s)}}({{{\mathit{\pmb{ θ}} }}_2})\parallel \leqslant {L_{{\text{v}}\_{N_{\text{m}}}}}\parallel {{{\mathit{\pmb{ θ}} }}_1} - {{{\mathit{\pmb{ θ}} }}_2}\parallel \hfill \\ \end{gathered} $ | (15) |
根据式(15)并结合向量范数三角不等式得到
| $ \begin{gathered} \parallel \nabla {J^{({\text{v}}\_1,s)}}({{{\mathit{\pmb{ θ}} }}_1}) + \nabla {J^{({\text{v}}\_2,s)}}({{{\mathit{\pmb{ θ}} }}_1})... + \nabla {J^{({\text{v}}\_{N_{\text{m}}},s)}}({{{\mathit{\pmb{ θ}} }}_1}) - \nabla {J^{({\text{v}}\_1,s)}}({{{\mathit{\pmb{ θ}} }}_2}) - \nabla {J^{({\text{v}}\_2,s)}}({{{\mathit{\pmb{ θ}} }}_2})... - \nabla {J^{({\text{v}}\_{N_{\text{m}}},s)}}({{{\mathit{\pmb{ θ}} }}_2})\parallel = \hfill \\ \parallel \nabla J_{\text{e}}^{(n,s)}({{{\mathit{\pmb{ θ}} }}_1}) - \nabla J_{\text{e}}^{(n,s)}({{{\mathit{\pmb{ θ}} }}_2})\parallel \leqslant \hfill \\ {{}}\,\parallel \nabla {J^{({\text{v}}\_1,s)}}({{{\mathit{\pmb{ θ}} }}_1}) - \nabla {J^{({\text{v}}\_1,s)}}({{{\mathit{\pmb{ θ}} }}_2})\parallel + ... + \parallel \nabla {J^{({\text{v}}\_{N_{\text{m}}},s)}}({{{\mathit{\pmb{ θ}} }}_1}) - \nabla {J^{({\text{v}}\_{N_{\text{m}}},s)}}({{{\mathit{\pmb{ θ}} }}_2})\parallel \leqslant \hfill \\ {{}}({L_{{\text{v}}\_1}} + ... + {L_{{\text{v}}\_{N_{\text{m}}}}})\parallel {{{\mathit{\pmb{ θ}} }}_1} - {{{\mathit{\pmb{ θ}} }}_2}\parallel \hfill \\ \end{gathered} $ | (16) |
由式(16)得到
| $ \begin{array}{l} \parallel \nabla J_{\text{e}}^{(n,s)}({{{\mathit{\pmb{ θ}} }}_1}) - \nabla J_{\text{e}}^{(n,s)}({{{\mathit{\pmb{ θ}} }}_2})\parallel \leqslant L_{\text{v}}^{(n)}\parallel {{{\mathit{\pmb{ θ}} }}_1} - {{{\mathit{\pmb{ θ}} }}_2}\parallel \hfill \\ L_{\text{v}}^{(n)} = {L_{{\text{v}}\_1}} + ... + {L_{{\text{v}}\_{N_{\text{m}}}}} \hfill \\ \end{array} $ | (17) |
则Je(n, s) (θ)也是Lipschitz连续的。
文献[23]中给出了强凸函数的充分必要条件:对于Rnp区间内任意的θ1、θ2满足以下不等式关系
| $ \,\,\,\,\,\,J_{}^{(n,s)}({{{\mathit{\pmb{ θ}} }}_2}) \geqslant J_{}^{(n,s)}({{{\mathit{\pmb{ θ}} }}_1}) + \nabla J_{}^{(n,s)}{({{{\mathit{\pmb{ θ}} }}_1})^{\text{T}}}({{{\mathit{\pmb{ θ}} }}_2} - {{{\mathit{\pmb{ θ}} }}_1}) + \tfrac{{{L_n}}}{2}\parallel {{{\mathit{\pmb{ θ}} }}_2} - {{{\mathit{\pmb{ θ}} }}_1}{\parallel ^2} $ | (18) |
则由(18)式得到
| $ \begin{gathered} \,{J^{({\text{v}}\_1,s)}}({{{\mathit{\pmb{ θ}} }}_2}) \geqslant {J^{({\text{v}}\_1,s)}}({{{\mathit{\pmb{ θ}} }}_1}) + \nabla {J^{({\text{v}}\_1,s)}}{({{{\mathit{\pmb{ θ}} }}_1})^{\text{T}}}({{{\mathit{\pmb{ θ}} }}_2} - {{{\mathit{\pmb{ θ}} }}_1}) + \tfrac{{{L_{{\text{v}}\_1}}}}{2}\parallel {{{\mathit{\pmb{ θ}} }}_2} - {{{\mathit{\pmb{ θ}} }}_1}{\parallel ^2} \hfill \\ \,{J^{({\text{v}}\_2,s)}}({{{\mathit{\pmb{ θ}} }}_2}) \geqslant {J^{({\text{v}}\_2,s)}}({{{\mathit{\pmb{ θ}} }}_1}) + \nabla {J^{({\text{v}}\_2,s)}}{({{{\mathit{\pmb{ θ}} }}_1})^{\text{T}}}({{{\mathit{\pmb{ θ}} }}_2} - {{{\mathit{\pmb{ θ}} }}_1}) + \tfrac{{{L_{{\text{v}}\_2}}}}{2}\parallel {{{\mathit{\pmb{ θ}} }}_2} - {{{\mathit{\pmb{ θ}} }}_1}{\parallel ^2} \hfill \\ {{ }} \vdots \hfill \\ \;\;\;\;\;\;{J^{({\text{v}}\_{N_{\text{m}}},s)}}({{{\mathit{\pmb{ θ}} }}_2}) \geqslant {J^{({\text{v}}\_{N_{\text{m}}},s)}}({{{\mathit{\pmb{ θ}} }}_1}) + \nabla {J^{({\text{v}}\_{N_{\text{m}}},s)}}{({{{\mathit{\pmb{ θ}} }}_1})^{\text{T}}}({{{\mathit{\pmb{ θ}} }}_2} - {{{\mathit{\pmb{ θ}} }}_1}) + \tfrac{{{L_{{\text{v}}\_{N_{\text{m}}}}}}}{2}\parallel {{{\mathit{\pmb{ θ}} }}_2} - {{{\mathit{\pmb{ θ}} }}_1}{\parallel ^2} \hfill \\ \end{gathered} $ | (19) |
根据式(19)得到
| $ \begin{gathered} J_{\text{e}}^{(n,s)}({{{\mathit{\pmb{ θ}} }}_2}) = {J^{({\text{v}}\_1,s)}}({{{\mathit{\pmb{ θ}} }}_2}) + {J^{({\text{v}}\_2,s)}}({{{\mathit{\pmb{ θ}} }}_2}) + \;\;\;\;\;\;... + {J^{({\text{v}}\_{N_{\text{m}}},s)}}({{{\mathit{\pmb{ θ}} }}_2}) \geqslant \hfill \\ {{ }}{J^{({\text{v}}\_1,s)}}({{{\mathit{\pmb{ θ}} }}_1}) + \cdots + {J^{({\text{v}}\_{N_{\text{m}}},s)}}({{{\mathit{\pmb{ θ}} }}_1}) + (\nabla {J^{({\text{v}}\_1,s)}}{({{{\mathit{\pmb{ θ}} }}_1})^{\text{T}}} + \hfill \\ {{ }} \cdots + \nabla {J^{({\text{v}}\_{N_{\text{m}}},s)}}{({{{\mathit{\pmb{ θ}} }}_1})^{\text{T}}})({{{\mathit{\pmb{ θ}} }}_2} - {{{\mathit{\pmb{ θ}} }}_1}) + \tfrac{{{L_{{\text{v}}\_1}} + ... + {L_{{\text{v}}\_{N_{\text{m}}}}}}}{2}\parallel {{{\mathit{\pmb{ θ}} }}_2} - {{{\mathit{\pmb{ θ}} }}_1}{\parallel ^2} \geqslant \hfill \\ {{ }}J_{\text{e}}^{(n,s)}({{{\mathit{\pmb{ θ}} }}_1}) + \nabla J_{\text{e}}^{(n,s)}{({{{\mathit{\pmb{ θ}} }}_1})^{\text{T}}}({{{\mathit{\pmb{ θ}} }}_2} - {{{\mathit{\pmb{ θ}} }}_1}) + \tfrac{{{L_{{\text{v}}\_1}} + ... + {L_{{\text{v}}\_{N_{\text{m}}}}}}}{2}\parallel {{{\mathit{\pmb{ θ}} }}_2} - {{{\mathit{\pmb{ θ}} }}_1}{\parallel ^2} \geqslant \hfill \\ {{ }}J_{\text{e}}^{(n,s)}({{{\mathit{\pmb{ θ}} }}_1}) + \nabla J_{\text{e}}^{(n,s)}{({{{\mathit{\pmb{ θ}} }}_1})^{\text{T}}}({{{\mathit{\pmb{ θ}} }}_2} - {{{\mathit{\pmb{ θ}} }}_1}) + \tfrac{{L_{\text{v}}^{(n)}}}{2}\parallel {{{\mathit{\pmb{ θ}} }}_2} - {{{\mathit{\pmb{ θ}} }}_1}{\parallel ^2} \hfill \\ \end{gathered} $ | (20) |
因此根据强凸函数的充分必要条件[23]可知Je(n, s)(θ)是强凸函数。进一步地,根据文献[10]可知存在μn常数满足
| $ {\mu _n}||{{{\mathit{\pmb{ θ}} }}^{(r - 1)}} - {{{\mathit{\pmb{ θ}} }}^*}|{|^2} \leqslant {({{{\mathit{\pmb{ θ}} }}^{(r - 1)}} - {{{\mathit{\pmb{ θ}} }}^*})^{\text{T}}}\nabla J_{\text{e}}^{^{(n,s)}} $ | (21) |
当学习率α=1/2MLv(n),r≥1时,且令收敛结果的最优点为
| $ \xi [||{{{\mathit{\pmb{ θ}} }}^{(r)}} - {{{\mathit{\pmb{ θ}} }}^*}|{|^2}] \leqslant {(1 - \frac{{{\mu _n}}}{{8L_{\text{v}}^{(n)}M}})^r}[3||{{{\mathit{\pmb{ θ}} }}^{(0)}} - {{{\mathit{\pmb{ θ}} }}^*}|{|^2} + \frac{{9{\sigma ^2}}}{{4L{{_{\text{v}}^{(n)}}^2}}}] $ | (22) |
| $ {(1 - \frac{{{\mu _n}}}{{8L_{\text{v}}^{(n)}M}})^r} \leqslant {\exp _{}}( - \frac{{r{\mu _n}}}{{8L_{\text{v}}^{(n)}M}}) \leqslant \frac{{8L_{\text{v}}^{(n)}M}}{{r{\mu _n}}} = O(M/r){{ }} $ | (23) |
则可以得到
式中:
对于细胞反应操作过程,进料操作的主要目的是最大化细胞生长和产物形成的速率,从而使产物形成的总速率(生产率)或产物收获率(选择性)最大化。通过调节限制底物、诱导剂、前体或中间体的投料速率和选择适当的初始条件来实现。给出了线性变化进料速率的基本细胞反应模型:
| $ \begin{array}{lc} \frac{\mathrm{d} V(t)}{\mathrm{d} t}=F_{0}(1+a t) \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;V\left(t_{0}\right)=V_{0} \\ \end{array} $ | (25a) |
| $ \frac{\mathrm{d} \rho_{\mathrm{X}}(t)}{\mathrm{d} t}=\mu V(t)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\rho_{\mathrm{X}}\left(t_{0}\right)=\rho_{\mathrm{X}, 0}+\boldsymbol{\eta}_{\mathrm{X}} \\ $ | (25b) |
| $ \frac{\mathrm{d} \rho_{\mathrm{S}}(t)}{\mathrm{d} t}=F_{0}(1+a t) S_{\mathrm{F}}-\frac{\mu \rho_{\mathrm{X}}(t)}{Y_{\mathrm{xS}}}\;\;\rho_{\mathrm{S}}\left(t_{0}\right)=\rho_{\mathrm{S}, 0}+\boldsymbol{\eta}_{\mathrm{S}} \\ $ | (25c) |
| $ \frac{\mathrm{d} \rho_{\mathrm{P}}(t)}{\mathrm{d} t}=\pi \rho_{\mathrm{X}}(t)=\frac{\mu \rho_{\mathrm{X}}(t)}{Y_{\mathrm{ps}}}\;\;\;\;\;\;\;\;\;\;\;\;\rho_{\mathrm{P}}\left(t_{0}\right)=\rho_{\mathrm{P}, 0}+\boldsymbol{\eta}_{\mathrm{P}} $ | (25d) |
模型中有4个状态变量,细胞培养液体积V(L)、细胞质量浓度
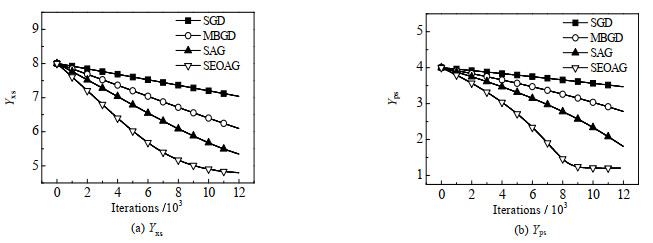
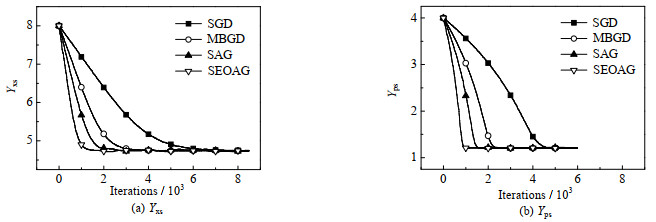
如图 1~ 3所示为e*=1.0×10−6以及Number为12 000时,选取不同学习率时不同算法对反应动力学参数θ=(Yxs,Yps)的估计情况。参数的初值θ0=(8.0, 4.0),图 1中,当学习率取0.000 1时,由于学习率偏小导致算法迭代估计速度较慢,其中SEOAG算法明显受学习率影响较小,参数估计值收敛至真值附近,而其余的算法均未收敛;各个算法单次参数估计的时间损耗分别为SGD:0.093 8 s,MBGD:0.103 2 s,SAG:0.101 5 s,SEOAG:0.115 4 s,表明相比其他算法,SEOAG在目标函数中扩展了Nm批次的数据量,导致SEOAG单次估计速度会偏慢一些;图 2中当学习率取0.001时,由于学习率选取适中,各个算法参数均能迭代估计到真值附近,而SEOAG算法比其他算法参数估计的收敛速度更快;增大学习率会增加收敛速度,但同时会在参数迭代估计中产生数值震荡,图 3中当学习率取0.01时,学习率过大导致不同算法对参数的估计值表现出明显的数值震荡,而SEOAG算法相比其他算法,有明显降低震荡的效果;具体参数估计值如表 1~ 3所示。
|
图 1 不同算法对Yxs,Yps迭代估计过程的比较(α=0.000 1) Fig.1 Comparison of Yxs and Yps iterative estimation processes by different algorithms(α=0.000 1) |
|
图 2 不同算法对Yxs,Yps迭代估计过程的比较(α=0.001) Fig.2 Comparison of Yxs and Yps iterative estimation processes by different algorithms(α=0.001) |

|
图 3 不同算法对Yxs,Yps迭代估计过程的比较(α=0.01) Fig.3 Comparison of Yxs and Yps iterative estimation processes by different algorithms(α=0.01) |
|
|
表 1 不同算法对Yxs,Yps估计值的比较(α=0.000 1) Table 1 Comparison of Yxs and Yps estimates by different algorithms(α=0.000 1) |
|
|
表 2 不同算法对Yxs,Yps估计值的比较(α=0.001) Table 2 Comparison of Yxs and Yps estimates by different algorithms(α=0.001) |
|
|
表 3 不同算法对Yxs,Yps估计值的比较(α=0.01) Table 3 Comparison of Yxs and Yps estimates by different algorithms(α=0.01) |
为了防止参数估计值受随机性的影响,表 1~ 3中分别列出了选取不同学习率时,不同算法分别运行10次,取10次终止时刻参数估计的平均值。表 1中由于学习率取值过小导致SGD、MBGD、SAG算法在终止时刻的估计值偏差较大、平均相对误差增大,而SEOAG算法的参数估计值偏差最小、估计精度最好;从表 2和3中的数据可知,增大学习率时,相比其他3种算法,SEOAG算法的参数估计精度也属于中上水平;从图 1~ 3以及表 1~3中的数据可知,SEOAG算法可以减小算法对学习率选取的依赖性,当学习率取值较大时,SEOAG在加快收敛速度的同时可以减缓数值震荡、减小估计误差;当学习率取值过小时,SEOAG在保证参数估计精度的同时可以明显增加收敛速度。
5.2 案例二考虑在一个体积固定的容器内发生的两步化学反应过程:
| $ {\text{A}} + {\text{B}}\xrightarrow{{{k_1}}}{\text{C}}\;\;\;\;\;\;2{\text{C}}\xrightarrow{{{k_2}}}{\text{D}} $ | (26) |
式中:物料A和物料B反应生成物料C,物料C反应生成物料D,k1、k2表示反应比率,A的初始浓度cA(t0)=1.5 mol⋅L−1,B的初始浓度cB(t0)=1.0 mol⋅L−1。假设该反应中物料C和物料D的浓度是可测量的,则输出量YC=cC+εC;YD=cD+εD,其中εC、εD都服从均值为0、方差为0.012的正态分布;假设A物料浓度初值存在随机扰动η,η服从均值为0、方差为0.012的正态分布。反应比率真值θ=(k1, k2)=(0.5, 2),假设该反应在实际生产过程中是批量反应的。基于多批次数据下运用联立求解框架重复案例一中求解的步骤,比较不同随机优化算法对反应动力学参数k1、k2估计结果。
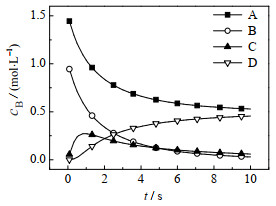
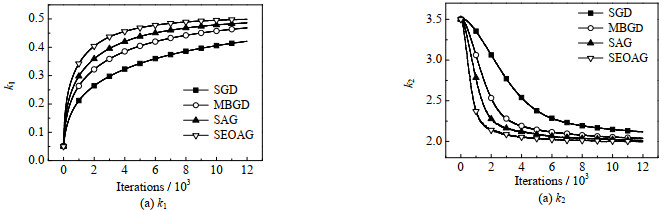
图 4给出了各个物料反应浓度cB的模拟数据,反应时间t为10 s,通过在A物料浓度初始时刻增加随机扰动η以及输出量添加给定噪声扰动ε,模拟出N=20的批次数据,e*=1.0×10−6,Number=12 000,采样率设为0.2,则Nm=N×0.2=4;参数的初值θ0=(0.05, 3.5),如图 5~7所示,当选择不同学习率时,不同算法对反应动力学参数k1、k2估计效果图。为了防止参数估计值受随机性的影响,表 4~ 6列出了选择不同学习率时,分别运行10次,对参数k1、k2估计值取平均值。
|
图 4 k1、k2为真值时各物质浓度的曲线 Fig.4 Concentration curve of substances for true values of k1 and k2 |
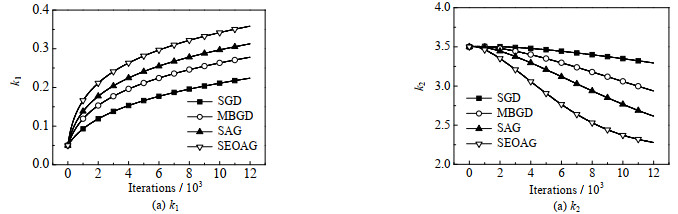
|
图 5 不同算法对k1,k2迭代估计过程的比较(α=0.001) Fig.5 Comparison of k1 and k2 iterative estimation processes by different algorithms(α=0.001) |
|
图 6 不同算法对k1,k2迭代估计过程的比较(α=0.01) Fig.6 Comparison of k1 and k2 iterative estimation processes by different algorithms(α=0.01) |
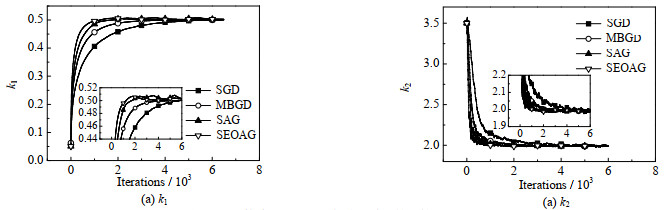
|
图 7 不同算法对k1,k2迭代估计过程的比较(α=0.1) Fig.7 Comparison of k1 and k2 iterative estimation processes by different algorithms(α=0.1) |
|
|
表 4 不同算法对k1,k2估计值的比较(α=0.001) Table 4 Comparison of k1 and k2 estimates by different algorithms(α=0.001) |
|
|
表 5 不同算法对k1,k2估计值的比较(α=0.01) Table 5 Comparison of k1 and k2 estimates by different algorithms(α=0.01) |
|
|
表 6 不同算法对k1,k2估计值的比较(α=0.1) Table 6 Comparison of k1 and k2 estimates by different algorithms(α=0.1) |
从图 5中可知学习率取0.001时,学习率取值过小导致各个算法对参数k1、k2的估计偏差较大,其中MBGD的样本批次大小为4,SEOAG算法在相同条件下,参数估计值的收敛效果更好;图 5中各算法单次参数估计时间损耗分别为SGD:0.120 6 s,MBGD:0.128 0 s,SAG:0.134 7 s,SEOAG:0.139 4 s,表明相比其他算法,由于SEOAG在目标函数中扩展了Nm批次的数据量,导致SEOAG单次估计速度会偏慢一些;图 6表示学习率取0.01时,各个算法收敛速度加快,而SEOAG算法则明显收敛速度更快;图 7表示学习率取0.1时,各个算法最后均能估计到真值附近、但由于学习率过大会导致明显的数值震荡,而SEOAG算法相比其他算法,有明显降低震荡的效果。表 4~ 6中列出了选取不同的学习率时,各个算法分别运行10次后,取参数估计的平均值以及估计值的平均相对误差,表 4和5中学习率取值过小,导致这4种算法在终止时刻参数估计值偏差都比较大,而基于表中数据可以发现SEOAG算法中估计值的平均相对误差最小;当学习率增大时,基于表 6中的数据可知SEOAG算法在估计精度上优势不太明显,但在取10次估计值的平均相对误差也是最小的。基于上述图 5~7以及表 4~6中的数据可知SEOAG算法可以减小算法对学习率取值的依赖性,在学习率取值过小时,SEOAG算法相比其他3种算法,收敛速度更快、更容易收敛到真值附近;在学习率取值较大时,可以减缓数值震荡、减小估计值的平均相对误差。
6 结论为了解决多批次数据下传统优化方法存在求解困难的情况,本研究通过对模型进行标度化处理解决了不同数据间的量纲差异,然后引入扩展目标函数提出了基于改进随机梯度下降的参数估计方法,并且给出了算法收敛的理论性分析。通过对主流的随机优化算法进行数值实验对比,验证了所提出的SEOAG算法在估计精度、收敛速度以及受学习率影响方面的优越性。
| [1] |
LIM H C, HENRY C, SHIN H S. Fed-batch cultures (principles and applications of semi-batch bioreactors)[M]. New York: Cambridge University Press, 2013.
|
| [2] |
MCLEAN K, MCAULEY K B. Mathematical modelling of chemical processes—obtaining the best model predictions and parameter estimates using identifiability and estimability procedures[J]. Canadian Journal of Chemical Engineering, 2012, 90(2): 351-366. DOI:10.1002/cjce.20660 |
| [3] |
KARIMI H, MCAULEY K B. A maximum-likelihood method for estimating parameters, stochastic disturbance intensities and measurement noise variances in nonlinear dynamic models with process disturbances[J]. Computers & Chemical Engineering, 2014, 67(4): 178-198. |
| [4] |
DUIJN M, GILE K J, HANDCOCK M S. A framework for the comparison of maximum pseudo-likelihood and maximum likelihood estimation of exponential family random graph models[J]. Social Networks, 2009, 31(1): 52-62. DOI:10.1016/j.socnet.2008.10.003 |
| [5] |
CANNARILE F, COMPARE M, ROSSI E, et al. A fuzzy expectation maximization based method for estimating the parameters of a multi-state degradation model from imprecise maintenance outcomes[J]. Annals of Nuclear Energy, 2017, 110(17): 739-752. |
| [6] |
HE L, HU M K, WEI Y J, et al. State of charge estimation by finite difference extended Kalman filter with HPPC parameters identification[J]. Science China (Technological Sciences), 2020, 63(3): 410-421. DOI:10.1007/s11431-019-1467-9 |
| [7] |
XIA W, DAI X X, FENG Y. Bayesian-MCMC-based parameter estimation of stealth aircraft RCS models[J]. Chinese Physics B, 2015, 24(12): 622-628. |
| [8] |
LI X L. Preconditioned stochastic gradient descent[J]. IEEE Transaction on Neural Networks and Learning Systems, 2018, 29(5): 1454-1466. DOI:10.1109/TNNLS.2017.2672978 |
| [9] |
ROBBINS H, MONRO S. A stochastic approximation method[J]. Annals of Mathematical Statistics, 1951, 22(3): 400-407. DOI:10.1214/aoms/1177729586 |
| [10] |
VAIDYA J, YU H, JIANG X Q. Privacy-preserving SVM classification[J]. Knowledge and Information Systems, 2008, 14(2): 161-178. DOI:10.1007/s10115-007-0073-7 |
| [11] |
SONG W J, ZHU J K, LI Y, et al. Image alignment by online robust PCA via stochastic gradient descent[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2016, 26(7): 1241-1250. DOI:10.1109/TCSVT.2015.2455711 |
| [12] |
KALANTZIS V, VASSILIS K. A spectral newton-schur algorithm for the solution of symmetric generalized eigenvalue problems[J]. Electronic Transactions on Numerical Analysis, 2020, 52: 132-153. DOI:10.1553/etna_vol52s132 |
| [13] |
ZHAO R B, TAN V. A unified convergence analysis of the multiplicative update algorithm for regularized nonnegative matrix factorization[J]. IEEE Transactions on Signal Processing, 2018, 66(1): 129-138. DOI:10.1109/TSP.2017.2757914 |
| [14] |
DUCHI J C, FENG R. Stochastic methods for composite optimization problems[J]. SIAM Journal on Optimization, 2017, 28(4): 3229-3259. |
| [15] |
QIAN N. On the momentum term in gradient descent learning algorithms[J]. Neural Networks, 1999, 12(1): 145-151. DOI:10.1016/S0893-6080(98)00116-6 |
| [16] |
MAZHAR H, HEYN T, NEGRUT D, et al. Using Nesterov's method to accelerate multibody dynamics with friction and contact[J]. ACM Transactions on Graphics, 2015, 34(3): 1-14. |
| [17] |
JOHNSON R, ZHANG T. Accelerating stochastic gradient descent using predictive variance reduction[J]. News in Physiological Sciences, 2013, 1(3): 315-323. |
| [18] |
SATO H, KASAI H, MISHRA B. Riemannian stochastic variance reduced gradient algorithm with retraction and vector transport[J]. SIAM Journal on Optimization, 2019, 29(2): 1444-1472. DOI:10.1137/17M1116787 |
| [19] |
SCHMIDT M, LE R N, BACH F. Minimizing finite sums with the stochastic average gradient[J]. Mathematical Programming, 2017, 162(1): 83-112. |
| [20] |
COURTY N, GONG X, VANDEL J, et al. SAGA: sparse and geometry-aware non-negative matrix factorization through non-linear local embedding[J]. Machine Learning, 2014, 97(1): 205-226. |
| [21] |
BAE J, JEONG D H, LEE J M. Ranking-based parameter subset selection for nonlinear dynamics with stochastic disturbances under limited data[J]. Industrial & Engineering Chemistry Research, 2020, 59(50): 21854-21868. |
| [22] |
CHEN W F, SHAO Z J, BIEGLER L T. A bilevel NLP sensitivity-based decomposition for dynamic optimization with moving finite elements[J]. AIChE Journal, 2014, 60(3): 966-979. DOI:10.1002/aic.14339 |
| [23] |
BOYD S, VANDENBERGHE L. Convex optimization[M]. New York: Cambridge University Press, 2004.
|
| [24] |
QIAN Q, JIN R, YI J F, et al. Efficient distance metric learning by adaptive sampling and mini-batch stochastic gradient descent (SGD)[J]. Machine Learning, 2015, 99(3): 353-372. DOI:10.1007/s10994-014-5456-x |




