机械蒸汽再压缩(mechanical vapor recompression, MVR)技术系统具有操作简单、能耗低等特点[1],广泛应用于海水淡化、化工、食品和废水处理等领域[2-5]。蒸发器作为MVR系统的核心设备,其传热性能对整套机组起着重要影响,由于MVR蒸发器小温差换热的特点(一般管内外温差8~12℃),客观上对换热器的传热效率提出了更高的要求,而当前传统光滑圆管折流板蒸发器存在效率低,体积大,造价高等问题。
三维变形管换热器是一种新型纵向纯逆流换热器,采用三维变形管作为换热元件,壳程不设折流板,达到管束自支撑与强化传热双重目的,制造方便,造价低,运行可靠无振动,得到广泛关注。Dzyubenko等[6-7]对三维变形管管内和管束间传热传质与流阻性能展开了研究,并拟合出关联式。思勤等[8]采用油和水为介质对三维变形管换热器管内外的传热性能进行实验研究,并将结果与Dzyubenko等的关联式进行了对比,两者在一定范围内吻合较好。孟继安等[9],Cheng等[10],采用理论分析与数值模拟的方法对三维变形管管内层流换热与流动特性进行了研究,发现三维变形管可较大程度地强化层流换热,而流阻增加较小。Yan等[11]将三维变形管用于强化高黏度流体环氧树脂的传热研究中也取得了令人满意的结果,谭详辉等[12],Bishara F等[13],朱冬生等[14]对三维变形管管内湍流换热过程进行了实验和数值研究,采用场协同理论分析了管内强化传热机理,并获得准则关联式。Zhang等[15]对三维变形管管外冷凝传热特性进行了实验研究,结果显示特定结构形式的三维变形管管外具有强化冷凝换热的特性。
MVR强制循环蒸发器主要应用于浓度要求较高的溶液,溶液循环流量大,液体在换热管内的循环流速通常在1.5~3.0 m·s-1,雷诺数Re > 60000,分析国内外相关文献可知,目前对三维变形管的研究主要集中在雷诺数Re < 60000,得到的传热与流阻准则关系式也存在一定的局限性。本文以水为介质,对三维变形管内雷诺数13000 < Re < 110000的传热与流阻特性进行数值研究,并利用数值模拟所得结果拟合出计算准则关联式,用于指导工程设计。
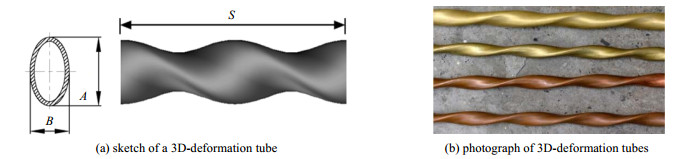
2 计算模型 2.1 计算模型与初始条件本文研究的三维变形管均由27 mm ×1.5 mm的光滑直圆管经过冷加工成型制成,首先建立7种不同的三维变形管的物理模型,并建立相应的普通直圆管模型,具体结构尺寸见表 1:
|
图 1 三维变形管 Fig.1 Profiles of the 3D-deformation tube |
|
|
表 1 换热管的结构参数 Table 1 Structural parameters of tubes |
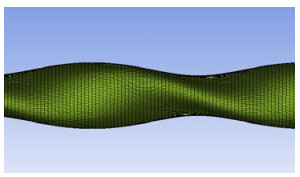
对换热管进行网格划分,采用结构化的六面体网格来划分,根据文献[16]推荐值,近壁区网格符合y+ ≈ 30的要求,保证计算结果的精度,图 2为网格示意图。
|
图 2 换热管网格示意图 Fig.2 Gridding scheme of the tube |
边界条件及物性:速度入口,给定相应的速度,湍流强度,以及入口温度;压力出口,给定相应的回流压力和回流温度;壁面恒定温度,无滑移。控制方程的离散采用二阶迎风格式,压力和速度耦合采用SIMPLE算法,Realizable k-ε湍流模型求解,采用标准壁面函法处理近壁区。管内流体介质为水,物性参数为等效温度下的常量。
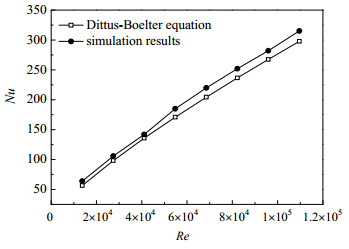
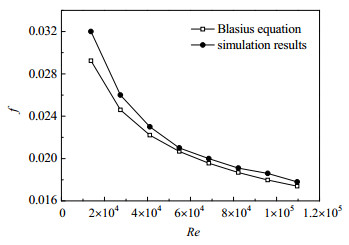
2.2 计算模型可靠性分析为了验证物理模型的可靠性,首先对光滑直圆管管内的传热与流阻进行了数值模拟,将所得结果与Dittus-Boelter (1),Blasius (2)经验式的计算结果比较,结果如图 3和图 4所示。从图中可以看出,两者计算结果接近,努塞尔数Nu与摩擦因子f的平均偏差分别为6.7%,5.2%,证明了该计算模型是可靠的。
| $ Nu = 0.023{{\mathop{ Re}\nolimits} ^{0.8}}{Pr ^{0.33}} $ | (1) |
| $ f = \frac{{0.3164}}{{{{{\mathop{ Re}\nolimits} }^{0.25}}}} $ | (2) |
|
图 3 努塞尔数Nu数值计算结果与经验公式计算对比 Fig.3 Comparison of Nu between numerical and empirical calculation results |
|
图 4 摩擦因子f数值计算结果与经验公式计算对比 Fig.4 Comparison of f between numerical and empirical calculation results |
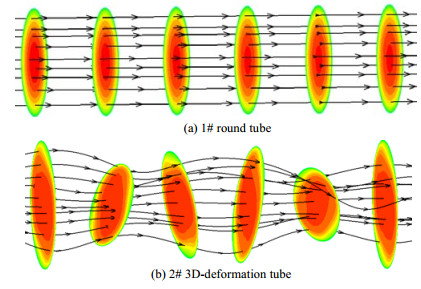
图 5为换热管内流线分布图,以等距离选取若干换热管切面,切面为速度分布图。通过对比图(a)和(b)可发现,在直圆管内,流体完全为轴向平行流动,而在三维变形管内,流体由于受到离心力的作用,呈现出轴向旋转流动形态,管中心处相对平缓,越靠近管壁,流体旋转越剧烈,从而增强了边界层与主流体质点间的径向混合,达到强化传热的效果。
|
图 5 换热管内流线图 Fig.5 Stream traces inside different tubes |
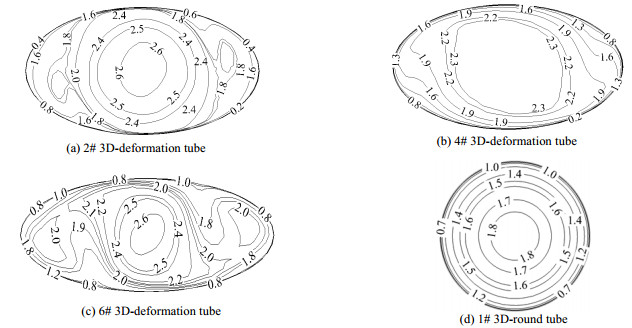
图 6为三维变形管2#,4#,6#和直圆管1#在距进口600 mm处的横截面合速度分布图。由图中可以看出,直圆管1#没有二次流出现,其合速度分布图呈现出一系列比较规整的同心圆形。而三维变形管2#,4#,6#合速度均产生了一定程度的扭曲,说明三维变形管内产生了垂直主流方向的二次流,由于4#三维变形管的长短轴A/B比较小,扭距S较大,其合速度仅在靠近长轴壁面处有轻微的扭曲;而扭距S相对较小的2#三维变形管和长短轴比A/B相对较大的6#三维变形管的合速度则扭曲较为明显,甚至出现了以横截面中心为轴的旋涡,流体对边界层的扰动更显著。
|
图 6 不同换热管横截面合速度分布图 Fig.6 Total velocity distributions at cross-sections of different tubes |
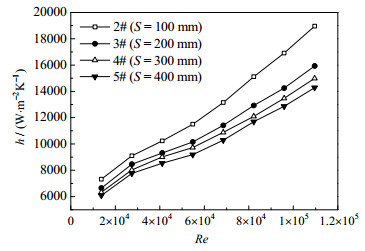
从图 7和图 8中可以看出,在相同雷诺数Re下,三维变形管的扭距S越小,传热效果越好,相应的压降ΔP也越大,当三维变形管扭距S由400 mm减小到200 mm时,管内传热膜系数h平均增大了10.2%,压降ΔP平均增大了17.8%,压降升高更快。分析原因主要是随着扭距S的减小,管内流体的旋转加剧,二次流增强,流体径向混合更充分,换热效果更好,但同时压降也相应增大。
|
图 7 扭距S对三维变形管管内传热膜系数h的影响 Fig.7 Effects of S on tube-side heat transfer coefficient h of 3D-deformation tubes |

|
图 8 扭距S对三维变形管管内压降ΔP的影响 Fig.8 Effects of S on tube-side pressure drop ΔP of 3D-deformation tubes |
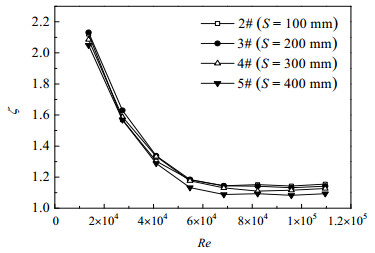
图 9为不同扭距S的三维变形管等泵功耗下的管内综合评价因子ζ [17]随雷诺数Re的变化情况。可以看出,随着雷诺数Re的增大,三维变形管的综合性能ζ下降,在13000 < Re < 60000,综合评价因子ζ急剧下降,但当Re > 60000时,综合评价因子ζ的下降趋势渐趋缓和。这是因为随着管内流速的增大,压降会急剧增大,导致强化传热效果下降。还可观察到,在本文研究的扭距S范围内,三维变形管的综合性能ζ大致呈现随着扭距S的减小而增大的趋势,但差别不明显,平均差别3.8%,且在13000 < Re < 80000,还出现了3# (S = 200 mm)的综合评价因子ζ比2# (S = 100 mm)稍大的现象。
|
图 9 扭距S对三维变形管管程综合性能ζ的影响 Fig.9 Effects of S on tube-side overall performance ζ of 3D-deformation tubes |
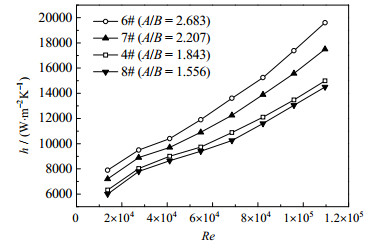
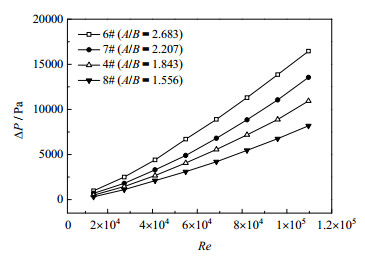
从图 10和图 11中可以看出,相同雷诺数Re下,长短轴比A/B越大,换热效果越好,同时压降ΔP也越大。长短轴比从1.556增大到2.683时,管内传热膜系数h平均增大29.1%,管内压降平均增长了125.7%。这主要是因为,A/B越大,代表换热管压扁程度越大,管内当量直径de越小,管内流体的速度场和温度场扭曲程度加剧,相同雷诺数Re下,流体流速也越大,换热效果增强的同时,导致管内压降也急剧增加。
|
图 10 长短轴比A/B对三维变形管管内传热膜系数的影响 Fig.10 Effects of A/B on tube-side heat transfer coefficient of 3D-deformation tubes |
|
图 11 长短轴比A/B对三维变形管管内压降特性的影响 Fig.11 Effects of A/B on tube-side pressure drop of 3D-deformation tubes |
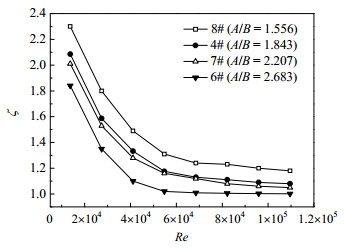
图 12为不同长短轴比A/B的三维变形管的管内综合评价因子ζ随雷诺数Re的变化情况,从图中可以看出,随着雷诺数Re的增大,三维变形管的综合性能ζ也是不断下降,在13000 < Re < 60000,管内综合评价因子ζ随着雷诺数Re的增大迅速减小;当雷诺数Re > 60000时,变形管的综合评价因子ζ随雷诺数Re增大而逐渐趋于平稳。从图 12中还可发现,相同雷诺数Re下,长短轴比A/B越大,管内综合评价因子ζ越小。长短轴比A/B从1.556增大到2.683时,综合评价因子ζ平均减小20.2%,即换热管的综合性能越差,这主要是因为在本文研究的长短轴比A/B范围内,管内综合性能的主导因子为压降,于是呈现出变形管压扁程度越小,综合性能反而越好的结果。
|
图 12 长短轴比 A/B 对三维变形管管程 综合性能的影响 Fig.12 Effects of A/B on tube-side overall performance of 3D-deformation tubes |
上文的模拟结果主要分析考察了三维变形管管内传热和压降特性与长短轴比A/B、扭距S以及雷诺数Re之间的对应关系。参考高学农等[18]对传热与压降计算准则关联式的拟合模型,采用多元线性回归的方法对数值计算结果进行拟合,得到了如下计算准则关系式:
| $ Nu = 1.023 \times {{\mathop{ Re}\nolimits} ^{0.432}}{Pr ^{0.33}} \times {(\frac{A}{B})^{{\rm{0}}{\rm{.131}}}}{(\frac{S}{{{d_{\rm{e}}}}})^{-{\rm{0}}{\rm{.1778}}}} $ | (3) |
| $ f = 15.292 \times {{\mathop{ Re}\nolimits} ^{-0.471}} \times {(\frac{A}{B})^{0.471}}{(\frac{S}{{{d_{\rm{e}}}}})^{-0.409}} $ | (4) |
适用范围:1.3×104 < Re < 11×104,5.1 < S/de < 20.3,1.566 < A/B < 2.683。
在上述适用范围内,拟合得到的管内Nu值计算准则关联式与数值模拟得到的Nu值结果最大偏差为9.44%,平均偏差为5.19%;拟合得到的管内f值计算准则关联式与数值模拟得到的f值结果最大偏差为6.34%,平均偏差为3.45%,说明拟合的准则关系式与数值模拟结果吻合度较高。
4 应用实例对比分析某化工厂的废水零排放项目中,末端高盐废水处理采用MVR蒸发结晶系统,蒸发器采用钛管TA2作为换热元件,壳体材质为316 L不锈钢,蒸发器投资约占整个MVR蒸发结晶系统的35%。图 13是装配中的三维变形管MVR蒸发器,管束实现自支撑结构,壳程无折流板,管外蒸汽纵向全空间流动,彻底消除振动,与管内废水实现纯逆流小温差换热,有效利用了传热温差,与普通光管蒸发器的性能参数对比如表 2所示,通过对比可以发现采用三维变形管MVR蒸发器换热面积减少33.9%,体积缩小43.6%,节省造价48.3万元,同时节约了运输成本和安装空间,通过现场标定证实已达到设计要求,表明采用三维变形管的MVR蒸发器具有良好的强化传热效果。

|
图 13 三维变形管MVR蒸发器现场装配图 Fig.13 Picture of the assembled 3D-deformation tube MVR evaporator |
|
|
表 2 性能参数对比表 Table 2 Comparison of performance parameters of different evaporators |
采用数值模拟方法,研究在MVR蒸发器管内流体运行工况范围内,三维变形管不同扭距S,长短轴A/B对传热与压降性能的影响,得到以下结论:
(1) 相比于光滑圆管,三维变形管具有优异的强化传热性能,三维变形管的S值越小,A/B值越大,强化传热效果越好,但同时压降也会增大。
(2) 在研究范围内,三维变形管的综合强化传热性能随着雷诺数Re的增大而将减弱,但均大于1,且减小S值比增大A/B值更有利于管内综合强化传热性能的提高。
(3) 根据模拟结果拟合出三维变形管管内传热与压降计算准则关系式,可为三维变形管MVR换热器的工程设计提供参考。
(4) 将三维变形管应用于高盐废水MVR蒸发器中,节材效益显著。
|
|
| [1] | YANG De-ming(杨德明), YE Meng-fei(叶梦飞), TAN Jian-kai(谭建凯), et al. Application progress for mechanical vapor recompression heat pump technology(机械蒸汽再压缩(MVR)热泵技术的应用进展)[J]. Journal of Changzhou University (Natural Science Edition)(常州大学学报(自然科学版)), 2015, 27(1): 76-80. DOI:10.3969/j.issn.2095-0411.2015.01.015. |
| [2] | Christopher C C E, Dutta A, Farooq S, et al. Process synthesis and optimization of propylene/propane separation using vapor recompression and self-heat recuperation[J]. Industrial & Engineering Chemistry Research, 2017, 56(49): 14557-14564. |
| [3] | QU Rui(瞿瑞), ZHANG Zhan-mei(张占梅), FU Ting(付婷). Pilot study on mechanical vapor recompression technology for treatment of saline wastewater(MVR法处理含盐废水中试研究)[J]. Chinese Journal of Environmental Engineering(环境工程学报), 2016, 10(7): 3671-3676. |
| [4] | QIU Ru-chen(仇汝臣), YUE Kun(岳坤), WANG Yu-shuang(王玉爽), et al. Research progress and prospect of seawater desalination technology(海水淡化技术研究进展及展望)[J]. Modern Chemical Industry(现代化工), 2017, 37(9): 49-51. |
| [5] | ZHAO Yuan-yuan(赵媛媛), ZHAO Lei(赵磊), QIAN Fang(钱方), et al. Application of the mechanical vapor recompression (MVR) evaporator in the food industry(机械蒸汽再压缩(MVR)蒸发器在食品工业中的应用)[J]. Dairy Industry(中国乳品工业), 2015, 43(1): 27-28. DOI:10.3969/j.issn.1001-2230.2015.01.007. |
| [6] | Dzyubenko B V. Influence of flow twisting on convective heat transfer in banks of twisted tubes[J]. Heat Transfer Research, 2005, 36(6): 449-59. DOI:10.1615/HeatTransRes.v36.i6. |
| [7] | Dzyubenko B V. Estimation of the thermohydraulic efficiency of heat exchanging apparatuses with twisted tubes[J]. Heat Transfer Research, 2006, 37(4): 349-363. DOI:10.1615/HeatTransRes.v37.i4. |
| [8] | SI Qin(思勤), XIA Qing(夏清), LIANG Long-hu(梁龙虎), et al. Investigation of heat transfer and flow resistance on twisted tube heat exchanger(螺旋扁管换热器传热与阻力性能)[J]. CIESC Journal(化工学报), 1995, 46(5): 601-608. |
| [9] | MENG Ji-an(孟继安), LI Zhi-xin(李志信), GUO Zeng-yuan(过增元), et al. Simulation and analysis on laminar flow and heat transfer in twisted ellipse-tube(螺旋扭曲椭圆管层流换热与流阻特性模拟分析)[J]. Journal of Engineering Thermophysics(工程热物理学报), 2002, 23(S1): 117-120. |
| [10] | Cheng J L, Qian Z Q, Wang Q. Analysis of heat transfer and flow resistance of twisted oval tube in low Reynolds number flow[J]. International Journal of Heat and Mass Transfer, 2017, 109: 761-777. DOI:10.1016/j.ijheatmasstransfer.2017.02.061. |
| [11] | Yan W B, Gao X N, Xu W D, et al. Heat transfer performance of epoxy resin flows in a horizontal twisted tube[J]. Applied Thermal Engineering, 2017, 127: 28-34. DOI:10.1016/j.applthermaleng.2017.08.013. |
| [12] | Tan X H, Zhu D S, Zhou G Y, et al. Experimental and numerical study of convective heat transfer and fluid flow in twisted oval tubes[J]. International Journal of Heat and Mass Transfer, 2012, 55(17-18): 4701-4710. |
| [13] | Bishara F, Jog M A, Manglik R M. Computational simulation of swirl enhanced flow and heat transfer in a twisted oval tube[J]. Journal Heat Tranfer, 2009, 131(8): 080902-080902. DOI:10.1115/1.3143015. |
| [14] | ZHU Dong-sheng(朱冬生), SHI Zhong-jing(石仲璟), QIAN Tai-lei(钱泰磊), et al. Numerical simulation and field synergy analysis of a twisted elliptical tube heat exchanger(扭曲椭圆管换热器的数值模拟及场协同分析)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2015, 29(1): 64-71. DOI:10.3969/j.issn.1003-9015.2015.01.009. |
| [15] | Zhang L, Yang S, Xu H. Experimental study on condensation heat transfer characteristics of steam on horizontal twisted elliptical tubes[J]. Applied Energy, 2012, 97(S1): 881-887. |
| [16] | WANG Fu-jun(王福军). Computational fluid dynamics-CFD software principles and applications(计算流体动力学分析-CFD软件原理与应用)[M].Beijing(北京): Tsinghua University Press(清华大学出版社), 2004. |
| [17] | Webb R L. Principles of enhanced heat transfer[M].New York: John Wiley & Son, 1995. |
| [18] | GAO Xue-nong(高学农), ZOU Hua-chun(邹华春), WANG Duan-yang(王端阳), et al. Heat transfer and flow resistance in a twisted flat tube with high twist ratio(高扭曲比螺旋扁管的管内传热及流阻性能)[J]. Journal of South China University of Technology (Natural Science Edition)(华南理工大学学报(自然科学版)), 2008, 11(36): 17-21. |




