在使用提升管进行催化裂解及炼焦的生产过程中,操作温度普遍高于500℃,在沥青蒸汽与焦炭颗粒接触的过程中常会发生颗粒团聚现象。团聚的结果一方面影响了焦炭粒子的流化效果,减弱了反应物间的热量传递,另一方面也对气力输送形成了阻碍,使设备能耗增加。因此有必要通过研究团聚现象下流态化过程所展现的特点来认识团聚机理,进而有效防治颗粒成团现象的发生。
由于工业过程难以实现提升管内流动过程的可视化,因此借助其内部压力波动信号来研究气固两相流动特性是一种可操作性强、准确度高的研究方法,得到了广泛的应用。Esmail[1],Stoyan[2],王晓萍[3]等基于压力信号波动特点实现了对流化床的流型识别。Bai[4],赵贵兵[5],吴贤国[6]等采用分形分析方法研究表明压力信号集中体现了流化床系统内介尺度上的相互作用。Zhao等[7]证明了压力信号具有某种非线性的确定机理,李晓祥[8, 9]基于压力信号对气固流动过程进行了非线性分析,并基于分析成果结合人工神经网络建立了颗粒浓度预测的非线性模型,实现了循环床颗粒浓度的短期预测。递归图[10]是一种适用于非线性动力系统的分析方法,它可以将表征系统特征的一维非线性时间序列转化为二维图像,给出系统相似性和预测性的相关信息。近年来很多学者采用递归图方法进行多相流领域的研究,洪文鹏[11]对管束间气液两相不同流型的压差信号进行递归分析,表明递归纹理结构能清晰演化系统内流型和动力学特征的变化。李洪伟[12]采用递归方法研究了气液两相的流动图像,表明递归特征量对流型识别具有重要意义。王肖祎[13]运用递归图及其定量分析研究了流化床内石英砂、生物质双组份混合流动特性,结果表明随生物质添加量的增加,系统的周期性呈现先减弱后增强的变化趋势。
本文为研究团聚物对气固两相流系统非线性特征所产生的影响,首先人工制造石英砂颗粒团聚现象,并对生成的团聚物经筛分法进行分区域辨识。此后,采用含不同种团聚物的石英砂进行流态化实验,对流动过程中压力波动信号进行递归定性与定量分析,着重研究了节涌床与湍动床状态下,系统混沌特征随团聚物种类及循环物料量的变化规律。
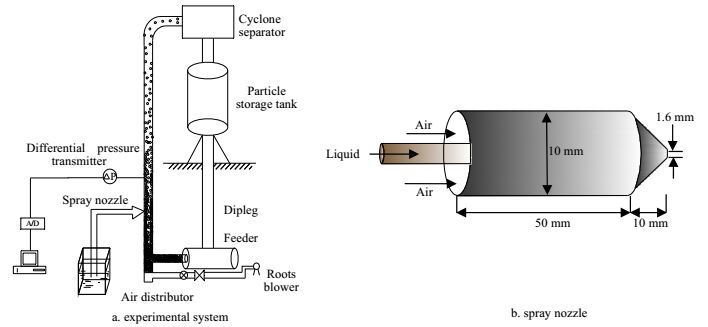
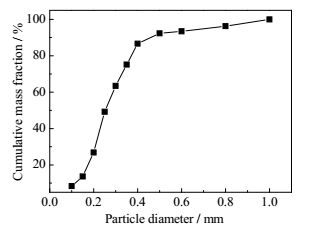
2 实验部分 2.1 实验装置及材料实验系统如图 1a所示,主要包括提升管实验台、雾化喷嘴装置[14]、压力测量装置、风机以及气固分离装置。其中,提升管高3.6 m,内径0.08 m,底部入风口装有圆形布风板并开有直径1 mm的小孔120个,促使流化均匀。雾化喷嘴安装在距布风板0.2 m高度位置,其结构如图 1 b所示,实验中可以通过控制时间来调节输送质量。测压孔中心位置位于布风板上方0.5 m处,压力波动信号由压力变送器测取。实验中以空气作为气相输送介质,以糖水溶液和石英砂分别代替沥青和催化剂颗粒来模拟工业炼焦过程,其中原始石英砂密度ρ = 2650 kg·m-3,平均筛分粒径dp= 0.26 mm,粒度分布如图 2所示,临界流化速度经计算为1.45 m·s-1,糖水溶液浓度为10.5%。
|
图 1 实验装置 Fig.1 Scheme of the experimental setup |
|
图 2 原始石英砂粒度分布 Fig.2 Profile of the original particle size distribution of quartz |
实验中,通过雾化喷嘴向处于流化状态的原始石英砂中喷入一定质量的糖水溶液来制造颗粒团聚,糖水喷入后继续流化一段时间,整个过程中保证加入糖水中的水分与受流化风作用而挥发的水分处于平衡状态,待形成稳定的颗粒团聚物后,将其全部取出,从中采样200 g进行结构筛分,以此来统计团聚物粒径分布。此后重新向提升管加入相同质量的原始石英砂并使之流化,改变注入糖水溶液质量并重复其余步骤。待全部结束后将各组含不同尺寸团聚物的石英砂颗粒分别作为物料颗粒进行实验。实验中,来自罗茨风机的空气经布风板携带物料颗粒向上运动,被提升的颗粒经旋风分离器气固分离后经由储料罐、下降管重新进入螺旋给料机,实现物料的循环,在此过程中进行压力信号的测取。本实验操作条件:静床高H = 0.28 m,操作气速范围Ug = 1.44~9.74 m·s-1,循环流量范围Gs= 20~43.2 kg·m-2·s-1。
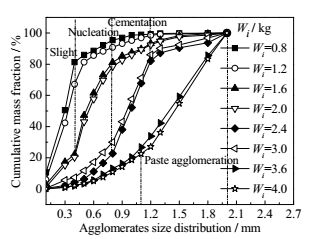
3 实验结果与分析 3.1 颗粒团聚的分区域辨识根据前人的研究,联系本实验可以预测,糖水溶液的注入质量会影响到生成的团聚结构种类。本实验中,第i次实验注入糖水质量分别为Wi= 0.8,1.2,1.6,2.0,2.4,3.0,3.6,4.0 kg,取样筛分的筛网直径分别为0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0,1.1,1.2,1.3,1.5,1.8,2.0 mm。对滞留在每一种筛孔直径的筛网上的样本进行称重,计算其占样本总质量的百分数,绘制各个工况下团聚物累计质量百分数,如图 3所示。
|
图 3 团聚结构粒度累计分布 Fig.3 Profiles of the agglomerates size distribution of quartz |
从图中可以发现,随注入糖水溶液质量的增加,可以将颗粒团聚物的尺寸分布划分为四个区域,第一区是当注入量Wi= 0~1.2 kg时,团聚结构粒度分布主要集中在0.2~0.45 mm,相对于原始颗粒,粒径的增长并不明显,只发生了轻微的聚团现象,称之为微团聚。第二区是在Wi= 1.6~2.0 kg条件下,团聚结构直径主要集中在0.4~0.8 mm,相比原始颗粒直径有所增加,但未发生粘结现象,称该结构为成核团聚。第三区是当注入质量达到2.4~3.0 kg时,团聚物直径已经有了显著增大,主要分布于0.8~1.3 mm,此状态可以看作是若干成核团聚物经物理作用发生了粘结后的结果,因此称之为黏结团聚,此时团聚物表面仍可以发现附着原始石英砂颗粒。继续增加注入量至3.6~4.0 kg,团聚物尺寸进一步增大,主要分布于1.2~2.0 mm,稠状糊质团聚结构开始显现,此时团聚物表面不再有附着的细小颗粒,称该结构为糊状团聚。
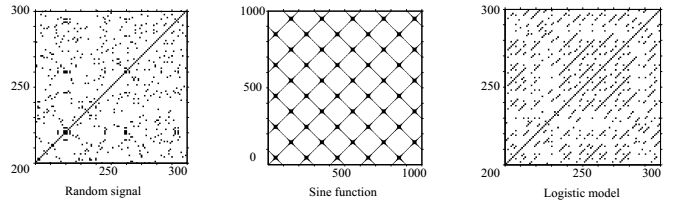
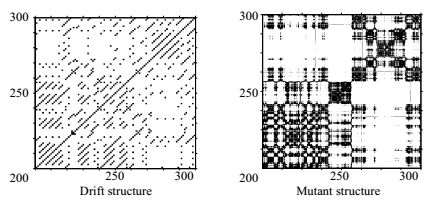
3.2 压力信号递归图分析图 4为基于随机信号、正弦信号、虫口模型信号所绘制的递归图,取样点个数为1000,其中对随机信号及虫口模型的递归图进行了放大处理。可以发现,随机信号的递归图属于宏观模式中的均态模式,除主对角线外其余点孤立分散且没有关联。正弦信号的递归图属于周期模式,其中出现了显著的网格状结构,网格的疏密反应了周期的长短。而虫口模型属于混沌信号,其递归图介于随机与周期信号之间,虽然没有显著的网格结构,但大量点形成了与主对角线平行的线段,其长度表示相空间中两条相邻轨迹相互逼近的快慢。图 5为递归图宏观模式中的漂移与突变模式,其中漂移模式是由于参数缓慢变化引起的,呈现沿对角线发展趋势,而突变模式是由于参数急剧变化引起的,图中出现白色与黑色块状区域。综上对比发现,递归图可以用于反映系统所处的状态以及混沌特征。
|
图 4 各类信号递归图 Fig.4 Recurrence plots of different signals |
|
图 5 漂移结构与突变结构 Fig.5 Drift and mutant structure in recurrence plot |
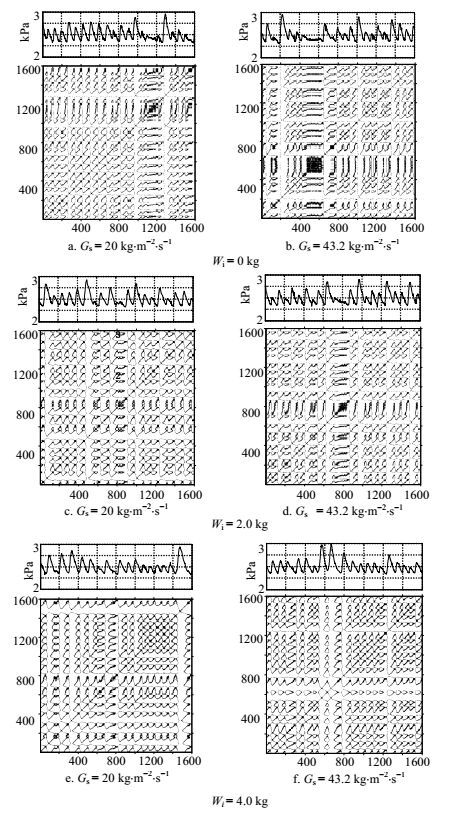
由于气固两相流动过程的复杂性,本文选取实验中观察到的节涌床与湍动床两种典型流型进行分析。图 6为选取原始石英砂、成核团聚石英砂、糊状团聚石英砂分别作为物料,保持Ug= 3.89 m·s-1,在不同Gs条件下所测得的压力波动信号及其递归图。从图中发现,含不同团聚结构的石英砂,压力信号及其递归图具有十分相似的特征,图中主要由较长的沿对角线方向线段组成,并包含部分黑色块状或白色条状结构,增大Gs对递归图内的结构特征并无显著影响。分析原因,当Ug= 3.89 m·s-1时,由于提升管直径小,高度高,此时管内气固两相均处于节涌流态化,气泡从布风板附近形成后,在上升过程中聚并、增大,直至其直径接近管径,到达一定高度后气泡破裂,尾涡夹带的颗粒受重力下落,下落过程正值另一个气栓的上升过程,以此往复。此过程中床层高度变化较规律,气泡的产生、合并、破裂过程周期性较强,且这种周期性特征不易受到团聚物尺寸以及颗粒浓度的影响。因此,各工况下压力信号递归图均表现出相似的周期性、间歇性特征。
|
图 6 节涌床状态下压力信号波动及其递归图 Fig.6 Recurrence plots of pressure fluctuation signals in slugging bed |
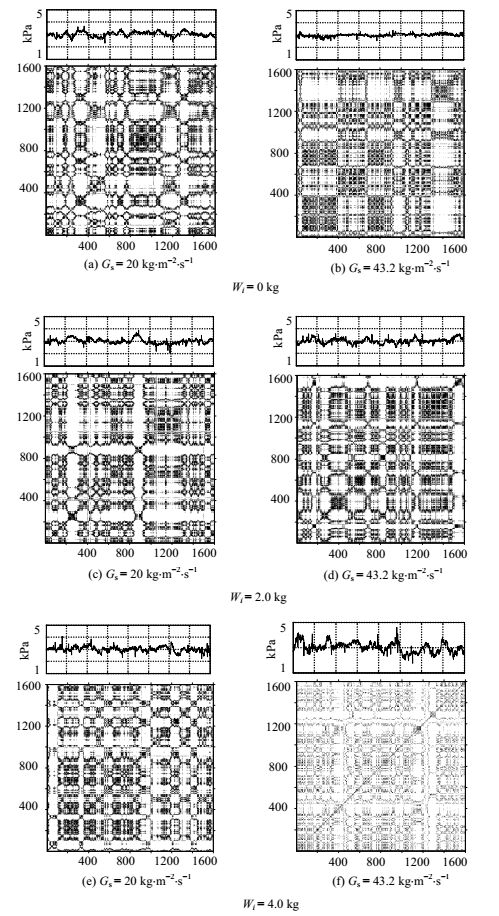
图 7为选取原始石英砂、成核团聚石英砂、糊状团聚石英砂分别作为物料,保持Ug= 7.58 m·s-1,在不同Gs条件下所测得的压力波动信号及其递归图。在此操作条件下,管内处于湍动流态化,气泡的产生与合并速度将加快,大量的气泡在床层表面破裂,导致气泡尾涡的夹带颗粒被抛洒到床层上方,床层表面已经开始弥漫。此过程中气固接触良好,压力脉动剧烈。对比图 7(a)、7(c)、7(e)可以发现,三幅图中压力波动的最大幅度以及递归图的结构组成较为一致,递归图主要由黑色与白色块状结构、竖直、水平线段组成,表明湍动床状态下系统具有显著的混沌特征且存在间歇与突变状态。同时也表明在Gs= 20 kg·m-2·s-1条件下,团聚结构的差异并未对两相流动过程造成显著影响。分别对比每一种团聚物的压力信号递归图发现:相对于图 7(a),图 7(b)中压力波动幅与频率明显降低,其递归图中孤立点减少,块状结构显著增加,沿对角线分布趋势增强,表明使用原始石英砂颗粒做循环物料的条件下,增大颗粒循环流量,系统虽仍具有混沌特征但随机性相对降低。图 7(d)相对图 7(c)无显著变化,表明使用含成核团聚结构的石英砂作为物料,两相流系统的混沌特征受物料循环量的影响较小。而相对于图 7(e),图 7(f)中孤立点数量显著增多,块状结构减少,沿对角线分布趋势减弱,同时压力脉动幅度与频率均显著增强,表明对于糊状团聚结构,随Gs增大流动过程的随机性增强,系统稳定性减弱。
|
图 7 湍动床状态下压力波动及其递归图 Fig.7 Recurrence plots of pressure fluctuation signals in turbulent bed |
分析产生以上现象的原因,由于系统混沌特性主要由气相脉动强度所决定,而气相脉动强度很大程度上受到物料粒径的影响。这里引入临界粒径dl,当团聚物平均粒径小于临界粒径时,由于其尺寸远小于最剧烈涡流的尺寸,因此会跟随涡流运动一段时间。在此过程中,由于曳力的存在会导致部分属于涡流的能量传递给颗粒,即涡流的湍流能转化为颗粒的动能,故气相涡流的湍动强度会随颗粒的浓度增大而相应削弱。当团聚物平均粒径大于临界粒径时,由于其直径接近于最剧烈的涡流而倾向于在漩涡尾部形成湍流,因此增大了气流的湍动强度。这种情况下,用于驱使颗粒运动的能量转化为涡流的动能,故湍动强度随颗粒循环流量的提高而增强。
Gore[16]在研究中,汇总了大量相关实验数据,发现d/le可以作为一个影响气固系统湍动强度的无量纲参数,其中d代表颗粒粒径,le代表气相最强涡流的特征长度。进而发现在d/le>0.1和d/le<0.1两种情况下,系统的湍动强度在受其他因素影响时,变化趋势截然相反,由此将0.1作为该无量纲参数的临界值,故本文中临界直径dl可以近似通过式(1) 计算。其中,在此前的研究中发现,对于单相气体射流以及气固两相管内流动的情况,在十分宽泛的实验条件范围内,气相最剧烈涡流的特征长度le与管径D存在近似式(2) 的数学关系,可以由式(2) 来计算。本实验中,提升管内径D = 80 mm,经计算,临界直径dl = 0.88 mm。当注入糖水质量Wi= 0 kg时,无团聚形成,物料直径0.26 mm明显小于dl,故Gs的增加会导致气体湍动强度的减弱,从递归图上表现为系统随机性的降低。当Wi= 2.0 kg时,形成成核团聚物的平均当量直径为0.85 mm,部分团聚物尺寸小于临界直径,另一部分团聚物尺寸大于临界直径,故随Gs增加,两部分团聚物对气相湍动强度起到了相反的作用,综合两种影响的结果,气体湍动能并未有显著改变,因此递归图也未发生结构突变。当Wi= 4.0 kg时,糊状团聚物的平均直径增大到2.0 mm,显然已超过临界直径dl,故此部分团聚物属于大粒径颗粒类别,颗粒浓度的提高会增强气体的湍动强度,导致系统随机性增强,周期性和确定性削弱,从而导致递归图中出现孤立点取代块状结构的现象。
| $\frac{{{d_{\rm{l}}}}}{{{l_{\rm{e}}}}} = 0.1$ | (1) |
| $\frac{{{l_{\rm{e}}}}}{D} = 0.11$ | (2) |
为了更精确地展现递归图纹理特征所反映的系统状态,采用基于递归图参数的定量分析方法。本文选取确定性(DET)以及分叉性(DIV)两种递归参数,其中确定性表示组成和主对角线平行的线段上的点与递归点总数的比值,DET值越大,表示图中沿主对角线方向发展的趋势越显著,块状结构越明显,系统内随机性越低。而分叉性定义为最大对角线长度的倒数,表示相空间内两条轨迹分离速率的快慢,与确定性相反,DIV值越大,表示系统越不稳定。
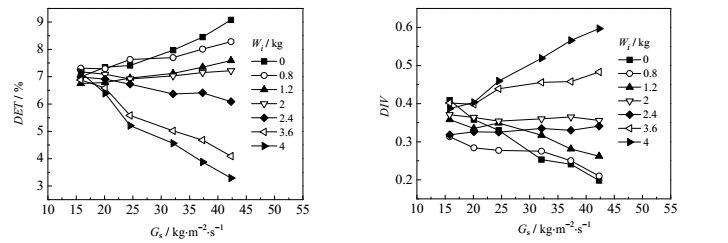
图 8给出了操作气速Ug= 7.58 m·s-1时,不同种团聚物压力信号DET与DIV变化情况。从中发现,随循环流量的增加,颗粒浓度增大,相应递归图参数变化规律因团聚物种类而相异。就确定性而言,对于原始石英砂及产生微团聚的石英砂,随Gs的增加,DET值有明显增长趋势,表明递归图中沿对角线分布及块状结构的显著增强,反映出系统不确定性的削弱。对于Wi= 1.2和2 kg条件下形成的成核团聚颗粒,DET仍随Gs增加有所增长,但增长量很少,表明此条件下系统受物料流量影响较小。而对于形成黏结团聚以及糊状团聚的物料颗粒,随Gs增加,DET呈与此前相反的减小趋势,且Wi越大,DET减小的趋势越明显。以上表明递归图孤立点状结构取代块状结构逐步增多,反映出系统不稳定性和随机性的增强。相比于确定性参数,分叉性的变化规律与之截然相反,对于微团聚及成核团聚的颗粒,DIV随Gs增加而减小,表明递归图最大对角线长度逐渐增加,系统稳定性增强。而对于粘结团聚及糊状团聚的颗粒,随Gs增加,DIV值随之增加,表明相空间内平行轨道正加速分离,系统稳定性减弱。此结论与上述通过递归图定性分析得出的结果相一致,印证了分析的正确性。
|
图 8 不同团聚结构下递归图DET及DIV变化规律 Fig.8 Profiles of DET and DIV under different agglomerate structures |
(1) 向石英砂颗粒中注入糖水溶液人工制造团聚现象,随注入糖水质量的增加,依次形成微团聚、成核团聚、黏结团聚以及糊状团聚,团聚物尺寸逐渐增加。
(2) 在节涌床流动过程中,压力信号递归图沿对角线发展的纹理特征显著,周期性较强,且不易受团聚物尺寸及颗粒循环流量的影响。
(3) 在湍动床状态下,对于原始及微团聚石英砂,随Gs提高,递归图块状结构增多,沿对角线发展趋势增强,DET提高,DIV减小,系统周期性增强,且团聚物尺寸越接近原始物料尺寸,这种变化越明显。对于成核团聚物料,颗粒循环流量对系统混沌特征影响不显著。而对于形成粘结团聚及糊状团聚的颗粒物,随Gs的提高,递归图孤立点状结构增多,对角线发展趋势减弱,DET减小,DIV提高,系统随机性增强,且团聚物尺寸越大,受Gs影响越显著。
符号说明:
| D | —提升管管径,mm | H | —静床高,m |
| DET | —递归图结构确定性 | le | —气象最剧烈涡流的特征长度,mm |
| DIV | —递归图结构分叉性 | Ug | —操作气速,m·s-1 |
| dl | —临界粒径,mm | Wi | —喷入糖水溶液质量,kg |
| dp | —原始颗粒平均筛分粒径,mm | ρ | —石英砂密度,kg·m-3 |
| Gs | —物料循环流量,kg·m-2·s-1 |
| [1] | Esmail R, Monazam , Lawrence J, et al. Identification and characteristics of different flow regimes in a circulating fluidized bed[J]. Powder Technology , 2005, 155(1): 17-25. DOI:10.1016/j.powtec.2005.03.019. |
| [2] | StoyanNedeltchev . New methods for flow regime identification in bubble columns and fluidized beds[J]. Chemical Engineering Science , 2015, 137(12): 436-446. |
| [3] | WANG Xiao-ping(王晓萍). The Hilbert-Huang transform and flow regimes identification for pressure fluctuation of gas-solid fluidized beds(气固流化床压力脉动信号的Hilbert-Huang变换与流型识别)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2005, 19(04): 474-479. |
| [4] | Bai D, Shibuya E, Nakagawa N, et al. Fractal characteristics of gas-solids flow in a circulating fluidized bed[J]. Powder Technology , 1997, 90(3): 205-212. DOI:10.1016/S0032-5910(96)03212-3. |
| [5] | ZHAO Gui-bing(赵贵兵), YANG Yong-rong(阳永荣). Characteristics of multi-scale and multi-fractal of pressure signals in a bubbling fluidized bed(流化床压力波动多尺度多分形特征)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2003, 17(06): 648-654. |
| [6] | WU Xian-guo (吴贤国). Application of fractal technology to the measurement of gas-solid fluidization (分形技术在气固流化床检测中的应用研究)[D]. Hangzhou (杭州): Zhejiang University (浙江大学), 2002. http://cdmd.cnki.com.cn/Article/CDMD-10335-2003051278.htm |
| [7] | Zhao G B, Chen J Z, Yang Y R. Predictive model and deterministic mechanism in a bubbling fluidized bed[J]. AIChE Journal , 2001, 47(07): 1524-1532. DOI:10.1002/(ISSN)1547-5905. |
| [8] | LI Xiao-xiang(李晓祥), SHI Yan-fu(石炎福), HUANG Wei-xing(黄卫星), et al. Nonlinear analysis of gas-solid flow behavior in fast fluidized bed riser(快速流化床提升管中气固流动行为的非线性分析)[J]. Journal of Chemical Industry and Engineering (China)(化工学报) , 2004, 55(02): 182-188. |
| [9] | LI Xiao-xiang(李晓祥), SHI Yan-fu(石炎福), HUANG Wei-xing(黄卫星), et al. Nonlinear model for generation of the solids holdup time series in the CFB riser based on combination of chaos with artificial neural network(基于混沌和人工神经网络方法建立计算气固循环流化床局部颗粒浓度时间序列的非线性模型)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2003, 17(5): 580-584. |
| [10] | Eckmann J P, Kamphorst S O, Rucllc D. Recurrence plots of dynamical systems[J]. Euro Physics Letters , 1987, 5(9): 973-977. |
| [11] | HONG Wen-peng(洪文鹏), ZHOU Yun-long(周云龙), LIU Yan(刘燕), et al. Chaotic recurrence characteristics analysis of differential pressure fluctuating signal across tube bundles(管束间压差波动信号的递归特性分析)[J]. Proceedings of the CSEE(中国电机工程学报) , 2011, 31(23): 74-78. |
| [12] | LI Hong-wei(李洪伟), ZHOU Yun-long(周云龙), SONG Qian(宋倩), et al. Recursive feature of gas-liquid two-phase flow pattern based on information entropy series of flow image(两相流流型图像信息递归特征分析)[J]. Journal of Chemical Industry and Engineering (China)(化工学报) , 2010, 61(6): 1431-1436. |
| [13] | WANG Xiao-yi(王肖祎), ZHONG Zhao-ping(仲兆平), WANG Chun-hua(王春华), et al. Chaotic recurrence analysis of two-component flow of mixed biomass particles and quartz sands in fluidized-bed(流化床内生物质石英砂双组分混合流动混沌递归分析)[J]. Journal of Chemical Industry and Engineering (China)(化工学报) , 2014, 65(3): 813-819. |
| [14] | Base T E, Chan E W, Kennett R D. Nozzle for atomizing liquid in two phase flow:US, 6003789[P]. 1999-12-21. |
| [15] | Saad M M, Barkouti A, Rondet E, et al. Study of agglomeration mechanisms of food powders:appliaction to durum wheat semolina[J]. Powder Technology , 2011, 208(2): 399-408. DOI:10.1016/j.powtec.2010.08.035. |
| [16] | Gore R A, Crowe C T. Effect of particle size on modulating turbulent intensity[J]. Multiphase Flow , 1989, 15: 279-285. DOI:10.1016/0301-9322(89)90076-1. |




