2, 4(或2, 6) -二氨基甲苯(TDA)及其混合物是生产甲苯二异氰酸酯(TDI)的重要原料[1, 2]。TDI是制备聚氨酯软泡沫材料、弹性材料、涂料和制胶辊等多种化工产品的重要有机中间体[3]。TDA通常是由相应的二硝基甲苯还原制得,但2, 6-TDA在制得的TDA混合物中所占比例较小。硝化邻硝基甲苯得到大约35%的2, 6-TDA,硝化对硝基甲苯,基本上没有2, 6-TDA生成。硝化未经分离的一硝基甲苯,可得到大约20% 2, 6-TDA。工业上,TDI有三种不同比例的异构体,即100%、 80% 和65% 的2, 4-TDA,其它组分为2, 6-TDA三种主要异构体。2, 6-TDA比2, 4-TDA反应速度要慢得多,在许多情况下,为了改善所得聚氨酯的性能,需要提高2, 6-TDA的含量,所以必须对2, 4-TDA和2, 6-TDA混合物进行分离,以得到2, 6-TDA含量更高的TDA产品。目前工业上TDA混合物的的分离方法主要有吸附分离[4]、化学分离[5]、精馏法分离[6]、重结晶[7]、反应结晶分离[8]、衍生化结晶法[9],以上方法虽能得到纯化的TDA,但生产工艺复杂、需要引入新的溶剂或反应物,过程能耗大、成本高、不环保。
无溶剂添加的新型分离技术熔融结晶,是一种高效节能的有机物分离提纯方法,由于该工艺不需要引入新的溶剂,减少了溶剂回收处理的成本,并且过程能耗较低、属于环境友好型工艺,是一种绿色的分离工艺。2, 4/2, 6-TDA的固液相平衡(SLE)数据,是该体系熔融结晶分离工艺最重要的基础数据之一,根据该体系的二元固液相平衡规律可对熔融结晶分离工艺做出正确的指导。
由于该体系的SLE数据未见报道,为此,本文采用差示扫描量热法(DSC)[10, 11]测定了2, 6-TDA与2, 4-TDA的SLE数据并进行关联。为研究熔融结晶分离极限,设备结构尺寸设计和操作条件的确定提供基础数据。
2 实验部分 2.1 实验试剂本实验所用试剂均为分析纯试剂。将采购试剂通过熔融结晶进一步提纯后,经色谱分析没有发现杂峰。 通过DSC测定精制后原料的熔点和熔化焓列于表 1,并与文献值进行了比较。可以发现文献中测定的2, 4-TDA的熔点数据和本文测定结果接近(相对偏差0.16%)。2, 6-TDA的熔点数据和本文测定结果偏差较大(相对偏差0.96%)。并补充了各物质的熔化焓数据。
| 表 1 试剂熔点及熔化焓 Table 1 Melting points and fusion enthalpies of the reagents |
Sartorius BT25S电子天平(精确度 = 0.01 mg),赛多利斯科学仪器(北京)有限公司;全自动多晶X-射线衍射仪(XRPD)XD-3,北京普析通用仪器有限责任公司;DSC-200F3型差示扫描量热仪,德国NETZSCH公司;傅里叶红外光谱仪,Vector22,德国布鲁克光谱仪公司。
2.3 实验步骤 2.3.1 仪器校正及可靠性验证(1) 仪器校正
实验中,首先按照仪器要求用仪器自带的标准物(Hg,In,Sn,Bi,Zn)对仪器进行了温度及热量校正,确定热焓和温度误差不超过2% 和0.20 K。
(2) 仪器可靠性验证
本实验选用标准样品In对其熔点和热焓值进行测定。其熔点值理论应为429.75 K,热焓值应为28.6 J⋅g-1。
DSC温度控制程序设定为:在373.15 K恒温20 min,然后以升温速率2.0 K⋅min-1升温至443.15 K。测定3次,其熔点值分别为430.15、430.25和430.45 K,其热焓值分别为28.50、28.40和28.50 J⋅g-1,平均值与理论值的误差分别为0.38%和0.47%,误差在0.50% 之内,证明本仪器准确度较高,测定结果可靠。
2.3.2 样品配制及预处理样品配制:在试管中称量不同组分比例的样品后进行预处理。
预处理:油浴上将样品熔化,搅匀,液氮极速冷却,室温下将固体在研钵中研磨,直至粉末状,确保样品混合均匀。
预处理的必要性验证:将同一个组成的样品分成两份,其中一份进行预处理,另外一份不作任何处理,将两份样品分别取样,并以相同的升温程序进行DSC测定,样品在测定DSC谱图时均消除了热记忆。对比两种制样方法得到的DSC谱图发现,未经过预处理得到的样品,由于2, 4-TDA和2, 6-TDA混合不均匀导致测得的DSC图谱中峰的形状波动太大、不圆滑,不能直接用于SLE的测定,由此验证了预处理的必要性。
2.3.3 样品测定(1) 实验中采用的是由NETZSCH公司提供的铝制坩埚(样品池),在坩埚中加入适量如上配制的不同比例样品,经压盖器密封后,放入炉体内热传感器的样品支撑位置上,以空的标准坩埚作参比物,以一定的升温速率扫描,所得DSC曲线的外推起始温度和峰温,即为固液平衡的实验数据。有关DSC法固液平衡测定原理见文献[13~16]。
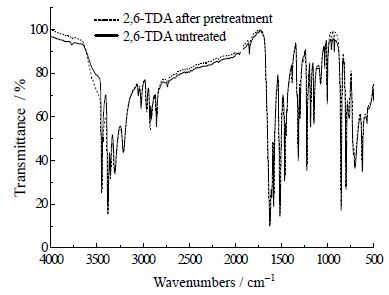
(2) 由于TDA物系本身的特殊性,即在高温下易被氧化变质,本实验采用氮气作为保护气,为验证预处理之后的样品是否发生变质,将预处理后的样品和没有经过处理的样品分别去做X-射线衍射(XRPD)分析、气相色谱分析以及红外光谱分析,得到的图谱如图 2所示。对比图谱可发现,预处理之后样品在经过XRPD分析、气象色谱分析、红外分析均没有产生新的特征峰,并且特征峰的位置没有发生移动,可证明在氮气保护下,原料在升温过程未变质。
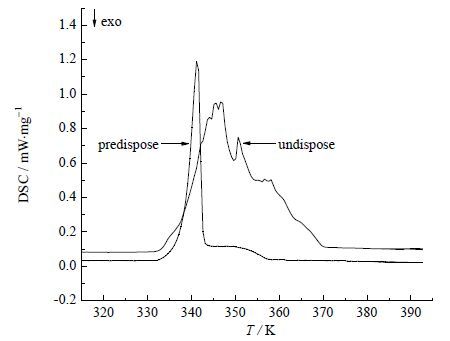
|
图 1 不同的制样方法得到的DSC 图谱 Fig.1 DSC thermograms of samples obtained with different preparation methods |
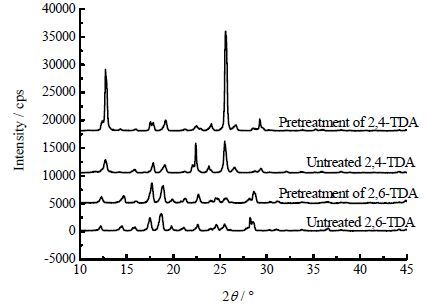
|
图 2(a) 样品的XRPD 图谱 Fig.2(a) XRPD patterns of different samples |
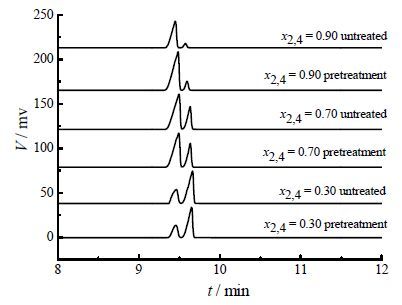
|
图 2(b) 样品的气相色谱图谱 Fig.2(b) GC spectra of different samples |
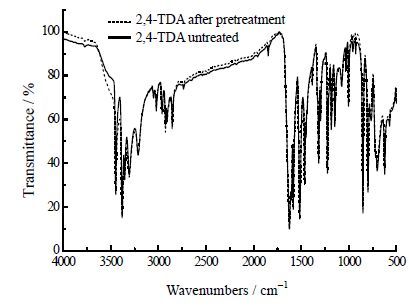
|
图 2(c) 样品2,4-TDA 的红外光谱图谱 Fig.2(c) 2,4-TDA IR spectra of different samples |
|
图 2(d) 样品2,6-TDA 的红外光谱图谱 Fig.2(d) 2,6-TDA IR spectra of different samples |
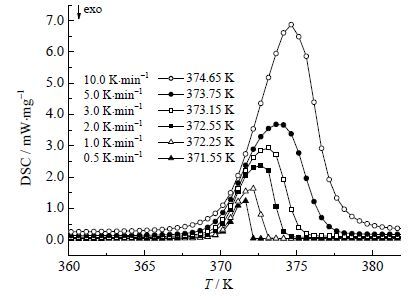
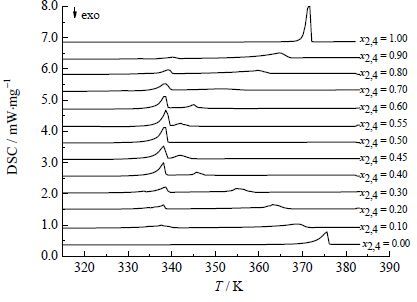
(1) 升温速率会影响分析过程的准确性,在测SLE前探究了不同的升温速率下2, 4-TDA纯品的熔点值的变化,如图 3所示,从图中可以看出熔融峰值温度随升温速率增大而增大,说明当升温速率过快时,熔化过程存在过热现象。当升温速率降到2.0 K⋅min-1时,随着升温速率的降低,熔融峰值温度变化不大,为了保证测温更接近实际相平衡温度,SLE测定过程中采用的升温速率为0.5 K⋅min-1。采用0.5 K⋅min-1的升温速率进行SLE的测定,得到各组成下的DSC图谱,如图 4所示。
|
图 3 纯品2,4-TDA 的DSC 热图谱 Fig.3 DSC thermograms of pure 2,4-TDA |
|
图 4 TDA 物系DSC 热图谱 Fig.4 DSC thermograms of TDA samples |
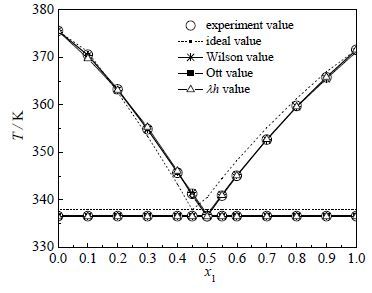
2, 4-TDA和2, 6-TDA的二元SLE数据列于下表 2中,图 5为其相应的二元相图。实验表明,所形成的固液平衡相图为简单低共熔型,2, 4-TDA(x1)+2, 6-TDA(1-x1)物系低共熔组成和温度为x1 = 0.4999,T = 336.56 K。
| 表 2 固液平衡数据表 Table 2 Solid-liquid equilibrium data |
SLE相平衡数据关联方法主要分为括经验模型法、活度系数法、状态方程法、拓扑法、人工神经网络法[17~19]
3.1 理想溶液模型计算简单低共熔型固液平衡计算的热力学基本方程[20]为
| $\ln {{x}_{i}}=\frac{{{H}_{m,i}}}{RT}(\frac{T}{{{T}_{m,i}}}-1)-\frac{\Delta {{C}_{p,i}}}{R}(1-\frac{{{T}_{m,i}}}{T}+\ln \frac{{{T}_{m,i}}}{T})-\ln {{\gamma }_{i}}$ | (1) |
|
图 5 2,4-TDA(x1)+2,6-TDA(1-x1)相图 Fig.5 Phase diagram of 2,4-TDA(x)+2,6-TDA(1-x1) |
若忽略溶液中组分与其纯组分的恒压热容的差别,上式可简化为
| $\ln {{x}_{i}}=\frac{{{H}_{m,i}}}{RT}(\frac{T}{{{T}_{m,i}}}-1)-\ln {{\gamma }_{i}}$ | (2) |
根据理想溶液模型lnγi=0,上式可简化整理为
| $T={{\left[ \frac{1}{{{T}_{m,i}}}-\frac{R}{{{H}_{m,i}}}\ln {{x}_{i}} \right]}^{-1}}$ | (3) |
所以理想溶液模型的温度Ti可通过式(3) 计算,计算结果列于表 2,在相图中以虚线表示,模型计算值与实验值的温度平均偏差为1.89 K,最大温度偏差3.95 K,与实验值有较大偏差。
3.2 Wilson方程基于分子的考虑,Wilson[21]提出了下列二元溶液过量自由焓表达式:
| $\frac{{{g}^{E}}}{RT}=-{{x}_{1}}\ln ({{x}_{1}}-{{\Lambda }_{12}}{{x}_{2}})-{{x}_{2}}\ln ({{x}_{2}}+{{\Lambda }_{21}}{{x}_{1}})$ | (4) |
由此导得的活度系数方程为:
| $\ln {{\gamma }_{1}}=-\ln ({{x}_{1}}+{{\Lambda }_{12}}{{x}_{2}})+{{x}_{2}}(\frac{{{\Lambda }_{12}}}{{{x}_{1}}+{{\Lambda }_{12}}{{x}_{2}}}-\frac{{{\Lambda }_{21}}}{{{\Lambda }_{21}}{{x}_{1}}+{{x}_{2}}})$ | (5) |
| $\ln {{\gamma }_{2}}=-\ln ({{x}_{2}}+{{\Lambda }_{21}}{{x}_{1}})-{{x}_{1}}(\frac{{{\Lambda }_{12}}}{{{x}_{1}}+{{\Lambda }_{12}}{{x}_{2}}}-\frac{{{\Lambda }_{21}}}{{{\Lambda }_{21}}{{x}_{1}}+{{x}_{2}}})$ | (6) |
在式(4) 中,过量自由焓是以拉乌尔定律意义上的理想溶液作为基准定义的。式(4) 服从当x1或x2变成零时gE等于零的边界条件。Wilson方程有两个可调参数Λ12和Λ21,在Wilson的推导中,它们与纯组分的摩尔体积和特征能之差有关。
| ${{\Lambda }_{12}}=\exp (-\frac{{{\lambda }_{12}}-{{\lambda }_{11}}}{RT})$ | (7) |
| ${{\Lambda }_{21}}=\exp (-\frac{{{\lambda }_{21}}-{{\lambda }_{22}}}{RT})$ | (8) |
其中活度系数γi由Wilson方程计算。二元Wilson活度系数方程的相互作用能参数λ12-λ11和λ21-λ22由实验数据根据通用全局优化法拟合得到,计算结果列于表 2,Wilson方程参数列于表 3。关联数据的计算值与实验值的温度平均偏差为0.15 K,最大温度偏差0.40 K,关联精度大于理想溶液模型。
| 表 3 Wilson方程参数 Table 3 Parameters for Wilson equation |
λh方程形式为
| $\ln \left[ 1+\lambda \left( 1-{{x}_{i}} \right)/{{x}_{i}} \right]=\lambda h\left( \frac{1}{T}-\frac{1}{{{T}_{m,i}}} \right)$ | (9) |
首次由Buchowski[22]提出,主要针对缔合物系的固液平衡。式中λ和h为方程参数,λ量纲为1,表示饱和溶液的非理想性,对理想缔合物系,可以认为是平均缔合度,h单位为K,与物系的焓变有关。对于本文物系,其参数λ和h根据单纯形加速法由实验数据回归得到。采用目标函数
| ${{F}_{obj}}=\sum\limits_{j}^{n}{{{({{T}_{\exp }}-{{T}_{cal,j}})}^{2}}}=\min $ | (10) |
计算结果列于表 2,所得到的方程参数列于表 4。关联数据的计算值与实验值的温度平均偏差为0.21 K,最大温度偏差0.80 K,关联精度大于理想溶液模型。
| 表 4 λh 方程参数 Table 4 Parameters for λh equation |
为了进一步提高实验数据关联精度,采用经验的Ott方程[23]对实验数据进行关联,方程形式为
| ${{T}_{cal}}={{T}_{m}}\left\{ 1+\sum\limits_{j=1}^{n}{{{b}_{j}}}{{({{x}_{1}}-x_{1}^{*})}^{j}} \right\}$ | (11) |
式中:Tcal为拟合计算结果;Tm为纯组分熔点;x1为Tm下组分的摩尔分数;bj为拟合分数;n为拟合系数个数。目标函数采用
| ${{T}_{obj}}=\sum\limits_{j=1}^{n}{{{({{T}_{\exp ,j}}-{{T}_{cal,j}})}^{2}}}=\min $ | (12) |
进行拟合,方程拟合参数bj列于表 5中。表中σ表示拟合值与实验值的标准偏差,且
| $\sigma =\left\{ {{\left. {{\sum\limits_{j}^{n}{\left( {{T}_{\exp ,j}}-{{T}_{cal,j}} \right)}}^{2}}/\left( m-n-1 \right) \right\}}^{1/2}} \right.$ | (13) |
| 表 5 2,4-TDA与2,6-TDA物系Ott方程参数bj Table 5 bj of 2,4-TDA + 2,6-TDA for Ott’s equation |
关联结果和试验测定的温度的平均偏差为0.05 K,最大偏差为0.13 K,显然拟合结果较好,完全可用于指导工业实践。
4 结论用差示扫描量热仪(DSC),测定了2, 4-TDA与2, 6-TDA的固液平衡温度-组成关系,并对二元体系实验结果进行数据拟合计算,结果显示该物系为简单低共熔类型,低共熔点摩尔分数组成和温度为:
x = 0.4999,T = 336.56 K。
采用理想溶液模型、Wilson方程、λh方程和Ott方程对SLE数据进行关联,所得固液平衡计算值与实验值比较接近,最大温度偏差不超过1.9 K,说明上述几种模型对本物系均适用,但基于Wilson方程的参数只有两个,所以优先选择Wilson方程进行数据关联。
符号说明:
| bj | — 拟合参数 | λ21-λ22 | — Wilson活度因子方程的相互作用能,J⋅mol-1 |
| ΔCp | — 纯组分的液固恒压热容差 | Λ12, Λ21 | — Wilson方程参数 |
| h | — λh | σ | — 标准偏差 |
| gE | — 自由焓,J | λ | — λh方程拟合参数 |
| Hm | — 纯组分的熔化热,J⋅mol-1 | δ | — 偏差 |
| m | — 实验数据点数 | 下标 | |
| R | — 气体常数(R = 8.314 J×K-1⋅mol-1) | cal | — 计算值 |
| R2 | — 相关系数 | eu | — 低共熔 |
| Tm | — 纯组分熔点,K | exp | — 实验值 |
| T | — 固液平衡温度,K | id | — 理想溶液模型 |
| x | — 组分摩尔分数 | i, j, k | — 组分 |
| γ | — 组分的活度系数 | m | — 纯物质 |
| λ12-λ11 | —Wilson活度因子方程的相互作用能参数,J⋅mol-1 | W | — Wilson方程 |
| [1] | BIAN Ai-fang(卞爱芳) . TDI production and market analysis at domestic and abroad(国内外TDI的生产及市场分析)[J]. Jiangsu Chemical Industry(江苏化工) , 2001, 29 (4) : 50-53 |
| [2] | Zinnen H A. Process for separating isomers of toluenndiamine:US, 4633018[P]. 1986-11-30. |
| [3] | XU Ke-xun(徐克勋) . Handbook of fine organic chemicals and inteimedia(精细有机化工原料及中间体手册)[M]. Beijing (北京): Chemical Industry Press(化学工业出版社), 1998 : 58 . |
| [4] | Zinnen H A. Process for separating isomers of toluenediamine:US, 4633018[P]. 1986-11-30. |
| [5] | Ibbotson A. Purification of amines:UK, 320879[P]. 1973-06-20. |
| [6] | Kirss V, Park J C. Purification of toluenediamine mixtures by vacuum distillation:US, 3420752[P]. 1969-1-7. |
| [7] | SU De-shui (苏德水), DUAN Li (段利), HUANG Jin (黄津), et al. Purified 2,4-diaminotoluene using recrystallization process(采用重结晶法提纯2,4-二氨基甲苯的工艺):CN, 104402732A[P]. 2015-3-11. |
| [8] | Hildreth J D, Haslam D G, Allen D E, et al. Production of 2, 4 and 2, 6-diaminotoluenes:US, 4256671[P]. 1981-3-7. |
| [9] | HU Yu-lai (胡雨来), WANG Gui (王珪), WU Cheng (武成), et al. Using derivatized crystallization process to separated and purified 2, 4-diaminotoluene and 2, 6-diaminotoluene(采用衍生化结晶法分离、提纯2, 4-二氨基甲苯、2, 6-二氨基甲苯的工艺):CN, 103319352A[P]. 2013-9-25. |
| [10] | Takiyama H, Suzuki H, Uchida H, et al. Determination of solid-liquid phase equilibria by using measured DSC curves[J]. Fluid Phase Equilibria, 2002, 194-197:1107-1117. |
| [11] | ZHANG You-wen(张友文), HE Qin-wei(何勤伟) . Determination of solid-liquid equilibrium of butynediol-water system(丁炔二醇-水体系固液平衡的测定)[J]. Petrochemical Technology(石油化工) , 1991, 20 (3) : 176-179 |
| [12] | Lide D R . CRC handbook of chemistry and physics. . |
| [13] | WEI Dong-wei(魏东炜), LI Fu-sheng(李复生), ZHANG Min-hua(张敏华) . Determination and correlation of solubilities of bisphenol A in phenol, phenol+acetone, phenol+water and phenol+acetone+water(双酚A在苯酚-丙酮-水中溶解度测定与关联)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2004, 18 (3) : 367-370 |
| [14] | JIA Xue-ting(贾雪婷), YANG Yi-chen(杨益辰), LIU Guo-zhu(刘国柱) . Measurement of the solubilities of 2-ethylanthraquinone and 2-amylanthraquinone in TMB/DIBC mixed solvents and their correlation with thermodynamic equations(2-乙基和2-戊基蒽醌在TMB/DIBC中溶解度的测定与关联)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2014, 28 (6) : 1183-1189 |
| [15] | JIN Ke-xin(金克新), CHEN Yong-qiang(陈勇强), WEI Dong-wei(魏东炜) . The measurement of solid-liquid equilibrium for dichlorobenzene isomers and 1, 2, 4-trichlorobenzene systems(二氯苯同分异构体及1, 2, 4, -三氯苯体系固液平衡测定)[J]. Chemical Industry and Engineering(化学工业与工程) , 1992, 9 (3) : 17-25 |
| [16] | JIN Ke-xin(金克新), WEI Dong-wei(魏东炜), LI Hong-xun(李洪勋) . Solid-liquid equilibria of the isomers of tetramethylbenzene(四甲苯物系固液平衡测定)[J]. Journal of Tianjin University(天津大学学报) , 1991, 24 (4) : 62-69 |
| [17] | QU Hong-mei(曲红梅), ZHOU Li-shan(周立山), WANG Wen-xi(王文喜) . Research progress theory of organic system's solid-liquid equilibrium(有机物系固-液相平衡理论研究进展)[J]. Chemical Propellants & Polymeric Materials(化学推进剂与高分子材料) , 2002 (6) : 10-13 |
| [18] | YUE Jin-cai(岳金彩), ZHU Nan-nan(朱南南), LIU Xian-hong(刘先红) . Research progress of solid-liquid equilibrium model(固液平衡模型研究进展)[J]. Speciality Petrochemicals(精细石油化工) , 2014, 31 (1) : 78-84 |
| [19] | LI Wen-chao(黎文超), XUAN Ai-guo(宣爱国), WU Yuan-xin(吴元欣) . Advance of research on solid-liquid equilibrium(固液平衡的研究进展)[J]. Petrochemical Technology(石油化工) , 2007, 36 (10) : 1067-1073 |
| [20] | Prausnitz J M, Ruediger N L, Edmundo G A . Molecular thermodynamics of fluid-phase equilibria[M]. 3rd ed. London: Prentice Hall PTR, 1999 . |
| [21] | Wilson G M. Vapor-liquid equilibrium. XI. A new expression for the excess free energy of mixing[J]. Journal of American Chemical Society, 964, 86(2):127-130. |
| [22] | Buchowski H, Ksiazcak A, Pietrzyk S . Solvent activity along a saturation line and solubility of hydrogen-bonding solids[J]. Physical Chemistry , 1980, 84 (9) : 975-979 DOI:10.1021/j100446a008 |
| [23] | Ott J B, Goates J R . (Solid+liquid) phase equilibria in binary mixtures containing benzene, a cycloalkane, an nalkane, or tetrachlormethane[J]. The Journal of Chemical Thermodynamics , 1983, 15 (3) : 267-278 DOI:10.1016/0021-9614(83)90119-2 |




