管壳式换热器作为一种热交换设备广泛应用于石油化工、能源动力等行业，其中以传统弓形折流板支撑多管束的弓形折流板换热器结构应用最为广泛，该结构具有加工制造简单、工作可靠等优点。然而，流体在其壳侧形成“Z”字形受限外流，流动死区大，沿程压降大，有效换热面积小^[1]，这种流动形式一定程度上降低了换热效率。

国内学者对优化和改进管壳式换热器壳侧受限外流做了大量工作，通过改变换热器壳程支撑结构以改进受限外流形式，从而研发新型节能换热器结构，主要结构形式有：多弓形折流板结构，圆盘-圆环形折流板结构、折流杆结构及螺旋折流板结构，主要思路是将流体横向流动转化为纵向流动或螺旋状流动。多弓形折流板结构和圆盘-圆环形折流板结构均由传统弓形折流板结构而来。这类换热器可减小弓形折流板壳程部分横向流动及死区面积，提高换热效率。然而，这些改良形式均未从根本上改变传统垂直弓形折流板管壳式换热器在壳侧形成“Z”字形受限外流外掠多管束的流动形式，在其折流板后方依然存在较大流动死区^[2~4]。折流杆是代替传统垂直折流板支撑结构的另一种形式，于20世纪70年代由美国Phillips石油公司首次研制成功，其壳程受限外流呈完全逆流，为理想塞柱流，有效增加了换热平均温差，提高换热效率，降低流动阻力，抗震抗结垢性能好。但结构不紧凑，加工工艺复杂，在低Re数下传热效果不佳^[5~8]，近年来有学者通过改变换热管形状或排列方式以提高其换热效率^{[9, 10]}。另一种支撑结构是螺旋折流板支撑结构，上世纪90年代捷克科学家提出采用螺旋状受限外流以有效降低流动阻力，提高换热效率的思想，并在欧美国家得到应用^[11~13]。这种流动形式依靠壳程螺旋折流板支撑结构来实现，流速变化平缓，可有效消除壳程流动死区，换热性能良好，但制造安装较困难。我国学者开展了交错搭接式螺旋折流板换热器和周向重叠三分螺旋折流板换热器的数值模拟及实验研究，并对其换热性能进行了系列研究比较^[14~22]。通过对螺旋折流板支撑多管束结构开展的大量研究，发现仍不能完全克服螺旋折流板换热器加工工艺复杂的缺点。

基于优化壳程流场以提高换热性能的核心思想，本文针对传统弓形折流板支撑多管束受限外流流动死区大，压降高的问题，提出新型斜百叶片折流板支撑结构。通过三维数值模拟，对斜百叶片折流板支撑多管束受限外流流场进行分析，详细研究了该受限外流阻力及传热性能。

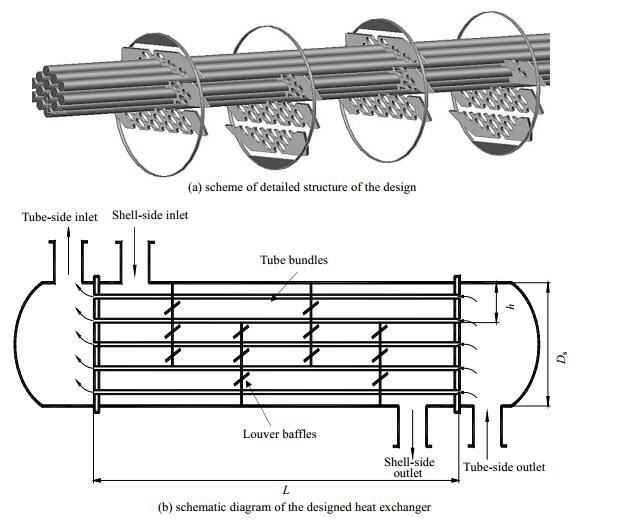
所研究斜百叶片折流板支撑结构由外壳，换热管束及百叶片折流板组成，如图 1所示。流体流经斜百叶片折流板后形成百叶片支撑多管束受限外流。折流板由若干与管束轴线倾斜角度相同的百叶片及折流圈组成。折流圈内部依各叶片角度及放置位置下轨，叶片插于导轨中并焊接以固定，确保叶片角度准确性，换热管束穿插于沿长度方向等距布置的折流板中，基本几何参数如表 1所示：

表 1(Tab. 1)

表 1 模型几何参数 Table 1 Geometric dimension of the design Item Dimension Item Dimension Item Dimension Item Dimension Diameter of shell Ds / mm 500 Tube effective length L / mm 2000 Tube numbers 61 Diameter of shell-side inlet/outlet dinlet / mm 150 Baffle number 4 Outer diameter of tube d0 / mm 38 Plate inclination angle 30~85° Width of each plate / mm 100 Tube pitch / mm 48 Baffle cut ratio 30% Plate pitch / mm 100 Arranging style for tubes Triangle

表 1 模型几何参数 Table 1 Geometric dimension of the design

图 1(Fig. 1)

图 1 斜百叶折流板与管束装配图 Fig.1 Schematic diagram of louver baffles and louver baffle supported tube bundles

本文通过三维数值模拟，对百叶片支撑多管束受限外流进行温度场、流场研究。模型计算流场为全三维流场，湍流模型采用k-ε湍流模型，标准壁面函数，无滑移壁面条件。用SIMPLE算法求解方程并采用QUICK格式。该计算模型边界条件与控制方程如下：

(1) 三维稳态湍流控制方程如下：

连续性方程

动量方程

能量方程

k方程

ε方程

式中：u_i为x_i方向上的平均速度分量；x_i为坐标；ρ为流体密度；P为平均压力；${\eta _{\rm{t}}} = \frac{{{c_{\rm{\mu }}}\rho {k^2}}}{\varepsilon }$为紊流黏性系数； k为湍流脉动动能；ε为流体脉动动能的耗散率；c₁、c₂、c_μ为经验系数；G_k为湍流动能的产生项。

(2) 边界条件

计算模型壳程进口为速度进口，给定进口温度、速度和湍流度，出口为压力出口。换热管束为恒壁温，壳程介质为水。固体壁面采用不可渗透，无滑移绝热边界条件。稳态不可压缩求解。本文进口流速为0.5~1.5 m·s^-1，温度为323 K。管壁温度为298 K。

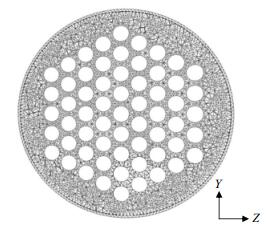
计算物理模型包括管壳、倾斜百叶折流板、换热管束等复杂结构，主体采用非结构化四面体网格，流体壳程进出口采用结构化网格。同时为保证计算准确可靠，精确捕捉换热管束和折流板处流动，在计算过程中对管壁和折流板处网格进行边界层自适应加密，截面网格如图 2所示。在划分网格确定尺寸时，本文建立了五套不同细密程度的网格以确定适用于计算的最优网格，网格数为：865937、1364075、1996600、2405828、2740513。进行网格独立性考核，计算结果如图 3所示。当相邻两套网格计算结果之间偏差小于1%时获得网格独立的解，综合考虑节省资源和计算准确性，拟采用第四套网格进行数值模拟计算。

图 2(Fig. 2)

图 2 网格截面图 Fig.2 Cross-section profile of the grid

图 3(Fig. 3)

图 3 网格独立性考核 Fig.3 Verification of grid independence

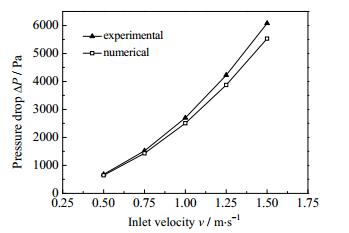
为验证本文模型和计算方法的可靠性，对具有相同几何参数的弓形折流板支撑多管束结构的换热器进行数值模拟，并采用Bell-Delaware法^[23]计算其压降，结果如图 4所示。计算表明：数值模拟压降随速度增大而增加，与实验经验公式结果所得趋势一致，由于实验经验公式所得到的压降时考虑了折流板、管束和管壳间漏流的影响，而数值模拟计算中部件紧密相连，使得实验公式计算结果小于模拟计算结果，两种结果偏差小于15%。数值模拟结果与公式计算结果相吻合，充分说明本文计算方法的可靠性。

图 4(Fig. 4)

图 4 模拟结果与实验数据对比 Fig.4 Comparison of experiment data and simulation results

图 5和图 6分别为弓形折流板支撑多管束及斜百叶片折流板支撑多管束受限外流中间截面流场图。图中模型，每组斜百叶折流片支撑结构由3片与换热管束轴线成60°夹角的百叶片组成，其宽度为100 mm，为了便于表示，采用“叶片个数—叶片宽度—叶片与轴线夹角”的形式表示该装配结构，即“3-100-60”。

图 5(Fig. 5)

图 5 弓形折流板支撑多管束受限外流流场纵剖图 Fig.5 Flow field of confined external flow within segmental baffle supported tube bundles

图 6(Fig. 6)

图 6 “3-100-60”百叶片支撑多管束受限外流流场纵剖图 Fig.6 Flow field of confined external flow within louver baffle supported tube bundles

从图 5可以看出，弓形折流板支撑多管束受限外流流动呈“Z”字形，其流场分布不均，流体流经折流板时，其流动方向发生突变，在缺口区流速较高，流体以较高速度横向冲刷换热管束；而当流体经过折流板后，在折流板背风面其流速大大降低，形成流动死区和回流区，这导致有效换热面积减小，流动阻力大大加大，从而使得泵功消耗增加。从图 6可以看出，对于新型斜百叶片折流板支撑多管束受限外流，与弓形折流板支撑多管束受限外流相比，其流场分布均匀，倾斜百叶片具有明显的导流作用，流速改变角度小；流体流经折流板组后分为多股流体流动，有效减小和消除了折流板背风面的流动死区，减小了流体由于横向阻挡和突然转向而产生的动能损失，使得其沿程阻力及折流板处的形体阻力均有所降低，进而减小其泵功消耗。

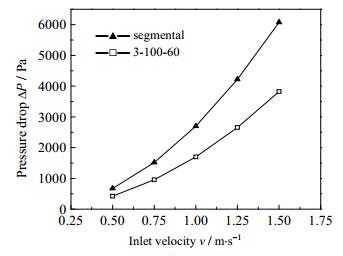
图 7为“3-100-60”结构的斜百叶片折流板支撑多管束和弓形折流板支撑多管束受限外流压降随入口流速的变化关系，入口流速为0.5~1.5 m·s^-1。可以看出，在相同入口流速下，斜百叶折流板支撑多管束受限外流压降远小于弓形折流板支撑多管束受限外流压降，在本文计算范围内，其压降与弓形折流板支撑多管束受限外流相比减小了36.9%~37%。主要原因在于斜百叶片折流板支撑多管束受限外流避免和减小了弓形折流板支撑多管束受限外流中流体的突然转向，折流板处的形体阻力大大降低，流体由横向冲击换热管改为斜向冲击，沿程阻力下降。为了更好说明和对比两种受限外流的优劣，相同压降下的传热系数比较如图 8所示。

图 7(Fig. 7)

图 7 压降随入口流速变化关系图 Fig.7 Pressure drop profiles as a function of inlet velocity

图 8(Fig. 8)

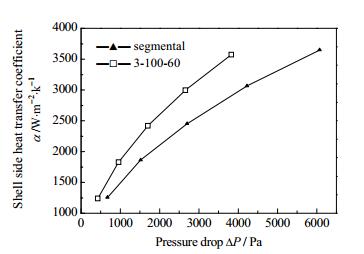
图 8 传热系数随压降变化关系 Fig.8 Profiles of heat transfer coefficient as a function of pressure drop

可以看出，在相同压降下斜百叶片折流板支撑多管束受限外流在相同压降下具有更高的传热系数，且压降越大其效果增强更为明显，与弓形折流板支撑多管束受限外流相比最大可提高22.7%。这也意味着在相同的泵功消耗下，与弓形折流板支撑多管束受限外流相比，斜百叶片折流板支撑多管束受限外流具有更高的传热效率，具有显著的节能效果。一方面，在相同压降下，斜百叶片折流板支撑多管束结构壳程流量大于弓形折流板支撑多管束结构，使得其平均流速高，换热管处换热边界层变薄，且斜百叶扰动作用明显，使得流速与温度梯度夹角较小，场协同作用明显，从而使得斜百叶片折流板支撑多管束受限外流综合性能优于弓形折流板支撑多管束受限外流。

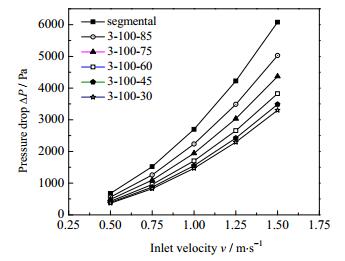
图 9为不同百叶片倾角下斜百叶折流板支撑多管束受限外流和弓形折流板支撑多管束受限外流压降随入口流速变化关系。可以看出，在相同进口流速下，斜百叶折流板支撑多管束受限外流压降均小于弓形折流板支撑多管束受限外流，并随叶片角度的增大而减小，且随角度减小其压降减小幅度变小。在本文研究角度范围内，较弓形折流板支撑多管束受限外流，压降最大可降低45.7%，最小可降低17.1%。在倾角较小时，两相邻两倾角的压降变化不大，当倾角小于60°时，相邻两角度的压降下降最小为5%。原因如下：随叶片倾角减小，两相邻叶片间流通截面积增加，有利于流体通过，使得折流板处形体阻力下降；同时叶片倾角减小，速度方向改变较小，动能损失下降；然而当叶片倾角较小时，改变倾角对叶片间的流通断面及流体流动方向影响减小。因此在角度较大时减小角度可显著减小阻力，而在角度较小时改变倾角对压降的影响变小。

图 9(Fig. 9)

图 9 压降随入口流速变化关系图 Fig.9 Pressure drop profiles as a function of inlet velocity

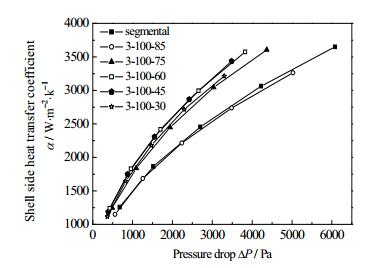
不同百叶片倾角下斜百叶折流板支撑多管束受限外流和弓形折流板支撑多管束受限外流相同压降下的传热系数如图 10所示。百叶片倾角大于45°时，斜百叶折流板支撑多管束受限外流相同压降下的传热系数随角度减小而增大；百叶片小于45°时，随角度减小而减小；当斜百叶折流板倾角达到85°时，相同压降下的传热系数与弓形折流板支撑多管束受限外流相近。对于相同压降斜百叶折流板支撑多管束受限外流，一方面，百叶片倾角越小其流动速度越大，换热管束表面扰动加强，其表面换热边界层变薄；但另一方面，百叶片倾角越小时折流板扰动作用减小，换热管局部表面换热边界层反而加厚，不同百叶片倾角下斜百叶折流板支撑多管束受限外流综合换热性能取决于两种作用的强弱。因此，其综合换热性能不随角度变化而单调变化在本文计算范围，百叶片倾角为45°时具有最优的综合性能，其相同压降下的传热系数最高，与弓形折流板支撑多管束受限外流相比可提高25.9%。

图 10(Fig. 10)

图 10 传热系数随压降变化关系图 Fig.10 Profiles of heat transfer coefficient as a function of pressure drop

提出一种新型斜百叶片支撑多管束结构，通过三维数值模拟对斜百叶片支撑多管束受限外流的传热和阻力性能进行了分析，主要结论如下：

(1) 斜百叶片支撑多管束受限外流流场分布均匀，与弓形折流板支撑多管束受限外流相比，倾斜叶片导流作用明显，其流场分布均匀，改善和减小了传统结构中的流动死区，提高了传热效率，大大降低了压降，从而降低了泵功消耗，具有显著节能效果。

(2) 本文研究范围内，倾斜叶片与管束轴线夹角越小其压降越小，与弓形折流板支撑多管束受限外流相比可减小17.1%~45.7%，但倾角度较小时改变角度对压降的影响程度变小。

(3) 相同压降下的传热系数不随角度单调变化，倾角大于45°时，随着角度减小，相同压降下传热热系数增大；倾角小于45°时，随角度减小，相同压降下传热系数下降；斜百叶片倾角为45°时具有最优的传热和阻力综合性能。传热系数较之弓形折流板支撑多管束受限外流可提高25.9%。