在化工生产工艺开发的早期阶段,需要评估工艺的风险信息,为确保评估过程在安全条件下进行,Regenass[1-2]设计开发了一种应用于实验室环境下的釜式反应量热系统,能够为反应风险评估、工艺开发与优化以及反应机理研究提供参考数据[3-4],是精细化工反应安全评估领域的重要科学仪器。
根据反应量热仪的工作原理,传热因子和系统热容是热安全评估的关键参数,一般需通过校正方法获取[5-6]。标准校正是目前应用最广泛的方法[7-8],依靠浸没在样品中的校正加热器输出已知功率完成传热因子的测量,并通过样品温度的阶跃变化来获取系统热容。由于这种方法要求测量过程中的反应体系长时间处于热平衡状态,因此花费时间较长,且样品前后的温度发生变化,可能会对化学过程产生干扰。Leveneur等[9]对标准校正方法进行改进,将传热因子和系统热容的测量步骤整合,提出一种更快速的校正方法,以下简称“快速校正方法”,通过减少校正方法步骤的方式提高了测量的效率。但是该方法是建立在校正过程中热散失程度不变的理论基础上,实际应用中的热散失应当随着样品与环境温度的变化而变化,忽略这点将会直接影响传热因子和系统热容的测量结果。
本文针对现有方法的弊端,提出一种功率振荡校正方法。主测量过程通过控制振荡周期的时间实现温度于基准状态下的短时小幅振荡,不需要长时间温度稳定的热平衡阶段,大大缩短了测量时间,短时且小幅变化的温度也降低了对反应过程的影响,并通过温度曲线反向对称区间测量值等效平均处理的方法降低热散失随温度变化对反应釜传热因子和系统热容测量的影响,最后通过实验验证了该方法的有效性。
2 理论 2.1 反应量热理论反应釜的热平衡分析是计算反应放热的依据[10-11],量热反应釜的结构及热量传递如图 1所示。
|
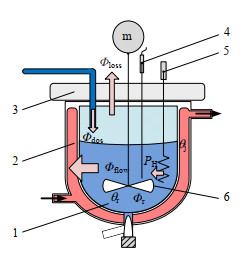
图 1 量热反应釜及其热量传递 Fig.1 Schematic diagram of the calorimetric reactor and heat transfer profile 1. sample 2. circulating oil 3. reactor cover 4. temperature sensor 5. calibration heater 6. stirrer |
样品1吸收的热流包括样品反应放热Φr、校正加热器5输出功率PH以及进料引起的热量效应Φdos。样品向外传递的热流包括由夹套循环油2带走的热量Φflow、反应釜内气相空间对流换热并经过反应釜盖3向外散失的热量Φloss。另外还包括反应釜随温度变化而产生热量累积率Φaccum,反应釜内热平衡方程为
| $ {\mathit{\Phi} _\rm{r}} + {P_\rm{H}} + {\mathit{\Phi} _{\rm{dos}}} = {\mathit{\Phi} _{\rm{accum}}} + {\mathit{\Phi} _{\rm{flow}}} + {\mathit{\Phi} _{\rm{loss}}} $ | (1) |
本研究提出的功率振荡校正方法处于无反应发生的稳定阶段内,即不涉及任何化学反应、加料等操作,故式(1)可简化为
| $ {P_\rm{H}} = {\mathit{\Phi} _{\rm{flow}}} + {\mathit{\Phi} _{\rm{accum}}} + {\mathit{\Phi} _{\rm{loss}}} $ | (2) |
式中:PH为校正加热器功率,W。
反应釜内样品与夹套内循环油之间传递的热量Φflow可表示为
| $ {\mathit{\Phi} _{{\rm{flow}}}} = UA({\theta _{\rm{r}}} - {\theta _{\rm{j}}}) $ | (3) |
式中:θr和θj分别为样品和夹套的温度,℃;UA为反应釜的传热因子,W·℃-1,其中U为传热系数,W·m-2·℃-1;A为热交换面积,m2。
反应釜的热累积Φaccum可表示为
| $ {\mathit{\Phi} _{\rm{accum}}} = {c_p}m \cdot \frac{{\rm{d}{\theta _r}}}{{{\rm{d}}t}} $ | (4) |
式中:cpm为样品及其内部的插入件,包括样品温度传感器4、搅拌桨6等总热容构成的系统热容,J·℃-1,其中cp为样品比定压热容,J·g-1·℃-1;m为系统的总质量,g;t为时间,min。
热散失Φloss与釜内对流条件及外界环境温度密切相关,关系可表示为
| $ {\mathit{\Phi} _{{\rm{loss}}}} = \alpha ({\theta _{\rm{r}}} - {\theta _\rm{a}}) $ | (5) |
式中:α为热散失系数,W·℃-1;θa为环境温度,℃。
由式(3)、(4)可知,夹套与样品间的UA及cpm是反应量热计算过程中的关键要素,准确性直接影响反应的热风险评估。
2.2 功率振荡式校正方法本文提出的功率振荡校正方法存在以下假设条件:
1) UA在各独立计算区间内近似不发生变化;
2) cpm在各独立计算区间内近似不发生变化。
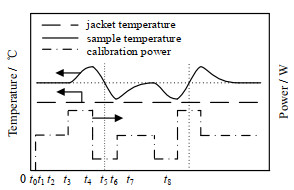
功率振荡校正方法的温度、功率控制策略如图 2所示。校正开始前(0~t0时刻),样品温度在校正功率和夹套油温共同作用下稳定在设定温度点,此时反应釜达到的热平衡状态称为基准状态。
|
图 2 功率振荡校正方法示意图 Fig.2 Scheme of the power oscillation calibration method |
基准状态下的热平衡方程为
| $ {P_\rm{H0}} = UA({\theta _\rm{r0}} - {\theta _\rm{j0}}){\rm{ + }}\alpha ({\theta _\rm{r0}} - {\theta _{\rm{a}}}) $ | (6) |
式中:PH0为基准状态下校正加热器功率,简称背景功率;θr0、θj0分别为基准状态下样品和夹套温度。
校正过程中固定夹套油温,控制校正加热器输出振荡功率使样品温度产生反向对称的两周期升降。由于校正过程中反应系统温度变化幅度较小,可视为处于准等温状态,散失的热量Φloss受温度振荡的影响较小,其变化暂不考虑。综上所述,当校正加热器进行振荡控制使样品偏离基准状态时,热平衡方程可简化为
| $ ({P_{{\rm{H0}}}} + \Delta {P_{\rm{H}}}) = {c_p}m\frac{{{\rm{d}}\Delta {\theta _{\rm{r}}}}}{{{\rm{d}}t}} + UA[({\theta _{{\rm{r0}}}} + \Delta {\theta _\rm{r}}) - ({\theta _\rm{j0}} + \Delta {\theta _{\rm{j}}})] $ | (7) |
式中:ΔPH为校正加热器偏离背景功率的量,W;Δθr和Δθj分别为样品和夹套温度偏离基准状态温度的量,℃。式(7)可简化为增量方程形式:
| $ \Delta {P_{\rm{H}}} = {c_p}m\frac{{{\rm{d}}\Delta {\theta _{\rm{r}}}}}{{{\rm{d}}t}} + UA(\Delta {\theta _{\rm{r}}} - \Delta {\theta _\rm{j}}) $ | (8) |
利用获得的样品、夹套温度及校正加热器功率数据,可进行UA的计算。式(7)的两侧在t0~t2、t2~t4、t4~t6、t6~t8阶段分别求积分。在这些阶段积分时,样品温度始末变化为0 ℃,因此系统热累积总量为0 J。
以t0~t2阶段为例,式(8)两侧同时积分的结果如式(9)所示:
| $ \int_{{t_0}}^{{t_{\rm{2}}}} {\Delta {P_{\rm{H}}}{\rm{d}}t} = {(UA)_1}\int_{{t_0}}^{{t_{\rm{2}}}} {(\Delta {\theta _{\rm{r}}} - } \Delta {\theta _\rm{j}}){\rm{d}}t $ | (9) |
式中:(UA)1为t0~t2阶段的等效传热因子,根据假设条件1),认为在积分阶段内(UA)1近似不变,且校正过程中夹套温度固定不变,即Δθj=0 ℃,由式(9)可得
| $ {(UA)_1} = \frac{{\int_{{t_0}}^{{t_2}} {\Delta {P_\rm{H}}{\rm{d}}t} }}{{\int_{{t_0}}^{{t_2}} {\Delta {\theta _\rm{r}}{\rm{d}}t} }} $ | (10) |
同理可分别求取t2~t4、t4~t6、t6~t8阶段的等效传热因子(UA)2、(UA)3和(UA)4。校正过程中,t0~t2阶段、t2~t4阶段分别与t4~t6阶段、t6~t8阶段的样品温度曲线相对于目标温度水平线反向对称,它们偏离基准状态的程度相同、方向相反,因此相互叠加的效果可近似抵消。采用上述4个阶段计算结果的平均值作为基准状态下目标温度点反应釜中样品与夹套间的传热因子:
| $ UA = \frac{1}{4}\sum\limits_{i{\rm{ = 1}}}^4 {{{(UA)}_i}} $ | (11) |
利用所求得的UA继续进行计算,式(8)的两侧分别在t0~t1、t1~t3、t3~t4、t4~t5、t5~t7、t7~t8阶段内求积分,以t0~t1阶段为例,积分结果如式(12)所示:
| $ \int_{{t_0}}^{{t_1}} {\Delta {P_{\rm{H}}}{\rm{d}}t} = {({c_p}m)_1}\int_{{t_0}}^{{t_1}} {{\rm{d}}\Delta {\theta _{\rm{r}}}} + \int_{{t_0}}^{{t_1}} {UA\Delta {\theta _{\rm{r}}}}{\rm{d}}t $ | (12) |
式中:(cpm)1为t0~t1阶段的等效热容,将式(11)代入(12),可得
| $ {({c_p}m)_1} = \frac{{\int_{{t_0}}^{{t_1}} {\Delta {P_{\rm{H}}}{\rm{d}}t - UA\int_{{t_0}}^{{t_1}} {\Delta {\theta _{\rm{r}}}} {\rm{d}}t} }}{{\int_{{t_0}}^{{t_1}} {{\rm{d}}\Delta {\theta _{\rm{r}}}} }} $ | (13) |
同理可求得t1~t3、t3~t4、t4~t5、t5~t7和t7~t8阶段的等效热容(cpm)2、(cpm)3、(cpm)4、(cpm)5和(cpm)6。校正过程中,t0~t1、t1~t3、t3~t4阶段分别与t4~t5、t5~t7、t7~t8阶段的样品温度曲线相对于目标温度水平线反向对称,它们偏离基准状态的程度相同、方向相反,因此相互叠加的效果也可近似抵消。采用上述6个阶段结果的平均值作为基准状态下目标温度点的系统热容:
| $ {c_p}m = \frac{1}{6}\sum\limits_{i{\rm{ = 1}}}^6 {{{({c_p}m)}_i}} $ | (14) |
功率振荡校正方法测量过程中采用样品温度小幅振荡的控制方法和反向对称区间多次等效测量值平均处理的方法,共同抑制了热散失随温度动态变化对UA和cpm结果的影响。
3 实验 3.1 实验材料与仪器 3.1.1 实验材料去离子水(H2O),纯度97%,密度1.00 g·mL-1,沸点100 ℃,CAS号:7732-18-5。二丙二醇(C6H14O3),纯度99%,密度为1.02 g·mL-1,沸点295 ℃,CAS号:110-98-5。2种物质均采购自阿拉丁试剂网。
3.1.2 实验仪器实验装置采用杭州仰仪科技有限公司研制的自动反应量热仪RC HP-1000A,实验装置见图 3。采用容积为1 L的夹套式玻璃釜,夹套进出口与外部的循环油浴连接,反应釜内的温度由夹套循环硅油控制。反应釜内插有最大功率为120 W的校正加热器、测温铂电阻及涡轮式磁力搅拌器,装置控温精度为±0.1 K,校正加热器功率分辨力为0.01 W。仪器由PC端上位机进行控制,数据的采样频率为1 Hz。

|
图 3 实验装置图 Fig.3 Pictures of the experimental device |
水是生活中常见的物质,用功率振荡校正方法实验测量了去离子水在不同温度、液位下的传热因子和比热容值,同时利用二丙二醇验证不同样品下的测量效果,并与现存2种校正方法进行对比。
以30 ℃温度点为例,3种校正方法的步骤设计如下:
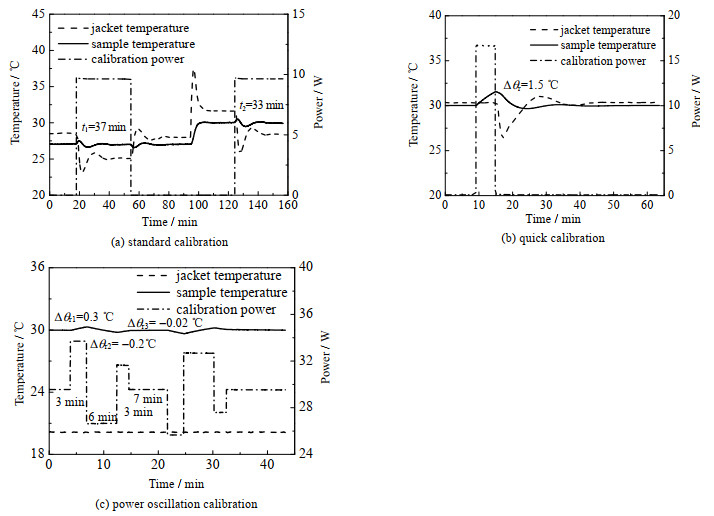
1) 标准校正方法:通过夹套油温将去离子水温度恒定在27 ℃,反应釜在该温度点下达到平衡状态后开启校正加热器,功率设定为10 W,向样品输出固定功率的同时维持样品温度不变,t1时间后关闭加热器,待反应釜恢复平衡状态后通过夹套油温提升样品温度至30 ℃,同样在达到新温度点的平衡状态后再次开启加热器,t2时间后关闭。其中加热器开启的时间为体系达到热平衡所花费的时间,2次开启的时间分别为t1=37 min和t2=33 min,实验曲线见图 4(a)。
|
图 4 去离子水实验曲线(30℃) Fig.4 Experimental results using deionized water as an example at 30 ℃ |
2) 快速校正方法:通过夹套油温将去离子水温度恒定在30 ℃,反应釜达到平衡状态后开启校正加热器,功率设定为17 W,向样品输出固定功率,并且维持夹套油温不变,样品温度上升Δθr=1.5 ℃后关闭校正加热器。
此处对快速校正方法之后的步骤进行改进,通过随样品温度变化的夹套油温控制策略,使样品温度更快地恢复至平衡状态,可进一步提升校正方法效率,同时不更改方法的计算原理,实验曲线见图 4(b)。
3) 功率振荡校正方法:通过夹套油温和校正加热器输出的30 W背景功率将去离子水的温度恒定在30 ℃,达到基准状态后固定夹套油温,开始主测量阶段。主测量分为2个周期,前半周期步骤为:t0~t1阶段内加热器输出偏离背景功率ΔPH1=4 W,样品温度偏离基准值Δθr1=0.3 ℃,时间为3 min;t1~t3阶段内输出偏离背景功率ΔPH2=-3 W,样品温度偏离基准值Δθr2=-0.2 ℃,时间为6 min。
为提高样品恢复速率改进了t3~t4阶段内的控制策略,将其划分为2个阶段:1)加热器输出偏离背景功率ΔPH3=2 W,直至样品偏离基准温度值Δθr3=-0.02 ℃,时间为3 min;2)功率更改为背景功率,等待样品温度恢复至基准状态,时间为7 min。控制策略改进后釜内并未引入其他热量,因此计算原理并不受影响。后半周期与前半周期输出功率及样品温度变化幅值关于基准状态反向对称,实验曲线见图 4(c)。
4 实验结果与讨论 4.1 去离子水实验取400 mL去离子水注入反应釜内,调整搅拌转速为400 r·min-1,利用实验平台进行不同温度下校正方法的对比实验,目标温度为30 ℃时3种方法的实测曲线如图 4所示。结果显示,样品温度对夹套油温变化的响应速度明显迟滞于加热器功率的变化。标准、快速和功率振荡校正方法测量实验花费时间分别为155、63、43 min,功率振荡校正方法效率要明显优于快速校正方法和标准校正方法。
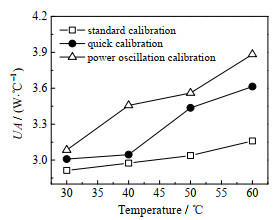
3种校正方法得到去离子水的UA随温度变化如图 5所示,UA都随着温度的增加而增大,表明样品在不同的温度下的物质属性发生了变化。相同温度点下的值有一定差别,是由于3种校正方法在实验过程中工况存在差异且等效UA与实际的UA也存在差别导致。
|
图 5 去离子水传热因子测量结果 Fig.5 Results of heat transfer factors of deionized water |
利用UA求取对应温度点下水的比热容值,由于系统热容无参考依据,本文以样品比热容作为测量的评判标准,具体结果见表 1,其中cp,sc、cp, qc和cp, poc分别为标准校正、快速校正以及功率振荡校正方法的比热容测量值。比热容测量值与文献值的相对误差(relative error,RE)计算如下:
| $ \rm{RE}{\rm{ = }}\frac{{{c_p} - {c_{p, {\rm{lit}}}}}}{{{c_{p, {\rm{lit}}}}}} \times 100\% $ | (15) |
式中:cp, lit为比热容文献值。REsc、REqc和REpoc分别为标准校正、快速校正以及功率振荡校正方法的相对误差。
|
|
表 1 不同温度下去离子水比热容测量结果 Table 1 Results of specific heat capacity of deionized water at different temperatures |
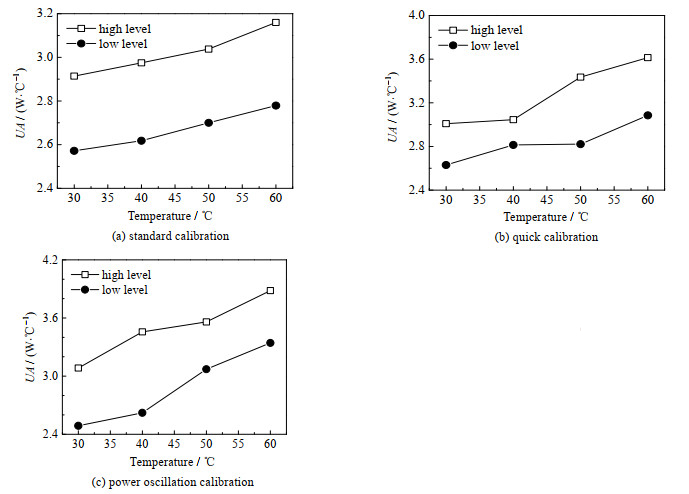
为研究液位对校正方法的影响,不更改其他实验条件,取300 mL去离子水注入反应釜内,再次进行对比实验。3种校正方法不同液位下的UA结果如图 6所示。在相同的温度条件下,液位越高,样品与夹套间的A越大,UA也越大。
|
图 6 3种校正方法传热因子-温度-液位关系 Fig.6 Relationship between heat transfer factor, temperature, and liquid level when using three calibration methods |
不同液位下的比热容测量结果见表 2,其中,cp, hl、cp, ll分别为高、低液位的比热容测量值,REhl、REll分别为高、低液位比热容测量值与文献值的相对误差。
|
|
表 2 不同液位下去离子水比热容测量结果 Table 2 Results of specific heat capacity of deionized water at different fluid levels |
为对比各方法的测量效果,分别计算平均相对误差(mean relative error,MRE),如下:
| $ {\rm{MRE}}{\rm{ = }}\frac{{\rm{1}}}{N}{\sum\nolimits_{i = 1}^N {\rm{RE}} _i} $ | (16) |
结果显示,功率振荡校正测量结果的MREpoc=-4.71%与标准校正的MREsc=-5.35%、快速校正的MREqc=-6.17%相差不大。
为评价实验结果的重复性,分别计算各方法相对误差的标准差(standard deviation, SD),如下:
| $ {\rm{SD}}{\rm{ = }}\sqrt {\frac{{\rm{1}}}{N}\sum\nolimits_{i = 1}^N {{({{\rm{RE}}_i} - {\rm{MRE}})}^2}} $ | (17) |
SD计算结果显示3种校正方法测量相对误差的离散程度也近似相等。
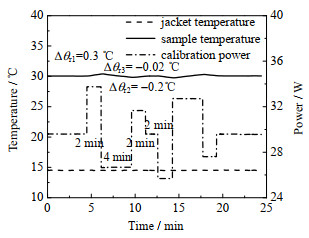
4.2 二丙二醇实验二丙二醇的黏度与导热性等属性与去离子水有较大差异,比热容随温度变化较为明显。因此将功率振荡校正方法应用于样品二丙二醇的测量。实验方法与去离子水保持一致,曲线如图 7所示。
|
图 7 二丙二醇功率振荡校正实验曲线(30℃) Fig.7 Results of power oscillation calibration using dipropylene glycol as an example at 30 ℃ |
由于醇类液体的热导率大于液态水,因此传热的效率也较高,校正操作共花费时间约为25 min,与去离子水实验相比减少了18 min。该现象在另外2种校正方法实验中得以验证。
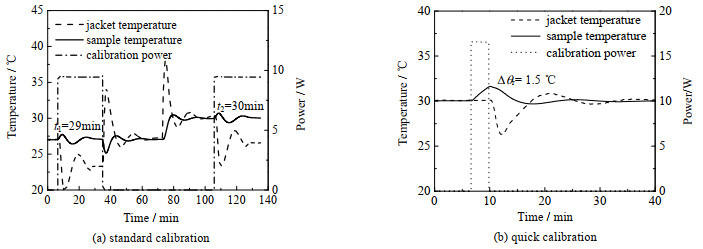
标准校正与快速校正方法所花费时间也同样减少了19和20 min,花费时间分别为136和43 min,实验曲线如图 8所示。
|
图 8 二丙二醇现存校正方法实验曲线(30 ℃) Fig.8 Results of traditional calibration methods on dipropylene glycol at 30 ℃ |
二丙二醇测量实验再次验证了功率振荡式校正的效率要高于标准校正方法与快速校正方法。
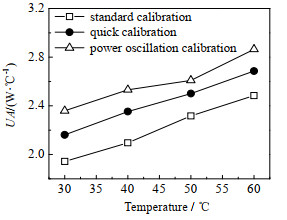
二丙二醇的UA测量结果如图 9所示。UA同样随着温度的增加而增大,但整体小于去离子水。由于醇类液体在此温度段的黏度要大于液态水,相同转速条件下引起的漩涡小,因此与夹套间的A较小,导致UA整体偏低。
|
图 9 二丙二醇传热因子测量结果 Fig.9 Results of heat transfer factors of dipropylene glycol |
分别使用3种校正方法对二丙二醇比热容进行测量,结果见表 3。结果显示,功率振荡校正方法测量结果的平均相对误差MREpoc=-5.69%与标准校正的MREsc=-5.03%、快速校正的MREqc=-7.21%也较为接近。
|
|
表 3 不同温度下二丙二醇比热容测量结果 Table 3 Results of specific heat capacity of dipropylene glycol at different temperatures |
综合去离子水实验结果可知,功率振荡校正方法的测量精度不低于现有的2种方法,但测量效率最高。
除此之外,根据Andersen[14-15]对功率补偿反应量热法的研究,功率补偿法是通过改变反应釜内校正加热器输出的功率来控制样品温度,样品与夹套在功率作用下始终维持一个固定的温差,样品的升降温通过功率的增减来实现,反应放热可直接根据加热器功率的变化量得到。不过功率补偿法仍需通过在反应开始前设计额外的校正方法步骤来获取UA及cpm。本文提出的功率振荡校正方法很好地贴合了功率补偿原理,可进一步完善功率补偿反应量热方法。
5 结论(1) 本研究提出一种应用于反应量热仪的功率振荡校正方法,通过校正加热器功率振荡周期控制使样品温度产生反向两周期的升降,结合多个温度对称区间的等效平均测量结果求取反应釜的UA及cpm。
(2) 去离子水和二丙二醇测量实验的结果显示,功率振荡校正方法测量精度与标准校正方法、快速校正方法基本相当,但功率振荡校正方法的效率要高于另外2种方法。
(3) 功率振荡校正方法采用小幅的功率及温度振荡的方式,为保证前后的基准状态不发生改变,对校正加热器功率精度以及反应釜控温精度有较高的要求。
(4) 采用功率振荡校正方法可快速获取釜内反应过程安全参数,为反应工艺的安全评估提供参考数据。
| [1] |
REGENASS W. Thermal and kinetic design data from a bench-scale heatflow calorimeter[J]. Chemical Reaction Engine ering-Houston, 1978, 65: 37-49. |
| [2] |
REGENASSW. The development of stirred-tank heat flow calorimetry:as a tool for process optimization and process safety[J]. Chimia, 1997, 51(5): 189-200. |
| [3] |
常佩, 周诚, 王伯周, 等. 二种NTO合成工艺的安全性分析[J]. 高校化学工程学报, 2018, 32(5): 1223-1227. CHANG P, ZHOU C, WANG B Z, et al. Safety analysis of two NTO synthesis processes[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(5): 1223-1227. DOI:10.3969/j.issn.1003-9015.2018.05.031 |
| [4] |
高宇鹏, 陈丽珍, 王建龙, 等. 反应量热仪在线探究硝酸硝解乌洛托品反应过程[J]. 科学技术与工程, 2017, 17(17): 288-291. GAO Y P, CHEN L Z, WANG J L, et al. The exploration of the reaction process of nitrifying methenamine by reaction calorimeter[J]. Science Technology and Engineering, 2017, 17(17): 288-291. DOI:10.3969/j.issn.1671-1815.2017.17.044 |
| [5] |
LANDAU R N, BLACKMOND D G. Scale up heat transfer based on reaction calorimetry[J]. Chemical Engineering Progress, 1994, 90(11): 43-48. |
| [6] |
RICHNER G, NEUHOLD Y M, PAPADOKONSTANTAKIS S, et al. Temperature oscillation calorimetry for the determination of the heat capacity in a small-scale reactor[J]. Chemical Engineering Science, 2008, 63(14): 3755-3765. DOI:10.1016/j.ces.2008.04.048 |
| [7] |
LANDAU R N, BLACKMOND D G, TUNG H H. Calorimetric investigation of an exothermic reaction:Kinetic and heat flow modeling[J]. Industrial & Engineering Chemistry Research, 1994, 33(4): 814-820. |
| [8] |
KUMPINSKY E. A method to determine heat-transfer coefficients in a heat-flow reaction calorimeter[J]. Thermochimica Acta, 1996, 289(2): 351-366. DOI:10.1016/S0040-6031(96)03007-9 |
| [9] |
LEVENEUR S, THÖNES M, HÉBERT J P, et al. From kinetic study to thermal safety assessment:application to peroxyformic acid synthesis[J]. Industrial & Engineering Chemistry Research, 2012, 51(43): 13999-14007. |
| [10] |
ZOGG A, STOESSEL F, FISCHER U, et al. Isothermal reaction calorimetry as a tool for kinetic analysis[J]. Thermochimica Acta, 2004, 419(1): 1-17. |
| [11] |
CREVATIN A, MASCARELLO F, LEUTHE B, et al. Kinetic investigations of a ketonization reaction using reaction calorimetry[J]. Industrial & Engineering Chemistry Research, 1999, 38(12): 4629-4633. |
| [12] |
刘光启, 马连湘, 刘杰. 化学化工物性数据手册·无机卷[M]. 北京: 化学工业出版社, 2013: 20-23. LIU G Q, MA L X, LIU J. Data handbook of physical and chemical properties of chemical engineering·inorganic volume[M]. Beijing: Chemical Industry Press, 2013: 20-23. |
| [13] |
刘光启, 马连湘, 刘杰. 化学化工物性数据手册·有机卷[M]. 北京: 化学工业出版社, 2013: 600-603. LIU G Q, MA L X, LIU J. Data handbook of physical and chemical properties of chemical engineering·organic volume[M]. Beijing: Chemical Industry Press, 2013: 600-603. |
| [14] |
ANDERSEN H M. Isothermal kinetic calorimeter applied to emulsion polymerization[J]. Journal of Polymer Science Part A-1 Polymer Chemistry, 1966, 4(4): 783-791. DOI:10.1002/pol.1966.150040405 |
| [15] |
ANDERSEN H M. Polymerization rates by calorimetry Ⅰ and Ⅱ[J]. Journal of Polymer Science Part A-1 Polymer Chemistry, 1969, 7(10): 2889-2896. DOI:10.1002/pol.1969.150071012 |




