扩展功能
文章信息
- 潘鹏程, 王红倩
- PAN Peng-cheng, WANG Hong-qian
- 基于直觉模糊集的公路PPP项目物有所值评价
- Evaluation of VFM of PPP Project Based on Intuitionistic Fuzzy Set
- 公路交通科技, 2018, 35(5): 142-150
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(5): 142-150
- 10.3969/j.issn.1002-0268.2018.05.019
-
文章历史
- 收稿日期: 2017-05-02
PPP模式是指政府部门与社会私营部门建立伙伴关系来提供公共产品或服务,该模式可以解决政府资金短缺的问题,提高项目效率,近两年在我国得到了大力的推广。但是并不是所有的项目都适合以PPP模式开展,物有所值(VFM)是国际通行的PPP项目评估标准,其核心意义在于评价PPP项目的效率能否高于传统经营模式。自2014年以来,PPP模式在我国得到了迅速的发展,根据财政部政府与社会资本合作中心2016年第3季度分析报告,公路类PPP项目发展迅速,新增投资额86.7%,投资总额占比24.4%。所以科学地选择公路PPP项目的实施模式是十分必要的。
公路基础设施PPP项目具有准公共产品特性,产生经济效益的同时具有社会效益[1],能带动经济发展、方便使用者出行、促进社会发展和减少环境污染。但因其投资规模大、资金回收期长、政府财政紧缺,公共部门很难在短时间内提供公路交通基础设施所需大量资金。通过PPP模式引入资金,缓解财政压力,使公路交通设施尽早实施满足公众需求。公路项目越早投入运营,公众就会越早享受其带来的社会效益,获得社会效益的时间价值。因此在VFM评价中, 应适当考虑项目采用PPP模式提前建设所带来的社会效益。
VFM评价是PPP项目前期决策的核心,用来判断是否采用PPP模式代替传统采购模式提供基础设施或公共服务。我国引入PPP模式较晚,VFM评价相对落后,VFM评价程序和方法尚不完善[2]。一些专家学者做了一些有益的探索,如刘雪婷等[3]构建了专门针对城市地下综合管廊PPP项目的VFM评价模型,指出可以考虑把PSC扩展成为包含外部性的评价。张家诚[4]引入不确定性分析,将PPP项目VFM评价从传统的确定性的点决策推向分布区间决策。吴洪樾等[5]指出我国VFM评价指标内容不完善,缺乏社会效益、环境政策等外部指标。尹超[6]在非自偿性PPP项目决策机制中建立了外部性效益评价指标。杜静等[7]以财政部VFM指引为基础设置了VFM评价指标、权重及评分标准, 并以北京地铁四号线为例进行了分析和讨论。罗涛等[8]构建了VFM评价指标体系,采用改进层次分析法确定指标权重,结合异权重专家打分法修正指标得分,对项目进行了评价。上述研究表明学者们普遍意识到需要依据项目具体类型调整和丰富VFM评价指标和内容。然而在评价过程中,由于专家主观思维的模糊性、不确定性和客观情况的复杂性,VFM评价时往往具有模糊性。直觉模糊集理论多用于项目的决策中,该种评价方法相对客观,使方案的选择更加接近实际。如夏英[9]建立了模糊多属性群决策的基本模型,使得决策更加贴近客观实际。孟俊娜[10]从城镇可持续发展的4个方面建立了专家评价信息模糊的最优权重计算方法,以确定最优方案。徐泽水[11]研究了决策者对方案有偏好的直觉模糊多属性决策问题,并通过案例进行了有效说明。S. T. Ng等[12]引入了模糊的多元目标决策模型在多种组合方案中选择最优。D. F. Li[13]提出的直觉模糊集对犹豫度进行了有效的数学表达,被广泛用来解决多属性决策。VFM评价需在多指标下对PPP模式和传统采购模式进行比较,其本质为多属性决策问题。
基于此,本研究在相关文献的梳理上,建立考虑综合社会效益的公路交通基础设施项目VFM评价指标体系,同时引入直觉模糊集理论,构建考虑公路项目社会效益的基于直觉模糊集的PPP项目VFM评价模型,并以实际案例验证该模型的可行性。
1 直觉模糊理论适用性分析VFM评价的关键在于有效评价方法的建立,只有在评价方法科学合理的前提下,才能够选择出公路交通基础设施项目最合适的实施模式。目前,我国的基础设施项目的VFM评价参照《PPP物有所值评价指引(试行)》的有关规定,使用专家赋权的方式确定评价指标的权重,将专家打分的算术平均值作为指标得分,忽略了专家差异,也未考虑项目的差异,可能造成评价结果与实际出现差异。在实际操作中需寻求一种能够依据项目具体情况客观地确定专家权重和指标权重的方法。因此本研究考虑将直觉模糊集理论引入VFM评价中。此方法具有以下优点:
(1) 针对专家在VFM评价中存在评价信息的不确定性、模糊性和决策过程中的犹豫度问题,引入直觉模糊多属性决策理论,解决以往的评价方法中专家决策信息存在犹豫度不能表达的问题,尽量完整地保存专家评分信息,以使专家评价结果尽量客观。
(2) 实际上VFM评价专家由于其知识结构、经验阅历和社会地位的不同,在专家评价中重要性程度也并不是完全相同的。专家权重的不同主要体现为专家内在的经验和专业能力,这属于内在特质,其判断具有一定的难度,在VFM评价的以往研究中少有提及。本研究引入直觉模糊集理论,依据专家评价的直觉模糊矩阵运用直觉模糊熵和直觉模糊加权平均算子IFWA计算专家权重,此种专家权重的确定方法较为客观,改进了以往赋权的主观性问题,并且专家权重依据具体项目的不同随之改变,使专家权重的确定更符合实际情况。
(3) 对于VFM评价的指标权重问题,在实际操作中和学术界都有一致的认识,也都考虑了指标权重的确定问题,但是往往在某一类型项目的VFM评价指标权重确定后很少依据具体项目调整,缺少针对性。本研究引入直觉模糊集理论,依据专家评价模糊矩阵,计算指标的权重,更能真实反映出不同项目中指标的重要程度和专家意见。此种方法的优点在于结合具体项目的特点,更客观地确定指标权重。
(4) 操作相对简单。传统评价方法中分别采用专家打分确定评价指标权重和专家权重,然后再依据专家的评价信息对方案作出决策。而直觉模糊的方法依据一次专家评价信息矩阵同时解决评价指标权重、专家权重和项目决策问题。该种评价方法较为便捷、可操作性更强。
2 VFM评价指标体系构建公路交通基础设施项目的建设,会使周边地区的居民、环境、经济和社会受到影响,而这种影响最终将转化成经济方面的影响,形成社会效益。很多学者已经对公路交通基础设施项目的综合社会效益进行了研究,考虑到社会效益评价指标的全面性和实用性,本研究采用陆建的评价指标体系,采用交通功能指标、社会经济适应性指标、环境影响指标和资源利用指标对公路项目的总体社会效益进行评价[14]。
依据《PPP物有所值评价指引(试行)》的规定,PPP项目的VFM评价指标包括6项基本评价指标和6项补充指标。本研究结合上述指标将其细化,并添加社会效益评价指标,建立VFM评价指标体系,见表 1。
| 一级指标 | 二级指标 | 评价内容 |
| 全生命周期整合程度 | 整合潜力 | 项目的设计、投融资、建设和运营维护等所有环节能否有机整合 |
| 全生命周期成本 | 市场主体能否统筹利用其承担的多个项目取得规模效应 | |
| 全生命周期效率 | 项目实施能否有效降低全生命周期的总成本 | |
| 风险识别与分配 | 风险识别 | 风险要素是否进行全面识别 |
| 风险分配 | 风险是否由政府和社会资本之间进行合理分配 | |
| 风险应对与管理 | 风险能否进行有效管理 | |
| 绩效导向与鼓励创新 | 产出绩效 | 产品/服务价格是否合理、能否调整,产品/服务的数量和质量能否与需求很好地匹配 |
| 鼓励创新 | 项目是否具有创新空间和创新能力 | |
| 潜在竞争程度 | 竞争积极性 | 能否引起市场主体广泛参与兴趣 |
| 竞争公平性 | 参与主体之间能否展开公平竞争 | |
| 政府机构能力 | 治理能力 | 能否促进政府转变职能,提高治理能力 |
| 监管能力 | 政府能否对项目进行有效监督 | |
| 履约能力 | 政府对项目的履约是否有保障 | |
| 可融资性 | 融资可行性 | 项目融资是否具备可行性,项目对金融机构(贷款和债券市场)的吸引力 |
| 补充指标 | 项目规模大小 | 项目的投资额或资产价值 |
| 预期使用寿命长短 | 项目的资产预期使用寿命 | |
| 主要固定资产种类 | PPP项目包含的资产种类 | |
| 全生命周期成本测算准确性 | 全生命周期成本(建设成本、运营成本、风险成本)被准确预估的可能性 | |
| 运营收入增长潜力 | 项目运营期收入增长可能性及程度 | |
| 行业示范性 | 项目实施是否符合法律和政策的要求,是否具有行业示范价值 | |
| 社会效益 | 交通功能效益 | 交通基础设施对居民交通需求的满足程度以及交通网络运行质量状况 |
| 社会经济适应性 | 从土地利用、交通投资、交通出行和交通安全4个方面反映社会经济与交通发展的协调性 | |
| 环境影响 | 交通系统对环境资源的影响程度以及交通-环境的协调性 | |
| 资源利用 | 空间资源消耗、交通时空资源消耗和能源消耗等方面 |
3 直觉模糊集的理论与算法研究 3.1 直接模糊集理论的概念
传统的模糊集所表达的信息并不全面,仅能表示肯定的程度,Atanassov[15]给出了直觉模糊集的概念,它包含肯定、否定和不确定的程度3方面信息,所表达的信息更加全面、详细。
定义1[15]:直觉模糊群的概念
设X为一个非空集合,其中的任意一个元素用x表示,A={[x, μA(x), vA(x)]|x∈X}为X的直觉模糊集,其中μA(x)和vA(x)分别表示元素x属于A的隶属度和非隶属度,可以表达为μA: X→[0, 1],x∈X→μA(x)∈[0, 1],vA:X→[0, 1],x∈X→vA(x)∈[0, 1]且同时满足0≤μA(x)+vA(x)≤1,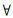
由此可见,元素x属于模糊集合A的程度由一组数字(μα(x), να(x))决定,显然α=(0, 1)为最小的直觉模糊值,α=(1, 0)为最大的直觉模糊集。
定义2[15]:直觉模糊群的运算
设α=(μα, να),β=(μβ, νβ)为直觉模糊数,则有如下运算:
(1) α=(vα, μα),
(2) α×β=(μα+μβ-μαμβ, vαvβ),
(3) λα=(1-(1-μα)λ, vαλ),λ>0, 其中λ为任意系数。
(4) α×β=(μαμβ, vα+vβ-vαvβ),
(5) αλ=(μαλ, (1-(1-vα)λ), λ>0。
验算可知这些运算在直觉模糊集的基础上具有封闭性,即获得的结果还是直觉模糊集。
定义3[16]:直觉模糊加权平均算子(IFWA)
设αj=(μαj, vαj)(j=1, 2, …, n)表示一组直觉模糊数,由直觉模糊加权平均算子得到的集成值也同样是直觉模糊数。且设IFWA:Ωn→Ω(表示含有n个元素的集合Ω),则:
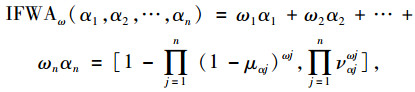
|
(1) |
式中,ω=(ω1, ω2, …, ωn)T为αj(j=1, 2, …, n)的权重向量,ωj∈[0, 1](j=1, 2, …, n),
定义4[17]:直觉模糊熵
已知U={x1, x2, …, xn},A=
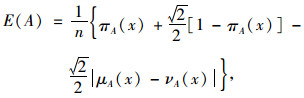
|
(2) |
则称E(A)为直觉模糊熵,μA(x),vA(x),πA(x)分别表示直觉模糊集A的隶属度、非隶属度和犹豫度,其中πA=1-μA(x)-vA(x)。
定义5[18]:直觉模糊数的得分函数
直觉模糊数的得分函数可以较好地反应直觉模糊数的大小,设α=(μα, να)为直觉模糊值,其中(μα, να)为直觉模糊数。则记分函数为:
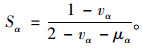
|
(3) |
定义6[19]:得分函数大小比较
设α=(μα, να)和β=(μβ, νβ)为两个直觉模糊值,Sα和Sβ分别为α和β的得分函数,若Sα>Sβ,则称α>β。
3.2 基于直觉模糊集的VFM评价算法(1) 问题描述
针对公路PPP项目VFM评价指标权重未知和评审专家权重未知的情况,运用直觉模糊信息集来解决其VFM评价问题。首先,通过专家评价,建立专家评价信息矩阵,利用直觉模糊熵和加权模糊熵,计算VFM评价指标体系的权重和评审专家权重。其次,通过直觉模糊加权平均算子IFWA集结不同专家给出的评价信息,运用记分函数对评价信息进行模糊化处理,建立记分矩阵,从而得到各个方案的综合得分。
假设某项目有m个实施方案组成的集合为M={m1, m2, …, mm},s个专家组成集合E={E1, E2, …, Es},专家的权重为ζ={ζ1, ζ2, …, ζs}T,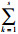
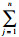
(2) 评价模型的计算步骤
在考虑公路项目社会效益的基础上,结合我国目前VFM评价指标体系,利用评审专家组的经验,进行PPP项目的VFM评价。VFM评价程序如图 1所示。
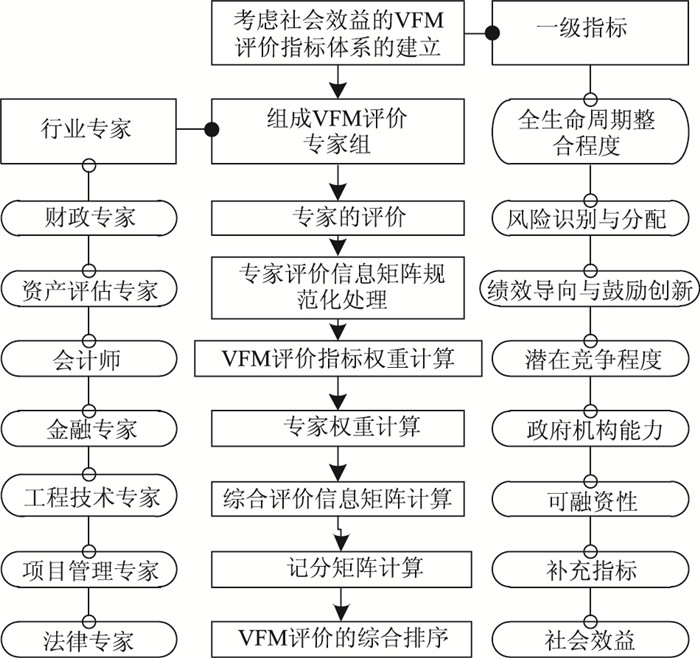
|
| 图 1 VFM评价程序 Fig. 1 VFM assessment program |
| |
步骤1:建立考虑社会效益的VFM评价指标体系。因项目类型不同,所建立的指标体系具有一定差别,本研究建立的公路项目VFM评价指标见表 1。
步骤2:组成VFM评价专家小组。该地区的财政部门(咨询机构)邀请s位资深专家,组成VFM评价专家小组。s位专家需包括财政专家、资产评估专家、注册会计师、金融专家、工程技术专家、项目管理专家、法律等方面专家,且为单数。
步骤3:专家评价。s位专家在熟悉了项目的基本情况、实施方案、财务测算以后,依据VFM评价指标体系分别对PPP模式和传统模式的实施方案进行评价。专家评价的直觉模糊矩阵如下:
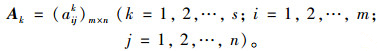
|
(4) |
第k个专家对m个实施方案在n个评价指标体系下的评价为:
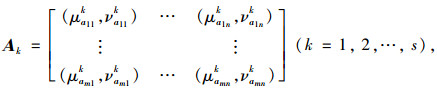
|
(5) |
则称Ak为专家评价的直觉模糊矩阵,式中aijk=(μaijk, νaijk)为专家Ek针对第j个指标对方案Mi评价的直觉模糊数。
步骤4:专家评价信息矩阵规范化。评价指标分为正向指标和负向指标两类,正向指标方案对其隶属度越大越好,负向指标方案对其隶属度越小越好,因此在对方案进行综合评价排序前,将两类指标进行规范化,将直觉模糊决策矩阵Ak=(αijk)m×n转化成正规范化矩阵Rk=(rijk)m×n(k=1, 2, …, s; i=1, 2, …m; j=1, 2, …, n)[20]。
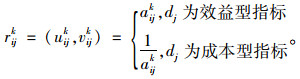
|
(6) |
第k个专家对m个实施方案在n个评价指标体系下的评价矩阵规范化后为:
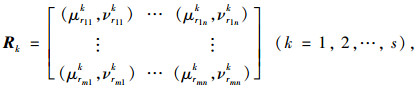
|
(7) |
则称Rk为规范化后的专家评价的直觉模糊矩阵,式中rijk=(μkrij, νrijk)为规范化后专家Ek针对第j个指标对方案Mi评价的直觉模糊数。
步骤5:计算评价指标权重。根据直觉模糊熵的定义,计算方案Dj在指标Mi下的熵值[21]:
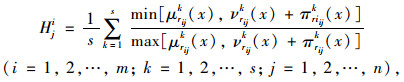
|
(8) |
式中,Hji为直觉模糊熵值;(μrijk(x), νrijk(x))为直觉模糊数; πrijk(x)=1-μrijk(x)-vrijk(x)。
依据式(8)可得指标的熵值矩阵:
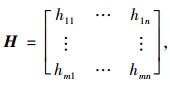
|
(9) |
则称H为直觉模糊熵矩阵,其中hij为直觉模糊熵值。
根据熵值的定义可以看出,数据中信息量越大,不确定性就越小,熵值也越小;相反熵值就越大,因此指标体系Dj的熵权可以表示为[20]:
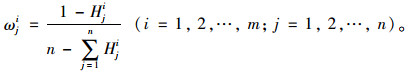
|
(10) |
依据式(10),方案Mi的权重矩阵为:
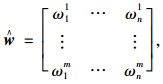
|
(11) |
式中,ŵ为直觉模糊熵权重矩阵;ωji为指标Dj方案Mi对应的熵权。
优化权重矩阵,得到VFM评价指标全局最优权重[21]:
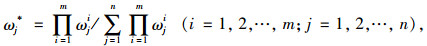
|
(12) |
式中ωj*为评价指标Dj的全局最优权重。
最终所得的VFM评价指标体系的权重向量为:
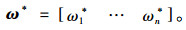
|
(13) |
步骤6:计算专家权重。专家权重表示为ξk(k=1, 2, …, 7), 专家的权重取决于专家判断信息的可靠性和确定性程度。专家提供的判断信息越模糊越不确定,说明专家对决策对象的了解程度相对较少,则赋予较小权重;反之,则赋予较大权重。
根据彭芳艳等基于不确定性和未知度的直觉模糊熵,第k个专家在第j个指标下给出的模糊熵为[17]:
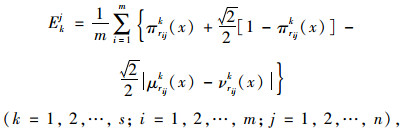
|
(14) |
式中Emj为对应的直觉模糊熵。
依据式(14)构造模糊熵矩阵:
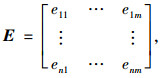
|
(15) |
则E为所构造模糊熵矩阵,eji为直觉模糊熵值。
将模糊熵矩阵与VFM指标权重向量集结计算加权模糊熵为[22]:
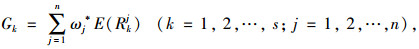
|
(16) |
式中,Gk为加权模糊熵;ω*为VFM评价指标体系的权重向量;E(Rkj)为第k个专家的直觉模糊熵值。
依据式(16)得到的加权模糊熵矩阵为:
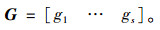
|
(17) |
利用加权模糊熵矩阵计算专家的权重[22]:
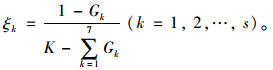
|
(18) |
专家的权重矩阵为ζ=[ζ1, ζ2, …, ζs]。其中ζk为第k位专家的权重。
步骤7:运用直觉模糊加权平均算子IFWA将专家评价信息矩阵Rk与对应的专家权重矩阵进行集结,得到综合评价信息矩阵T[10]:
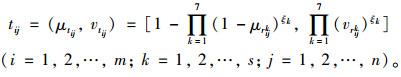
|
(19) |
依据式(19)得到的综合评价信息矩阵如下:
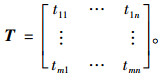
|
(20) |
步骤8:直觉模糊数的得分能够较好地反映直觉模糊数的大小,依据前人结论给出直觉模糊决策矩阵的得分矩阵,将直觉模糊矩阵T转换成记分矩阵[18]:
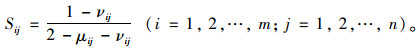
|
(21) |
利用式(20)得到记分矩阵如下:

|
(22) |
步骤9:对VFM评价进行综合排序。将记分函数矩阵S和指标权重向量w进行集结,得到方案Mi的群评价综合得分[10]:
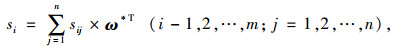
|
(23) |
式中ω*T为VFM指标权重向量ωT的转置。
根据上述综合得分的大小,比较si的大小,对方案的VFM评价结果进行综合排序,若sp>sq,则方案Mp优于方案Mq。
本研究使用专家评分信息的模糊性和不确定程度代替传统的专家决策信息的偏差程度,利用专家决策信息确定VFM评价指标权重和评审专家权重。不同于传统的权重方法,基于直觉模糊信息集成的计算权重是一种相对客观的赋权方法。
4 VFM评价案例分析某地区公路交通项目拟采用PPP模式进行VFM专家评审,判别是选择PPP模式还是传统模式实施。该项目具体的VFM决策系统可以表述为选取7名专家构成决策者集E={E1, E2, E3, E4, E5, E6, E7}对公路项目的两个实施模式M={M1, M2}进行VFM评价,其中M1代表PPP模式,M2代表传统模式。财政部门选取本研究所建立的VFM评价指标体系中8个一级指标生命周期整合程度d1、风险识别与分配d2、绩效导向与鼓励创新d3、潜在竞争程度d4、政府机构能力d5、可融资性d6、补充指标d7、社会效益d8作为评分标准D={d1, d2, d3, d4, d5, d6, d7, d8},具体的VFM评价程序如下。
(1) 邀请专家进行VFM评价
依据上述描述,该地区的财政部门(咨询机构)邀请7位资深专家组成评价小组。评审小组在熟悉了项目情况后,依据VFM评价指标体系分别对PPP模式和传统模式的实施方案进行评价。本研究VFM评价体系的7个指标均属于效益型指标,本案例中社会效益指标也为正,因此专家评价信息矩阵不需要规范化操作,即Ak=Rk,所建立的专家评价信息直接模糊矩阵如下:

|
(2) 根据步骤4和步骤5,利用式(6)~(13)计算VFM评价:
ω*=[0.191 1 0.076 9 0.061 7 0.043 3 0.147 5 0.157 6 0.157 6 0.164 2]。
(3) 根据步骤6,利用式(14)~(18)计算专家权重如下:
ξ=[0.140 7 0.124 4 0.149 7 0.157 7 0.141 0 0.133 5 0.153 0]
(4) 依据步骤7,利用式(19)~(20)将专家评价信息矩阵Rk与对应的专家权重矩阵ξ进行集结,得到综合评价信息矩阵T:

|
(5) 依据步骤8,利用记分函数(21)~(22)将直觉模糊矩阵T转换成记分矩阵:

|
(6) 依据步骤9,利用式(23)将记分函数矩阵S和指标权重向量w进行集结,得到方案Mi的群评价综合得分,对VFM评价进行综合排序:
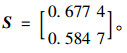
|
即sm1=0.677 4>sm2=0.584 7,方案M1优于方案M2表明专家针对VFM指标体系对PPP模式的评价较高,因此根据VFM评价结果应选择PPP模式实施项目。
5 结论目前PPP项目VFM评价中尚未考虑项目的社会效益,也没有考虑评价指标和评审专家的模糊性。本研究尝试将直觉模糊群决策模型应用于考虑社会效益的公路交通基础设施项目VFM评价中。利用前人对社会效益的分类,结合《PPP物有所值评价指引(试行)》中VFM评价的基本指标和补充指标,建立了公路交通基础设施项目的VFM评价指标体系,以期我国的VFM评价指标能够有所改进,更加完善。
将直觉模糊集理论引入公路基础设施项目VFM评价中,可以充分表达专家评价信息中的模糊性和犹豫度,还可以依据项目的具体情况较为客观地计算专家权重和评价指标的权重,综合专家评价信息矩阵,计算方案综合得分,以使评价结果更加接近实际。
在实际应用中, 专家评价的隶属度、非隶属度应该是一个区间范围,在今后的研究中应该充分考虑非平衡评价语言值,以及考虑区间直觉模糊决策环境下的区间模糊信息集算子,融合更多更全面的信息来解决VFM评价问题,以使我国的VFM评价更加贴近实际。
| [1] |
朱婉璐, 郑彭军, 黄正锋, 等. 考虑社会效益的高速公路PPP项目特许期研究[J]. 科技与管理, 2016, 18(4): 8-12. ZHU Wan-lu, ZHENG Peng-jun, HUANG Zheng-feng, et al. Determination of Concession Period for PPP Freeway Infrastructure Project Considering Social Benefits[J]. Science-Technology and Management, 2016, 18(4): 8-12. |
| [2] |
崔彩云, 王建平, 刘勇. 基础设施PPP项目物有所值(VFM)评价研究综述[J]. 土木工程与管理学报, 2016, 33(4): 57-62. CUI Cai-yun, WANG Jian-ping, LIU Yong. Literature Review on Value-for-money Assessment for PPP Project[J]. Journal of Civil Engineering and Management, 2016, 33(4): 57-62. |
| [3] |
刘雪婷, 李明顺. 地下综合管廊PPP项目物有所值定量评价模型的构建[J]. 价值工程, 2017(10): 27-29. LIU Xue-ting, LI Ming-shun. Quantitative Evaluation Model of the PPP Project in Pipe Gallery[J]. Value Engineering, 2017(10): 27-29. |
| [4] |
张家诚. 考虑不确定性的PPP项目物有所值定量评价研究[D]. 成都: 西南交通大学, 2016. ZHANG Jia-cheng. Research of Value for Money Quantitative Evaluation for PPP Project Based on Uncertainiy[D]. Chengdu: Southwest Jiaotong University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10613-1016168836.htm |
| [5] |
吴洪樾, 袁竞峰, 杜静. 国际PPP项目物有所值定性评价及对我国的启示[J]. 建筑经济, 2017, 38(3): 38-42. WU Hong-yue, YUAN Jing-feng, DU Jing. Qualitative Evaluation of Value for Money of International PPP Project and Enlightenment to China[J]. Construction Economy, 2017, 38(3): 38-42. |
| [6] |
伊超. 基于资金价值(VFM)的非自偿性PPP项目决策机制研究[D]. 济南: 山东建筑大学, 2014. YI Chao. Study on Decision-making Mechanism of Non-self Reimbursement PPP Projects Based on Value for Money[D]. Jinan: Shandong Jianzhu University, 2014. http://cdmd.cnki.com.cn/article/cdmd-10430-1015517097.htm |
| [7] |
杜静, 吴洪樾. 轨道交通PPP项目物有所值(VFM)定性评价研究:以北京地铁四号线为例[J]. 项目管理技术, 2016, 14(10): 19-25. DU Jing, WU Hong-yue. Analysis of VFM Quantitative Evaluation of Urban Rail Transit PPP Project:A Case Study of Beijing Metro Line 4[J]. Project Management Technology, 2016, 14(10): 19-25. |
| [8] |
罗涛, 李晓鹏, 汪伦焰, 等. 城市水生态PPP项目物有所值定性评价研究[J]. 人民黄河, 2017, 39(1): 87-91. LUO Tao, LI Xiao-peng, WANG Lun-yan, et al. Qualitative Evaluation for the VFM Research of Urban Water Ecological PPP Project[J]. Yellow River, 2017, 39(1): 87-91. |
| [9] |
夏英. 基于直觉模糊集的多属性群决策问题的模型及其方法研究[D]. 武汉: 武汉理工大学, 2006. XIA Ying. Study on Multi-attribute Group Decision-making Models and Methods Using Intuitionistic Fuzzy Set[D]. Wuhan: Wuhan Ligong University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10497-2006061757.htm |
| [10] |
孟俊娜, 房宁, 刘炳胜, 等. 基于直觉模糊集的城镇基础设施项目可持续性评价[J]. 模糊系统与数学, 2015, 29(1): 167-174. MENG Jun-na, FANG Ning, LIU Bing-sheng, et al. Sustainability Evaluation Model for Urban Infrastructure Projects Based on Intuitionistic Fuzzy Sets[J]. Fuzzy Systems and Mathematics, 2015, 29(1): 167-174. |
| [11] |
徐泽水. 直觉模糊偏好信息下的多属性决策途径[J]. 系统工程理论与实践, 2007, 27(11): 62-71. XU Ze-shui. Approaches to Multiple Attribute Decision Making with Intuitionistic Fuzzy Preference Information[J]. Systems Engineering-Theory & Practice, 2007, 27(11): 62-71. |
| [12] |
NG S T, XIE J, SKITMORE M, et al. A Fuzzy Simulation Model for Evaluating the Concession Items of Public-private Partnership Schemes[J]. Automation in Construction, 2007, 17(1): 22-29. |
| [13] |
LI D F. A Ratio Ranking Method of Triangular Intuitionistic Fuzzy Numbers and Its Application to MADM Problems[J]. Computers & Mathematics with Applications, 2010, 60(6): 1557-1570. |
| [14] |
陆建, 王炜. 面向可持续发展的城市交通系统综合评价方法研究[J]. 土木工程学报, 2004, 37(3): 99-104. LU Jian, WANG Wei. The Study of Urban Transportation System Sustained Development Evaluation Method[J]. China Civil Engineering Journal, 2004, 37(3): 99-104. |
| [15] |
ATANASSOV K T. Intuitionistic Fuzzy Sets[J]. Fuzzy Sets & Systems, 1989, 33(1): 37-45. |
| [16] |
ZESHUI X. Intuitionistic Fuzzy Aggregation Operators[J]. IEEE Transactions on Fuzzy Systems, 2007, 15(6): 1179-1187. |
| [17] |
彭芳艳, 梁家荣, 伍华健. Vague集模糊熵的新构造方法[J]. 计算机工程与应用, 2009, 45(29): 52-54. PENG Fang-yan, LIANG Jia-rong, WU Hua-jian. New Construction Method of Fuzzy Entropy of Vague Sets[J]. Computer Engineering and Applications, 2009, 45(29): 52-54. |
| [18] |
黎华, 王周敬. 基于直觉模糊集的多属性决策问题[J]. 昆明理工大学学报:自然科学版, 2008, 33(6): 109-112. LI Hua, WANG Zhou-jing. Multiattribute Decision Making Method Using Intuitionistic Fuzzy Sets[J]. Journal of Kunming University of Science and Technology:Science and Technology Edition, 2008, 33(6): 109-112. |
| [19] |
丁晓阳. 基于直觉模糊集的多属性群决策方法及其应用[D]. 海口: 海南师范大学, 2013. DING Xiao-yang. Multi-attribute Group Decision Making and Its Applications Based on Intuitionistic Fuzzy Sets[D]. Haikou: Hainan Normal University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-11658-1013327614.htm |
| [20] |
王毅, 雷英杰. 一种直觉模糊熵的构造方法[J]. 控制与决策, 2007, 22(12): 1390-1394. WANG Yi, LEI Ying-jie. A Technique for Constructing Intuitionistic Fuzzy Entropy[J]. Control and Decision, 2007, 22(12): 1390-1394. |
| [21] |
LIU B, HUO T, WANG X, et al. The Decision Model of the Intuitionistic Fuzzy Group Bid Evaluation for Urban Infrastructure Projects Considering Social Costs[J]. Canadian Journal of Civil Engineering, 2013, 40(3): 263-273. |
| [22] |
赵萌, 任嵘嵘, 邱菀华. 基于直觉模糊熵的专家权重确定方法及其验证[J]. 控制与决策, 2015, 30(7): 1233-1238. ZHAO Meng, REN Rong-rong, QIU Wan-hua. Experts' Weights Method and Computational Experiment Analysis Based on Intuitionistic Fuzzy Entropy Measures[J]. Control and Decision, 2015, 30(7): 1233-1238. |
 2018, Vol. 35
2018, Vol. 35
