扩展功能
文章信息
- 林丽, 冯辉
- LIN Li, FENG Hui
- 基于Ring-barrier相位的干线公交协调控制
- Coordination Control for Traffic on Arterial Based on Ring-barrier Phase
- 公路交通科技, 2018, 35(5): 128-134
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(5): 128-134
- 10.3969/j.issn.1002-0268.2018.05.017
-
文章历史
- 收稿日期: 2017-01-16
城市路网中,由于各交叉口相距较近且独立运行各自的信号配时方案使得车辆在行驶过程中通行不畅,在带来行车延误增加的同时也造成了城市日益拥堵,其中环境污染问题尤为突出。面对存在的问题,越来越多的交通研究者从信号控制的角度出发,结合干线通行提出了干线协调控制[1]。该方法通过将干线上一批相邻的交通信号统一于线控系统之中,并在确定的行驶速度与相位差的基础上使得干线车辆实现畅行的目的。相对于小汽车的发展,公交车在缓解城市问题上具有无可比拟的优势并能产生更好的正环境效应[2],因此,结合公交优先发展的背景,通过对干线公交车辆进行协调控制也是一种有效的优先策略。
国内外学者对干线公交协调控制已进行了一些研究,如:文献[3]引入公交专用相位并在确保干线上直行、左转公交车具有优先权的情况下,根据交叉口公交车辆的分布模式,通过寻找理想交叉口间距的方法来确定公交相序,结果表明该方法能够为直行、左转相位提供足够的绿波带宽,提高公交车辆运行效率,然而在面对干线交叉口饱和度较高或公交车流量较少的情况时,还需进一步考虑研究。针对上述情况,文献[4]分别从干线协调和公交优先角度提出了干线公交信号优化的两层优化方法,建立了公交优先的控制流程并充分考虑不同交通状态下(低峰、中峰、高峰)优先相位公交车流量的变化。通过仿真模拟表明,实施干线公交优先后,公交车辆延误和人均延误均得到显著降低。文献[5]针对多相位公交到达时的冲突问题,提出了就近原则进行公交优先排序,同时在各相位饱和度不超过0.95时,结合绿灯延长与绿灯提前启动两种方法进行优化算法建立。该策略不仅能很好地降低路网公交车辆的延误,还能有效限制其对社会车流的干扰。文献[6]提出了一种干线公交协调的优化模型,该模型能够有效地降低公交车辆的总延误,在提高车辆到达准点率的同时,最大限度地减少在不同交通需求条件下对其他社会车流量的干扰。
本研究基于Ring-barrier相位模式并结合干线公交协调控制理论,通过改进传统单环相位结构设计,提出有利于公交协调控制的专用相位设计,以公共周期信号、相位绿灯时间和相位差等参数分析为基础,建立相应的控制参数模型。为验证协调控制效果,结合实际案例,运用两种工具软件对模型方案进行算法的优化求解。
1 相位设置方法简介在信号周期变换的过程中,每个信号灯都会保持一段显示时间,而相位则是将这段连续的显示时间分配给道路上无冲突的组合车流并反映交叉口车辆运行状态的变化,相序则是表现相位运行顺序优先的排列[7]。
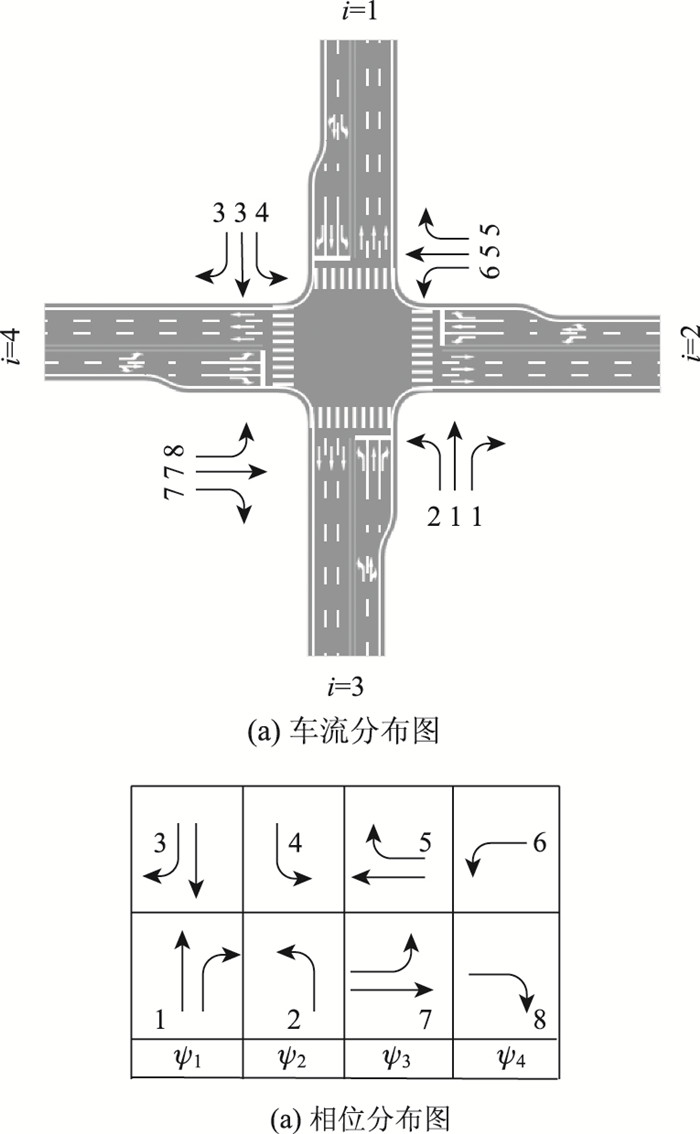
1.1 传统交叉口相位设置方法传统交叉口信号相位布局属于单环方式(Ring)且一般采用对称式设置,即:相对方向的互补车流采用同一相位进行设置。如图 1所示,1和3、2和4、5和7、6和8分别为各自的互补车流,ψj(j=1, 2, 3, 4)为每股互补车流所对应的相位。
|
| 图 1 传统交叉口布局形式 Fig. 1 Layout form of traditional intersection |
| |
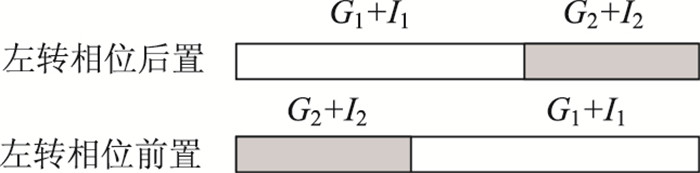
相序的表现形式多种多样,图 1(b)中仅是控制相序的一种形式。如图 2所示,为方便阐述,若仅考虑南-北方向车流,即ψ1和ψ2相位,根据左转相位前置与后置[8]则会产生〈G2+I2|G1+I1〉和〈G1+I1|G2+I2〉两种相序布局,其中Gj和Ij分别为相位ψj的有效绿灯时间和绿灯间隔时间,具体相序的选择应根据实际交通条件和优先控制目标而定。
|
| 图 2 南-北方向下左转相位前置、后置 Fig. 2 Left-turn phase lead and lag in south-north direction |
| |
1.2 双环相位(Ring-barrier)布局形式
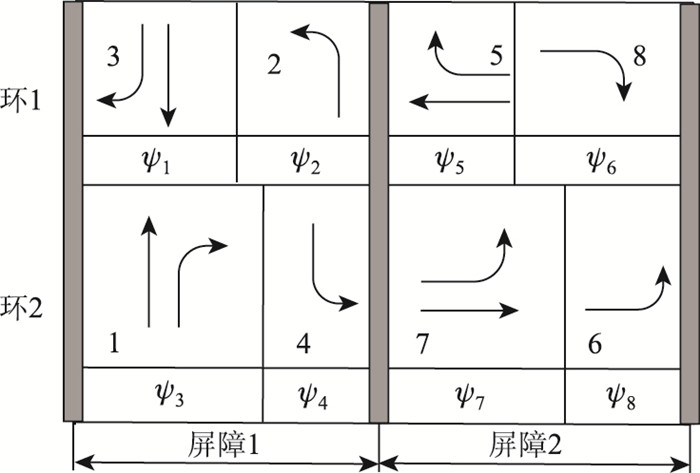
双环相位布局方法又称非对称式布局方法。该方法源于NEMA[9]所制定的交通控制指标,通过将每股车流分别单独设置一个相位,然后根据车流的冲突、非冲突情况进行相位间的相互组合,常见相位结构如图 3所示。对于相位的组合来说,若只考虑南-北方向的相位,则共有4种组合方案:〈G3+I3, G2+I2|G1+I1, G4+I4〉,〈G3+I3, G2+I2|G4+I4, G1+I1〉,〈G2+I2, G3+I3|G1+I1, G4+I1〉,〈G2+I2, G3+I3|G4+I4, G1+I1〉。
|
| 图 3 双环相位结构示意图 Fig. 3 Schematic diagram of dual-loop phase structure |
| |
双环相位设置过程中的主要特点:(1)在同一屏障(Barrier)而不同环(Ring)的相位之间可以相互组合,但处于同一屏障和环的相位则不能同时运行。(2)不同屏障内的相位不能同时运行,即不能跨屏障组合;同一屏障内的不同环,其相位运行时间必须相等,且满足周期为屏障1与屏障2两者时间之和。(3)相较于传统相位设置,双环相位则能够根据交通变化灵活采取控制方案,因此,相对传统相位设置的方法,其在减少相位车辆等待时间上能够实现更好的控制效果。
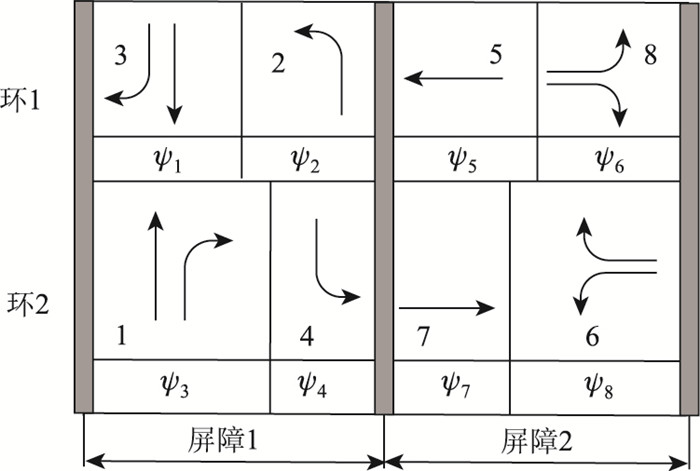
公交协调控制的目的是为了减少公交车在各个交叉口间的停车次数与行车延误,提高运行效率,因此,在设定以南-北方向作为协调控制的情况下,结合双环相位结构的特点,从相位结构、相序的角度提出适合于干线公交协调控制的相位结构设计方案,如图 4所示。
|
| 图 4 干线公交协调控制的相位结构设计 Fig. 4 Phase structure design for coordinated control for traffic on arterial road |
| |
采用该相位设置方法的优点:(1)在实施干线公交协调控制后,将直行与右转相位相配合,使得右转公交车辆能与直行相位公交车辆享有同样的通行权,从而既能保证协调相位直行车辆的优先,也能兼顾其他社会车辆的通行效益;(2)在交叉口处,当直行相位面对左转公交到达较多的情况时,采用干线方向左转相位后置则有利于等待左转公交在下一个相位的及时疏散、减少延误的增加;(3)干线非协调方向上左转-右转相位的组合则有利于缩短非协调方向汇入干线的公交车在下一个信号处的延误。
2 干线公交协调控制模型的建立干线公交协调控制中,各个交叉口的绿灯启动时刻都存在一个滞后时间段,这个时间段就是相位差。相位差是保持干线协调控制的重要参数,而这个重要参数又由干线控制路段上交叉口的公共周期所决定,在此基础上,通过对各交叉口的有效绿灯时间进行调整达到更贴近于实际的控制效果。因此,从干线公交协调控制参数角度出发,需要对其中的公共周期、绿灯时间、相位差等重要参数进行优化[10]。
(1) 公共周期信号的确立。干线公交路段上通常选取公交负荷最大的交叉口(关键交叉口)作为协调信号的参考点进行周期的选取。若采取协调周期则会造成与之相交的非协调相位(行人过街或次干路)上行人/车辆的延误增加,对此一般采用公共周期的1/2或1/3进行周期设置。在确定公共周期范围之前,首先需要确定各个交叉口的最小周期Cimin,即满足交叉口各相位最小绿灯时间Gi, jmin。Gi, jmin的确定不仅要保障车辆的行车安全,还需考虑行人过街的安全。从行人安全过街的角度出发,最小绿灯时间Gi, jp, min满足[1]:
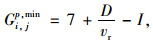
|
(1) |
式中,Gi, jp, min为行人过街最短绿灯时间;D为人行横道长度;vr为采用15百分步行速度,在我国可取1.2 m/s[11];I为绿灯间隔时间,可取5 s。
从车辆行驶安全角度出发,相位最小绿灯时间Gi, js, min可取直-右相位15 s,左转相位可取12 s。因此对于最小绿灯时间Gi, jmin,有:
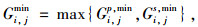
|
(2) |
式中,i和j分别为第i交叉口的第j相位(i为整数, j∈[1, 8])。依据第1部分的原理和图 4所示干线公交协调控制的相位结构设计,可以确定最小周期Cimin的范围:
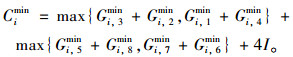
|
(3) |
因此,干线协调控制系统之下共周期时间C0的选择满足:
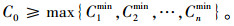
|
(4) |
(2) 相位绿灯时间的确定。干线公交协调控制过程中,除了考虑各交叉口处绿灯的选择外,还需考虑与干线相交的次要道路、人行横道处的过街需求。绿灯时间的选择关键在于确保绿灯时间足够长,从而确保其通行绿波带宽,因此结合相位有效绿灯时间与图 4的相位结构设计方案,以南-北方向作为协调控制干线,建立优化模型:
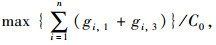
|
(5) |
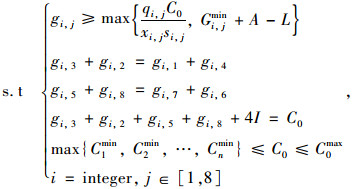
|
(6) |
式中,gi, j,qi, j,xi, j,si, j分别为第i交叉口的第j相位的有效绿灯时间、关键相位下车流的到达率、饱和度及饱和流率,协调控制下xi, j取0.85;A为黄灯时间;L为周期损失时间;C0max为公共周期极限最大值;integer为取整数。
(3) 双向相位差的确定。干线协调的过程中,相位差的确定直接影响到干线控制效果的好坏,且相对于单向相位差来说,双向相位的确定也更加复杂。相位差主要包括内部相位差和外部相位差[12-13],内部相位差Δi由上下行协调方向绿灯起始时刻之间的一段错位时间所确定,且根据相序选择的不同,也会有不同的控制结果,即:Δi=0,Δi=gi, 2,Δi=-gi, 4,Δi=gi, 2-gi, 4。
由于公交在行驶过程中受到中间停靠站及自身行驶特性的影响,使得在公交车辆行驶过程中存在更多不确定性。因此,在实际协调过程中,并不能直接套用确定小汽车相位差的方法来衡量干线上的公交协调控制。针对上述问题,将结合遗传算法的全局搜索与优化方法对相位差进行优化,具体过程将在第4部分中介绍。
(4) 对于干线公交协调控制效果的评价,主要选用公交车在交通信号处的延误作为评价指标。假设协调控制路段满足非饱和状态,依据延误三角形法建立公交车辆在交叉口处的延误模型[14]:
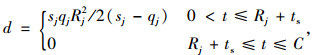
|
(7) |
式中,d为交叉口延误;t为时间;sj为第j相位的饱和流率;qj为第j相位下车流的到达率;Rj为第j相位的红灯时间;ts为车流的疏散时间,C为周期时长。
(5) 干线公交车行程时间特性分析。考虑到实际公交运行情况,需分析公交车在路段上的行驶时间及站点的停靠时间。当公交在协调路段行驶时,若路段设置了公交专用道,则公交车行驶过程中所受到来自路边行人、非机动车及周边社会车辆的干扰较少,则可视其行程时间为常数;若路段未设置公交专用道,受周边车辆、行人、非机动车的影响,则其行程时间即呈现一种随机波动的特性。因此,可以看出公交车的行程时间包括了在两种不同状态下行驶特性的组合,即[15]:
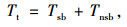
|
(8) |
式中,Tt为公交车的行程时间;Tsb为设置了公交专用道后公交车的行程时间;Tnsb为未设置公交专用道公交车的行程时间,Tsb可通过专用道设置长度同公交车正常行驶速度之间的比值获得。
公交站点的停靠时间是从公交车从进站停车开启车门上下乘客到乘客上车完毕车门关闭过程结束所经历的一个完整时间段。其中,上下乘客人数对于公交停靠时间的长短起至关重要的作用。我国公交车在乘客上下车的模式一般为前上后下,因此公交车站点停靠时间[16]为:
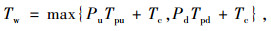
|
(9) |
式中,Tw为站点停靠时间;Pu和Pd分别为车辆停靠时的上、下车乘客数;Tpu和Tpd分别为人均上、下车乘客时间;Tc为公交车门关闭时间。
3 模型求解(1) 对于式(6)中相位有效绿灯时间的ILP问题,借助Lingo软件,依据分支定界的原理进行模型求解。第1步:将求解的ILP问题转化为LP问题,并输入相应参数qi, j,xi, j,si, j,L,I获取最优解C0k(其中k=1, 2, …, n,表示迭代次数)。第2步:对C0k进行分支并在最优解中任选一个不符合整数条件的变量gi, j进行整数约束,若C0k+1≥C0k且gi, j仍不是整数时,则循环第2步,否则进入第3步。第3步:将求出的某一分支问题的一个整数可行解作为是否淘汰其他分支的界限。第4步:将最大整数解作为原问题最优解,并获取其所对应的gi, j值。
(2) 结合MATLAB工具箱,运用遗传算法确定相位差。遗传算法是模拟自然界生物进化而发展起来的随机全局和优化方法,它能在搜索过程中智能优化搜索空间,并自适应地控制搜索过程用以求得最优解[17]。与传统的优化方法相比,遗传算法的主要优点在于:它以群体为基础,而非以单点搜索为基础,因此能从不同点获得极值,相对于传统优化方法所采用的爬山策略来说,不易陷入局部最优情况;遗传算法只需利用目标函数来区别群体中的个体好坏而不需事先描述求解问题的全部特点,从而减少不必的附加操作。遗传算法设计中常规的运算流程包括创建原始种群、染色体的编码与解码、选择与遗传策略、遗传算子的确定、优化的数集[18]。
4 算例分析选取南京市城区某条城市干线,该干线从南到北共有4个交叉口组成,分别命名为A,B,C,D。通过实际调查获取相关数据,如表 1所示。
| 编号 | 间距/m | 东进口/(pcu·h-1) | 西进口/(pcu·h-1) | 南进口/(pcu·h-1) | 北进口/(pcu·h-1) | |||||||||||
| 左 | 直 | 右 | 左 | 直 | 右 | 左 | 直 | 右 | 左 | 直 | 右 | |||||
| A | — | 45 | 467 | 110 | 140 | 777 | 37 | 226 | 773 | 34 | 25 | 850 | 274 | |||
| B | 595 | 92 | 346 | 135 | 227 | 398 | 268 | 274 | 708 | 67 | 114 | 793 | 284 | |||
| C | 870 | 326 | 478 | 333 | 228 | 585 | 148 | 102 | 482 | 478 | 146 | 724 | 255 | |||
| D | 908 | 146 | 347 | 275 | 25 | 304 | 184 | 265 | 561 | 225 | 188 | 792 | 38 | |||
依据图 4中关于干线公交协调控制的相位结构设计以及式(1)~(4)中的控制模型,根据表 1计算出CAmin=85, CBmin=66, CCmin=78, CDmin=85,因此公共周期范围满足C0≥85。在计算干线相位有效绿灯时间时,取相位损失时间l=3 s和A=3 s,且道路左、直、右饱和流率依次为1 500,1 600,1 200 pcu/h,根据式(5)~(6)计算可得公共周期C0=146 s,各相位有效绿灯时间结果如表 2所示。
| 交叉口 | 相位 | |||||||
| ψ1 | ψ2 | ψ5 | ψ6 | ψ3 | ψ4 | ψ7 | ψ8 | |
| A | 81 | 11 | 25 | 17 | 68 | 24 | 25 | 17 |
| B | 66 | 12 | 21 | 35 | 48 | 30 | 21 | 35 |
| C | 42 | 16 | 25 | 51 | 46 | 12 | 30 | 46 |
| D | 51 | 21 | 37 | 25 | 43 | 29 | 25 | 37 |
对于干线相位差的优化,首先用8位二进制对干线上行方向4个交通信号的外部相位差进行编码,然后将这4个交叉口上的每个相位的二进制合并成一个长串,这样每代种群中的基因型xk可表示为:

|
(10) |
式中λi, j为第i交叉口第j相位的二进制基因表现型。
对于相位差的解码则可使用下面的解码函数:
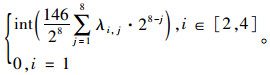
|
(11) |
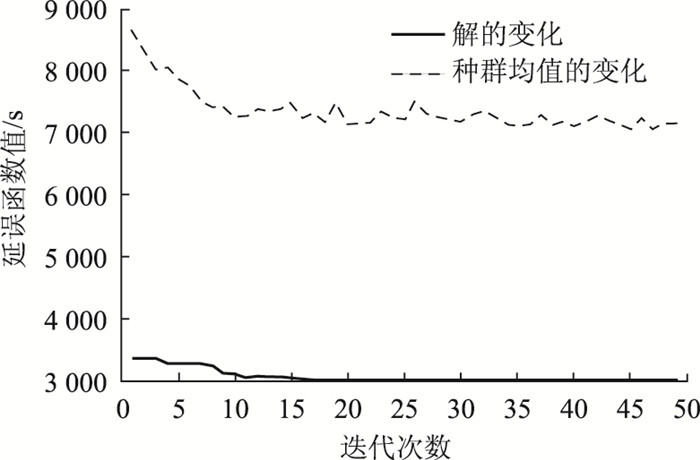
适应度函数的选取则依据式(6)中对于干线公交车协调控制延误最小作为目标函数并考虑干线公交车行程时间特性;选择二进制中的遗传算子和变异算子作为遗传算子的确定;选取种群规模为100、杂交率0.8、变异概率0.2、最大迭代次数50。为实现上述算法以及对干线公交相位差的优化,将利用MATLAB中的遗传算法工具箱对干线公交的优化效果进行分析与评价,其目标函数值变化趋势如图 5所示。
|
| 图 5 目标函数值变化趋势 Fig. 5 Change trend of objective function value |
| |
从图 5中可以看出,随着迭代次数的不断增加,延误函数值总体上呈现不断下降的趋势,其中略有波动。其主要原因在于公交行驶过程中受到了其他社会车辆驶入与驶出的干扰、满载率变化所带来的公交车在停靠站点时间的变化等多方面影响。第1次迭代的过程中,初始值为8 784 s,第50次迭代的结果为7 016 s,优化了20.13%。此外,算法整体上的收敛速度较快,其中在迭代第15次以后就接近于曲线底部,越往后曲线的变化趋势也越稳定。通过分析上图,将迭代第20次以后的值(即将相位差方案作为算法最优解的结果)进行输出,结果为[0,70,45,0,44,27,30,64]。
5 结论从干线公交协调角度出发,通过分析传统相位布局形式及相序前置、后置时所产生的不同控制效果,结合双环相位布局的特点,提出了适合于干线公交协调控制的相位结构设计方案。在此基础上,从协调控制参数的角度出发,分别对公共周期与相位有效绿灯时间建立了协调控制模型。为更好地评价协调控制效果,将延误三角形理论作为建模基础,建立了公交车延误模型。对于非线性整数规划模型的求解主要借助分支定界的思想,运用Lingo软件进行求解。此外,针对公交车行驶过程存在波动性的特点,相位差的选取则依据遗传算法中自然选择与遗传理论思想进行。通过理论与实际案例结合,该模型能使公交车的运行延误降低20.13%,从而使得公交运行效益得到了一定的优化。
| [1] |
吴兵, 李晔. 交通管理与控制[M]. 北京: 人民交通出版社, 2009. WU Bing, LI Ye. Traffic Management and Control[M]. Beijing: China Communications Press, 2009. |
| [2] |
卓健. 公交优先发展战略的几个认识误区[J]. 国际城市规划, 2013(4): 51-52. ZHUO Jian. Misunderstandings on the Prioritization of Public Transit Development in Chinese Cities[J]. Urban Planning International, 2013(4): 51-52. |
| [3] |
杨震, 王炜, 陈淑燕, 等. 干线公交绿波通行控制中公交专用相位的设置方法[J]. 东南大学学报:自然科学版, 2014, 44(4): 854-858. YANG Zhen, WANG Wei, CHEN Shu-yan, et al. Setting Methods of Bus Exclusive Phase in Bus Green-wave Control of Urban Arterial[J]. Journal of Southeast University:Natural Science Edition, 2014, 44(4): 854-858. |
| [4] |
王殿海, 朱慧, 别一鸣, 等. 干线公交优先信号协调控制方法[J]. 东南大学学报:自然科学版, 2011, 41(4): 859-865. WANG Dian-hai, ZHU Hui, BIE Yi-ming, et al. Bus Signal Priority Method at Arterial Signal Progression[J]. Journal of Southeast University:Natural Science Edition, 2011, 41(4): 859-865. |
| [5] |
别一鸣, 王殿海, 赵莹莹, 等. 干线协调交叉口多相公交信号优先控制策略[J]. 华南理工大学学报:自然科学版, 2011, 39(10): 111-118. BIE Yi-ming, WANG Dian-hai, ZHAO Ying-ying, et al. Multiple-phase Bus Signal Priority Strategy for Arterial Coordination Intersection[J]. Journal of South China University of Technology:Natural Science Edition, 2011, 39(10): 111-118. |
| [6] |
MA W, NI W, HEAD L, et al. Effective Coordinated Optimization Model for Transit Priority Control under Arterial Progression[J]. Transportation Research Record, 2013, 2356: 71-83. |
| [7] |
翟润平, 周彤梅, 刘广萍. 道路交通控制原理及运用[M]. 北京: 中国人民公安大学出版社, 2011. ZHAI Run-ping, ZHOU Tong-mei, LIU Guang-ping. Principle of Road Traffic Control and Application[M]. Beijing: Chinese People's Public Security University Press, 2011. |
| [8] |
徐洪峰, 郑明明, 李克平. 机动车相位固定最小绿灯时间计算方法[J]. 公路交通科技, 2008, 25(5): 105-110. XU Hong-feng, ZHENG Ming-ming, LI Ke-ping. Absolute Minimum Green Time Calculation for Vehicle Phase[J]. Journal of Highway and Transportation Research and Development, 2008, 25(5): 105-110. |
| [9] |
Trafficware Ltd. Signal Timing[EB/OL]. [2017-01-16]. http://www.trafficware.com/assets/pdfs.
|
| [10] |
曲大义, 万孟飞, 王兹林, 等. 基于交通波理论的干线绿波协调控制方法[J]. 公路交通科技, 2016, 33(9): 112-119. QU Da-yi, WAN Meng-fei, WANG Zi-lin, et al. A Coordinate Control Method for Arterial Green Wave Traffic Based on Traffic-wave Theory[J]. Journal of Highway and Transportation Research and Development, 2016, 33(9): 112-119. |
| [11] |
裴玉龙, 冯树民. 城市行人过街速度研究[J]. 公路交通科技, 2006, 23(9): 104-107. PEI Yu-long, FENG Shu-min. Research on Design Speed of Urban Pedestrian Crossing[J]. Journal of Highway and Transportation Research and Development, 2006, 23(9): 104-107. |
| [12] |
GARTNER N H, ASSMAN S F, LASAGA F, et al. A Multi-band Approach to Arterial Traffic Signal Optimization[J]. Transportation Research Part B:Methodological, 1991, 25(1): 55-74. |
| [13] |
朱和, 常玉林. 基于灵活相位的双向绿波协调控制[J]. 公路交通科技, 2013, 30(7): 140-143. ZHU He, CHANG Yu-lin. Bidirectional Green Wave Coordinative Control Based on Flexible Phase[J]. Journal of Highway and Transportation Research and Development, 2013, 30(7): 140-143. |
| [14] |
李海姣, 陆建. 基于交通流理论的公交站点间行程时间预测[J]. 交通信息与安全, 2012, 30(3): 29-32. LI Hai-jiao, LU Jian. Travel Time Prediction between Bus Stops Based on Traffic Flow Theory[J]. Computer and Communications, 2012, 30(3): 29-32. |
| [15] |
DURÁN-HORMAZÁBAL E, TIRACHINI A. Estimation of Travel Time Variability for Cars, Buses, Metro and Door-to-door Public Transport Trips in Santiago, Chile[J]. Research in Transportation Economics, 2016, 59: 26-39. |
| [16] |
美国交通运输研究委员会, 杨晓光, 滕靖, 等. 公共交通通行能力和服务质量手册[M]. 2版. 北京: 中国建筑工业出版社, 2010. American Transportation Research Council, YANG Xiao-guang, TENG Jing, et al. Manual of Transit Capacity and Service Quality[M]. 2nd.ed. Beijing: China Archi-tecture & Building Press, 2010. |
| [17] |
陈秋莲, 王成栋. 基于Matlab遗传算法工具箱的优化计算实现[J]. 现代电子技术, 2007, 30(2): 124-126. CHEN Qiu-lian, WANG Cheng-dong. Optimization of Genetic Algorithm Toolbox Based on Matlab[J]. Modern Electronics Technique, 2007, 30(2): 124-126. |
| [18] |
曹交交, 韩印, 姚佼. 城市交通干线动态双向绿波优化控制模型[J]. 公路交通科技, 2015, 32(9): 115-120. CAO Jiao-jiao, HAN Yin, YAO Jiao. A Dynamic Dual-direction Green Wave Optimization Control Model for Urban Arterial Roads[J]. Journal of Highway and Transportation Research and Development, 2015, 32(9): 115-120. |
 2018, Vol. 35
2018, Vol. 35
