扩展功能
文章信息
- 马超群, 艾倩楠, 张俊
- MA Chao-qun, AI Qian-nan, ZHANG Jun
- 不完备信息下公交断面客流的推算模型
- A Model for Calculating Bus Route Section Passenger Volume under Incomplete Information
- 公路交通科技, 2018, 35(5): 121-127
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(5): 121-127
- 10.3969/j.issn.1002-0268.2018.05.016
-
文章历史
- 收稿日期: 2018-01-03
2. 同济大学 交通运输工程学院, 上海 201804
2. School of Transportation Engineering, Tongji University, Shanghai 201804, China
公交断面客流指的是一定时间内某一道路断面的一条公交线路的断面公交客运量或者该断面所有公交线路的断面客运量[1]。公交断面客流是公交系统优化设计线路网和调配车辆不可或缺的基础数据[2]。单条公交线路断面客流分布及其时变特征是规划公交车发车频次、考量是否设置区间车的重要依据。
传统的公交断面客流调查方法主要是人工调查法。人工调查法耗费较多的人力,成本较高,且受外部环境因素干扰较大,要求调查人员具有较高的责任心。国内外有部分学者提出了在人工调查基础之上的基于历史数据的客流预测方法。Zhao等人[3]首先对吉林公交历史客流曲线进行小波分解,然后采用神经网络模型对分解的曲线进行客流预测。Chen等人[4]利用Huang transform(HHF)方法对台北公交换乘客流数据进行预测分析。杨军等人[5]以各类大型活动的历史OD客流数据为基础,利用灰色预测算法对客流数据建立灰色模型,然后建立马尔可夫修正模型,最后利用预测误差对灰色预测结果进行修正得到最终的预测大客流值。Umlauf等人[6]提出了一种公交走廊客流的估算模型;Antunes等人[7]运用神经网络和GIS建立了公交用户偏好模型;Lam S W等人[8]提出了一种基于综合仿真模型和服务可靠性测度的多响应优化方法,以优化公交服务调度规则;张红[9]对IC卡的数据分析以及公交调度进行了研究;胡继华等[10]构建了公交IC卡乘客下车站点判断概率模型;Bure等[11]在假定进出客流强度已知时对交通特征进行估计;赵晖[12]利用公交IC卡信息推算居民出行OD;Shi Junqing等[13]对金华市公共交通客流进行分析。
虽然国内外学者尝试采用其他方法进行客流预测,但是这些方法的数据来源依然是人工调查。近年来,随着公交车IC卡收费系统和GPS系统在全国各地陆续投入使用[14],为研究乘客的出行轨迹提供了大量的数据,对个体出行轨迹进行集计研究为获取公交断面客流提供了一种新的思路[15]。但是,我国大部分城市的公交线路采取一票制收费系统,乘客只在上车时刷卡,下车时无需刷卡,无法直接通过数据融合来获取乘客下车站点,而公交站点下车客流量的计算直接关系到断面客流量,从而影响到发车频率以及资源的合理配置,使得有些线路车辆满载率过高、发车频率不足,有些线路出现空载或者几辆车赶在一起到站的情况发生,而有些线路出现很长时间无车辆到达的情况,使得乘客的等待时间过长,车辆满载率过高。为此,本研究通过分析公交车站周边土地利用情况,在仅有上车刷卡数据的情况下,构建各个车站下车客流的预测模型,进而求得公交线路断面客流。
1 建立模型 1.1 模型基础断面客流量的计算以各个站点的上下车客流量为基础,由于本研究是依据公交IC卡数据为基础推算断面客流,在高峰小时内以通勤客流为主,为简化计算不考虑各站投币上车的乘客。根据刷卡数据推算可得各个车站的上车客流量,对于下车客流需要建立一定的模型进行测算。本研究以单一方向(上行或下行)建立断面客流的计算模型,如图 1所示。

|
| 图 1 单一方向公交运行示意图 Fig. 1 Schematic diagram of bus operation in single direction |
| |
根据断面客流量的计算公式可得:
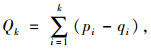
|
(1) |
式中,pi为车站i的上车客流量;qi为车站i的下车客流量;Qk为第k个断面的断面客流量。
同时断面客流量和平均运距之间存在如下关系:
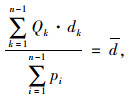
|
(2) |
式中,dk为第k个断面的运输距离,即第k个站点与第k+1个站点之间的公交路线长度;d为该公交线路的平均运输距离。
将式(1)代入式(2)可得:
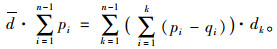
|
(3) |
式(3)反映了各站点上车客流量pi与已知各站点下车客流量qi、站间距dk、线路平均运距d之间的相互关系。
1.2 建模思路由于公交线路具有的站点数量多、线路长,一条公交线路存在多个大型客流集散点,每一个大客流集散点具有较强的吸引范围,客流集散点吸引范围内公交路段为该集散点的覆盖区段。本研究以存在3个客流集散点为例进行讨论,结合各站点周边用地、人口数据构建出各车站用地范围内公交的分担率模型。模型需作以下假设:
(1) 本模型的应用对象为高峰时期的公交线路,以日常通勤客流为主,上车乘客均持有公交IC卡。
(2) 由于公交车站的站间距较小,根据《城市道路交通规划设计规范GB50220—95》中3.3.2,公交车站服务面积取站点周边300 m的范围作为公交乘客下车后的吸引范围;
(3) 各集散点覆盖区段范围并不严格以集散点对称,覆盖半径按照最大覆盖半径取值;
(4) 各个车站的公交分担率与车站所处的覆盖区段及区位相关;
(5) 各车站的下车客流与站点的公交吸引强度成正比。
根据区位理论,站点吸引强度由离中心距离、周边用地强度、人口密度、经济发展水平等因素有关。由于线路各个站点均处于西安市主城区范围内,各个站点周边经济发展水平差异较小,故本研究只考虑用地、距离和人口密度3类影响因素。
首先统计各公交站点服务半径覆盖范围内的各类用地性质。并按照各类用地的吸引系数对各站点周边总的交通吸引量进行估算。如图 2所示,站点服务半径通常取值为站间距的一半。在城市公交系统中,站间距通常在500~700 m,因此站点平均服务半径约为300 m。

|
| 图 2 公交车站服务半径 Fig. 2 Service radius of a bus station |
| |
因此可得站点i周边300 m半径覆盖范围内高峰小时总的吸引人数为:
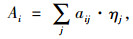
|
(4) |
式中,Ai为站点i周边300 m半径覆盖范围内高峰小时总的吸引人数;aij为站点i范围内第j类用地总的建筑面积;ηj为第j类用地高峰小时内吸引率的采纳值。
在得到各个站点周边用地总吸引人数的基础之上,需要确定各站点的下车客流量,但是并不能将不同区域的分担率视为定值,需要考虑站点在线路中的位置以及人口密度等因素来进行确定。通常情况下,站点越靠近线路大型客流集散点下车人数越多、人口密度越大公交分担率(吸引强度)越大。
当车站i位于第m个客流集散点的覆盖区段[ms, me]时,车站用地范围内公交的分担率根据式(5)进行计算:
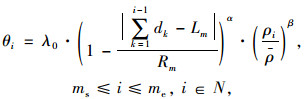
|
(5) |
式中,θi为站点i所在区域内的公交出行分担率;Lm为第m个大客流集散点至起点的距离;Rm为第m个集散点的最大覆盖半径;ρi为站点i范围内的人口密度;ρ为线路各个站点周边用地人口密度的均值;λ0为公交线路整体分担率。
α和β为待确定的参数,虽然缺乏吸引强度和距离系数、人口密度具体的变化关系,但是由式(1)~式(3)可知在各站点上车人数、站间距已知的情况下,各站点下车人数与平均运距存在平衡制约关系,进而可通过判定线路客运周转量的差值最小进行α和β求解:
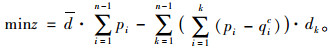
|
(6) |
通过总量控制法使总下车人数和总上车人数一致,结合式(5)可得式(6)中车站i的理论下车人数qic的计算式为:
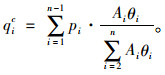
|
(7) |
综上所述,在以IC卡数据推算得到的上车客流的基础之上,当车站i位于第m个客流集散点的覆盖区段时,常规公交线路各站点的下车客流计算模型为:
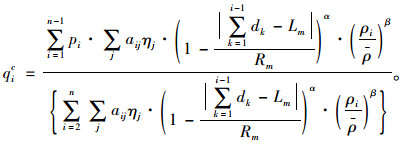
|
(8) |
根据上述构建的下车客流模型,则可得到断面n处的客流为:
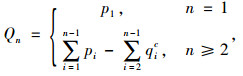
|
(9) |
式中,Qn为第n个断面的客流量;qic为车站i计算所得下车人数;pi为车站i上车人数。
1.4 参数求解考虑站间距离与平均运距之间的关系,根据式(3)可得如下关系式:
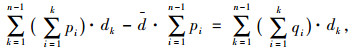
|
其中:
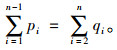
|
(10) |
最终求解的参数应使得等式两边的结果尽可能接近,即使得等式两边差值最小:
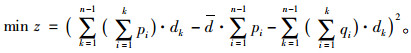
|
(11) |
本研究以西安市16路公交车2012年5月16日的早高峰上行刷卡数据进行研究,线路总长18.7 km,共有29个站点,采用一票式IC卡计费模式。将公交五公司至辛家庙公交枢纽站记为上行方向,辛家庙公交枢纽站至公交五公司记为下行方向。16路公交线路走向图如图 3所示。线路服务于西安市主城区内部居民出行,两端区段沿线用地以居住为主,中段沿线用地以商业、办公为主。
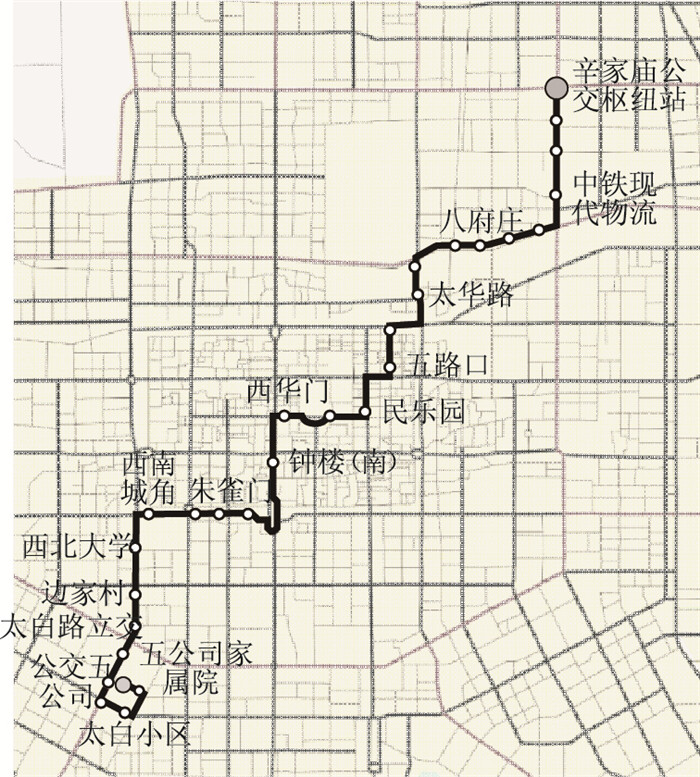
|
| 图 3 16路公交线路走向图 Fig. 3 Diagram of line of Bus No. 16 |
| |
在Transcad软件中绘制公交线路,并得出其300 m吸引范围图,如图 4所示。根据16路公交线路走向及其300 m覆盖半径图,统计各站点300 m范围内的用地性质以及人口密度。
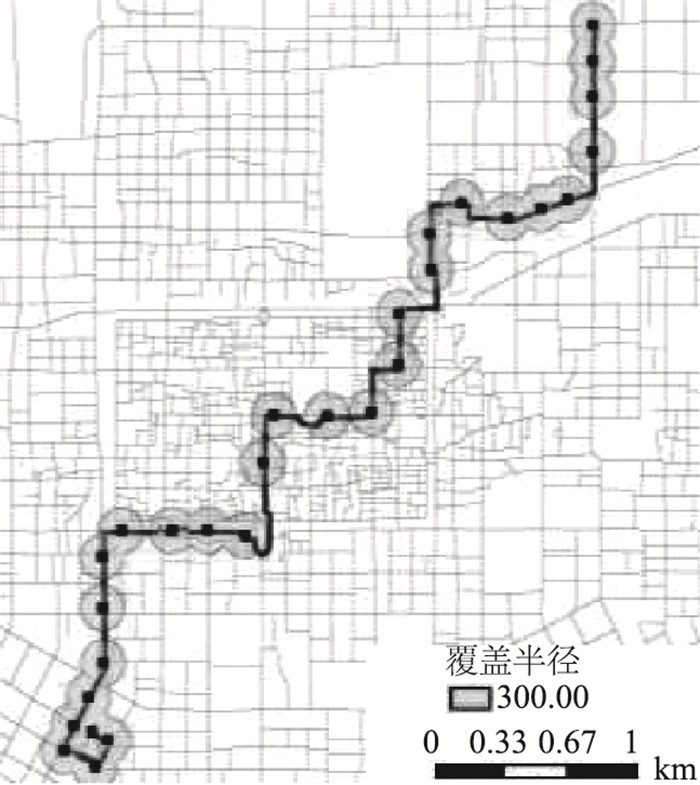
|
| 图 4 16路公交300 m吸引范围图 Fig. 4 Diagram of 300 m attract range of Bus No. 16 |
| |
2.2 客流集散点
根据16路公交线的路由走向,以明城墙区为边界,将线路分为3个区段,同时依据附表中的统计结果,在3个区段内确定出3个客流集散点,如图 5所示。
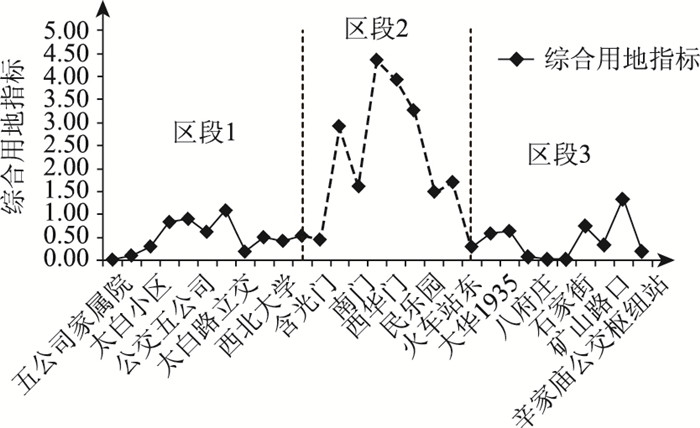
|
| 图 5 综合用地指标 Fig. 5 Comprehensive land use index |
| |
客流集散点1:太白路立交,覆盖区段:五公司家属院至西北大学,最大覆盖半径R1为2.87 km;
客流集散点2:西华门,覆盖区段:西南城角至火车站东,最大覆盖半径R2为6.50 km;
客流集散点3:辛家庙,覆盖区段:太华路至辛家庙公交枢纽站,最大覆盖半径R3为3.73 km。
3 参数标定本研究构建的目标函数式(11)包含各个车站上下车人数和站间距,其中下车人数由包含参数α,β的理论计算模型代入,增加了最终目标函数的多样性与复杂性,难以使用传统的数值算法精确求解,因此采用启发式算法进行求解。本研究采用改进的遗传算法进行求解。
3.1 遗传算法概述依据本研究所构建的模型以及模型检验的目标,模型求解思路是获得参数α,β的最优组合,使得目标函数的值最小。求解最优的方法有蚁群算法[16]、粒子群算法[17]、模拟退火法[18]、遗传算法等[19],本研究采用遗传算法进行求解。和这些方法相比,选用遗传算法进行求解的优点在于:
(1) 搜索种群中的点是并行的,以面为单位进行搜索优于传统的以点为单位的搜索;
(2) 不需要辅助信息,只需要影响搜索方向的目标函数和相应的适应度;
(3) 强调使用概率转换规则来引导搜索过程,并非确定性规则;
(4) 使用数字化编码参数集,建立表现型和基因型的关系。
和传统的遗传算法相比,本研究采用的混合遗传算法应用如下改进:编码方式采用格雷码,和传统的二进制编码相比,格雷码能够提高算法的局部搜索能力,且使得交叉、变异等操作易于实现;适应度函数依据目标函数采用界限构造法进行设计,能够在保证概率非负的同时避免目标函数值在分布上差距过大,使平均适应度能体现种群的平均性能;交叉方式为两点交叉,在保证优良基因结构延续的基础之上提高运算效率。具体步骤如下:
Step 1.编码:将解空间的数据表示为遗传空间中基因串结构数据,采用格雷码。
Step 2.生成初始种群,设置最大进化代数。
Step 3.选择(复制):根据个体的适应度值大小进行选择,适应度较高的个体被遗传到下一代群体中的概率较高,使群体中个体适应度不断接近最优解,适应度函数形式如下:
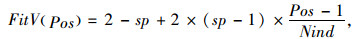
|
(12) |
式中,FitV为适应度;Pos为每个个体在排序种群中的位置;Nind为种群中个体的数量;sp为选择的压差。
Step 4.交叉(重组):按照较大的概率从群体中选择2个个体,在个体编码串位中随机设置2个交叉点,然后进行个体间部分基因交换,产生子代。
Step 5.变异:以较小的概率对个体编码串上的某个或某些位值进行改变,产生新的个体,能避免由于选择和交叉运算造成的某些信息的丢失,保证算法的有效性。
3.2 模型求解根据西安市居民出行调查数据,主要交通方式的出行距离和出行速度分布如图 6所示。由于线路长度、线路路由、乘客属性不同,西安市常规公交的旅行速度分布于15~20 km/h,乘客的出行距离多分布于4~10 km,综合判定出公共交通的平均出行速度约为17 km/h, 平均出行距离约为6.14 km。
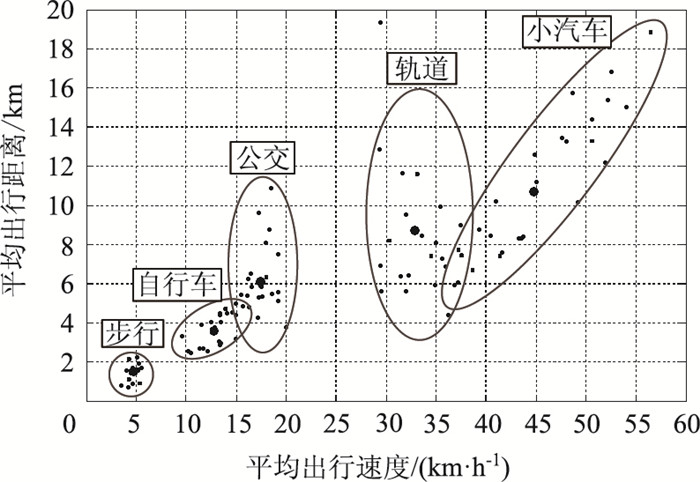
|
| 图 6 西安市各方式的出行距离和速度散点分布图 Fig. 6 Travel distances and velocity scatter distributions of different trip modes in Xi'an |
| |
因此,常规公交的平均运距d取6 km,代入目标函数式(11)进行未知参数的计算。可得求解的目标函数为:
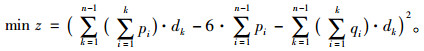
|
(13) |
根据统计所得到的各车站周边用地性质以及人口密度,编写遗传算法的迭代程序,相关参数设置为:交叉概率0.7,变异概率0.01,为使得目标函数达到全局最优最大迭代次数设置为50。本研究的调查数据在MATLAB中的运算过程如图 7所示,同时根据迭代收敛图可知,当迭代至9代时目标函数值开始收敛,达到理论最小值0,如图 8所示。此时α和β值即为最优解。
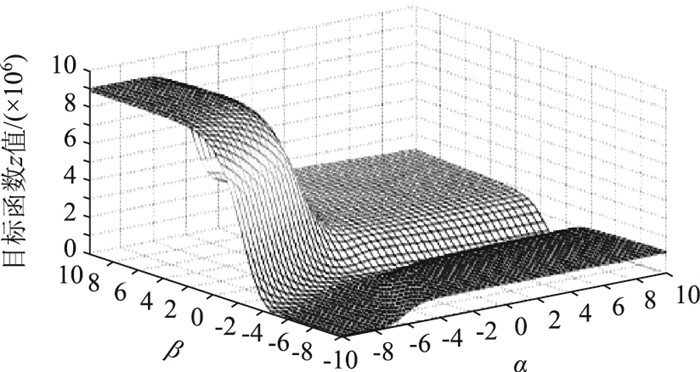
|
| 图 7 目标函数曲线 Fig. 7 Target function curve |
| |
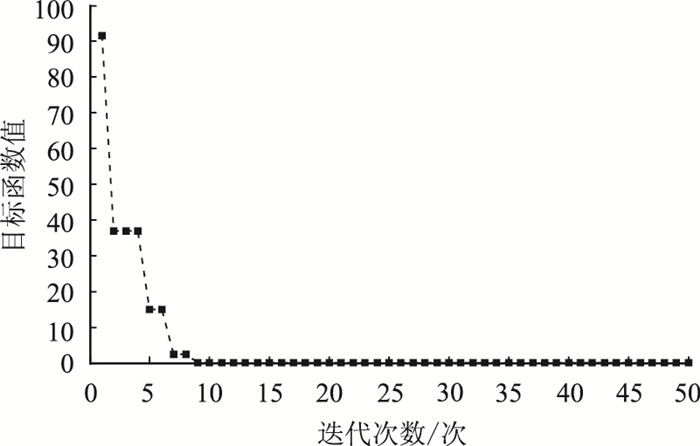
|
| 图 8 目标函数值随进化代数的变化 Fig. 8 Objective function value varying with iterations |
| |
解得最优解为:α=0.419 1,β=0.482 3,目标值z取极小值0。
4 断面客流的计算根据16路公交的高峰小时上行方向运营IC卡数据,统计各车站的上车人数,利用遗传算法标定的参数结果以及上车客流量,代入下车客流预测模型计算各车站的下车人数。通过构建的下车客流计算模型所计算得到的各个公交车站的下车客流,以及各个车站的上车客流,则可以得到各个断面的客流量,与调查实际得到的断面客流结果对比如图 9所示。
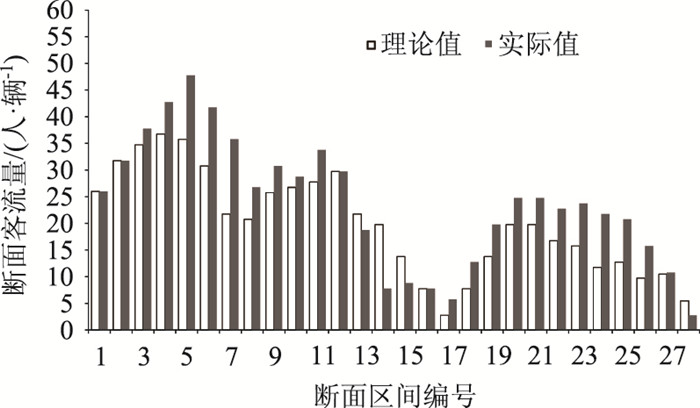
|
| 图 9 16路高峰小时公交断面客流计算值与实际值比较 Fig. 9 Comparison of calculated value and actual value of bus section passenger volumes of Bus No. 16 in peak hour |
| |
根据图 9分析可知,本模型推算出的公交断面客流量与实际调查所得公交断面客流存在一定的差异,个别区段的变动差异较为明显,断面客流平均相对误差为22.6%,平均绝对误差约为5人/断面。
同时可以看出理论计算出的断面客流整体小于实际的断面客流,在高客流断面较为显著,这是由于大客流集散点车站下车客流理论计算值过大所致。实际情况下客流集散点处用地、交通、客流情况较为复杂,需要对此类车站节点的下车客流模型进行后续优化研究,以减小理论结果与实际的偏差。
尽管存在22.6%的相对误差,但是对于每一辆车而言在每个断面平均存在5人的误差。误差是不可避免的,但是从结果整体来看客流断面的变化趋势与实际基本一致,因此文中基于综合土地指标划分的覆盖区间合理,构建的下车客流量模型的计算结果可以作为公交线路运能匹配分析及车辆运用的基础依据。
5 结论本研究在认真分析城市公交线路客流特征的基础之上,在仅有上车刷卡数据条件下,构建公交车站下车客流推算模型,进而通过累计上车人数与累计下车人数之差计算各断面客流量,为公交线路的布设、车辆调度提供依据。通过选取一条公交线路的刷卡数据,统计其300 m服务覆盖半径内的土地利用情况,以求解模型参数,并且计算出该条线路各车站的下车客流以及断面客流。在模型求解时对传统的遗传算法进行改进,使得算法的收敛性和结果可靠性得到一定程度的改善,得到的结果理论可应用于一票制公交线路断面流量的计算,说明模型具有一定的可行性。
依据公交车上车刷卡数据结果以及所构建的各车站下车客流计算模型能够计算出断面客流,并结合同时段实际调查的数据进行对比分析。由于本模型是面向高峰小时的通勤客流,基于公交IC卡数据构建,模型假设日常通勤客流均持有公交IC卡,需要补充调查全线上车投币乘客的比例后,对断面客流结果进行一定的修正处理。同时,本研究在确定主要集散点对应通道上的下车客流时未考虑多条线路共线及换乘的情况,使得计算结果也与实际存在一定的差异,需要进一步研究通道内多线客流的分担率和换乘情况。
| [1] |
吴祥国. 基于公交IC卡和GPS数据的居民公交出行OD矩阵推导与应用[D]. 济南: 山东大学, 2011. WU Xiang-guo. Derivation and Application of OD Matrix Based on Public Transport IC Card and GPS Data for Resident Trip[D]. Jinan: Shandong University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10422-1011227743.htm |
| [2] |
舒国辉. 基于数据挖掘的公交客流规律研究[D]. 北京: 北京交通大学, 2009. SHU Guo-hui. Research on Rules of Public Transport Passenger Flow Based on Data Mining[D]. Beijing: Beijing Jiaotong University, 2009. http://cdmd.cnki.com.cn/article/cdmd-10004-2009204673.htm |
| [3] |
ZHAO S Z, NI T H, WANG Y, et al. A New Approach to the Prediction of Passenger Flow in a Transit System[J]. Computers & Mathematics with Applications, 2011, 61(8): 1968-1974. |
| [4] |
CHEN M C, WEI Y. Exploring Time Variants for Short-term Passenger Flow[J]. Journal of Transport Geography, 2011, 19(4): 488-498. |
| [5] |
杨军, 侯忠生. 一种基于灰色马尔科夫的大客流实时预测模型[J]. 北京交通大学学报:自然科学版, 2013, 37(2): 119-123, 128. YANG Jun, HOU Zhong-sheng. A Grey Markov Based on Large Passenger Flow Real-time Prediction Model[J]. Journal of Beijing Jiaotong University:Nature Science Edition, 2013, 37(2): 119-123, 128. |
| [6] |
UMLAUF T, GALICIA L D, CHEU R L, et al. Ridership Estimation Procedure for a Transit Corridor with New Bus Rapid Transit Service[J]. Journal of Advanced Transportation, 2016, 50(4): 473-488. |
| [7] |
ANTUNES R, YAMASHITA Y, DANTAS A, et al. Modeling User's Preferences of Public Bus Transportation Using Neural Networks and GIS[C]//International Conference on Urban Transport and the Environment for the 21st Century. Cambridge: [s. n. ], 2001.
|
| [8] |
LAM S W, TANG L C, GOH T N, et al. Multiresponse Optimization of Dispatch Rules for Public Bus Services[J]. Computers & Industrial Engineering, 2009, 56(1): 77-86. |
| [9] |
张红. 基于公交IC卡信息的客流数据分析及调度研究[D]. 西安: 西安电子科技大学, 2012. ZHANG Hong. Data Analysis of Public Transit Passenger Flow and Static Scheduling of Vehicle Based on Information of Public Transportation IC Cards[D]. Xi'an: Xidian University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10701-1013297574.htm |
| [10] |
胡继华, 邓俊, 黄泽. 结合出行链的公交IC卡乘客下车站点判断概率模型[J]. 交通运输系统工程与信息学报, 2014, 14(2): 62-67. HU Ji-hua, DENG Jun, HUANG Ze. Trip-chain Based Probability Model for Identifying Alighting Stations of Smart Card Passengers[J]. Journal of Transportation System Engineering and Information Technology, 2014, 14(2): 62-67. |
| [11] |
BURE V M, MAZALOV V V, PLAKSINA N V. Estimating Passenger Traffic Characteristics in Transport Systems[J]. Automation and Remote Control, 2015, 76(9): 1673-1680. |
| [12] |
赵晖. 基于公交IC卡信息的居民出行OD推算研究[D]. 西安: 长安大学, 2009. ZHAO Hui. Research on OD Calculation of Inhabitant Trips Based on Data of Bus Intelligent Card[D]. Xi'an: Chang'an University, 2009. http://cdmd.cnki.com.cn/article/cdmd-11941-2009210355.htm |
| [13] |
SHI J, CHENG L. A Study and Analysis of Passenger Flow of Urban Public Transport in the City of Jinhua, China[C]//International Conference on Civil. New York: Transportation and Environmental Engineering, 2013: 177-181. http://cn.bing.com/academic/profile?id=8b68af2fa5cb32d09a7664f17746769f&encoded=0&v=paper_preview&mkt=zh-cn
|
| [14] |
DUAN W J, CHEN Y Y, LAI J H. Analysis of Single-line Passenger Flow Based on IC Data and GIS Data[C]//International Conference of Transportation Professionals. Reston: The American Society of Civil Engineers, 2012: 1350-1357.
|
| [15] |
胡继华, 邓俊, 黄泽. 一种基于乘客出行轨迹的公交断面客流估算方法[J]. 计算机应用研究, 2015, 31(5): 1398-1402. HU Ji-hua, DENG Jun, HUANG Ze. Travel Path Based Method for Estimating Public Transit Section Flow[J]. Application Research of Computers, 2015, 31(5): 1398-1402. |
| [16] |
LI Z C, ZHOU X, DAI Z, et al. Identification of Protein Methylation Sites by Coupling Improved Ant Colony Optimization Algorithm and Support Vector Machine[J]. Analytica Chimica Acta, 2011, 703(2): 163-171. |
| [17] |
KIA S, SEBT M H, SHAHHOSSEINI V. Optimization of the Infrastructure of Reinforced Concrete Reservoirs by a Particle Swarm Algorithm[J]. Slovak Journal of Civil Engineering, 2015, 23(1): 14-22. |
| [18] |
SUMAN B, HODA N, JHA S. Orthogonal Simulated Annealing for Multiobjective Optimization[J]. Computers & Chemical Engineering, 2010, 34(10): 1618-1631. |
| [19] |
HUGHES J A, HOUGHTEN S, ASHLOCK D. Recentering and Restarting a Genetic Algorithm Using a Generative Representation for an Ordered Gene Problem[J]. International Journal of Hybrid Intelligent Systems, 2014, 11(4): 257-271. |
 2018, Vol. 35
2018, Vol. 35
