扩展功能
文章信息
- 许雪琦, 姜柯, 黄超
- XU Xue-qi, JIANG Ke, HUANG Chao
- 过饱和状态的潮汐车道交叉口群协同控制及仿真
- Cooperative Control and Simulation for Intersection Group of Over-saturated Tidal Lane
- 公路交通科技, 2018, 35(5): 108-114
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(5): 108-114
- 10.3969/j.issn.1002-0268.2018.05.014
-
文章历史
- 收稿日期: 2017-02-27
根据高德地图近两年发布的《中国主要城市交通分析报告》,杭州稳列中国拥堵城市前4位。针对职住分离所造成的潮汐式交通拥堵问题,可变车道技术是有效的解决手段之一。杭州于2014年在居民较密集的西湖区设立了潮汐走廊,但由于车流量的不断增加及路口信号灯设置的不合理性,个别路段仍极易出现拥堵; 而且由于交通流的流动性及路网的延伸性,拥堵会逐渐蔓延,导致整个潮汐走廊陷入交通瘫痪,给杭州市区早晚高峰的交通带来极大压力。本研究基于对潮汐走廊实际交通数据的定量分析,剖析造成拥堵的症结,并提出瓶颈路段的信号协同配时解决方案。
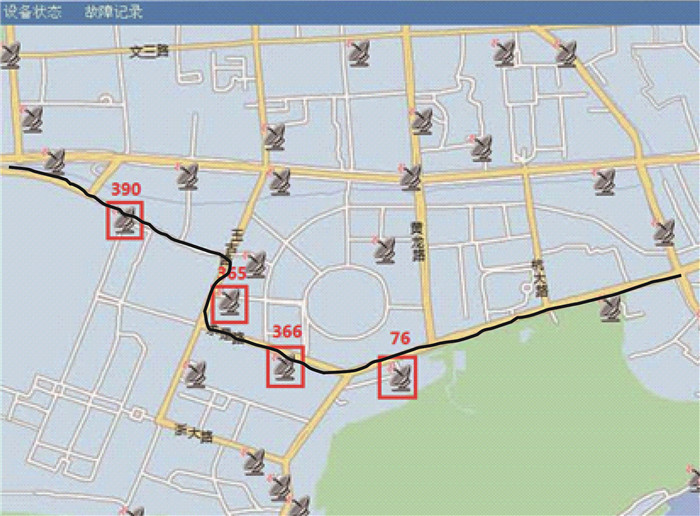
1 潮汐走廊拥堵原因分析 1.1 路段设置及交通数据来源说明杭州西湖区潮汐走廊的具体路段为“西溪路-玉古路-求是路-曙光路”,如图 1所示。潮汐走廊是杭州市区的交通要道,在早晚高峰承担着巨大的交通流量,影响着整个西湖区的交通状况。
|
| 图 1 潮汐走廊微波监控点分布图 Fig. 1 Distribution of microwave monitoring points of Tidal Corridor |
| |
对上述4个路段进行实地调研,记录潮汐车道路段名称、长度、车道数、交通指示标志、交叉口等基础信息以及信号灯的设置位置、红绿灯时长。此外,采集了交警部门微波检测监控平台1周内(2016-04-06~2016-04-10)早高峰(7:00—9:00)时段的交通数据,包括具体时段内的断面流速和流量。根据杭州交警部门的微波检测平台监控点的布置,潮汐走廊的监控点布置及其监测的路段如图 1所示。
1.2 潮汐特征分析潮汐走廊的基本路况及早晚高峰行车方向如表 1所示。
| 路段名称 | 路段长度/km | 路段方向 | 车道数 | 早高峰时间车道分配 | 晚高峰时间车道分配 |
| 西溪路 | 3 | 东西 | 4 | 7:00—9:00 (西3东1) |
17:00—19:00 (东3西1) |
| 玉古路 | 0.34 | 南北 | 5 | 7:00—9:00 (北4南1) |
17:00—18:30 (南3北2) |
| 求是路 | 0.64 | 东西 | 5 | 7:00—9:00 (西3东2) |
17:00—18:30 (东3西2) |
| 曙光路 | 1.4 | 东西 | 5 | 7:00—9:00 (西3东2) |
17:00—19:00 (东3西2) |
潮汐车道数的设置是否合理直接关系到潮汐车道的运行效果。潮汐特征是指早晚高峰时段道路上两个方向交通量的不均衡程度,用方向分布系数K表示,“K≥2/3”表示道路潮汐特征明显[1]。在实施潮汐车道之前,西湖区潮汐走廊的各路段除曙光路外,其余路段的K值为0.68~0.76。根据实施潮汐车道之后1周内早高峰时段的流量数据,各路段的K值为0.74~0.89,车道设置的合理性使得潮汐特征更为显著。
1.3 瓶颈路段的判定根据文献[2]设计车速路段的通行能力标准,经计算得出潮汐走廊的设计通行能力为1 300~1 350 pcu/h。而根据实际交通流量与其设计通行能力的比较结果,西溪路、玉古路和求是路的早高峰流量在1 555~2 758 pcu/h,远大于其设计通行能力,因此极易发生拥堵。
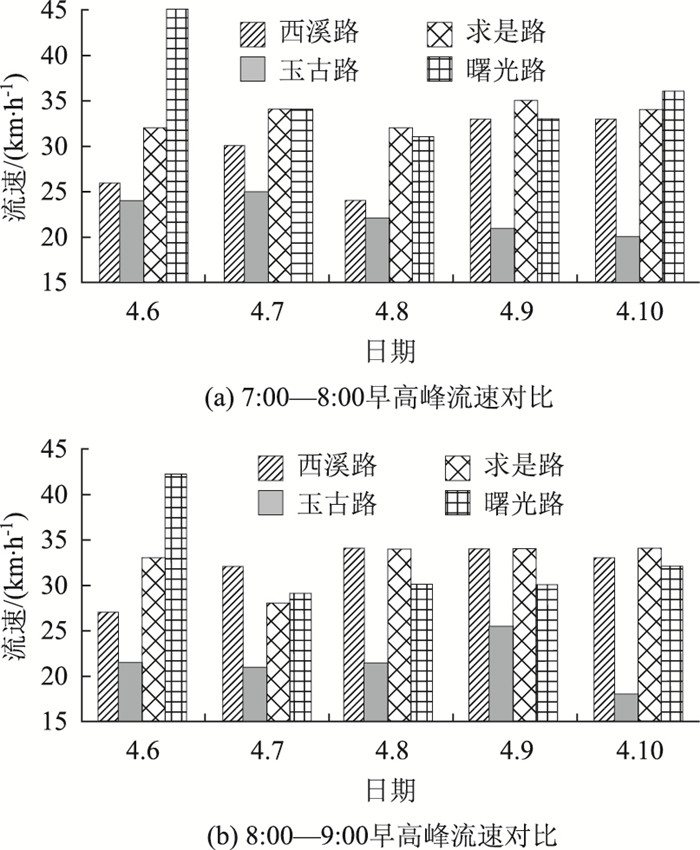
针对1周内潮汐走廊的交通流量、流速数据的时间序列分析,玉古路和曙光路流速没有明显的谷值,玉古路除了深夜时段车速较快,其他时段车速均低于25 km/h。曙光路的车速波动较大,但基本高于25 km/h,较其他路段相对通畅。对比各路段早高峰流速,玉古路的车速明显低于其他路段,为瓶颈路段,如图 2所示。根据文献[3]对杭州道路交通运行状态的评价标准,从而判断玉古路早高峰时段处于中度拥堵状况。
|
| 图 2 杭州西湖区潮汐走廊各路段早高峰车速对比 (2016年4月) Fig. 2 Comparison of vehicle speeds on each road of Tidal Corridor in West Lake District of Hangzhou in morning rush (April, 2016) |
| |
作为潮汐走廊的中间路段,玉古路的拥堵状况会随着交通流的不断增加以及路网的扩散,导致整个路网的拥堵。由表 1可知,玉古路-求是路,实施潮汐车道路段分别只有0.34 km和0.64 km,在早高峰时段玉古路两端的路口(西溪路-玉古路-求是路的两个交叉口)信号灯各自孤立,导致车辆在340 m路段间滞留,不能有效通行,更加重了交通拥堵状况。
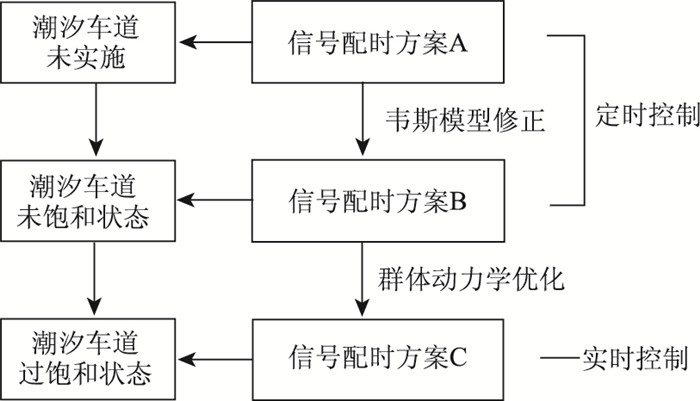
2 多路段潮汐车道的信号配时方案设计 2.1 信号配时方案说明由于早高峰拥堵情况较晚高峰严重,故以早高峰为例,针对潮汐车道未实施、潮汐车道未饱和-饱和、过饱和3种情况讨论。系统信号配时方案如图 3所示。
|
| 图 3 潮汐车道3种信号配时方案 Fig. 3 Three signal timing schemes for tidal lane |
| |
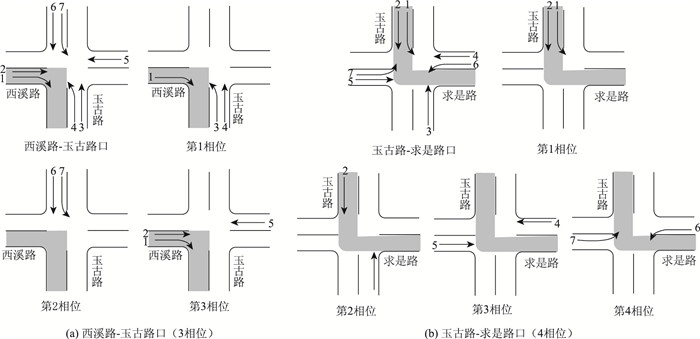
工作日早7:00后,潮汐车道的实施使得原车道行车方向发生了变化。图 4为瓶颈路段玉古路两端的西溪路口、求是路口潮汐时段信号相位示意图,图中省略了次要的右转方向,灰色表示早高峰潮汐路段。
|
| 图 4 早高峰时段玉古路两端路口信号相位示意图 Fig. 4 Schematic diagrams of signal phases for intersections at both ends of Yugu Road in morning rush |
| |
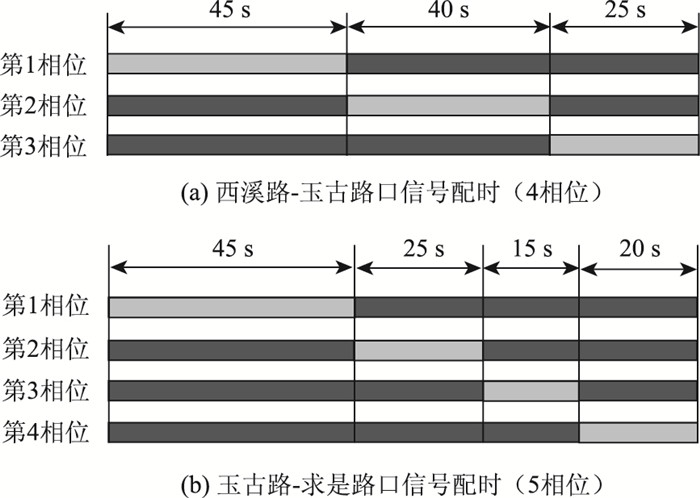
对信号相位及配时方案A做出调整,采用经韦伯斯特模型修正[4]的潮汐配时方案B(见图 5),深色部分为红灯时长,灰色部分为绿灯时长。在1个信号周期内,图中的绿灯时长包括了黄灯。
|
| 图 5 玉古路两端路口信号配时方案B Fig. 5 Signal timing scheme B for both intersections of Yugu Road |
| |
随着交通流量的不断增大,道路逐渐趋于饱和,进而发展到过饱和。此时,采用群体动力学模型对信号配时方案B进行修正,生成自适应的实时配时方案C,以应对潮汐车道的过饱和状态。
2.2 过饱和状态下的配时方案饱和流量是指单位时间内经过道路某截面的最大车流量,一般采用饱和度界定道路是否处于过饱和状态。饱和度是流量与路段通行能力的比值,若饱和度大于1,则道路处于过饱和状态[5]。针对潮汐走廊的玉古路仅有340 m长的具体路况,除了流量和流速外,过饱和程度的判断还必须考虑路口车辆排队长度。参考文献[4]的计算方法,依据两个条件判断过饱和状态:玉古路北至南流量超过1 300 pcu/h的设计通行能力,或玉古路-求是路北口的车辆排队在两个信号周期内无法消散。当道路出现过饱和状态时,则采用实时控制的协同配时方案C,直至车流排队能够在1个信号周期内消散。
3 过饱和状态下的交叉口群协同控制研究 3.1 群体动力学与多交叉口群群体动力学(Group Dynamics)是以群体的演化规律及群体与个人、群体与群体间的影响关系为研究对象,通过描述群体运动和群体控制规律以发现一般规律的学科[5]。近年来该理论的应用在交通控制领域得到较大的发展。
交通道路的交叉口协同控制主要是研究交叉口与交叉口之间、交叉口群与交叉口之间的互相影响和互相牵制的关系,两者在本质上具有较强的相似性。基于群体动力学算子及交通仿真技术的研究目的,是使饱和或过饱和状态尽可能平稳地过渡到未饱和状态,以保证潮汐车道达到交通状态的稳定性。
3.2 过饱和状态下的交叉口群间关系分析基于群体动力学理论分析交叉口群间的关系。当道路出现过饱和状态时,需要采用一个群体动力学算子,将后一周期相位的绿信比在前一周期该相位的绿信比上进行调整,尽可能快速消散车流排队,并且以交叉口群总延误时间最少为目标,以求解各交叉口的信号配时。文献[6]结合潮汐走廊早高峰的实际交通情况,对交叉口群的模型进行了定义。
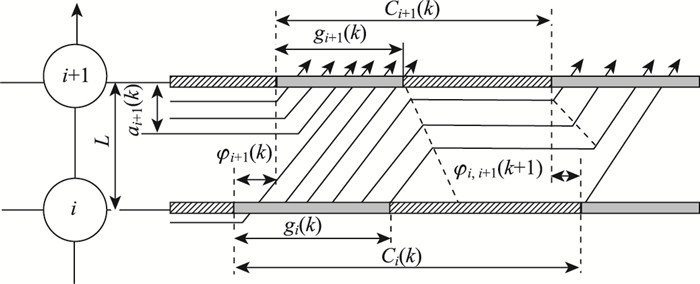
两个相邻交叉口的各个相位之间存在合并、分离两种关系。如图 6所示,合并状态协调的目标是形成车流的连续流动,分离状态协调的目标是避免邻接路段出现拥堵和尽量降低延误[7]。因此,潮汐方向的相邻两交叉口应该是合并关系,其余为分离关系。
|
| 图 6 相邻交叉口信号协同控制示意图 Fig. 6 Schematic diagram of cooperative signal control for adjacent intersections |
| |
基于群体演化的过饱和交通控制方法,对各交叉口的相位绿灯时间做出调整,以减轻过饱和区域的交通压力。将相邻两交叉口的潮汐方向Ii-Ii+1设置成理想相位差,参考文献[8-10],为了使车流排队能够在1个信号周期内消散,则在第k和k+1周期的相位差需要满足:
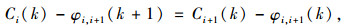
|
(1) |
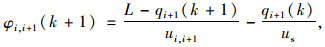
|
(2) |
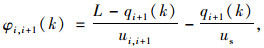
|
(3) |
式中,Ci(k)和Ci+1(k)分别为第k周期交叉口Ii与交叉口Ii+1的周期时长;φi, i+1(k)为第k+1周期交叉口Ii与交叉口Ii+1的理想相位差;L为第交叉口Ii的与交叉口Ii+1的公共路段长度;ui, i+1为交叉口Ii与交叉口Ii+1公共路段上的平均车速;us为车辆启动波波速; qi+1(k)与qi+1(k+1)分别为第k和k+1周期内车辆启动波波速,车流排队长度越长,启动波速越低。
3.3 过饱和状态下交叉口协同控制算法由上述分析,过饱和状态下潮汐走廊过饱和状态的交叉口实时动态协同控制配时算法如下。
Step 1:根据潮汐车道流量饱和之前的信号配时方案B得到初始路段参数,包括路段长度、车道数、信号周期、相位数、绿灯时间、交通量、车流通行权分配等,同时令k=0,采用群体动力学算子,计算出各交叉口协调相位的绿信比。
Step 2:确定第1个交叉口的初始信号周期C1(k),令i=2。
Step 3:根据式(1)~(2),计算交叉口Ii第k周期的周期时长Ci(k)。
Step 4:判断i与N,若i>N,得出各交叉口第k周期的信号周期时长序列;否则返回Step 3。检验各交叉口是否满足最大最小周期的约束条件,若不满足,则返回Step 2,重新生成第k周期的信号时长序列。
Step 5:从交叉口的末端依次往前计算各交叉口第k周期对向交通流的反向相位差。
Step 6:计算交叉口第k周期的总延误,同时更新各项参数。判断k=K是否成立,若满足,则输出总延误,算法结束;否则,令k=k+1,返回Step 1,重新开始计算。
4 双交叉口信号配时优化及仿真分析 4.1 双交叉口协同控制模型关键交叉口的信号配时控制是基于群体演化的过饱和路网交通协调控制研究的关键[7]。针对潮汐走廊的瓶颈路段玉古路,其两端的交叉口即双关键交叉口。对这两个交叉口间的潮汐方向绿灯相位差进行优化,将有助于玉古路潮汐交通的最优化运行。
双交叉口的协同控制模型的目标是使该路段交通流的总行程时间最短,同时通行能力最大, 即:
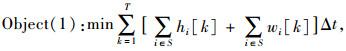
|
(4) |
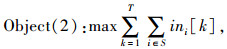
|
(5) |
式中,hi[k]为在第k时间段内路段i的容量;在双交叉口协同控制方案S中,i实际为两个路段;wi[k]为在第k时间段内排队等待进入路段i的车辆数;ini[k]为在第k时间段内进入路段i的平均车流密度。限于篇幅,车道组信号状态、相位差规范等约束条件不赘述。
主要的约束条件有:
(1) 周期和绿时范围约束C∈[Cmin, Cmax]; gip∈[gmin, gmax]其中gip为第i交叉口的第p相位的有效绿灯时长。
(2) 相邻两交叉口的相位差约束gi+1+φi, i+1+ti+1≥gi, i∈SN,对于所有的交叉口控制方案SN,gi为第i交叉口的相关相位绿灯时长,交叉口i与i+1的相位差φi, i+1∈[0, C],i∈SN,ti+1为交叉口i+1的停车波传至上游交叉口i的最大时间,等于交叉口i与i+1之间路段长度Li与交通流在路段i的停车波λi的比值。
(3) 过饱和路况下主要相位的绿灯时长,应大于该相位车流控制的实际有效绿灯时间[11],即gip≥gi-kcnt, flow(k)∈p, p∈P,其中第k周期内的车流flow(k)属于交叉口i的第p相位,p属于所有相位集合P。在下文的仿真模型中,由于输入的交通流为实际的限定数据,因此除需要优化的潮汐方向绿时外,假设其余相位绿灯时长不变。
4.2 VISSIM仿真模型的建立将2016年4月6日~10日一周工作日早高峰时段的实际交通流数据,以及交叉口信号灯配时、车道数量、行车方向等作为VISSIM仿真模型的输入参数,选取流量和流速作为校准参数,构建潮汐走廊早高峰瓶颈路段玉古路及其两端交叉口的基础路况仿真模型。
工作日早7:00实施潮汐车道瓶颈路段玉古路南北两端的交叉口实施配时方案B,至过饱和状态,其主干方向北-南平均流量为1 843 pcu/h,平均流速为22.4 km/h,经校准后的基础模型流量为1 773 pcu/h,流速为23.1 km/h,误差分别为-3.9%及3.1%。饱和状态配时方案B的仿真输出参数见表 2。
| 配时方案 | 流量/(pcu·h-1) | 平均延误时间/s | 停车次数 | 排队长度/m | 流速/(km·h-1) |
| 饱和-定时B | 1 773 | 63.14 | 3.12 | 39.3 | 22.7 |
| 过饱和-实时C | 1 862 | 35.05 | 1.24 | 10.3 | 28.2 |
4.3 过饱和状态下实时协同配时方案的仿真分析
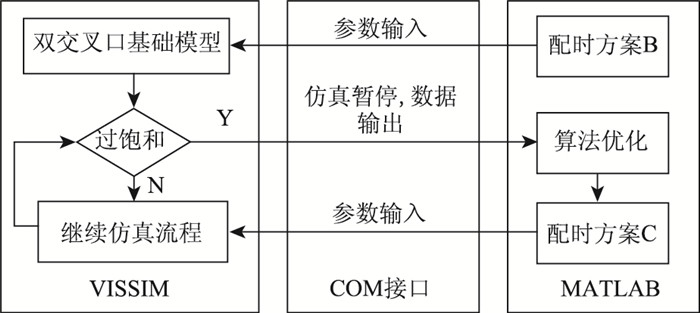
基于基础模型,选取VISSIM的VAP信号控制模块,如图 7所示,进行VISSIM+MATLAB的自适应实时控制仿真,采用过饱和状态下交叉口协同控制算法求解实时配时方案C。控制目标是使车辆由北向南通过玉古路-求是路口的总行程时间最小,同时通行能力最大,即单向绿波[12-14]。约束条件为信号周期小于130 s(方案B为110 s),潮汐相位的绿灯时长最大不超过65 s,其他相位绿灯时长不变。
|
| 图 7 VISSIM+MATLAB的自适应实时控制仿真流程 Fig. 7 Process of adaptive real-time control simulation based on VISSIM+MATLAB |
| |
最优配时方案使仿真系统内的双交叉口潮汐方向车流延误最低,即求是路口北-东的平均延误时间最短。根据2.2节所述条件及文献[15-16],仿真程序通过COM接口调用双交叉口协同控制算法,进行信号重新配时,直至过饱和车流能够在1个信号周期内消散,取通行能力接近实际交通需求且平均延误时间最短最优解,生成方案C实时绿信比。
4.4 仿真结果的输出仿真过程经历了14个信号周期之后,过饱和流量造成的路况拥堵情况得到缓解,此时,方案C玉古路-求是路口第1相位的有效绿灯时长分别为58,62 s,相位差为7 s。仿真结果经整理后,对比饱和状态定时方案B与过饱和状态实时方案C,玉古路北-南流量和流速、求是路口北-东的平均延误时间、停车次数、排队长度如表 2所示。
由仿真数据可见,在满足实际交通流量的前提下(1 843 pcu/h),玉古路北-南的流速由22.7 km/h提高至28.2 km/h,提速24.23%。根据文献[2],作为城市主干道,28.2 km/h的流速在轻度拥堵的25~35 km/h范围,即瓶颈路段由原先的中度拥堵改善为轻度,而行车时间、平均延误时间等参数也均达到了不同程度的优化。
5 结论随着我国汽车保有量的持续增长,国内大中城市的通勤交通拥堵问题日趋严重,进行有效的智能交通实时控制迫在眉睫。在近年来对城市潮汐车道的定量分析中,信号配时实时控制方法的研究尚为空白[17]。经仿真分析验证,当潮汐车道出现过饱和状态时,基于群体动力学算法和VISSIM+MATLAB的自适应仿真控制技术的多交叉口信号配时协同控制,能够有效缓解交通拥堵。
在仿真过程中发现,过饱和状态的瓶颈路段两端的双交叉口协同配时控制达到了一定的效果,但下一路段的车辆流速降低了12.35%,平均延误时间增加了8.96%。这说明,基于群体动力学算法的多交叉口协同配时方案设计,必须强调上下游交通流的关联关系[18],从全局角度进行全路段的交叉口群的协同控制,然而这将大大提高系统的复杂性和仿真建模的难度。此外,在通勤交通中,非机动车和行人对道路的影响也是不可忽略的,今后的研究工作需要同时考虑上述两个方面的影响。
| [1] |
王勇. 城市交通网络可变车道设置方案研究[D]. 成都: 西南交通大学, 2014. WANG Yong. Research on Plan of Reversible Lane in Urban Traffic Network[D]. Chengdu: Southwest Jiaotong University, 2014. http://cdmd.cnki.com.cn/article/cdmd-10613-1014254838.htm |
| [2] |
祝付玲. 城市道路交通拥堵评价指标体系研究[D]. 南京: 东南大学, 2006. ZHU Fu-ling. Research on Index System of Urban Traffic Congestion Evaluation[D]. Nanjing: Southeast University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10286-2007031831.htm |
| [3] |
杨莹莹. 杭州市道路交通高峰拥堵成因分析与对策研究[J]. 城市道桥与防洪, 2012(7): 15-18. YANG Ying-ying. Study on Cause Analysis and Countermeasure of Traffic Jam in Peak Time in Hangzhou[J]. Urban Roads Bridges & Flood Control, 2012(7): 15-18. |
| [4] |
代磊磊, 姜桂艳, 裴玉龙. 饱和信号交叉口排队长度预测[J]. 吉林大学学报:工学版, 2008, 38(6): 1287-1290. DAI Lei-lei, JIANG Gui-yan, PEI Yu-long. Prediction of Queue Length at Saturate Signalized Intersection[J]. Journal of Jilin University:Engineering and Technology Edition, 2008, 38(6): 1287-1290. |
| [5] |
楚天广, 杨正东, 邓魁英, 等. 群体动力学与协调控制研究中的若干问题[J]. 控制理论与应用, 2010, 27(1): 86-93. CHU Tian-guang, YANG Zheng-dong, DENG Kui-ying, et al. Problems in Swarm Dynamics and Coordinated Control[J]. Control Theory & Applications, 2010, 27(1): 86-93. |
| [6] |
黄超. 杭州西湖"潮汐走廊"交通模型及评价研究[D]. 杭州: 杭州电子科技大学, 2016. HUANG Chao. Research on Traffic Model and Evaluation of "Tidal Corridor" in West Lake, Hangzhou[D]. Hangzhou: Hangzhou Dianzi University, 2016. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D824278 |
| [7] |
张敏捷. 基于群体动力学的交通协调控制理论与方法研究[D]. 广州: 华南理工大学, 2013. ZHANG Min-jie. Research on Traffic Coordination Control Theories and Methods Based on Group Dynamics[D]. Guangzhou: South China University of Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10561-1014153504.htm |
| [8] |
JAHANGIRI A, AFANDIZADEH S, KALANTARI N. The Optimization of Traffic Signal Timing for Emergency Evacuation Using the Simulated Annealing Algorithm[J]. Transport, 2011, 26(2): 133-140. |
| [9] |
张邻, 吴伟明, 黄选伟. 基于动态信号配时的非线性规划模型[J]. 公路交通科技, 2014, 31(8): 134-137. ZHANG Lin, WU Wei-ming, HUANG Xuan-wei. A Nonlinear Programming Model Based on Dynamic Signal Timing[J]. Journal of Highway and Transportation Research and Development, 2014, 31(8): 134-137. |
| [10] |
裴玉龙, 蒋贤才. 饱和交通状态下的绿信比优化及其应用研究[J]. 哈尔滨工业大学学报, 2005, 37(11): 1499-1502. PEI Yu-long, JIANG Xian-cai. Green Ratio Optimizing and Application in Saturated Traffic Flow[J]. Journal of Harbin Institute of Technology, 2005, 37(11): 1499-1502. |
| [11] |
王莉, 王明哲, 周丰. 实时自适应交通信号控制CPN建模分析[J]. 公路交通科技, 2008, 25(6): 115-119. WANG Li, WANG Ming-zhe, ZHOU Feng, et al. Modeling and Analyzing of Real-time Adaptive Traffic Signal Control with CPN[J]. Journal of Highway and Transportation Research and Development, 2008, 25(6): 115-119. |
| [12] |
ABU-LEBDEH G, CHEN H, BENEKOHAL R. F. Modeling Traffic Output for Design of Dynamic Mu1ti-cycle Control in Congested Conditions[J]. Journal of Intelligent Transportation Systems, 2007, 11(1): 25-40. |
| [13] |
BEDE Z, SZABÓ G, PÉTER T. Optimalization of Road Traffic with the Applied of Reversible Direction Lanes[J]. Periodica Polytechnica Transportation Engineering, 2010, 38(1): 31-38. |
| [14] |
陈东静, 李林波, 朱锐, 等. 信号交叉口可变车道主预信号配时协调关系研究[J]. 重庆交通大学学报:自然科学版, 2013, 32(2): 252-256. CHEN Dong-jing, LI Lin-bo, ZHU Rui, et al. Coordinate Relationship between Main Signals and Pre-Signals of the Variable Lane at Signalized Intersection[J]. |
| [15] |
王曦, 祝付玲. 基于高斯混合分布的交通拥堵评价模型[J]. 公路交通科技, 2011, 28(2): 127-132. WANG Xi, ZHU Fu-ling. Evaluation Model of Traffic Congestion Based on Gaussian Mixture Distribution[J]. Journal of Highway and Transportation Research and Development, 2011, 28(2): 127-132. |
| [16] |
邵娟, 程琳. 基于Synchro系统的干线绿波控制优化技术[J]. 公路交通科技, 2013, 30(9): 116-121. SHAO Juan, CHENG Lin. Green-wave Control Optimization Technique of Arterial Roads Based on Synchro[J]. Journal of Highway and Transportation Research and Development, 2013, 30(9): 116-121. |
| [17] |
南天伟, 敖梦雅, 魏丽英. 基于模糊神经网络的城市干道信号协调控制[J]. 公路交通科技, 2012, 29(1): 145-149. NAN Tian-wei, AO Meng-ya, WEI Li-ying. Traffic Signal Coordination for Urban Arterial Roads Based on Fuzzy Neural Network[J]. Journal of Highway and Transportation Research and Development, 2012, 29(1): 145-149. |
| [18] |
谢正全. 基于VISSIM的实时数据交通仿真技术的应用研究[D]. 成都: 西南交通大学, 2010. XIE Zheng-quan. Research on Application of Real Time Data Traffic Simulation Technology Based on VISSIM[D]. Chengdu: Southwest Jiaotong University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10613-2010122283.htm |
 2018, Vol. 35
2018, Vol. 35
