扩展功能
文章信息
- 陈一飞, 孙宗光, 邵元
- CHEN Yi-fei, SUN Zong-guang, SHAO Yuan
- 基于长期监测的北方跨海斜拉桥钢箱梁截面温差特性分析
- Analysis on Temperature Difference Characteristic of Steel Box Girder Cross-section of Cable-stayed Bridge over North Sea Based on Long-term Monitoring
- 公路交通科技, 2018, 35(5): 65-72
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(5): 65-72
- 10.3969/j.issn.1002-0268.2018.05.009
-
文章历史
- 收稿日期: 2017-02-20
钢箱梁斜拉桥是受力状态非常复杂,也很容易受到环境侵害的的大型结构。在钢箱梁受到的各种外界荷载中,由太阳辐射、环境温度、风速变化等环境条件所引发的热效应尤其难以预测[1]。对于钢箱梁,由热效应导致的温度应力之大甚至可以与桥梁自身静载应力相比拟[2-3]。由于钢箱梁斜拉桥的结构受力特征,不均匀的温度应力会在主梁、拉索、主塔处产生远比其他桥型严重得多的问题[4-6],对大跨度桥梁的安全性、耐久性产生不利影响。
我国规定大跨度桥梁应有100年的使用寿命,在桥梁的全寿命周期内,温度荷载始终伴随其中。因此,研究由环境因素引起的钢箱梁斜拉桥温度场变化有助于我们揭露与掌握温度荷载对桥梁的影响,一方面为采用钢箱梁作为主梁构造的大跨度桥梁提供设计参考,另一方面为桥梁运营期结构损伤识别、预警以及全寿命周期预测提供支持。
如今,已有越来越多的团队参与到钢箱梁温度荷载效应的研究中来。丁幼亮等人以苏通大桥为研究对象,针对扁平钢箱温差分布特征进行了研究[7],再通过对润扬大桥上的长期监测数据的分析,提出了扁平钢箱梁横截面温差形式,并在此基础上提出了建立扁平钢箱梁温度场全寿命模拟的方法[8-9]。张玉平等应用有限元,模拟江东大桥无铺装层钢箱梁温度梯度分布,采用拟合公式反映无铺装层钢箱梁日照温度梯度[10]。缪长青等对润扬大桥悬索桥钢箱梁进行了现场温度测试,提出了一种适用于六角形扁平钢箱梁的温度梯度分布曲线。通过有限元进行温度效应分析,认为现行规范与实际温度梯度不符[11]。Sang-Hyo Kim等从太阳辐射与环境参数角度出发,分别研究了曲线钢箱梁与施工过程中的钢箱梁斜拉桥问题,并使用了数值模拟的方法进行了钢箱梁温度预测[12-13]。M.T.Yarnold等通过对温度变化及由此引发的结构应变与位移,建立健康监测系统框架下的评价体系,通过实测长期监测数据,在三维空间中建立温度-应变、温度-位移间的非线性关系[14]。
随着桥梁监测数据的积累以及数值模拟工具的引入,钢箱梁温度分布特征、日照辐射热效应等问题已经有了显著的突破。根据设计需求,国内外结构设计相关规范也先后将温度效应引入。然而,针对钢箱梁截面的温差基准值的研究却十分有限,国内外规范大多没有明确定义[15-18]。温差基准值是研究箱梁截面内应力分布的重要参数,确立可靠的温差基准值计算方法将为钢箱梁结构的耐久性与可靠性提供保障。
本研究以坐落于我国北方冰冻海域地区的胶州湾大桥上三座航道桥之一的沧口航道桥为研究对象。大桥安装有大型长期监测系统,自2011年通车以来积累了丰富的响应数据,以主梁跨中截面温度测点数据为基础探讨我国北方跨海钢箱桥梁截面温差基准值的计算方法。
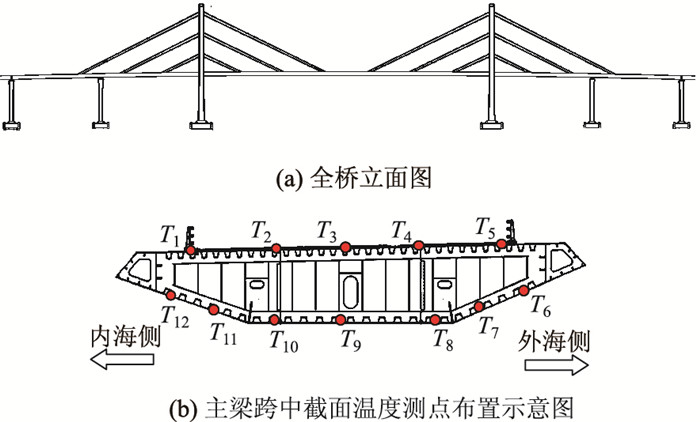
1 主梁截面温度特征 1.1 工程背景胶州湾大桥是中国北方冰冻海域首座特大型桥梁集群工程,全桥长36.48 km。其中沧口航道桥为一座分离双箱梁双塔双索面斜拉桥,主跨为260 m,全桥主梁均为带有加劲肋的钢箱梁。如图 1(a)所示为沧口航道桥立面图,全桥共计8个截面布有温度传感器,图 1(b)所示测点为跨中截面钢结构温度传感器布置位置,截面共计12个温度传感器,其中T1~T5安装于箱梁顶板,T6~T12安装于箱梁底板,在同截面处钢箱梁以外还布有大气温度传感器T0。
|
| 图 1 沧口航道桥立面图与跨中截面温度测点布置示意图 Fig. 1 Elevation and layout of mid-span section temperature measuring points of Cangkou channel bridge |
| |
1.2 年环境温度
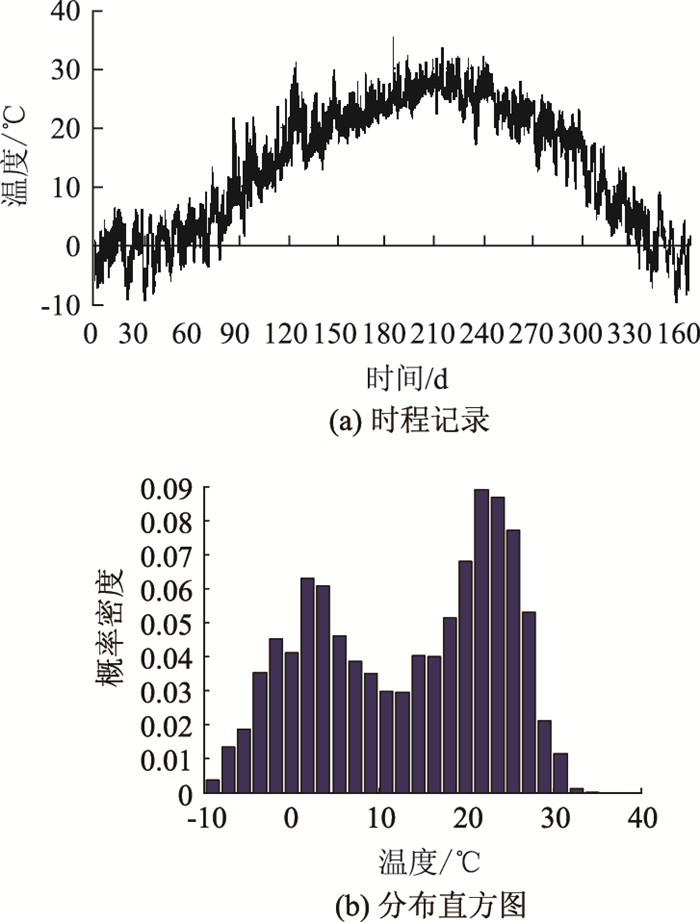
取2012年全年监测数据作为分析样本,温度传感器采样频率为1 Hz,每测点全年共计约316万个数据,为方便分析处理同时满足精度要求,取10 min均值对数据进行压缩,将2012年测点数据重新整理为52 704个数据,如图 2所示为跨中桥面2012全年大气温度时程曲线与概率密度直方图。
|
| 图 2 2012年实测跨中桥面处大气温度 Fig. 2 Measured atmospheric temperature of mid-span of bridge deck in 2012 |
| |
1.3 主要测点间年温差变化
由不均匀的温度分布引发的内应力被称为温度应力,温度应力与温差呈正相关,研究温度应力须分析各温度测点间的温度差异。选取顶板底板各3个测点作为主要测点,即顶板中央与边缘(T1,T3,T5),底板中央与边缘(T6,T9,T12),共6个测点来分析截面温度差异。使用T1,T2等符号表示对应图 1(b)的温度测点,Ti-j±作为温差表达符号,其中i为当前测点,j为对比测点,Ti-j即为i点与j点的温度差,+代表正温差,-代表负温差。
由2012年全年各测点温差整理得到表 1所示数据,可知顶板横向温差最大值20.6 ℃出现在T3-1+,其他顶板测点横向温差也较为明显。顶底板间纵向温差T3-9+十分显著,达到27.9 ℃。底板间横向温差则较小,最高不超过3.1 ℃。综上所述,顶板横向温差与顶底板间温差均十分显著,而底板间横向温差则可忽略不计。
| T3-1 | T3-2 | T3-4 | T3-5 | T3-9 | T9-12 | |
| 最大正温差 | 20.6 | 7.35 | 6.86 | 8.6 | 27.9 | 3.1 |
| 最大负温差 | -3.02 | -3.29 | -2.91 | -1.59 | -5.66 | -1.72 |
| 正温差数据占比/% | 57.22 | 48.37 | 65.04 | 90.51 | 57.04 | 92.95 |
| 负温差数据占比/% | 42.78 | 51.63 | 34.96 | 9.49 | 42.96 | 7.05 |
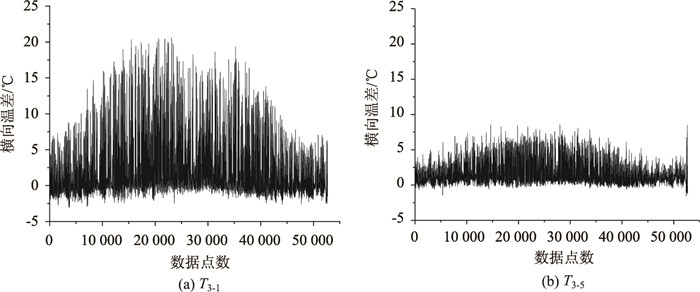
如图 3所示为2012年顶板T1,T3,T5共3个温度测点中T3-1与T3-5变化曲线。由图 3(a)可知,顶板横向温差显著,通常在10 ℃以上,极值超过20 ℃;顶板中央与顶板边缘的温差呈现明显季节性变化,整体趋势与图 2所示年温度变化形式接近,但峰值出现位置有所不同,说明温差变化曲线除受环境温度影响外,还受其他因素影响。此外,由表 1可知T3-1的统计数据中正温差和负温差的数据点数量相差不大,而T3-5的正温差数据则远远多于负温差数据,说明顶板横向温差是不对称的,这与现有其他桥梁统计数据有所不同[5-6],说明顶板横向温度分布可能与桥址地理位置或其他因素有关,并非全为对称分布。
|
| 图 3 2012年主梁跨中截面顶板测点横向温差 Fig. 3 Transverse temperature difference at measuring points of roof of main girder mid-span section in 2012 |
| |
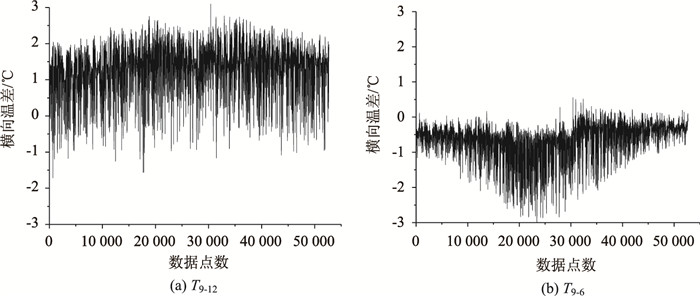
如图 4所示为2012年底板T6,T9,T12共3个温度测点中T9-12与T9-6变化曲线。可知底板中央与边缘的温度差异较小,最大温差不超过3 ℃。由图 4(a)(b)对比可知随时间变化T9-12没有显著变化特征,而T9-6则具有明显的季节性变化规律。
|
| 图 4 2012年主梁跨中截面底板测点横向温差 Fig. 4 Transverse temperature difference at measuring points of bottom of main girder mid-span section in 2012 |
| |
综合图 3与图 4,截面顶板横向温差变化显著、季节特征明显,底板则相对规律性较差、特征不明显,且顶底板中央与两侧边缘温度测点的温差并不对称。
1.4 年温差分布拟合根据上述测点历史数据可知,同一截面上各测点温差随时间变化呈平稳随机过程。可以将温差视为随机变量,通过统计学方法获取对应温差的概率密度分布函数,用以描述各测点间温差特性。由图 3、图 4可知,顶底板的正负温差分布规律有所不同,而产生正温差或负温差对结构带来的影响也不一致,因此分析时应当将温差分正负情况讨论。
通过对各主要测点温差数据分布特征观察并对比拟合误差,最终选择由两个WeiBull分布加权和用于描述正负温差概率密度分布。其计算公式如式(1)所示:
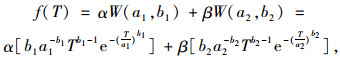
|
(1) |
式中,W(a, b)为Weibull分布函数;a1,b1与a2,b2分别为两个Weibull分布的控制参数;α, β为两个Weibull分布的权重,且α+β=1。
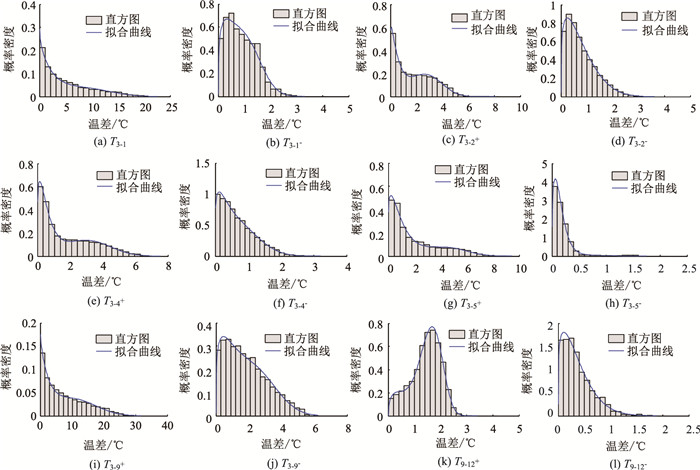
对主梁截面各主要节点间温差实测数据分布进行非线性拟合,如图 5所示,其中顶板横向及顶底板温差以测点T3为参考点。拟合曲线均通过显著性水平0.05的皮尔逊检验,证明加权威布尔分布可以用于描述截面内温差分布,拟合概率密度函数参数如表 2所示。
|
| 图 5 截面各测点正负温差概率密度分布及拟合函数曲线 Fig. 5 Probability density distributions and fitting function curves of positive and negative temperature difference of measuring points on cross-section |
| |
| 温差模式 | 概率密度函数参数 | ||||||||||||
| 正温差 | 负温差 | ||||||||||||
| α | a1 | b1 | β | a2 | b2 | α | a1 | b1 | β | a2 | b2 | ||
| T3-1 | 0.703 | 2.951 | 0.954 | 0.297 | 11.297 | 2.621 | 0.576 | 0.686 | 1.309 | 0.424 | 1.380 | 2.672 | |
| T3-2 | 0.468 | 0.656 | 1.067 | 0.532 | 3.214 | 2.830 | 0.537 | 0.573 | 1.230 | 0.463 | 1.170 | 1.810 | |
| T3-4 | 0.549 | 0.645 | 1.185 | 0.451 | 3.606 | 2.732 | 0.578 | 0.444 | 1.181 | 0.422 | 1.151 | 2.163 | |
| T3-5 | 0.717 | 1.057 | 1.160 | 0.283 | 4.901 | 3.238 | 0.145 | 0.423 | 0.893 | 0.855 | 0.163 | 1.374 | |
| T3-9 | 0.527 | 3.212 | 0.985 | 0.473 | 14.397 | 2.382 | 0.559 | 1.267 | 1.261 | 0.441 | 3.065 | 2.601 | |
| T9-12 | 0.226 | 0.822 | 1.397 | 0.774 | 1.788 | 4.504 | 0.291 | 0.497 | 1.626 | 0.709 | 0.360 | 1.174 | |
2 温差基准值 2.1 极值分布与重现期
温度的基准值是确定温度作用最主要的参数,大气温度基准值一般由气象台记录所得的某年极值气温数据为样本,经统计得到具有一定年超越概率的最高和最低气温。而关于如何确定结构上的极值温差,还没有统一的方案[12-15]。我国行业标准《铁路桥涵设计基本规范》(TB 10002.1—2005)采用7月份和1月份的月平均气温;《公路桥涵设计通用规范》(JTG D60—2015用有效温度并将全国分为3个区来规定;《建筑结构荷载规范》(GB 50009—2012)将基本气温定义为50年一遇的月平均最高和月平均最低气温,根据最近30年历年最高温度月的月平均最高和最低温度月的月平均最低气温为样本。欧洲规范(EN1991-1-5:—2003)采用小时最高和最低气温为样本,并将气温基准值确定为具有50年重现期的作用值。
参阅相关规范并结合统计学方法整理出如下思路。根据温度基准值的定义,由已知的N年温差数据确定极值样本的概率分布,再分别计算年极大值温差的取值超过特定值的发生概率或年极小值温差低于特定值的发生概率,最后通过指定重现期获得对应的温差基准值。需要注意的是,极值分布要求各次观测必须相互独立且服从同一分布。
根据以往记录数据拟合的某测点组间年温差分布函数为F(x),即原始分布函数,每次从原始温差中抽取n个样本x1, x2,…,xn,他们满足独立同分布,则其极大值和极小值分别为:
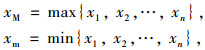
|
(2) |
则根据极值分布理论,其极大值和极小值分布函数可由原始分布函数F(x)确定:
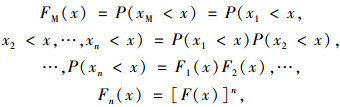
|
(3) |
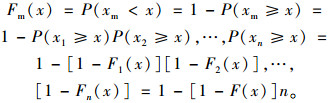
|
(4) |
可见,极值分布只与原始分布函数F(x)和抽样样本容量n有关。
得到极值分布后,由于极大极小极值重现期定义为正负温差超过某一指定值的概率的倒数,如式(5)所示,通过指定特定重现期即可计算出对应重现期的温差极值。
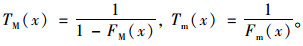
|
(5) |
基于上述方案,对钢箱梁截面各测点间温差基准值进行计算。使用加权威布尔分布描述温差分布模型,其概率密度函数为式(1),公式内各参数如表 2所示,则原始分布函数如式(6)所示:
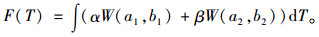
|
(6) |
将式(6)分别代入式(3)、式(4),可得对应温差的极大、极小分布函数。根据2.4节的结论,钢箱梁截面上顶板横向温差和顶底板间温差最为显著,远远高于其他温度测点间温差,因此着重关注顶板横向温差T3-1及顶底板温差T3-9。
由于极值分布计算结果受原始分布函数F(x)影响显著,故取2012-2015共4年监测数据作为样本,以获得更为精确的计算结果。而影响计算结果的另一参数,抽样样本容量n,如图 6所示,为T3-9+与T3-9-的温差极值分布与抽样本容量n不同取值时的对比。
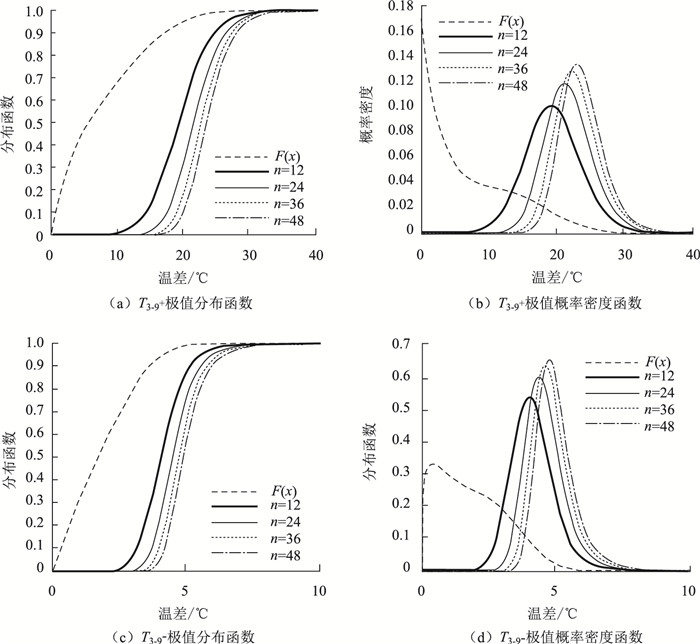
|
| 图 6 T3-9极值分布函数与样本容量n的关系 Fig. 6 Relationship between T3-9 extreme distribution function and sample size n |
| |
由图 6可知,随抽样样本容量n的上升,分布函数曲线及概率密度函数曲线逐步向极端靠近,其方差逐步缩小,说明更高温差极值出现的几率上升,意味着以相同重现期计算的温差基准值要更大。基于现有规范,假定以每月极值作为样本,年样本抽样n=12,在此基础上计算箱梁截面温差最为显著的两组测点温差T3-1与T3-9在不同重现期条件下的极值温差。计算结果如表 3所列。其中50年重现期的顶板横向温差达21.42 ℃,顶底板竖向正温差达28.53 ℃。
| 重现期/年 | T3-1+ | T3-1- | T3-9+ | T3-9- |
| 10 | 18.35 | 3.29 | 24.68 | 5.17 |
| 20 | 19.71 | 3.72 | 26.40 | 5.57 |
| 30 | 20.46 | 4.03 | 27.35 | 5.81 |
| 40 | 21.00 | 4.34 | 28.02 | 6.00 |
| 50 | 21.42 | 4.68 | 28.53 | 6.15 |
| 100 | 22.77 | 6.94 | 30.18 | 6.66 |
箱梁温度测点差异主要来源于日照辐射作用,根据桥面顶板测点历史温度数据,顶板横向温差与竖向温差最为显著的时段为12:00—15:00,该区间为日照最为强烈的时段,沧口航道桥桥面为沥青铺装,对日照辐射吸收较多,故T3温度上升显著;T1所处位置为护栏与斜拉索锚固区,太阳辐射吸收较少,升温较小;T9位于箱梁底板处,无日光直射,温度与大气温度接近,故此顶板横向与顶底板竖向均形成了显著的温度差异。
《公路桥涵设计通用规范》(JTG D60—2015)对于沥青混凝土铺装层,竖向正温差基准值为20 ℃,表 3所示计算值(28.53 ℃)超过规范值,说明将现行规范用于青岛地区梁截面竖向温差基准值的确定是不够准确的。
3 结论(1) 沧口航道桥钢箱梁顶板横向温差与顶底板竖向温差均较大,且主梁截面顶底板温度分布呈明显不对称性,说明横向温度分布与桥址环境等因素有关。
(2) 采用加权Weibull分布对胶州湾大桥沧口航道跨中截面顶板与底板各主要测点温差进行概率密度分布拟合,拟合结果良好。
(3) 基于极值分布的箱梁截面温差基准值计算方法,先根据完整连续实测数据建立原始温差分布函数,再计算极值分布确定极大、极小值分布函数,最终通过给定重现期计算对应温差基准值,其中抽样样本容量n取值对结果存在一定影响。
(4) 根据算例,得到年样本抽样n=12时,50年重现期下钢箱梁截面温差最为显著的两组测点的温差基准值:T3-1+为21.42 ℃,T3-9+为28.53 ℃,其中竖向温差T3-9+超过了规范给定的20 ℃。对于钢箱梁,这样的温差将产生显著的温度应力,应当在设计与监测时给予足够的重视。
| [1] |
LEE J H. Behavior of Precast Prestressed Concrete Bridge Girders Involving Thermal Effects and Initial Imperfections During Construction[J]. Engineering Structures, 2012, 42(12): 1-8. |
| [2] |
孙君, 李爱群, 丁幼亮. 润扬长江大桥钢箱梁的温度分布监测与分析[J]. 公路交通科技, 2009, 26(8): 94-98. SUN Jun, LI Ai-qun, DING You-liang. Observation and Research on Temperature Distribution in Steel Box Girders of Runyang Yangtse River Bridge[J]. Journal of Highway and Transportation Research and Development, 2009, 26(8): 94-98. |
| [3] |
陈权, 王丽娟, 张元海, 等. 连续箱梁的日照温差应力计算研究[J]. 公路交通科技, 2009, 26(8): 99-104. CHEN Quan, WANG Li-juan, ZHANG Yuan-hai, et al. Study on Calculation of Sunshine Thermal Stress in Continuous Box-girders[J]. Journal of Highway and Transportation Research and Development, 2009, 26(8): 99-104. |
| [4] |
TONG M, THAM L G, AU F T K, et al. Numerical Modelling for Temperature Distribution in Steel Bridges[J]. Computers and Structures, 2001, 79(6): 583-593. |
| [5] |
吴六政. 混凝土箱梁桥温度场的模拟[J]. 公路交通科技, 2011, 28(10): 65-69. WU Liu-zheng. Simulation of Temperature Field of Concrete Box-girder Bridge[J]. Journal of Highway and Transportation Research and Development, 2011, 28(10): 65-69. |
| [6] |
LIU H B, CHEN Z H, ZHOU T. Theoretical and Experimental Study on the Temperature Distribution of H-shaped Steel Members under Solar Radiation[J]. Applied Thermal Engineering, 2012, 37: 329-35. |
| [7] |
王高新, 丁幼亮, 王晓晶, 等. 苏通大桥扁平钢箱梁温度场长期监测与统计分析[J]. 公路交通科技, 2014, 21(2): 69-73. WANG Gao-xin, DING You-liang, WANG Xiao-jing, et al. Long-term Monitoring and Statistical Analysis of Temperature Field of Flat Steel-box Girder of Sutong Bridge[J]. Journal of Highway and Transportation Research and Development, 2014, 21(2): 69-73. |
| [8] |
周广东, 丁幼亮, 李爱群, 等. 基于长期实测数据的大跨悬索桥扁平钢箱梁温差特性研究[J]. 土木工程学报, 2012, 45(5): 114-125. ZHOU Guang-dong, DING You-liang, LI Ai-qun, et al. Thermal Difference Characteristic Analysis of a Flat Steel Box Girder in Long-span Suspension Bridge Based on Long-term Field Measurement Data[J]. China Civil Engineering Journal, 2012, 45(5): 114-125. |
| [9] |
丁幼亮, 王高新, 周广东, 等. 基于现场监测数据的润扬大桥斜拉桥钢箱梁温度场全寿命模拟方法[J]. 土木工程学报, 2013, 46(5): 129-136. DING You-liang, WANG Gao-xin, ZHOU Guang-dong, et al. Life-cycle Simulation Method of Temperature Field of Steel Box Girder for Runyang Cable-stayed Bridge Based on Field Monitoring Data[J]. China Civil Engineering Journal, 2013, 46(5): 129-136. |
| [10] |
张玉平, 杨宁, 李传习. 无铺装层钢箱梁日照温度场分析[J]. 工程力学, 2011, 28(6): 156-162. ZHANG Yu-ping, YANG Ning, LI Chuan-xi. Research on Temperature field of Steel Box Girder without Pavement Caused by the Solar Radiations[J]. Engineering Mechanics, 2011, 28(6): 156-162. |
| [11] |
缪长青, 史长华. 大跨悬索桥扁平钢箱梁温度梯度与温度影响研究[J]. 中国科学:技术科学, 2013, 43(10): 1155-1164. MIU Chang-qing, SHI Chang-hua. Temperature Gradient and Its Effect on Flat Steel Box Girder of Long-span Suspension Bridge[J]. Scientia Sinica:Technologica, 2013, 43(10): 1155-1164. |
| [12] |
KIM S H, CHO K I, WON J H, et al. A Study on Thermal Behaviour of Curved Steel Box Girder Bridges Considering Solar Radiation[J]. Archives of Civil and Mechanical Engineering, 2009, 9(3): 59-76. |
| [13] |
KIM S H, PARK S J, WU J X, et al. Temperature Variation in Steel Box Girders of Cable-stayed Bridges During Construction[J]. Journal of Constructional Steel Research, 2015, 112: 80-92. |
| [14] |
YARNOLD M T, MOON F L. Temperature-based Structural Health Monitoring Baseline for Long-span Bridges[J]. Engineering Structures, 2015, 86: 157-167. |
| [15] |
TB 10002. 1-2005, 铁路桥涵设计基本规范[S]. TB 10002. 1-2005, Fundamental Code for Design on Railway Bridge and Culvert[S]. |
| [16] |
JTG D60-2015, 公路桥涵设计通用规范[S]. JTG D60-2015, General Code for Design of Highway Bridges and Culverts[S]. |
| [17] |
GB 50009-2012, 建筑结构荷载规范[S]. GB 50009-2012, Load Code for the Design of Building Structures[S]. |
| [18] |
BS EN 1991-1-5: 2003, Eurocode 1: Actions on Structures-Part 1-5: General Actions-Thermal Actions[S].
|
 2018, Vol. 35
2018, Vol. 35
