扩展功能
文章信息
- 王荣霞, 任腾腾, 宋娃丽, 张宇明
- WANG Rong-xia, REN Teng-teng, SONG Wa-li, ZHANG Yu-ming
- 斜交连续T梁桥的动力特性分析及试验
- Analysis and Experiment on Dynamic Characteristics of Skew Continuous T-beam Bridge
- 公路交通科技, 2018, 35(5): 57-64, 72
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(5): 57-64, 72
- 10.3969/j.issn.1002-0268.2018.05.008
-
文章历史
- 收稿日期: 2017-09-29
2. 廊坊市交通勘察设计院, 河北 廊坊 065000
2. Langfang Transport Survey and Design Institute, Langfang Hebei 065000, China
近年来,在高等级公路与城市立交桥中,为满足安全及线形要求,修建了大量斜桥。由于斜交角的存在,斜桥的力学特性与正桥有明显不同,其设计计算也与正桥有所不同[1]。
目前,国内外学者对斜桥的动力特性进行了较为广泛的研究。刘华[2]通过对一座斜桥进行固有模态分析,认为斜交角是影响公路桥梁冲击系数的一个重要因素;张等[3]提出了斜交T形简支梁桥的基频随斜交角度变化的修正公式;刘小燕[4]和吴桥[5]对规范中的基频公式进行了修正,提出了预应力简支空心板桥的基频修正公式,并分析了预应力筋效应对频率的影响;夏樟华[6]以某三跨简支T梁桥为背景,分析了不同斜交角时该类桥动力特性的差异;夏桂云[7]建立了单跨斜梁桥的理论解析,总结了单跨斜梁桥频率的变化特征;Makle[8]和Afshin[9]分析了斜桥的自振特性;卢明奇[10]分析了斜度和支座剪切刚度对斜交连续梁桥自振周期的影响;许永吉[11]的试验研究表明在斜交桥设计中,合理选择斜交角对桥梁动力性能有很大影响;何旭辉[12]通过对实桥模型试验研究,总结了斜交箱梁振动的变化规律。综上所述,已有文献缺乏对连续斜交T梁桥动力特性的深入研究。
众所周知,现行《公路桥涵设计通用规范》(JTG D60—2015)(以下简称“桥规”)在计算连续梁桥的冲击系数时,给出了结构基频的通用计算公式,但是这一公式并未区分正桥和斜桥,因此并不能得到斜交桥梁准确的基频值。这就需要深入研究连续斜交T梁桥结构的动力特性,为此类桥梁设计提供科学的理论指导。
本研究以河北省某高速公路上的一座三跨连续斜交T梁桥为背景,应用Midas Civil建立空间梁格模型,计算分析结构的振型与自振频率在不同斜交角度下的变化规律,并根据计算结果对《桥规》中计算连续梁桥冲击系数时所采用的基频公式进行了修正,提出了适用于三跨连续斜交T梁桥基频计算的修正公式,最后结合实桥试验验证了该公式的合理性。本研究结论可为此类桥梁结构设计提供指导,具有重要的理论和实用价值。
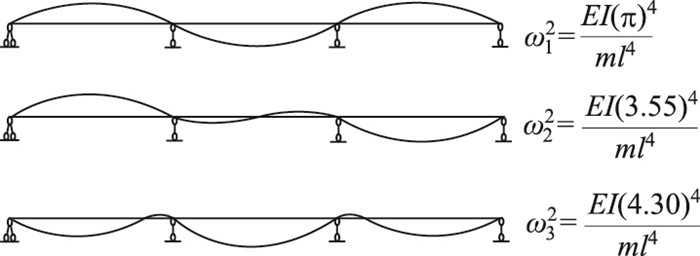
1 三跨连续梁的弯曲固有振动分析 1.1 三跨均匀正交连续梁的振动分析根据文献[13]对于正交三等跨连续梁结构,若每跨采用相同截面,且假设每跨连续梁具有均匀分布的质量和刚度,其前三阶振型及其相应的固有频率(ω1,ω2,ω3)计算公式如图 1所示。
|
| 图 1 三等跨连续梁的振型及固有频率 Fig. 1 Vibration modes and natural frequencies of 3-equal-span continuous beam |
| |
然而,上述连续梁自振频率的计算公式只适用于等跨正交连续梁桥,并不完全适用于所有连续梁桥结构,尤其是对于斜交连续梁桥,其斜交角度的影响并未考虑其中,不能有效指导斜桥的实际工程设计。
1.2 三跨连续斜梁桥的振动分析文献[14]和文献[15]根据多跨斜梁桥振动分析的递推算法[14]与刚度矩阵法[15],得到了三跨连续斜梁结构关于自振频率的超越方程,并进行了自振频率的求解。但是该求解公式只针对于单梁的振动求解是有效的,它忽略了主梁数量及主梁之间的联结方式、支座约束、阻尼的存在等因素的影响,使得实际斜梁桥结构不能直接应用所提出的公式得到基频的精确解,需依靠有限元方法进行求解。
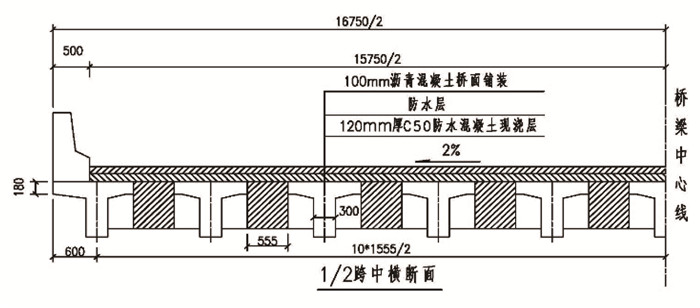
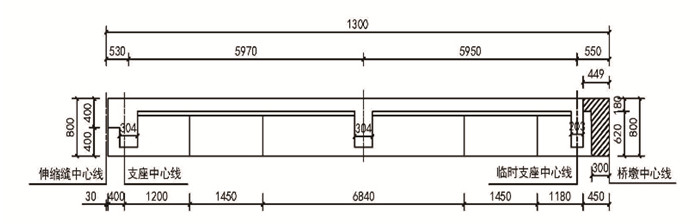
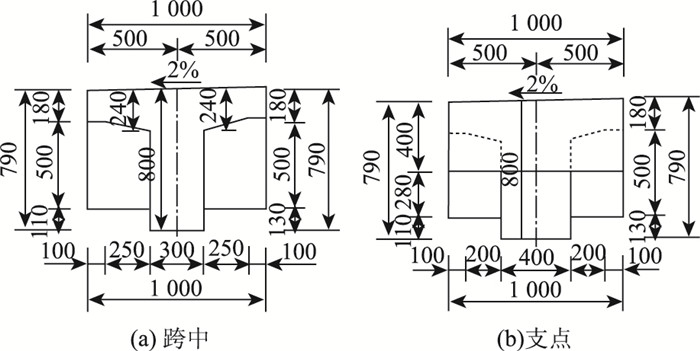
2 工程背景及有限元模型的建立 2.1 工程背景该桥为3×13 m预应力钢筋混凝土连续斜交T梁桥,设计荷载为公路-Ⅰ级,采用圆板式橡胶支座,斜交角度为40°,行车道宽15.75 m,上部结构由11片T梁组成,其纵横断面布置及主梁几何尺寸见图 2~图 4。
|
| 图 2 主梁跨中横断面图(单位:mm) Fig. 2 Cross-section of mid-span of main girder (unit:mm) |
| |
|
| 图 3 主梁纵断面图(单位:mm) Fig. 3 Longitudinal section of main girder (unit: mm) |
| |
|
| 图 4 主梁截面尺寸(单位:mm) Fig. 4 Dimensions of girder section (unit: mm) |
| |
2.2 有限元模型的建立 2.2.1 斜桥梁格模型
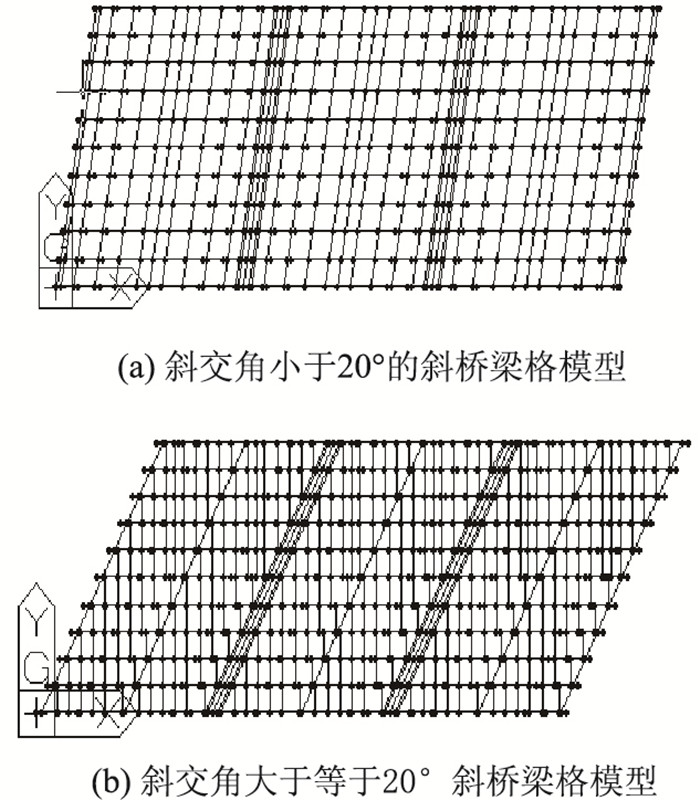
根据梁格法的基本原理[16],本研究建立的有限元模型中,除了实际设置的横隔板外还设置了虚拟横梁。当斜交角小于20°时,虚拟横梁为平行于横隔板(或支承线)方向,如图 5(a)所示;当斜交角大于20°时,梁格中的纵横向构件设置成正交的[16],如图 5(b)所示。
|
| 图 5 斜桥的梁格模型 Fig. 5 Grillage models of skew bridge |
| |
应用梁格法建立不同角度的斜桥有限元模型,其斜交角为0°~60°(间隔相差5°)。模型中共设11根纵梁,每一纵梁代表一片T梁,纵梁之间的连接方式分为刚性连接和铰接[17]。
为尽可能准确地模拟实际结构,本研究所建模型考虑了桥面铺装(包括水泥混凝土现浇层和沥青混凝土)对结构质量的影响,以及水泥混凝土桥面铺装对截面惯性矩的影响[18-19]。
2.2.2 模型中设计参数的确定模型中各设计参数为:混凝土强度为C50,弹性模量3.45×104 MPa,质量密度2 600 kg/m3。预应力筋抗拉强度标准值fpk=1 860 MPa,公称直径d=15.2 mm,弹性模量Ep=1.95×104 MPa,设计张拉控制力为0.75fpk。支座采用点弹簧模拟,桥台处弹簧刚度系数SDx=2 718 685.95 kN/m,SDy=SDz=1 359.34 kN/m,SRx=SRy=Sz=0;桥墩处弹簧刚度系数SDx=3 054 326.19 kN/m,SDy=SDz=1 527.16 kN/m,SRx=SRy=SRz=0。
3 有限元计算结果与分析将第2节的三跨连续斜交T形梁结构,按主梁之间采用刚接和铰接两种不同的连接方式分为两组,共计算了斜交角φ从0°~60°(间隔相差5°)共13×2种有限元模型的固有振型及相应的自振频率。
3.1 主梁之间为刚接的模型计算结果及分析 3.1.1 振型结果及分析表 1所示为不同斜交角度的三跨连续斜交T梁桥有限元模型的前7阶固有振型图。
| 模态 | 正桥 (斜交角度为0°) |
斜桥 (斜交角度为5°~10°) |
斜桥 (斜交角度为15°~60°) |
| 1阶 | 
|

|

|
| 2阶 | 
|
|

|
| 3阶 | 
|

|

|
| 4阶 | 
|

|

|
| 5阶 | 
|
|

|
| 6阶 | 
|

|

|
| 7阶 | 
|

|

|
根据连续梁固有振动理论[13],《桥规》中计算连续梁冲击力采用的自振频率应是与竖弯振型相对应的自振频率值。从表 1中可以看出,随着斜交角度的增大,模型的前两阶竖弯振型恒定为固有振型的一、三阶,而第三阶竖弯振型从固有振型的第五阶变化到了第七阶。因此,当斜交角较大时,其结构动力特性的变化是不容忽视的,需要在设计时注意。
3.1.2 自振频率结果及分析根据第3.1.1节,竖弯振型相对应的自振频率是设计者更为关注的参数,因此表 2给出了不同斜交角度三跨连续斜交T梁桥模型的前三阶竖弯振型相对应的自振频率计算结果。
| 斜交角φ/(°) | fs1/Hz | 相对正桥增大百分比/% | fs2/Hz | 相对正桥增大百分比/% | fs3/Hz | 相对正桥增大百分比/% |
| 0 | 7.769(7.589) | 0.00 | 10.075(9.691) | 0.00 | 13.885(14.219) | 0.00 |
| 5 | 8.046 | 3.57 | 10.426 | 3.48 | 14.441 | 4.00 |
| 10 | 8.049 | 3.61 | 10.433 | 3.55 | 14.429 | 3.92 |
| 15 | 8.109 | 4.38 | 10.505 | 4.27 | 14.518 | 4.56 |
| 20 | 8.186 | 5.37 | 10.616 | 5.37 | 14.616 | 5.26 |
| 25 | 8.318 | 7.07 | 10.793 | 7.13 | 14.799 | 6.58 |
| 30 | 8.481 | 9.17 | 11.018 | 9.36 | 15.032 | 8.26 |
| 35 | 8.730 | 12.38 | 11.334 | 12.50 | 15.355 | 10.58 |
| 40 | 9.072 | 16.78 | 11.766 | 16.78 | 15.787 | 13.69 |
| 45 | 9.529 | 22.66 | 12.144 | 20.54 | 16.246 | 17.00 |
| 50 | 10.215 | 31.49 | 12.603 | 25.09 | 16.791 | 20.93 |
| 55 | 11.085 | 42.70 | 13.150 | 30.52 | 17.133 | 23.39 |
| 60 | 12.120 | 56.02 | 13.932 | 38.28 | 17.637 | 27.02 |
| 注:括号内的数值为斜交角0°(正桥)时应用动力学理论公式(2)计算的自振频率结果。 | ||||||
由表 1和表 2可以看出,当斜交角为0°时,该桥有限元模型的前三阶竖弯振型及其相应的自振频率值与图 1中的理论振型和理论频率基本一致,前三阶竖弯自振频率的理论值与计算值的相对误差均小于5%,且由于本研究模型考虑了铺装层和支座刚度影响,其频率计算值稍大于理论计算值,说明考虑这些因素影响后模型的刚度是有所增加的。
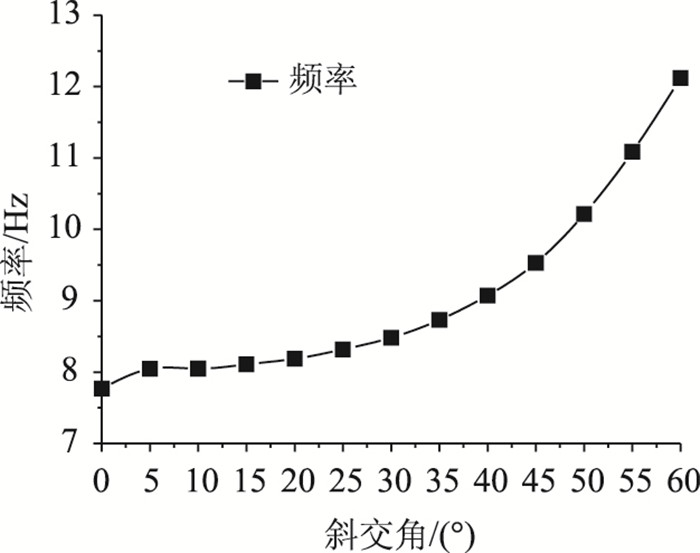
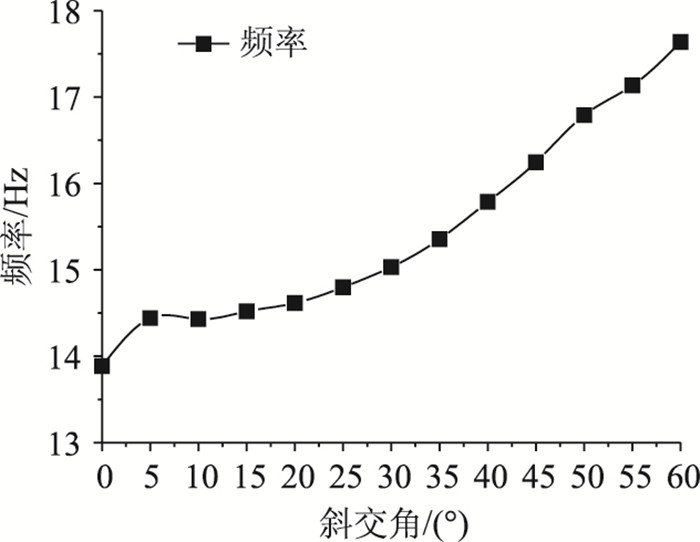
根据已有研究结论,在计算三跨连续梁桥冲击力引起的正弯矩效应及剪力效应时,冲击系数应按表 2中第一阶竖弯振型对应的基频fs1计算,计算负弯矩效应时冲击系数应按表 2中第三阶竖弯振型对应的自振频率fs3计算[20]。采用最小二乘法对表 2中的数据进行拟合,得到频率fs1和fs3随斜交角变化的拟合曲线如图 6和图 7所示。
|
| 图 6 基频fs1拟合曲线 Fig. 6 Fitting curve of fundamental frequency fs1 |
| |
|
| 图 7 基频fs2拟合曲线 Fig. 7 Fitting curve of fundamental frequency fs3 |
| |
由图 6、图 7曲线可知,结构各阶自振频率值均随着斜交角度的增加而增大,且从0°到5°的频率值有一个小突变,在5°~30°区段,频率增加的幅度缓慢,当大于30°时,频率随斜交角增大的幅度逐渐加大。分析表明,在斜交角小于30°时,斜桥基频值与正桥相近,可以按正桥考虑;当斜交角大于30°时,应按斜桥进行计算,否则将会产生较大的误差。如斜交角为45°的斜桥基频比正桥增大22.66%,若按《桥规》公式计算冲击系数将比正桥增大10.42%,这在设计时必须引起注意。
此外,根据连续梁固有振动理论[13],对于图 1中正交三跨连续梁桥的前三阶竖弯自振频率,存在比例关系为fs1: fs2:fs3=π2:3.552:4.32(即竖弯振型前三阶频率的比值)。而本研究中对不同斜交角度的三跨连续斜梁桥的计算结果进一步表明,这一比例关系对于在某斜交角度范围内的斜交连续梁桥仍然适用。表 3列出了由模型计算出的一阶竖弯自振频率按照上述比例关系推出的二、三阶竖弯自振频率,并将按比例计算的数值与有限元模型计算结果进行了比较。
| 斜交角/(°) | 一阶自振频率fs1/Hz | 二阶自振频率fs2/Hz | ①和②的误差/% | 三阶自振频率fs3/Hz | ①和②的误差/% | ||
| ①按比例计算 | ②模型计算 | ①按比例计算 | ②模型计算 | ||||
| 0 | 7.769 | 9.920 | 10.075 | 1.5 | 14.554 | 13.885 | 4.8 |
| 5 | 8.046 | 10.274 | 10.426 | 1.5 | 15.073 | 14.441 | 4.4 |
| 10 | 8.049 | 10.278 | 10.433 | 1.5 | 15.079 | 14.429 | 4.5 |
| 15 | 8.109 | 10.354 | 10.505 | 1.4 | 15.192 | 14.518 | 4.6 |
| 20 | 8.186 | 10.453 | 10.616 | 1.5 | 15.336 | 14.616 | 4.9 |
| 25 | 8.318 | 10.621 | 10.793 | 1.6 | 15.582 | 14.799 | 5.3 |
| 30 | 8.481 | 10.830 | 11.018 | 1.7 | 15.889 | 15.032 | 5.7 |
| 35 | 8.730 | 11.148 | 11.334 | 1.6 | 16.356 | 15.355 | 6.5 |
| 40 | 9.072 | 11.584 | 11.766 | 1.5 | 16.996 | 15.787 | 7.7 |
| 45 | 9.529 | 12.168 | 12.144 | 0.2 | 17.852 | 16.246 | 9.9 |
| 50 | 10.215 | 13.043 | 12.603 | 3.5 | 19.137 | 16.791 | 14.0 |
| 55 | 11.085 | 14.155 | 13.150 | 7.6 | 20.768 | 17.133 | 21.2 |
| 60 | 12.120 | 15.477 | 13.932 | 11.1 | 22.707 | 17.637 | 28.7 |
由表 3可以看出,对于二阶自振频率fs2,当斜交角小于50°时,由一阶频率按比例计算的数值与模型计算值无明显差距;当斜交角为55°~60°时,两者误差则变得明显。对于三阶自振频率fs3,当斜交角小于40°时,由一阶频率按比例计算的数值与模型计算值相差不太大,而大于40°以后两者误差变得明显。因此可以认为,当斜交角度小于40°时,三跨斜交连续梁桥的前三阶竖弯振型频率仍然满足和正桥相同的比例关系:fs1: fs2:fs3=π 2:3.552:4.32。
在实际工程中,对于预应力混凝土梁桥,在进行动载试验时,由于跑车或跳车荷载的频率低于结构的第三阶固有频率,无法激起结构的高频振动;且结构的阻尼使结构高频振动迅速衰减[20],很难测得第三及更高阶的模态,只能测得第一阶频率。因此对斜交角小于40°的预应力混凝土连续斜交梁桥,可利用测得的一阶自振频率通过上述比例关系推导得出第三阶自振频率,作为在计算连续梁桥冲击力引起的负弯矩效应时采用的自振频率数值。此结论对实际工程设计具有重要的参考和指导意义。
3.2 主梁之间为铰接的模型计算结果及分析 3.2.1 振型结果及分析当主梁之间的连接为铰接时,结构固有振型及其竖弯振型分布规律与刚接模型相同(见表 1)。
3.2.2 自振频率结果及分析当主梁之间为铰接时,结构竖弯振型对应的自振频率计算结果以及与刚接模型的计算结果对比见表 4。
| 斜交角/(°) | ①刚接模型竖弯振型频率/Hz | ②铰接模型竖弯振型频率/Hz | ①和②结果相对误差/% | ||||||||
| 1阶 | 2阶 | 3阶 | 1阶 | 2阶 | 3阶 | 1阶 | 2阶 | 3阶 | |||
| 0 | 7.769 | 10.075 | 13.885 | 7.769 | 10.075 | 13.885 | 0.00 | 0.00 | 0.00 | ||
| 5 | 8.046 | 10.426 | 14.441 | 8.046 | 10.426 | 14.441 | 0.00 | 0.00 | 0.01 | ||
| 10 | 8.049 | 10.433 | 14.429 | 8.049 | 10.432 | 14.427 | 0.00 | 0.01 | 0.01 | ||
| 15 | 8.109 | 10.505 | 14.518 | 8.109 | 10.505 | 14.518 | 0.00 | 0.00 | 0.00 | ||
| 20 | 8.186 | 10.616 | 14.616 | 8.185 | 10.611 | 14.609 | 0.02 | 0.05 | 0.05 | ||
| 25 | 8.318 | 10.793 | 14.799 | 8.314 | 10.783 | 14.785 | 0.04 | 0.09 | 0.09 | ||
| 30 | 8.481 | 11.018 | 15.032 | 8.476 | 11.001 | 15.010 | 0.07 | 0.15 | 0.15 | ||
| 35 | 8.730 | 11.334 | 15.355 | 8.720 | 11.307 | 15.320 | 0.12 | 0.24 | 0.22 | ||
| 40 | 9.072 | 11.766 | 15.787 | 9.055 | 11.725 | 15.738 | 0.19 | 0.35 | 0.31 | ||
| 45 | 9.529 | 12.144 | 16.246 | 9.499 | 12.078 | 16.161 | 0.32 | 0.54 | 0.52 | ||
| 50 | 10.215 | 12.603 | 16.791 | 10.174 | 12.533 | 16.708 | 0.40 | 0.56 | 0.49 | ||
| 55 | 11.085 | 13.150 | 17.133 | 11.021 | 13.066 | 17.012 | 0.58 | 0.64 | 0.71 | ||
| 60 | 12.120 | 13.932 | 17.637 | 12.013 | 13.818 | 17.445 | 0.89 | 0.82 | 1.09 | ||
从表 4可以看出,总体上铰接T梁结构的自振频率略低于刚接T梁结构,T梁之间刚接或铰接的不同连接方式,对结构自振频率的影响很小,最大相对误差在1%左右,此影响可忽略不计。该结论与文献[16]中的研究结论是一致的。
4 三跨连续斜交T梁桥基频修正公式根据表 2中数据及图 6、图 7所示的曲线关系,在考虑斜交角影响的基础上对《桥规》中计算冲击系数时所采用的基频计算公式进行修正,得到考虑斜交角φ影响的基频修正公式。
(1) 计算连续梁桥冲击力引起的正弯矩效应及剪力效应时采用的基频fx1:
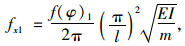
|
(1) |
式中f(φ)1为考虑斜交角φ影响的正弯矩及剪力效应计算时采用的基频修正系数。
当0°≤φ≤5°时:
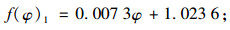
|
(2) |
当5° < φ≤30°时:
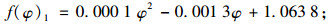
|
(3) |
当30° < φ≤60°时:
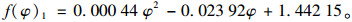
|
(4) |
(2) 计算连续梁桥冲击力引起的负弯矩效应时采用的基频fx2:
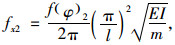
|
(5) |
式中f(φ)2为考虑斜交角φ影响的负弯矩效应计算时采用的基频修正系数。
当0°≤φ≤5°时:
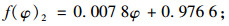
|
(6) |
当5° < φ≤30°时:
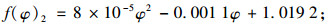
|
(7) |
当30° < φ≤60°时:
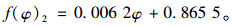
|
(8) |
对于公式(1)~(8),当斜交角度小于30°时频率计算可按正桥考虑,式(2),(3)和式(6),(7)可仅作为参考。当斜交角度大于30°时,则需要应用式(4)和式(8)计算得到更精确的频率值。根据第4节的研究结论,同样适用于主梁之间为铰接的三跨连续斜交T梁桥基频的计算。
5 实桥动载试验 5.1 试验方案对所依托的工程——三跨连续斜交T梁桥(斜交角为40°)进行现场动载试验。试验现场采用TST5926E无线环境激励试验模态采集分析系统采集和处理信号数据,包括数据采集仪器(如图 8所示)和数据分析系统软件。

|
| 图 8 TST5926系列大型结构动态特性测试采集器 Fig. 8 TST5926 series large structure dynamic characteristic test collector |
| |
试验测点选取边跨跨中和中跨跨中位置。两辆试验车重量分别为448.2 kN和414 kN。试验工况如下:
工况一:试验车以60 km/h匀速驶过该桥,分别在边跨和中跨跨中测得该桥自振频率f1和f2;
工况二:试验车以70 km/h匀速驶过该桥,分别在边跨和中跨跨中测得该桥自振频率f3和f4;
工况三:两辆不同重量的试验车分别在中跨跨中进行跳车试验得到该桥的有载频率,然后将该桥的有载频率经公式换算[20]得到该桥基频f5。
对于该类预应力混凝土梁桥,由于跑车和跳车荷载的频率低于结构的第三阶固有频率,因此本次试验只测得了该桥的基频fx1。
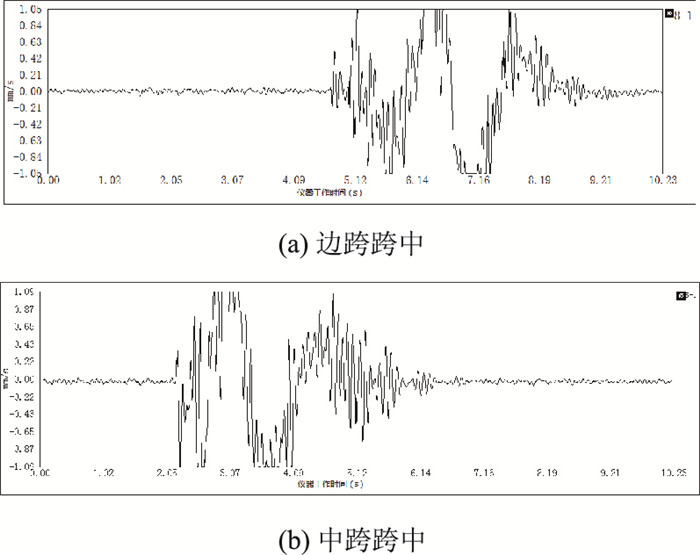
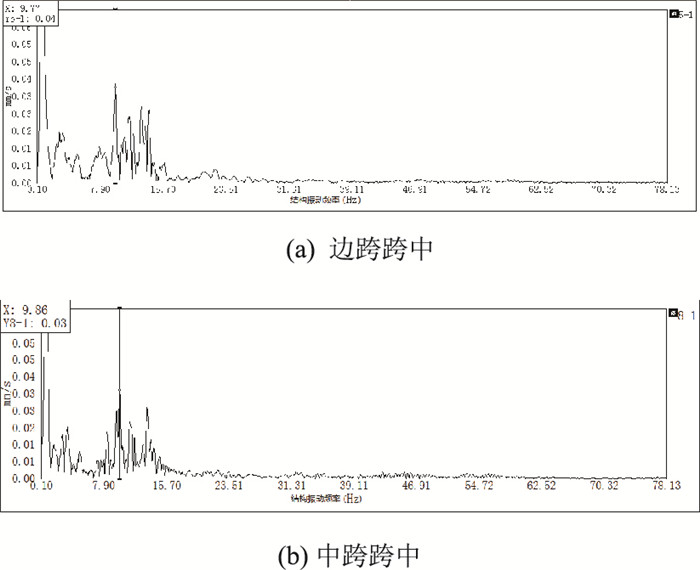
5.2 试验结果及分析图 9和图 10分别表示试验车以60 km/h时速跑过该桥(工况一)时,边跨跨中和中跨跨中采集器得到的动态时域信号波形图和对应的频谱分析图。经数据分析测得该桥基频f1=9.77 Hz, f2=9.86 Hz。
|
| 图 9 跑车车速60 km/h(工况一)动态时域曲线图 Fig. 9 Dynamic time domain curves at vehicle speed of 60 km/h (case 1) |
| |
|
| 图 10 跑车车速60 km/h(工况一)频谱分析图 Fig. 10 Spectrum analysis charts at vehicles peed of 60 km/h (case 1) |
| |
工况二与工况一属于同性质的试验,在此不再赘述,试验结果见表 5。
| 项目 | 现场测试结果 | 拟合公式结果 | ①与③的相对误差/% | ②与④的相对误差/% | ||||
| ①基频fx1/Hz | ②冲击系数μ | ③基频fx1/Hz | ④冲击系数μ | |||||
| 工况1 | 中跨跨中 | 9.86 | 0.389 | 8.42 | 4.03 | |||
| 边跨跨中 | 9.77 | 0.387 | 7.57 | 3.63 | ||||
| 工况2 | 中跨跨中 | 9.42 | 0.381 | 9.03 | 0.373 | 4.14 | 2.00 | |
| 边跨跨中 | 9.96 | 0.390 | 9.34 | 4.47 | ||||
| 工况3 | 中跨跨中 | 9.84 | 0.388 | 8.23 | 3.94 | |||
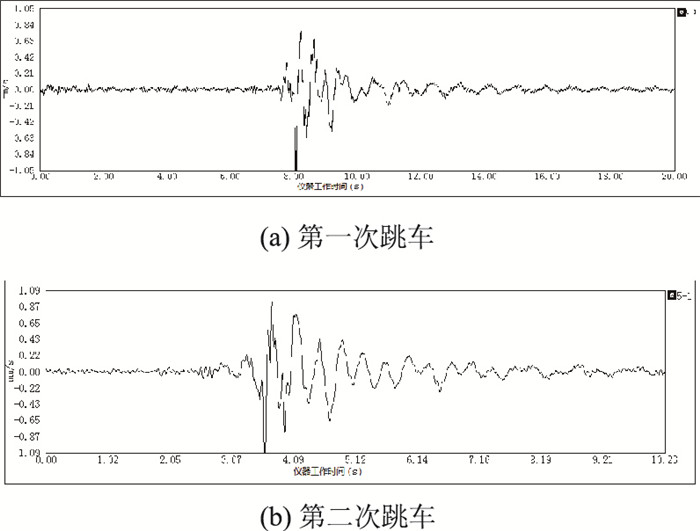
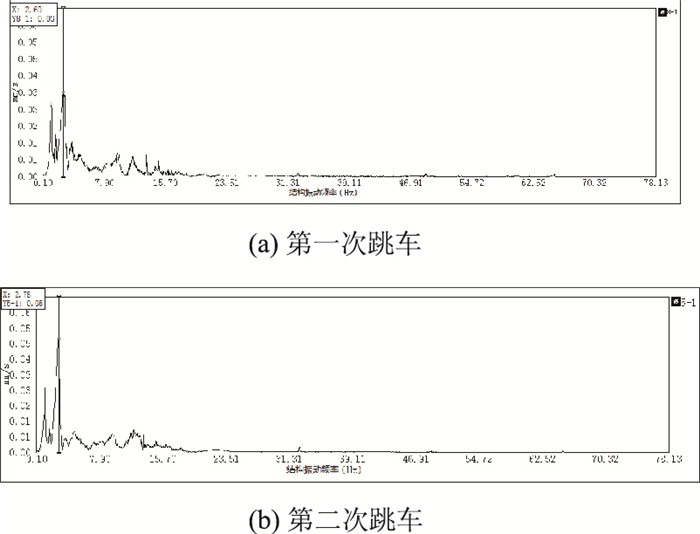
图 11和图 12表示两辆试验车分别在中跨跨中位置进行跳车试验(工况三)时,在中跨跨中采集得到的动态时域信号波形图和对应的频谱分析图。由频谱分析得到该桥有载振动频率分别为f′=2.69 Hz,f″=2.78 Hz。再由两试验车车重及《公路桥梁荷载试验规程》[21](JTGTJ2101—2015)中第6.6.2条公式经换算得结构基频fs=9.84 Hz。
|
| 图 11 中跨跨中跳车(工况三)动态时域曲线 Fig. 11 Dynamic time domain curves when vehicle jumping at mid-span of central span (case 3) |
| |
|
| 图 12 中跨跨中跳车(工况三)频谱分析图 Fig. 12 Spectrum analysis charts when vehicle jumping at mid-span of central span (case 3) |
| |
将以上各工况的基频测试结果与本研究提出的基频修正式(4)的计算结果进行比较,同时将两种基频结果分别代入《桥规》公式计算出冲击系数并进行比较,结果列于表 5中。
由表 5可知,实测基频与式(4)计算结果基本接近,两者得出的冲击系数相差最大为4.47%,说明本研究提出的公式可以较为准确地计算三跨连续斜交T形梁桥的基频值,其结果较为合理。
6 结论(1) 三跨连续斜交T梁桥,随着斜交角度的增大,其前三阶竖弯振型由固有振型的一、三、五阶逐渐变化到了一、三、七阶。
(2) 在斜交角小于30°时,结构基频值与正桥相近,可以按正桥考虑;当斜交角大于30°时,应按斜桥进行具体计算,否则将会产生较大的误差。
(3) 在实际工程中,对于斜交角小于40°的混凝土连续斜交T梁桥,可利用实测的一阶自振频率通过比例关系(fs1: fs2:fs3=π 2:3.552:4.32)得出第三阶自振频率,作为在计算连续梁桥因冲击力引起的负弯矩效应时采用的自振频率值。
(4) 经分析得出了计算三跨连续斜交T梁桥冲击系数时采用的基频修正公式,并通过实际桥梁的现场动载试验,验证了该基频修正公式是合理的。
(5) 主梁之间的连接方式对斜交T梁桥的动力特性的影响非常小,可忽略不计。因此本研究结论适用于主梁之间为刚接或铰接的中小跨径三跨连续斜交T梁桥结构。
| [1] |
周东, 于向东. 斜交角对斜交箱梁桥横梁内力的影响分析[J]. 公路交通科技, 2011, 28(4): 61-66. ZHOU Dong, YU Xiang-dong. Analysis on Inner Forces of Transverse Beams of Skew Box Girder Bridge Affected by Skew Angle[J]. Journal of Highway and Transportation Research and Development, 2011, 28(4): 61-66. |
| [2] |
刘华, 叶见曙, 钱培舒. 混凝土公路斜桥的动反应研究[J]. 公路交通科技, 2006, 23(10): 60-64. LIU Hua, YE Jian-shu, QIAN Pei-shu. Dynamic Response Research of Concrete Highway Skew Bridge[J]. Journal of Highway and Transportation Research and Development, 2006, 23(10): 60-64. |
| [3] |
张等. 不同斜交角度简支T形梁桥基频计算与试验[J]. 湖南交通科技, 2016, 42(1): 74-77. ZHANG Deng. Calculation and Experiment of Fundamental Frequency of Simply Supported T-beam Bridge with Different Skew Angles[J]. Hunan Communications Science and Technology, 2016, 42(1): 74-77. |
| [4] |
刘小燕, 袁龙文, 何志军. 斜交空心板桥基频计算与实验[J]. 中外公路, 2012, 32(3): 189-191. LIU Xiao-yan, YUAN Wen-long, HE Zhi-jun. Calculation of Fundamental Frequency and Experiment of Skew Hollow Slab Bridge[J]. Journal of China & Foreign Highway, 2012, 32(3): 189-191. |
| [5] |
吴桥. 斜交空心板桥的动力特性分析[J]. 湖南交通科技, 2016, 42(4): 82-85. WU Qiao. Analysis on Dynamic Characteristic of Skew Hollow Slab Bridge[J]. Hunan Communication Science and Technology, 2016, 42(4): 82-85. |
| [6] |
夏樟华, 宗周红. 三跨斜交T梁动力特性分析[J]. 振动与冲击, 2007, 26(4): 147-150. XIA Zhang-hua, ZONG Zhou-hong. Dynamic Analysis of a Skewed T-girder Bridge with Three-spans[J]. Journal of Vibration and Shock, 2007, 26(4): 147-150. |
| [7] |
夏桂云, 俞茂宏, 李传习, 等. 斜桥动力特性[J]. 交通运输工程学报, 2009, 9(4): 15-21. XIA Gui-yun, YU Mao-hong, LI Chuan-xi, et al. Vibrating Characteristics of Skew Bridge[J]. Journal of Traffic and Transportation Engineering, 2009, 9(4): 15-21. |
| [8] |
MALEKI S. Free Vibration of Skewed Bridge[J]. Journal of Vibration and Control, 2001, 7: 935-952. |
| [9] |
KALANTARI A, AMJADIAN M. An Approximate Method for Dynamic Analysis of Skewed Highway Bridges with Continuous Rigid Deck[J]. Engineering Structures, 2010, 32(9): 2850-2860. |
| [10] |
卢明奇, 郭建虎, 杨庆山, 等. 斜度和支座剪切刚度对斜交连续梁桥自振周期的影响[J]. 地震工程与工程振动, 2014, 34(增1): 379-372. LU Ming-qi, GUO Jian-hu, YANG Qing-shan, et al. Effects of Skew Angles and Shear Stiffness of Bearing on Vibration Periods of Skew Bridges[J]. Earthquake Engineering and Engineering Dynamics, 2014, 34(S1): 379-372. |
| [11] |
许永吉, 卓卫东, 孙颖. 两跨连续斜交梁桥振动台实验研究[J]. 振动与冲击, 2016, 35(5): 228-233. XU Yong-ji, ZHUO Wei-dong, SUN Ying. Shaking Table Tests for a Two-span Continuous Skew Girder Bridge[J]. Journal of Vibration and Shock, 2016, 35(5): 228-233. |
| [12] |
何旭辉, 盛兴旺, 陈政清. 高速铁路PC斜交箱梁桥振动特性模型试验研究[J]. 铁道学报, 2002, 24(5): 89-92. HE Xu-hui, SHENG Xing-wang, CHEN Zheng-qing. Model Test Study of Vibration Characteristics on PC Skew Box Girder Bridge of Civil High Speed Railway[J]. Journal of the China Railway Society, 2002, 24(5): 89-92. |
| [13] |
宋一凡. 公路桥梁动力学[M]. 北京: 人民交通出版社, 2000. SONG Yi-fan. Dynamics of Highway Bridges[M]. Beijing: China Communications Press, 2000. |
| [14] |
夏桂云, 李传习, 张建仁. 多跨连续斜桥动力特性分析[J]. 重庆大学学报, 2011, 34(8): 121-127. XIA Gui-yun, LI Chuan-xi, ZHANG Jian-ren. Analysis of Vibrating Characteristics of Multi-span Continuous Skew Bridges[J]. Journal of Chongqing University, 2011, 34(8): 121-127. |
| [15] |
何朝晖, 廖林清. 多跨连续梁的振动[J]. 重庆工业管理学院学报, 1995, 9(4): 68-76. HE Zhao-hui, LIAO Lin-qing. Vibration of Multi-span Continuous Beam[J]. Journal of Chongqing Institute of Technology Management, 1995, 9(4): 68-76. |
| [16] |
汉勃利E C. 桥梁上部构造性能[M]. 北京: 人民交通出版社, 1982. HAMBLY E C. Property of Super Structure of Bridge[M]. Beijing: China Communications Press, 1982. |
| [17] |
丁瑞, 赵剑. MIDAS CIVIL中连续T梁结构桥梁模型梁格法释放梁端约束的简化应用[J]. 黑龙江交通科技, 2013(5): 104. DING Rui, ZHAO Jian. Simplified Application of Beam End Release Constraint of Continuous T-beam Bridge Model Grillage Method in MIDAS CIVIL[J]. Communications Science and Technology Heilongjiang, 2013(5): 104. |
| [18] |
高建军, 王长材. 水泥混凝土桥面铺装对桥梁自振频率的影响[J]. 山东交通科技, 2014(4): 67-68. GAO Jian-jun, WANG Chang-cai. The Influence of Cement Concrete Deck Pavement on Bridge Natural Vibration Frequency[J]. Shandong Transport Science and Technology, 2014(4): 67-68. |
| [19] |
徐小明. 桥梁结构动力学性能的研究[J]. 黑龙江交通科技, 2015(9): 152-154. XU Xiao-ming. Study on Dynamic Performance of Bridge Structure[J]. Communications Science and Technology Heilongjiang, 2015(9): 152-154. |
| [20] |
袁向荣. 基于连续梁振动分析的桥梁冲击系数研究[J]. 四川建筑科学研究, 2013, 39(4): 190-194. YUAN Xiang-rong. Study of the Impact Factor Based on the Dynamic Analysis of the Continuous Beam[J]. Sichuan Building Science, 2013, 39(4): 190-194. |
| [21] |
JTG/T J21-01-2015. 公路桥梁荷载试验规程[S]. JTG/T J21-01-2015. Load Test Methods for Highway Bridges[S]. |
 2018, Vol. 35
2018, Vol. 35
