扩展功能
文章信息
- 赵明华, 刘湘宁, 杨超炜, 肖尧
- ZHAO Ming-hua, LIU Xiang-ning, YANG Chao-wei, XIAO Yao
- 基于非线性规划法的单桩受扭研究
- Study on Single Pile Subjected to Torsion Based on Nonlinear Programming Method7
- 公路交通科技, 2018, 35(5): 49-56
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(5): 49-56
- 10.3969/j.issn.1002-0268.2018.05.007
-
文章历史
- 收稿日期: 2017-02-21
2. 中国建筑第五工程局有限公司, 湖南 长沙 410004
2. China Construction Fifth Engineering Division Co., Ltd., Changsha Hunan 410004, China
随着我国经济的迅速发展以及对交通能源需求的不断扩大,近年来,立交桥、跨海大桥、海上平台和风力发电塔等大型基础建设规模正在不断扩大。在这些结构物中,桩基础得到了较多的应用。在复杂的受力环境中,这些结构物除了受到自身重力和上部结构荷载之外,还会受到风荷载、波浪荷载以及高速行驶的车辆和船舶的影响,使桩基础受到扭转力作用[1]。若是工程实际中的桩基础抗扭转设计不当或是忽略这类扭矩荷载,会影响到基础的安全性和适用性,从而带来灾难性的后果[2]。并且,与其他形式受力相比,扭转更容易导致桩身破坏[3-4]。因此,对桩基础在扭转荷载作用下的反应特性研究就显得尤为重要。
目前,国内外许多学者对受扭桩基础进行了研究。在试验研究方面,Stoll[5]通过在砂土中对两根外径0.273 m的管桩进行现场扭转试验,获得了桩体的扭矩转角曲线,并首次研究了桩扭转受荷与竖向受荷之间的关系;国内刘云云等[6]进行了扭矩作用下嵌岩桩基础模型试验,Zhang等[3, 7]对单桩和群桩进行了扭转加载离心机模型试验,进一步研究了基桩受扭特性。在理论研究方面,Poulos[8]和Randolph[9]基于弹性理论求得了受扭单桩的解析解,但只局限于均质地基中桩头的扭转;Guo等[10-11]考虑到桩土界面的滑移以及地基土的非均匀性,根据荷载传递法和剪切位移法,获得了桩身的扭矩转角解析解;邹新军等[12]考虑地基土剪切模量在地面处为非零值,导出了桩周土处于不同受力状态下桩身的扭矩-扭转角解析解。这类方法虽然计算相对简单,但对于多层地基以及复杂边界条件,仍有局限性。数值计算方法能更好地弥补理论研究的不足,不仅能考虑复杂边界条件和地基分层的影响,还能考虑地基土各向异性,能更真实地模拟桩土间的相互作用。Chow[13]提出了计算受扭单桩的离散元法;Basack等[14]首次用边界元法进行了受扭单桩的计算。
本研究根据荷载传递法,将桩身离散成若干单元,基于最小势能原理,建立了用于受扭单桩变形计算的非线性规划模型。运用最优化计算方法对模型进行求解,获得桩身扭矩和扭转角的分布以及桩顶的扭矩-扭转角关系曲线。
1 单桩受扭的非线性规划模型 1.1 简化模型和单元的划分为便于分析,假定桩为弹性梁,土体对桩的摩阻力用非线性弹簧代替,在扭转作用下,桩体只发生纯扭转,不发生翘曲。
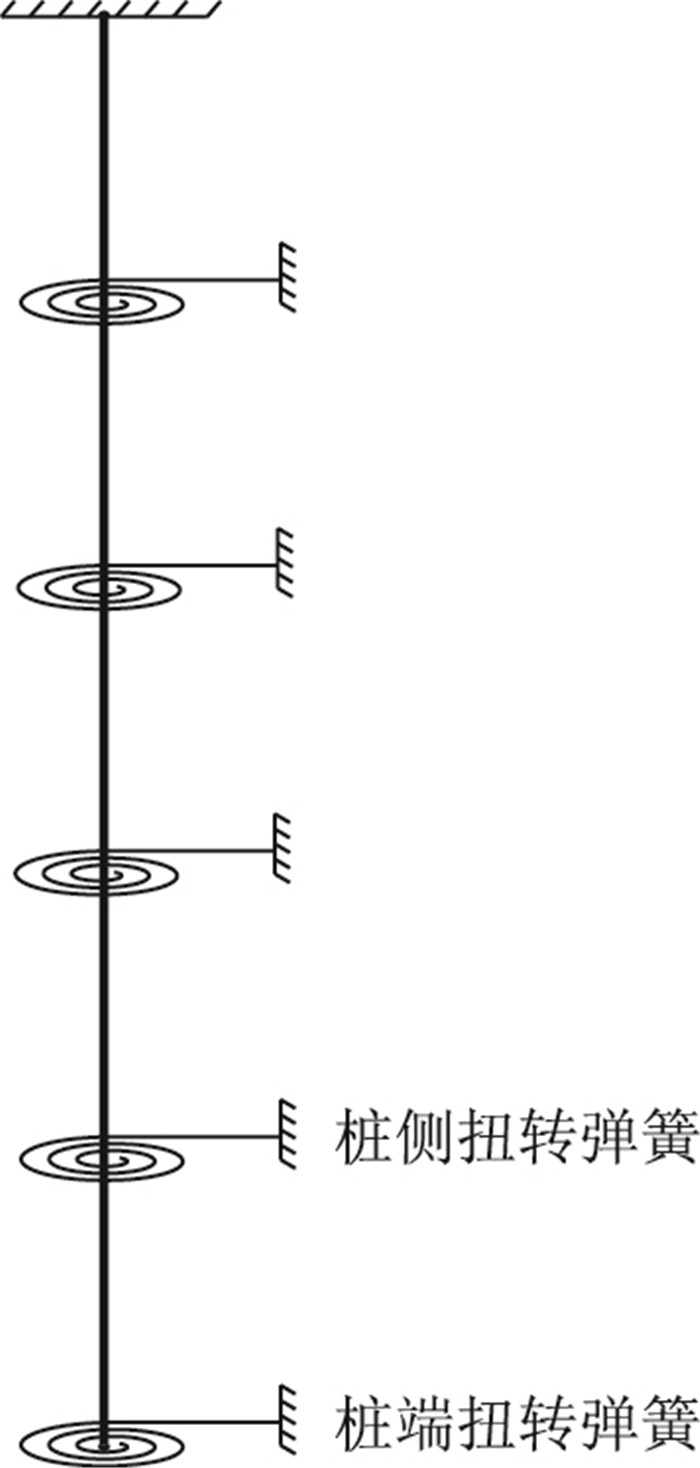
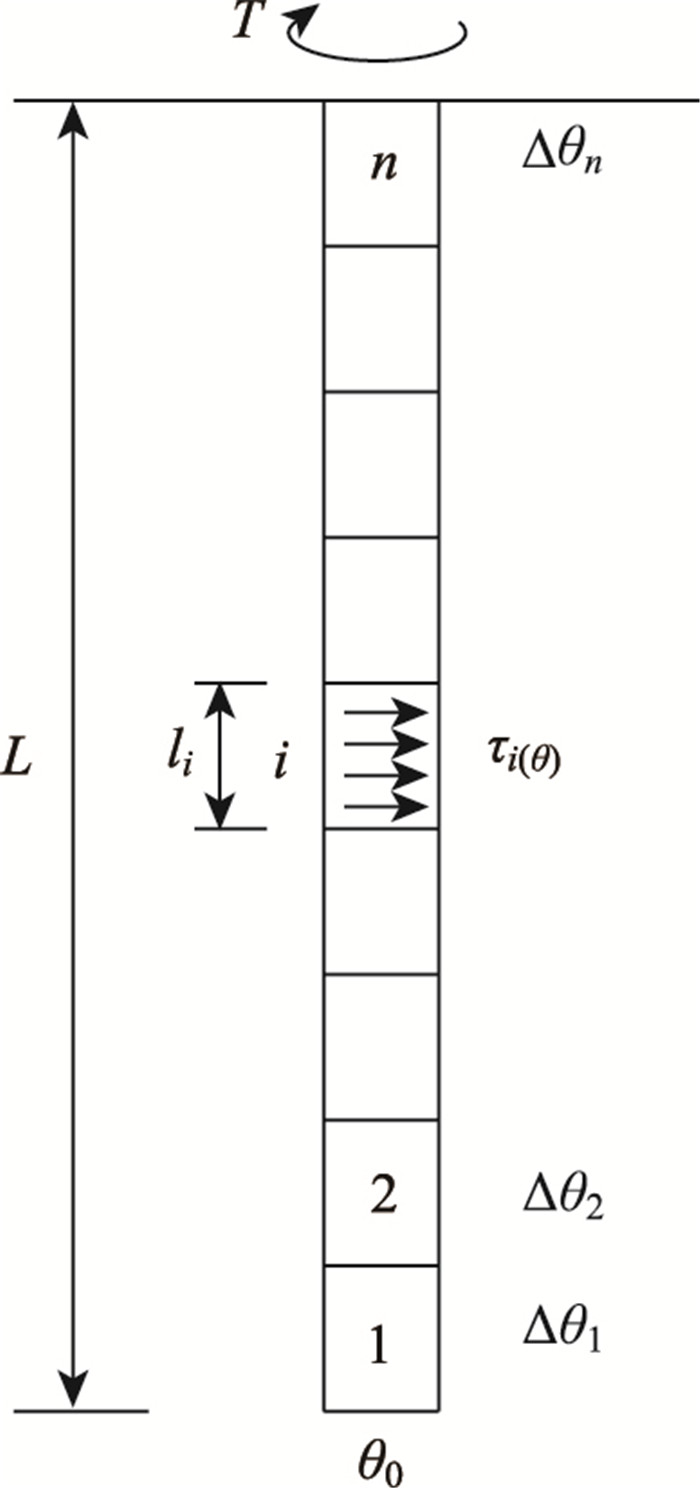
在桩土系统中,最小势能原理可以表述为:在给定的扭矩作用下,满足边界条件的所有桩身可能的变形状态中,桩身实际变形应使桩土系统的总势能成为极小值。为获得桩土系统的总势能,将桩土离散化,并用非线性弹簧表示桩土间的摩阻力,如图 1所示,土弹簧的受力特征用τ-θ曲线表示。将桩身划分为n个单元,桩单元自下而上进行编号,如图 2所示。假定每个单元上土体剪应力均匀分布,集中作用在桩单元上。从而,为获得桩身的变形,可建立以桩土体系的总势能为目标函数,并以边界条件作为约束方程的非线性规划模型。
|
| 图 1 计算模型 Fig. 1 Calculation model |
| |
|
| 图 2 单元划分 Fig. 2 Element division |
| |
1.2 目标函数的建立
根据前述单元划分结果,取任一桩单元为分析对象。桩身假定为弹性材料,桩单元的形变势能可以表示为:
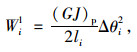
|
(1) |
式中,Δθi为第i桩单元的变形扭转角增量,即第i桩单元上下平面的相对扭转角;(GJ)p为桩身的扭转刚度;li为桩单元长度。
桩身摩阻力做功等于非线性扭转弹簧的势能,该势能可以通过τ-θ曲线的积分表示出来, 则桩单元上桩侧单位面积摩阻力做功为:
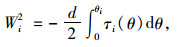
|
(2) |
桩端摩阻力做功为:
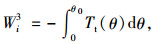
|
(3) |
式中,τi(θ)为第i桩单元桩侧曲线的函数;Tt(θ)为桩端扭转反力函数;θ0为桩端的扭转角,桩端嵌固时,θ0取为0;θi为第i桩单元扭转角。负号表示土体剪切摩阻力做负功。
单桩受外力扭矩作用,桩土系统的广义总势能可以表示为:
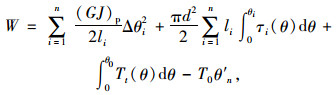
|
(4) |
式中,d为桩的直径;T0为作用在桩顶的扭矩荷载;θ′n为地面处桩身的扭转角,即第n个桩单元上节点处的扭转角。
根据桩体的扭转变形协调条件,桩身任一单元上节点处扭转角为:
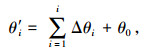
|
(5) |
桩身任一单元的扭转角为:
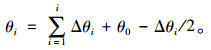
|
(6) |
将式(5)和式(6)代入式(4),式(4)中将只存在θ0,Δθ1,Δθ2,…,Δθn这一组变量。式(4)即为所建立的非线性规划模型的目标函数,通过求得使该目标函数值最小的一组θ0,Δθ1,Δθ2,…,Δθn,从而得到桩身的扭矩、扭转角以及桩顶的扭矩-扭转角曲线。
1.3 约束条件桩身除了应该满足变形协调条件,还应满足荷载和位移边界条件,例如已知的某一桩单元的扭矩,或是扭转角等等。桩身受力平衡和边界条件可以作为目标函数的约束条件。由于非线性规划模型可以包含多个约束条件,因而使得这种算法的适用性较强,但应注意避免相互冲突的约束。有效的约束条件可以大大缩小模型求解的可行域。
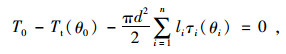
|
(7) |
式(7)为桩身应满足的受力平衡方程,可作为非线性规划模型的一个约束条件。
桩身扭矩计算式为:
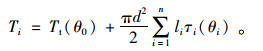
|
(8) |
目前应用较多的包括以下两类曲线:
(1) Kong[7]基于在砂土中进行的单桩受扭的离心机试验,整理出了砂土的双曲线型τ-θ曲线以及桩端扭转曲线,表达式如下:
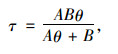
|
(9) |
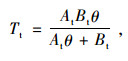
|
(10) |
式中,A,At分别为τ-θ曲线和桩端扭转曲线的初始斜率。B,Bt分别为桩侧极限扭转剪应力和桩端极限扭转抗力。B可表示为:
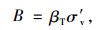
|
(11) |
式中,βT为考虑初始有效应力和孔隙比的修正系数;σ′v为竖向有效应力。Bt可表示为:
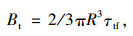
|
(12) |
式中τtf为桩端桩土极限摩擦力。
(2) 对于非均质地基,可先假定土体的剪切模量为幂函数分布形式[15]:
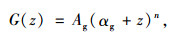
|
(13) |
或是指数函数分布形式[16]:
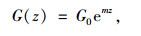
|
(14) |
式中,n,Ag为待定系数,Ag通过地表处的土体剪切模量换算得到,其单位随n的取值不同而变化;αg为地面处剪切模量非零因子,在(0~1)L内取值;G0为地面处土体剪切模量,可由桩的实测初始扭转刚度换算得到[10];m为非线性系数,m=α/h,h为土层厚度,α为非负的无量纲常数,取决于上覆土层的特性,α=0时表示均质土,具体可按文献[16]取值。
式(13)和式(14)可模拟工程中的常见土体[17]:无实测资料时,对于一般土可采用线性幂函数模拟,即取n=1,转化为广义Gibson地基[18],结合经验数据,可换算获得部分参数的取值范围如表 1所示;若有实测剪切模量,可按幂函数(n>0)或指数函数(m>0)拟合出相应参数;若是较特殊的软基上硬层地基,可采用非线性幂函数(n < 0)进行模拟[18],部分参数取值见表 1。
| 土类 | αg(αt)/m | Agαg/MPa | Atαt/kPa |
| 粗砂 | (0~1)L | 57.8~80.5 | 74~116 |
| 中砂 | 56.0~78.1 | 54~95 | |
| 细砂 | 39.4~60.7 | 48~88 | |
| 粉砂 | 16.4~23.0 | 24~48 | |
| 粉土 | 18.0~37.7 | 26~88 | |
| 黏土 | 16.6~42.3 | 24~105 |
桩土界面无滑移,基于剪切位移法,桩侧剪应力与扭转角的关系可按下式确定[9]:
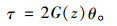
|
(15) |
桩土界面产生滑移,桩侧土进入塑性状态,桩侧摩阻力达到极限摩阻力。为简化问题,引入与土体剪切模量分布模式相同的极限摩阻力的分布形式[15],即:
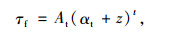
|
(16) |
或:
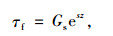
|
(17) |
式中,At,αt为常数,与式(13)中的Ag,αg对应,通常取αt=αg;t,s为常系数,分别与式(13)中的n和式(14)中的m对应,通常可取t=n,s=m;Gs为取决于土质条件的常数。
对于桩底截面,桩端扭转曲线可表示为[9]:
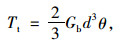
|
(18) |
式中Gb为桩底深度处土体的剪切模量。
所以,τ-θ曲线和桩端扭转曲线可表示为:
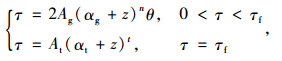
|
(19) |
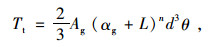
|
(20) |
或:
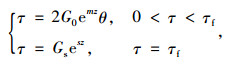
|
(21) |
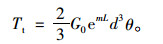
|
(22) |
上文已经将受扭单桩的变形计算转化成了如下非线性数学规划问题:
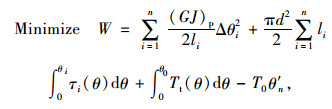
|
(23) |
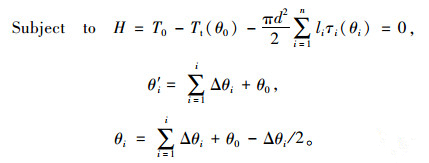
|
(24) |
求解这种有约束非线性规划模型的方法大致分为3类,第1类是可行方向法。这类方法的思想是:从一个可行点出发,沿着目标函数减小的方向,搜索得到一个新的改进了的可行点,通过迭代使可行点逐渐逼近目标函数的极小值点。第2类是序列无约束极小化方法。这类方法是将约束条件随同一个参数并入到目标函数而形成一个新的无约束问题,当参数变化时就得到了一系列无约束问题,用求解这一系列无约束问题而得到的解来逼近原有约束问题的解。第3类是割平面方法。这类方法的思想是将带有约束的非线性规划问题化为一个将约束区域包含在某一多胞形内的线性规划问题,当多胞形逐渐缩小时,用相应得到的一系列线性规划问题的解去逼近原问题的解。本研究采用第2类方法中的乘子法求解上述非线性规划模型。
首先令x =(θ0, Δθ1, Δθ2, …, Δθν)T,构造乘子罚函数:
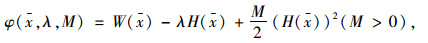
|
(25) |
式中,W(x)为目标函数;H(x)为约束函数;λ为Lagrange乘子;M为罚因子。
如果知道最优Lagrange乘子为λ′,给定一个足够大的罚因子M就可以通过极小化φ(x, λ′, M)来获得原问题的解。但实际上λ′未知,故先给定Lagrange乘子的初始值λ(1)和x 的一组初始值x0,通过不断修正使其逐渐趋于λ′。Lagrange乘子修正公式为:

|
(26) |
约定x j为λ第j次迭代时计算minφ(x, λ(j), M)所得到的一组自变量值;若λ不收敛或收敛速度很慢,可以增大罚因子再进行迭代。
当λ第j次迭代时,取x的初始值为xj-1,Lagrange乘子为λ(j),初始罚因子为M,求解minφ(x, λ(j), M)。
首先需确定搜索方向,若搜索方向d选取为函数φ(x, λ(j), M)的负梯度方向,则有:
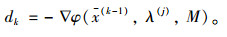
|
(27) |
约定dk为沿φ(x, λ(j), M)第k次下降的方向,x(k-1)为k-1次下降后所得到的自变量值。
之后要确定每次下降的步长t,先构造函数:
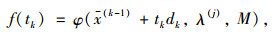
|
(28) |
并令f(tk)′=0。求得下降的步长t,则新的迭代点为:
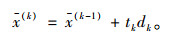
|
(29) |
然后令k=k+1,进行下一次的下降搜索。当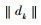
将xj代入式(26)修正Lagrange乘子,并令j=j+1,重新求解minφ(x, λ(j), M)。当|H(xj)|在精度范围之内时,则认为λ(j)为最优Lagrange乘子,此时求得的xj即为原问题的解。
在求解minφ(x, λ(j), M)的过程中,搜索方向的选取方法有多种,如Rosenbrock法、单纯形搜索法、共轭梯度法、拟牛顿法等等,可参见文献[19]。在实用计算软件MATLAB的优化工具箱中,可以根据所选的算法调用相应的函数求解,较为方便。
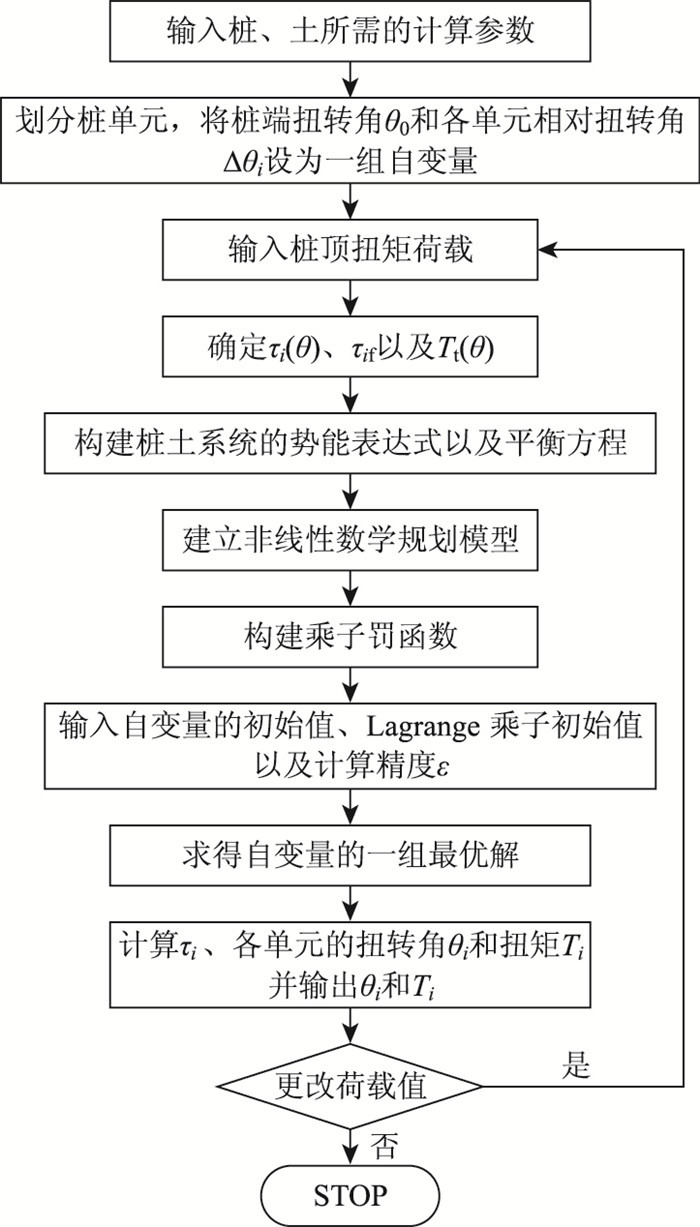
2.2 计算流程为分析单桩在扭转荷载作用下的受力特性,以上述分析为基础,采用乘子法,编制计算程序,计算流程如图 3所示。
|
| 图 3 计算流程图 Fig. 3 Flowchart of calculation |
| |
3 算例
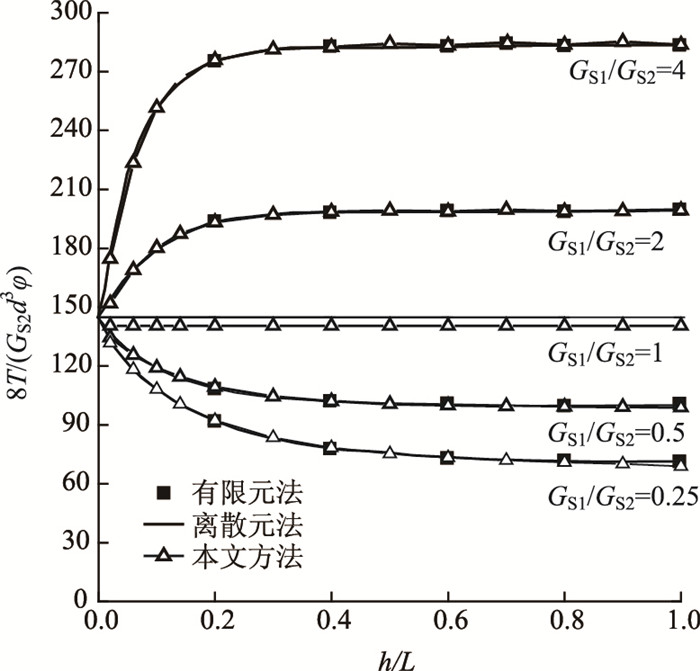
为验证本研究方法对层状地基单桩受扭分析的解答,本研究拟基于文献[13]中的双层地基模型进行验证。各参数如下:取桩径d=1 m,桩长L=50 m,桩身剪切模量GP=8 GPa,底层土剪切模量GS2=8 MPa。图 4给出了相同荷载作用下,在顶层土的厚度h和剪切模量GS1分别取不同值时,采用不同方法计算的结果。
|
| 图 4 双层地基中单桩受扭对比分析 Fig. 4 Comparison of mechanical properties of torsional single pile in double-layered foundation |
| |
图 4结果表明采用本研究方法的计算结果与文献[13]中所报道的采用离散元法及有限元法的计算结果吻合度较高;桩的抗扭刚度约与桩周土剪切模量的0.5次方成正比例关系;其次,顶层土的剪切模量对桩身的抗扭性能影响较大,对于上软下硬地基土,影响最大的深度约为0.4~0.5倍桩长,对于上硬下软地基土,影响最大的深度约为0.2~0.3倍桩长,通过提高这部分地基土的剪切模量来提升桩的抗扭能力,是实际工程可以采取的经济且有效的手段。
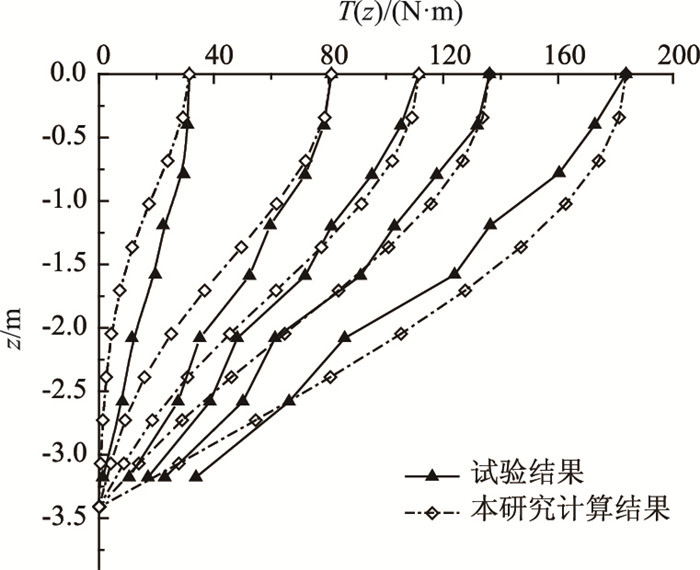
为了进一步验证本研究方法的有效性,将基于非线性规划模型对受扭单桩的变形进行计算,并将计算结果进行对比分析。采用文献[20]中所报道的扭转受荷单桩模型试验:试验采用钢管桩,管径为114 mm,壁厚4.5 mm,桩长为6 m,埋入深度和自由长度分别为3.41 m和2.59 m;桩弹性模量E=2.06×105MPa,剪切模量GP=7.9×104 MPa;试验土体为杭州粉土,内摩擦角30°,浮重度为8.8 kN/m3,极限侧摩阻为8 kPa,极限端阻力为1 200 kPa。由试验结果拟合取A=4.5×104 kN/m2,B=8 800×0.23z(N/m2),At=1 090 N/m,Bt=52 N/m。将桩身划分为10个桩单元,用本研究方法在MATLAB中编程计算。图 5、图 6分别给出了几组扭矩荷载作用下桩身的扭矩分布和桩头扭矩转角曲线计算结果,并与实测结果进行了比较。
|
| 图 5 桩身扭矩分布 Fig. 5 Distribution of torque along pile shaft |
| |
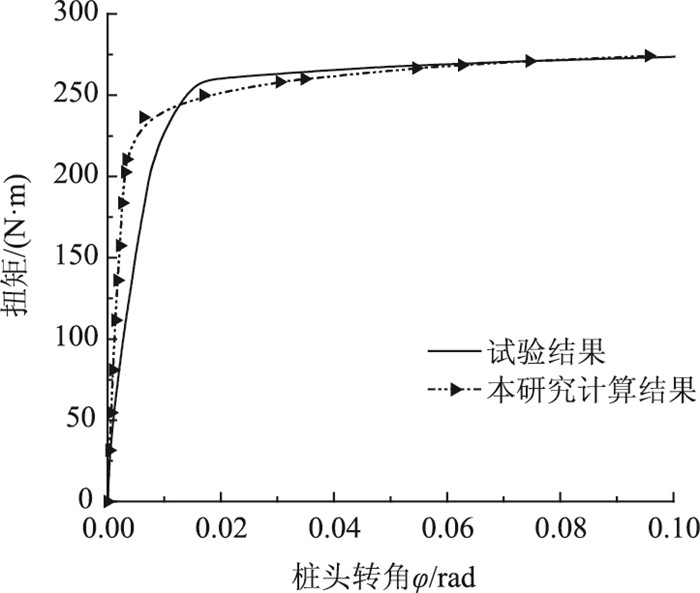
|
| 图 6 桩头扭矩-扭转角曲线 Fig. 6 Curves of torque vs. torsion angle at pile top |
| |
由分析结果可知,采用本研究方法计算得到的桩身扭矩分布和桩头扭矩-扭转角曲线与试验结果吻合较好,体现了单桩受扭转荷载作用下明显的非线性性状。在桩顶扭矩荷载较小时,计算得到的桩头扭转角比试验值小,但在单桩接近于破坏的时候,计算得到的单桩极限扭矩荷载以及极限扭转角与试验结果几乎完全吻合。
4 参数分析影响桩土体系的扭转响应的参数主要包括桩身参数和桩侧土参数。以上述模型试验为基础,下面主要讨论桩身剪切模量GP、桩径d以及桩侧土极限剪应力B对单桩受扭性能的影响。
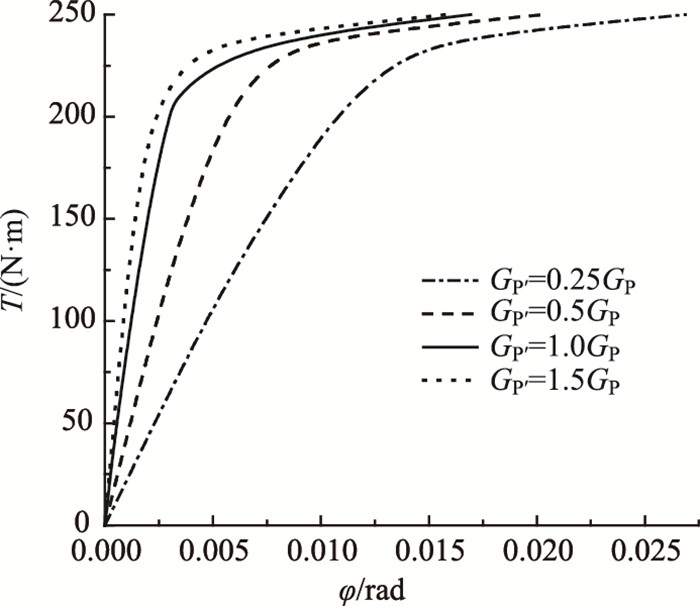
4.1 桩身剪切模量Gp的影响上述模型试验中桩身的剪切模量GP=7.9×104 MPa,为探讨桩身剪切模量GP对单桩扭转性能的影响,分别取桩身的剪切模量为0.25GP,0.5GP,1.5GP,保持其余桩土参数不变来进行计算,并与原计算结果进行比较分析。图 7为不同的桩身剪切模量下计算得到的桩顶的扭矩-扭转角曲线。
|
| 图 7 桩身剪切模量Gp对桩头扭矩-扭转角曲线的影响 Fig. 7 Influence of pile shaft shear modulus GP on T-φ curves |
| |
图 7中结果表明:桩身剪切模量GP越大,在相同的扭转荷载作用下,桩头的扭转角越小,但当桩身剪切模量值达到1.0GP后,增大桩身剪切模量对桩头扭转角的影响会变得很小;在达到同一桩头扭转角时,桩身剪切模量越大,桩身受到的扭转荷载越大,同样的,当桩身剪切模量值达到1.0GP后,增大桩身剪切模量对桩的承载能力的影响会变得很小,同时也证明了模型试验中桩身剪切模量的取值是经济合理的;增大GP能提高桩的抗扭性能,但提高GP对整个桩土体系所能承受的极限扭矩影响较小。
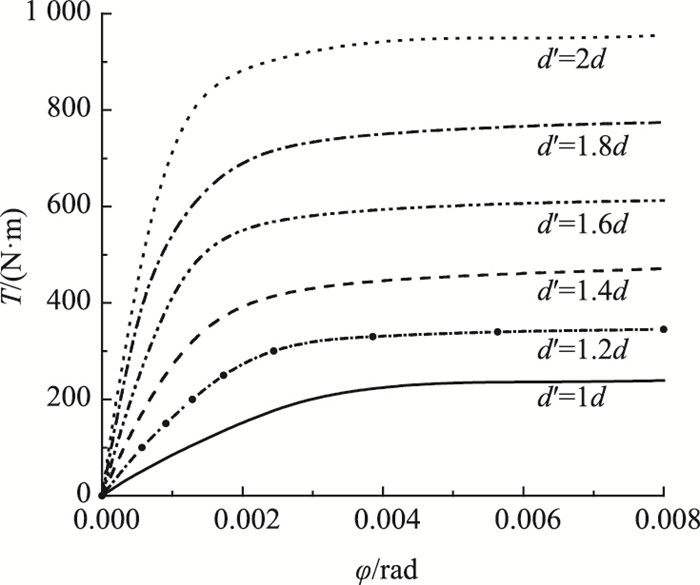
4.2 桩径d的影响上述模型试验中桩径d=0.114 m,为探讨桩径d的影响,分别取桩径为1.2d,1.4d,1.6d,1.8d,2d进行计算,并与原计算结果进行比较。图 8为不同的桩径取值下计算得到的桩顶的扭矩-扭转角曲线。分析图 8可知:桩径d越大,在相同的扭转荷载作用下,桩头的扭转角越小;桩径d越大,桩土体系所能承受的极限扭矩越大,且极限扭矩值的变化约与桩径的变化率的平方成比例关系。
|
| 图 8 桩径d对桩头扭矩-扭转角曲线的影响 Fig. 8 Influence of pile diameter d on T-φ curves |
| |
4.2 桩侧土极限剪应力B的影响
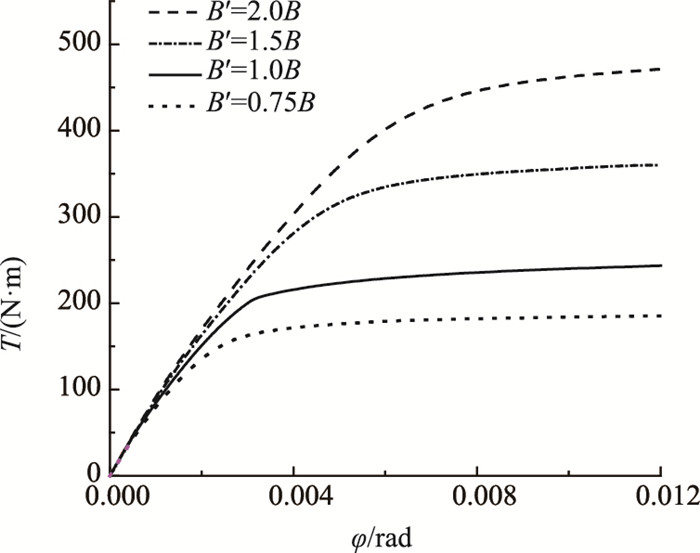
为探讨桩侧土极限剪应力B的影响,分别取桩侧土极限剪应力为0.75B,1.5B,2.0B,2.5B,保持其余桩土参数不变来进行计算,并与原计算结果进行比较。图 9为桩侧土极限剪应力B取不同值时计算得到的桩顶扭矩-扭转角曲线。
|
| 图 9 桩侧土极限剪应力B对桩头扭矩-扭转角曲线影响 Fig. 9 Influence of ultimate shear stress B of pile soil on T-φ curves |
| |
图 9中的结果表明:桩侧土极限剪应力B对受扭桩的抗扭刚度基本无影响,但会影响桩土体系所能承受的极限扭矩值;B越小,受扭桩越早进入弹塑性变形阶段,桩的抗扭承载力也越小,且受扭桩的极限承载力的大小与B值成正比例关系。
5 结论(1) 本研究基于荷载传递法,将桩身离散化,以桩土体系的总能量方程为目标函数,提出了用于受扭单桩变形计算的非线性规划模型,并基于MATLAB软件编制了计算程序。
(2) 根据非线性规划法,利用MATLAB计算程序,对受扭单桩变形进行了求解:通过在双层地基中的受扭计算分析,验证了该方法在层状地基中的适用性;将基于模型试验的计算结果与试验结果进行对比分析,进一步验证了本研究方法的正确性。
(3) 通过对影响桩身扭转响应的主要参数进行分析可得:在相同的扭转荷载作用下,桩身剪切模GP越大,桩头的扭转角越小;增大GP对整个桩土体系所能承受的极限扭矩值影响较小。在相同的扭转荷载作用下,桩径d越大,桩头的扭转角越小,且桩土体系所能承受的极限扭矩越大,极限扭矩值的变化率约与桩径的变化率的平方成比例关系;桩侧土极限剪应力B越小,桩的抗扭承载力也越小,且受扭桩的极限承载力的大小与B值成正比例关系。
| [1] |
AZADI M R E, NORDAL S, SADEIN M. Nonlinear Behavior of Pile-soil Subjected to Torsion due to Environmental Loads on Jacket Type Platforms[J]. Journal of WSEAS Transaction on Fluid Mechanics, 2008, 3(4): 390-400. |
| [2] |
VICKERY B J. Wind Effects on Building and Structures-Critical Unsolved Problems[J]. Practical Experiences with Flow-induced Vibrations Symposium. New York:Springer-Verlag, 1979, 823-828. |
| [3] |
ZHANG L M, KONG L G. Centrifuge Modeling of Torsional Response of Piles in Sand[J]. Canadian Geotechnical Journal., 2006, 43(5): 500-515. |
| [4] |
ZHANG L Y. Nonlinear Analysis of Torsionally Loaded Piles in a Two-layer Soil Profile[J]. International Journal of Geomechanics, 2010, 10(2): 65-73. |
| [5] |
STOLL U W. Torque Shear Test on Cylindrical Friction Piles[J]. Civil Engineering, 1972, 42(4): 63-64. |
| [6] |
刘云云, 陈竹昌. 扭矩作用下嵌岩桩桩顶内力分布的模型试验[J]. 岩土力学, 2000, 21(2): 119-122. LIU Yun-yun, CHEN Zhu-chang. Model Simulation of Internal Load Distribution in Rock-socketed Piles Subject to Torsion[J]. Rock and Soil Mechanics, 2000, 21(2): 119-122. |
| [7] |
KONG L G, ZHANG L M. Centrifuge Modeling of Torsionally Loaded Pile Groups[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(11): 1374-1384. |
| [8] |
POULOS H G. Torsional Response of Piles[J]. Journal of Geotechnical Engineering Division, 1975, 101(10): 1019-1035. |
| [9] |
RANDOLPH M F. Piles Subjected to Torsion[J]. Journal of Geotechnical Engineering Division, 1981, 107(8): 1095-1111. |
| [10] |
GUO W D, RANDOLP M F. Torsional Piles in Non-homogeneous Media[J]. Computers and Geotechnics, 1996, 19(4): 265-287. |
| [11] |
GUO W D, RANDOLPH M F. Rationality of Load Transfer Approach for Pile Analysis[J]. Computers and Geotechnics, 1998, 23(1): 85-112. |
| [12] |
邹新军, 徐洞斌, 王亚雄, 等. 非均质地基中单桩受扭弹塑性分析[J]. 土木工程学报, 2015, 48(11): 103-110. ZOU Xin-jun, XU Dong-bin, WANG Ya-xiong, et al. Torsional Elasto-plastic Analysis of Single Piles in Heterogeneous Ground[J]. China Civil Engineering Journal, 2015, 48(11): 103-110. |
| [13] |
CHOW Y K. Torsional Response of Piles in Non-Homogeneous Soil[J]. Journal of Geotechnical Engineering, 1985, 111(7): 942-947. |
| [14] |
BASACK S, SEN S. Numerical Solution of Single Piles Subjected to Pure Torsion[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(1): 74-90. |
| [15] |
GUO W D. Vertically Loaded Single Piles in Gibson Soil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(2): 189-193. |
| [16] |
尚守平, 李刚, 任慧. 剪切模量沿深度按指数规律增大的场地土的地震放大效应[J]. 工程力学, 2005, 22(5): 153-157. SHANG Shou-ping, LI Gang, REN Hui. Seismic Amplification of Sites with Exponentially Increasing Shear Modulus with Depth[J]. Engineering Mechanics, 2005, 22(5): 153-157. |
| [17] |
RAJAPAKSE R K N D. A Torsion Load Transfer Problem for a Class of Non-homogeneous Elastic Solids[J]. International Journal of Solids and Structures, 1988, 24(2): 139-151. |
| [18] |
杜秦文. 土体剪切模量随深度连续变化非均质地基解析研究[D]. 杭州: 浙江大学, 2005. DU Qin-wen. Analytical Study on Non-homogeneous Subgrade with Continuous Variation of Shear Modulus Versus Depth[D]. Hangzhou: Zhejiang University, 2005. |
| [19] |
陈宝林. 最优化理论与算法[M]. 2005. CHEN Bao-lin. Optimization Theory and Algorithm[M]. 2nd ed.. Beijing: Tsinghua University Press, 2005. |
| [20] |
王书行. 水平偏心荷载下群桩受荷性状模型试验及设计方法研究[D]. 杭州: 浙江大学, 2011. WANG Shu-xing. Model Test and Design Method of Behavior of Pile Group under Eccentrically Lateral Loading[D]. Hangzhou: Zhejiang University, 2011. |
 2018, Vol. 35
2018, Vol. 35
