扩展功能
文章信息
- 李传习, 周群, 董创文
- LI Chuan-xi, ZHOU Qun, DONG Chuang-wen
- 顶推钢箱梁的梁段制造构形与无应力线形实现
- Fabrication Configuration and Unstressed Geometry Achievement of Beam Segment of Incrementally Launched Steel Box Girder
- 公路交通科技, 2018, 35(5): 40-48
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(5): 40-48
- 10.3969/j.issn.1002-0268.2018.05.006
-
文章历史
- 收稿日期: 2017-01-09
许多学者对预制拼装桥梁的理论无应力线形确定[1-3]、现场实现[1, 3-7],以及施工过程结构安全确保[1, 8-11]等施工控制的3个方面进行了探讨,取得了丰硕成果。
文献[12-13]在上述研究基础上,提出了顶推梁体理论无应力线形确定的简便方法、顶推梁体各梁段制造构形确定的矩形法和带直角梯形法、顶推梁体无应力线形实现的相位变换法,并进行了良好的工程应用。
虽然制造构形确定的矩形法和带直角梯形法简单实用,但理论上矩形法存在梁段间上下焊缝宽度不一致、带直角梯形法存在邻边不等(梁高相等)或梁高不等(邻边长度相等)的不足。对此,本研究将研究矩形法和带直角梯形法不足的影响与其适用范围,并提出理论上更为完备的梁段制造构形确定方法。
虽然相位变换法能高精度实现顶推梁体的无应力线形,概念清晰简明,但使用的基本变量为各控制点高程,工程应用稍有不便。虽然传递矩形法在结构分析与现代控制领域得到了深刻认识,并具有易理解和编程等优点,但其应用于顶推梁体待拼梁段就位标高确定[14-15],因缺乏基准相位及相位变换思想而未能有效考虑已有梁体线形偏差的修正。对此,本研究将基于相位变换思想,以梁段前后端的高差为基本变量,分析待拼梁段与已拼梁段间的传递关系,明确线形偏差修正,简单实用地实现顶推钢箱梁主梁高精度线形控制。
1 顶推梁体各梁段制造构形的确定钢梁的无应力线形采用先在工厂进行梁段制作,再在顶推平台上加以拼接的方式实现。在梁体以短直代曲的理论无应力线形确定后,各梁段制造构形的确定可采用文献[13]的矩形法或带直角梯形法,也可采用1.3节提出的等高等邻边梯形法。下面分析矩形法和带直角梯形法的不足与适应范围,并给出等高等邻边梯形法。
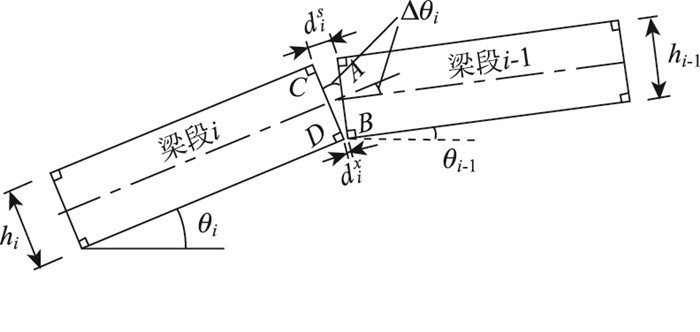
1.1 “矩形法”适应性分析矩形法必然带来具有转角的相邻梁段间的焊缝上下宽度不同(见图 1),根据规范《钢结构焊缝外形尺寸》(JB/T 7949—1999)[16]要求,在整个焊缝长度范围内缝宽差不得大于5 mm。根据矩形法的定义,由几何关系(图 1)可得,不同梁高、不同拼转角Δθi(无应力状态下梁段i-1与梁段i水平倾角之差,即:Δθi=θi-1-θi,i=2, 3, …, n),梁体焊缝上下宽度差Δdi(上下是指顶、底面点)见表 1。
|
| 图 1 矩形法上下缝宽差计算简图 Fig. 1 Calculation diagram of weld width difference between top and bottom by "rectangle method" |
| |
| Δθi | hi | ||||
| 2 000 | 2 500 | 3 000 | 3 500 | 4 000 | |
| 0.02° | 0.70 | 0.87 | 1.05 | 1.22 | 1.40 |
| 0.04° | 1.40 | 1.74 | 2.09 | 2.44 | 2.79 |
| 0.06° | 2.09 | 2.62 | 3.14 | 3.66 | 4.19 |
| 0.08° | 2.79 | 3.49 | 4.19 | 4.88 | 5.58 |
| 0.10° | 3.49 | 4.36 | 5.23 | 6.11 | 6.98 |
| 0.12° | 4.19 | 5.23 | 6.28 | 7.33 | 8.37 |
由表 1可见,当转角相同时,随着梁高的增大,相邻梁段间的焊缝上下宽度差增加(宽度差按Δdi=dis-dix=hi·tanΔθi计算)。对梁高3.5 m的桥梁,焊缝上下5 mm宽度差对应拼转角不超过0.082°。
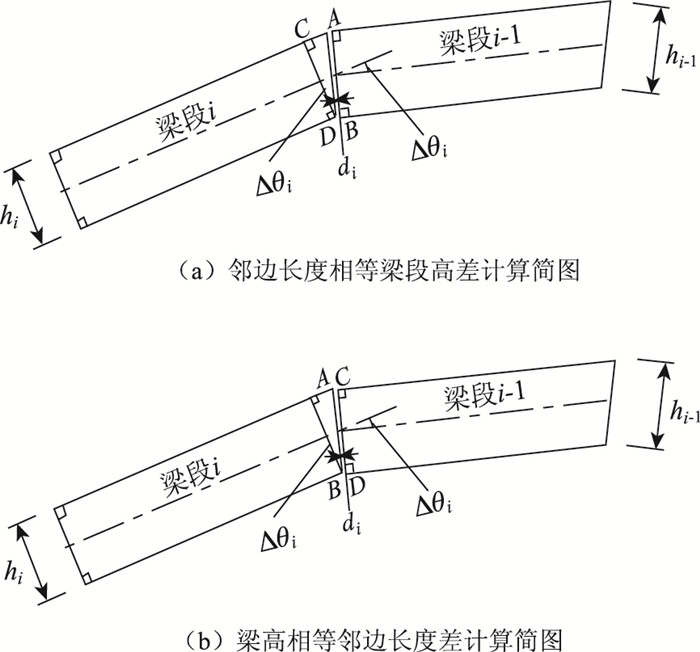
1.2 带直角梯形法适应性分析带直角梯形法虽克服了顶底板焊缝宽度不一致的缺陷,却带来具有转角的相邻梁段梁高不等(邻边长度相等)或者邻边不等(梁高相等)的问题。根据《公路桥钢箱梁制造验收规范》(DB32/T947—2006)[17]的要求,其高差或者邻边长度差不应超过2 mm。根据带直角梯形法的定义,由几何关系,不同梁高、不同转角的相邻梁段的高差(邻边长度相等,见图 2(a))或者邻边长度差(梁高相等,见图 2(b))ΔSi见表 2。
|
| 图 2 带直角梯形法相邻梁段高差或邻边长度差计算简图 Fig. 2 Calculation diagram of differences of beam heights or adjacent edge lengths by right-angled trapezoid method |
| |
| Δ θi | hi | ||||
| 2 000 | 2 500 | 3 000 | 3 500 | 4 000 | |
| 1.4° | 0.60 | 0.75 | 0.89 | 1.04 | 1.19 |
| 1.6° | 0.78 | 0.97 | 1.17 | 1.36 | 1.56 |
| 1.8° | 0.99 | 1.23 | 1.48 | 1.73 | 1.97 |
| 2.0° | 1.22 | 1.52 | 1.83 | 2.13 | 2.44 |
| 2.2° | 1.47 | 1.84 | 2.21 | 2.58 | 2.95 |
| 2.4° | 1.75 | 2.19 | 2.63 | 3.07 | 3.51 |
| 2.6° | 2.06 | 2.57 | 3.09 | 3.60 | 4.12 |
由表 2可见,当转角相同时,随着梁高的增大,带直角梯形法相邻梁段高差或邻边长度差增加(差值按ΔSi=SAB-SCD=hi·(secΔθi-1)计算)。对梁高3.5 m的桥梁,其高差或者邻边长度差不应超过2 mm差值对应的拼转角不超过1.937°。
1.3 梁段制造构形确定的等高等邻边梯形法如图 3所示,设折线ABCDEF为以短直代曲的无应力梁轴线(多个线段组成,下同,略),作该轴线中所有相邻直线段的角平分线,由相交于角平分线的平行无应力梁轴线的梁顶线、梁底线和相邻角平分线组成的梯形必然等高等邻边,该梯形减去两端沿梁高等值的焊缝宽度(一般为8 mm), 再增加沿梁高等值的焊接收缩量,即为梁段的制造构形:等高等邻边的梯形。

|
| 图 3 等高等邻边梯形法梁段制造构形示意图 Fig. 3 Schematic diagram of segment fabrication configuration by method of trapezoid with equal heights and equal adjacent edge lengths |
| |
2 基于传递矩形法和相位变换思想的顶推梁体线形控制
顶推施工桥梁的梁体拼接(或浇注,下同,略)均在顶推平台上进行[8, 18];拼接后即把已拼梁体向前顶推一定距离,再在顶推平台上安装下一批次的梁段,循环往复,最终形成整个梁体。同文献[12-13]一样,本研究将处于接拼其他梁段位置的已拼梁体末端梁称为接拼梁段,将在顶推平台上安裝即将拼接的梁段称为待拼梁段。通常,可使或可视接拼梁段和待拼梁段为无应力状态[9]。
为了保证最终实现的梁体无应力线形与理论无应力线形一致,每个待拼梁段前后端的就位高差需考虑其对应的接拼梁段的即时相位(倾角)。由于已成梁体线形偏差的不可避免,该就位高差还需考虑该偏差修正。
显然,已拼梁体无应力线形在顶推过程中是不变的,可看作随任一梁段无应力线形作刚体位移,即无应力状态下已拼各梁段之间的相对方位不变。特别地,以第1个梁段为基准,确定其他接拼梁段相位(相对方位或相对倾角)和已成梁体线形偏差, 继而确定待拼梁段两端就位高差和就位相位,这就是相位变换法。详细思想可参考文献[12-13]。下面将依据该思想分析相邻梁段前后端高差间的传递关系,建立待拼梁段就位高差的确定方法。
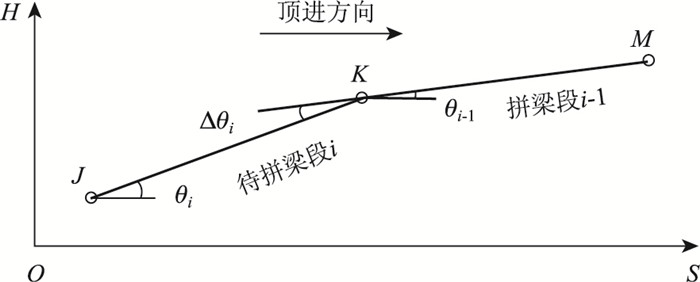
2.1 相邻梁段间传递关系的建立如图 4所示,用梁顶线或1/2梁高线等表示梁体位置(下同,略),设S为里程(顺桥向)方向坐标,H为高程方向坐标,组成顶推梁体梁段数为n,沿着与顶推方向相反由前至后依次编号为1, 2, …, n,各梁段长为li(i=1, 2, …, n),各梁段的前后端高差为ΔHi,水平倾角为θi;同前文所述,定义无压力状态下梁段间拼转角Δθi=θi-1-θi(i=2, 3, …, n,下同,略)。显然,理论无应力状态下拼转角ΔθiN、各梁段前后端高差ΔHiN、梁段长li均可由设计图纸确定的成桥线形与各控制点计算所得的累计挠度求得[10],本研究视为已知。由于顶推过程中各梁段无论处于待拼就位状态,还是焊后状态或接拼状态,其水平投影长几乎不变,故均用li表示,不再区分。
|
| 图 4 梁段拼接示意图 Fig. 4 Schematic diagram of assembling beam segments |
| |
由几何关系得:
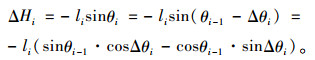
|
(1) |
一般情况下,桥梁纵坡坡度均小于4%,梁段水平倾角很小,相邻梁段水平倾角差则更小,余弦值接近为1,故可取小角度角的余弦值为1作近似计算(后文相关计算均作此近似)。
所以,式(1)中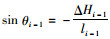
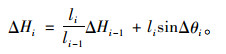
|
(2) |
顶推施工的钢箱梁桥,梁体一般有以下几种线形状态:理论无应力状态、预拼就位状态(计算确定的就位状态)、焊后状态、接拼状态等。不论结构处于何种状态,其几何位形均可采用梁段顶推方向前后端高差与梁段长度两个量来描述。若接拼梁段i-1与待拼梁段i的几何位形分别用φi-1=(ΔHi-1, li-1)T、φi=(ΔHi, li)T描述,则可用φN,φC,φA,φC′分别表示顶推梁体理论无应力状态、预拼状态、焊后状态、接拼状态的几何位形。由几何和数学知识有:
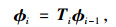
|
(3) |
式(3)即为状态传递方程,Ti为状态传递矩阵。
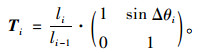
|
(4) |
在式(3)和式(4)中,梁段i,i-1的水平投影长为已知;接拼梁段i-1两端的高差可通过实测得到,拼转角则需在理论无应力拼转角基础上,减去线形偏差所需修正的角度。
式(3)和式(4)对理论无应力状态自然满足,即:
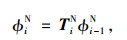
|
(5) |
式中TiN为理论无应力状态传递矩阵。
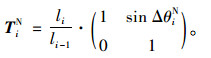
|
(6) |
梁段i-1处于接拼状态时,其前后端高差可通过实测得到,设该高差测量值为ΔHi-1C′,则待拼梁段i就位高差ΔHiC应根据ΔHi-1C′,并考虑线形偏差修正获得, 其公式为:
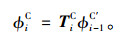
|
(7) |
通过式(7)即可求得考虑线形偏差修正和刚体转动后的待拼梁段i前后端就位高差ΔHiC,TiC为实际预拼状态传递矩阵。
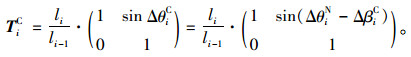
|
(8) |
式(8)中,ΔβiC为梁段线形偏差修正角;ΔθiC为考虑线形偏差修正后的拼转角,后文2.2节将对其线形偏差修正过程作详细的分析。
2.2 梁段1#就位高差确定与焊后偏差计算待拼梁段1#的就位高差ΔH1C可直接采用其理论高差ΔH1N,即ΔH1C=ΔH1N。
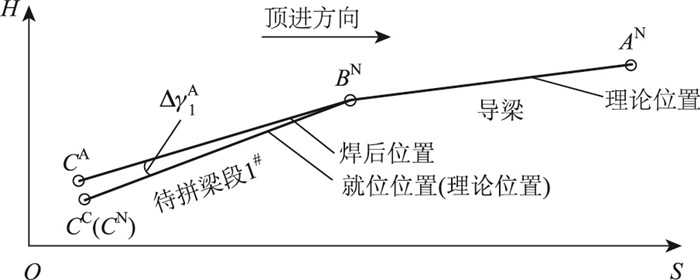
由于施工误差、温度变形、焊接变形等,梁段1#与导梁拼接焊接(或拼接)后,其两端实测高差,即焊后高差ΔH1A与就位高差ΔH1C或多或少存在偏差,该偏差可描述成梁段1#绕其梁顶线(或1/2梁高线)前端点(即图 5中BN点)在竖直平面内发生的微小转动引起,记该微小转动角为Δγ1A,即梁段1#焊后位置与其就位位置间的夹角差为Δγ1A,规定梁段由就位位置顺时针转到焊后位置为正(图 5中的Δγ1A为正),则由几何关系有:
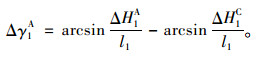
|
(9) |
|
| 图 5 待拼梁段1#拼接及线形偏差确定示意图 Fig. 5 Schematic diagram of assembly and determination of geometry deviation for beam segment No.1 to be assembled |
| |
由于ΔH1C与ΔH1N相同,故就位状态下待拼梁段1#位置(简称就位位置,下同,略)与其理论位置(无应力线形随梁段1#刚体转动,下同,略)间夹角差Δφ1C为0,梁段1#焊后位置与其理论位置夹角差Δφ1A为:
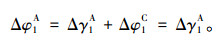
|
(10) |
同理,焊后待拼梁段1#后端高程与其理论差值Δh1A由几何关系有:
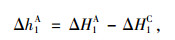
|
(11) |
式(11)即为梁段1#拼接焊后的线形偏差值。
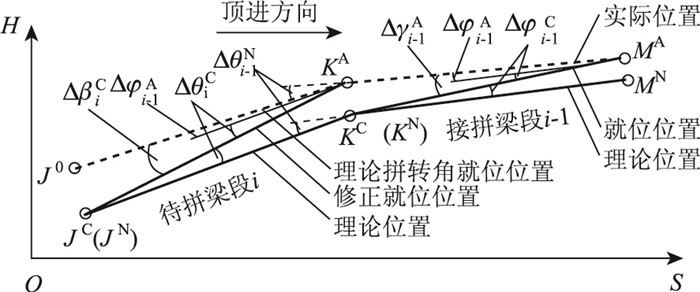
2.3 梁段i就位高差确定与线形偏差的修正梁段i-1(i=2, 3, …, n,下同,略)焊后随导梁顶推前行一定距离,变为接拼梁段。如前所述,已拼梁体无应力线形在顶推过程中是不变的,可看作均随无应力状态的梁段1#刚体位移,即已拼各梁段与1#梁体的相对方位不变,亦即梁段i-1焊后位置与其就位位置间的夹角差Δγi-1A、梁段i-1焊后位置与其理论位置(无应力线形随梁段1#刚体转动后,下同,略)间的夹角差Δφi-1A保持不变(图 6中Δφi-1C为负,Δγi-1A为正,Δφi-1A为正)。
|
| 图 6 待拼梁段i拼接及线形偏差修正示意图 Fig. 6 Schematic diagram of assembly and geometry deviation for beam segment i to be assembled |
| |
如图 6所示,KNJN线段代表与接拼梁段i-1理论位置MNKN线段间拼转角为理论值ΔθiN确定的待拼梁段i理论位置,KAJ0线段代表与接拼梁段i-1实际位置MAKA线段间拼转角亦为理论值ΔθiN确定的待拼梁段i实际预拼位置。由几何关系可知,若待拼梁段i拼转角Δθi取理论值ΔθiN,则待拼梁段i的就位位置(该位置称为理论拼转角就位位置)与其理论位置间夹角差为Δφi-1A(图 6中KAJ0线段与KNJN线段间夹角差),其后端与其理论偏差值ΔhiC(图 6中J0与JN之间差值)由几何关系为:
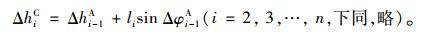
|
(12) |
因此,待拼梁段i拼转角Δθi不能直接取理论值ΔθiN,应在其理论值基础上减去一个线形偏差修正角ΔβiC,使待拼梁段i后端与其理论后端位置重合,保证后端无偏差,从而完成对线形偏差的修正(待拼梁段的该位置称为其修正就位位置,对应状态称为考虑线形偏差修正后的就位状态)。则待拼梁段i线形偏差修正角ΔβiC由几何关系有:
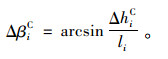
|
(13) |
待拼梁段i实际拼转角ΔθiC为ΔθiN-ΔβiC。
若实测所得梁段i-1处于接拼状态时其前后端高差为ΔHi-1C,则由式(7),(8)即可确定线形偏差修正后的待拼梁段i预拼状态φiC为:
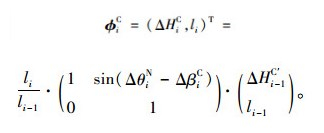
|
(14) |
由此,即可确定考虑线形偏差修正后的待拼梁段i就位高差ΔHiC。考虑线形偏差修正后,就位状态下待拼梁段i位置与其理论位置夹角差ΔφiC为:
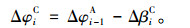
|
(15) |
待拼梁段i前后高差按ΔHiC就位,再焊接拼接,实测所得的焊后高差为ΔHiA,则待拼梁段i焊后位置与其就位位置间的夹角差ΔγiA由几何关系有:
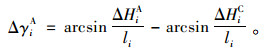
|
(16) |
待拼梁段i焊后实际位置与其理论位置夹角差ΔφiA为:
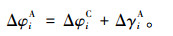
|
(17) |
焊后待拼梁段i后端高程与其理论差值ΔhiA,由几何关系有:
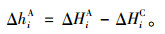
|
(18) |
式(18)即为梁段i拼接焊后的线形偏差值。
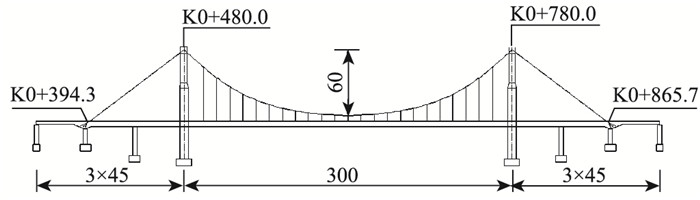
3 工程应用实例 3.1 工程概况株洲枫溪大桥主桥为3×45 m+300 m+3×45 m自锚式悬索桥(见图 7),边跨和锚跨为支架现浇混凝土箱梁,主跨主梁为单箱三室扁平流线型钢箱梁。
|
| 图 7 桥梁立面布置图(单位:m) Fig. 7 Layout of bridge elevation (unit:m) |
| |
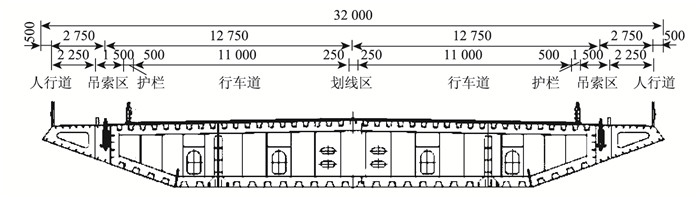
钢箱梁中心梁高3.5 m(内轮廓),全宽:2×(0.5 m风嘴+2.25 m人行道+1.5 m吊索区+0.5 m护栏+11.0 m行车道划线区+0.25 m双黄线)=32 m,桥面设2%的双向横坡,底板水平,标准横断面如图 8所示。
|
| 图 8 标准横断面图(单位:mm) Fig. 8 Standard cross-section (unit:mm) |
| |
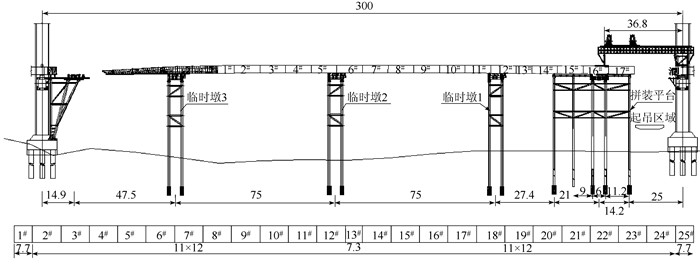
钢箱梁总长298 m,沿桥纵向划分为27个梁段,标准梁段长12 m,最短梁段长7.3 m。中间1#~23#梁段分23批次进行提升顶推架设,顶推总长259 m。顶推导梁长54 m,拼装平台长35.4 m,设3个临时墩,最大跨径75 m,墩顶标高依梁底成桥标高设置,梁钢箱梁步履式顶推施工流程及箱梁整体分段情况如图 9所示。
|
| 图 9 钢箱梁步履式顶推施工流程及箱梁整体分段图(单位:m) Fig. 9 Diagram of steel box girder segments and incremental launching construction process (unit:m) |
| |
此外,由于两侧主塔均位于湘江水中,离河岸百米有余,拼装平台上提升钢箱梁的设备遮挡了部分测量视线,综合考虑后最终采取相邻梁段高差控制梁体线形。
3.2 梁段制造构形确定该桥梁体理论无应力线形为半径R=14 000 m常曲率竖曲线,设计采用矩形法确定梁段制造构形,梁段上下焊缝理论宽度差见表 3。
| 编号 | 轴线长/mm | ΔθiN/(°) | 梁高(内轮廓)/mm | 上下焊缝宽度差/mm |
| 1# | 7 700 | 0 | 3 500 | 0 |
| 2# | 12 000 | -0.040 4 | 3 500 | 2.5 |
| 3#~12 #15#~24# |
12 000 | -0.049 1 | 3 500 | 3.0 |
| 13# | 7 300 | -0.039 5 | 3 500 | 2.4 |
| 14# | 12 000 | -0.039 5 | 3 500 | 2.4 |
| 25# | 7 700 | -0.040 4 | 3 500 | 2.5 |
由表 3知,钢箱梁制造梁段间理论上下焊缝宽度差在3 mm左右。但由于制造误差因素的存在,实际拼接时,某两梁段间上下焊缝宽度差超规范值(5 mm),这时现场采用了本研究所提“等高等邻边梯形法”对该两梁段进行必要切割处理,其拼转角采用线形修正后的实际拼转角ΔθiC。
3.3 待拼梁段2#就位高差确定1#梁长l1=7 700 mm,待拼梁段1#焊后位置与其理论位置夹角差为0,顶推前行该梁段长,形成新的接拼梁段1#,接拼梁段1#前后端高差ΔH1C′=-83.9 mm(纵向坡度1.09%);待拼梁段2#梁长为l2=12 000 mm,理论拼转角Δθ2N=-0.040 4°。
则:φ1C′=(ΔH1C′, l1)T=(-83.9, 7 700)T,
传递矩阵: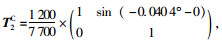
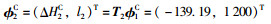
现场实际施工时,在接拼梁段2#前后端距离端口一定距离处各布置控制点,由ΔH2C即可确定待拼梁段2#上两控制点相对高差。
3.4 后续典型梁段就位高差确定后续梁段就位高差确定均采用自编程序计算,限于篇幅,下面仅列举第12#,13#,14#梁段拼装情况(见表 4),其余批次类似处理。
| 梁段号 | li/mm | ΔθiN /(°) | ΔβiC /(°) | ΔθiC /(°) | ΔHiC /mm | ΔHiA /mm | ΔγiA /(°) | ΔφiA /(°) | ΔhiA /mm |
| 12#拼装就位 | |||||||||
| 接拼梁段11# | 12 000 | -0.049 1 | -0.031 9 | -0.017 2 | -99.4 | -99.4 | -0.004 8 | 0.082 4 | -1.1 |
| 待拼梁段12# | 12 000 | -102.9 | -104.0 | ||||||
| 13#拼装就位 | |||||||||
| 接拼梁段12# | 12 000 | -0.039 5 | -0.074 6 | 0.035 1 | -91.4 | -91.4 | 0.002 3 | 0.010 1 | 0.2 |
| 待拼梁段13# | 7 300 | -60.8 | -60.6 | ||||||
| 14#拼装就位 | |||||||||
| 接拼梁段13# | 7 300 | -0.039 5 | 0.011 1 | -0.050 6 | -56.4 | -56.4 | -0.013 4 | -0.172 6 | -2.8 |
| 待拼梁段14# | 12 000 | -103.3 | -106.1 | ||||||
3.5 梁体拼接顶推全部完成后的控制效果
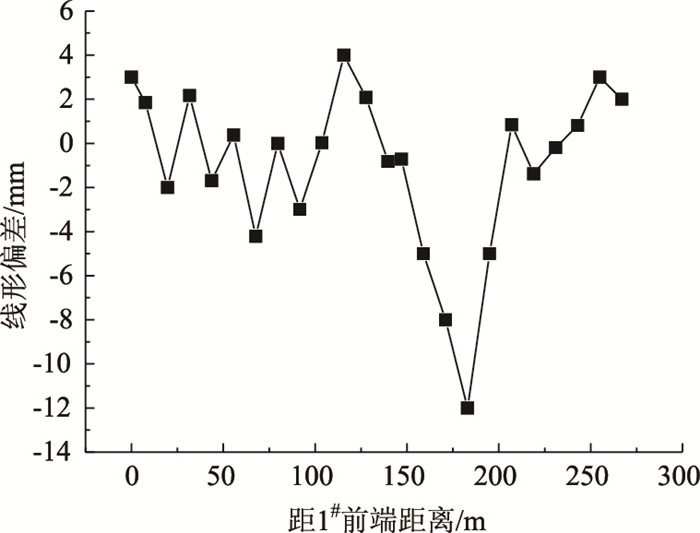
梁体全部顶推到位后,根据整体测量数据叠加上自重挠度的反向曲线得到实际无应力线形,其与目标线形(理论无应力线形)的偏差如图 10所示。由图 10可知,除极少数几个测点由于测量时局部误差的存在,偏差值超过了10 mm,其他测点误差值都在10 mm之内,线形精度完全在设计与规范要求之内,说明高精度实现了梁体无应力线形。
|
| 图 10 顶推完成后实际无应力线形与目标线形的偏差 Fig. 10 Deviations between practical unstressed geometry and object geometry after incremental launching |
| |
4 结论
(1) 带直角梯形法适应性远大于矩形法;矩形法确定的制造构形相邻梁段间的焊缝宽度差、带直角梯形法确定的梁高差或邻边差均随梁高及拼转角增大而增大。
对梁高3.5 m的梁段,当拼转角超过0.082°时,其焊缝宽度差超5 mm,带直角梯形法确定的梁高差或邻边差随梁高及拼转角增大而增大,对梁高3.5 m的梁段,当拼转角超过1.937°时,其梁高差或邻边差已超过2 mm,均不再合适。
(2) 等高等邻边梯形法对任意梁高、任意转角梁体各梁段制造构形均适用。不仅适用顶推,而且适用大节段吊装、悬臂拼装等原位拼装的桥梁。
(3) 以梁段两端高差为基本变量,以传递矩阵形式表示的待拼梁段就位高程确定方法,拓展了相位变换法的表达形式,编程简化,更直观实用。
成果在依托工程中应用,效果良好。
| [1] |
梁鹏, 肖汝诚, 徐岳. 超大跨度斜拉桥的安装构形与无应力构形[J]. 长安大学学报:自然科学版, 2006, 26(4): 49-53. LIANG Peng, XIAO Ru-cheng, XU Yue. Assembled Geometry and Unstrained Geometry of Super Long Span Cable-Stayed Bridges[J]. Journal of Chang'an University:Natural Science Edition, 2006, 26(4): 49-53. |
| [2] |
秦顺全. 桥梁施工控制:无应力状态法理论与实践[M]. 北京: 人民交通出版社, 2007. QIN Shun-quan. Bridge Construction Control:Theory and Practice of Un-stress State Method[M]. Beijing: China Communications Press, 2007. |
| [3] |
李乔, 卜一之, 张清华. 基于几何控制的全过程自适应施工控制系统研究[J]. 土木工程学报, 2009, 42(7): 69-77. LI Qiao, BU Yi-zhi, ZHANG Qing-hua. Whole-procedure Adaptive Construction Control System Based on Geometry Control Method[J]. China Civil Engineering Journal, 2009, 42(7): 69-77. |
| [4] |
周绪红, 吕忠达, 狄瑾, 等. 大跨径简支转连续箱梁桥的线形观测与控制[J]. 中国公路学报, 2007, 20(3): 54-59. ZHOU Xu-hong, LÜ Zhong-da, DI Jin, et al. Line Shape Observation and Control of Simple-supported-to-continuous Long-span Box Girder Bridges[J]. China Journal of Highway and Transport, 2007, 20(3): 54-59. |
| [5] |
吴皋, 颜东煌, 许红胜, 等. 大跨度桥梁钢箱梁拼接顶推施工过程线形控制的若干问题[J]. 北京交通大学学报, 2006, 30(增): 150-152. WU Hao, YAN Dong-huang, XU Hong-sheng, et al. Several Linear-control Questions of Long Span Steel Box Girder in Spelling and Thrusting Case[J]. Journal of Beijing Jiaotong University, 2006, 30(S): 150-152. |
| [6] |
黄伟. 顶推钢箱梁施工中拼接线形控制的实践研究[J]. 中外建筑, 2007(6): 85-86. HUANG Wei. Practice Research of Splicing Line Shape Control in Construction of Incremental Launching Steel Box Beam[J]. Chinese and Overseas Architecture, 2007(6): 85-86. |
| [7] |
颜东煌, 陈常松, 董道福, 等. 大跨度钢主梁斜拉桥的自适应无应力构形控制[J]. 中国公路学报, 2012, 25(1): 55-58, 82. YAN Dong-huang, CHEN Chang-song, DONG Dao-fu, et al. Control of Self-adaptive Zero-stress Configuration for Long-span Cable-stayed Bridge with Steel Main Girders[J]. China Journal of Highway and Transport, 2012, 25(1): 55-58, 82. |
| [8] |
张晔芝, 谢晓慧. 铁路特大桥钢箱梁顶推过程受力分析及改善方法[J]. 中国铁道科学, 2009, 30(3): 21-26. ZHANG Ye-zhi, XIE Xiao-hui. The Mechanical Behaviors and Improvement Measures of Railway Grand Bridge during Incremental Launching of the Steel Box Girder[J]. China Rrailway Science, 2009, 30(3): 21-26. |
| [9] |
张玉平, 董创文. 江东大桥双塔单跨空间主缆自锚式悬索桥的施工控制[J]. 公路交通科技, 2010, 27(4): 76-82. ZHANG Yu-ping, DONG Chuang-wen. Construction Control of Self-anchored Suspension Bridge with Two Pylons and Single Span Spatial Cables in Jiangdong Bridge[J]. Journal of Highway and Transportation Research and Development, 2010, 27(4): 76-82. |
| [10] |
王俊, 李传习. 变曲率竖曲线钢箱梁顶推施工临时墩标高调整方案确定[J]. 中外公路, 2011, 31(3): 177-181. WANG Jun, LI Chuan-xi. Determination of Elevation Adjustment of Temporary Pier in Construction of Curved Vertical Curved Steel Box Girder[J]. Journal of China & Foreign Highway, 2011, 31(3): 177-181. |
| [11] |
董创文, 李传习, 张玉平, 等. 变曲率竖曲线梁顶推过程支点标高调整方案确定的单步模数搜索合成法[J]. 土木工程学报, 2015, 48(1): 101-111. DONG Chuang-wen, LI Chuan-xi, ZHANG Yu-ping, et al. Single-step Modulus Search and Composition Method for Determining the Scheme of Support Elevation Adjustment during Girder Launching with Vertically Varied Curvatures[J]. China Civil Engineering Journal, 2015, 48(1): 101-111. |
| [12] |
董创文, 李传习, 王琛. 考虑相位变化及组拼高程偏差的顶推梁体无应力线形的实现[J]. 土木工程学报, 2013, 46(8): 74-82. DONG Chuang-wen, LI Chuan-xi, WANG Chen. Achieving Unstressed Geometry of Incrementally Launched Girders Considering Phase Shift and Elevation Deviation during Assembly Stage[J]. China Civil Engineering Journal, 2013, 46(8): 74-82. |
| [13] |
李传习, 王琛, 董创文, 等. 基于相位变换的顶推曲梁桥自适应无应力构行控制[J]. 中国公路学报, 2014, 27(2): 45-53. LI Chuan-xi, WANG Chen, DONG Chuang-wen, et al. Control of Self-adaptive Unstressed Configuration for Incrementally Launched Curved Girder Bridge Base on Phase Transformation[J]. China Journal of Highway and Transport, 2014, 27(2): 45-53. |
| [14] |
林建平, 汪劲丰, 陈春雷, 等. 槽形组合钢梁桥顶推施工线形控制[J]. 桥梁建设, 2014, 44(4): 102-106. LIN Jian-ping, WANG Jin-feng, CHEN Chun-lei, et al. Geometric Shape Control of Trough Steel Girder Composite Bridge Constructed by Incremental Launching Method[J]. Bridge Construction, 2014, 44(4): 102-106. |
| [15] |
熊正强. 变曲率竖曲线连续钢梁桥顶推施工线形控制研究[J]. 中外公路, 2015, 35(4): 187-191. XIONG Zheng-qiang. Study on Geometry Control during Incremental Launching of Variable Curvature Vertical Curve Continuous Beam Bridge[J]. Journal of China & Foreign Highway, 2015, 35(4): 187-191. |
| [16] |
JB/T 7949-1999, 钢结构焊缝外形尺寸[S]. JB/T 7949-1999, Weld Outer Dimensions for Steel Construction[S]. |
| [17] |
DB32/T947-2006, 公路桥钢箱梁制造规范[S]. DB32/T947-2006, Cob for Manufacture of Highway Bridge Steel Box Girder[S]. |
| [18] |
JUNG K H, KIM K S, SIM C W, et al. Verification of Incremental Launching Construction Safetyfor the Ilsun Bridge the World's Longest and Widest Prestressed Concrete Box Girder with Corrugated Steel Web Section[J]. Journal of Bridge Engineering, 2011, 12(3): 453-460. |
 2018, Vol. 35
2018, Vol. 35
