扩展功能
文章信息
- 谭小刚, 张洪伟
- TAN Xiao-gang, ZHANG Hong-wei
- 基于小尺度分形维数的裂缝图像分割方法
- A Crack Image Segmentation Method Based on Small Scale Fractal Dimension
- 公路交通科技, 2018, 35(5): 34-39
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(5): 34-39
- 10.3969/j.issn.1002-0268.2018.05.005
-
文章历史
- 收稿日期: 2018-02-06
2. 内蒙古自治区道路结构与材料重点实验室, 内蒙古 呼和浩特 010051
2. Key Laboratory of Road Structures and Materials, Hohhot Inner Mongolia 010051, China
公路路面破损程度评估是公路养护工作中一项非常关键的任务。传统的人工检测方法不仅费时费力,而且易受检测人员主观判断因素的影响,检测结果通常不太准确。目前,随着计算机技术的不断发展和数字图像处理技术的不断完善,基于图像的路面裂缝检测系统已被广泛应用于公路路面的养护工作中。
国内外很多学者针对裂缝检测这项工作做过大量的研究和试验。早在2003年,初秀民等[1]将路面破损图像进行分块处理,求得了子块图像的灰度方差值、所有子块灰度方差的均值和最小值来描述纹理。随后,美国托莱多大学的Katakam[2]在2006年通过将图像划分为不同的区域,针对每个区域采用局部阈值方法进行阈值分割,从而得到图像的裂缝信息。李清泉等[3]也在2010年提出了基于最小代价路径的图论的路面裂缝检测算法。
近年来,随着图像技术的迅速普及,越来越多的图像处理算法也应用于路面裂缝检测中。Xu等[4]提出了基于显著性检测的裂缝检测方法,根据裂缝的结构特征构建显著图,并根据所获得的显著图提取出裂缝信息。2016年,Amhaz等[5]利用最短路径搜索算法,并根据裂缝具有全局跟踪亮度最小的特征来提取裂缝信息,并取得了不错的结果。基于张量投票的方法也常应用于裂缝自动检测中,Shi等[6]将张量投票方法与Random变换相结合检测裂缝信息。Cho等[7]研究了光照强度、场景距离等因素对裂缝成像效果的影响,并进行了室外试验验证。Li等[8]提出了基于活动轮廓模型和支持向量机的裂缝检测方法,该方法首先选取裂缝种子点,再将裂缝图像进行分类。
虽然关于路面裂缝检测的研究成果很多,但所采集的裂缝图像容易受到光照不均、噪声、天气等因素的影响,使得裂缝提取效果不尽如人意。本研究在前人研究的基础上,提出了一种基于小尺度分形维数理论的裂缝图像分割方法,并通过试验验证所提出算法的有效性。
1 路面图像滤波实际获取的路面图像中往往含有不同的噪声,这就给裂缝的提取与分析带来了困难。为了得到更好的裂缝图像分割结果,首先需要进行图像滤波去噪,即在保留裂缝信息的前提下对路面图像中的噪声进行抑制。图像滤波的效果将对后续裂缝检测和分析的有效性和可靠性产生直接影响,常见的图像滤波方法有均值滤波、高斯滤波和中值滤波。
1.1 均值滤波均值滤波也称线性滤波[9]。其主要方法是邻域平均法,即通过计算邻域内的所有像素平均值代替该点的像素值,起到去除突变的像素点进而达到去除噪声的目的。具体的实现方法是给定模板中全体像素的平均值代替原来的像素值。
1.2 高斯滤波高斯滤波是一种线性平滑滤波[10]。由于可以有效消除高斯噪声,广泛应用于图像处理的减噪过程。在图像中,每个像素点的灰度不仅与邻域内像素的灰度值有关,而且也与邻域内像素的位置有关。均值滤波虽然考虑了邻域内像素的灰度,却没考虑邻域内由于位置不同对该像素的影响效果也不尽相同,只是简单地将邻域内所有位置的像素点进行相同的处理,因此会导致处理后的图像变得模糊。而高斯滤波考虑到不同像素点的位置对该像素影响效果的不同,引入了加权系数,距离中心元素越近的点,加权系数越大,对像素点的影响效果越大。
1.3 中值滤波中值滤波是一种非线性平滑技术[11],其基本原理是把将要处理像素点的某个邻域内的所有像素按照灰度值的大小进行排列,取排列的中值作为该像素点的新值,进而让周围的像素接近真实值,从而消除孤立的噪声点。如图 1所示。
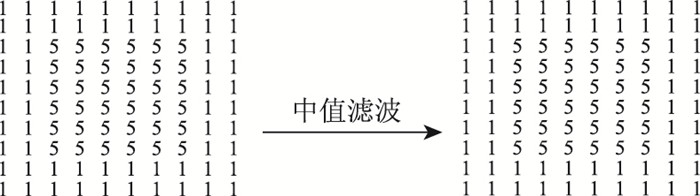
|
| 图 1 中值滤波模板举例 Fig. 1 Examples of median filtering template |
| |
1.4 选择中值滤波的原因
路面图像中的裂缝不仅拥有非常丰富的边界信息,而且图像中还有孤立点的噪声及随机分布噪声的存在。
通过对3种的滤波方法分析得出,经过均值滤波后的整个图像不仅变得模糊,而且对去除孤立点的噪声几乎没有效果。高斯滤波后的图像可以有效消除高斯噪声,但是裂缝的边界变得模糊,而且对去除孤立点噪声的效果也不明显。而经过中值滤波后的图像可以保留裂缝边缘信息,还能有效地去除孤立点的噪声。
经过对图像滤波技术比较分析,本研究选择中值滤波实现裂缝图像分割的去噪处理。
2 基于分形学的路面裂缝图像分割算法分形几何学由法国数学家Mandelbrot[12]于1973年首次提出,分形几何学主要是通过一种定量描述的方式表述自然界中不规则的、具有自相似性和自仿射性的对象。比较而言,传统几何在分形几何图形的不同尺度上有着相同的规则性,分形图形整体又有着处处不规则的特性。
2.1 分形维数定义分形维数是用来衡量自然界不规则程度的度量参数,通过将图像的几何信息和图像的灰度信息进行关联,使其在描述自然界物体的规则度上具有稳定性。其定义并不唯一,在欧几里得n维空间中,将1个有界集A的分维数表示为:
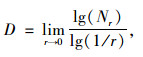
|
(1) |
式中,Nr为尺度r上集合A不同副本的最小数目,且Nr不同副本的集合必须包含集合A;r为小立方体的边长;D为集合A的分形维数。
2.2 路面分形维数的裂缝图像分割算法路面裂缝信息可以看作自相似性确定的目标,整个裂缝信息都具有相似的分形维数特征。因此,本研究采用基于分形维数的理论实现对裂缝图像的分割[13]。在图像处理中,一般采用差分计盒维数的方法实现对图像分形维数的估算。
在图像处理中,首先将二维图像用三维空间重新表示图像,如图 2所示。平面上的像素位置用(x, y)表示,像素灰度级用坐标z表示。在传统的DBC方法中,(x, y)平面被划分成大小为s×s的不重叠的块,每个块的尺度为r=s/M,大小为s×s×h,h为每个盒子的高度,M根据公式G/h=M/s计算得到,G为灰度级别总数,M/2≥s>1,s为整数。
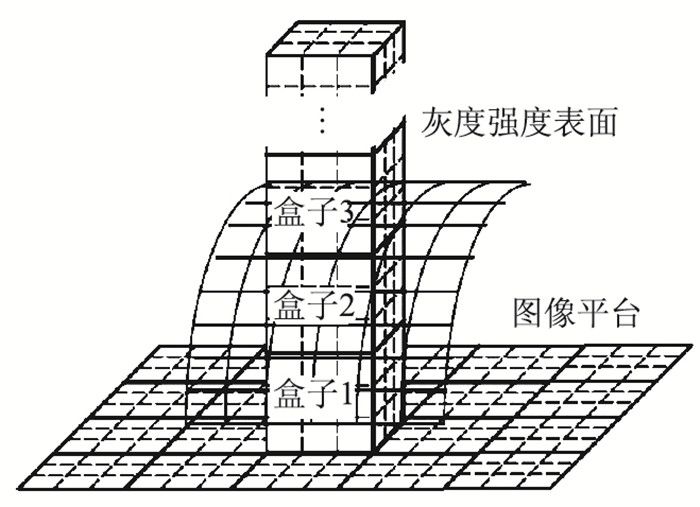
|
| 图 2 裂缝图像分割示意图 Fig. 2 Schematic diagram of crack image segmentation |
| |
在计算分形维数时,尺度r越小,体现图像的细节越真实。当r值取最小值1时,图像细节最好,但是传统的方法无法适应。因此,对于r=1时的小尺度分形维数的计算方法做出如下定义[14-16]。
当计算某像素的分形维数时,通过计算(i, j)的2×2四邻域的像素来计算分形维数。在对应的第(i, j)个块中的最小和最大灰度级分别为gmax和gmin,则中心像素点的分形维数计算公式为:
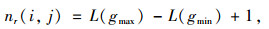
|
(2) |
式中,L(gmax)和L(gmin)分别为像素点(i, j)相邻邻域中像素点中灰度最大和最小值所在位置。
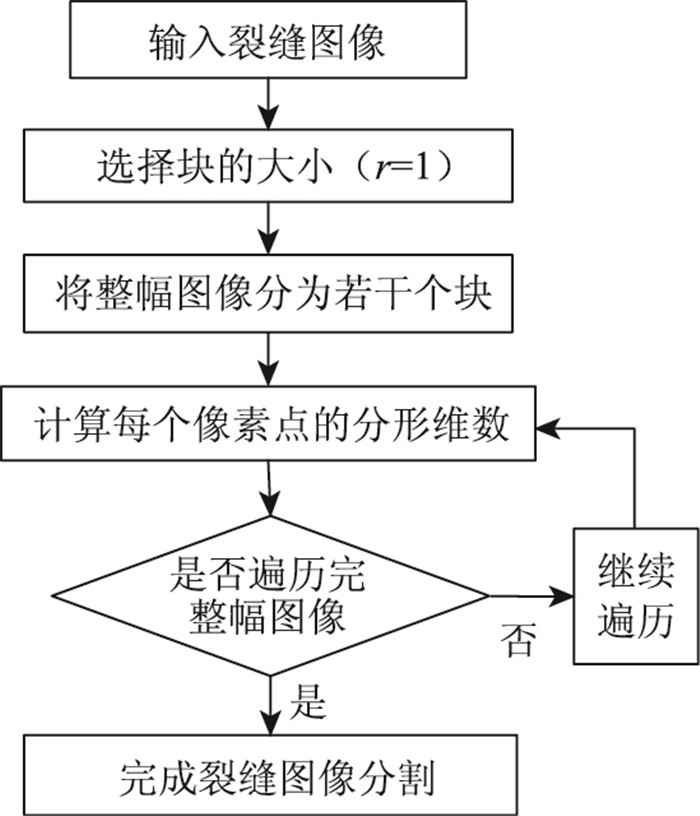
基于小尺度的分形维数计算流程图如图 3所示。
|
| 图 3 小尺度的分形维数计算流程图 Fig. 3 Flowchart of fractal dimension calculation at small scale |
| |
可以看出,本研究方法可以计算路面图像中所有像素点的分形维数特征,该算法将其维数细化到最小值使其图像细节得到最大的体现。比较传统的分形维数算法,该算法可以使裂缝的不规则性得到更好的体现,能够对于裂缝不规则的特征进行分割,得到更好的效果。
3 试验结果对比为了更好地体现算法的性能,通过与阈值分割(二值化)、大津法(OTSU)、边缘检测(Canny)及传统的分形维数(FD)等经典图像算法进行分析对比。结果如图 4所示。

|
| 图 4 裂缝图像分割结果对比 Fig. 4 Comparison of crack image segmentation results |
| |
从裂缝图像分割结果来看,因为如图 4(a)所示的路面较为粗糙,二值化算法和OTSU算法对图像进行分割处理时,都将裂缝形态本身和大量噪声混合在一起,无法分辨出裂缝的原本形态,无法正确提取裂缝,如图 4(b)和图 4(c)所示。采用Canny算子的边缘检测虽然勉强可以体现出裂缝信息,但是也同样伴随着许多噪声的边缘信息,无法满足裂缝图像分割的要求,如图 4(d)所示。而使用传统FD算法处理图像同样也无法得到有效的裂缝信息,如图 4(e)所示。最后,使用本研究算法可以很好地去除噪声的影响,同时完整地分割出裂缝的原本形态,试验结果较为清晰,如图 4(f)所示。
可以看出,在传统图像分割算法中不会计算每个像素的分形维数,故而不会注重图像的细节处理,在边缘处理的过程中并不占优势,但是裂缝图像的关键信息存在于边缘中。这些方法都只能提取目标区域的大概范围,而不能准确提取。而本研究算法中加入了对像素自身的分析和计算,可以尽可能地得到目标区域的特征信息,保留其边缘特征。
4 试验结果分析现有研究多釆用准确率衡量图像识别算法的优劣,但它具有一定的局限,如:识别结果为100个裂缝像素点,准确率100%,实际上却有1 000个裂缝像素点,算法只识别了10%的目标物,综合来看算法并不好。算法分类结果既要准确又要全面,因此,引入了准确率、召回率(Precision and Recall)这样一组指标评价裂缝分类算法的性能[17-18]。
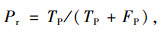
|
(3) |
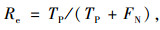
|
(4) |
式中,Pr为准确率;Re为召回率;TP为正确检测出来的目标物数目(True Positive);FP为不是目标物却检测为目标物的数目(False Positive);FN为目标物却没检测出来的数目(False Negative)。
最终的F-测度计算公式为:
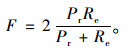
|
(5) |
裂缝图像分割的对应准确率、召回率参数如表 1所示。
| 方法分类 | 准确率 | 召回率 | F-measure |
| 二值化 | 0.413 | 0.862 | 0.558 |
| Otsu | 0.452 | 0.851 | 0.591 |
| Canny | 0.437 | 0.703 | 0.538 |
| FD | 0.365 | 0.624 | 0.462 |
| 本研究方法 | 0.897 | 0.915 | 0.916 |
可以看出,在召回率上,4种经典方法并没有表现出很大的区别,其中二值化和Otsu的召回率分别达到了0.862和0.581,而本研究方法(0.915)并没有表现出较大的优越性。然而在准确率上,本研究方法可以达到0.897,比其余的方法高出了很多。其中二值化和FD方法的准确率分别只有0.413和0.365,而Canny方法也只达到了0.437。因此,在综合召回率和准确率的基础上,造成了本研究方法在F-测度上达到0.916,而其余的方法都在0.6以下。
为了更好地验证裂缝图像的分割的效果,选取了一系列图像数据进行验证,其准确率和召回率数据如图 5所示。从图 5(a)可以看出,所有的方法都可以在召回率上得到较好的结果,其中的二值化方法(数据4)和Canny算子(数据6)几乎和本研究方法拥有同样的检测性能。然而图 5(b)显示,这些传统方法在准确率上并不能有较好的结果。传统方法与本研究方法仍然存在着一定的差距。在F-测度上本研究方法基本都稳定在0.9左右,而传统方法的F-测度大多都徘徊在0.7以下,甚至有些结果(二值化的数据15)竟然下降到0.3以下,如图 5(c)所示。因此总体上看,相比于传统的方法,本研究方法可以取得较好裂缝提取结果。
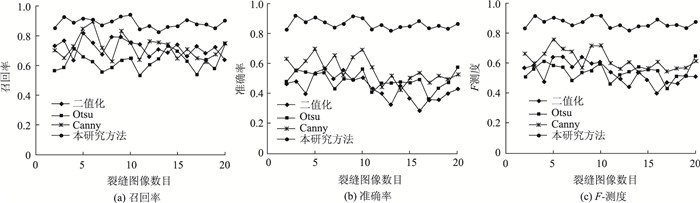
|
| 图 5 不同算法的裂缝图像分割性能比较曲线图 Fig. 5 Comparison curves of crack image segmentation performance obtained by different algorithms |
| |
5 结论
针对路面图像中裂缝噪声较多或形态较复杂的特点,在传统分割方法的基础上,提出了小尺度分形维数裂缝图像分割方法。通过试验结果和分析,相比于常用的图像分割算法,本研究提出的方法能够有效地提取裂缝形态和特征值,并在准确率和召回率上有着优良的表现,可以满足裂缝图像分割的高精度要求。
| [1] |
初秀民, 王荣本, 储江伟, 等. 沥青路面破损图像分割方法研究[J]. 中国公路学报, 2003, 16(3): 11-14. CHU Xiu-min, WANG Rong-ben, CHU Jiang-wei, et al. Study of Asphalt Pavement Surface Distress Image Segmentation[J]. China Journal of Highway and Transport, 2003, 16(3): 11-14. |
| [2] |
KATAKAM N. Pavement Crack Detection System through Localized Thresholding[D]. Toledo: University of Toledo, 2009.
|
| [3] |
李清泉, 邹勤, 毛庆洲. 基于最小代价路径搜索的路面裂缝检测[J]. 中国公路学报, 2010, 23(6): 28-33. LI Qing-quan, ZOU Qin, MAO Qing-zhou. Pavement Crack Detection Based on Minimum Cost Path Searching[J]. China Journal of Highway and Transport, 2010, 23(6): 28-33. |
| [4] |
XU W, TANG Z, ZHOU J, et al. Pavement Crack Detection Based on Saliency and Statistical Features[C]//IEEE International Conference on Image Processing. Melbourne: IEEE, 2013.
|
| [5] |
AMHAZ R, CHAMBON S, IDIER J, et al. Automatic Crack Detection on Two-dimensional Pavement Images:An Algorithm Based on Minimal Path Selection[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(10): 2718-2729. |
| [6] |
SHI Y, CUI L, QI Z, et al. Automatic Road Crack Detection Using Random Structured Forests[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(12): 3434-3445. |
| [7] |
CHO H W, YOON H J, YOON J C. Analysis of Crack Image Recognition Characteristics in Concrete Structures Depending on the Illumination and Image Acquisition Distance through Outdoor Experiments[J]. Sensors, 2016, 16(10): 1646-1650. |
| [8] |
LI G, ZHAO X, DU K, et al. Recognition and Evaluation of Bridge Cracks with Modified Active Contour Model and Greedy Search-based Support Vector Machine[J]. Automation in Construction, 2017, 78: 51-61. |
| [9] |
王科俊, 熊新炎, 任桢. 高效均值滤波算法[J]. 计算机应用研究, 2010, 27(2): 434-438. WANG Ke-jun, XIONG Xin-yan, REN Zhen. Highly Efficient Mean Filtering Algorithm[J]. Application Research of Computers, 2010, 27(2): 434-438. |
| [10] |
王怀野, 张科, 李言俊. 一种自适应各项异性高斯滤波方法[J]. 计算机工程与应用, 2004, 40(10): 18-19. WANG Huai-ye, ZHANG Ke, LI Yan-jun. An Adaptive Anisotropic Gaussian Filter for Noise Reduction[J]. Computer Engineering and Applications, 2004, 40(10): 18-19. |
| [11] |
黄颖, 王卫星. 分类中值滤波算法的研究[J]. 计算机工程与应用, 2009, 45(11): 34-36. HUANG Ying, WANG Wei-xing. Research on Classification Median Filter Algorithm[J]. Computer Engineering and Applications, 2009, 45(11): 34-36. |
| [12] |
MANDELBROT B B, AIZENMAN M. Fractals:Form, Chance, and Dimension[J]. Physics Today, 1979, 32(5): 65-66. |
| [13] |
法尔科内K. 分形几何: 数学基础及其应用[M]. 曾文曲, 等. 译. 北京: 人民邮电出版社, 2007. FALCONE K. Fractal Geometry: Mathematical Foundations and Its Application[M]. ZEN Wen-qu, et al. translated. Beijing: People's Posts and Telecommunications Press, 2007. |
| [14] |
SARKAR N, CHAUDHURI B B. An Efficient Approach to Estimate Fractal Dimension of Textural Images[J]. Pattern Recognition, 1992, 25(9): 1035-1041. |
| [15] |
刘晟, 王卫星, 曹霆, 等. 基于差分计盒维数及最大熵阈值的裂缝提取[J]. 长安大学学报:自然科学版, 2015, 35(5): 13-21. LIU Sheng, WANG Wei-xing, CAO Ting, et al. Road Crack Extraction Based on Differential Box Dimension and Maximum Entropy Threshold[J]. Journal of Chang'an University:Natural Science Edition, 2015, 35(5): 13-21. |
| [16] |
KING G, MAY R. New Approaches to Tack Application[C]//The 83rd Annual Meeting of the Transportation Research Board. Washington, D. C. : TRB, 2003.
|
| [17] |
KRUNTCHEVA M R, COLLOP A C, THOM N H. Effect of Bond Condition on Flexible Pavement Performance[J]. Journal of Transportation Engineering, 2005, 131(11): 880-888. |
| [18] |
TASHMAN L, NAM K, PAPAGIANNAKIS T, et al. Evaluation of Construction Practices That Influence the Bond Strength at the Interface between Pavement Layers[J]. Journal of Performance of Constructed Facilities, 2008, 22(3): 154-161. |
 2018, Vol. 35
2018, Vol. 35
