扩展功能
文章信息
- 严圆, 李洛克, 周亦唐, 保亮
- YAN Yuan, LI Luo-ke, ZHOU Yi-tang, BAO Liang
- 混凝土路面传力杆疲劳松动行为的试验研究与数值模拟
- Experimental Study and Numerical Simulation of Fatigue Looseness Behavior of Dowel Bars in Concrete Pavement
- 公路交通科技, 2018, 35(5): 8-15
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(5): 8-15
- 10.3969/j.issn.1002-0268.2018.05.002
-
文章历史
- 收稿日期: 2017-02-22
2. 昆明理工大学, 云南 昆明 650500
2. Kunming University of Science and Technology, Kunming Yunnan 650500, China
水泥混凝土路面的横向缩缝结构是整个路面结构的最薄弱环节之一[1]。为提高缩缝的耐久性,设置光圆金属传力杆装置是最有效措施[2-3]。传力杆可将部分车轮荷载传递到相邻路板上,从而减少受荷板边的应力和挠度,使缩缝两侧路板变形协调,将错台和卿泥等早期病害减小到最低程度[4-5]。然而,荷载传递过程中传力杆与周围混凝土间存在明显的应力集中,在车轮荷载往复作用下不可避免地引起传力杆周边混凝土内出现损伤累积并发展成为传力杆的疲劳松动。传力杆松动的出现会导致路面板边缘的挠度和应力集中迅速增加,降低缩缝的传荷能力,最终可引起板边混凝土开裂。因此,研究传力杆装置在我国典型道路交通荷载条件出现松动现象的成因及疲劳扩展规律,提出合理的控制措施,对提高水泥混凝土路面缩缝结构的服役寿命具有一定的理论意义和应用价值。
基于上述原因,本研究应用数值方法研究了传力杆的力学特性与传力杆周边混凝土内应力响应,确定了水泥混凝土路面缩缝结构易发生损坏的最不利位置。在此基础上,通过试验方法模拟了传力杆的疲劳松动行为,以试验现象为基础探讨了传力杆在疲劳松动模式下的传荷失效过程。最后,应用数值方法模拟了疲劳松动过程中传力杆周边混凝土的疲劳开裂过程,给出了基于有限元仿真技术的路面缩缝结构临界车辆轴载计算方法。
1 荷载传递过程传力杆的力学特性分析 1.1 道路缩缝结构的三维有限元模型针对我国水泥混凝土路面典型结构尺寸,基于ABAQUS有限元平台建立缩缝结构三维有限元模型。
(1) 几何模型与材料参数
取行车方向相邻的两块路板为分析对象,定义X轴为行车方向,Y轴为沿横缝方向,Z轴垂直于路板平面。路板尺寸为5 m×4.5 m×0.26 m,缩缝宽度为5 mm,15根长度500 mm、直径φ32 mm的Q235钢质传力杆以圆心间距300 mm沿行车方向布置在板厚中间。基层尺寸为11.1 m×5.5 m×0.2 m,土基尺寸为11.1 m×5.5 m×2 m。混凝土面层弹性模量Ey=2.8×104 MPa,泊松比νy=0.2,密度ρy=2 400 kg/m3;基层弹性模量Et=4×102 MPa,泊松比νt=0.3,密度ρt=2 000 kg/m3;土基弹性模量Es=1.5×102 MPa,泊松比νs=0.35,密度ρs=2 100 kg/m3;传力杆弹性模量Ed=2.1×105 MPa, 泊松比νd=0.3, 密度ρd=7 800 kg/m3。
(2) 接触设置的可靠性验证
传力杆锚固端与周边混凝土设为Tie连接,可滑动端与混凝土在X方向设为摩擦系数0.1的滑动摩擦接触,Z方向为硬接触。结合肖益民[6]的混凝土板滑动摩擦试验,将面层与基层的接触面在X方向设为系数0.5的滑动摩擦接触,Z方向为硬接触。基层与土基间设为Tie连接。滑动接触应用库伦模型。
应用上述接触设置方法,对美国海军工程实验室进行的机场水泥路面缩缝传荷能力试验[7]进行模拟,通过数值解与试验解的对比来验证建模方法的正确性,如表 1所示。
| 距荷载作用位置距离/mm | 最大正弯矩/(kN·m) | 误差/% | 最大负弯矩/(kN·m) | 误差/% | 最大剪力/kN | 误差/% | |||
| 数值解 | 试验解 | 数值解 | 试验解 | 数值解 | 试验解 | ||||
| 0 | 0.306 | 0.288 | 6.250 | 0.201 | 0.189 | 6.349 | 20.66 | 22.87 | 9.663 |
| 304.8 | 0.274 | 0.259 | 5.792 | 0.177 | 0.184 | 3.804 | 13.65 | 14.65 | 6.390 |
| 609.6 | 0.179 | 0.174 | 2.287 | 0.108 | 0.122 | 11.475 | 8.79 | 9.79 | 10.018 |
| 914.4 | 0.166 | 0.185 | 10.270 | 0.060 | 0.052 | 15.385 | 3.88 | 4.08 | 8.520 |
| 1 219.2 | 0.109 | 0.128 | 14.844 | 0.046 | 0.059 | 22.034 | 2.3 | 2.4 | 10.448 |
从表 1中的对比结果可以看出,分别考虑传力杆、混凝土、面层、基层、土基间不同接触状态的道路缩缝结构建模方法,在分析传力杆与混凝土接触面力学行为方面具有良好的计算精确度。
(3) 荷载条件、边界条件、单元选择及网格划分
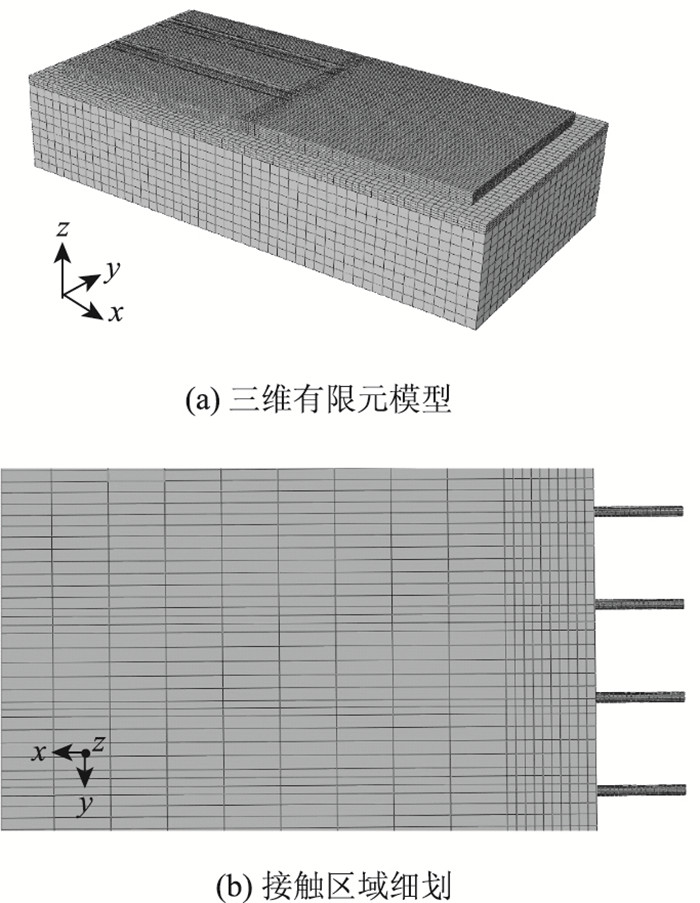
采用单轴双轮轴载模式作用于板边中部,轮胎压印(接地形状)为矩形,选择轴载100 kN,200 kN和300 kN共3种车辆轴载作为荷载条件,模拟标准车辆、重载车辆及严重超载车辆。根据Himeno[8]提出的轮胎接地压强、轮重与充气压力间的经验关系式计算轮胎接地压力。设置两个分析步,先施加各结构层重力载荷,然后再施加车轮荷载。道路缩缝结构的三维有限元模型具有147 212个C3D8R单元、170 086个节点,如图 1(a)所示。对面层板与轮胎接触区域的有限元网格进行细划,如图 1(b)所示。
|
| 图 1 传力杆路面缩缝结构有限元模型 Fig. 1 FE model of shrink joint structure of dowel bar and pavement |
| |
1.2 荷载传递过程中传力杆的力学特性分析
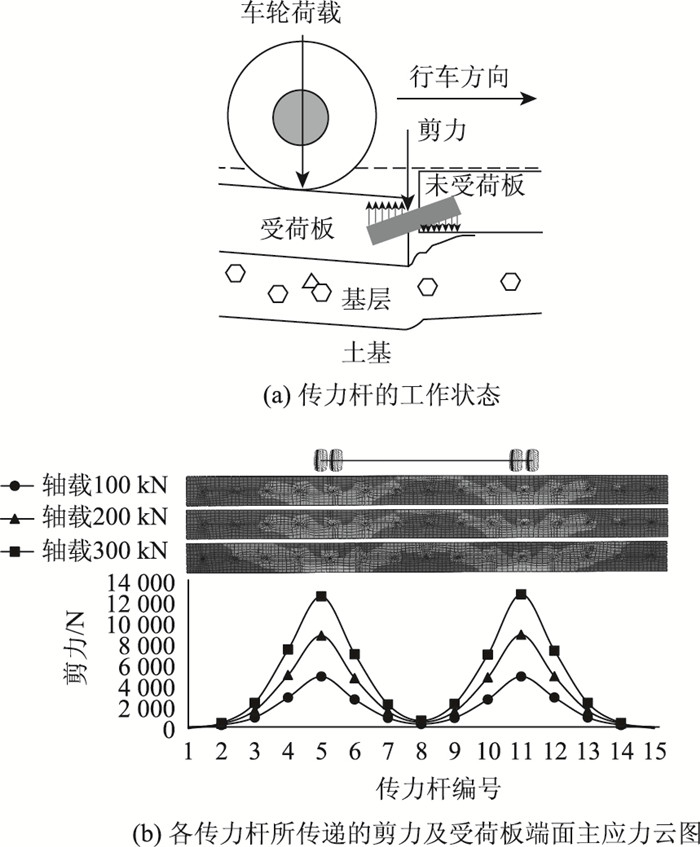
Timoshenko认为车辆荷载作用于混凝土路面受荷板边时,传力杆装置在缩缝两端路面板内依靠剪力和弯矩来传递部分车辆载荷,同时需要靠周边的混凝土提供支反力。基于经典理论,本研究通过数值模型分别提取3种轴载条件下路面缩缝每根传力杆所传递的剪力,应用剪力传递系数LTE(V)评价整组传力杆装置以剪力形式在缩缝两侧路面板内传递车辆轴载的能力,应用剪力传递分配比LTE(D)评价不同位置传力杆在整套传力杆装置荷载传递过程中的分配比例,如式(1)所示。图 2为传力杆的工作状态与3种计算工况中轮载作用一侧路面板缩缝Y-Z端面上的最大主应力云图。
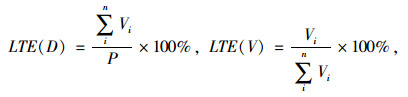
|
(1) |
|
| 图 2 传力杆的工作状态 Fig. 2 Working condition of dowel bar |
| |
式中,Vi为各传力杆所传递的剪力;P为车辆轴载;本研究模型n=15。
从模型中提取各传力杆在荷载作用时所受的最大剪力,3种计算工况中传力杆装置的剪力传递系数分别为23.72%,21.42%,20.96%,传荷分配比LTE(D)的计算结果如表 2所示。
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 工况1 | Vi | -69 | 122 | 812 | 2 642 | 4 560 | 2 463 | 770 | 211 | 770 | 2 463 | 4 560 | 2 642 | 812 | 122 | -69 |
| LTE(D) | -0.3 | 0.5 | 3.6 | 11.6 | 19.9 | 10.8 | 3.4 | 0.9 | 3.4 | 10.8 | 19.9 | 11.6 | 3.6 | 0.5 | -0.3 | |
| 工况2 | Vi | -126 | 236 | 1 525 | 4 886 | 8 654 | 4 596 | 1 424 | 405 | 1 411 | 4 665 | 8 736 | 4 770 | 1 506 | 259 | -108 |
| LTE(D) | -0.3 | 0.6 | 3.6 | 11.7 | 20.7 | 11.0 | 3.4 | 1.0 | 3.4 | 11.1 | 20.9 | 11.4 | 3.6 | 0.6 | -0.3 | |
| 工况3 | Vi | -204 | 322 | 2 243 | 7 323 | 12 386 | 6 883 | 2 094 | 549 | 2 138 | 6 841 | 12 589 | 7 215 | 235 | 40 | -252 |
| LTE(D) | -0.3 | 0.5 | 3.6 | 11.6 | 19.7 | 10.9 | 3.3 | 0.9 | 3.4 | 10.9 | 20.0 | 11.5 | 3.7 | 0.6 | -0.4 | |
数值计算结果表明,车辆荷载作用于缩缝一侧板边时,轮胎与路面接触位置下方传力杆所受剪力最大,3种工况中传力杆所受最大剪力分别为4.56,8.73 kN和12.81 kN,增加幅度超过180%。车辆轴载改变对不同位置传力杆的传荷分配比影响并不明显。由于混凝土作为承载材料为传力杆提供支反力,因此在受荷面层板一侧5#和11#传力杆上半圆周区域内的混凝土存在明显的应力集中现象,其中传力杆顶部混凝土以受压为主,两侧混凝土以受拉为主,混凝土内的应力集中情况随车辆轴载增加迅速加剧。考虑实际道路运营过程中存在的渠化交通现象,本研究将轮胎与路面接触位置下方传力杆附近应力集中区域定义为荷载传递过程中缩缝结构的最不利位置。
2 传力杆的疲劳松动行为的试验研究 2.1 传力杆试件的疲劳试验以荷载传递过程中路面缩缝最不利位置的传力杆作为研究对象,将其周边400 mm×300 mm×260 mm体积区域作为缩缝试验子结构。按质量配合比为m(水泥):m(沙子):m(石料):m(水):m(减水剂)=1:2.05:3.5:0.45:0.015制作C30混凝土与直径32 mm的R235级圆钢组合的传力杆试件,如图 3(a)所示。采用基于ABAQUS的子结构拟静力加速加载试验方法[9],设计传力杆试件的疲劳试验设备如图 3(b)所示。为保证传力杆试件具有缩缝试验子结构相同的受力状态,基于圣维南原理,设计顶板、边板与拉压传感器相连构件模拟边界条件;将数值计算3种工况中最不利位置传力杆所受的剪力转化为脉动循环的等幅交变动力荷载,通过专门的加载装置施加至试验子结构试件的相应位置进行拟静力加速加载试验,如图 3(c)所示。100 kN标准车辆轴载对应的疲劳工况1加载制度为:Pmax=4.56 kN,Pmin=10%Pmax,ΔP=90%Pmax,f=1 Hz。200 kN重载车辆轴载对应的疲劳工况2加载制度为:Pmax=8.73 kN,Pmin=10%Pmax,ΔP=90%Pmax,f=1 Hz。300 kN严重超载车辆轴载对应的疲劳工况3加载制度为:Pmax=12.59 kN,Pmin=10%Pmax,ΔP=90%Pmax,f=1 Hz。循环次数均为3万次。用LVDTs传感器采集加载点在疲劳循环中的位移变化,用声发射技术监测试件应力集中区域动态损伤过程的声发射特征参数,如图 3(d)所示。

|
| 图 3 疲劳试验装置 Fig. 3 Fatigue experimental device |
| |
2.2 传力杆的疲劳松动行为分析
经过30 000次荷载循环后,疲劳工况1与疲劳工况2加载点最大位移无显著变化,而疲劳工况3加载点在试验结束阶段峰值荷载时的最大位移比试验初始时增加了0.21 cm,传力杆出现了疲劳松动现象。在疲劳工况1与疲劳工况2试验过程中,传力杆试件仅在循环加载初期可采集到少量的声发射信号,而在疲劳工况3试验全程中均有声发射信号产生。
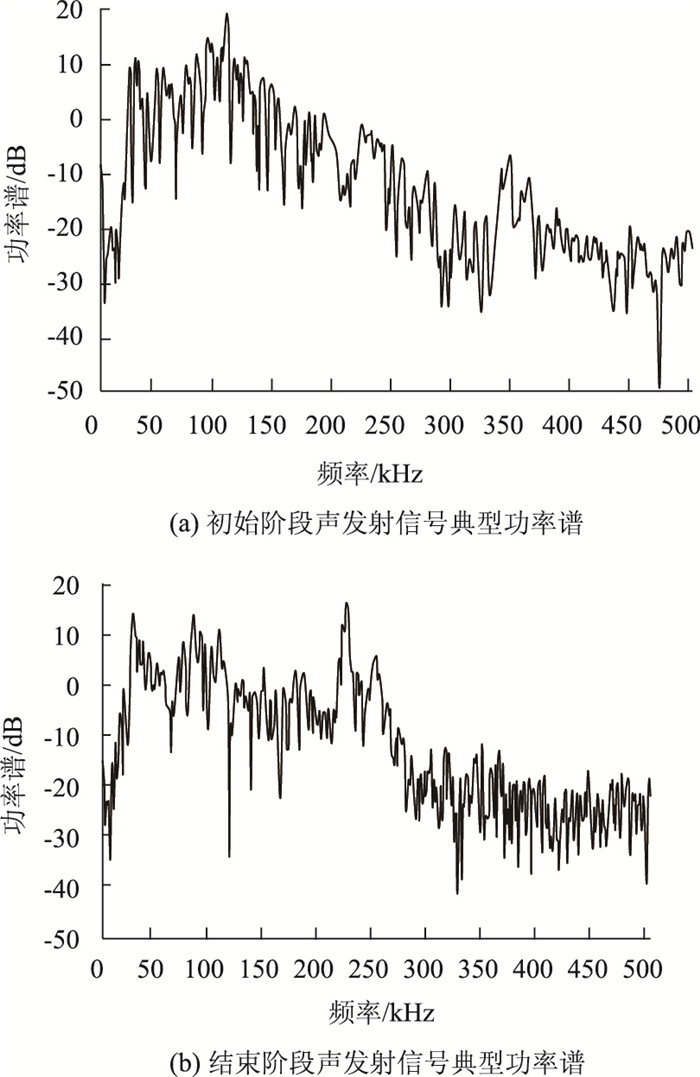
声发射监测技术的本质是根据声发射信号波形的各项特征分析来解释声发射源的损伤信息[10]。纪洪广认为混凝土在荷载作用下出现的内部骨料开裂、砂浆开裂及两者交界面微裂纹扩展都会产生声发射信号[11]。吴胜兴通过试验发现骨料破坏的声发射信号峰值频率较高,砂浆破坏的声发射信号峰值频率相对较低,交界面破坏的声发射信号峰值频率居中[12]。依据上述研究成果,提取疲劳工况3初始阶段和结束阶段中的典型声发射信号的功率谱进行对比,如图 4所示。
|
| 图 4 典型功率谱对比 Fig. 4 Comparison of typical power spectra |
| |
由图 4可以看出,在疲劳工况3的初始阶段,声发射信号的峰值频率在50~150 kHz之间,属于低频峰值信号与高频峰值信号同时存在阶段,说明该阶段试件内部损伤由传力杆与混凝土接触面脱粘及混凝土微裂纹起裂扩展两部分组成。在疲劳工况3的结束阶段,声发射信号的峰值频率上升至150~250 kHz区间,说明由混凝土微裂纹的萌生、扩展所引起的高频信号成为第2阶段试件内部的主要损伤源。
综合分析可以发现,在与100,200 kN两种车辆轴载相对应的疲劳加载制度下,传力杆与混凝土虽然在交界面上存在着不匹配的应变水平,但由于疲劳荷载峰值与幅值较低,因此二者接触面附近区域的力学性能未显著退化,传力杆的力学特性没有发生改变。在与300 kN车辆轴载相对应的疲劳加载条件下,传力杆与混凝土接触面附近区域的应力水平显著加剧,造成两种材料在接触面持续脱粘,同时混凝土内微裂纹不断起裂并发生疲劳扩展,出现累积损伤。试验现象表明车辆轴载通过缩缝可导致传力杆与混凝土间处于高接触应力的加卸载状态,重载车辆的长期作用将不可避免地引起传力杆周边混凝土材料发生龟裂与剥落,最终造成传力杆疲劳松动量的不断增加。
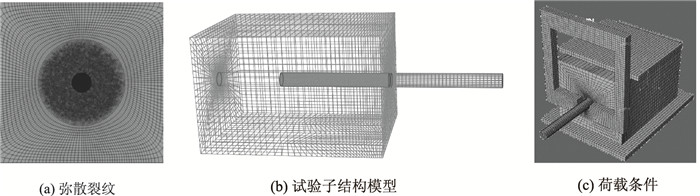
3 传力杆疲劳松动行为的数值模拟 3.1 含弥散裂纹体的缩缝试验子结构有限元模型为模拟传力杆周边应力集中区域内混凝土材料在疲劳应力加卸载过程中内部微裂纹的起裂、疲劳扩展行为,本研究以弥散分布裂纹体模拟混凝土材料内的原有裂纹状缺陷。通过对有限元软件二次开发,在传力杆周边3倍半径应力集中区域内生成192条0.05 mm至0.5 mm随机长度非线性分布的初始微裂纹,建立含弥散裂纹体的混凝土二维平面模型如图 5(a)所示。在ABAQUS有限元平台上利用实体单元建立缩缝的试验子结构足尺三维有限元模型,将弥散裂纹体平面模型嵌入三维模型距端面2.5 mm的Y-Z断面上,如图 5(b)所示。数值模型的荷载条件与疲劳试验工况3相同,如图 5(c)所示。根据本研究道路缩缝结构的三维有限元模型计算结果插值出试验子结构边界上各节点的位移值作为子模型的位移边界。材料参数为:混凝土弹性模量Ey=2.8×104 MPa,泊松比νy=0.2,密度ρy=2 400 kg/m3;传力杆弹性模量Es=2.1×105 MPa, 泊松比νs=0.3, 密度ρs=7 800 kg/m3。采用扩展有限元法模拟裂纹在任意方向的扩展行为,应用Heaviside函数联系裂纹两侧不连续的位移场,使裂纹扩展独立于网格划分。
|
| 图 5 缩缝子结构有限元模型 Fig. 5 Shrink joint substructure FE model |
| |
3.2 混凝土疲劳裂纹的起裂、扩展准则
疲劳应力幅值不变,混凝土内微裂纹疲劳扩展行为可分为初始起裂、稳定疲劳扩展、失稳扩展3个阶段。第1阶段内裂纹扩展较快,第2、3阶段扩展速率服从Paris准则[13]。在有限元分析时,采用虚拟裂纹闭合法,根据裂纹尖端的节点位置与节点力,计算裂纹尖端的应变能释放率分量GⅠ,GⅡ。
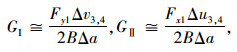
|
(2) |
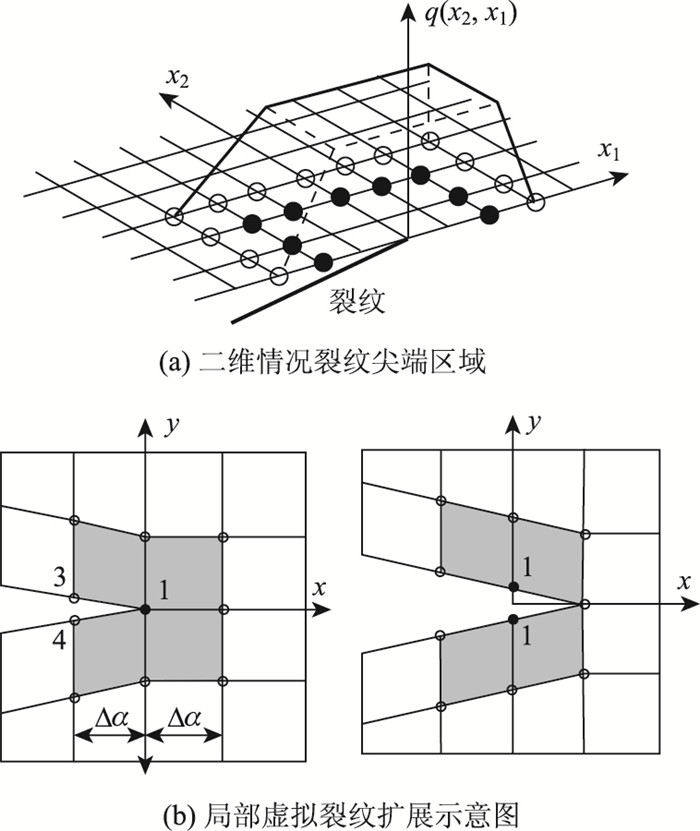
式中,Fx1与Fy1为裂尖节点1位置X、Y方向节点力;Δu3, 4与Δv3, 4是裂尖节点3、4后方张开位移;B为裂纹厚度;Δa为虚拟裂纹扩展量,如图 6所示。
|
| 图 6 虚拟裂纹闭合法示意图 Fig. 6 Schematic diagram of virtual crack closure method |
| |
由于传力杆周边应力集中区域的混凝土承载材料在荷载传递过程中处于复合受力状态,本研究应用B-K准则[14]计算混凝土内微裂纹尖端等效应变能释放率Gequiv来描述这类复合型疲劳裂纹的扩展行为:
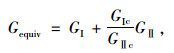
|
(3) |
式中,GΙc为模式Ι临界应变能释放率;GⅡc为模式Ⅱ临界应变能释放率。应力循环中混凝土微裂纹尖端对应的最大能量释放率Gmax小于裂纹疲劳起裂应变能释放门槛值Gthresh时裂纹不扩展;当Gmax大于Gthresh时疲劳裂纹扩展,疲劳扩展速率da/dN符合Pairs准则:
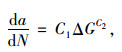
|
(4) |
式中,C1与C2是混凝土的材料参数,取值与加载频率、应力比及环境条件等因素相关。
根据徐世烺提出的断裂韧度计算方法[15],依据美国RILEM协会的E399-09试验规范[16],开展三点弯曲粱疲劳加载试验,在应力比R= 0.3,f=1 Hz加载条件下获得混凝土裂纹疲劳起裂应变能释放门槛值为10 J/m2。为获取混凝土内微裂纹在第二阶段稳定疲劳扩展时的材料参数,分别对Ⅰ型与Ⅱ型混凝土疲劳裂纹开展应变能释放率试验[17-18],测得C1=4.876 8×10-6,C2=1.15。
3.3 传力杆疲劳松动行为的数值模拟计算1万次荷载循环后传力杆上部应力集中区域混凝土内的疲劳裂纹扩展情况如图 7(a)所示,3万次循环后的疲劳裂纹扩展情况如图 7(b)所示,拟静力疲劳试验3万次后传力杆上部应力集中区域混凝土的龟裂现象如图 7(c)所示, 10万次循环后的疲劳裂纹扩展情况如图 7(d)所示。

|
| 图 7 混凝土内微裂纹的疲劳扩展情况 Fig. 7 Fatigue propagation of micro-crack in concrete |
| |
从图 7(a)中可以看出,经过1万次荷载循环后,传力杆上部应力集中区域混凝土内预制的弥散分布初始微裂纹体已经发生扩展现象,但并未贯穿成为主裂缝,说明在该疲劳应力幅值下裂尖位置的能量释放率已达到或超过裂纹疲劳扩展的门槛值。从图 7(b)中可以看出,经过3万次荷载循环,传力杆顶部受压区混凝土内出现3条贯通主裂纹,右侧受拉区出现1条贯穿主裂纹,说明该阶段应力集中区域混凝土内疲劳裂纹处于亚临界稳定扩展状态,其初始微裂纹发生集中扩展并贯通形成多条主裂纹的疲劳扩展行为与图 7(c)试验中混凝土表面出现网状裂纹的现象相吻合;同时,传力杆加载点在峰值荷载时的位移比初始阶段增加0.28 mm,与试验测试值0.21 mm也较为接近。从图 7(d)中可以看出,经过10万次荷载循环,传力杆周边应力集中区域出现多条贯通裂纹,混凝土表面出现明显的龟裂现象,此时传力杆加载点在峰值荷载时的位移比初始阶段已增加0.71 mm,表明传力杆已出现疲劳松动现象。
通过数值计算结果与试验结果的对比可以看出:采用具有真实混凝土保护层内部细观结构特征的弥散分布初始裂纹模型, 应用Paris准则描述微裂纹在疲劳荷载条件下的起始扩展及亚临界稳态扩展规律,以最大能量释放率作为微裂纹疲劳起裂与扩展判定准则,基于扩展有限元方法模拟裂纹的演化行为,可准确地描述传力杆周边应力集中区域混凝土内裂纹的疲劳扩展行为。
4 基于传力杆疲劳松动模型的临界车辆轴载数值计算方法为在实际使用条件下长期保持传力杆装置的荷载传递能力,避免因重载车辆长期通行引起传力杆产生疲劳松动,本研究将造成传力杆周边混凝土内微裂纹发生疲劳扩展的峰值荷载定义为单根传力杆的极限承载力Vmax,即在混凝土路面的缩缝结构中,任何传力杆所传递的荷载不超过Vmax时,整个缩缝结构内部无损伤发生。在此基础上,通过计算最不利位置传力杆的剪力传递分配比LTE(D)与缩缝处整套传力杆装置的剪力传递系数LTE(V),按式(5)可反演得到水泥混凝土路面缩缝结构的临界车辆轴载Pmax:
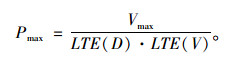
|
(5) |
以本研究水泥混凝土路面缩缝组合为例,基于建立的含弥散裂纹体的缩缝子结构有限元模型,在保持其他参数不变的条件下以每级500 N渐进的方式逐级进行试算,获得不引起最不利位置传力杆周边混凝土材料出现损伤的极限承载力Vmax为9 500 N。采用本研究建立的道路缩缝结构的三维有限元模型,试算得到最不利位置传力杆承受9 500 N剪力时所对应的LTE(V)为21.17%,LTE(D)为20.40%,据式(5)可计算本研究路面缩缝结构的临界车辆轴载约为单轴双轮轴重为220 kN。当道单轴双轮车辆轴重控制在220 kN以内时,传力杆装置不会出现疲劳松动现象,路面缩缝结构将长期保持良好的荷载传递能力。
5 结论本研究通过试验研究与数值模拟相结合的方法,研究了水泥混凝土路面传力杆在车辆轴载作用下的受力特性与疲劳松动扩展行为,提出了设传力杆的路面缩缝临界车辆轴载的数值计算方法,得到以下结论:
(1) 重载车辆的长期作用将引起传力杆周边应力集中区域混凝土材料内微裂纹不断出现起裂并发生疲劳扩展,造成传力杆周边混凝土材料出现龟裂与剥落现象,最终形成传力杆的疲劳松动并引起路面缩缝结构的挠度传荷能力下降。
(2) 应用弥散分布裂纹体模拟混凝土材料内的原有裂纹状缺陷,以能量释放率作为混凝土内微裂纹发生起裂和疲劳扩展的判定指标,通过扩展有限元技术模拟裂纹的疲劳扩展与贯通过程,可有效地模拟路面缩缝传力杆装置在重载交通环境中出现疲劳松动的过程。
(3) 基于本研究建立的道路整体结构有限元模型与缩缝子结构有限元模型,可计算得到水泥混凝土路面缩缝结构的临界车辆轴载,避免严重超载车辆通行造成传力杆周边混凝土承载材料出现损伤累积,防止传力杆出现疲劳松动,保证路面缩缝结构长期具有良好的荷载传递能力。
| [1] |
黄仰贤. 路面分析与设计[M]. 北京: 人民交通出版社, 1998. HUANG Yang-xian. Pavement Analysis and Design[M]. Beijing: China Communications Press, 1998. |
| [2] |
JTG D40-2011, 公路水泥混凝土路面设计规范[S]. JTG D40-2011, Specification for Design of Highway Cement Concrete Pavement[S]. |
| [3] |
AASHTO. AASHTO Guide for Design of Pavement Structures, 1993[M]. Washington, D.C.: AASHTO, 1993.
|
| [4] |
BRONUELA L, LEE H, RYU S, et al. Cantilever and Pull-out Tests and Corresponding FEM Models of Various Dowel Bars in Airport Concrete Pavement[J]. Construction & Building Materials, 2015, 83(2): 181-188. |
| [5] |
周正峰. 水泥混凝土路面接缝传荷能力的研究现状和发展趋势[J]. 公路, 2011(7): 49-53. ZHOU Zheng-feng. Current Status and Development Trend for Study on Load Transfer Efficiency at Joints for Cement Concrete Pavement[J]. Highway, 2011(7): 49-53. |
| [6] |
肖益民, 丁伯承. 水泥混凝土路面与基层接触状况的研究[J]. 公路, 2000(9): 32-34. XIAO Yi-min, DING Bo-cheng. Study on Contact Condition between Cement Concrete Pavement and Basecourse[J]. |
| [7] |
KEETON J R, BISHOP J A, FRIBERG B F. Load Transfer Characteristics of a Dowelled Joint Subjected to Aircraft Wheel Loads[C]//Proceedings of the Thirty-sixth Annual Meeting of the Highway Research Board. Washington, D. C. : Highway Research Board, 1957: 190-198.
|
| [8] |
HIMENO K, KAMIJAIMA T, IKEDA T, et al. Distribution of Tire Contact Pressure of Vehicles and Its Influence on Pavement Distresses[C]//Eighth International Conference on Asphalt Pavements. Seattle: [s. n. ], 1997.
|
| [9] |
陈再现, 陈芍桥, 吴斌, 等. 缩尺模型子结构混合模拟试验方法数值模拟研究[J]. 哈尔滨工业大学学报, 2016, 48(6): 51-57. CHEN Zai-xian, CHEN Shao-qiao, WU Bin, et al. Numerical Simulation of Substructure Hybrid Simulation Test Method for the Scale Model[J]. Journal of Harbin Institute of Technology, 2016, 48(6): 51-57. |
| [10] |
ABDELRAHMAN M, ELBATANOUNY M K, ZIEHL P H. Acoustic Emission Based Damage Assessment Method for Prestressed Concrete Structures:Modified Index of Damage[J]. Engineering Structures, 2014, 60(60): 258-264. |
| [11] |
纪洪广. 混凝土材料声发射性能研究与应用[M]. 北京: 煤炭工业出版社, 2004. JI Hong-guang. Performance Research and Application of Acoustic Emission of Concrete Material[M]. Beijing: China Coal Industry Publishing House, 2004. |
| [12] |
吴胜兴, 王岩, 沈德建. 混凝土及其组成材料轴拉损伤过程声发射特性试验研究[J]. 土木工程学报, 2009, 46(7): 21-27. WU Sheng-xing, WANG Yan, SHEN De-jian. Experimental Study on Acoustic Emission Characteristics of the Damage Process of Concrete and Its Components under Uniaxial Tension[J]. China Civil Engineering Journal, 2009, 46(7): 21-27. |
| [13] |
PARIS P C, BUCCI R J, WESSEL E T, et al. Extensive Study of Low Fatigue Crack Growth Rates in A533 and A508 Steels[C]//Appeared in Stress Analysis and Growth of Cracks, Proceedings of the 1971 National Symposium on Fracture Mechanics, Part I. Urbana-Champaign, US: University of Illinois, 1971.
|
| [14] |
BENZEGGAGH M L, KENANE M. Measurement of Mixed-mode Delamination Fracture Toughness of Unidirectional Glass/Epoxy Composites with Mixed Mode Bending Apparatus[J]. Composites Science and Technology, 1996, 56(4): 439-449. |
| [15] |
赵艳华, 徐世烺, 吴智敏. 混凝土结构裂纹扩展的双G准则[J]. 土木工程学报, 2004, 37(10): 14-18. ZHAO Yan-hua, XU Shi-lang, WU Zhi-min. A Dual-Gcriterion For Crack Propagation in Concrete Structures[J]. China Civil Engineering Journal, 2004, 37(10): 14-18. |
| [16] |
ASTM E399-09, Standard Test Method for Linear-elastic Plane-strain Fracture Toughness KIC of Metallic Materials[S].
|
| [17] |
XU Y, HUANG Y. Computational Analysis of Mixed-mode Fatigue Crack Growth in Quasi-brittle Materials Using Extended Finite Element Methods[J]. Engineering Fracture Mechanics, 2009, 76(2): 165-181. |
| [18] |
MALL S, KOCHHAR N K. Characterization of Debond Growth Mechanism in Adhesively Bonded Composites under Mode Ⅱ Static and Fatigue Loadings[J]. Engineering Fracture Mechanics, 1988, 31(5): 747-758. |
 2018, Vol. 35
2018, Vol. 35
