扩展功能
文章信息
- 杜长东
- DU Chang-dong
- 低频动态载荷理论分析及称重精度提高算法研究
- Theoretical Analysis of Low Frequency Dynamic Load and Research on the Algorithm of Weighing Accuracy Improvement
- 公路交通科技, 2018, 35(4): 153-158
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(4): 153-158
- 10.3969/j.issn.1002-0268.2018.04.020
-
文章历史
- 收稿日期: 2017-06-12
公路运输车辆超限超载一直是一个世界性的难题,其引发的各类严重社会问题受到了广泛关注。为了避免超限超载车辆对公路造成破坏,早在20世纪50年代末,美国、法国、德国等欧共体国家对动态称重(weigh in motion,WIM)系统[1]进行了研究,并取得了一定的成果。目前国外的产品单轴载荷平均误差从±5.0%~±30%不等,相应置信度为90%或95%,最好的动态称重系统单轴载荷误差可以优于±5.0%,但成本太昂贵且主要适应于低速场合。
我国“八五”期间开始引进和消化国外公路动态称重技术,同时也开始对动态称重系统进行研制,发展速度较快。1999年,德国PAT载荷监控产品开始进入中国市场,云南航天新技术工程有限公司引进其技术并于1999年8月获得了国家质量技术监督局颁发的《计量器具型式批准证书》。基于动态称重技术,我国自2001年开始试行高速公路计重收费至今已达15年,至2011年已全面实行高速公路货车计重收费[2-3],并取得一定成效。但由于我国研究起步晚,对车辆动态称重过程中的各种干扰未作深入分析,轴重检测精度平均误差一般在±1%~±30%之间[4-5]。
近年来,动态称重设备经历了多次技术升级,依次为弯板(称量部分轮载)、单台面秤(称量轴重)、双台面秤(称量轴重)、轴组秤(称量轴组重)与整车秤(称量整车重)。长期以来,动态称重技术的主要研究方向通过延长秤体承载器长度,增大车辆称重时间来提高动态称重精度[6-7]。从车辆匀速行驶的动态称重精度来看,目前整车秤已达到动态1级,基本满足了市场需求。但是,此研究方向存在2个问题:一是没有从理论上分析秤体承载器长度,导致秤体越来越大,成本越来越高,占地面积越来越大,施工周期越来越长,通行效率也变差;二是占据大半市场的存量设备单台面秤、双台面秤的动态称重精度得不到有效提高,若更换已有设备成本又非常高,如果能通过理论算法分析动态称重干扰,将节省大量硬件成本。
通过分析车辆与秤体设备振动特性,建立了动态称重信号的滑动平均滤波和B样条最小二乘法的数学模型处理低频周期动态载荷,在此基础上,计算了车辆匀速运动下的最小秤体长度,并针对现有秤体承载器较短的单台面秤、双台面秤,经大量试验提出一种在车辆匀速运动下满足动态称重精度为1级的理论方法。
1 汽车和秤体振动力学模型 1.1 汽车和秤台等效二阶系统模型动态称重的振动信号主要由稳态荷载、动态荷载及高频噪声3部分组成[8-9]。其中,动态载荷产生的原因主要是汽车振动和秤体振动,表现为低频周期动态载荷,它是影响车辆动态称重准确度的关键因素之一,使真实静态轴重信号淹没在各种复杂的动态轴重信号中,因此需要有效消除或减缓。
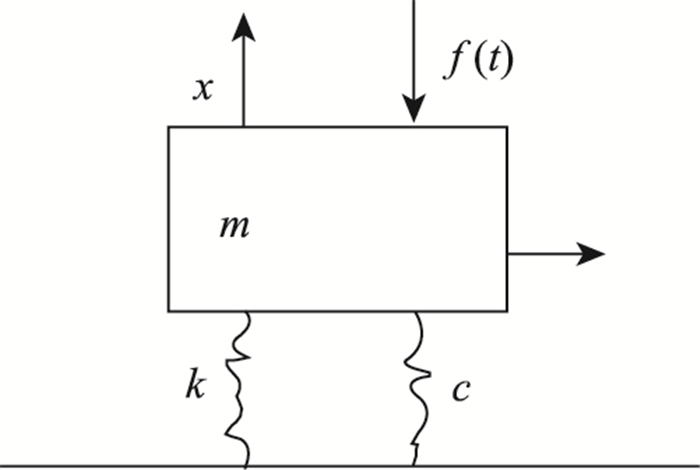
车辆行驶通过秤台时,秤台和汽车均处于振动状态,使称重信号夹杂一个由于振动引起的波动分量,从而造成测量误差。为了便于数学分析,可以将汽车和秤体的振动力学模型等效为由弹簧、阻尼器组成的二阶系统[10-12],如图 1所示。
|
| 图 1 汽车和秤台等效二阶系统模型图 Fig. 1 Equivalent 2-order system model of vehicle and scale |
| |
图 1中m为汽车质量; f(t)为汽车振动载荷; K为汽车结构的弹性系数; C为汽车的阻尼系数; x为汽车振动产生的垂向位移。用二阶系统微分方程描述该系统为:

|
(1) |
设系统的固有角频率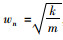
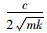
汽车的阻尼非常小,可以忽略不计。假设汽车在外力作用下获得向下的速度v0,代入初始条件可得:
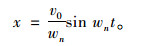
|
(2) |
由上述可得:汽车的振动是一个自由无阻尼振动,主要来于悬挂系统,而汽车的振动频率与汽车的质量、载重及弹簧刚度等因素有关,大约为2.5~10 Hz,振幅则与车辆速度和路面状况有关,其峰值一般为恒定分量的10%左右[13-14]。
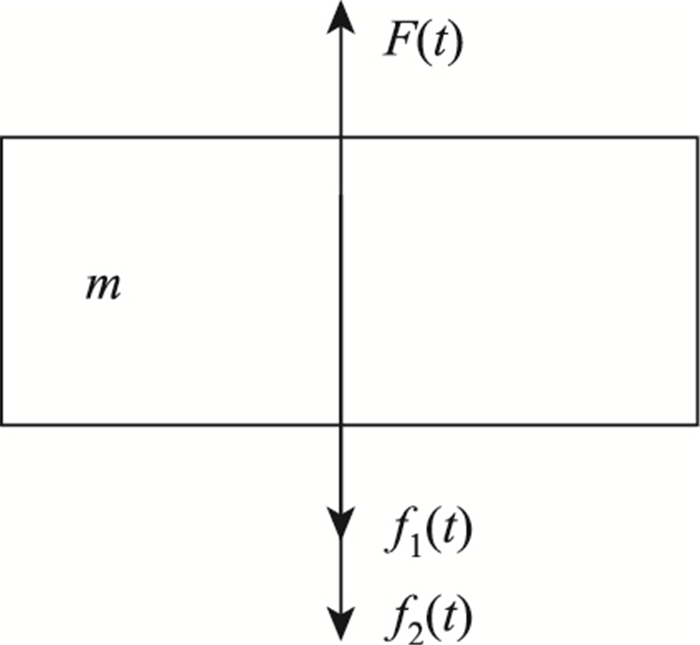
1.3 秤体的振动特性汽车上秤后,秤体受到的外力可看作阶跃函数f1(t)的汽车重力和汽车作无阻尼自由振动的力f2(t),如图 2所示。
|
| 图 2 秤体受力示意图 Fig. 2 Force diagram of scale |
| |
设ω0为秤体的固有频率,依据线性系统的叠加原理,分别求出在力f1(t)和力f2(t)的作用下的位移x1,x2,进而求出秤台的总位移为:
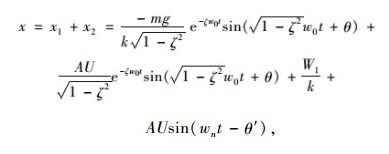
|
(3) |
式中W1=mg,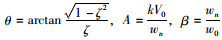
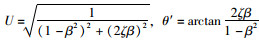
由此可看出,秤体衰减振荡的频率以及衰减幅度的大小与秤台的固有频率ω0、重量及阻尼有关。一般情况下,秤台的重量越大,衰减过程就会越慢,且振荡的频率也越低。秤体的振动频率和振幅与车辆轮胎状况和自身特性有关,频率大约为10~20 Hz,振幅大约为恒定分量的5%左右[15]。
2 低频干扰消除 2.1 滑动平均法为了抑制秤台振动和车辆振动叠加以后产生的随机误差e(t)的影响, 常对动态称重数据y(t)作平滑和滤波处理[16-17],即沿全长N个数据逐一小区间上进行不断的局部平均,得出较平滑的测量结果{fj}, 而滤掉频繁起伏的随机误差。对于N个非平稳数据{yi},视之为每h个相邻数据的小区间内是接近平稳的,即其均值接近于常量。通常多用该均值来表示其中点数据或端点数据的测量结果或信号。可得一般表达式为:
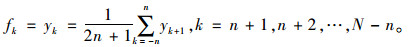
|
(4) |
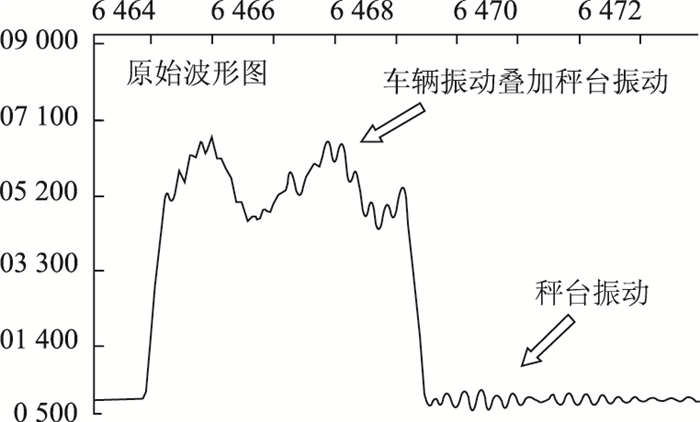
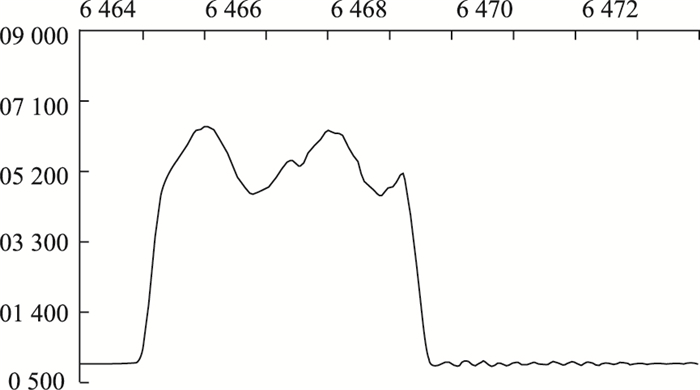
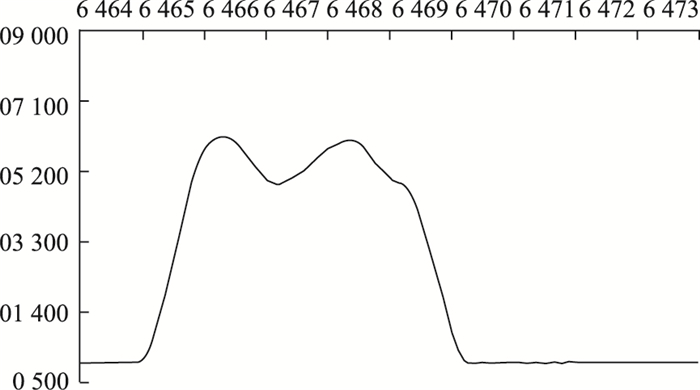
根据式(4), 分别取图 3动态称重数据信号的1倍周期和2倍周期作为滑动窗口,得到处理后的效果如图 4、图 5所示。
|
| 图 3 原始动态称重数据信号 Fig. 3 Original WIM data signal |
| |
|
| 图 4 1倍周期平滑效果 Fig. 4 Effect of 1 times cycle smoothing |
| |
|
| 图 5 2倍周期平滑效果 Fig. 5 Effect of 2 times cycle smoothing |
| |
但在实际试验观测中,夹杂振动干扰的原始动态称重信号,周期特征数会随车速增加而减少。并且,当滑动窗口过小时,秤台振动信号无法滤除,当滑动窗口过大时,实际动态称重周期特征会消失,降低动态称重结果准确度。
2.2 B样条最小二乘法为了减少滑动平均滤波本身所引起的方法误差,采用B样条最小二乘法[18]消除秤体振动信号。设有g个平面有序数据点集{qi(xi, yi)}i=0g-1,对应参数向量R={r0, r1, r2…,rg-1}, 在非递减的节点向量T={t0, t1, t2…,tn+k}已知的情况下讨论B样条曲线的最小二乘拟合, 其中g>n,定义一条k次B样条曲线:
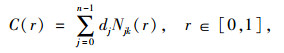
|
(5) |
式中,C(r)为k次B样条曲线多项式,{d0, d1, …, dn-1}为控制顶点,可用向量D表示;Njk(r)为定义在节点向量T上的B样条基函数,其递推关系式为:

|
(6) |
节点向量T满足如下周期性条件:
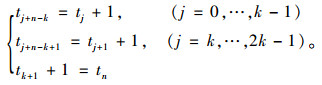
|
(7) |
设qic为拟合曲线上对应参数ri的点,应用标准的最小二乘技术,则要找到qic的函数使:
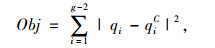
|
(8) |
达到最小,其中Obj为目标函数。若点集落在B样条曲线上, 即qi=C(ri),则问题可归结为求解线性方程组:
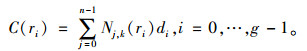
|
(9) |
记B样条矩阵:
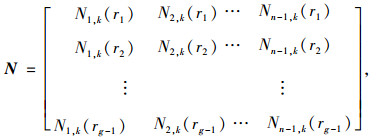
|
有序数据点阵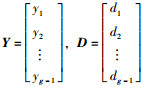
则式(5)写成矩阵形式有:
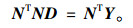
|
(10) |
通过式(10)可求得控制顶点集D,最后由:
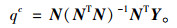
|
(11) |
得到插值于端点的最小二乘拟合曲线。
设车辆上秤的原始动态称重信号为y1(n),车辆刚下秤时,秤体振动信号较均匀,设为y2(n),将y1(n)和y2(n)分别代入式(11)进行最小二乘拟合,最后求取二者差值,即为消除秤体振动后的动态称重信号。
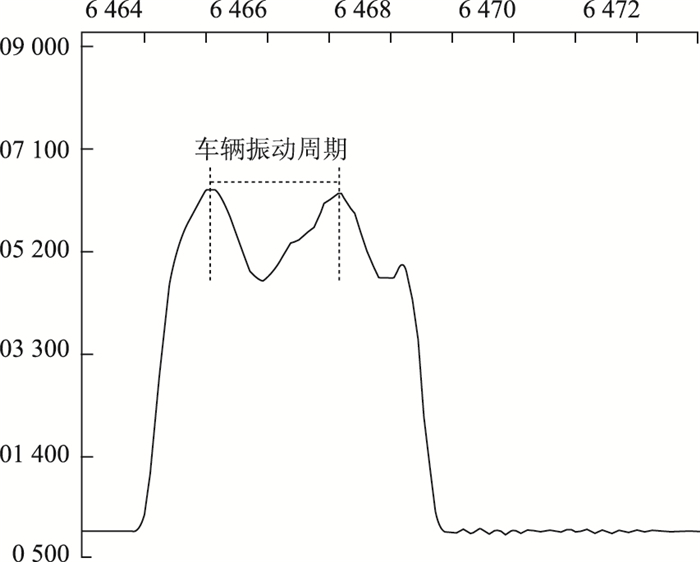
针对图 3的原始动态称重信号,由B样条最小二乘法消除秤台振动后的效果如图 6所示,与图 4、图 5相比,不仅秤台振动得到明显抑制,车辆振动周期特征也得到了有效保护。
|
| 图 6 采用B样条最小二乘法消除秤台振动效果 Fig. 6 Effect by using B spline least square method to eliminate scale vibration |
| |
结合汽车振动特性,设汽车振动频率为fv,通行速度vt,轮胎着地宽度为wv可计算秤体承载器长度L为:
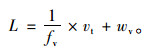
|
(12) |
根据交通运输部《收费公路联网电子不停车收费技术要求》,ETC车道的限速为20 km/h。汽车振动频率大约为2.5~10 Hz,轮胎着地宽度0.3 m,那么由式(12)可知,保证全周期波形的最小秤体长度约为2.5 m。
3 试验结果及分析在上述理论分析基础上,一是针对目前大部分已安装长度分别为0.8 m和1.6 m的单台面秤、双台面秤,试验统计满足1级秤的速度范围。二是在限速20 km/h情况下,试验验证车辆匀速运动下的最小秤体理论长度。因此,试验制造了0.8,1.6,2.6及3 m长度的4种秤体规格。
试验车辆采用两轴刚性货车,实际重量为17 955 kg,根据奈奎斯特定理,试验采样频率为1 kHz。车辆匀速通过秤体时,经采样处理后的部分动态称重试验统计数据如表 1所示。
| 秤体长度规格/m | 速度段/ (km·h-1) |
试验车次 | 重量误差0~0.5%车次统计/% | 重量误差0.5%~1%车次统计/% | 重量误差1%~2%车次统计/% |
| 0.8 | 0~5 | 40 | 99.72 | 0.28 | 0.00 |
| 5~8 | 30 | 97.40 | 2.47 | 0.13 | |
| 1.6 | 0~5 | 40 | 99.63 | 0.37 | 0.00 |
| 5~10 | 40 | 99.53 | 0.47 | 0.00 | |
| 10~12 | 30 | 98.92 | 1.05 | 0.03 | |
| 12~15 | 30 | 97.65 | 1.60 | 0.75 | |
| 2.6 | 0~20 | 60 | 99.50 | 0.50 | 0.00 |
| 3 | 0~25 | 60 | 99.52 | 0.48 | 0.00 |
由试验数据可知,车辆分别以0~5 km/h和0~12 km/h范围内的速度通过长度为0.8 m和1.6 m的秤体,重量误差在0.5%以内,即国家1级秤标准,与式(12)计算的理论值4.5 km/h,11.7 km/h相符。同理,由式(12)计算的2.6 m和3 m的理论速度限值分别为20.7和24.3,试验车辆在这样的限速内通过后,统计可得出重量误差在0.5%以内。
4 结论动态称重能够有效缓解公路运输事业发展带来的超载、交通拥堵、环境污染等诸多严重问题,但为了限制通行费流失,动态称重准确度仍然有待提高。从分析汽车和秤台振动特性出发,结合实际观测数据,得到了汽车和秤台振动产生的低频干扰规律。为了有效消除汽车和秤台振动干扰,建立了滑动平均滤波和B样条最小二乘法相比较的数学模型,推导出了车辆在匀速行驶下保证秤体1级准确度的最小秤体长度,不仅为动态汽车衡的长度设计提供理论依据,也为现有已安装的单台面秤、双台面秤的动态称重精度提高具有重要的参考意义。
| [1] |
李晓松. 动态称重技术的应用[J]. 公路交通科技, 1991, 8(3): 65-67. LI Xiao-song. Application of Weighing in Moving Technique[J]. Journal of Highway and Transportation Research and Development, 1991, 8(3): 65-67. |
| [2] |
张剑勇, 周尚儒, 杨军. ETC模式货车计重收费系统设计[J]. 中国测试, 2016, 42(7): 84-87. ZHANG Jian-yong, ZHOU Shang-ru, YANG Jun. Design of Truck Weighing Toll System Based on ETC Mode[J]. China Measurement & Test, 2016, 42(7): 84-87. |
| [3] |
程保喜. 高速公路ETC模式的货车计重收费方案浅析[J]. 现代工业经济和信息化, 2013(4): 59-61. CHENG Bao-xi. Analysis on the Freight Vehicle Toll by Weight Based on ETC Mode[J]. Modern Industrial Economy and Informationization, 2013(4): 59-61. |
| [4] |
贾海庆, 辛星, 高雪池, 等. 动态称重系统数据采集及分析[J]. 公路交通科技, 2010, 27(6): 138-142. JIA Hai-qing, XIN Xing, GAO Xue-chi, et al. Data Collection and Analysis by Using Weigh-in-motion[J]. Journal of Highway and Transportation Research and Development, 2010, 27(6): 138-142. |
| [5] |
张瑞, 吕文红, 张瑞玺. 基于神经网络自适应滤波的车辆动态称重系统研究[J]. 公路交通科技, 2010, 27(7): 138-141. ZHANG Rui, LÜ Wen-hong, ZHANG Rui-xi. Research of Vehicle Weigh-in-motion System Based on Neural Network Self-adaptive Filtering[J]. Journal of Highway and Transportation Research and Development, 2010, 27(7): 138-141. |
| [6] |
HAN L D, KO S S, GU Z, et al. Adaptive Weigh-in-motion Algorithms for Truck Weight Enforcement[J]. Transportation Research Part C:Emerging Technologies, 2012, 24(9): 256-269. |
| [7] |
陈超波, 沈辰, 高嵩. 公路超载车辆动态预检系统的研究[J]. 国外电子测量技术, 2014, 33(12): 49-52. CHEN Chao-bo, SHEN Chen, GAO Song. Study of Highway Overload Vehicle Dynamic Triage System[J]. Foreign Electronic Measurement Technology, 2014, 33(12): 49-52. |
| [8] |
翟丽霞. 动态汽车衡称重系统动态特性分析及数据处理的研究[D]. 天津: 天津理工大学, 2012. ZHAI Li-xia. Study on Dynamic Characteristics Analysis and Data Processing of Dynamic Vehicle Weighing System[D]. Tianjin: Tianjin University of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10060-1012347690.htm |
| [9] |
黄丹, 唐练, 张洪明, 等. 弯板动态称重信号的多分辩率分析及去噪[J]. 自动化与仪器仪表, 2014(5): 181-183. HUANG Dan, TANG Lian, ZHANG Hong-ming, et al. Multi-resolution Analysis and De-noising Bending Plate WIM Signal[J]. Automation and Instrumentation, 2014(5): 181-183. |
| [10] |
毛建东. 动态称重系统的建模及其参数估计[J]. 传感器与微系统, 2006, 25(6): 72-74. MAO Jian-dong. Model Establishment and Parameter Identification for Dynamic Weighing System[J]. Transducer and Microsystem Technologies, 2006, 25(6): 72-74. |
| [11] |
胡春海, 陈静. 用于动态称重的模型参数估计方法[J]. 自动化与仪表, 2005, 20(4): 23-25. HU Chun-hai, CHEN Jing. Model Parameter Estimation Method for Dynamic Weighing[J]. Automation and Instrumentation, 2005, 20(4): 23-25. |
| [12] |
张雨, 贺曙新, 文绍波, 等. 汽车动态称重信号的两个处理方法[J]. 南京工程学院学报:自然科学版, 2004, 2(4): 17-21. ZHANG Yu, HE Shu-xin, WEN Shao-bo, et al. The Two Measurements of Signal Processing for Weigh-in Motion of Vehicle[J]. Journal of Nanjing Institute of Technology:Natural Science Edition, 2004, 2(4): 17-21. |
| [13] |
汪小朋, 刘文彬, 黄俊杰, 等. 路面随机激励下的汽车振动仿真分析[J]. 山东交通学院学报, 2010, 18(3): 7-11. WANG Xiao-peng, LIU Wen-bin, HUANG Jun-jie, et al. Simulation Analysis of Vehicle Vibration under Randomly Road Excitation[J]. Journal of Shandong Jiaotong University, 2010, 18(3): 7-11. |
| [14] |
孙璐. 运动车辆随机荷载及其激励下的地面动力响应的理论研究[M]. 南京: 东南大学, 1996. SUN Lu. Theoretical Study on Ground Dynamic Responses of Moving Vehicles under Random Loads and Excitations[M]. Nanjing: Southeast University, 1996. |
| [15] |
马应林. 车辆超载动态监测系统的研究与实现[D]. 北京: 北京交通大学, 2010. MA Ying-lin. Research and Implementation of Vehicle Overloading Dynamic Monitoring System[D]. Beijing: Beijing Jiaotong University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10004-2010119893.htm |
| [16] |
SINHA N K, KUSZTA B. Modeling and Identification of Dynamic Systems[M]. Princeton: Van Nostrand Company Inc, 1983.
|
| [17] |
赵毅. 数字滤波的算术平均法和加权平均法[J]. 仪表技术, 2001(4): 41. ZHAO Yi. Arithmetic Mean Method and Weighting Mean Method of Digital Filter[J]. Instrument Technology, 2001(4): 41. |
| [18] |
李蓓蕾. 多次自适应最小二乘曲线拟合方法及其应用[D]. 荆州: 长江大学, 2014. LI Bei-lei. Multiple Adaptive Least Squares Curve Fitting Method and Its Application[D]. Jingzhou: Yangtze University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10489-1014345371.htm |
 2018, Vol. 35
2018, Vol. 35
