扩展功能
文章信息
- 王征宇, 任建伟, 马钰淇, 张红红
- WANG Zheng-yu, REN Jian-wei, MA Yu-qi, ZHANG Hong-hong
- 基于城市共同配送系统的托盘共用调度随机规划模型
- A Stochastic Programming Model for Pallet Pooling Based on Urban Collaborative Distribution System
- 公路交通科技, 2018, 35(4): 146-152
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(4): 146-152
- 10.3969/j.issn.1002-0268.2018.04.019
-
文章历史
- 收稿日期: 2017-08-29
2. 内蒙古大学数学科学学院, 内蒙古 呼和浩特 010070;
3. 大连海事大学北京研究院, 辽宁 大连 116026
2. School of Mathematical Sciences, Inner Mongolia University, Hohhot Inner Mongolia 010070, China;
3. Beijing Research Institute, Dalian Maritime University, Dalian Liaoning 116026, China
由商务部、财政部联合推行的城市共同配送项目正受到越来越多的关注。所谓城市共同配送是指外来商品进入一个城市后,经过同城化统一配送送达用户手中,它是解决物流“最后一公里”问题的有效途径。城市共同配送是一个复杂的系统,需要以托盘为基础,实现物品包装的单元化、规范化和标准化。然而“托盘共用”这一关系城市共同配送能否高效运行的基础如何实现却仍未解决[1]。
托盘共用,英文名为Pallet pooling,它是指供应链上的企业通过租赁和交换等形式实现对托盘的高效重复利用,以提高物流作业效率。这种共用实质上是指在物流作业中,作为承载工具的托盘能够随货物在供应链上移动,直至最终必需将货物和托盘拆开,即实现“单元化物流”的理念[2-3]。国内外的企业越来越愿意选择这种方式来管理托盘,因为它能够显著地降低托盘使用量,从而减少对木材、钢和塑料等原材料的使用,保护生态环境;也能减少无效装卸作业,减少对货物的损害;更能提高物流作业效率,加速物资周转,产生可观的经济效益[4-6]。
托盘调度问题是关系托盘共用系统成败的最重要问题。C.Brindley对CHEP,iGPS等托盘共用企业调研发现调度问题是所有这些企业都未解决的难题[7]。J.Wu等认为托盘共用系统调度方案非常重要[8]。然而长期以来学术界未给予该问题足够的重视,研究文献非常少。R. LeBlanc[9]和C.Brindley[7]分别对加拿大最大的托盘共用系统CPC和美国PECO公司进行了调研,两个公司的高层领导人均认为毁坏率是影响托盘调度效率的最主要因素。D. Roy等基于成本关系模型与行业收集的数据,构建了一个两阶段模型[10]。周康等基于铁路托盘共用系统构建了空盘调度模型,模型考虑了调运时间约束[11]。紧接着,他们又去除了铁路托盘共用系统这一限制,将模型扩展到了普通的托盘共用系统,构建了调度优化模型[12]。K.Zhou则设计了一套克隆免疫算法求解托盘共用调度模型,较传统的遗传算法更加有效[13]。L.Ni等基于托盘生命周期的分析,建立了考虑生产、分派、再分派、回收、维修等托盘全生命周期的调度模型[14]。N. Doungpattra等针对宠物食品行业的托盘调度问题进行了研究,构建了以成本最小为目标的调度优化模型[15]。任建伟等研究了极端不确定条件下的托盘共用调度问题[16]。目前尚没有文献对城市共同配送系统中的托盘共用调度模型进行研究。
由于城市共同配送托盘共用系统涉及到跨企业调度问题,面临着一系列不确定因素,而随机性是最普遍存在的一种不确定性,因此本文将研究当城市共同配送系统的决策者面临随机因素时如何制定最优的托盘共用调度方案。
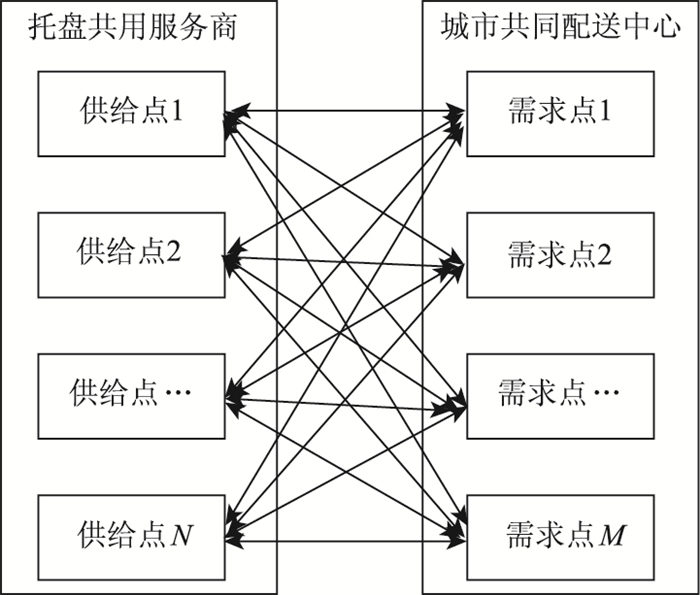
1 模型构建 1.1 问题描述城市共同配送系统中,托盘将主要服务于2种情景:一是托盘供城市共同配送中心各网点使用,此种情况下托盘的需求方是城市共同配送中心各网点,如图 1所示;二是托盘在整个供应链中循环使用,此种情况下托盘的需求方不仅包括城市共同配送中心各网点,还有供应链中的零售商、批发商等,如图 2所示。
|
| 图 1 托盘仅供城市共同配送中心各服务网点使用 Fig. 1 Pallets only used at service stations of an urban collaborative distribution center |
| |
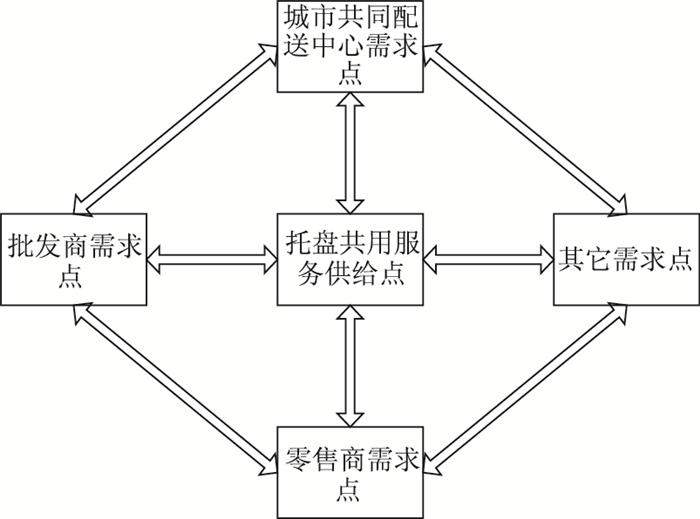
|
| 图 2 托盘在供应链中循环使用 Fig. 2 Pallets reused in a supply chain |
| |
一般来说城市共同配送中心和托盘共用服务商是战略合作伙伴关系,因此当托盘仅供城市共同配送中心各网点使用时,管理者在决策时基本可以掌握所需的数据,此种情况较为简单。但当托盘在整个供应链中循环使用时,由于涉及到多级用户,管理者在决策时面临的情况非常复杂,有些因素是确定的(如自身的装卸能力),而有些因素则是随机的(如季节性原因等导致的供给、需求、库存随机;交通事故原因等导致的运输能力随机)。
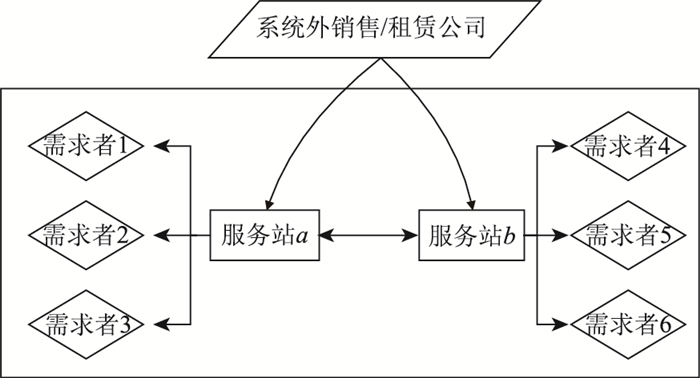
本研究将对托盘在整个供应链中循环使用的情况进行研究,调度流程如图 3所示。城市共同配送托盘共用服务商通过其托盘服务站就近向需求者提供托盘共用服务,并在托盘服务站之间通过统一调度实现托盘的最优化配备。为构建模型,做出如下假设:
|
| 图 3 城市共同配送系统托盘调度流程 Fig. 3 Pallet allocation process of an UCDS |
| |
(1) 城市共同配送系统中的托盘有很多种,且只能用客户指定型号的托盘满足它的需求。因为,托盘的型号不具备可替代性,如果用不同材质的托盘进行替代也基本不可行(如果用价值高的托盘替代价值低的托盘,如塑料托盘替代木托盘,服务商一般不会接受;反之,客户不会接受),因此本研究不考虑托盘的替代。
(2) 所有客户的需求都应该被满足,如若系统内可使用的空托盘不能满足需求,服务站可以向系统外购买或租借托盘。
(3) 城市共同配送系统中各托盘服务站拥有托盘的数量和最大库存能力、服务站间的最大运输能力、客户的需求数量等均存在部分确定和部分随机的情况(如若实践中决策者面临的是较为理想的情况,不存在随机因素,则只需将随机因素的值设为0即可)[17]。
(4) 单位托盘所需的购买(租借)成本、库存成本、运输成本均已知。
(5) 单位托盘所需的库存能力和运输能力均已经过严格测量确定,服务站间的运输时间也已确定。
1.2 标量、变量和参数定义(1) 标量
I为托盘服务站的集合;T为运营周期的集合;P为托盘型号的集合。
(2) 决策变量
Xijpt为在t期从服务站i运到服务站j的p种型号托盘的数量;Yipt为在t期服务站i用来满足需求的p种型号托盘的数量;Hipt为t期服务站i因可供给托盘不足而必须购买(租借)的托盘数。
(3) 参数
Cijp为将一个p种型号托盘从服务站i运到j的费用;Chp为p种型号托盘的单位购买(租借)费用;CKip为一个p种型号托盘在服务站i的库存费用;Sipt为t期新进入服务站i的p种型号托盘的确定数量;αipt为t期服务站i新进的p种型号托盘的随机数量;Dipt为t期服务站i对p种型号托盘的确定需求量(该需求量是其服务的所有客户确定需求量的总和);βipt为t期服务站i的p种型号托盘的随机需求量(该需求量是其根据历史数据估计的所有客户的随机需求量的总和);Kipt为服务站i在t期末剩余的p种型号托盘的数量;K0it和κ0it分别为服务站i在t期的确定库存能力和随机库存能力;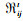
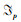
为了解决本问题,采用随机机会约束规划的方法构建模型[18-19]。因为本研究不涉及定价问题,因此模型以调度总成本最小为目标函数,如式(1)所示。对巴运集团、集托网等10多家相关企业管理者的调研发现,城市共同配送系统中的托盘调度问题中,最主要的3个成本是运输成本、购买(租借)成本和库存成本,因此模型考虑这3个成本。目标函数中的第1部分为运输成本,第2部分为购买(租借)成本,第3部分为库存成本。
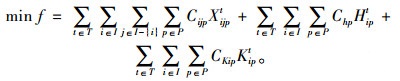
|
(1) |
根据管理者的分析,城市共同配送系统中的托盘共用调度优化模型应考虑需求约束、供给约束、运输能力约束和库存能力约束,如式(2)~(7)所示。
约束条件式(2)表示所有客户的所有型号托盘的确定和随机需求都应该被满足。
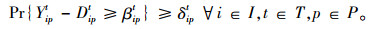
|
(2) |
约束条件式(3)表示Yipt不能超过服务站i∈I在t∈T时所能够使用的p∈P种型号托盘的数量。该数量等于上期末服务站i∈I的库存+服务站i∈I在t∈T时确定新进的托盘量+服务站i∈I在t∈T时随机新进的托盘量+从其他服务站运来的在t∈T时到达服务站i∈I的托盘数量+服务站i∈I在t∈T时从系统外购买或租借的托盘量-服务站i∈I在t∈T时再分派到其它服务站的托盘数量。
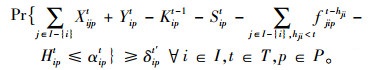
|
(3) |
约束条件式(4)表示服务站i∈I在t∈T期末的库存。服务站i∈I在t∈T时的库存=上期末服务站i∈I的库存+服务站i∈I在t∈T时确定新进的托盘量+服务站i∈I在t∈T时随机新进的托盘量+从其他服务站运来的在t∈T时到达服务站i∈I的托盘数量+服务站i∈I在t∈T时从系统外购买或租借的托盘量-服务站i∈I在t∈T时再分派到其它服务站的托盘数量-t期服务站i∈I用来满足需求的托盘的数量。
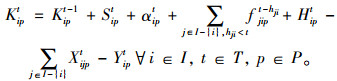
|
(4) |
约束条件式(5)表示服务站i∈I在t∈T期末的库存不能大于其库存能力。
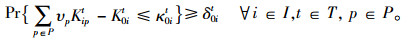
|
(5) |
约束条件式(6)表示从服务站i∈I到服务站j∈I-{i}之间的运输能力约束。
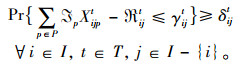
|
(6) |
约束条件式(7)表示决策变量必须为非负整数。
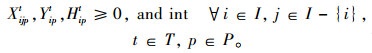
|
(7) |
为便于求解模型,将机会约束式(2),(3),(5),(6)转化为其确定等价形式,如式(8)~(11)所示:
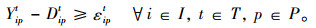
|
(8) |
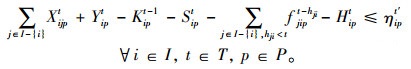
|
(9) |
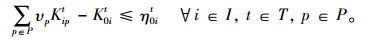
|
(10) |
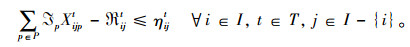
|
(11) |
式中,η=sup{η|η=ϕ-1(1-δ)}为选择ϕ-1(1-δ)的最大值,ϕ-1(1-δ)为对应约束条件中随机变量的分布函数的逆函数;ε=inf{η|η=ϕ-1(δ)}为选择ϕ-1(δ)的最小值。
2 算例假定某城市共同配送系统中有6个托盘共用服务站(a, b, c, d, e, f∈I),2种型号的托盘(p1, p2∈P),决策期为4期(t=t1, t2, t3, t4),系统中的托盘在整个供应链中循环使用。管理者在决策时仅有第3期面临的是随机情况。从系统外购买(租借)p1和p2两种型号托盘的单位成本分别为1元和1.1元。各服务站的p1和p2型号的托盘在期初均没有库存。p1和p2两种型号托盘耗用库存系数和耗用运输能力系数均分别为1.1和1。p1和p2两种型号托盘在所有服务站的库存成本均分别为1,2,3,4,5,6元。所有机会约束条件的置信水平均设为0.95。其它参数如表 1~6所示。
| p1/p2 | a | b | c | d | e | f |
| a | — | — | 3/5 | 4/5 | 5/7 | 6/7 |
| b | — | — | ∞/∞ | 2/3 | 4/5 | 5/7 |
| c | 3/5 | ∞/∞ | — | — | 7/8 | 8/8 |
| d | 4/5 | 2/3 | — | — | 2/4 | 1/1 |
| e | 5/7 | 4/5 | 7/8 | 2/4 | — | — |
| f | 6/7 | 5/7 | 8/8 | ∞/∞ | — | — |
| a | b | c | d | e | f | |
| a | — | — | 1 000 | 1 000 | 400 | 500 |
| b | — | — | 0 | 700 | 300 | 500 |
| c | 1 000 | 0 | — | — | 400 | 700 |
| d | 1 000 | 700 | — | — | 250 | 0 |
| e | 400 | 300 | 400 | 250 | — | — |
| f | 500 | 500 | 700 | 0 | — | — |
| a | b | c | d | e | f | |
| a | — | — | 1 000/N (10, 4) |
1 000/N (10, 9) |
400/N (20, 9) |
500 |
| b | — | — | 0 | 700/N (20, 9) |
300 | 500/N (10, 4) |
| c | 1 000/N (10, 4) |
0 | — | — | 400/N (10, 9) |
700 |
| d | 1 000/N (10, 9) |
700/N (20, 9) |
— | — | 250/N (20, 4) |
0 |
| e | 400/N (20, 9) |
300 | 400/N (10, 9) |
250/N (20, 4) |
— | — |
| f | 500 | 500/N (10, 4) |
700 | 0 | — | — |
| 注:N(ψ, υ)表示随机变量服从均值为ψ、方差为υ的正态分布。 | ||||||
| p1(t1/t2/t3/t4) | p2(t1/t2/t3/t4) | |
| a | 95/100/(105/N(10, 9))/- | 45/50/(55/N (20, 9))/- |
| b | 150/200/200/- | 90/100/110/- |
| c | 100/200/300/- | 100/200/300/- |
| d | 400/400/(400/N(10, 4))/- | 100/100/(100/N(20, 4))/- |
| e | -/-100/-200/-300 | -/0/-100/-200 |
| f | -/-200/(-400/N(20, 9))/-600 | -/0/-200/-400 |
| 注:负数表示需求。 | ||
| a | b | c | d | e | f | |
| a | — | — | 1 | 2 | 1 | 2 |
| b | — | — | ∞ | 1 | 2 | 1 |
| c | 1 | ∞ | — | — | 2 | 1 |
| d | 2 | 1 | — | — | 1 | 1 |
| e | 1 | 2 | 2 | 1 | — | — |
| f | 2 | 1 | 1 | ∞ | — | — |
| t1/t2/t3/t4 | |
| a | 2 000/2 000/(2 000/N(10, 9))/2 000 |
| b | 1 800/1 800/(1 800/N (10, 4))/1 800 |
| c | 2 000/2 000/2 000/2 000 |
| d | 1 800/1 800/1 800/2 000 |
| e | 2 000/2 000/2 000/2 000 |
| f | 2 000/2 000/2 000/2 000 |
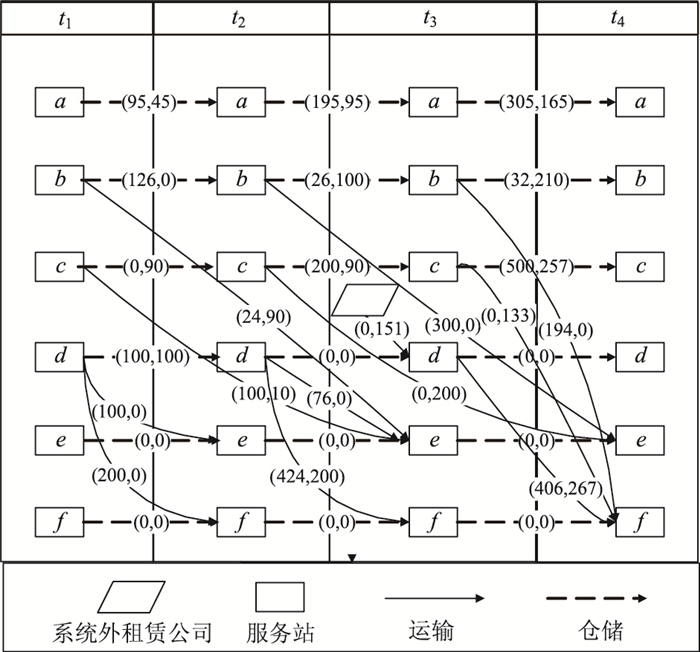
利用Lingo软件编写程序求解模型,得到全局最优解14 274,最优调度方案如图 4所示。结果表明,该问题的最低期望调度成本为14 274元,无需向系统外购买和租赁托盘,所有客户的期望需求均得到了满足。
|
| 图 4 最优调度方案 Fig. 4 Optimum allocation scheme |
| |
进一步研究表明,置信水平的设置对模型解的影响较大,城市配送系统管理者应根据实际情况合理地设置置信水平,提高模型解的精确性。事实上,如果托盘共用系统管理者如果能够采用信息化的手段加强信息管理(如构建RFID监控系统),实现供应链的可视化(即通过信息化的手段实现与供应链中的零售商、批发商等客户的信息互联互通),则可更精确地设置置信水平,甚至降低各因素的不确定性,从而提高决策水平。
3 分析影响城市物流效率的一个重要因素是“交通拥堵”。交通拥堵的“随机性”会导致运输能力随机,因此模型中将“运输能力”设置为随机变量。模型假设运输能力的分布函数已知,但有些情况下这一假设未必成立,管理者可能只能估计一个发生拥堵的概率。这种情况下可以将约束条件式(6)变更为式(12),同时增加约束条件式(13)。
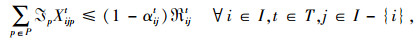
|
(12) |
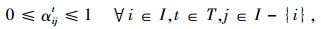
|
(13) |
式中αijt为拥堵因子。当αijt等于1时,(1-αijt) 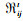
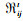
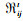
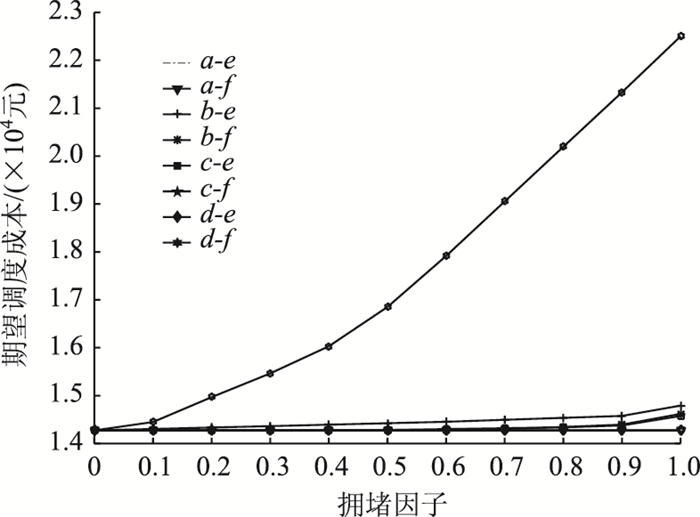
为了进一步分析交通拥堵对城市共同配送系统中托盘共用调度决策的影响,在其它条件不变的情况下,将第3期服务站间的运输线路交通拥堵因子分别设置为[0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1],求解模型。结果如图 5所示。
|
| 图 5 拥堵因子与期望调度成本的关系 Fig. 5 Relationship between congestion factor and expect allocation cost |
| |
由图 5可知,除a到e,a到f,c到f和d到e外,其它服务站间的运输线路交通拥堵因子从小到大变化时,最低期望调度成本亦普遍逐步变大。其中b到e交通拥堵因子为1时,期望调度成本为14 792元;b到f交通拥堵因子为1时,期望调度成本为14 619元;c到e交通拥堵因子为1时,期望调度成本为14 575元;d到f交通拥堵因子为1时,期望调度成本为22 500元。进一步分析可知,a到e,a到f,c到f和d到e的调度成本之所以不受交通拥堵因子变化的影响,是因为在最优方案中,第3期这些服务站间无需调度托盘。因此可以得出结论:最低期望调度总成本与关键线路的交通拥堵情况呈正相关关系。管理者在规划服务站时就应充分考虑周边线路的交通情况,尽可能将服务站避开交通拥堵路段;在运营过程中,应密切关注交通情况,用科学的方法分析交通拥堵规律,在满足客户时间要求的前提下,尽可能避开高峰时段运输托盘。
4 结论研究了一个城市共同配送系统中的托盘共用调度问题,在该系统中有多个托盘服务站,多种托盘型号,决策者面临的是存在诸多随机因素的多周期决策问题。采用随机机会约束规划的方法构建了基于城市共同配送系统的托盘共用调度最优化模型,并用算例证明该模型能帮助决策者制订出科学的决策方案。通过分析交通拥堵对期望调度成本的影响,得出结论:最低期望调度成本与关键线路的交通拥堵情况呈正相关关系。
没有托盘共用系统的支撑,城市共同配送将难以有效开展,具体表现为:供应链各环节之间无法实现全程托盘一贯化作业;无法避免货物交割环节上反复倒换托盘的现象,增加无效劳动;频繁装卸导致商品损耗增加,提高货损成本;为避免商品损耗,需加强产品包装强度,提高包装成本;低效的物流活动导致交通拥堵,环境污染。在《物流业调整与振兴规划》和《物流业发展中长期规划(2014—2020年)》等近年来国务院出台的有关物流业的重要政策文件中均提出要支持发展托盘共用。希望更多的专家能加入到有关托盘共用问题的研究中来。
| [1] |
HARRIS J S, WORRELL J S. Pallet Management System: A Study of the Implementation of UID/RFID Technology for Tracking Shipping Materials within the Department of Defense Distribution Network[D]. Monterey: Naval Postgraduate School, 2008.
|
| [2] |
吴清一. 论中国托盘共用系统的建立[J]. 物流技术与应用, 2003, 8(12): 1-4. WU Qing-yi. Discussion on Setup of China Pallet Pool System[J]. Logistics & Material Handling, 2003, 8(12): 1-4. |
| [3] |
ELIA V, GNONI M G. Designing an Effective Closed Loop System for Pallet Management[J]. International Journal of Production Economics, 2015, 170(5): 730-740. |
| [4] |
TREBILCOCK B. Pallet Survey:What Moves Our Readers?[J]. Modern Materials Handling, 2010(9): 24-29. |
| [5] |
TORNESE F, CARRANO A L, THORN B K, et al. Carbon Footprint Analysis of Pallet Remanufacturing[J]. Journal of Cleaner Production, 2016, 126(3): 630-642. |
| [6] |
CARRANO A L, PAZOUR J A, ROY D, et al. Selection of Pallet Management Strategies Based on Carbon Emissions Impact[J]. International Journal of Production Economics, 2015, 164(11): 258-270. |
| [7] |
BRINDLEY C. Position is Everything:Rising Transport Costs Make Pallet Logistics More Critical for Success[J]. Pallet Enterprise, 2011(6): 24-28. |
| [8] |
WU J, REN J W, LIU B, et al. Deterministic and Multi-scenario Models for Pallet Allocation over a Pallet Pool in a City Joint Distribution System[J]. Advances in Mechanical Engineering, 2016, 8(1): 1-8. |
| [9] |
LEBLANC R. Effective Pallet Management=Data Management:CPC Embraces Data-centric Approach, Third Party Certification as Keys to Success[J]. Pallet Enterprise, 2010(11): 21-23. |
| [10] |
ROY D, CARRANO A L, PAZOUR J A, et al. Cost-effective Pallet Management Strategies[J]. Transportation Research Part E:Logistics & Transportation Review, 2016, 93(7): 358-371. |
| [10] |
周康, 何世伟, 宋瑞, 等. 共用模式下的铁路空托盘调运优化模型[J]. 北京交通大学学报, 2014, 38(3): 22-26. ZHOU Kang, HE Shi-wei, SONG Rui, et al. Optimization Model of Railway Empty Pallet Dispatching Based on the Mode of Pallet Pool[J]. Journal of Beijing Jiaotong University, 2014, 38(3): 22-26. |
| [12] |
周康, 何世伟, 宋瑞, 等. 共用模式下的空托盘调配决策方案优化[J]. 控制与决策, 2015, 30(11): 2009-2013. ZHOU Kang, HE Shi-wei, SONG Rui, et al. Decision Scheme Optimization for Empty Pallets Dispatching Based on Pallet Pool Mode[J]. Control and Decision, 2015, 30(11): 2009-2013. |
| [13] |
ZHOU K, HE S W, SONG R. Optimization for Service Routes of Pallet Service Center Based on the Pallet Pool Mode[J]. Computational Intelligence and Neuroscience, 2016(3): 1-11. |
| [14] |
NI L, HE Y D, ZHOU L, et al. Robust Control Optimization of Triple-echelon Closed-loop Pallet Pool System in Multi-uncertain Environment[J]. Journal of Information and Computational Science, 2015, 12(7): 2635-2645. |
| [15] |
DOUNGPATTRA N, JARUPAN L, ONGKUNARUK P. Simulation for Transport Pallet Cost Reduction in Pet Food Manufacturing:An Empirical Case Study[J]. Packaging Technology and Science, 2012, 25(6): 311-319. |
| [16] |
任建伟, 章雪岩, 张锦, 等. 托盘共用系统调度多情景规划模型[J]. 系统工程理论与实践, 2014, 34(7): 1788-1798. REN Jian-wei, ZHANG Xue-yan, ZHANG Jin, et al. A Multi-scenario Model for Pallets Allocation over a Pallet Pool[J]. Systems Engineering Theory & Practice, 2014, 34(7): 1788-1798. |
| [17] |
任建伟. 托盘共用系统调度优化研究[D]. 成都: 西南交通大学, 2012. REN Jian-wei. Study on Pallet Allocation Optimization over a Pallet Pool[D]. Chengdu: Southwest Jiaotong University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10613-1013252709.htm |
| [18] |
LIU B D, IWAMURA K. Chance Constrained Programming with Fuzzy Parameters[J]. Fuzzy Sets and Systems, 1998, 94(2): 227-237. |
| [19] |
李红启, 常馨玉, 朱晓宁, 等. 城际干线甩挂运输的公路牵引车调度问题及其求解[J]. 公路交通科技, 2016, 33(2): 151-158. LI Hong-qi, CHANG Xin-yu, ZHU Xiao-ning, et al. Intercity Line-haul Tractor Dispatching Problem in Trailer Pick-up Transport and Its Solving Method[J]. Journal of Highway and Transportation Research and Development, 2016, 33(2): 151-158. |
 2018, Vol. 35
2018, Vol. 35
