扩展功能
文章信息
- 王鹏, 卢小钊, 闫章存, 张敏捷
- WANG Peng, LU Xiao-zhao, YAN Zhang-cun, ZHANG Min-jie
- 基于Ordered Probit模型的追尾事故严重性影响因素分析
- Analysis on Influencing Factors of Rear-end Crash Severity Based on Ordered Probit Model
- 公路交通科技, 2018, 35(4): 102-107, 122
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(4): 102-107, 122
- 10.3969/j.issn.1002-0268.2018.04.013
-
文章历史
- 收稿日期: 2017-05-05
2. 宁波工程学院, 浙江 宁波 315211
2. Ningbo University of Technology, Ningbo Zhejiang 315211, China
随着我国社会经济的快速发展,机动车拥有率的迅猛提高,道路安全形势日趋严峻,交通事故频繁发生。据世界卫生组织统计,全球每年约有130万人死于道路交通事故,2010年我国道路交通伤亡人数分别为254 075人和65 225人。道路安全事故成为社会发展的巨大负担。为了减少道路交通事故的发生,降低事故中伤亡人数,国内外学者尝试通过构建模型来分析交通事故探究诱因以制定合理有效对策。
Abdel-Aty等[1]利用ORP模型来解释在不同地点影响交通事故严重性的因素之间的相同点与不同点。Kockelman等[2]采用ORP模型检验在不同事故类型下的驾驶员受伤风险程度。Quddus等[3]利用ORP模型分析摩托车事故中各影响因素与驾驶员受伤程度以及车辆损毁程度的关系。Riffat与Chor等[4]基于ORP模型研究穿越地点与光照条件对交通事故中行人受伤严重程度的影响。Savolainen等[5]指出ORP模型和Ordered Logit(ORL)模型是交通事故分析中最具代表性的2种模型。宗芳等[6]通过建立有序回归模型对交通事故中受伤的人数进行回归分析。文元桥等[7]将有序模型应用到船舶碰撞危险度的研究,对于减小事故发生率有很大的指导意义。
根据美国公路安全管理局统计,追尾事故是最普遍的一类事故类型,占总交通事故的35%。Yan等[8]提出道路条件、驾驶员特性和车辆特性会对追尾事故产生影响;Harb等[9]评估了无信号交叉口汽车的车型对追尾事故的影响程度;Meng和Qu等[10]利用反高斯回归的方法分析城市道路的追尾事故。王华荣[11]提出坡长与追尾事故率呈正相关。孟祥海[12]分析了道路线型特征交通状态,对山区高速公路的追尾事故进行预测。刘鑫鑫[13]构建了基于累积Logistic的高速公路追尾事故严重程度概率预测模型和基于SVM的高速公路追尾事故严重程度预测模型分别从驾驶员、车辆、道路、环境4个方面对高速公路追尾事故严重程度影响因素进行了分析。目前,尚未有学者从事故严重程度的角度分析追尾事故。引入Ordered Probit模型并结合事故记录数据,本研究分析了影响追尾事故严重程度的各类因素,为道路的安全管理和控制措施提供了一定的理论依据。
1 追尾事故特征分析追尾事故是指事故车辆在道路行驶过程中由于各种原因导致其车正面部分与其他机动车尾部发生碰撞接触的过程。其发生实质在于后车驾驶员没能及时发现前车进入制动状态,等发现时两车间距离小于后车制动所需的最小的距离,从而导致后车撞上前车[14]。追尾事故一般有以下特征:
(1) 由于追尾事故中车身变形常发生在尾部,一般后座人员的受伤几率要大于前座人员,且更严重;
(2) 追尾事故通常由多种因素共同作用互相影响而发生,因此带有随机性;
(3) 被追尾车辆驾驶员通常感知较晚,因此常常规避不及。
2 数据描述考虑到数据的完整性统一性,本研究采用了HSIS(Highway Safety Information System)中北卡罗来纳州2010—2015年公路上所有的车辆事故数据。原始数据包括4个子部分,分别为事故特征、车辆特征、乘客特征以及道路特征(包含AADT)。在HSIS数据集中,事故严重性分为5种等级,为了方便研究分析,将其综合为3类,分别为:死亡,受伤和财产损失。其中,“死亡”表示事故中有人员死亡;“受伤”表示事故中有人员受伤(重伤或轻伤,但没有死亡);“财产损失”表示事故中没有人员伤亡,只有财产损失。在HSIS数据集中有各种类型的事故,本研究仅选择追尾事故作为研究对象。根据实际经验,选择了11种有可能影响事故严重性的因素作为解释变量。这些变量包括驾驶员特征(年龄、是否饮酒、是否使用安全带以及身体情况)、环境特征(光照条件、路面交通条件、限速值)以及道路特征(地形、道路线形、路面条件)。在数据文件的集成处理过程中,排除了信息缺失的数据条目。最终得到了包含1 315条完整事故信息的数据集,详见表 1。
| 变量名称 | 变量解释 | 变量的分类或取值 | 频数/ 均值 |
百分比%/ 标准差 |
| SEVERITY | 追尾事故的严重程度 | 1:无人员受伤 2:人员受伤 3:人员死亡 |
722 588 5 |
54.9 44.7 0.4 |
| DRV_ALCO | 驾驶员是否饮酒 | 0:没有饮酒 1:饮酒 |
176 1 139 |
13.4 86.6 |
| PHY_COND | 驾驶员的身体生理情况 | 0:情况正常 1:身体情况欠佳(疲劳、情绪低落、困倦等) |
1 166 149 |
88.7 11.3 |
| DRV_REST | 驾驶时是否使用安全带 | 0:没有使用安全带 1:使用安全带 |
94 1 221 |
7.1 92.9 |
| RD_SURF | 事故发生时发生地点的路表情况 | 0:不利的路面情况(冰雪、雨水等) 1:路表干燥 |
199 1 116 |
15.1 84.9 |
| LIGHT | 事故发生时发生地点的光线条件 | 0:不利的光线条件(黄昏、黎明、黑暗) 1:白天 |
737 578 |
56.0 44.0 |
| RD_AL | 事故发生地点的道路线型条件 | 0:曲线线型 1:直线线型 |
264 1 051 |
20.1 79.9 |
| TRF_CNTL | 事故发生地是否采用相关交通控制措施 | 0:没有采用交通控制措施 1:采用交通控制措施 |
582 733 |
44.3 55.7 |
| TERRAIN | 事故发生地点的地形条件 | 0:崎岖、坡度较大 1:平坦 |
1 084 267 |
79.7 20.3 |
| DRV_AGE | 驾驶员的年龄值 | 年龄分布: 17-80 |
平均值= 37.2 |
SD= 13.3 |
| SPD_LIMT | 事故发生路段的限速值 | 限速分布: 15-70 |
平均值= 50.6 |
SD=10 |
| AADT | 事故发生路段的年平均日交通量 | 交通量分布: 200-183 000 |
平均值= 32 659 |
SD= 35 574 |
| 注:SD,标准差(Standard Deviation) | ||||
3 模型分析 3.1 Ordered Probit模型
鉴于追尾事故中的受伤类型是次序变量,因此拟采用顺序模型进行数据拟合、参数估计、分析预测。根据误差扰动项的设定分布不同,常见的顺序型模型有ORL模型和ORP模型。ORP模型通过对边缘影响的估计,判断具体某个变量对于决策变量的影响程度,结果简单明确,适用于对追尾事故影响变量的分析。最基本的顺序型离散模型的框架为随机效用模型或隐性回归模型,其基本表达式为:
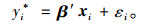
|
(1) |
通过判断隐性变量yi*的阈值范围,确定决策变量yi的取值,判断标准如下:
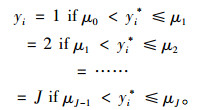
|
(2) |
式中,εi为随机误差项,是各种与解释变量有关但又无法具体表达的影响因素的综合,假设其为正态分布;向量xi为由K个与εi严格独立的解释变量构成;向量β为各解释变量对决策变量的影响程度。N为样本总量,i=1, …, N。
当εi服从标准正态分布时,其概率密度函数f(εi)=ϕ(εi),累计分布函数F(εi)=Φ(εi) [E(εi)=0, Var(εi)=1]。因此,第i个事故的严重性为j的条件概率为:
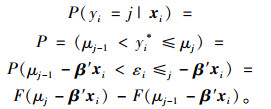
|
(3) |
鉴于ORP模型自身的特性,β难以解释自变量与因变量之间的关系。因此,对于ORP模型,在估计得出参数β之后,需要计算出每一个变量的边际影响值。边际影响表示,假设其他变量为固定值,当某一个变量增加或减少一个单位时,因变量为某一类别的概率的变化,其计算公式为:
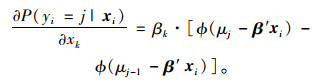
|
(4) |
最大似然估计是最普遍也是最直接的用来估计参数β值的一种方法,最基本的ORP模型自然对数形式的似然方程为:
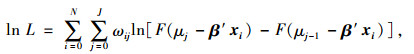
|
(5) |
式中,ωij为指示函数,
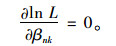
|
(6) |
对于所建立的模型,需要对其进行平行线假设检验和似然比检验。
(1) 平行线假设检验:在累积概率的J-1个二分类probit模型方程中回归系数保持不变,而只有临界点μm变化,称为Ordered Probit模型的平行线假设(Parallel Line Assumption)。即在不同等级的有序多分类结果中,解释变量的效应保持一致,不会随等级的不同而变化。
平行线假设的检验方法一般有2种,分别为得分检验(Score Test)和Wald检验。对于J个等级分类的有序结果变量,建立累积二分类Probit回归模型:
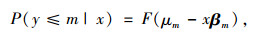
|
(7) |
式中,m=1, 2, …, J-1。得分检验估计了在回归系数相等的限制条件取消时,式(5)的对数似然改变值。统计量服从自由度为k(J-2)的χ2分布。在平行线假设成立的条件下,β1=β2=…=βJ-1应与β一致或接近,不存在系统性的差别。
(2) 似然比检验:检验似然函数所得估计参数β是否等于零的假设。检验方法为比较包含待检验变量的两个回归模型的对数似然值,表示为:
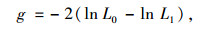
|
(8) |
当对单个变量进行检验时,g近似服从自由度为1的χ2分布。当实际似然比统计量的绝对值大于给定显著性水平(一般为5%)下的χ2值时,则拒绝零假设H0:βm=0,零假设不成立,即ORP模型的参数β不全为零。
3.4 模型的评价由于变量的不同,可能结果会产生数种模型,因此,判断最佳拟合数据的模型至关重要。赤池信息准则(Akaike Information Criterion,AIC)[15]是一种评价统计模型优劣的标准,其建立在熵的概念基础上,可以权衡所估计模型的复杂度和此模型拟合数据的优良性。AIC值计算方法为:
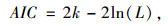
|
(9) |
式中,k为模型中自由参数的数量;L为似然值。AIC为模型对于数据拟合优劣的程度,并且认为当AIC值越小时,模型对数据的拟合表现越佳。
AICc[16]为当样本量较小时AIC的修正量,其表达式为:
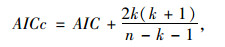
|
(10) |
式中,n为样本量;k为自由参数的数量。当n的值较小时,AICc比AIC的判断效果更好。
与AIC类似,贝叶斯信息准则(Bayesian information criterion,BIC)[17-18]也是一项评价模型优劣性的标准。通常认为,当BIC值较小时,模型最佳。结合AIC与BIC进行综合判断,能够更有效、可靠地得出最佳模型。BIC的计算公式为:
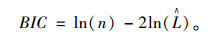
|
(11) |
对于初始模型,一般采用向后删除变量法选出具有显著影响的变量,即从包含所有变量开始,计算各个变量的p值,通过判定p值是否合理来逐步删除变量,最终得到所有统计学显著的变量。一般认为,当变量的p值小于0.05时,变量在统计上显著,即此变量在95%置信水平上影响事故的严重程度。当模型中变量的p值均小于0.05时,则得到了全部的具有显著影响的变量,结合AIC, AICc与BIC值,可以得到最优的模型结果。
4 结果分析表 2总结了模型估计的演化进程。模型演化结果显示,从模型M1到M4,变量依次减少。在剔除了DRV_ALCO,PHY_COND,SPD_LIMT等变量后,最终模型包含5个解释变量,分别为DRV_REST,LIGHT,RD_AL,TRF和AADT(p值分别为0.040 3,0.003 9,0.033 4,0.026 3和0.03,均小于0.05)。这5个变量可以被认为显著影响追尾事故的严重性,即驾驶员的饮酒情况、生理情况、光照条件、交通控制以及道路交通量这5类因素与事故严重程度密切相关。
| 解释变量 | 模型参数估计(p值) | 边际影响 | ||||||
| M1 (K=11) | M2 (K=8) | M3 (K=6) | M4 (K=5) | 无人员受伤 | 人员受伤 | 人员死亡 | ||
| DRV_ALCO | 0.080(0.456 8) | |||||||
| PHY_COND | 0.080(0.492 5) | |||||||
| DRV_REST | 0.284(0.032 1) | 0.280(0.034 5) | 0.274(0.038 3) | 0.271(0.040 3) | -0.053 7 | 0.013 8 | 0.039 9 | |
| RD_SURF | 0.001(0.995 9) | |||||||
| LIGHT | 0.196(0.005 8) | 0.193(0.006 4) | 0.202(0.004) | 0.202(0.003 9) | -0.040 1 | 0.010 3 | 0.029 8 | |
| RD_AL | 0.150(0.089 1) | 0.150(0.087 5) | 0.167(0.055) | 0.182(0.033 4) | -0.036 1 | 0.009 3 | 0.026 8 | |
| TRF_CNTL | 0.153(0.047 9) | 0.152(0.048 9) | 0.176(0.019 8) | 0.166(0.026 3) | -0.032 9 | 0.008 5 | 0.024 4 | |
| TERRAIN | 0.116(0.209 5) | 0.109(0.235 7) | 0.087(0.331 6) | |||||
| DRV_AGE | 0.003(0.308 6) | 0.003(0.292 9) | ||||||
| SPD_LIMT | -0.004(0.287) | 0.005(0.256 6) | ||||||
| AADT | 3.10E-6(0.01) | 3.16E-6(0.02) | 2.53E-6(0.02) | 2.28E-6(0.03) | -4.5E-7 | 1.17E-7 | 3.33E-7 | |
| Intercept γ1 | -0.519(0.085 3) | -0.427(0.117 8) | -0.551(0.000 8) | -0.529(0.001 2) | ||||
| Intercept γ2 | 2.09(< 0.000 1) | 2.18(< 0.000 1) | 2.05(< 0.000 1) | 2.066(< 0.000 1) | ||||
| -2LL | 1 841.888 | 1 842.659 | 1 845.023 | 1 845.969 | ||||
| AIC | 1 867.888 | 1 862.659 | 1 861.023 | 1 859.969 | ||||
| AICc | 1 868.091 | 1 862.769 | 1 861.08 | 1 860.014 | ||||
| BIC | 1 935.249 | 1 914.475 | 1 902.476 | 1 896.24 | ||||
| Score test for equal slope assumption | 10.718 (0.467 2) |
9.469 0 (0.304 3) |
5.241 (0.513 3) |
5.232 (0.388 2) |
||||
| χ2 likelihood ratio test | 16.129 (0.006 2) |
25.358 (0.001 4) |
22.994 (0.000 8) |
22.048 (0.000 5) |
||||
估计结果显示,从模型M1到M4,模型的AIC值从1 867.888下降到1 859.969,BIC值也从1 935.249下降到1 896.24。指标模型从M1到M4不断优化,模型M4比其他3个模型更精确。对于平等斜坡假设,模型M4的p值为0.513 3,表明其累计概率的回归线是平行的,即模型能充分拟合追尾事故数据。对于似然比检验,模型M4的p值为0.000 5(远小于0.05),表明全局零假设不成立,ORP模型的参数β不全为0,即拥有5个变量的模型比无变量的模型更能反映数据特性。综上,模型M4可视为针对记录数据的最佳模型,模型表示为:
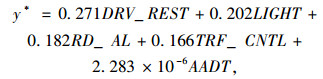
|
(12) |
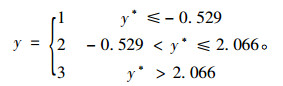
|
(13) |
根据式(4),可以计算得出不同变量对于3种受伤程度的边际影响:
(1) 变量DRV_REST显著影响受伤严重性(p值=0.040 3 < 0.05),意味着车内人员是否正确使用安全带与追尾事故的严重性关系密切。边际影响的符号与预计基本一致,当DRV_REST增加一个单位,“无人员受伤”的概率增加0.053 7,同时,“人员受伤”和“人员死亡”的概率分别下降0.013 8和0.039 9。可以得出,当使用安全带时(肩带或腰带),追尾事故的潜在受伤程度将会减轻;当未使用安全带时,受伤程度明显加重。因此,在车内严格使用安全带至关重要。
(2) 模型拟合的结果显示光照条件的p值为0.003 9(远小于0.05),即光照条件与追尾受伤的严重性密切相关。同时,边际影响计算结果显示:变量“LIGHT”每增加一个单位,“无人员受伤”的概率即增加0.040 1,“人员受伤”和“人员死亡”的概率分别下降0.010 3和0.029 8。解释为,在昏暗的环境下,驾驶员视线较为模糊,当注意到前方有车辆时,允许自身减速的时间也较为紧张,因此不利的光照条件易导致更严重的追尾事故,这与经验认知相一致。
(3) 变量RD_AL(p值=0.033 4 < 0.05)和TRF_CNTL(p值=0.026 3 < 0.05)皆统计上显著,说明道路线型与交通控制条件对于追尾事故的严重程度有一定的影响。变量RD_AL的边际影响值表明:道路线型每增加一个单位,“无人员受伤”的概率即增加0.036。也就是说,道路线型的优劣对追尾事故的严重程度影响较为明显。急转弯、半径较小的曲线路段等线型较差的道路路段将会导致更加严重的追尾事故;相反,流畅的直线线型将会潜在降低追尾事故的严重性。变量TRF_CNTL的边际影响值显示其每增加一个单位,“无人员受伤”的概率即增加0.032 9,而“人员受伤”和“人员死亡”的概率分别下降0.008 5和0.024 4。结果表明,在相关路段采取合适的交通控制措施,对降低事故的严重性(特别是对减少死亡数)效果显著。
(4) 由于AADT的值较大(平均值=32 659),因此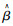
本研究采用实际追尾事故的记录数据,结合分析软件SAS对ORP模型参数进行了估计,估计结果表明选择ORP模型分析相关影响因素是可行有效的,且主要影响因素分别为光照条件、安全带使用情况、道路线型条件、交通控制条件和AADT。结合分析结果,从普遍意义上而言,为了避免发生严重的追尾事故,相关交通管理部门应该着力改善道路的光照条件。在道路设计阶段,注意道路线型的平稳流畅。在运营阶段,合理安排交通控制策略,并控制道路的最大交通量。
本研究存在以下缺陷:(1)只考虑了ORP模型的适应性,并证明了ORP模型具有较高的精度,今后可以考虑参量的特性选择其他的模型(比如ORL模型、多项Probit模型等),并作比较分析;(2)在数据方面,仅仅选取了11个影响变量并分析其对事故严重性的影响,今后应结合实际选取更多的变量以完善模型。
| [1] |
ABDELATY M. Analysis of Driver Injury Severity Levels at Multiple Locations Using Ordered Probit Models[J]. Journal of Safety Research, 2003, 34(5): 597-603. |
| [2] |
KOCKELMAN K M, KWEON Y J. Driver Injury Severity:An Application of Ordered Probit Models[J]. Accident Analysis and Prevention, 2002, 34(3): 313. |
| [3] |
QUDDUS M A, NOLAND R B, CHIN H C. An Analysis of Motorcycle Injury and Vehicle Damage Severity Using Ordered Probit Models[J]. Journal of Safety Research, 2002, 33(4): 445-62. |
| [4] |
RIFAAT S M, CHIN H C. Analysis of Severity of Single-vehicle Crashes in Singapore[C]//Proceedings of the 84th Annual Meeting of Transportation Research Board. Washington, D. C. : Transportation Research Board, 2005.
|
| [5] |
SAVOLAINEN P, MANNERING F. Probabilistic Models of Motorcyclists' Injury Severities in Single and Multi-vehicle Crashes[J]. Accident Analysis and Prevention, 2007, 39(5): 955-63. |
| [6] |
宗芳, 许洪国, 张慧永. 基于Ordered Probit模型的交通事故受伤人数预测[J]. 华南理工大学学报:自然科学版, 2012, 40(7): 41-45. ZONG Fang, XU Hong-guo, ZHANG Hui-yong. Forecast of Injury Number due to Traffic Accident Based on Ordered Probit Model[J]. Journal of South China University of Technology:Natural Science Edition, 2012, 40(7): 41-45. |
| [7] |
文元桥, 张恒, 万品. 基于序次Probit模型的航道船舶碰撞危险度研究[J]. 中国安全科学学报, 2012, 22(2): 134. WEN Yuan-qiao, ZHANG Heng, WAN Pin. Risk Degree Analysis of Ship Collision Risk in Channel Based on Ordered Probit Model[J]. China Safety Science Journal, 2012, 22(2): 134. |
| [8] |
YAN X, RADWAN E, ABDEL-ATY M. Characteristics of Rear-end Accidents at Signalized Intersections Using Multiple Logistic Regression Model[J]. Accident Analysis and Prevention, 2005, 37(6): 983-95. |
| [9] |
HARB R, RADWAN E, YAN X, et al. Light Truck Vehicles (LTVs) Contribution to Rear-end Collisions[J]. Accident Analysis and Prevention, 2007, 39(5): 1026-1036. |
| [10] |
MENG Q, QU X. Estimation of Rear-end Vehicle Crash Frequencies in Urban Road Tunnels[J]. Accident Analysis and Prevention, 2012, 48(5): 254. |
| [11] |
王华荣, 孙小端, 贺玉龙, 等. 山区双车道公路尾随相撞事故与道路线形的关系[J]. 北京工业大学学报, 2010, 36(9): 1236-1241. WANG Hua-rong, SUN Xiao-duan, HE Yu-long, et al. Effects of Geometric Features of Rear-end Crash Accidents on Mountainous Two-lane Highways[J]. Journal of Beijing University of Technology, 2010, 36(9): 1236-1241. |
| [12] |
孟祥海, 张晓明, 郑来. 基于线形与交通状态的山区高速公路追尾事故预测[J]. 中国公路学报, 2012, 25(4): 113-118. MENG Xiang-hai, ZHANG Xiao-ming, ZHENG Lai. Prediction of Rear-end Collision on Mountainous Expressway Based on Geometric Alignment and Traffic Conditions[J]. China Journal of Highway and Transport, 2012, 25(4): 113-118. |
| [13] |
刘鑫鑫. 高速公路追尾事故严重程度影响因素分析及预防对策研究[D]. 长春: 吉林大学, 2016. LIU Xin-xin. Research on Influencing Factors of Severity of Rear-end Accident on Freeway and Countermeasures[D]. Changchun: Jilin University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10183-1016084039.htm |
| [14] |
赵军芳. 基于PC-Crash的车辆偏置追尾事故仿真分析[D]. 哈尔滨: 东北林业大学, 2015. ZHAO Jun-fang. Simulation of Vehicle Bias Rear-end Collision Based on PC-Crash[D]. Harbin: Northeast Forestry University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10225-1015665650.htm |
| [15] |
BURNHAM K, ANDERSON D, BURNHAM P, et al. Model Selection and Multimodel Inference:A Practical Information-theoretical Approach[M]. New York: Springer New York, 2010.
|
| [16] |
HURVICH CM, TSAI C. Regression and Time Series Model Selection in Small Samples[J]. Biometrika, 1989, 76(2): 297-307. |
| [17] |
SCHWARZ G. Estimating the Dimension of a Model[J]. Annals of Statistics, 1978, 6(2): 15-18. |
| [18] |
WIT E, HEUVEL E V D, ROMEIJN J W. 'All Models Are Wrong...':An Introduction To model Uncertainty[J]. Statistica Neerlandica, 2012, 66(3): 217-236. |
 2018, Vol. 35
2018, Vol. 35
