扩展功能
文章信息
- 李颖, 朱昌锋, 张正坤
- LI Ying, ZHU Chang-feng, ZHANG Zheng-kun
- 基于前景理论的城市轨道交通停站方案研究
- Study on Stopping Schedule for Urban Rail Transit Based on Prospect Theory
- 公路交通科技, 2018, 35(4): 85-92
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(4): 85-92
- 10.3969/j.issn.1002-0268.2018.04.011
-
文章历史
- 收稿日期: 2017-03-22
随着我国城市轨道交通的快速发展,城轨列车停站方案日益成为热点话题。一个合理的停站方案,对方便市域内居民出行、减少运营成本具有重要作用,为此,有关专家及学者对城市轨道列车的停站方案展开大量的研究。其中,文献[1]认为停站方案是影响旅客出行时间的主要因素,为研究和优化城市轨道交通的停站方案提供了一定的依据;文献[2]在分析客流需求时变特征和旅客等待行为的基础上,通过考虑列车与运行线的匹配关系,对城市轨道交通的开行方案进行了研究;文献[3]以节省旅客出行时间为优化目标,建立了跨站停站方案的0-1整数规划模型;文献[4]构建了基于乘客广义时间效益和运营收益最大化的快慢车停站方案模型;文献[5]对快慢车的组合模式、追踪间隔及避让站的设置等内容作了研究,对进一步研究快慢车停站方案具有借鉴意义;文献[6]利用灰色定权聚类模型对车站进行了分级,并根据分级结果建立了快慢车停站方案的0-1非线性规划模型。
综上所述,既有文献对城市轨道交通停站方案的研究较为全面,但仍存有不足之处。主要体现在以下两个方面:第一,大部分研究是基于旅客出行完全理性的条件下展开,对旅客出行的选择行为考虑不足;第二,有关文献均为城市轨道交通运营前的停站方案研究,缺乏对运营后停站方案的进一步优化分析。基于此,本文以既有停站方案与客流实际需求存有偏差为背景,通过考虑旅客出行选择行为,以旅客出行时间和拥挤程度作为旅客选择的影响因素,利用前景理论对城市轨道交通的停站方案作进一步研究。
1 有关问题分析城市轨道交通在运营过程中,标准停站凭借其组织简单、无需同线换乘等优势而成为主要的组织模式,但随着城市发展和设施完善,对于有些线路而言,域内实际客流量与起初预测量会有明显偏差,因此,标准停站方案已难以满足现行区段内客流波动较大的乘客出行需求。
1.1 停站方案分析既有城市轨道交通停站方案,除了标准停站方案,还有一些特殊的停站方案,主要有跨站停站方案、区域停站方案及快慢车方案等。不同停站方案示意图如图 1所示。
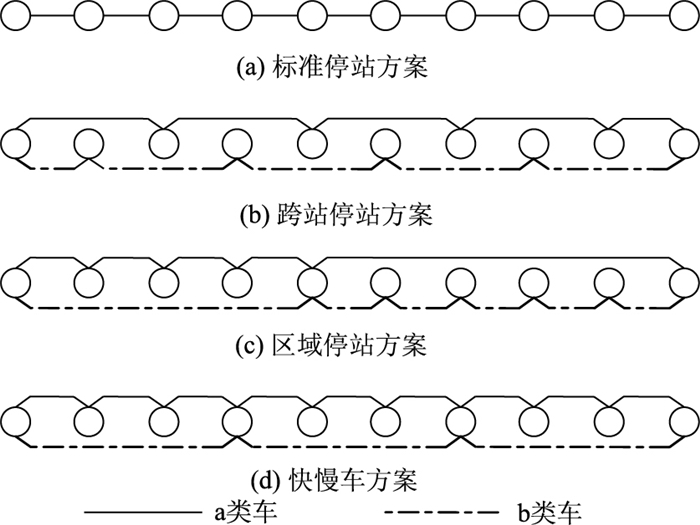
|
| 图 1 不同停站方案示意图 Fig. 1 Schematic diagram of different stopping schedules |
| |
从图 1中可以看出,非标准停站的行车组织模式因减少停站次数而提高列车的旅行速度,进而节省了乘客的总出行时间。但是,跨站停站方案和区域停站方案的可达性较差,且必须设有越行站才可满足行车需求,而快慢车则是一种相对比较灵活的组织模式,具有很好的可达性,通过开行快车,在降低拥挤程度的同时还可节省客流较大车站的旅客等待时间,此外,通过优化快慢车的发车间隔,还可避免两车越行。基于以上分析,本文认为在区段内客流波动较大且依旧采用标准停站方案的线路上,可以通过开行快慢车更为经济合理。
1.2 快慢车运行分析根据快慢车停站方案特征,慢车在区段各站均有停靠,因此,乘客出行时间的节省主要取决于快车的停站序列。根据快、慢车以相同的运行速度最优为依据[5],设ti表示列车在i站的停站时间(含制动和启动时间);变量xi表示快车在i站是否停留,即:

|
设TQi和THi分别表示快车与其前后慢车在i站的出站时间间隔,则:
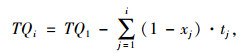
|
(1) |
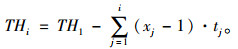
|
(2) |
结合式(1)、式(2)发现,对于车站i,两慢车的开行间隔时间T(周期)均为定值,即:

|
(3) |
鉴于既有标准停站运营模式进一步优化所采取的快慢车停站方案不具有越行能力,为了确保行车安全,快、慢车之间必须存有一定的追踪间隔时间I,即:
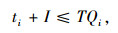
|
(4) |
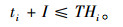
|
(5) |
广义出行费用一般包括票价、旅行时间及拥挤费用等[7]。在城市轨道交通中,票价并不是影响运营组织模式的主要因素,因此,下面主要对乘客的旅行时间和拥挤费用进行分析。
时间是除票价外乘客出行最重要的支出[8]。设fi(t)表示周期T内,i站乘客随时间的一个到达规律函数;客流分配比pij表示时间段内从i站前往j站的人数占到达i站总人数的比,且有:
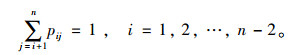
|
(6) |
对于车站i(i=2, …, n-1)而言,快车在该站停靠与否对区段内旅客的出行时间具有一定的影响。当快车在i站停靠时,可以上车的乘客,其到站必须是快车停靠的车站,否则,乘客上车后必须中途换乘慢车至到站,而这与无快车停靠、直接在i站乘坐慢车至到站所需的出行时间是一样的。因此,快车在i站停靠节省了可上车乘客等待后续慢车的时间TJi,其求解如式(7)所示:
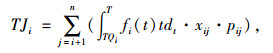
|
(7) |
式中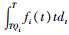
但是,对于快车上非i站下车的乘客而言,快车在该站上的停靠造成了他们无效的等待时间TSi,其求解如式(8)所示:
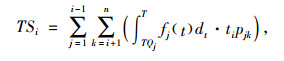
|
(8) |
式中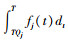
根据式(7)和式(8)可以发现,对于区段内的非始发站和终到站而言,快车在站的停靠与否都会对乘客的出行时间造成影响,如果用ΔTi表示i站的乘客出行时间节省情况,则有:

|
(9) |
很显然,当ΔTi > 0时,说明快车在i站停靠对区段内乘客总的出行时间是节约的,即停站是合理的;反之,则说明具有损失,不宜停站。
由于列车的载客能力有限,当区间断面客流量较大时往往会出现拥挤,进而影响乘客的舒适性。拥挤程度一般用列车满载率或断面满载率指标进行评价[9],设M表示列车的额定载客量,ηi1和ηi2分别表示在i站时快车和后续慢车的满载率,则当列车行进至i站时,则有:
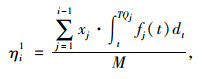
|
(10) |

|
(11) |
式中tj表示一个周期T内,i站的起始时间,取tj=0。
式(10)和式(11)分别体现了快车和后续慢车到达i站时的拥挤程度,如果用Δηi表示i站处快车与慢车的拥挤程度差值,即:
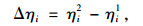
|
(12) |
很明显,当Δηi > 0时,说明慢车比快车拥挤;当Δηi < 0时,说明快车比慢拥挤。
综上所述,式(9)和式(12)分别从时间和拥挤程度反映了乘客的出行费用。这两个指标虽然是制订城轨列车停站方案的主要依据,但不能直接用于停站方案的制订,因为它们具有不同的量纲,且无法体现出乘客在有限理性条件下的选择行为,进而决策出的结果不能符合人本身所固有的思维习惯[10],基于此,本文利用前景理论对该问题展开研究。
2 基于前景理论的停站方案优化 2.1 前景理论介绍前景理论是通过修正主观期望效益理论发展而来的,其将决策分为编辑和评估两个阶段,并最终得到决策方案,其中,决策阶段主要是数据处理和参考点的选取,评估阶段则是依赖价值函数和权重函数对信息进行计算,并以前景值对结果进行判断[11-12]。
(1) 价值函数
价值函数又称为主观效用函数,它是收益的凹函数和损失的凸函数。该函数体现了决策者在面临收益时是风险规避的,而在面临损失时是风险偏好的,且决策者对损失比收益更具敏感。本文采用文献[11]中提出的价值函数,其定义如下:

|
(13) |
式中,参数α, β(0 < α, β≤1)为风险敏感系数,其中,α为收益敏感系数,β为损失敏感系数;λ为损失规避系数,且λ≥1,通常α=β=0.88,λ=2.25。
(2) 权重函数
权重函数为一个单调递增的函数,其图像表现为反S形状[13]。该函数反映了决策者往往会重视小概率事件而忽略重大概率事件,权重函数的形式较多,本文依旧采用文献[11]中所提出的权重函数,其定义如下:
当决策者获得收益时:
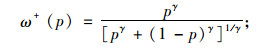
|
(14) |
当决策者获得损失时:

|
(15) |
式中,ω(p)为事件发生的感知概率,p为事件发生的实际概率。通常,γ取0.61,δ取0.69。
2.2 乘客选择行为描述已有相关说明,时间和拥挤程度是乘客选乘过程中的主要决策因素,结合前景理论中的价值函数和权重函数所表达的含义,现对乘客的选择行为分析如下。
(1) 时间价值选择分析
基于行为心理学的研究,当快车节省时间时,大多数乘客往往会以“见好就收”的心态而保守地选择快车;而当快车有时间损失时,他们则会以“试试看”的心态而选择快车。结合前景理论中价值函数的定义,现给出乘客出行时间的价值函数如式(16)所示:
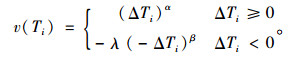
|
(16) |
(2) 拥挤程度选择分析
与时间价值选择分析一样,拥挤越小对乘客而言是收益的,反之则为损失。当快车的拥挤程度相对慢车较小时,大多数乘客会保守地选择快车,反之,则会以“试试看”的心态而选择快车。同样地,给出乘客拥挤程度的价值函数如式(17)所示。
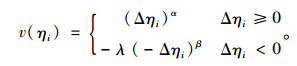
|
(17) |
(3) 选择概率分析
在有限理性条件下,乘客在快车和慢车的选择过程中往往会遵循“重视小概率事件而忽略重大概率事件”的决策行为。在停站方案实施前,乘客只能凭借经验,依客流量来判断快车停站与否,因此,本文以i站客流量占区段总客流量的比例作为权重函数中实际概率pi的值,即:

|
(18) |
基于本研究假设条件下的研究和说明,方案中快车停站序列由一系列组合(Ti, ηi, pi)组成。快车是否在i站停靠取决于该站的前景值vi,该值可通过式(19)和式(20)求解。

|
(19) |
式中v(Ti)为乘客出行时间无量纲化的前景值。

|
(20) |
式中,σ为决策偏好系数,且0≤σ≤1,很显然,当σ的值越大时,说明决策者对出行时间更具偏好,基于时间比拥挤的重要性,本研究拟取σ=0.7。可见,对于前景值vi,当vi > 0时,说明快车停靠i站是满足乘客需求的,因为这有利于乘客出行时间和拥挤费用的节省;反之,则应避免快车在该站停靠。对于区段而言,通过前景值vi判断所得出的停站序列往往有多个,因此,最优的停站序列还需满足综合前景值V最大,即:

|
(21) |
可见,以式(21)为优化目标,通过式(20)便可以得到区段内乘客广义出行费用最优的快车停站方案。结合上述研究可以看出,该问题是利用前景理论来判断快车的停站序列,而并非利用前景理论来求解停站序列,因此,需要设计可行的算法,以期产生快车的停站序列。
3 算法设计结合上述研究说明,前景理论中的前景值是评价快车停站合理性的主要依据,而各站前景值的计算又必须要求在快车停站序列确定的条件下进行,因此,快车停站序列的确定具有明显的并行性。基于初始搜索的遗传算法在求解并行性问题方面的优势[14],结合区段内各站和停站序列分别与遗传算法中基因及染色体的对应关系,本研究采用遗传算法对该问题进行求解。
3.1 遗传算法及说明遗传算法借鉴生物界自然选择和遗传机制,利用遗传算子(选择、交叉和变异)对候选解集中的个体进行组合,进而产生新一代候选解集,重复此过程,直到满足某种收敛指标为止。遗传算法具有很强的全局并行搜索能力,简单通用、鲁棒性强,并且不受优化函数联系性的约束[15-16],因此,对本研究快车停站方案的求解具有很好的优势。
本研究在传统遗传算法的基础上,结合问题实际,现作如下说明。
第一,以表示快车在i站停靠与否的变量xi作为遗传基因,以站序为基因座,进而形成表示n维决策向量的染色体。
第二,将综合前景值V作为算法的适应度函数值,以期前景值较大的停站序列能有较高的概率被选择传递至下一个阶段。
第三,考虑到单点交叉算子对个体性状破坏较小,本研究采用单点交叉算子对个体进行交叉操作;在进行变异操作时,以对应车站的前景值vi作为依据,对前景值vi较小的基因座具有较大概率为思想进行变异操作。
第四,影响遗传算法搜索效果的主要参数有:个体编码串长度l、种群大小G、交叉概率Pc、变异概率Pm以及终止迭代次数Te。本文根据文献[17]中的研究成果,取G=30,Pc=0.8,Pm=0.01及迭代次数Te=100。
3.2 算法步骤设计根据遗传算法求解问题的过程,结合本研究内容,现给出求解快车停站序列的遗传算法的计算步骤如下所示:
Step 1 有关数据初始化。
Step 2 随机产生初始种群G,计算个体的适应度值V[18]。
Step 3 根据适应度值,判断是否符合最优化准则,若是,转至Step7;否则,继续。
Step 4 判断是否满足迭代次数,若是,转至Step7;否则,继续。
Step 5 以一定的交叉概率Pc和变异概率Pm对种群中的个体按对应规则进行交叉或者变异操作,以产生新的个体。
Step 6 重新评估个体的适应度值V,并进行选择操作产生新的种群G,返回Step3。
Step 7 操作结束,输出种群G中最佳个体。
需要特殊说明的是,为了避免有效解的损失,步骤中的最优化准则通过经验而预设给定。
4 实例验证及分析 4.1 线路介绍某城市轨道交通共设11座车站,全程约50 km。标准停站运营时,列车均为8节编组,其定员为240人,运行时间约35 min,发车间隔为10 min,停站时间为1 min。根据统计,沿线各车站客流到达规律如图 2所示。
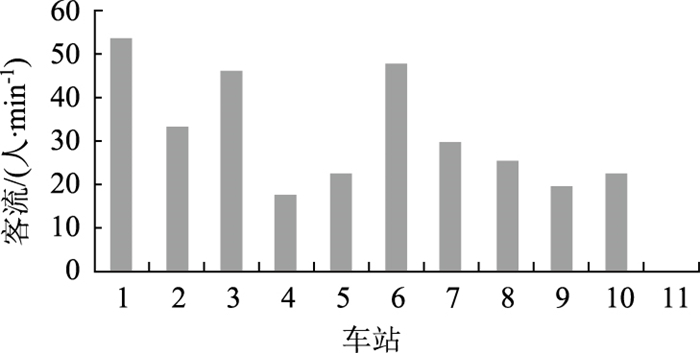
|
| 图 2 各车站客流到达规律 Fig. 2 Passenger arrival rule for each station |
| |
在图 2所示的客流到达规律的基础上,各车站的客流分配比pij如表 1所示。
| 车站 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 1 | 0 | 0.08 | 0.11 | 0.09 | 0.11 | 0.07 | 0.17 | 0.02 | 0.13 | 0.12 | 0.11 |
| 2 | 0 | 0 | 0.21 | 0.06 | 0.02 | 0.03 | 0.16 | 0.01 | 0.30 | 0.21 | 0.02 |
| 3 | 0 | 0 | 0 | 0.07 | 0.06 | 0.07 | 0.26 | 0.02 | 0.26 | 0.19 | 0.07 |
| 4 | 0 | 0 | 0 | 0 | 0.06 | 0.05 | 0.15 | 0.27 | 0.10 | 0.31 | 0.05 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0.10 | 0.28 | 0.12 | 0.18 | 0.10 | 0.22 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.23 | 0.13 | 0.26 | 0.19 | 0.19 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.21 | 0.37 | 0.40 | 0.02 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.41 | 0.30 | 0.29 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.78 | 0.22 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.00 |
因区段内客流需求,经评估决定,在不变更线路设备的条件下,在两列车之间加开一列快车,快车为4节编组,最小列车追踪间隔I=1 min,且快车与前续慢车发车间隔为TQ1=8 min,快车与后续慢车发车间隔为TH1=2 min。
4.2 方案求解与分析根据该区段统计数据和评估决定,结合本研究提出的理论及算法,利用Visual C++6.0进行编程求解,程序运行约5.7 s,最终得到较为合理的编码序列及停站方案。编码序列及停站方案如图 3所示。
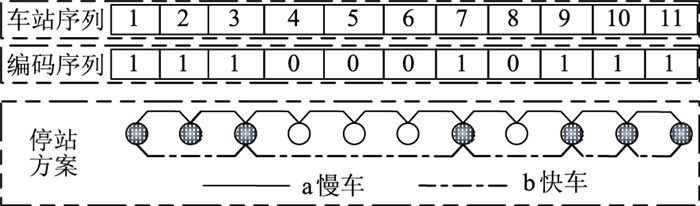
|
| 图 3 编码序列及停站方案 Fig. 3 Coding sequence and stopping schedule |
| |
从图 3可以看出,快车沿线共停靠7站,缓解了区段内的客流压力。根据算结果,现给出各站的时间前景值、拥挤费用前景值及综合费用前景值。区段内各站前景值如图 4所示。
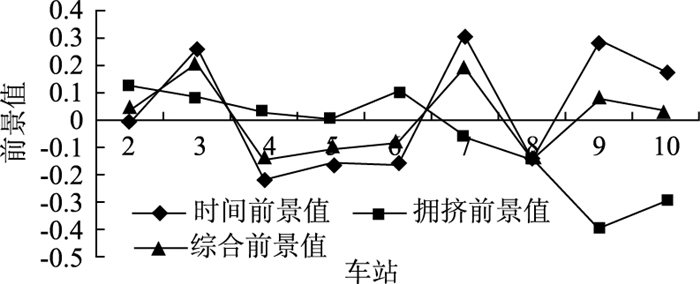
|
| 图 4 区段内各站前景值 Fig. 4 Prospect value for each station in interval |
| |
从图 4可以看出,区段内各站的前景值具有明显的波动性,且综合前景值与时间前景值的变化趋势接近,这是由于本研究拟定时间较拥挤偏好的缘故。根据其变化趋势,可以得出:快车的开行主要是分担了区段内较后车站的客流,进而导致后续车站拥挤程度的前景值较低。然而,根据图 2的表示,序列为6车站的到达客流明显大于7站,却将快车设于7站停靠,这主要是因为前景值是以乘客时间节省和区段拥挤为评价指标的,这也体现着乘客出行时的选择行为。
此外,本研究加开的是小编组快车,计算结果表明:通过开行快慢车停站方案比既有标准停站方案节约乘客时间共计约6 238 min,而这也比直接压缩发车时间间隔5 min条件下,加开慢车(编组和快车一样,为4节编组)的标准停站方案节省1 958 min,因此,上述分析说明了本研究理论及算法具有一定的合理性。
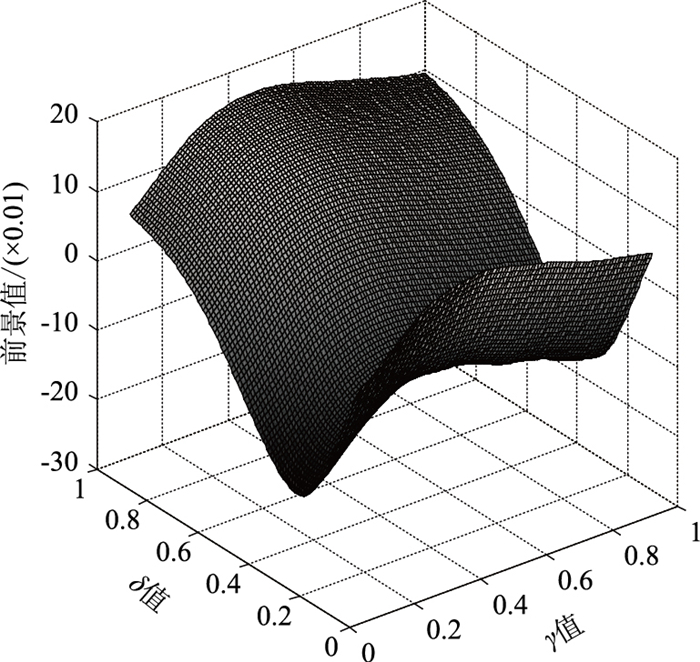
最后,考虑到价值敏感系数α,β以及权重系数γ,δ对综合前景值的影响,有必要对其敏感度作一分析。敏感系数及权重系数对综合前景值的影响,分别如图 5和图 6所示。
|
| 图 5 价值敏感系数对前景值的影响 Fig. 5 Influence of sensitivity coefficient on prospect value |
| |

|
| 图 6 权重系数对前景值的影响 Fig. 6 Influence of weight coefficient on prospect value |
| |
从图 5和图 6可以看出,在价值函数中,收益敏感系数对前景值的影响要远大于损失敏感系数所产生的影响;在权重函数中,权重损失系数对前景值的影响要远大于权重收益系数所产生的影响。基于仿真结果分析,本研究在计算过程中,上述参数的取值均在合理范围内。
5 结论本研究通过利用前景理论,以乘客广义出行费用为前景值,采用快慢车停站方案对既有城市轨道交通停站方案进行了分析研究。研究结果表明:第一,前景理论所反映的思维习惯符合于城市轨道交通的乘客出行选择行为。第二,对于原定标准停站方案与客流实际需求不符的轨道运营线路,可通过开行快慢车来节省对乘客的出行费用。其中,对于发车间隔较大的标准停站方案,在满足追踪间隔的条件下,可直接加开快车来进行优化,此外,也可适当优化标准停站方案的发车间隔以达到满足间隔的条件,进而开快车来进行优化。在研究过程中,没有深入研究快慢车间的发车间隔及快车的编组,这是本文不足之处,也是下一步研究的重点。
| [1] |
程婕, 彭其渊. 基于弹性客流的城市轨道交通组合停站方案优化[J]. 计算机应用研究, 2014, 31(11): 3361-3364. CHENG Jie, PENG Qi-yuan. Combined Stop Optimal Schedule for Urban Rail Transit with Elastic Demand[J]. Application Research of Computers, 2014, 31(11): 3361-3364. |
| [2] |
牛惠民, 陈明明, 张明辉. 城市轨道交通列车开行方案的优化理论及方法[J]. 中国铁道科学, 2011, 32(4): 128-133. NIU Hui-min, CHEN Ming-ming, ZHANG Ming-hui. Optimization Theory and Method of Train Operation Scheme for Urban Rail Transit[J]. China Railway Science, 2011, 32(4): 128-133. |
| [3] |
郑锂, 宋瑞, 何世伟, 等. 城市轨道交通跨站停车方案优化模型及算法[J]. 铁道学报, 2009, 31(6): 1-8. ZHENG Li, SONG Rui, HE Shi-wei, et al. Optimization Model and Algorithm of Skip-stop Strategy for Urban Rail Transit[J]. Journal of the China Railway Society, 2009, 31(6): 1-8. |
| [4] |
谭小士. 城市轨道交通快慢车运行组织研究[D]. 成都: 西南交通大学, 2014. TAN Xiao-shi. Research of Express-local Train Operation Organization in Urban Rail Transit[D]. Chengdu: Southwest Jiaotong University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10613-1014254835.htm |
| [5] |
孙元广, 史海欧. 市域线快慢车组合运营模式研究与实践[J]. 都市快轨交通, 2013, 26(2): 14-17. SUN Yuan-guang, SHI Hai-ou. Study and Practice of Operating Express/Slow Trains on Urban Railway Lines[J]. Urban Rapid Rail Transit, 2013, 26(2): 14-17. |
| [6] |
王智鹏, 罗霞. 城市轨道交通快慢车停站方案优化[J]. 华南理工大学学报:自然科学版, 2015, 43(12): 91-98. WANG Zhi-peng, LUO Xia. Stopping Schedule Optimization of Express/Local Trains in Urban Rail Transit[J]. Journal of South China University of Technology:Natural Science Edition, 2015, 43(12): 91-98. |
| [7] |
禹丹丹, 韩宝明, 张琦, 等. 基于灵活编组的轨道交通列车开行方案优化方法[J]. 北京交通大学学报, 2015, 39(6): 21-31. YU Dan-dan, HAN Bao-ming, ZHANG Qi, et al. Optimization Method for Train Plan of Urban Rail Transit Based on the Flexible Length of Train Formation[J]. Journal of Beijing Jiaotong University, 2015, 39(6): 21-31. |
| [8] |
陈虎, 贾俊芳. 高速铁路旅客列车停站方案问题的研究分析[J]. 物流技术, 2011, 30(7): 14-15. CHEN Hu, JIA Jun-fang. Analysis of the Stop Plan of High-speed Railway Passenger Trains[J]. Logistics Technology, 2011, 30(7): 14-15. |
| [9] |
张钰梅. 城市轨道交通路网客流拥挤传播特性及疏解策略研究[D]. 北京: 北京交通大学, 2015. ZHANG Yu-mei. Study on Passenger Congestion Propagation Properties and Solving Strategies of Urban Rail Transit Network[D]. Beijing: Beijing Jiaotong University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10004-1015611117.htm |
| [10] |
赵坤, 高建伟, 祁之强, 等. 基于前景理论及云模型风险型多准则决策方法[J]. 控制与决策, 2015, 30(3): 395-402. ZHAO Kun, GAO Jian-wei, QI Zhi-qiang, et al. Multi-criteria Risky-decision-making Approach Based on Prospect Theory and Cloud Model[J]. Control and Decision, 2015, 30(3): 395-402. |
| [11] |
KAHNEMAN D, TVERSKY A. Prospect Theory:An Analysis of Decision under Risk[J]. Econometrica, 1979, 47(2): 263-292. |
| [12] |
李小静, 刘林忠. 基于累积前景理论的通勤者路径选择模型[J]. 交通运输系统工程与信息, 2015, 15(1): 173-178. LI Xiao-jing, LIU Lin-zhong. Route Choice Model for Commuters Based on Cumulative Prospect Theory[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(1): 173-178. |
| [13] |
夏金娇, 隽志才, 高晶鑫. 基于前景理论的出行路径选择行为[J]. 公路交通科技, 2012, 29(4): 126-131. XIA Jin-jiao, JUAN Zhi-cai, GAO Jing-xin. Travel Routing Behaviors Based on Prospect Theory[J]. Journal of Highway and Transportation Research and Development, 2012, 29(4): 126-131. |
| [14] |
马永杰, 云文霞. 遗传算法研究进展[J]. 计算机应用研究, 2012, 29(4): 1202-1206. MA Yong-jie, YUN Wen-xia. Research Progress of Genetic Algorithm[J]. Application Research of Computers, 2012, 29(4): 1202-1206. |
| [15] |
边霞, 米良. 遗传算法理论及其应用研究进展[J]. 计算机应用研究, 2010, 27(7): 2426-2429. BIAN Xia, MI Liang. Development on Genetic Algorithm Theory and Its Applications[J]. Application Research of Computers, 2010, 27(7): 2426-2429. |
| [16] |
贺毅朝, 王熙照, 李文斌, 等. 基于遗传算法求解折扣{0-1}背包问题的研究[J]. 计算机学报, 2016, 39(12): 2614-2630. HE Yi-chao, WANG Xi-zhao, LI Wen-bin, et al. Research on Genetic Algorithms for the Discounted {0-1} Knapsack Problem[J]. Chinese Journal of Computers, 2016, 39(12): 2614-2630. |
| [17] |
张国辉, 高亮, 李培根, 等. 改进遗传算法求解柔性作业车间调度问题[J]. 机械工程学报, 2009, 45(7): 146-151. ZHANG Guo-hui, GAO Liang, LI Pei-gen, et al. Improved Genetic Algorithm for the Flexible Job-shop Scheduling Problem[J]. Journal of Mechanical Engineering, 2009, 45(7): 146-151. |
| [18] |
冷亮, 杜庆东. 基于遗传算法解决车辆最优路径诱导问题[J]. 信息通信, 2012(2): 14-15. LENG Liang, DU Qing-dong. Solving Optimal Vehicle's Routing Guidance Problem Based on Genetic Algorithm[J]. Information and Communication, 2012(2): 14-15. |
 2018, Vol. 35
2018, Vol. 35
