扩展功能
文章信息
- 胡祖平, 何建佳
- HU Zu-ping, HE Jian-jia
- 基于网络可靠性的街区开放适宜度研究
- Study on Suitable Size of Block Opening Based on Network Reliability
- 公路交通科技, 2018, 35(4): 77-84
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(4): 77-84
- 10.3969/j.issn.1002-0268.2018.04.010
-
文章历史
- 收稿日期: 2017-03-24
2. 上海理工大学 超网络研究中心(中国), 上海 200093
2. Super Network Research Center(China), University of Shanghai for Science and Technology, Shanghai 200093, China
街区是城市形态的重要组成部分,是构成城市生活与城市环境的基本面状单元,也是城市健康有机发展的基础[1]。当社会私有经济的活性得到充分释放,又在传统“家”文化的催化下,一系列大型封闭居住社区、大型综合体、城市产业片区,城中村等城市体如雨后春笋林立而起,人与人、人与环境的阻隔严重影响了公共资源的有效配置与布局[1];当前我国正处于经济转型的重要战略时期,互联网经济下的电商与物流行业正蓬勃发展,大面积封闭小区的存在已成为物流与电商“最后一公里”的瓶颈[3-4]。2014年10月,李克强总理签批了快递业第一部纲领性文件《国务院关于促进快递业发展的若干意见》,围绕推进“互联网+”发展、完善服务网络、衔接综合交通体系,打通电商“最后一公里”,完善资源配置等问题进行了广泛的阐述[5];2016年2月,政府又出台了《中共中央国务院关于进一步加强城市规划建设管理工作的若干意见》,“意见”中提出原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院要逐步打开,树立“窄马路、密路网”的城市道路布局理念[6]。随着相关政策的出台,街区开放的理念也应运而生,拆除围墙,开放街区,建立城市“微空间”成为时下大多数人关注的焦点[7]。因此打开封闭小区,推广街区制已经势在必行,这既是促进城市公共空间优化,人居模式可持续发展的手段之一[8],也是对社会经济发展过程中所出现的问题的一种修正和调整,如何推行和实施街区开放也便成为当前一项紧迫的议题。
对街区的研究,最早源自西欧,之后在美国得到发展,目前对于街区研究的理论脉络大体可概括为3个方向。一是在和谐社会的背景下从城市交通优化的角度研究街区,随着20世纪中后期人本主义的兴起,国外学者将“人-社会-环境”的和谐理念融入了街区的研究,认为大规模的道路会影响城市的结构和肌理,而且会给城市道路交通带来拥堵,随后提出了“城市功能街区”、“环境功能街区”、“开放式街区”的概念及构想,倡导建立功能性空间环境,解决道路交通的拥堵[9];二是基于城市形态的角度研究街区问题,城市的形态及轮廓各不相同,伴随政治、经济、文化等方面的影响,城市形态并非一成不变,而是处于不定形状态,因此部分学者对街区尺度进行了合理判断与选择,从模式与肌理两个方面展开研究[10],也有学者针对城市形态的分离及趋同问题,从整体上分析路径、影响因子、分形等指标,从而得到不同形态街区的量化表达[11-12];三是基于中国特色的单位街区研究,“单位”指的是给城市居民提供就业机会的生产组织及有关的政府和公共机关部门,自20世纪50年代“新居住单元”的提出后形成了新的社会性城市聚落,之后又趋于弱化,很多学者从我国城市变迁的视角出发,探究其影响及利弊[13]。
上述研究都是属于城市规划设计的领域范围,涉及了城市形态学、地理学,以及建筑学等相关问题,而对于街区开放这一议题而展开的开放方式及适宜度研究却少有涉及。张义荣等在借鉴信息论中提出了评价网络性能的“网络熵”理论,“网络熵”是对网络安全性能和稳定性的一种描述,网络熵值越小,表明该网络系统的可靠性越高、稳定性越强[14];反之,网络熵值越大,表明该网络系统的可靠性越低、稳定性越弱。从网络可靠性出发,引入基于网络熵的最大流、最短路熵理论[15],以封闭小区为代表,将封闭小区及周围场所虚拟为网络节点,并以各场所之间的可达路径视为连接节点的边,构建其功能型路网[16-17],对该小区从封闭到打开围墙的过程分开讨论,分别计算开放过程中构成的各个路网的最大流、最短路熵,并根据网络可靠性判定标准对各个网络的可靠性进行判定,以此作为判定街区开放适宜度的依据,这将会成为研究街区开放的新思路,也将成为一个重要而富有挑战性的课题。
1 基于最大流、最短路熵理论下街区路网的构建及可靠性分析网络系统在人们行为生活中已然触目皆是,多样的网络形态表述不同的网络特征,网络系统中也包含着各种各样的流量问题,例如公路系统中的车流、金融系统中的现金流、控制系统中的信息流等等[18]。类似这些系统,通常会考虑其流量问题,求出其网络系统的最大流和最短路,从而加深对系统的认识并对其进行改造,对于街区而言,引入网络系统也将会是其研究思路之一[19]。购物商场、餐厅、银行、公交地铁等都是除居住场所外人们经常活跃的场所,这些场所的存在构成了城市的区域性经济,成为城市经济的组成部分,也是城市居民日常生活不可或缺的一部分。从网络视角出发,我们可以将这些场所看作虚拟的节点,各场所之间的可达路径可以看作连接节点之间的边,每条边的赋权即是节点之间的距离,这样由节点和边构成的一个功能型路网,则成为研究街区开放的对象,分析构成该路网的可靠性作为判定街区开放适宜度的依据[20]。
传统网络熵在研究网络可靠性问题时存在很多的不足,例如网络节点受到攻击是随机的,具有不确定性,用传统网络熵则无法计算该网络的网络吞吐量、信道利用率等,这样一来则无法计算其网络熵;其次传统网络熵在计算各指标的权重时大多使用专家打分法来给出判断矩阵的值,并利用几何平均来综合给出专家的判断,掺杂过多的主观成分,从而影响求解结果的准确性,而且在实施过程中困难也较大[21]。最大流、最短路熵则是基于传统网络熵上的改进,利用最大流、最短路熵值来判断网络稳定性,并给出百分制网络可靠等级判断标准,具有更强的实用性和有效性[22]。
街区路网的最大流问题就是给一个带收发点的网络,其每条边的赋权称为流量,在不超过每条边流量的前提下,求从出发地到目的地的最大流量。最短路就是对一个赋权的,有n个节点的,有向图D的起点v1和终点vn找到一条从v1到vn的路,使得这条路上所有边的距离总和最小,这条路就被称为从v1到vn的最短路。这条路上所有边的距离之和称为从v1到vn的距离。
对于一个有n个场所构成的街区路网图D=(V, A, C),其中V={vi|i=1, 2, …, n}为该街区路网范围内的场所节点集,A={aij|aij为节点vi指向节点vj的边,i,j=1, 2, …, n},C={cij|cij为边aij的流量,i,j=1, 2, …, n}。当该路网受到“攻击”时,将会有两种情况发生:(1)当某一场所遭遇故障无法通行时,即节点vi受到“攻击”时失效,那么与节点vi相连的边aij和aki均断裂;(2)当连接场所间的道路遭遇故障无法通行时,即该边aij受到“攻击”时失效,那么边aij将断裂。
当街区网络的节点受到攻击时,该网络的最大流和最短路必然会减小(增大)或不变,因此该网络的可靠性能也可能会受到影响。此时可以引入网络的最大流熵和最短路熵来体现街区路网的可靠性,网络熵越大,该路网的可靠性就越差,反之可靠性就越好。这里将讨论街区路网节点受到攻击时网络最大流熵和网络最短路熵,限于篇幅,不讨论网络边受到攻击时的情况。
由于在街区路网中形成的有向图与无向图有所不同,有向图确定了从某一场所到另一场所的方向,而无向图没有确定的方向,所以无法计算起点和终点间的最大流和最短路,其最大流、最短路熵的计算需分开讨论。
1.1 有向街区路网图的网络熵定义有向街区路网的最大流熵和最短路熵步骤如下:
(1) 对形成的街区路网中的n个场所节点进行编号,依次为v1, v2,…,vn,v1为起点,vn为终点;
(2) 利用网络图论的相关方法计算出含有n个场所节点的有向街区路网图的最大流df(最短路dp);
(3) 利用网络图论的相关方法计算出含有n个场所构成的的有向街区路网图的节点vi受到“攻击”后的最大流dfi(最短路dpi)。
考虑到有向街区路网图受到攻击时,其起始场所v1和终止场所vn受到“攻击”的概率较小,不予考虑。所以当路网受到“攻击”时,剩下的n-2个场所都有受到“攻击”的可能,每个场所受到“攻击”的概率为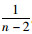
(4) 网络最大流熵为:
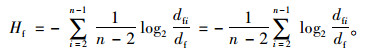
|
(1) |
最短路熵为:
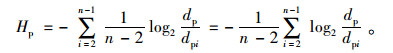
|
(2) |
对于无向街区网络图,在n个场所中先随机设定一个起点和一个终点,则共有An2=n(n-1)种选择,然后按照上述有向街区路网图网络熵的计算方法进行计算,最后将n(n-1)种路网的最大流熵和最短路熵分别相加求其平均值得到该无向街区路网图的最大流熵和最短路熵。步骤如下:
(1) 对原街区路网中的n个场所进行编号,依次为v1, v2, …, vn。
(2) 随机选择两个场所vj和vk,分别定为起点和终点,j, k=1, 2, …,n,且j≠k。
(3) 利用网络图论的相关方法计算上述以场所vj为起点,场所vk为终点的有向街区路网图的最大流dfjk(最短路dpjk)。
(4) 利用网络图论的相关方法计算上述以场所vj为起点,场所vk为终点的有向街区路网图中的场所vi受到“攻击”后的最大流dfijk(最短路dpijk),其中i=1, 2,…,n,且i≠j, k。
(5) 场所vj到场所vk的网络最大流熵为:
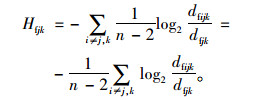
|
(3) |
起点vj到终点vk的网络最短路熵为:
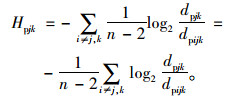
|
(4) |
(6) 原无向街区路网的网络最大流熵为:
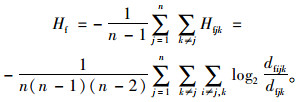
|
(5) |
原无向街区路网的网络最短路熵为:
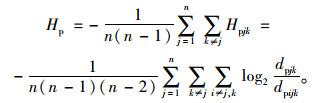
|
(6) |
街区路网的可靠性可根据计算网络熵的得分结果来进行排序及等级划分,我们可以认为如果街区路网中某场所受到“攻击”之后依然能够保持其路网性能90%以上,则认为该路网可靠性为“优”,如果受到“攻击”之后能够保持其路网性能80%~90%之间,则认为该路网可靠性为“良”,以此类推,70%~80%之间为“中”,60%~70%之间为“及格”,0~60%之间为“不及格”。
根据传统网络熵的计算可知,当受到“攻击”之后能够保持其路网性能90%~100%时,计算得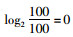
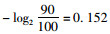
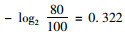
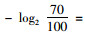
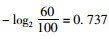
| 百分制区间 | [90, 100] | [80, 90) | [70, 80) | [60, 70) | [0, 60) |
| 网络熵区间 | [0, 0.152] | (0.152, 0.322] | (0.322, 0.515] | (0.515, 0.737] | (0.737,∞) |
| 可靠性等级 | 优 | 良 | 中 | 及格 | 不及格 |
2 实例分析
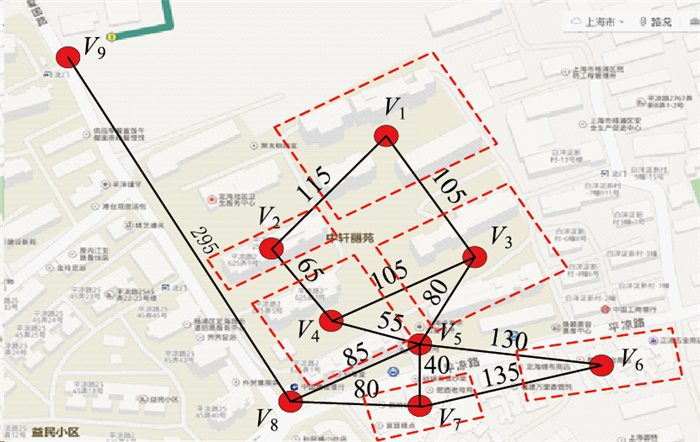
中轩丽苑是位于上海市杨浦北外滩的定海居住区,是该区域为数不多几个新式高档生态型住宅区,中轩丽苑由9幢错落而置的酱红色的14~19层的小高层组成,住宅区四周由围墙围住,朝南方向设有小区门禁以供出入,是个传统典型的封闭式居民区。该居民区东南方向有聚集而成的购物商场,正对小区南门的是餐饮饭馆类的集中区,西南路口设有银行,且距离小区最近的地铁口位于西北方向,如图 1所示。中轩丽苑共有居民500多户,区内居民及车辆都由小区南门出入,该路段一直以来都较为拥堵和嘈杂。由于封闭小区的围墙缘故,居民出行也受到了很大的限制。比如说距离小区最近的地铁口位于小区西北侧,与该小区仅因为一墙之隔,却使居民前往地铁站的路途增加了数倍,极大地削弱了交通的便利性。本研究即从街区开放的角度出发,以中轩丽苑为例拆除封闭围墙,构建区域内功能型路网,并利用上述基于网络熵的最大流、最短路熵理论对其街区路网进行可靠性检验,分析该小区街区开放的适宜度。
|
| 图 1 中轩丽苑及其周边路网图 Fig. 1 Road network of Zhongxuanliyuan and its surrounding |
| |
下面以中轩丽苑为例,为了便于分析计算,将住宅区内的9幢楼划分为4个区域,并表示为节点V1,V2,V3,V4,如图 1所示。节点V5表示该居民区的门禁出入口,节点V6表示购物商场,节点V7表示餐饮休闲集中区,节点V8表示银行,节点V9表示地铁口,图中连接各节点的边表示各节点间的可达路径,赋予这些边的权值表示场所间的距离,由这些节点构成的路网从空间维度反映了该居民区及其附近的生活、休闲、出行等方面,构成一个由9个节点12条边组成的路网。由于篇幅限制,本研究只将该街区路网看作无向街区路网图,分析计算其最短路熵,此结果更具有普适性。
由上述对网络熵的讨论可以看出,如果在一个街区路网中,存在一个节点Vi,当该节点受到“攻击”后网络最大流为0,最短路为无穷大,即该网络系统面临瘫痪,此时的节点称为高危节点,此时的网络是极不稳定的。据上述网络熵的计算公式可作如下推算,当节点Vi受到攻击后,最大流dfi趋向于0,最短路dpi趋向于正无穷,则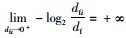
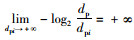
在现实的视角下,从路网节点之间的连接边可以看出各场所之间的来往路径,该封闭式小区的正门作为小区的唯一出入点,是居民前往附近公交和地铁站、购物场所、餐饮休闲中心、银行等场所的唯一通道,也承载着该居民区日常内部与外界所有的供需来往,当此唯一出入点遭遇修缮,改造或其他故障时,将会严重影响到该小区内及附近人们的日常生活。在我国当前的大中型城市中,类似于此封闭类型的住宅区不甚枚举,下面仅以中轩丽苑为例,打开封闭的围墙,实施街区开放,尝试探索该街区路网的可靠性。
在原街区路网的基础上,通过实施街区开放,拆除封闭围墙,从而增加了场所间的可达路径,即增加节点之间的边,不改变原网络节点之间的连接边,构建新的街区路网。由于不同城市,不同街区的形态各有不同,街区开放的尺度也将有所不同,在不同开放尺度下分别计算其最短路熵并分析其路网可靠性,将会确定该小区推行街区开放的最佳适宜度。如图 2所示,(a)为拆除西北方向围墙而构建的新路网;(b)为拆除西北,西南方向围墙而构建的新路网;(c)为拆除拆除东南方向围墙而构建的新路网。分别计算各个街区路网的最短路熵,分析其网络可靠性。

|
| 图 2 封闭小区逐步开放路网图 Fig. 2 Road networks formed in process of block opening |
| |
在matlab中运用Floyd算法[23]计算上图路网(1)中的场所节点之间的最短路径,得出场所间的最短距离矩阵如表 2所示。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 0 | 115 | 105 | 180 | 185 | 315 | 225 | 270 | 220 |
| 2 | 115 | 0 | 170 | 65 | 120 | 250 | 160 | 205 | 200 |
| 3 | 105 | 170 | 0 | 105 | 80 | 210 | 120 | 165 | 325 |
| 4 | 180 | 65 | 105 | 0 | 55 | 185 | 95 | 140 | 265 |
| 5 | 185 | 120 | 80 | 55 | 0 | 130 | 40 | 85 | 320 |
| 6 | 315 | 250 | 210 | 185 | 130 | 0 | 135 | 215 | 450 |
| 7 | 225 | 160 | 120 | 95 | 40 | 135 | 0 | 80 | 360 |
| 8 | 270 | 205 | 165 | 140 | 85 | 215 | 80 | 0 | 295 |
| 9 | 220 | 200 | 325 | 265 | 320 | 450 | 360 | 295 | 0 |
根据表 2数据可计算出路网遭遇“攻击”后各节点间的最短路径,将计算结果代入公式:
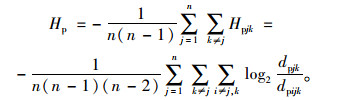
|
计算得出路网1的最短路熵为Hp1=0.116 4,根据基于网络熵的路网可靠性等级判断标准,可以得知Hp1=0.116 4 < 0.152,该网络可靠性为优;且根据计算2-0.116 4=0.922 5,可知该网络节点在受到攻击后的网络可靠性能够保持92.25%。相比小区未拆除围墙之前的封闭状态,推行街区开放后构成路网的稳定性明显提升,由此可以判断该小区适宜推行街区开放。
按以上计算方法,依次对路网2、3进行计算,如下所示:
根据表 3计算可得路网2的最短路熵为Hp2=0.054,由网络熵的网络可靠性等级判断标准可知,其网络可靠性为优,且网络节点在受到攻击后的网络可靠性为:2-0.054=0.963 3=96.33%,较于路网1而言,其网络稳定性能更高,因此该小区适宜在路网1基础上继续推行街区开放。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 0 | 115 | 105 | 180 | 185 | 315 | 225 | 250 | 220 |
| 2 | 115 | 0 | 170 | 65 | 120 | 250 | 160 | 135 | 200 |
| 3 | 105 | 170 | 0 | 105 | 80 | 210 | 120 | 165 | 325 |
| 4 | 180 | 65 | 105 | 0 | 55 | 185 | 95 | 70 | 265 |
| 5 | 185 | 120 | 80 | 55 | 0 | 130 | 40 | 85 | 320 |
| 6 | 315 | 250 | 210 | 185 | 130 | 0 | 135 | 215 | 450 |
| 7 | 225 | 160 | 120 | 95 | 40 | 135 | 0 | 80 | 360 |
| 8 | 250 | 135 | 165 | 70 | 85 | 215 | 80 | 0 | 295 |
| 9 | 220 | 200 | 325 | 265 | 320 | 450 | 360 | 295 | 0 |
根据表 4计算可得路网3的最短路熵为Hp3=0.044 5,根据网络熵的网络可靠性等级判断标准判断,其网络可靠性为优,且网络节点在受到攻击后的网络可靠性为:2-0.044 5=0.969 6=96.96%,相比于路网1和2,其网络稳定性能又有所提高,所以该小区应当在路网1和2的基础之上进一步推行街区开放。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 0 | 115 | 105 | 180 | 185 | 230 | 225 | 250 | 220 |
| 2 | 115 | 0 | 170 | 65 | 120 | 250 | 160 | 135 | 200 |
| 3 | 105 | 170 | 0 | 105 | 80 | 125 | 120 | 165 | 325 |
| 4 | 180 | 65 | 105 | 0 | 55 | 185 | 95 | 70 | 265 |
| 5 | 185 | 120 | 80 | 55 | 0 | 130 | 40 | 85 | 320 |
| 6 | 230 | 250 | 125 | 185 | 130 | 0 | 135 | 215 | 450 |
| 7 | 225 | 160 | 120 | 95 | 40 | 135 | 0 | 80 | 360 |
| 8 | 250 | 135 | 165 | 70 | 85 | 215 | 80 | 0 | 295 |
| 9 | 220 | 200 | 325 | 265 | 320 | 450 | 360 | 295 | 0 |
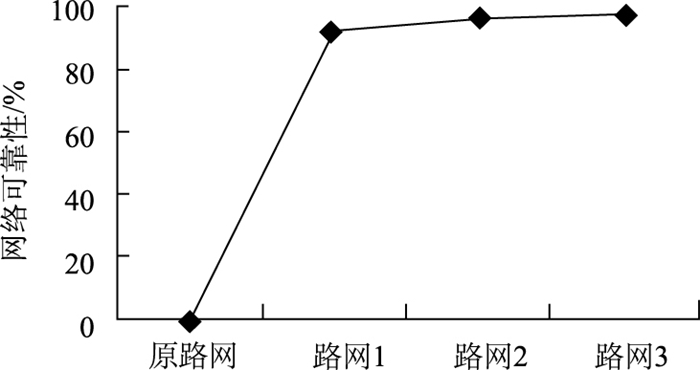
通过上述计算,可知中轩丽苑小区通过逐步拆除围墙推行街区开放后,其构成的街区路网逐渐趋于稳定状态,如图 3所示。推行街区开放后,避免了原始路网中高危节点的存在,其路网实现了从极不可靠到可靠的状态,由此得知中轩丽苑适宜开放,并根据计算的各路网可靠性比较,可知应当对其西北、西南、东南方向的封闭围墙都进行拆除,推行开放,这样有利于构建街区路网的稳定性。这不仅在理论视角下,有利于构建区域可靠性路网,对于实现坊市合一,以及构建更加灵活的区域发展体系也有着重要的意义。
|
| 图 3 街区开放网络可靠性趋势图 Fig. 3 Trend of block opening network reliability |
| |
3 结论
本研究从网络可靠性出发,通过构建街区路网,运用基于网络熵的最大流、最短路熵理论,对路网进行分析并计算,且根据网络可靠性的判定标准确定其网络可靠性,从而确定实施街区开放的适宜度,并结合了实例分析,旨在为研究街区开放寻找新的切入点,为街区开放研究提出建设性的实施策略,以期推动我国街区制的发展和多功能街区的完善。从文中中轩丽苑的实例分析得知,该封闭小区及其周边构成的路网中存在高危节点,最短路熵趋向于无穷大,该网络具处于极不稳定的状态,经过对其分阶段实施街区开放,分别计算各路网的最短路熵,可以得知网络逐渐趋于稳定,可靠性逐渐增加,因此可以认为对该小区实施开放的适应性及必要性,且应当对此推行进一步,多方位的街区开放。
近年来,大面积封闭小区的存在造成了城市交通堵塞、土地资源浪费、经济转型缓慢等问题,严重制约了我国的城市经济发展,推动街区制改革已经成为必然。研究街区开放的思路也越来越多,当前大多数研究思路都是从理论角度出发,来论述街区开放的必要性。城市除了具备经济、市场、管理等功能外,更加具备的是社会关系,社会组织形式才是城市的基本元素,人是城市的主体。在封闭小区的盛行下,城市区域间的隔阂越来越多,严重阻碍了人的关系发展,大量封闭空间将城市的整体分割为部分,社区邻里之间的交流已经日渐式微。从社会关系的角度出发,通过构建街区供需关系网来探析街区开放,将会成为一种新的思路。除此之外,实施街区开放过程中面对更多的是复杂的社会问题,例如开放社区后的城市安全问题、城市道路的与街区道路的管理问题,以及公共停车问题等,都将成为学者们研究街区开放的后续议题。
| [1] |
芒福德L. 城市发展史:起源、演变和前景[M]. 北京: 中国建筑工业出版社, 2005. MUMFORD L. The City in History:Its Origins, Its Transformation, and Its Prospects[M]. Beijing: China Architecture & Building Press, 2005. |
| [2] |
刘伟, 徐晓童. 浅谈开放街区制度的可实施性意见[J]. 科技经济导刊, 2016(30): 252. LIU Wei, XU Xiao-tong. Opinions on Implementation of Open Block System[J]. Technology and Economic Guide, 2016(30): 252. |
| [3] |
臧鑫宇. 生态城街区尺度研究模型的技术体系构建[J]. 城市规划学刊, 2013(4): 81-87. ZANG Xin-yu. The Construction of Technical Indicator System for Eco-cities at Blocks Scale[J]. Urban Planning Forum, 2013(4): 81-87. |
| [4] |
王振坡, 张颖, 梅林. 我国城市推广街区制的路径及对策研究[J]. 学习与实践, 2016(7): 108-115. WANG Zhen-po, ZHANG Ying, MEI lin. A Study on Path and Countermeasures of Urban Street Block in China[J]. Study and Practice, 2016(7): 108-115. |
| [5] |
刘晖, 于澄. 低碳视角下的"单位大院"街区空间模式反思[J]. 低碳世界, 2015(19): 36-37. LIU Hui, YU Cheng. Reflections on Spatial Pattern of "Unit Courtyard" in Perspective of Low Carbon[J]. Low Carbon World, 2015(19): 36-37. |
| [6] |
白鸽, 刁艳. 街区开放环境下可持续城市规划研究[J]. 门窗, 2016(4): 147-149. BAI Ge, DIAO Yan. Study on Sustainable Urban Planning in Block Open Environment[J]. Doors and Windows, 2016(4): 147-149. |
| [7] |
王少婧. 锦里街区开放空间的探访[J]. 四川建筑, 2013, 33(4): 47-48. WANG Shao-jing. A Visit to Open Space of Jinli Street Blocks[J]. Sichuan Architecture, 2013, 33(4): 47-48. |
| [8] |
郑悦. 开放街区式住区规划设计策略探析[D]. 北京: 北京建筑大学, 2016. ZHENG Yue. Planning and Design Strategy Anal-ysis for Residential Open Block[D]. Beijing: Beijing University of Civil Engineering and Architecture, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10016-1016082218.htm |
| [9] |
LEMANSKI C. Spaces of Exclusivity or Connection? Linkages between a Gated Community and Its Poorer Neighbour in a Cape Town Master Plan Development[J]. Urban Studies, 2006, 43(2): 397-420. |
| [10] |
ZHANG T, ARRIGONI S, GAROZZO M, et al. A Lane-level Road Network Model with Global Continuity[J]. Transportation Research Part C:Emerging Technologies, 2016, 71: 32-50. |
| [11] |
黄烨勍, 孙一民. 街区适宜尺度的判定特征及量化指标[J]. 华南理工大学学报:自然科学版, 2012, 40(9): 131-138. HUANG Ye-qing, SUN Yi-min. Judgement Char-acteristics and Quantitative Index of Suitable Block Scale[J]. Journal of South China University of Technology:Natural Science Edition, 2012, 40(9): 131-138. |
| [12] |
黄烨勍, 谢青. 广州城市中区心街区尺度适宜性探讨:以天河体育中心片区街区为例[J]. 华南理工大学学报:社会科学版, 2015, 7(3): 70-75. HUANG Ye-qing, XIE Qing. Investigation into Suitability of Block Scale in Urban Central Districts in Guangzhou:Taking the Block in the District of Tianhe Sports Center as an Example[J]. Journal of South China University of Technology:Social Science Edition, 2015, 7(3): 70-75. |
| [13] |
肖亮. 城市街区尺度研究[D]. 上海: 同济大学, 2006. XIAO Liang. Study on Scale of Urban Blocks[D]. Shanghai: Tongji University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10247-2006058791.htm |
| [14] |
张义荣, 鲜明, 王国玉. 一种基于网络熵的计算机网络攻击效果定量评估方法[J]. 通信学报, 2004, 25(11): 158-165. ZHANG Yi-rong, XIAN Ming, WANG Guo-yu. A Quantitative Evaluation Technique of Attack Effect of Computer Network Based on Network Entropy[J]. Journal on Communications, 2004, 25(11): 158-165. |
| [15] |
吴六三. 基于网络熵的网络可靠性研究[D]. 南京: 南京航空航天大学, 2014. WU Liu-san. Research on Network Reliability Based on Network Entropy[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10287-1015951829.htm |
| [16] |
邬尚霖. 低碳导向下街区尺度和路网密度规划研究[J]. 华中建筑, 2016(7): 29-33. WU Shang-lin. Research on the Block Scale and Density of Road Network Planning under the Guidance of Low-carbon[J]. Huazhong Architecture, 2016(7): 29-33. |
| [17] |
FREIRIA S, RIBEIRO B, TAVARES A O. Under-standing Road Network Dynamics:Link-based Topological Patterns[J]. Journal of Transport Geography, 2015, 46: 55-66. |
| [18] |
吴六三, 谭清美. 基于网络熵的应急物流网络稳定性研究[J]. 当代财经, 2012(7): 60-68. WU Liu-san, TAN Qing-mei. A Study of the Stability of Emergency Logistics Network Based on Network Entropy[J]. Contemporary Finance & Economics, 2012(7): 60-68. |
| [19] |
苗鑫, 西宝. 基于云理论的路网可靠性评估方法[J]. 公路交通科技, 2008, 25(8): 132-136. MIAO Xin, XI Bao. Road Network Reliability Evaluation Method Based on Cloud Theory[J]. Journal of Highway and Transportation Research and Development, 2008, 25(8): 132-136. |
| [20] |
赵国锋, 苑少伟, 慈玉生. 城市路网的复杂网络特性和鲁棒性研究[J]. 公路交通科技, 2016, 33(1): 119-124. ZHAO Guo-feng, YUAN Shao-wei, CI Yu-sheng. Analysis of Complex Network Property and Robustness of Urban Road Network[J]. Journal of Highway and Transportation Research and Development, 2016, 33(1): 119-124. |
| [21] |
曾伟渊. 一种基于网络熵的计算机网络攻击效果定量评估方法[J]. 长春师范大学学报, 2016(8): 24-29. ZENG Wei-yuan. A Quantitative Evaluation Method of Computer Network Attack Effects Based on Network Entropy[J]. Journal of Changchun Normal University, 2016(8): 24-29. |
| [22] |
CHELLAPPAN V, SIVALINGAM K M, KRITHIVASAN K. A Centrality Entropy Maximization Problem in Shortest Path Routing Networks[J]. Computer Networks, 2016, 104: 1-15. |
| [23] |
张德全, 吴果林, 刘登峰. 最短路问题的Floyd加速算法与优化[J]. 计算机工程与应用, 2009, 45(17): 41-43. ZHANG De-quan, WU Guo-lin, LIU Deng-feng. Accelerated and Optimized Method of Floyd Algorithm to Find out Shortest Path[J]. Computer Engineering and Applications, 2009, 45(17): 41-43. |
 2018, Vol. 35
2018, Vol. 35
