扩展功能
文章信息
- 魏瑞, 曹周阳, 顾安全
- WEI Rui, CAO Zhou-yang, GU An-quan
- 高填方钢波纹管涵变形计算及涵土相对刚度系数研究
- Calculation of Deformation of High-filling Steel Corrugated Pipe Culvert and Study on Culvert Soil Relative Stiffness Coefficient
- 公路交通科技, 2018, 35(4): 67-76, 92
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(4): 67-76, 92
- 10.3969/j.issn.1002-0268.2018.04.009
-
文章历史
- 收稿日期: 2018-01-11
2. 郑州航空工业管理学院 土木建筑工程学院, 河南 郑州 450015;
3. 四川高速公路建设开发总公司, 四川 成都 610041
2. School of Civil and Architecture Engineering, Zhengzhou Institute of Aeronautical Industry Management, Zhengzhou Henan 450015, China;
3. Sichuan Expressway Construction & Development Corporation, Chengdu Sichuan 610041, China
在我国山岭重丘地带修筑公路时,为了满足线型与填挖平衡的要求,并兼顾排水与出行,设置了较多的高填方涵洞,过去此类涵洞多为钢筋混凝土刚性涵洞,近年来,随着我国钢波纹管涵洞的推广应用,因结构自身在荷载作用下的压缩变形量不可以忽略不计,此类涵洞可以被看作为柔性涵洞,而高填方涵洞的受力性状与涵洞的刚柔性有着密切的关系,因此开展钢波纹管涵变形计算及涵土相对刚度的研究,对于理解涵洞受力具有重要的意义。
自Marston在高填方涵洞上采用摩擦理论与极限平衡方程推导得出的上埋式管道土压力计算公式以来,诸多学者教授对上埋式涵洞所受垂直土压力进行了全面而深入的研究与探讨[1-5],多涉及上埋式的刚性涵洞,不考虑涵洞自身的变形计算,因此涵侧土体的压缩变形量较大,涵顶不但要承受其上的土柱压力,还要承担因摩擦产生的附加压力,使得涵顶土压力过大。而对于涉及涵土相对刚度的柔性涵洞的判别,多是根据地埋管道设计规范[6]中的要求进行判断,此类管道以PVC塑料管材和钢材为主,直径较小,管壁较薄,刚度较小,在填土荷载作用下,管道的竖向压缩变形较大,且向两侧土体膨胀挤压,同时侧向土体也给予管道一定的弹性抗力阻止其持续变形[7],在填土增加的过程中,管土变形协调发展,使得管周土压力会重新分布,当管道竖向变形量大于两侧土体的变形量时,通过摩擦传递作用,使得涵顶垂直土压力将小于其上的土柱压力,变形会起到减荷的效应,由此可见刚性涵洞与柔性涵洞因变形引起的土压力受力模型区别较大,这为判断涵土相对刚度提出了严格的要求。
钢波纹管涵的应用最早起始于美国,自1892年开始,针对高填方下钢波纹管的材料性质、动静荷载变化与土压力、收敛变形与涵土相互作用、耐久性与防护等进行了测试与分析[8-13],并取得了一定的理论研究成果,形成了设计与施工指导规范,具有重要应用价值。2000年以后,随着我国高填方钢波纹管涵洞的推广与应用,部分学者也针对钢波纹管的性质进行了研究,如李祝龙教授[14-15]持续十多年在现场试验与理论分析的基础上,对钢波纹管材进行了系统的受力与变形研究,并撰写了《公路钢波纹管涵洞设计与施工技术》专著。季文玉教授[16]对高填方下的钢波纹管及拱桥结构形式差异、材料应力应变、管涵压力与变形、设计参数与施工工艺进行了详细的研究。方亚非[17]等对上埋式钢波纹管涵结构设计计算方法进行了分析。王艳丽[18]指出应用薄壳中旋转对称壳理论对钢波纹管进行分析是可行有效的。研究人员彭立等[19],朱旭阳,何欢等[20],张允海,曾水生等[21],赵中连, 王志刚[22]依托实际工程,分别针对高填方下大直径钢波纹管进行了现场测试工作,得到管材应变值及土压力值随填高的变化规律,部分涉及管涵变形规律。但是以上研究内容,针对钢波纹管涵自身的收敛变形计算及其与周围土体相互作用的研究开展较少,也很少涉及涵土相对刚度的计算。因此,拟在考虑波纹管材料惯性矩变化的基础上,利用管土相互作用模型,对管涵变形进行定量计算,并给出管涵刚柔性的判定方法。
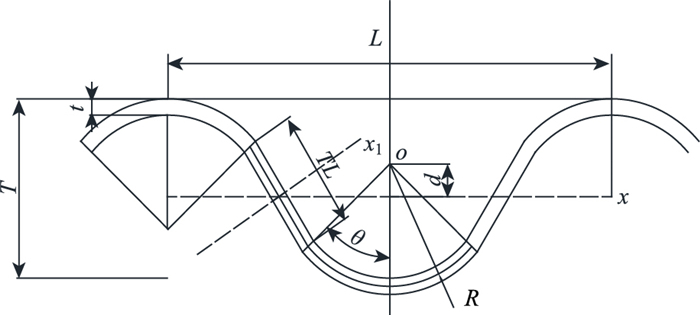
1 钢波纹管涵变形及相对刚度系数计算 1.1 钢波纹管涵惯性矩计算钢波纹管是由波形钢板组合拼接而成,沿管长方向呈波形状,增大了钢板的抗弯惯性矩,使之具有较高的抗弯性能,一定程度上提高了抗压性能。其波形如图 1所示。波形参数包括:波长L;波高T;直线段长度TL;波峰与波谷半径R;圆弧角度θ;圆心偏离x轴距离d;板厚t。
|
| 图 1 钢波纹板标准波形示意图 Fig. 1 Schematic diagram of standard waveform of steel corrugated plate |
| |
在钢波纹板结构中用到的惯性矩是相对于中性轴(x轴)的惯性矩,材料力学中惯性矩的表达公式为:
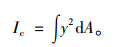
|
(1) |
式中,dA为截面内的面积元素;y2dA为面积元素对x轴的惯性矩。
由于钢波纹板形状较为复杂,直接积分不易得到。但根据惯性矩的定义可知,组合截面对于某坐标轴的惯性矩,等于其各组成部分对于同一坐标轴的惯性矩之和。因此,可将一个波长内的波纹分解成圆弧段和直线段分别求其惯性矩再求和[23],并采用转轴公式,将圆弧部分和直线部分所得结果求和,经计算得到一个波长相对x轴的惯性矩Ic,即
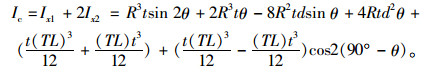
|
(2) |
式中,Ix1为L长度内圆弧部分对圆心所在水平轴的惯性矩;Ix2为L长度内直线部分对圆心所在水平轴的惯性矩。
同时也可以得到一个波长内的钢波纹板单位长度惯性矩Ic:
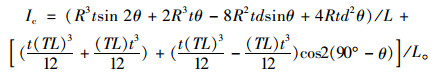
|
(3) |
国际上为了评价热塑性管道环向刚度,采用了如下的计算[24]:
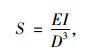
|
(4) |
式中,S为环刚度;E为材料的弹性模量;I为惯性矩;D为管环的平均直径。其物理意义为管道环向断面的刚度,国际标准规定,管材的环刚度用公称环刚度SN表示,分为2,4,8,16和32共5个标准等级。
将钢波纹管涵看作柔性结构,必须考虑管涵材料的环向刚度,若环向刚度不足,其过大的内力将会引起大的变形,甚至局部曲屈或开裂。对钢波纹管而言,材质的弹性模量比较稳定,其惯性矩又有计算公式,EI值可以通过公式计算获取,所以可以通过式(4)来评价钢波纹管涵材料的环向刚度。
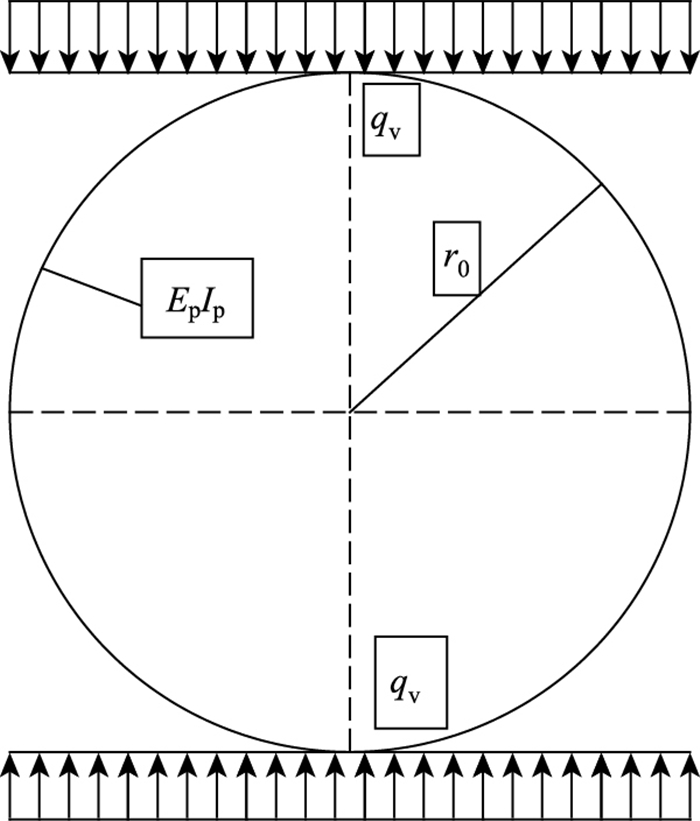
1.3 钢波纹管涵相对刚度系数“规范”计算方法《给水排水工程管道结构设计规范》(GB 50332—2002)中:“对地埋圆形管道结构,应根据管道结构刚度与管周土体刚度的比值αs判别刚性管道或柔性管道”[6]。管土相对刚度系数αs=Δs/Δp,Δp为管道的压缩变形量;Δs为管侧土体的压缩变形量。当αs > 1时, 属于刚性管道;当αs < 1时,属于柔性管道,然后依此确定管道的受力计算模型,如图 2所示。在计算Δp时,常忽略管周土体的弹性抗力,只考虑管顶均布垂直土压力的影响,同时假定管道底部地基竖向反力水平均匀分布,且与管顶土压力值相等,将管道看作无重材料,利用结构力学中超静定结构位移计算方法可得管顶竖向变形计算公式为:
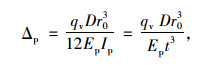
|
(5) |
|
| 图 2 结构计算模型示意图 Fig. 2 Schematic diagram of structure calculation model |
| |
式中,D=2r0;Ep为管道材料的弹性模量;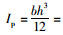
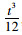
在相同的竖向压力作用下,管道两侧土体的竖向压缩变形量均为:
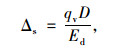
|
(6) |
式中,Ed为管周土体的综合变形模量,当为上埋式管涵方式修筑时,可采用土的变形模量Eh进行替代。
如果管顶平面内、外土柱压力相等,假设qv=γH,γ为土体的重度,H为涵洞顶部填土高度,则管土相对刚度系数αs为:
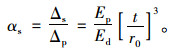
|
(7) |
式(7)为《规范》中计算地埋管道管土相对刚度系数计算公式,于是各种地下管道[6, 25-26]均将此公式作为设计依据,同时也被研究文献广泛引用。但是该公式存在如下不足:①在公式推导过程中,将管道的压缩变形与管侧土体的压缩变形分开考虑,没有将两者的相互影响考虑进去,且对管顶平面两侧土柱压力采用了相同的qv=γH,使得管道压缩变形计算结果偏大,导致计算出来的相对刚度系数αs偏小,在用其进行刚柔性判别时容易将刚性管涵定为柔性管涵,低估了管顶土压力,使管涵设计偏于不安全;②天然地基、垫层地基、有无基座、基座形式等对管道的变形影响很大,但公式中没有考虑;③管涵压缩变形的计算公式,是按结构力学中结构位移计算的方法,将管涵分解为上下两个三次超静定结构进行挠度计算,仅考虑了竖向挠度,而没有考虑在竖向压力下管侧壁的挠曲变形,也没有考虑土体的弹性抗力对侧壁的约束影响;④公式是针对无波纹的圆弧形薄钢板管涵或混凝土圆管涵情况,采用的是单位长度上的惯性矩: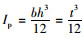
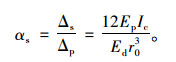
|
(8) |
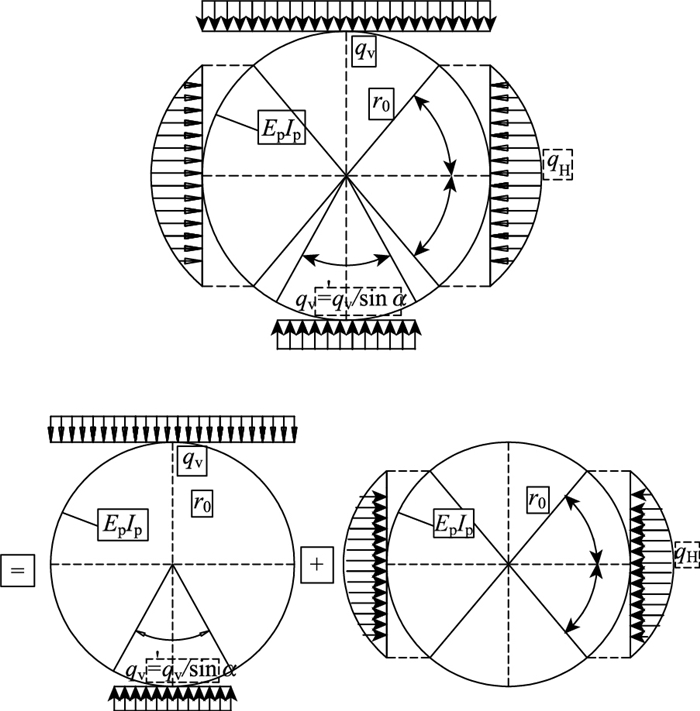
在考虑管涵侧向土体弹性抗力和基床形式对管道压缩变形影响的基础上,采用Spangler的管土相互作用模型进行分析,该模型假设[27]:作用于管顶的垂直荷载qv沿管道直径横向水平分布,作用于管底上的竖向反力沿基床宽度水平分布,作用于管道两侧的弹性抗力为抛物线分布,其最大压力qH等于管侧填土的被动土压力系数乘以管道水平挠度Δx的一半,管侧被动土压力圆心角为2β,基床包角为2α,计算模型如图 3所示。
|
| 图 3 Spangler管道计算模型示意图 Fig. 3 Schematic diagram of Spangler pipeline calculation model |
| |
在竖向压力作用下,受弯构件的挠度主要由弯曲变形产生,运用结构力学方法,对管顶、管底和管侧压力作用下的变形进行计算并叠加,得到管道的压缩变形Δp为:
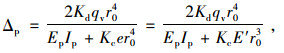
|
(9) |
式中,Kd,Kc分别为基床系数和侧压力系数。
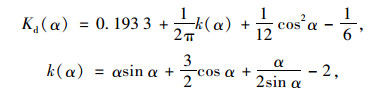
|
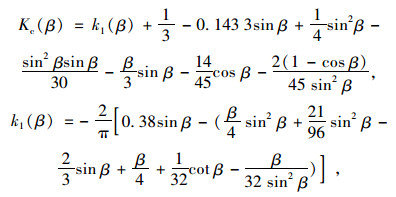
|
式中,r0,Ip,Ep的含义同前,e为管侧填土的弹性抗力系数;E′=er0,为管侧填土在管道侧向挠曲变形引起的侧压力作用下土的模量,故可用土的变形模量Eh来代替,而土的变形模量可由室内侧限压缩试验测得的压缩模量Es换算而得,如果没有试验依据时,可参照表 1取值,相关参数及意义参照文献[28]的取值标准。
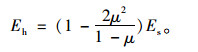
|
(10) |
| 土的类别 | 填土压实度/% | 85 | 90 | 95 | 100 |
| 原状土标准贯入垂击数N63.5 | 4 < N≤14 | 14 < N≤24 | 24 < N≤50 | > 50 | |
| 砾石、碎石 | 5 | 7 | 10 | 20 | |
| 细粒土含量少于12%的粗颗粒土,中粗砂,砂夹石,土夹石 | 3 | 5 | 7 | 14 | |
| 细粒土含量少于12%的粗颗粒土,中粗砂,黏质砂土粉砂 | 1 | 3 | 5 | 10 | |
| 中到无塑性的细颗粒土(WL < 50%),粗颗粒土含量不小于25%,无机黏土,粉土 | 1 | 2 | 5 | 10 | |
| 中到无塑性的细颗粒土(WL < 50%),粗颗粒土含量不小于25%,无机黏土与粉土混合土 | — | 1 | 3 | 7 | |
当2β=100°时,式(9)可换简化成
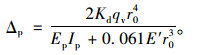
|
(11) |
此公式与Spangler的Iowa公式类似,Spangler认为填土的压实度会随着时间的推移而增加,埋设于地下的管道变形也会因此增大,故在式(9)中加入了一个变形延滞系数DL,可按管道两侧填土密实程度,取1.2~1.5;当设计要求管侧填土压实系数大于95%时,DL可取1.5,公式变换成:
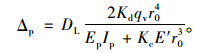
|
(12) |
在弹性力学中,对于平面应变问题,须将平面应力问题表达式中的弹性模量Ep换成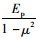
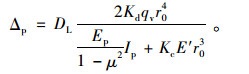
|
(13) |
对钢波纹管,公式中的惯性矩Ip可改为钢波纹管的惯性矩Ic,则
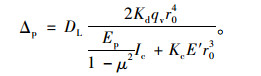
|
(14) |
将式(6)、(14)代入式(8)中,于是管土相对刚度系数为:
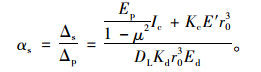
|
(15) |
假设E′和Ed同为管周填土的综合变形模量,对于上埋式涵洞(管道),可以认为其相等且为管侧土的变形模量Eh,于是:
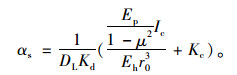
|
(16) |
若不考虑延滞系数,式(16)可改写为:
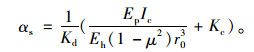
|
(17) |
如果考虑波纹管的环向刚度,则将式(4)代入式(16)可得
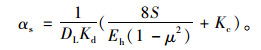
|
(18) |
如果不考虑变形延滞系数的影响,则上式可变换为:
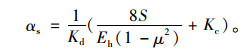
|
(19) |
式(19)计算结果相对于式(18)来讲是偏大的,对结构设计而言是偏于安全的。
将变形模量换成压缩模量,则上式变换为:
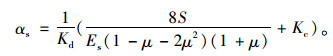
|
(20) |
| β/(°) | 40 | 50 | 60 | 70 | 80 | 90 |
| Kc | 0.055 | 0.061 | 0.066 | 0.068 | 0.069 | 0.070 |
| α/(°) | 0 | 15 | 30 | 45 | 60 | 75 | 90 |
| Kd | 0.11 | 0.108 | 0.103 | 0.096 | 0.089 | 0.085 | 0.083 |
1.5 钢波纹管涵现场试验与变形计算 1.5.1 钢波纹管涵现场试验
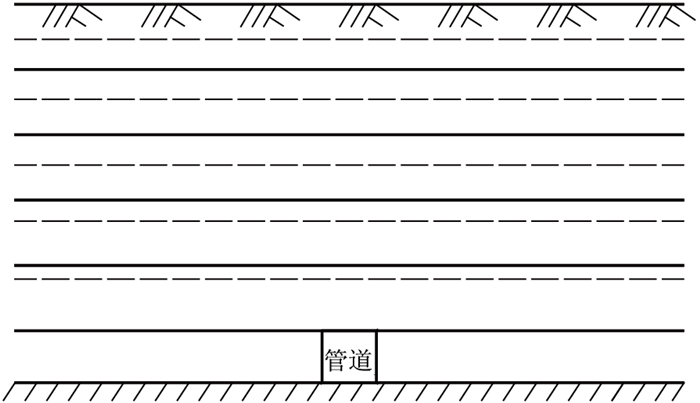
所选涵洞位于广陕广巴高速公路连接线LJ4标段K9+423,波纹管涵顶最大填方高度为11.7 m,管径为5.5 m,钢波纹板厚为6.5 mm,波形采用200 mm×55 mm;采用热轧镀锌钢板加工成型的Q345钢材,为防腐对管涵做了镀锌和刷沥青强化处理,涵洞施工采用波纹板现场吊装、螺栓拼接,总长度约为89.87 m,原地基位于沟谷稻田中,土质为软黏土,经碎石挤密桩加固处理后在局部形成复合地基,如图 4所示。

|
| 图 4 波纹管涵现场照片 Fig. 4 Field photos of steel corrugated pipe culvert |
| |
管涵纵向与路堤填方最高处的路面宽度相对应,沿涵周设置了4个土压力观测断面,其中A断面为不减荷断面,B,C,D断面为减荷断面,选用了钢弦式JXY-1型单膜土压力盒,每个断面布设了16个压力盒,共计64个压力盒,并对压力盒进行了位置编号;频率数据采集选用了QLA-2型钢弦式智能测频仪。
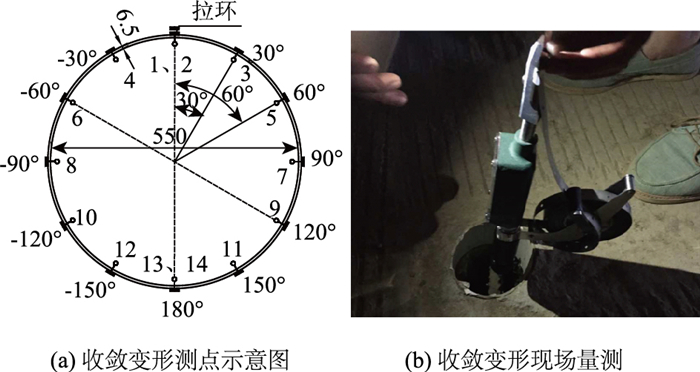
为了量测钢波纹管自身的变形,选用了SWJ-Ⅳ隧道收敛计,配合拉环与拉钩,在各试验段A,B,C和D断面依0°,30°,60°,90°,120°,150°方向过圆心沿对角线焊接布设对拉环,如图 5所示。
|
| 图 5 管涵收敛变形量测点位布置图 Fig. 5 Location layout of measuring points of pipe culvert convergent deformation |
| |
施工中的分层填筑高度增量采用水准仪测量。因试验内容较多,计算未涉及涵洞减荷及变形情况,故仅采用了A断面未减荷时的试验数据。
1.5.2 钢波纹管变形计算根据式(14),弹性抗力系数E′用变形模量Eh替换,不考虑变形延滞系数,公式变换为:
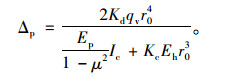
|
(21) |
结合工程实例计算钢波纹管涵洞的竖向变形量,算例基本参数:涵顶填土高度H为11.5 m,填料容重为21.5 kN/m3,管道或钢波纹管涵直径5.5 m,半径为2 750 mm,壁厚6.5 mm,钢材的弹性模量为200 000 MPa,式中Eh均采用土体的变形模量为12 MPa,钢波纹管的波距与波高为:200 mm×55 mm,根据式(3)计算得惯性矩为:2 875.411 mm4/mm,泊松比为0.3,Kc=0.061,Kd=0.089。
假设qv=γH,分别计算:涵侧土体变形模量为12 MPa不变情况下,涵洞在土柱压力作用下的涵洞竖向收敛变形计算值;涵侧土体变形模量以文献[31]中的计算过程随填高呈直线性增加的方式进行求解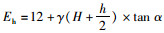
|
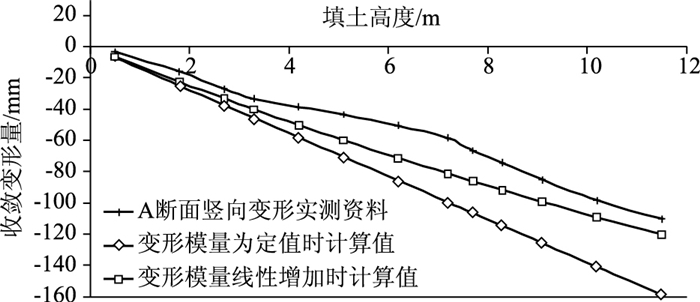
| 图 6 涵洞竖向收敛变形量随填高增加之变化曲线 Fig. 6 Curves of culvert vertical convergence deformation varying with filling height |
| |
实测的涵洞竖向收敛变形量并不是从零开始计算的,在涵洞侧向填筑过程中,土体对涵洞有水平向的挤压作用,涵洞竖直方向有鼓胀而形成竖向椭圆形,而涵洞竖向收敛变形在涵顶填高为零时的起始读数应为一正值,随着填高增加,椭圆形涵洞在竖向土压力作用下逐渐收敛至圆形,随着压力的增大,涵洞在水平方向对涵侧土体有鼓胀而形成水平向椭圆形。因此,实际上涵洞的收敛变形量需要减去初始的正值部分,并没有图 6中的变形量大,而图中公式计算值部分理论上仅考虑初始变形量为零时的情况。实测的涵洞收敛变形量为80.64 mm,收敛变形率1.47%。
从图 6可以看出:钢波纹管涵洞的竖向收敛变形量随着填土高度的增加而增大,其中当涵侧填筑土体的压缩变形模量为固定值时,收敛变形量计算值在填土后期较实测值增加快;当涵侧土体的压缩变形量为线性增加时,涵洞的收敛变形计算值与实测值较为一致,尤其是填土结束时变形量相差最小,理论计算结果与实测结果规律一致,基本能够满足工程建设中对涵洞收敛变形的预估计算,为设计与施工提供理论支撑。最终涵洞的竖向收敛变形量计算值分别为:158.75 mm,120.22 mm,与涵洞直径之比的变形率分别为:2.19%,1.96%。图 6中钢波纹管涵洞实测收敛变形量为110.20 mm,变形率为2.0%,均大于以零起算的涵洞的实测收敛变形率1.47%,所以涵洞受侧向土压力作用先竖向鼓起,后受竖向土压力作用收敛变形,抵消了一部分鼓起变形,有利于结构与土协调变形与受力。而且试验与计算结果值均小于各类规范规定[28-30]的3%或5%的变形率。结果表明:试验工点管涵的收敛变形满足规范要求,同时,在考虑涵侧填土变形模量随填高线性增加的基础上,所推导的理论公式可以计算管涵的收敛变形。
1.6 钢波纹管涵相对刚度系数算例分析计算参数与1.5节中所列保持一致,表 4表示采用不同公式后管土相对刚度系数随管径变化时的变化规律,表 5和表 6分别表示钢管或混凝土管管径与壁厚改变时采用式(7)计算的管土相对刚度系数变化规律,表 7表示钢波纹管涵壁厚不变管径变化时管土相对刚度系数的变化规律。
| 管壁厚度6.5 mm | 管涵直径/mm | ||||||
| 编号 | 管土相对刚度系数计算公式 | 250 | 500 | 1 000 | 2 000 | 2 750 | |
| 1 | 式(7) | 0.292 9 | 0.036 6 | 0.004 6 | 0.000 6 | 0.000 2 | |
| 2 | 式(8) | 36.805 3 | 4.600 7 | 0.575 1 | 0.071 9 | 0.027 7 | |
| 3 | 式(17) | 38.555 6 | 5.419 2 | 1.277 1 | 0.759 4 | 0.713 8 | |
| Ep=200 000 MPa, Ed=12 MPa | 壁厚/mm | |||||||
| 编号 | 管土相对刚度系数计算公式 | 管涵半径/mm | 5 | 10 | 50 | 100 | 200 | |
| 1 | 式(7) | 250 | 0.133 3 | 1.066 7 | 133.333 3 | 1 066.666 7 | 8 533.333 3 | |
| 2 | 500 | 0.016 7 | 0.133 3 | 16.666 7 | 133.333 3 | 1 066.666 7 | ||
| 3 | 1 000 | 0.002 1 | 0.016 7 | 2.083 3 | 16.666 7 | 133.333 3 | ||
| 4 | 2 000 | 0.000 3 | 0.002 1 | 0.260 4 | 2.083 3 | 16.666 7 | ||
| 5 | 2 750 | 0.000 1 | 0.000 8 | 0.100 2 | 0.801 4 | 6.411 2 | ||
| Ep=30 000 MPa, Ed=12 MPa | 壁厚/mm | |||||||
| 编号 | 管土相对刚度系数计算公式 | 管涵半径/mm | 5 | 10 | 50 | 100 | 200 | |
| 1 | 式(7) | 250 | 0.020 0 | 0.160 0 | 20.00 | 160.00 | 1 280.00 | |
| 2 | 500 | 0.002 5 | 0.020 0 | 2.50 | 20.00 | 160.00 | ||
| 3 | 1 000 | 0.000 3 | 0.002 5 | 0.312 5 | 2.50 | 20.00 | ||
| 4 | 2 000 | 0.000 0 | 0.000 3 | 0.039 1 | 0.312 5 | 2.50 | ||
| 5 | 2 750 | 0.000 0 | 0.000 1 | 0.015 0 | 0.120 2 | 0.961 7 | ||
| 管壁厚度6.5 mm | 钢波纹管惯性矩/(mm4·mm-1) | |||||||
| 编号 | 管土相对刚度系数计算公式 | 管涵半径/mm | 150×50 | 200×55 | 300×110 | 380×140 | 400×150 | |
| 2 428.6 | 2 875.4 | 12 978 | 19 740 | 22 841 | ||||
| 1 | 式(8) | 250 | 31.086 | 36.805 | 166.13 | 252.675 | 292.367 | |
| 500 | 3.885 8 | 4.600 6 | 20.766 | 31.584 3 | 36.545 9 | |||
| 1 000 | 0.485 7 | 0.575 1 | 2.595 8 | 3.948 0 | 4.568 2 | |||
| 2 000 | 0.060 7 | 0.071 9 | 0.324 5 | 0.493 5 | 0.571 0 | |||
| 2 750 | 0.023 4 | 0.027 7 | 0.124 8 | 0.189 8 | 0.219 7 | |||
| 2 | 式(17) | 250 | 32.671 | 38.555 | 171.622 | 260.67 | 301.51 | |
| 500 | 4.683 6 | 5.419 1 | 22.053 | 33.184 | 38.289 | |||
| 1 000 | 1.185 2 | 1.277 1 | 3.356 3 | 4.747 7 | 5.385 8 | |||
| 2 000 | 0.747 9 | 0.759 4 | 1.019 3 | 1.193 2 | 1.272 9 | |||
| 2 750 | 0.709 4 | 0.713 8 | 0.813 8 | 0.880 7 | 0.911 4 | |||
从表 4可以看出,当管涵壁厚为6.5 mm时,管土相对刚度系数随着管涵半径的增加而减小,变化幅值较大,且与管涵半径的三次方成反比。由此可知,管涵半径对管土相对刚度系数的影响最大。另外,从表中数据还可以看出,式(17)不但考虑了惯性矩的变化,而且考虑了管侧土体的抗力影响,其可用于普通管涵的管土相对刚度系数进行计算,也可用于钢波纹管涵的管土相对刚度系数计算;且式(17)较式(8)计算得的管土相对刚度系数要大一些;现场试验中所用钢波纹管涵的半径为2 750 mm,表中计算的相对刚度为0.713 8,其值小于1.0,故此管涵为柔性涵洞,同时试验测得的垂直土压力约为0.9土柱压力,故此也可以判定此涵洞在垂直土压力作用下为柔性管涵,所以,此值也与柔性涵洞标准相互验证。虽然式(7)或式(8),也可得到涵洞为柔性涵洞,但是其相对刚度系数非常小,表明管涵柔性很大,这与实际情况有一定的差距,实际情况是管涵虽然是柔性涵洞但具有相当的承担土压力的能力。
表 5与表 6表明:管涵壁厚越厚其相对刚度系数越大,直径越大其相对刚度系数越小;同时,钢材的弹性模量为200 000 MPa,C30混凝土的弹性模量为30 000 MPa,由于材料性质的不同,造价与施工工艺的不同,其使用范围也各有一定的限制。通常钢管涵直径小于2 m,管壁较薄,大多小于20 mm,多属柔性管;而混凝土管涵壁较厚,多在50 mm~300 mm范围,公路中使用的管径多在0.5 m~2.5 m范围,这样才能确保管涵为刚性管。
从表 7可以看出,管土相对刚度系数随着管径的增大而减小,也随着钢波纹管的惯性矩的增大而增大;直径相同的波纹管,由于惯性矩的增大,管土相对刚度系数可以小于1.0,也可能大于1.0,即可以由柔性管变为刚性管。同样,惯性矩相同的波纹管,因直径的变化,也可以由柔性管变为刚性管。
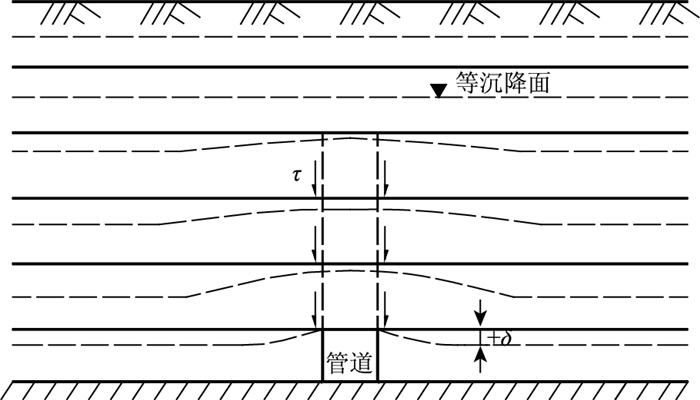
2 应用高填方刚性涵洞减荷技术对涵土相对刚度进行判定对于高填方大直径的波纹管涵,当填土由低到高变化时,管涵将显示出由刚性向柔性的转化过程,及其最终垂直土压力计算模型的确定,可用涵顶平面内外土柱沉降差±δ这一参数分析判定,其原理如图 7~图 9所示,对于未减荷的涵洞,垂直土压力系数可表示为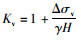
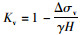
|
| 图 7 平埋式涵洞不减荷受力图 Fig. 7 Force diagram of flat buried culvert without loading reduction |
| |
|
| 图 8 上埋式涵洞不减荷受力图 Fig. 8 Force diagram of positive buried culvert without loading reduction |
| |
|
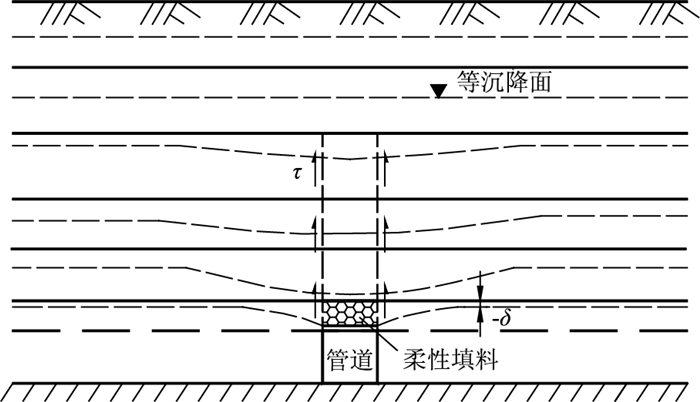
| 图 9 上埋式涵洞减荷受力图 Fig. 9 Force diagram of positive buried culvert with loading reduction |
| |
因此,根据以上减荷技术原理,针对高填方涵洞,当δ > 0时,引起涵顶产生附加应力者,均属于刚性涵洞;若不采用减荷措施,如果涵洞自身的压缩变形量大于两侧填土的压缩变形时,此类情况当然满足δ < 0的条件,此时涵顶垂直土压力小于土柱压力,此类涵洞均属于柔性涵洞。
针对未采取减荷措施的涵洞,不考虑柔性材料的影响,仅考虑涵洞结构本身,实际上根据涵土相对刚度系数公式αs =Δs/Δp可知,αs是与单位1.0相比较后来判定涵洞刚柔性的,此时,当αs=Δs/Δp > 1时,即δ=Δs-Δp > 0,为+δ的情况;当αs=Δs/Δp < 1时,即δ=Δs-Δp < 0,为-δ的情况。由此可知,沉降差±δ与涵土相对刚度系数αs是相统一的,均可以用来判定涵洞的刚柔性,当计算或量测得到+δ时为刚性涵洞,当计算或量测得到-δ时为柔性涵洞。故此,±δ又反映涵顶填土压力,可以延伸应用垂直土压力大小与土柱压力相比较或垂直土压力系数来判定涵洞的刚柔性。
3 结论(1) 在考虑涵侧填土变形模量随填高线性增加的基础上,通过涵土相互作用模型推导的管涵变形计算公式,得到的管涵收敛变形计算值变化规律与试验实测计算规律基本一致,验证了理论公式计算的有效性。
(2) 推导的高填方钢波纹管涵涵土相对刚度系数计算公式,得到试验管涵的相对刚度系数为0.713 8,小于1.0,将其判定为柔性涵洞;同时试验测得的垂直土压力约为0.9倍的土柱压力,故此也可以判定此涵洞在垂直土压力作用下为柔性管涵,由此验证了计算公式的可行性。
(3) 对涵土相对刚度系数理论计算公式进行变换,可得涵顶平面内外土柱沉降差±δ与涵土相对刚度系数αs本质上是相通的,故可用±δ对涵土相对刚度进行判定,依此确定为刚性涵洞或柔性涵洞,这为判定管涵的刚柔性又提供了一个新的计算途径。
| [1] |
顾安全. 上埋式管道垂直土压力的研究[D]. 西安: 陕西工业大学, 1963: 50-50. GU An-quan. Research of Vertical Earth Pressure on Buried Pipeline[D]. Xi'an: Shaanxi University of Technology, 1963: 50-50. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=ytgc198101000&dbname=CJFD&dbcode=CJFQ |
| [2] |
曾国熙. 土坝下管道竖向土压力的计算[J]. 浙江大学学报, 1960, 4(1): 79-97. ZENG Guo-xi. Calculation of Vertical Soil Pressure on Pipeline under an Earth Dam[J]. Journal of Zhejiang University, 1960, 4(1): 79-97. |
| [3] |
林选青. 高填土下结构物的竖向土压力及结构设计计算方法[J]. 土木工程学报, 1989, 22(4): 27-37. LIN Xuan-qing. Calculation Method of Vertical Earth Pressure and Structure of Constructions under High Earth Embankment[J]. China Civil Engineering Journal, 1989, 22(4): 27-37. |
| [4] |
田文铎. 地下管垂直土压力计算探讨[J]. 水利水电技术, 1994, 24(3): 9-13. TIAN Wen-duo. A Discussion on Computation of Vertical Soil Pressure Acting on Buried Pipes[J]. Water Conservancy and Hydropower Technology, 1994, 24(3): 9-13. |
| [5] |
刘全林, 杨敏. 上埋式管道上竖向土压力计算的探讨[J]. 岩土力学, 2001, 22(2): 214-218. LIU Quan-lin, YANG Min. Study of Vertical Soil Pressure on Positive Buried Pipeline[J]. Rock and Soil Mechanics, 2001, 22(2): 214-218. |
| [6] |
GB 50332-2002, 给水排水工程管道结构设计规范[S]. GB 50332-2002, Structural Design Code for Pipeline Water Supply and Waste Water Engineering[S]. |
| [7] |
温特科恩H F, 方晓阳. 基础工程手册[M]. 北京: 中国建筑工业出版, 1983. WINTER COHN H F, FANG Xiao-yang. Basic Engineering Manual[M]. Beijing: China Architecture & Building Press, 1983. |
| [8] |
KJARTANSON B H, HEILERS G A, LOHNES R A, et al. Soil-structure Interaction Analysis of Longitudinal Uplift of Culverts[J]. Journal of Geothchnical and Geoenvironmental Engineering, 1998, 124(2): 128-139. |
| [9] |
TRICKEY S A, MOORE I D, ASCE M. Three-dimensional Response of Buried Pipes under Circular Surface Loading[J]. Journal of Geothchnical and Geoenvironmental Engineering, 2007, 133(2): 219-223. |
| [10] |
SATGAND S, MASADA T, MORELAND A. Measured Field Performance and Computer Analysis of Large-diameter Multiplate Steel Pipe Culvert Installed in Ohio[J]. Journal of Performance of Constructed Facilities, 2008, 22(6): 391-397. |
| [11] |
YEAU K Y, SEZEN H, FOX P J. Load Performance in Situ Corrugated Steel Highway Culverts[J]. Journal of Performance of Constructed Facilities, 2009, 23(1): 32-39. |
| [12] |
American Iron and Steel Institute. Modern Sewer Design[M]. 4th ed. Washington, D. C.: American Iron and Steel Institute, 1999, 251-270.
|
| [13] |
CAN/CSA-S6-06, Canadian Highway Bridge Design Code[S].
|
| [14] |
李祝龙. 公路钢波纹管涵洞设计与施工技术研究[D]. 西安: 长安大学, 2006. LI Zhu-long. Study on Design and Construction Technology of Steel Corrugated Pipe Culvert for Highway[D]. Xi'an: Chang'an University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-11941-2006163392.htm |
| [15] |
李祝龙. 公路钢波纹管涵洞设计与施工技术[M]. 北京: 人民交通出版社, 2007. LI Zhu-long. Design and Construction Technology of Corrugated Pipe Culvert in Highway[M]. Beijing: China Communications Press, 2007. |
| [16] |
季文玉. 金属波纹管涵洞受力行为理论分析与计算分析[D]. 北京: 北京交通大学, 2004. JI Wen-yu. Theoretical Analysis and Calculation Analysis of Stress Behavior of Metal Corrugated Pipe Culvert[D]. Beijing: Beijing Jiaotong University, 2004. |
| [17] |
方亚非, 温学钧. 埋置式波纹钢板管结构的计算方法比较[J]. 城市道桥与防洪, 2007(5): 126-129. FANG Ya-fei, WEN Xue-jun. Comparison of Calculation Methods for Embedded Corrugated Sheet Pipe Structure[J]. Urban Roads Bridges and Flood Control, 2007(5): 126-129. |
| [18] |
王艳丽, 李祝龙, 吴大中. 钢波纹管涵洞的薄壳效应[J]. 公路交通科技, 2008, 25(5): 86-90. WANG Yan-li, LI Zhu-long, WU Da-zhong. Thin Shell Effect of Corrugated Steel Culvert Performance[J]. Journal of Highway and Transportation Research and Development, 2008, 25(5): 63-67. |
| [19] |
彭立, 张阳, 穆程, 等. 高填土大跨钢波纹管涵力学性能分析与测试[J]. 中外公路, 2016, 36(6): 103-108. PENG Li, ZHANG Yang, MU Cheng, et al. Mechanical Analysis and Test of High-filling Large Span Steel Corrugated Pipe Culvert[J]. Journal of China & Foreign Highway, 2016, 36(6): 103-108. |
| [20] |
朱旭阳, 何欢, 高文学, 等. 大直径钢波纹管管顶土压力分析[J]. 中外公路, 2015, 35(4): 39-43. ZHU Xu-yang, HE Huan, GAO Wen-xue, et al. Analysis on Earth Pressure on Large Diameter Steel Corrugated Pipe[J]. Journal of China & Foreign Highway, 2015, 35(4): 39-43. |
| [21] |
张允海, 曾水生, 郝铁宝. 大直径高填方钢波纹管涵洞现场试验分析[J]. 公路, 2015(6): 19-25. ZHANG Yun-hai, ZENG Shui-sheng, HAO Tie-bao. Experimental Analysis of Large Diameter Steel Corrugated Pipe Culvert under High filling[J]. Highway, 2015(6): 19-25. |
| [22] |
赵中连, 王志刚. 散拼大直径钢波纹管涵回填变形的观测与分析[J]. 施工技术, 2015, 44(增2): 204-208. ZHAO Zhong-lian, WANG Zhi-gang. Monitoring and Analysis of Backfill Deformation of Large-diameter Steel Corrugated Pipe Culvert[J]. Construction Technology, 2015, 44(S2): 204-208. |
| [23] |
张敏, 李百建. 波纹钢板截面几何性质计算[J]. 科学技术与工程, 2012, 12(10): 2400-2403. ZHANG Min, LI Bai-jian. Geometrical Properties Calculation of the Corrugated Steel Plate Section[J]. Science Technology and Engineering, 2012, 12(10): 2400-2403. |
| [24] |
张玉川. 塑料管环向刚度的定义、标准、选择和实现[J]. 塑料, 2002, 31(1): 50-57. ZHANG Yu-chuan. Definitions, Standards, Selections and Realization of Ring Stiffness for Plastics Pipes[J]. Plastics, 2002, 31(1): 50-57. |
| [25] |
中交第一公路勘察设计院有限公司. 公路桥涵施工手册[M]. 北京: 人民交通出版社, 2000. CCCC First Highway Engineering Co., Ltd. Construction Manual of Highway Bridge and Culvert[M]. Beijing: China Communications Press, 2000. |
| [26] |
JTG/T D65-04-2007, 公路涵洞设计细则[S]. JTG/T D65-04-2007, Guidelines for Design of Highway Culvert[S]. |
| [27] |
邓道明, 李育光. 埋地柔性管道的应力和变形分析[J]. 油气储运, 1998, 17(6): 11-15. DENG Dao-ming, LI Yu-guang. Analysis on Stress and Distortion of Buried Flexible Pipeline[J]. Oil & Gas Storage and Transportation, 1998, 17(6): 11-15. |
| [28] |
CECS 122-2001, 埋地硬聚氯乙烯排水管道工程技术规程[S]. CECS 122-2001, Technical Specification for Buried PVC-U Pipeline for Sewer Engineering[S]. |
| [29] |
GB 50251-2015, 输气管道工程设计规范[S]. GB 50251-2015, Code for Design of Gas Transmission Pipeline Engineering[S]. |
| [30] |
DB 15/T 654-2013, 公路波纹管(板)桥涵设计与施工规范[S]. DB 15/T 654-2013, Specifications for Design and Construction of Corrugated Steel Pipe and Plate for Highway Bridges and Culverts[S]. |
| [31] |
顾安全. 上埋式管道及洞室垂直土压力的研究[J]. 岩土工程学报, 1981, 3(1): 3-15. GU An-quan. Investigation of the Vertical Earth Pressure on Projecting Conduit and Underground Chamber under a High Embankment[J]. Chinese Journal of Geotechnical Engineering, 1981, 3(1): 3-15. |
 2018, Vol. 35
2018, Vol. 35
