扩展功能
文章信息
- 凌立鹏, 唐亮
- LING Li-peng, TANG Liang
- 钢桥面板顶板-U肋焊接接头热点应力的精细有限元分析
- Refined Finite Element Analysis on Hot Spot Stresses of Deckplate-U-rib Weld Joints in Steel Bridge Deck
- 公路交通科技, 2018, 35(4): 58-66
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(4): 58-66
- 10.3969/j.issn.1002-0268.2018.04.008
-
文章历史
- 收稿日期: 2016-11-30
2. 中交公路规划设计院有限公司, 北京 100088
2. CCCC Highway Consultants Co., Ltd., Beijing 100088, China
在国内外大跨径桥梁结构中,正交异性钢桥面板(简称“钢桥面板”)凭借重量轻、承载能力大、工厂化程度高、施工速度快、结构造型美观等优点而被广泛采用[1-3]。但由于本身应力状况复杂且存在不可避免的焊接缺陷,在车辆荷载的反复直接作用下,各焊接接头处极易萌生各类疲劳裂纹[4-6]。其中,出现最多且危害最大的一类就是顶板-U肋焊接接头的疲劳问题,具体表现为分别萌生于顶板焊趾、焊根和肋板焊趾、焊根的疲劳裂纹C.1~C.4[7-8],如图 1所示。
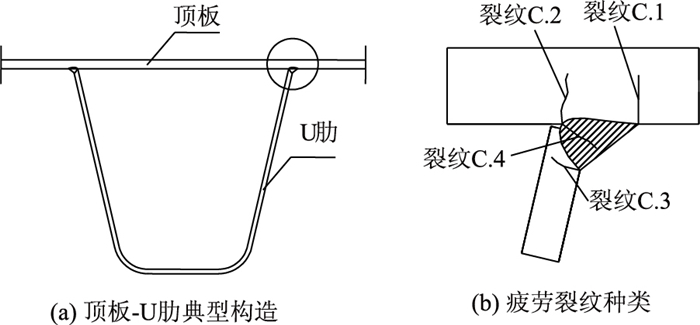
|
| 图 1 顶板-U肋焊接接头的疲劳裂纹示意图 Fig. 1 Schematic diagram of fatigue cracks in deckplate-U-rib weld joints |
| |
在钢桥面板疲劳性能的评估方法中,名义应力法应用最广,通常忽略焊接接头引起的局部应力集中,以距离焊接接头较远处的某点应力来名义上代表焊接接头等处的疲劳应力,因而不能有效反映焊接接头附近的真实应力特征且细节分类繁多[10]。而热点应力法采用距焊趾固定位置的外推点插值得到焊接接头焊趾等处的疲劳应力,考虑了焊接接头几何尺寸引起的应力集中特征且应用相对便利[11],因而近年来越来受到关注。而其他评定方法虽然概念上能更好地反映疲劳应力特征,但在实际应用过程较为复杂[13-15]。
对此,本研究以广东虎门二桥坭洲水道桥标准梁段钢桥面板为例,基于有限元软件ANSYS建立的参数化热点应力精细有限元分析模型,对顶板-U肋焊接接头热点应力受顶板厚度、熔透率、组装间隙等参数的影响进行了精细有限元分析,并基于一种新兴的U肋内焊技术,即将传统的顶板-U肋单面焊接接头发展为双面焊接头,通过扩展上述参数化热点应力精细有限元分析模型,对采用U肋内焊技术后的顶板-U肋焊接接头热点应力的变化及受熔透率、内焊趾高度、内焊趾角度等参数的影响进行了精细有限元分析,以为今后U肋内焊技术在正交异性钢桥面板结构的工程应用提供一些合理化建议。
1 参数化热点应力精细有限元分析模型已知虎门二桥坭洲水道桥钢桥面标准梁段(B梁段)实腹式横隔板的间距为3 200 mm,顶板U肋上口宽300 mm,下口宽170 mm,高280 mm,U肋中心距600 mm,纵U肋厚8 mm,顶板在外侧重车道厚18 mm,内侧快车道厚16 mm,标准横隔板板厚10 mm,吊索处加厚为14 mm。该钢桥面结构在我国应用较多,具有广泛的代表性。为尽可能获得实桥钢桥面板顶板-U肋焊接接头的实际应力分布,设计如图 2所示的钢桥面板模型,计算中约束所有横隔板翼缘底部自由度[16]。
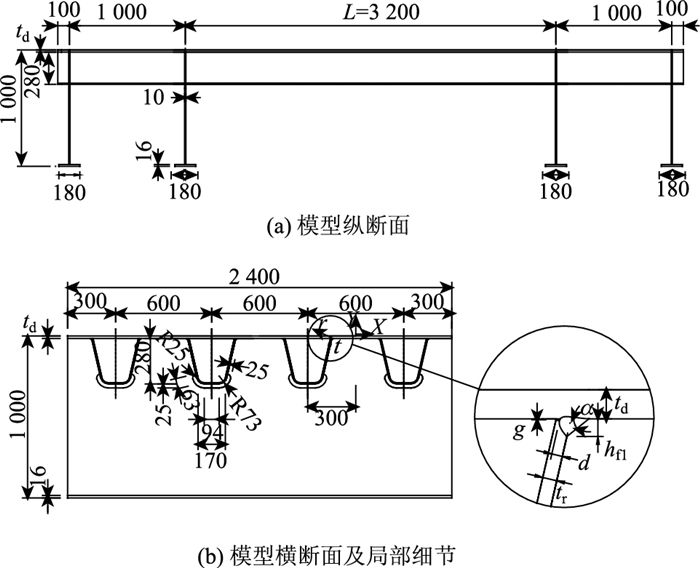
|
| 图 2 钢桥面板模型(单位:mm) Fig. 2 Steel bridge deck model (unit:mm) |
| |
已知图 2中,X-Y为描述顶板的直角坐标系,t-r为描述U肋的曲线坐标系,td表示顶板厚度,g表示组装间隙,α表示焊趾角度,hf1表示焊趾高度,d表示熔透深度,tr表示肋板厚度。
关注目标位置位于纵桥向中跨跨中(Z=L/2)与3号U肋交叉位置的顶板-U肋焊接接头,加载方式参考《公路桥涵设计通用规范》(JTG D60-2015)中的车辆双轮胎轴载及顶板-U肋接头处各应力影响线[8],采用在3、4号U肋间的正上方加载,加载大小为70 kN,加载宽度和长度为600 mm×200 mm(未考虑桥面铺装层的荷载分布),如图 3所示。
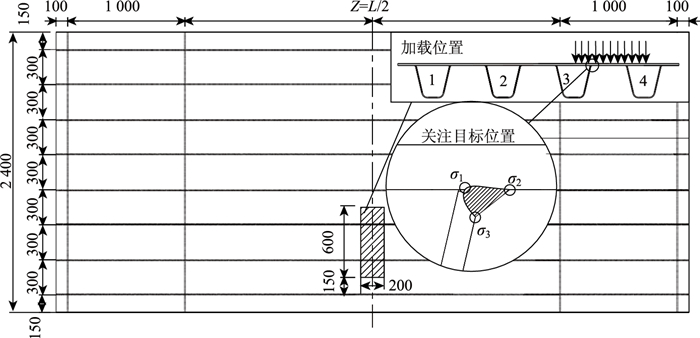
|
| 图 3 加载位置及关注目标位置(单位:mm) Fig. 3 Loading position and concerned target position(unit:mm) |
| |
已知图 3中,σ1沿X方向的应力分量σ1_x为控制顶板焊根萌生疲劳裂纹C.2的热点应力,σ2沿X方向的应力分量σ2_x为控制顶板焊趾萌生疲劳裂纹C.1的热点应力,σ3点沿t方向的应力分量σ3_t为控制肋板焊趾、焊根萌生疲劳裂纹C.3、C.4的热点应力[17-18]。上述热点应力采用国际焊接协会(International Institute of Welding,IIW)推荐的热点应力法计算得到,即根据距离焊趾0.4t和1.0t(t为板厚)位置的应力分量线性插值得到。
在有限元软件ANSYS上,基于APDL编程语言建立可变参数包括顶板厚度td、肋板厚度tr、组装间隙g、焊趾角度α、焊趾高度hf1和熔透率(d/tr)的热点应力有限元分析模型,其中,有限单元采用20节点实体单元Solid95,关注目标位置的网格精度采用1 mm[11],具体建模过程如图 4所示。
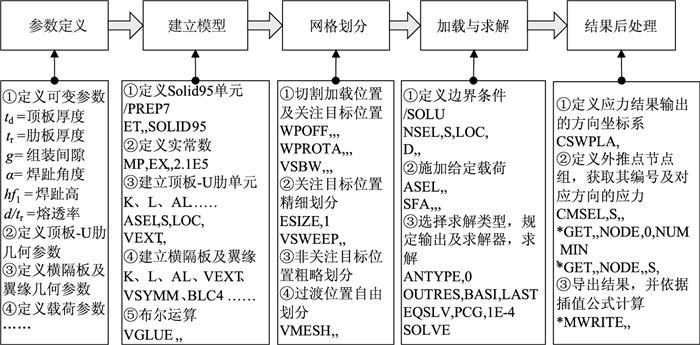
|
| 图 4 建模过程 Fig. 4 Modeling process |
| |
参考虎门二桥坭洲水道桥钢桥面板,可变参数取td=16 mm,tr=8 mm,g=0.5 mm,α=40°,hf1=8 mm,d/tr=0.8时,建立的精细有限元模型如图 5所示,共有236 842个单元,并将其作为基准参数模型。单元尺寸的敏感性测试表明,关注目标位置的网格精度由1.2 mm逐步减小到0.8 mm,热点应力计算结果的变化在1%范围以内,说明已收敛。
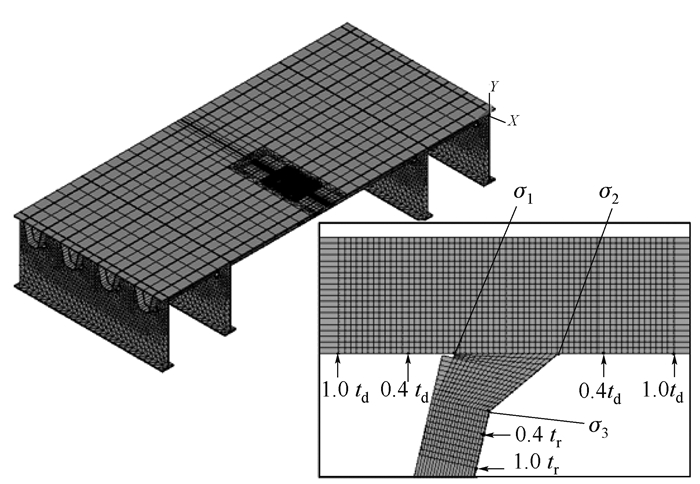
|
| 图 5 精细有限元模型 Fig. 5 Refined finite element model |
| |
2 热点应力的精细有限元分析 2.1 顶板厚度分析
依次改变基准参数模型中的顶板厚度参数td为12, 14, 18 mm和20 mm,计算得到不同位置热点应力大小,如图 6所示。
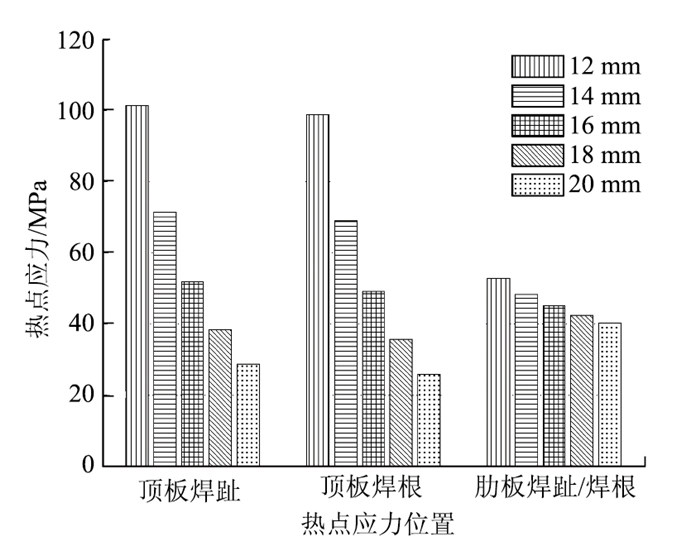
|
| 图 6 随顶板厚度变化的热点应力 Fig. 6 Hot spot stress varying with deck thickness |
| |
图 6中计算结果表明:
(1) 顶板厚度由16 mm增加到18,20 mm,顶板焊趾、焊根热点应力降低约26%,28%和45%,47%,肋板焊趾、焊根热点应力降低约6%, 11%。
(2) 顶板厚度由16 mm减小到14,12 mm,顶板焊趾、焊根热点应力增加约38%,40%和96%,101%,肋板焊趾、焊根热点应力增加约7%、17%。
2.2 肋板厚度分析依次改变基准参数模型中的肋板厚度参数tr为6 mm和10 mm,计算得到不同位置热点应力大小,如图 7所示。
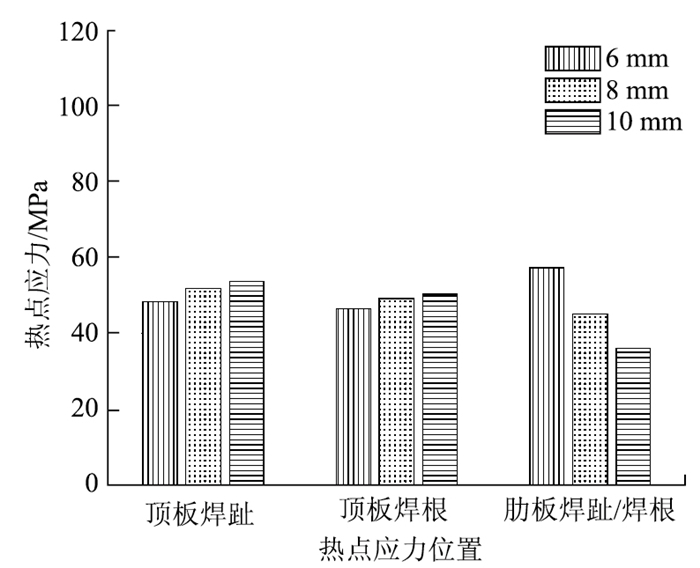
|
| 图 7 随肋板厚度变化的热点应力 Fig. 7 Hot spot stress varying with rib thickness |
| |
图 7中的计算结果表明:
(1) 肋板厚度由8 mm增加到10 mm,肋板焊趾、焊根热点应力降低约20%,而顶板焊趾、焊根热点应力增加约2%、4%。
(2) 肋板厚度由8 mm减小到6 mm,顶板焊趾、焊根热点应力幅减小约5%,7%,肋板焊趾、焊根热点应力增加约27%。
2.3 熔透率分析依次改变基准参数模型中熔透率参数d/tr为0%(角焊缝),30%,50%,60%,70%,80%和100%(全熔透),计算得到不同位置的热点应力大小,如图 8所示。
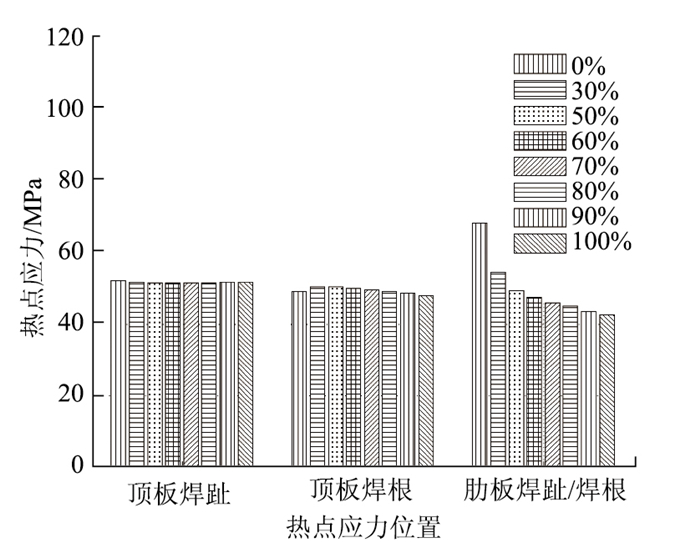
|
| 图 8 随熔透率变化的热点应力 Fig. 8 Hot spot stress varying with penetration rate |
| |
图 8中的计算结果表明:
(1) 随熔透率的变化,顶板焊趾、焊根热点应力变化最大在3%以内,表明顶板焊趾、焊根热点应力基本不受熔透率变化的影响。
(2) 熔透率由60%增加到80%和100%(全熔透),肋板焊趾、焊根热点应力降低约6%,10%。
(3) 熔透率由60%减小到30%和0%(角焊缝),肋板焊趾、焊根热点应力增加约14%和43%。
2.4 组装间隙分析为全面分析组装间隙参数g,在三种不同熔透率下,依次改变基准参数模型中组装间隙参数g为0.5,1.0,1.5,2.5 mm和3.5 mm,计算得到不同位置热点应力大小,如图 9所示。
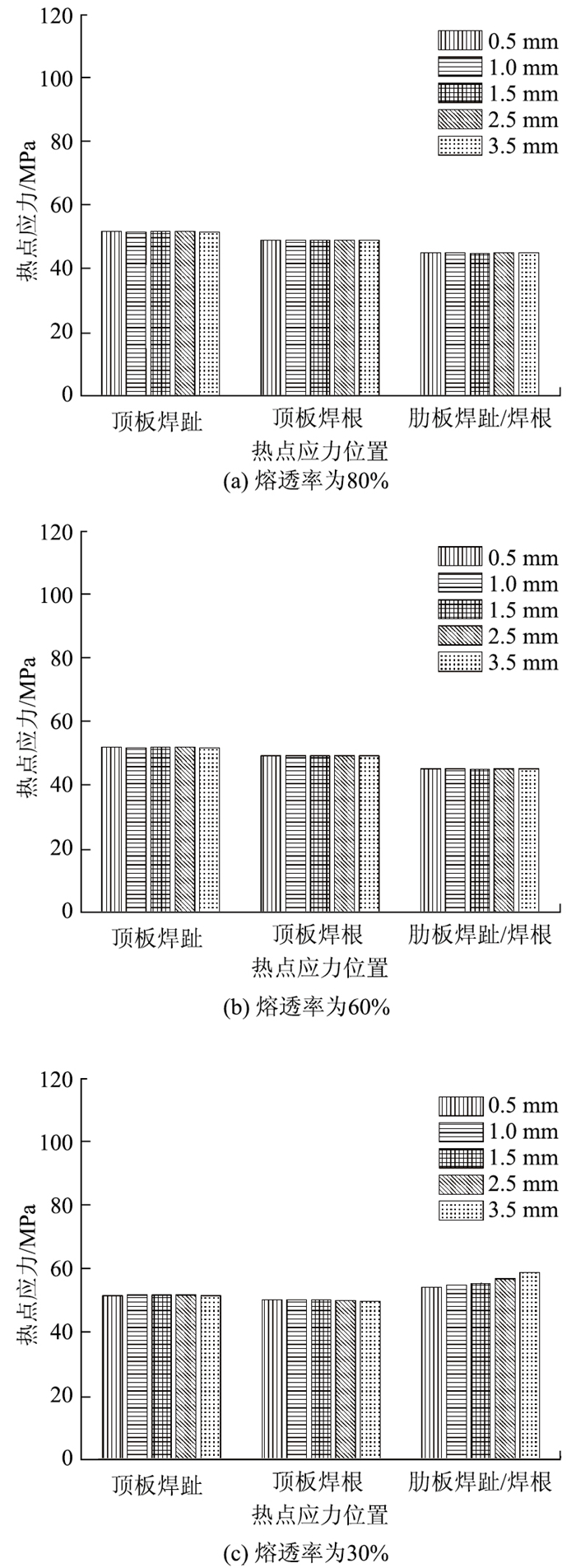
|
| 图 9 随组装间隙变化的热点应力 Fig. 9 Hot spot stress varying with assembly gap |
| |
图 9中的计算结果表明:
(1) 熔透率为60%,80%时,组装间隙由0.5 mm增加到3.5 mm,各热点应力变化最大在2%以内。
(2) 熔透率为30%时,组装间隙由0.5 mm增加到3.5 mm,肋板焊趾、焊根热点应力增加约9%。
2.5 焊趾高度分析依次改变基准参数模型中焊趾高度参数hf1为6 mm和10 mm,计算得到不同位置热点应力大小,如图 10所示。
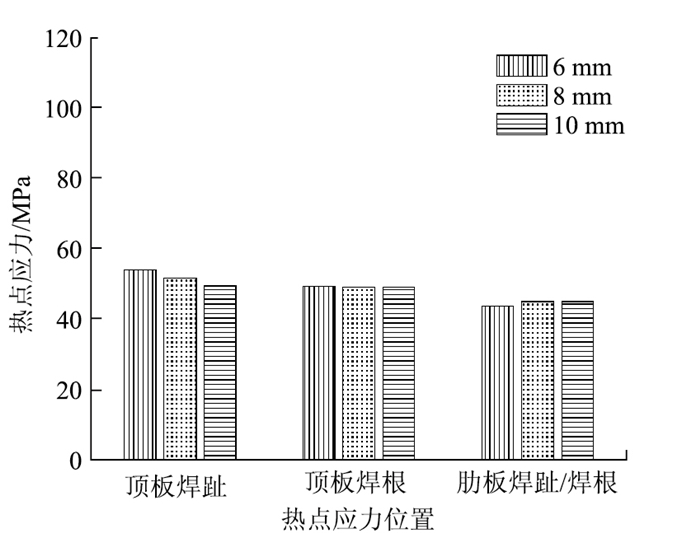
|
| 图 10 随焊趾高度变化的热点应力 Fig. 10 Hot spot stress varying with height of weld toe |
| |
图 10中的计算结果表明:
(1) 随焊趾高度的变化,顶板焊根热点应力变化最大在1%以内,表明顶板焊根热点应力基本不受焊趾高度变化的影响。
(2) 焊趾高度由8 mm减小到6 mm,顶板焊趾热点应力增加约4%,肋板焊趾、焊根热点应力降低约3%。
(3) 焊趾高度由8 mm增加到10 mm,顶板焊趾热点应力幅减小约4%,肋板焊趾、焊根热点应力变化最大在1%以内。
2.6 焊趾角度分析依次改变有基准参数模型中焊趾角度参数α为30°,35°,45°,50°和60°,计算得到不同位置热点应力,如图 11所示。
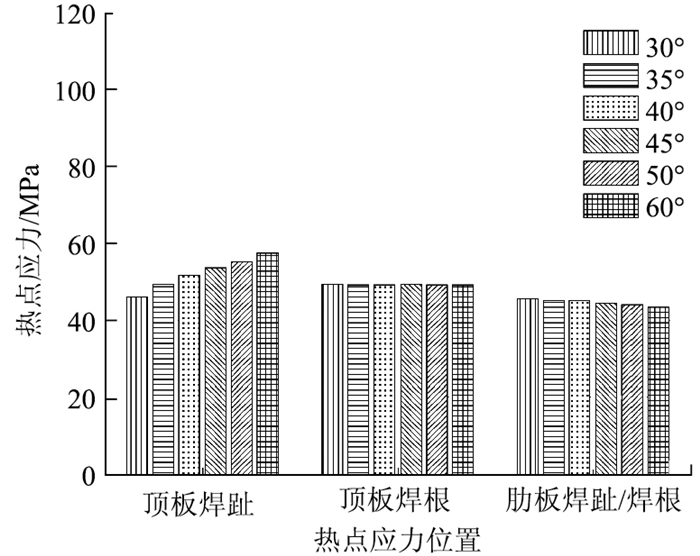
|
| 图 11 随焊趾角度变化的热点应力 Fig. 11 Hot spot stress varying with angle of weld toe |
| |
图 11中的计算结果表明:
(1) 随焊趾角度的变化,顶板焊根热点应力变化最大在1%以内。
(2) 焊趾角度由40°减小到30°,顶板焊趾热点应力幅减小约11%,肋板焊趾、焊根热点应力幅增加约3%。
(3) 焊趾角度由40°增加到60°,顶板焊趾热点应力幅增大约11%,肋板焊趾、焊根热点应力幅减小约4%。
3 一种新型双面焊接头的热点应力分析最近,武汉两家公司联合开发了一种U肋内焊技术,将传统的顶板-U肋单面焊接接头发展为双面焊接头,具体如图 12所示。
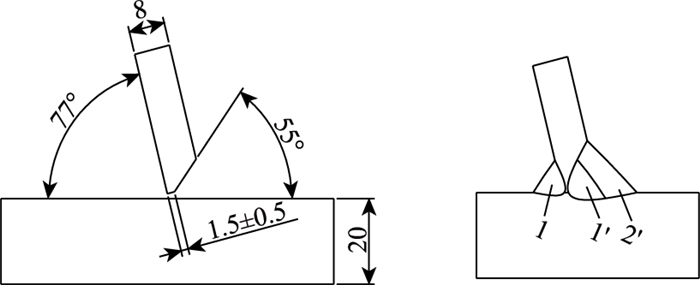
|
| 图 12 U肋内焊技术示意图 Fig. 12 Schematic diagram of U-rib internal welding technology |
| |
从理论上分析,采用该U肋内焊技术后,原顶板焊根和肋板焊根的疲劳性能将得到大幅提高,顶板-U肋焊接接头将不再易萌生疲劳裂纹C.2和C.4,但与此同时,新引入的内焊缝也可能导致萌生新的疲劳裂纹C.2N和C.4N,具体如图 13所示。
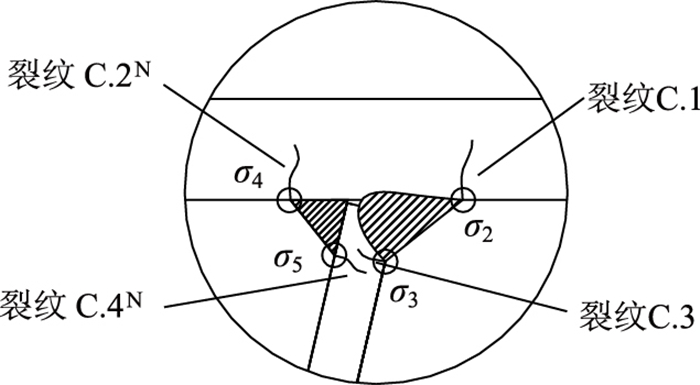
|
| 图 13 新型双面焊接头的疲劳裂纹示意图 Fig. 13 Schematic diagram of fatigue cracks in new double-sided welded joint |
| |
对此,扩展上述参数化热点应力精细有限元模型,新定义内焊焊趾角度参数β和内焊焊趾高度参数hf2,将σ4沿X方向的应力分量σ4_x作为控制顶板焊根萌生疲劳裂纹C.2N的热点应力,σ5沿t方向的应力分量σ5_t作为控制顶板焊趾萌生疲劳裂纹C.4N的热点应力。共计算完成如表 1所示的10种不同双面焊接头的热点应力分析,具体如图 14和表 1所示。
| 编号 |
td/ mm |
tr/ mm |
d/tr |
g/ mm |
α/ (°) |
hf1/ mm |
β/ (°) |
hf2/ mm |
| A | 16 | 8 | 80% | 0.5 | 40 | 8 | 40 | 6 |
| B | 16 | 8 | 100% | 0.5 | 40 | 8 | 40 | 6 |
| C | 16 | 8 | 60% | 0.5 | 40 | 8 | 40 | 6 |
| D | 16 | 8 | 80% | 0.5 | 40 | 8 | 40 | 8 |
| E | 16 | 8 | 80% | 0.5 | 40 | 8 | 40 | 4 |
| F | 16 | 8 | 80% | 0.5 | 40 | 8 | 30 | 6 |
| G | 16 | 8 | 80% | 0.5 | 40 | 8 | 50 | 6 |
| H | 18 | 8 | 80% | 0.5 | 40 | 8 | 40 | 6 |
| J | 16 | 6 | 80% | 0.5 | 40 | 8 | 40 | 6 |
| K | 16 | 10 | 80% | 0.5 | 40 | 8 | 40 | 6 |
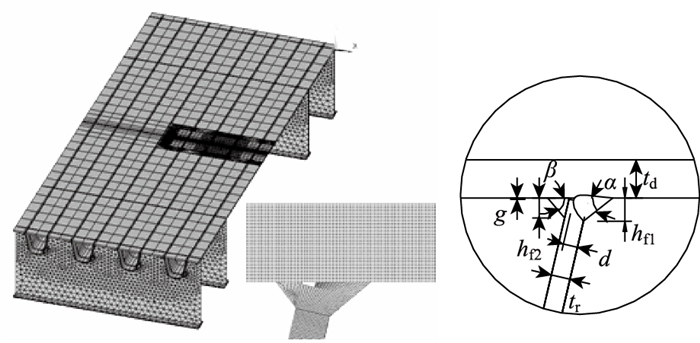
|
| 图 14 精细有限元模型及新参数 Fig. 14 Refined finite element model and new parameters |
| |
计算结果表明:
(1) 采用新型双面焊接头,肋板焊趾热点应力降低约15%,顶板焊趾热点应力变化最大在2%以内,同时,顶板内焊趾、肋板内焊趾热点应力与肋板焊趾热点应力相当,如图 15所示。
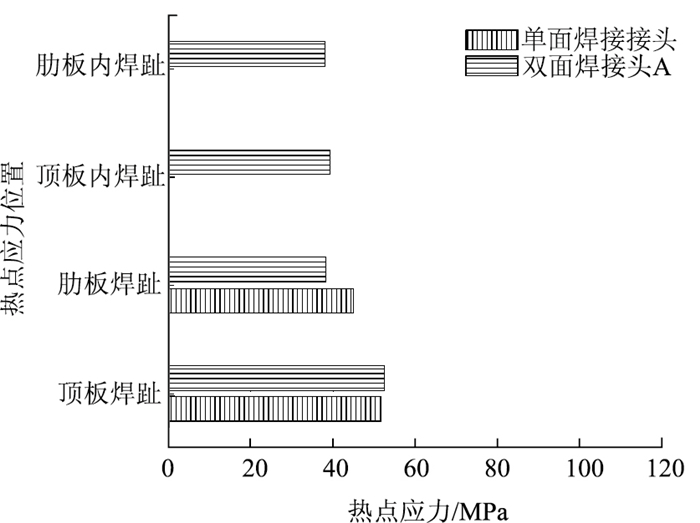
|
| 图 15 采用新型双面焊接头前后的热点应力 Fig. 15 Hot spot stresses before and after using new double-sided weld joint |
| |
(2) 采用新型双面焊接头,熔透率为60%、80%和100%(全熔透)时,各热点应力变化最大在1%以内,如图 16所示。
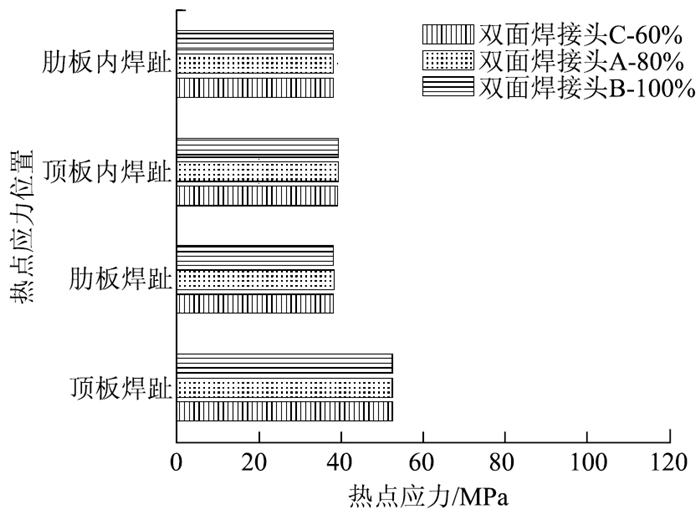
|
| 图 16 新型双面焊接头随熔透率变化的热点应力 Fig. 16 Hot spot stress in new double-sided weld joint varying with penetration rate |
| |
(3) 采用新型双面焊接头,内焊趾高度由6 mm增加到8 mm,顶板内焊趾、肋板内焊趾、肋板焊趾热点应力降低约7%,3%,4%,顶板焊趾热点应力变化最大在1%以内;而当内焊趾高度由6 mm减小到4 mm,顶板内焊趾、肋板内焊趾热点应力增加约7%,22%,肋板焊趾、顶板焊趾热点应力变化最大在2%以内,如图 17所示。
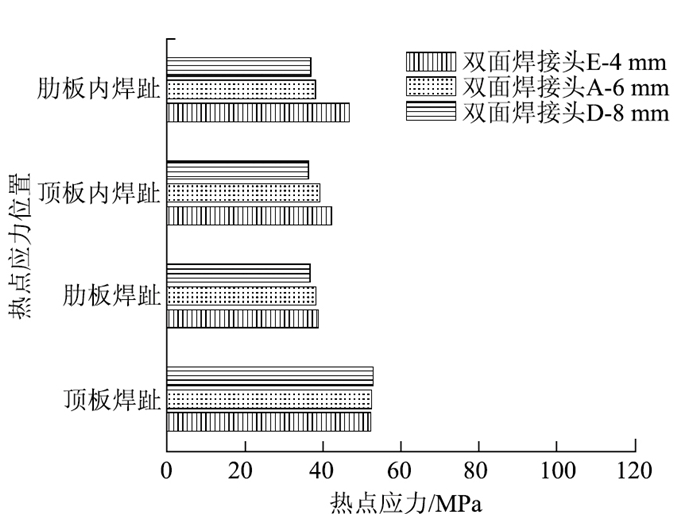
|
| 图 17 新型双面焊接头随内焊趾高度变化的热点应力 Fig. 17 Hot spot stress in new double-sided weld joint varying with height of inner weld toe |
| |
(4) 采用新型双面焊接头,内焊趾角度由40°减小到30°,顶板内焊趾降低约9%,其余热点应力变化最大在3%以内;当内焊趾角度由40°增加到50°,顶板内焊趾热点应力增加约6%,其余热点应力变化最大在2%以内,如图 18所示。
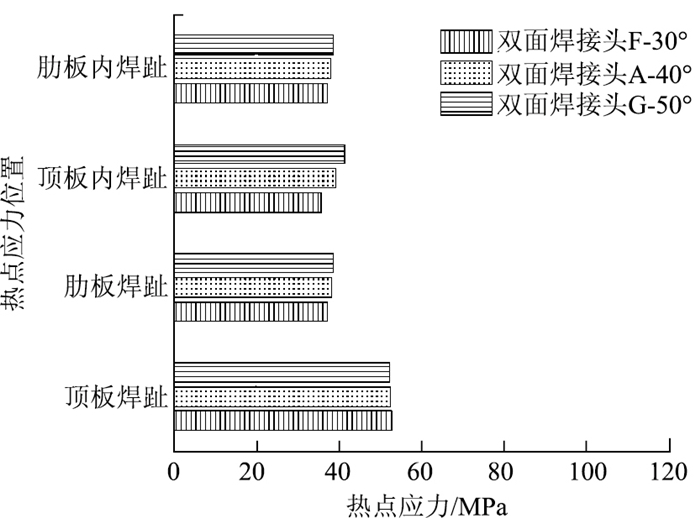
|
| 图 18 新型双面焊接头随内焊趾角度变化的热点应力 Fig. 18 Hot spot stress in new double-sid weld joint varying with angle of inner weld toe |
| |
(5) 采用新型双面焊接头,D18U8(18 mm顶板厚度与8 mm肋板)较D16U8板厚组合,顶板焊趾、内焊趾热点应力降低约26%,28%,肋板焊趾、内焊趾热点应力均降低约3%;D16U6较D16U8板厚组合,顶板焊趾、内焊趾热点应力降低约7%、6%,肋板焊趾、内焊趾热点应力增加低约33%、36%;D16U10较D16U8板厚组合,顶板焊趾热点应力增加约4%,肋板焊趾、内焊趾热点应力均降低约22%,顶板内焊趾热点应力变化最大在1%以内,如图 19所示。
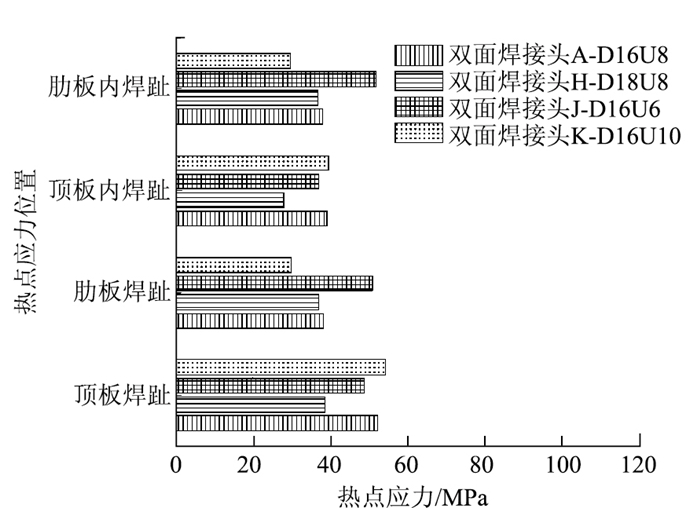
|
| 图 19 新型双面焊接头采用不同板厚组合的热点应力 Fig. 19 Hot spot stresses of new double-sided weld joint using different deck thickness combinations |
| |
4 结论与建议
针对顶板-U肋焊接接头的疲劳问题,以广东虎门二桥坭洲水道桥标准梁段钢桥面板为例,基于有限元软件ANSYS建立的参数化热点应力有限元分析模型,对顶板-U肋焊接接头及新型双面焊接头热点应力进行了精细有限元分析,得出以下主要结论:
(1) 顶板厚度由16 mm逐步增加到18 mm,顶板焊趾、焊根热点应力降低约26%,28%,采用新型双面焊接头后,顶板焊趾热点应力同样降低约26%。
(2) 肋板厚度由8 mm增加到10 mm,顶板焊趾、焊根热点应力增加约2%,4%,肋板焊趾、焊根热点应力降低约20%,采用新型双面焊接头后,肋板焊趾热点应力降低约22%。
(3) 熔透率由60%增加到80%,100%(全熔透),肋板焊趾、焊根热点应力降低约6%,10%,采用新型双面焊接头后,各热点应力变化最大在1%以内。
(4) 当熔透率为60%,80%,组装间隙由0.5 mm增加到3.5 mm,各热点应力变化最大在2%以内。
(5) 焊趾高度由8 mm增加到10 mm或焊趾角度由40°减小到30°,顶板焊趾热点应力降低约4%或11%。
(6) 基于本研究热点应力变化规律的分析,本研究形成如表 2所示的相关设计建议,以为今后相关工程应用提供一定的参考价值。
| 设计参数 | 疲劳裂纹 | |||||
| C.1 | C.2 | C.3 | C.4 | C.2N | C.4N | |
| 顶板厚度 | 增加 | 增加 | 增加 | 增加 | 增加 | 增加 |
| U肋厚度 | 减小 | 减小 | 增加 | 增加 | 减小 | 增加 |
| 熔透率 | — | — | 增加 | 增加 | — | — |
| 组装间隙 | — | — | 减小* | 减小* | — | — |
| 焊趾高度 | 增加 | — | — | — | — | — |
| 焊趾角度 | 减小 | — | 增加 | 增加 | — | — |
| 内焊焊趾高度 | — | — | 增加 | — | 增加 | 增加 |
| 内焊焊趾角度 | — | — | 减小 | — | 减小 | 减小 |
| 注:“*”代表在一定条件下,“-”无关或本文没有涉及。 | ||||||
| [1] |
WOLCHUK R. Steel Orthotropic Decks:Developments in the 1990s[J]. Transportation Research Record, 1999, 1688: 30-37. |
| [2] |
HOBBACHER A. Recommendations for Fatigue Design of Welded Joints and Components[M]. Berlin: Springer International Publishing, 2016.
|
| [3] |
张喜刚, 刘高, 马军海, 等. 中国桥梁技术的现状与展望[J]. 科学通报, 2016(4): 415-425. ZHANG Xi-gang, LIU Gao, MA Jun-hai, et al. Status and Prospect of Technical Development for Bridges in China[J]. Chinese Science Bulletin, 2016(4): 415-125. |
| [4] |
JONG F B P D. Overview Fatigue Phenomenon in Orthotropic Bridge Decks in the Netherlands[C]//Proceedings of Orthotropic Bridge Decks. Sacramento, US: 2004 Orthotropic Bridge Conference ASCE, 2004: 489-512.
|
| [5] |
鋼構造委員会鋼床版の疲労小委員会. 鋼床版の疲労[J]. 土木学会論文集, 1989, 410(Ⅰ-12): 25-36. Subcommittee of Fatigue Investigation of Orthotropic Decks, JSCE. Fatigue of Orthotropic Decks[J]. Journal of Japan Society of Civil Engineers, 1989, 410(Ⅰ-12): 25-36. |
| [6] |
唐亮, 黄李骥, 刘高. 正交异性钢桥面板横梁弧形切口周边应力分析[J]. 公路交通科技, 2011, 28(6): 83-90. TANG Liang, HUANG Li-ji, LIU Gao. FEA of Stress along Cope Hole Edge of Crossbeam in Orthotropic Steel Deck[J]. Journal of Highway and Transportation Research and Development, 2011, 28(6): 83-90. |
| [7] |
王迎军, 朱桂新, 陈旭东. 虎门大桥钢桥面铺装的使用和维护[J]. 公路交通科技, 2004, 21(8): 64-67. WANG Ying-jun, ZHU Gui-xin, CHEN Xu-dong. The Using and Maintenance of the Steel Deck Pavement in Humen Bridge[J]. Journal of Highway and Transportation Research and Development, 2004, 21(8): 64-67. |
| [8] |
唐亮, 黄李骥, 刘高, 等. 正交异性钢桥面板顶板贯穿型疲劳裂纹研究[J]. 公路交通科技, 2012, 29(2): 60-66. TANG Liang, HUANG Li-ji, LIU Gao, et al. Research on Fatigue Cracks through Deck-plate in Orthotropic Steel Deck[J]. Journal of Highway and Transportation Research and Development, 2012, 29(2): 60-66. |
| [9] |
猛森, 志保鴫原, 宏中村. 溶接溶け込み深さを考慮した鋼床版デッキプレート·トラフリブ溶接部の疲労試験[J]. 土木学会論文集A, 2006, 62: 570-581. MORI T, SHIGIHARA S, NAKAMURA H. Fatigue Tests on Welded Connections between Deck Plate and Trough Rib in Steel Plate Deck in Consideration of Weld Penetration[J]. Journal of Japan Society of Civil Engineers, Ser. A, 2006, 62(3): 570-581. |
| [10] |
PYTTEL B, GRAWENHOF P, BERGER C. Application of Different Concepts for Fatigue Design of Welded Joints in Rotating Components in Mechanical Engineering[J]. International Journal of Fatigue, 2012, 34(1): 35-46. |
| [11] |
韩冰, 蒲黔辉, 施洲, 等. 桥梁正交异性板焊接构造热点应力计算方法研究[J]. 桥梁建设, 2015(1): 56-61. HAN Bing, PU Qian-hui, SHI Zhou, et al. Study of Calculation Methods for Hot Spot Stress of Welded Structure of Bride Orthotropic Plate[J]. Bridge Construction, 2015(1): 56-61. |
| [12] |
傅中秋, 吉伯海, 王满满, 等. 钢桥面板疲劳热点应力计算模型精度分析[J]. 南京工业大学学报:自科版, 2016, 38(1): 83-88. FU Zhong-qiu, JI Bo-hai, WANG Man-man, et al. Analysis on Precision of Hot Spot Stress Calculation Model of Steel Bridge Deck Weld Fatigue[J]. Journal of Nanjing Tech University:Natural Science Edition, 2016, 38(1): 83-88. |
| [13] |
WANG C, CHEN W, CHEN A. Fatigue Safety Assessment of Existing Steel Bridges in China[J]. Structural Engineering International, 2009, 19(2): 174-179. |
| [14] |
CARPINTERI A, SPAGNOLI A, VANTADORI S, et al. Multiaxial Fatigue Life Estimation in Welded Joints Using the Critical Plane Approach[J]. International Journal of Fatigue, 2009, 31(1): 188-196. |
| [15] |
LIU G, LIU Y, HUANG Y. A Novel Structural Stress Approach for Multiaxial Fatigue Strength Assessment of Welded Joints[J]. International Journal of Fatigue, 2014, 63(4): 171-182. |
| [16] |
唐亮, 黄李骥, 刘高, 等. 正交异性钢桥面板足尺模型疲劳试验[J]. 土木工程学报, 2014, 47(3): 112-122. TANG Liang, HUANG Li-ji, LIU Gao, et al. Fatigue Experimental Study of a Full-scale Steel Orthotropic Deck Model[J]. China Civil Engineering Journal, 2014, 47(3): 112-122. |
| [17] |
BS EN 1993-1-9: 2005 Eurocode 3: Design of Steel Structures-Part 1-9: Fatigue[S].
|
| [18] |
EN 1993-2: 2006 Eurocode 3: Design of Steel Structures-Part 2: Steel Bridges[S].
|
 2018, Vol. 35
2018, Vol. 35
