扩展功能
文章信息
- 陈永高, 钟振宇
- CHEN Yong-gao, ZHONG Zhen-yu
- 基于改进EEMD算法的桥梁结构模态参数识别
- Modal Parameter Identification of Bridge Structure Based on Improved EEMD Algorithm
- 公路交通科技, 2018, 35(4): 49-57
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(4): 49-57
- 10.3969/j.issn.1002-0268.2018.04.007
-
文章历史
- 收稿日期: 2017-01-03
由于实际桥梁结构处于环境激励[1]下,以致传感器[2]采集的振动响应信号[3]内部会含有一定的噪声,噪声部分主要包括:非线性影响、外部结构噪声以及电子设备内部噪声;噪声的存在会直接影响信号分解的精确性,已有不少学者对如何消除响应信号内部的噪声进行了大量的研究,现阶段常用的信号预处理算法是由WU和Huang[4]提出的总体经验模态分解[5](Ensemble Empirical Mode Decompo-sition, EEMD),虽然该分解法能弥补经验模态分解(Empirical Mode Decomposition,EMD)[6]的一些不足之处,但其依然存在一些缺陷,本研究针对这些缺陷,提出了一种新的算法,即互补自适应噪声的EEMD算法(Ensemble Empirical Mode Decomposition With Complementary Adaptive Noise, EEMDCAN),以实现更好的降噪效果以及信号的重构。
1 EEMD算法EEMD是对EMD的进一步完善改进,即在信号中加入白噪声,使信号预白化,再对其进行EMD分解。
通过对EEMD算法的深入了解,发现该算法依然存在以下几点缺陷,分别是:
(1) 添加白噪声的幅值标准差和次数并无统一标准;
(2) 所得本征模态函数(Intrinsic Mode Function, IMF)间存在一定的模态混叠现象;
(3) 难以区分有效IMF分量和噪声分量,以致无法实现对信号的自适应重构。
针对上述3方面的问题,提出了“互补自适应噪声的集合经验模态分解算法”,该算法能够实现信号的自适应分解与重构,即能够自动根据待分解信号的特性确定添加白噪声的幅值标准差和集成次数,并能保证所得IMF之间不存在模态混叠现象,同时还能智能化筛选有效IMF分量,以实现待分解信号的自适应分解和重构。该算法的主要优点在于,能够有效避免人为参与信号的分解,进而达到提高信号分解效率和准确性的目的。
2 EEMD算法的改进 2.1 信号分解参数的确定在利用EEMD算法对信号进行模态分解时,由于需要先添加白噪声再进行模态分解,所以最后的分解结果(IMFs)中也会相应的含有部分白噪声,白噪声的存在会在一定程度上影响识别结果的精确性。基于此,在EEMD算法的基础上通过添加正、负白噪声的方式来减少所得IMFs中白噪声存在的程度,以下就如何添加正、负白噪声[7]进行详细的流程分析:
(1) IMF1的求解
在原始信号中添加正、负2种白噪声((-1)qa0ni(t)),并对添加了正负白噪声的信号进行一次EMD分解,并筛选出本征模态函数分量(IMF1),数学表达式如式(1):
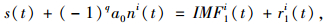
|
(1) |
式中,q=1为加入的是负的白噪声,q=2为加入的是正的白噪声;i=1, 2, …, M/2,M为加入白噪声的总次数;a0为添加白噪声的幅值标准差;ni(t)为第i次添加的白噪声;s(t)为原始信号。
利用M个本征模态函数分量IMF1i(t)取平均值以便求得新的第一阶本征模态函数分量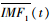
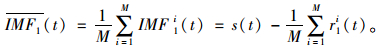
|
(2) |
对原始信号进行上述处理的原因在于:通过在M次集合平均中能将加入的正、负白噪声(-1)qa0ni(t)相互抵消,进而在一定程度上减少残留在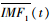
(2) 求取剩余的本征模态函数
根据步骤(1)可以分解得到原始信号的第一阶本征模态函数分量,接着利用相同的方法计算出剩余量r1(t)的第一阶本征模态函数分量,具体计算式子如式(3):
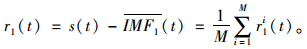
|
(3) |
在剩余量r1(t)中添加经过EMD分解的正负的自适应噪声IMF分量对(-1)qa1E1(ni(t)),构成新的信号即r1(t)+(-1)qa1E1(ni(t))。利用EMD对其进行模态分解,求解得到新的第一阶本征模态函数分量,计算式如式(4):
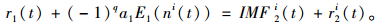
|
(4) |
最后对上述得到的本征模态函数取平均值以便得到原始信号的第2阶本征模态函数分量:
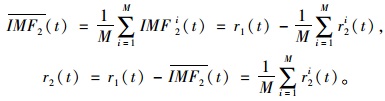
|
(5) |
按照上述原理可以得到剩余的本征模态函数分量,具体的公式如式(6)所示:

|
(6) |
重复上述流程直到求解出最后一阶本征模态函数分量以及剩余量R(t)。
相比EEMD算法而言,上述算法流程具有以下几方面的优点:
(1) 无需大幅的增加集成平均次数,提高信号分解的效率;
(2) 能有效地降低每个IMF分量中的噪声;
(3) 能在一定程度上确保各IMF分量之间不存在模态混叠现象。
2.2 聚类分析的运用为了保证分解结果中各IMF分量间不存在模态混叠现象,本研究引入多元统计学中的“聚类分析”算法[8]。首先利用该算法计算得到每组分解结果中各IMF分量间的欧式距离;并利用该欧式距离绘制聚类谱图,以辨识IMF分量间是否存在混叠现象,当该组IMF分量间存在混叠现象时,则剔除这组分解结果,如此对所有分解结果进行辨识筛选,以保留分解结果中不存在混叠现象的结果;最后根据EEMD算法中的“均值”原理对保留的多组分解结果取均值,获得最终的分解结果。
2.3 有效IMF分量的筛选为实现有效IMF分量的智能化筛选,借鉴模糊数学中的“模糊综合评价法”提出了一种新筛选算法,该方法不仅能考虑各IMF分量与原始信号之间的相关系数[9],还能兼顾各IMF分量对应的能量密度和平均周期[10]。以下首先分别分析相关系数准则、能量密度以及平均周期,最后论述如何将这三者进行有效结合。
(1) 相关系数准则
引入相关性分析求解每个IMF与原始信号之间的整体相似程度r。
① 分别求解出各IMF分量的互相关函数(Rj)和原始信号的自相关函数(Rx),计算式子如式(7):

|
(7) |
式中,s(i)为信号第i时刻对应的数据值;N为信号序列的长度值;m为IMF分量的个数。
② 归一化处理上述所得的自相关函数(Rx),并求出Rj和Rx的互相关系数rj,计算式如式(8):
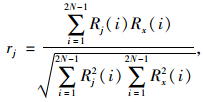
|
(8) |
式中,j为IMF分量的总个数;rj的数值大小为IMF分量与原始信号之间的的相似程度。
(2) 求解能量密度和平均周期
① 对待分解信号进行EEMD分解,并分别计算各IMF分量对应的能量密度(E)、平均周期(T)以及能量系数(ET):
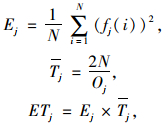
|
(9) |
式中,N为各IMF分量对应的序列长度;fj为IMFj分量对应的振幅值;Oj为IMFj分量内部的极值点个数。
② 利用能量系数计算用于筛选有效IMF分量的新指标——有效系数(X):
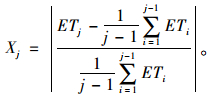
|
(10) |
根据该式可知:当Xj值越大时,表明该IMF分量为有效IMF分量的几率越大。根据文献[8],本研究假定当Xj≥0.8时,该IMFj属于有效成分,能被用于信号的重构。
(3) 有效IMF分量的筛选
利用模糊综合评价算法[11]将这3项参数进行结合,即利用式(11)求解各IMF分量对应的有效程度Y:
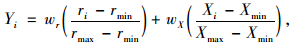
|
(11) |
式中,Yi为第i个IMF与原始信号之间的有效程度系数;wr, wX分别为相关系数r和有效系数对应的权重,考虑到这两参数具有相同的重要性,所以将其分别取值为0.5。
综合上述可知,当Yi越接近1则表示该第i个IMF分量与原始信号的相似程度越高,当Yi≥0.6时[11],则认为该IMF为有效IMF。再对保留下来的k个IMF分量进行重构,计算式如式(12):
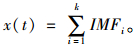
|
(12) |
综合上述,梳理EEMDCAN算法的基本流程图,如图 1所示。

|
| 图 1 EEMDCAN算法流程图 Fig. 1 Flowchart of EEMDCAN algorithm |
| |
3 试验仿真
为验证本研究所提算法具有可行性,利用如下模拟信号进行相关验证,该信号由1 Hz和5 Hz的余弦信号叠加噪声水平约为15%的随机噪声组成,时间共20 s,采样频率为100 Hz。叠加信号的计算式见式(13),各叠加信号对应的时程图如图 2所示。
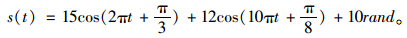
|
(13) |

|
| 图 2 信号与噪声 Fig. 2 Signal and noise |
| |
根据2.1节所提算法可计算出添加的白噪声的幅值标准差和集成平均次数分别为0.083和18次。
3.1 本征模态函数基于相同的白噪声幅值标准差和集成平均次数,分别利用EEMD和本研究算法对模拟信号进行模态分解,所得结果见图 3和图 4。

|
| 图 3 EEMD分解结果 Fig. 3 Decomposition result by EEMD |
| |
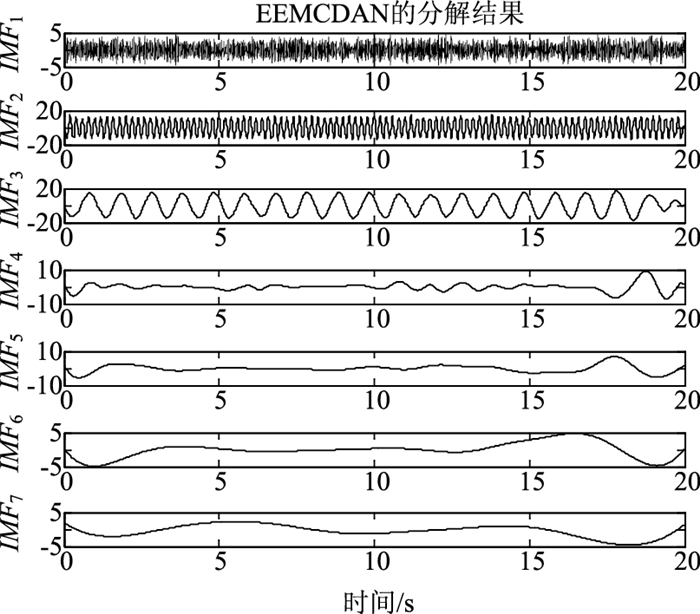
|
| 图 4 EEMDCAN分解结果 Fig. 4 Decomposition result by EEMDCAN |
| |
为直观地观察所得本征模态函数间是否存在模态混叠现象,利用2.2节所提“聚类分析”对所得结果进行分析,聚类结果见图 5和图 6,图中横坐标代表各IMF分量,纵坐标代表各IMF分量间的欧式距离。
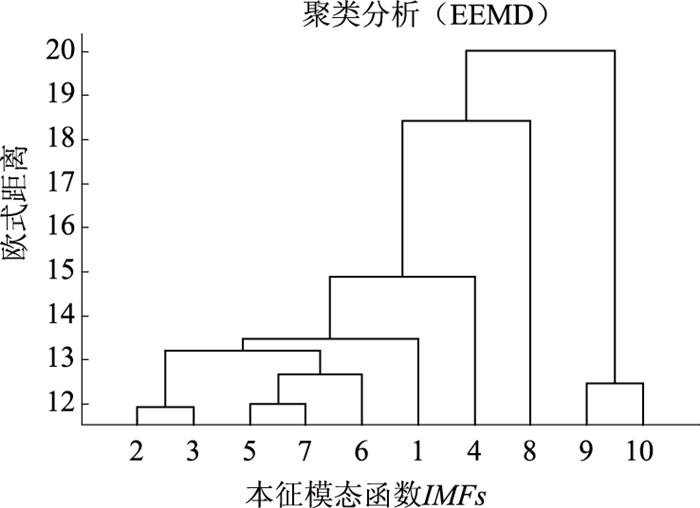
|
| 图 5 聚类结果(EEMD) Fig. 5 Clustering result (EEMD) |
| |
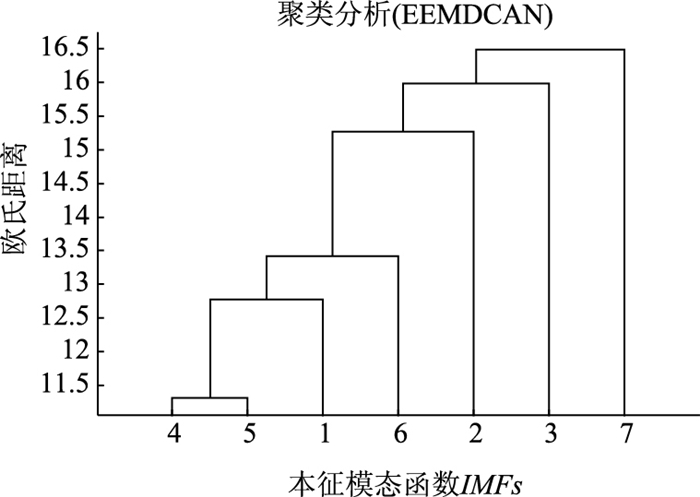
|
| 图 6 聚类结果(EEMDCAN) Fig. 6 Clustering result (EEMDCAN) |
| |
对比上述分解结果可得如下结论:
(1) 分解效率方面:EEMD分解共得10个IMF分量,而本研究算法仅得7个IMF分量,可见本研究算法具有更高的分解效率;
(2) 模态混叠现象:EEMD分解结果中IMF5和IMF7以及IMF9和IMF10间均存在模态混叠现象,即这两IMF分量结果中含有一定的相似信息;本研究算法所得IMF分量间不存在模态混叠现象。
(3) 本征模态函数:本研究算法所得结果中的IMF2分量与原始信号中的5 Hz信号基本一致,同时IMF3与原始信号中的1 Hz信号基本一致;而EEMD分解结果只有IMF4分量与原始信号中的1 Hz信号基本一致,却不存在与5 Hz信号相似的分量结果;
3.2 有效IMF分量的筛选首先分别求解出各IMF分量对应的相关系数、能量密度以及平均周期,其次基于“模糊综合评价算法”的原理筛选出最终的有效IMF分量,具体结果如下。
(1) 相关系数
分别计算各IMF分量与原始信号、5 Hz信号以及1 Hz信号之间的相关系数,结果如表 1所示。
| IMF分量 | 叠加信号 | 1 Hz信号 | 5 Hz信号 |
| IMF1 | 0.183 | 0.015 | 0.005 |
| IMF2 | 0.618 | -0.004 | 0.978 |
| IMF3 | 0.745 | 0.972 | 0.005 |
| IMF4 | 0.394 | 0.395 | 0.000 |
| IMF5 | 0.027 | 0.035 | 0.002 |
| IMF6 | 0.002 | 0.013 | 0.001 |
| IMF7 | 0.003 | 0.003 | 0.000 |
由表 1可知:
① 根据叠加信号与各IMF分量之间的相关系数可知:IMF2~IMF4与叠加信号的相关系数大于0.3,即可以被认为是有效地IMF分量。
② 考虑到叠加信号中含有噪声,如果只是根据叠加信号与IMF分量之间的相关系数来选择有效IMF分量是否准确,为了验证①中所得结论,则可以通过观察各IMF分量与真实信号之间的相关系数,根据各分量与1 Hz信号之间的相关系数可选出IMF3和IMF4属于有效分量;根据各分量与5 Hz信号之间的相关系数可选出IMF2属于有效分量。
③ 可以利用各IMF分量与原始信号的相关系数来筛选有效IMF分量。
为了进一步验证本研究所提算法较现有EEMD算法的分解结果更好,计算出了EEMD分解结果与叠加信号、5 Hz和1 Hz信号之间的相关系数,具体结果见表 2。
| IMF分量 | 叠加信号 | 1 Hz信号 | 5 Hz信号 |
| IMF1 | 0.183 | 0.002 | 0.013 |
| IMF2 | 0.581 | 0.000 | 0.917 |
| IMF3 | 0.646 | 0.543 | 0.379 |
| IMF4 | 0.731 | 0.949 | 0.001 |
| IMF5 | 0.122 | 0.149 | 0.001 |
| IMF6 | 0.036 | 0.056 | 0.003 |
| IMF7 | 0.023 | 0.035 | 0.002 |
| IMF8 | -0.006 | 0.001 | 0.000 |
| IMF9 | -0.009 | -0.001 | 0.000 |
| IMF10 | 0.029 | 0.031 | 0.002 |
由表 2可知:叠加信号与IMF分量中的IMF2-4的相关系数均大于0.5,由各IMF分量与1 Hz信号的相关系数可选出IMF3和IMF4为有效分量,由IMF分量与5 Hz信号的相关系数可选出IMF2和IMF3为有效分量。这也再一次证明:虽然信号中含有一定的噪声,但是依然能够利用各IMF分量与叠加信号之间的相关系数来筛选出有效IMF分量。
(2) 能量密度与平均周期
利用相关系数能够从IMF分量中筛选出有效的分量,但如果只是利用一种算法对有效IMF分量进行筛选,则筛选结果并不完全正确。基于此,利用每个IMF分量的能量密度与其平均周期的乘积为一个常量这一特点,提出了一种新的筛选算法,以下是该算法对模拟信号的结果分析。
首先分别求出EEMDCAN分解结果中各IMF分量的能量密度和平均周期,并利用所得结果计算能量系数和有效系数,具体的计算结果见表 3。
| 各IMF分量 | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 |
| 能量密度 | 4.31 | 72.58 | 102.15 | 5.07 | 4.89 | 4.54 | 2.52 |
| 平均周期 | 0.03 | 0.17 | 0.98 | 1.11 | 2.35 | 5.71 | 8.00 |
| 能量系数 | 0.12 | 12.00 | 99.66 | 5.64 | 11.51 | 25.92 | 20.12 |
| 有效系数 | 0.12 | 0.92 | 0.89 | 0.85 | 0.61 | 0.01 | 0.22 |
由表 3可知:IMF2和IMF3对应的有效系数均大于0.8,表明这两个IMF分量属于有效成分,能被用于信号的重构。
(3) 模糊综合评价算法
相关系数和有效系数都能被用于筛选有效IMF分量,当利用相关系数进行选择时,则保留IMF2~IMF4;而利用有效系数的相关准则则保留的分量只有IMF2和IMF3。这时就出现了分歧,即IMF4分量到底是保留还是删除。基于此,使用模糊综合评价算法,该算法的特点在于不仅需要靠相关系数同时还能兼并有效系数,表 4为综合评价算法的具体结果。
| 各项系数 | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 |
| 相关系数 | 0.18 | 0.62 | 0.75 | 0.39 | 0.03 | 0.00 | 0.00 |
| 有效系数 | 0.12 | 0.92 | 0.89 | 0.85 | 0.61 | 0.01 | 0.22 |
| 有效程度系数 | 0.18 | 0.77 | 0.82 | 0.62 | 0.32 | 0.00 | 0.11 |
由表 4可知;
① IMF2,IMF3和IMF4的有效程度系数都大于0.6,则被认为是有效的IMF分量,能被运用于重构信号;
② 模糊综合评价算法能有效的避免单独利用相关系数和单独利用有效系数对有效IMF分量筛选出现的偏差。
3.3 EEMD与EEMDCAN结果的对比以下将从2个方面来验证EEMDCAN分解结果要优于EEMD结果,首先是重构信号的误差,其次是瞬时频率Hilebert-Huang谱。
(1) 信号重构误差
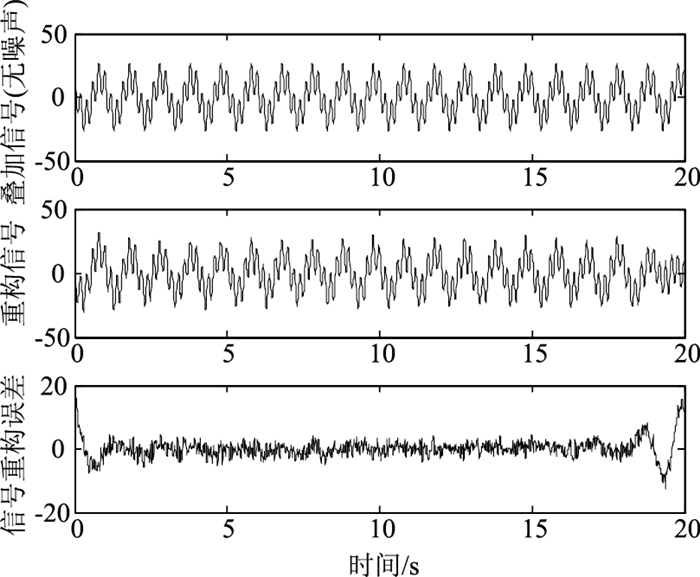
根据2.3节所提算法确定2种分解算法对应的有效IMF分量,并对其进行重构,绘制各重构信号对应的时程曲线,结果如图 7和图 8所示。对比两图可知:
|
| 图 7 EEMD重构信号误差 Fig. 7 Errors of EEMD signal reconstruction |
| |
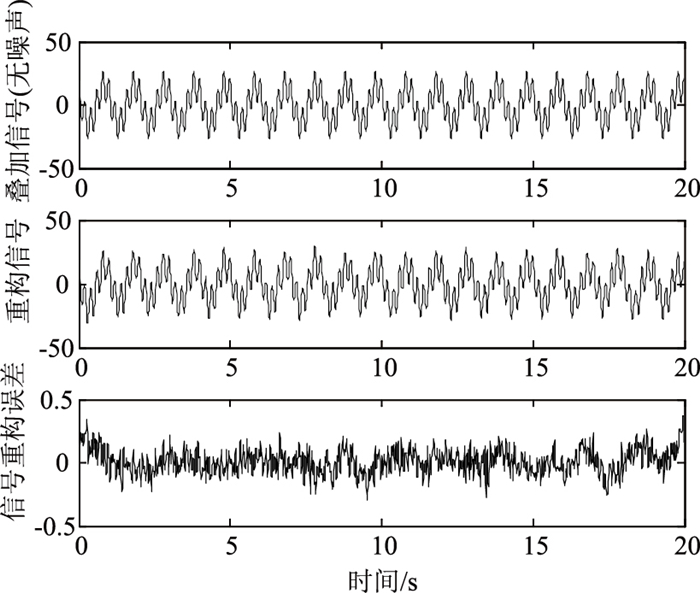
|
| 图 8 EEMDCAN重构信号误差 Fig. 8 Errors of EEMDCAN signal reconstruction |
| |
① 对比2种分解算法所得重构信号在端点处的误差值可知,相比EEMD算法而言,EEMDCAN算法具有更好的端点效应处理效果;
② 观察2种分解算法所得重构信号整体误差值可知,EEMDCAN算法得到的重构误差较EEMD算法更小,表明所得重构信号更接近真实值,即本研究算法所得分解结果更接近实际值。
(2) 瞬时频率Hilebert-Huang谱
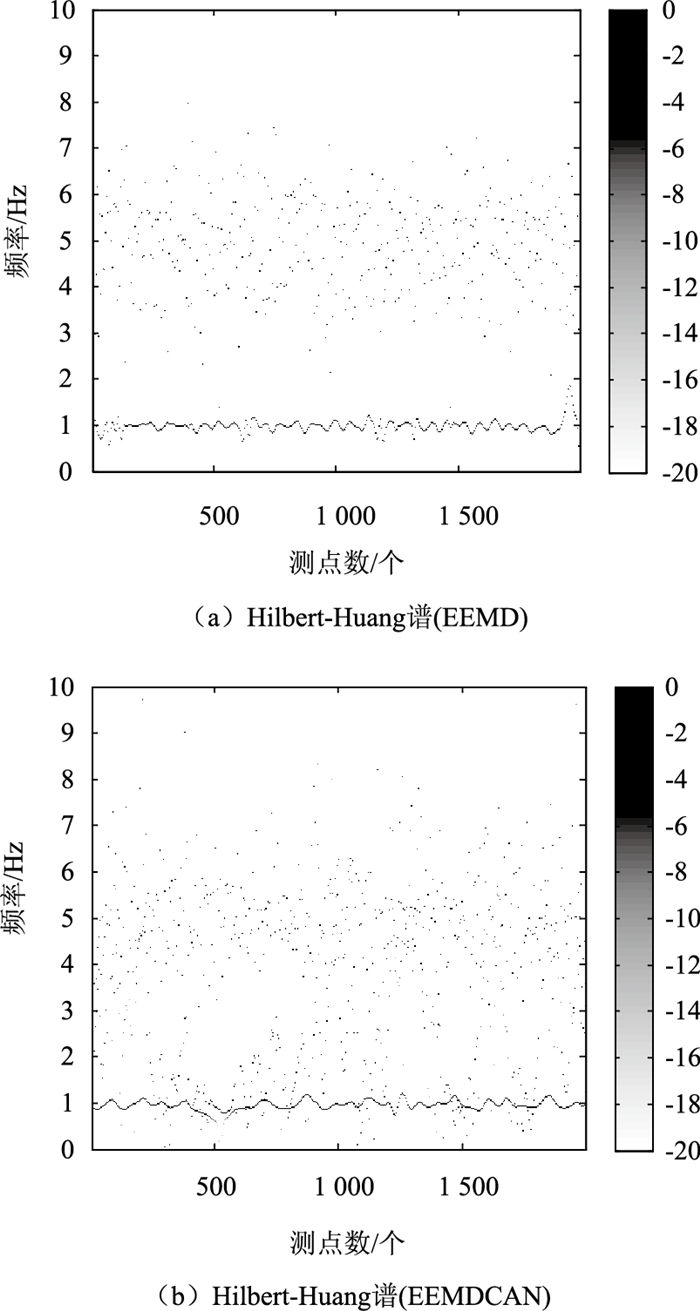
对比2分解算法结果中有效IMF分量对应的瞬时频率Hilebert-Huang谱[12],结果见图 9,图中横坐标为测点个数。
|
| 图 9 Hilbert-Huang谱 Fig. 9 Hilbert-Huang spectrum |
| |
对比Hilbert-Huang谱图可知:EEMDCAN所得频率的连续性更好,且上下变化的浮动也小于EEMD的结果,即说明本研究算法得到的频率更为精确;
综合上述分析可知:本研究分解算法无论是在模态混叠现象处理、端点效应处理效果还是分解效率均优于现有的EEMD算法,同时该EEMDCAN算法能够实现信号的自适应分解和重构,且重构信号具有可靠性。
4 某大型斜拉桥模态参数识别结果为验证EEMDCAN算法能对实际桥梁结构响应信号进行很好的降噪与重构,现以长江上某大型斜拉桥为研究对象,先分别运用EEMD算法和本研究算法对传感器采集的加速度响应信号进行降噪与重构,再将重构的信号作为AMRA识别算法[13]的输入进行模态参数识别[14]。
4.1 工程背景该斜拉桥的主跨径为1 088 m,该桥主梁上共布置14个竖向加速度传感器,总体布置图如图 10所示;加速度信号采样频率为20 Hz,采样时间为2 000 min。选取加速度传感器采集的实测响应信号为对象进行信号分解,再对重构信号进行模态参数识别[15]。

|
| 图 10 加速度传感器布置图(单位:m) Fig. 10 Acceleration sensor arrangement (unit:m) |
| |
4.2 模态参数识别结果对比分析
首先分别利用EEMD和EEMDCAN 2种分解算法对信号进行分解,并进行信号的重构,其次再利用ARMA模型时间序列分析法[16]对重构信号进行模态参数识别[17]。由于该桥梁结构的跨度大,结构柔,模态密集,所以本研究只提取了各算法结果的前8阶频率值进行对比分析,结果见表 5。
| 模态 | 未预处理 | EEMD处理 | EEMDCAN处理 | 真实值 | 差值百分比1 | 差值百分比2 | 差值百分比3 |
| 1阶竖向 | 0.237 9 | 0.208 4 | 0.198 0 | 0.186 4 | 21.6 | 10.6 | 5.8 |
| 2阶竖向 | 0.274 9 | 0.247 4 | 0.236 9 | 0.228 4 | 16.9 | 7.7 | 3.6 |
| 3阶竖向 | 0.387 5 | 0.347 1 | 0.312 4 | 0.298 3 | 23.0 | 14.1 | 4.5 |
| 4阶竖向 | 0.414 0 | 0.380 8 | 0.360 8 | 0.320 8 | 22.5 | 15.7 | 11.1 |
| 5阶竖向 | 0.454 9 | 0.432 1 | 0.413 1 | 0.386 8 | 15.0 | 10.5 | 6.4 |
| 6阶竖向 | 0.532 2 | 0.493 2 | 0.454 3 | 0.431 2 | 19.0 | 12.6 | 5.1 |
| 7阶竖向 | 0.599 1 | 0.571 5 | 0.532 6 | 0.484 6 | 19.1 | 15.2 | 9.0 |
| 8阶竖向 | 0.673 2 | 0.609 5 | 0.573 4 | 0.535 6 | 20.4 | 12.1 | 6.6 |
| 注:“未预处理”指的是直接利用ARMA算法对实际信号进行识别;“EEMD处理”指的是先利用EEMD对实际信号进行降噪处理,再利用ARMA算法对重构信号进行识别;“EEMDCAN处理”指的是先利用EEMDCAN对实际信号进行降噪处理,再利用ARMA算法对重构信号进行识别;“真实值”是文献[18]中所得结果;“差值百分比1”代表真实值与未预处理所得结果之间的差值百分比;“差值百分比2”代表真实值与EEMD处理所得结果之间的差值百分比;“差值百分比3”代表真实值与EEMDCAN处理所得结果之间的差值百分比。 | |||||||
(1) 对比差值百分比1~3的数值大小可知:
① EEMD能消除原始振动信号中的部分噪声。
② EEMDCAN的预处理效果比EEMD预处理效果更好。
(2) 利用EEMDCAN算法先预处理原始振动信号,再利用ARMA模型时间序列分析法进行模态参数识别,识别得到的桥梁结构频率值与真实值之间的差值百分比能控制在10%以下。
综合上述结论可知:本研究所提算法能运用于实际桥梁结构的信号预处理中,能对传感器采集的振动响应信号进行降噪处理,且降噪结果优于现有的EEMD算法。
5 结论基于EEMD算法存在的缺陷,本研究通过引入相关性分析、聚类分析以及模糊综合评价算法,能够实现信号的自我分解与重构,提高了信号分解的效率与精度。
(1) EEMDCAN算法的计算效率以及分解精度均高于EEMD算法,且能在得到更少的IMF分量的前提下,减小分解误差。
(2) 根据聚类分析的结果可知,经过EEMDCAN分解得到的IMF之间并不存在模态混叠现象,即本研究算法能够克服EEMD算法存在的模态混叠现象。
(3) 通过将本研究算法运用于实际桥梁结构的响应信号中,并利用相关参数识别法识别结构的频率值,最后对比分析识别值与真实值之间的差值百分比。可知,本研究所提的EEMDCAN算法能被运用于实桥响应信号的预处理,且能保留响应信号中的有用信息。
| [1] |
刘宇飞, 辛克贵, 樊健生, 等. 环境激励下结构模态参数识别方法综述[J]. 工程力学, 2014, 31(4): 46-53. LIU Yu-fei, XIN Ke-gui, FAN Jian-sheng, et al. A Review of Structure Modal Identification Methods through Ambient Excitation[J]. Engineering Mechanics, 2014, 31(4): 46-53. |
| [2] |
杨小森, 闫维明, 陈彦江, 等. 基于振动信号统计特征的损伤识别方法[J]. 公路交通科技, 2013, 30(12): 99-106. YANG Xiao-sen, YAN Wei-ming, CHEN Yan-jiang, et al. Damage Detection Method Based on Statistics Characteristics of Vibration Signal[J]. Journal of Highway and Transportation Research and Development, 2013, 30(12): 99-106. |
| [3] |
康俊涛, 张亚州, 秦世强. 桥梁安全状态评估有限元模型修正方法[J]. 中国安全科学学报, 2016, 26(11): 99-103. KANG Jun-tao, ZHANG Ya-zhou, QIN Shi-qiang. A Method for Modifying Bridge Security Condition Evaluation FEA Model[J]. China Safety Science Journal, 2016, 26(11): 99-103. |
| [4] |
WU Z, HUANG N E. Ensemble Empirical Mode Decomposition:A Noise-assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. |
| [5] |
郑近德, 程军圣, 杨宇. 改进的EEMD算法及其应用研究[J]. 振动与冲击, 2013, 32(21): 21-26. ZHENG Jin-de, CHENG Jun-sheng, YANG Yu. Modified EEMD Algorithm and Its Applications[J]. Journal of Vibration and Shock, 2013, 32(21): 21-26. |
| [6] |
WU Z, HUANG N E. A Study of the Characteristics of White Noise Using the Empirical Mode Decomposition Method[J]. Proceedings:Mathematical, Physical & Engineering Sciences, 2004, 460(2046): 1597-1611. |
| [7] |
蔡艳平, 李艾华, 徐斌, 等. 集成经验模态分解中加入白噪声的自适应准则[J]. 振动.测试与诊断, 2011, 31(6): 709-714. CAI Yan-ping, LI Ai-hua, XU Bin, et al. Adaptive Guideline of Ensemble Empirical Mode Decomposition with Gauss White Noise[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(6): 709-714. |
| [8] |
唐东明. 聚类分析及其应用研究[D]. 成都: 电子科技大学, 2010. TANG Dong-ming. Cluster Analysis and Its Application[D]. Chengdu: University of Electronic Science and Technology of China, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10614-2010234406.htm |
| [9] |
林丽, 余轮. 基于相关系数的EMD改进算法[J]. 计算与数学工程, 2008, 36(12): 28-29. LIN Li, YU Lun. Improvement on Empirical Mode Decomposition Based on Correlation Coefficient[J]. Computer and Digital Engineering, 2008, 36(12): 28-29. |
| [10] |
周晶. 基于环境振动模态参数识别随机子空间方法与应用[D]. 兰州: 兰州理工大学, 2008. ZHOU Jing. A Method and Application of Identification of Stochastic Subspace Based on Ambient Vibration Modal Parameters[D]. Lanzhou: Lanzhou University of Technology, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10731-2008113330.htm |
| [11] |
许顺国, 牟瑞芳, 张雪梅. 模糊数学综合评判法在水质评价中的应用:以成都市府河为例[J]. 唐山师范学院学报, 2007, 29(2): 68-70. XU Shun-guo, MOU Rui-fang, ZHANG Xue-mei. The Application of Fuzzy Mathematical Comprehensive Judgment to the Evaluation of Water Quality:About the Fu River in Chengdu City[J]. Journal of Tangshan Normal University, 2007, 29(2): 68-70. |
| [12] |
JING Hang, YUAN Hai-qing, ZHAO Yi, et al. Applying Hilbert-Huang Transform to Identifying Structural Modal Parameters[C]//2008 International Workshop on Education Technology and Training & 2008 International Workshop on Geoscience and Remote Sensing. Washington, D. C. : IEEE, 2008: 617-621.
|
| [13] |
PAPPAS S S, EKONOMOU L, KARAMOUSANTAS D C, et al. Electricity Demand Loads Modeling Using Auto Regressive Moving Average (ARMA) Models[J]. Energy, 2008, 33(9): 1353-1360. |
| [14] |
CARDEN E P, MITA A. Challenges in Developing Confidence Intervals on Modal Parameters Estimated for Large Civil Infrastructure with Stochastic Subspace Identification[J]. Structural Control and Health Monitoring, 2011, 18(1): 53-78. |
| [15] |
VELAZQUEZ A, SWARTZ R A. Output-only Cyclo-stationary Linear Parameter Time Varying Stochastic Subspace Identification Method for Rotating Machinery and Spinning Structures[J]. Journal of Sound & Vibration, 2015, 337: 45-70. |
| [16] |
LIN P, ZHANG N, NI B. On-line Modal Parameter Monitoring of Bridges Exploiting Multi-core Capacity by Recursive Stochastic Subspace Identification Method[C]//2008 American Control Conference. Seattle, WA: IEEE, 2008: 632-637.
|
| [17] |
LARDIES J, MINH-NGI T. Modal Parameter Identification of Stay Cables from Output-only Measurements[J]. Mechanical Systems and Signal Processing, 2011, 25(1): 133-150. |
| [18] |
单德山, 李乔, 黄珍. 桥梁动力测试信号的自适应分解与重构[J]. 振动与冲击, 2015, 34(3): 1-6. SHAN De-shan, LI Qiao, HUANG Zhen. Adaptive Decomposition and Reconstruction for Bridge Structural Dynamic Testing Signals[J]. Journal of Vibration and Shock, 2015, 34(3): 1-6. |
 2018, Vol. 35
2018, Vol. 35
