扩展功能
文章信息
- 张宝龙, 范文
- ZHANG Bao-long, FAN Wen
- 土-岩混合边坡的破坏模式研究
- Study on Failure Mode of Soil-rock Composite Slope
- 公路交通科技, 2018, 35(4): 33-39
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(4): 33-39
- 10.3969/j.issn.1002-0268.2018.04.005
-
文章历史
- 收稿日期: 2017-08-29
2. 内蒙古交通设计研究院有限责任公司, 内蒙古 呼和浩特 010010
2. Inner Mongolia Transport Design and Research Institute Co., Ltd., Huhehot Inner Mongolia 010010, China
随着我国基础设施建设的繁荣发展,与之相伴的各种边坡工程大量涌现,这些边坡的稳定性对其所附属的具体工程意义重大。一直以来,边坡的稳定性分析都是岩土工程领域一项重要的研究内容,学者们也在此方面做了大量工作。总结来看,目前的研究主要集中在模型试验研究[1]、极限平衡分析[2]、非线性理论分析[3]以及数值分析[4]几个方面,当然除了单一研究方法之外,多种方法相融合的分析方法也逐渐得到了发展,如有限元数值极限分析法[5]、可靠度-有限元法[6]等,这些方法的出现为边坡的稳定性分析不断带来新思路。
然而,对于一个工程边坡而言,再精准的稳定性计算结果都不是第一位的。众所周知,无论是稳定性分析、还是加固治理工程的方案设计、或是预测预警方案的提出,准确的失稳模式判定是首要任务,也是以上这些工作的前提条件。
早期对边坡破坏模式的研究,主要以一些简单的破坏模式为主,比如黏土的圆弧破坏[7-8]、岩块的平移块滑破坏[9]、风化黏土或斜坡基岩碎屑上的片滑破坏[10]、泥流破坏[11],以及崩塌破坏模式等[12]。以这些经典的破坏模式为基础,边坡的破坏模式研究逐渐发展得更为精细、全面,罗国煜等将火成岩地区边坡变形破坏归为15种破坏模式,对已有的圆弧破坏、崩塌等破坏模式作了进一步的细分同时,又增加了岩体松动破坏模式,发展和促进了破坏模式的研究[13]。更为复杂的组合式破坏模型也大量涌现,例如,岩崩-碎屑流组合破坏模式[14],转动滑坡-土流组合破坏模式[15]、滑动-倾倒破坏模式等[16]。与此同时,随着计算机技术的不断发展,分析过程中公式的迭代计算变得更加容易处理,一些算法的数学意义变得更加严格,采用数值计算分析边坡破坏模式已成为比较普遍的方法[17-18],使得复杂边坡工程的分析成为可能。
已有研究成果对于边坡破坏模式的研究主要以土质边坡、岩质边坡为主。然而在黄土地区,黄土大多覆盖在基岩或者冲积层之上,在公路建设过程中就常会形成土-岩二元结构的边坡,定性来看,其破坏模式大致可有滑坡、崩塌两大类,但是在具体的情况下何时发生滑动?何时产生崩塌?这就值得我们去进行理论探索。
基于此,首先从力学机制上对边坡发生不同破坏模式的条件进行界定,在此基础上借助数值模拟对实际工程中某土-岩混合边坡的破坏模式进行研究,并探讨不同因素对于土-岩二元结构边坡破坏模式的影响,为边坡工程实践提供依据。
1 破坏模式判别依据对于土-岩二元结构的边坡,其稳定性与下伏基岩的倾斜程度、土-岩接触带的含水状况,以及上覆土层自身性质有关,一般定性理解其最有可能的破坏方式就是沿基底接触面的滑动破坏、上覆土层内部的滑动破坏,以及崩塌破坏[19],至于具体发生何种破坏,首先就需要从力学上对发生不同破坏形式的条件进行界定。
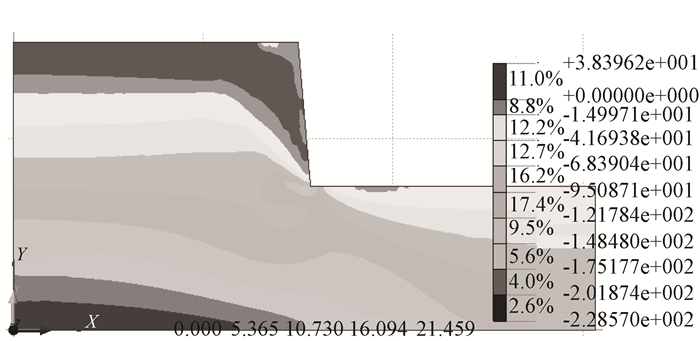
在重力作用下,边坡坡顶岩土体受到水平张拉应力作用,张应力区主要分布在离坡面一定距离处,从坡顶近似向下发展(图 1)。往往实验室强度测试时土体可以表现出一定的抗拉强度[20],然而在现场,坡体表面存在的水、裂缝都可以破坏土体的抗拉强度,所以土体的抗拉强度是不可靠的,在对边坡破坏模式进行分析时,可以将较陡边坡坡面附近的张应力区简化为一条张性裂缝。
|
| 图 1 坡体内张拉应力分布(单位:kN/m2) Fig. 1 Distribution of tension stresses in slope(unit:kN/m2) |
| |
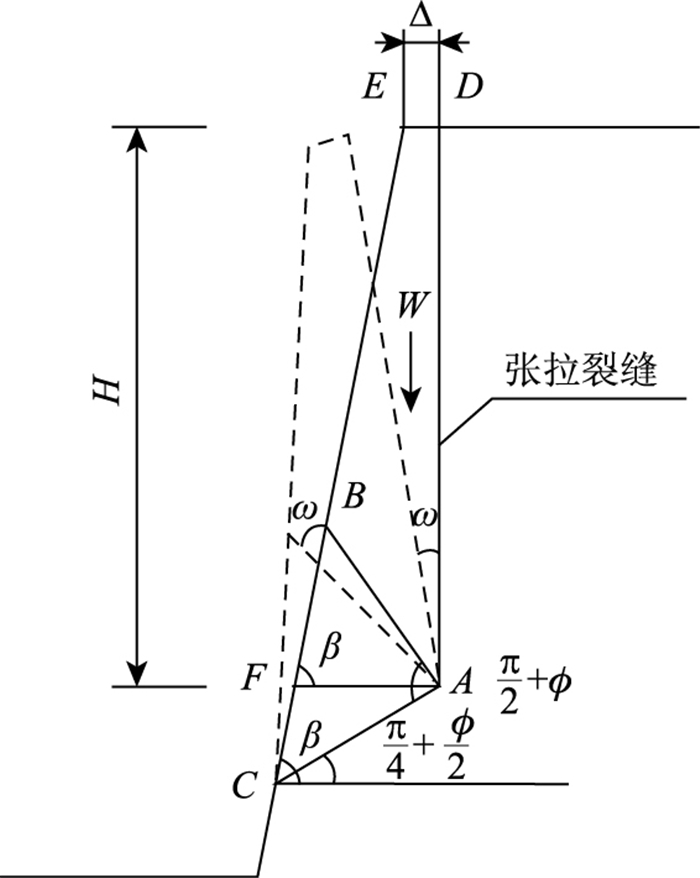
由于崩塌破坏形式上主要表现为岩土体的翻转、滚动和弯曲折断,因此可以把边坡发生崩塌破坏的结构模型简化为如图 2所示的一个包含简单张裂缝和均匀剪切区ABC的旋转机构,即厚度为Δ的土坯可能以角速度ω绕A点倾倒发生崩塌破坏。其中:ϕ是材料的内摩擦角;H可以认为是张应力发展深度;Δ为拉应力外边界到坡面的距离。
|
| 图 2 边坡崩塌破坏的旋转机构 Fig. 2 Rotation mechanism of slope collapse failure |
| |
由于发生崩塌破坏的边坡坡度较陡,可以近似的认为大主应力的方向是竖直方向,所以均匀剪流场ABC的下边界AC为一与水平面呈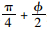
根据极限分析的上限定理,如果任意假想破坏机构的外力所做的功率,超过了内部能量耗损率,则土体不可能承受所施加的荷载。对任意有效的破坏机构,令外功率等于内功率,便可得到破坏荷载或者极限荷载的一个不安全的上限。
假设土体不能抗拉,此时,在简单张裂缝内,没有能量耗损,在裂缝面上,正应力和剪应力均等于零。则均匀剪切区ABC内部的单位体积能量耗损可根据式(1)[21]:
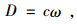
|
(1) |
式中,c为土体的黏聚力;ω为剪切应变率。
若ABC厚度取1时,总的内部能量耗损率恰是D与三角形ABC面积的乘积,根据几何关系有:
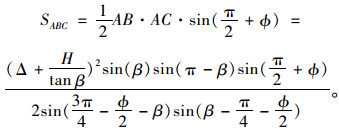
|
(2) |
则均匀剪切区总的能量耗损率D内可按下式计算:
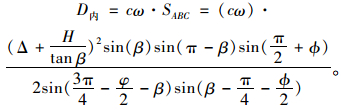
|
(3) |
重力所做的外功率是土坯ACED向下运动的重量与速度竖直分量的乘积,则重力所做的外功率为:
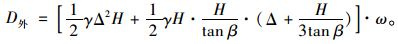
|
(4) |
令外功率等于内部能量耗损,即,式(3)=式(4);且令
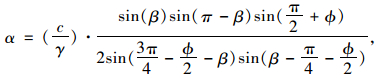
|
则可得式(5):

|
(5) |
解此方程有:
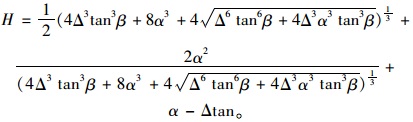
|
(6) |
当β=π/2时,(7)式也就是不抗拉竖直土质边坡的临界高度,此时
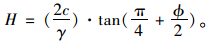
|
(7) |
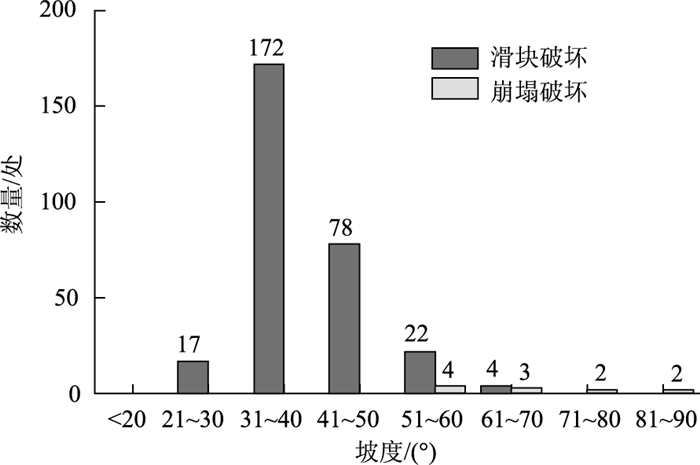
式(6)和式(7)给出了存在张性裂缝土质边坡维持自稳的极限高度,那么从理论上来看,当张性裂缝的发育深度大于该式计算值时,土坯将发生翻转产生崩塌破坏;而小于此计算值时则剪切滑移破坏,破坏模式表现为滑坡。从式(6)还可以看出,边坡张性裂缝土坯自稳的极限高度H受边坡坡角β影响较大,这符合崩塌一般发生在较陡边坡这一普遍规律。根据张茂省等人[22]对黄土边坡破坏模式的调查结果(图 3),可以发现在坡度小于50°时,边坡的破坏模式主要为滑坡破坏,坡度在51°~70°之间时,不稳定边坡破坏模式仍以滑坡为主,并伴有崩塌;当边坡大于70°时,基本不发生滑坡,主要破坏模式为崩塌。
|
| 图 3 滑坡、崩塌初始坡度对比 Fig. 3 Comparison of initial slopes of collapse and landslide |
| |
2 算例分析
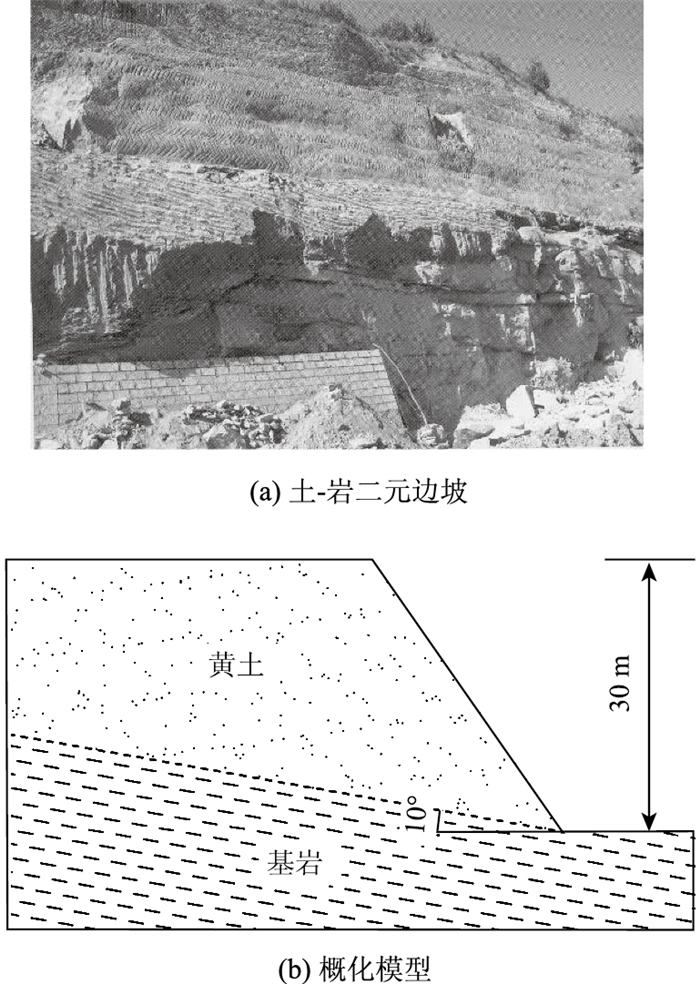
借助某实际工程中土-岩二元结构边坡,对其破坏模式开展研究,如图 4所示。坡高30 m,上覆土层黏聚力C1=22 kPa,摩擦角ϕ1=24°,土-岩接触面黏聚力C2=11 kPa,摩擦角ϕ2=12°,接触面倾角β2=10°,其他岩土体参数见表 1。数值计算借助Midas-GTS计算软件,此处数值模型中保持边坡土-岩接触面的产状不变,着重考察坡高、坡角对此类边坡破坏模式的影响。
|
| 图 4 某土-岩二元边坡及其概化模型 Fig. 4 A soil-rock dual structure slope and its simplified model |
| |
| 材料 | 重度γ/(kN·m-3) | 弹性模量E/MPa | 泊松比ν |
| 上覆土层 | 19 | 28 | 0.3 |
| 接触面 | 18 | 20 | 0.32 |
| 下覆基岩 | 23 | 10 000 | 0.25 |
2.1 坡角对破坏模式的影响
首先借助有限元计算软件,对边坡坡角β在40°~90°区间变化时,坡体内拉张应力区的分布及变化进行计算。计算模型采用摩尔-库仑屈服准则和相关联的流动准则。
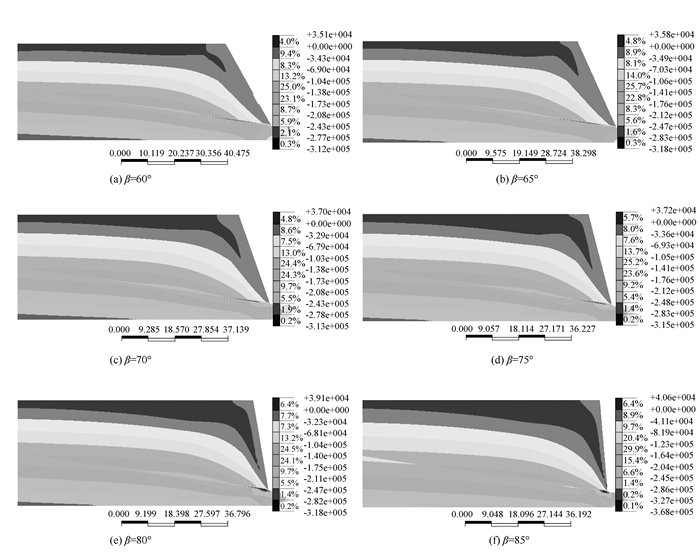
图 5给出了不同坡角时边坡内拉张区的分布,由图可见,随着坡度的增加,边坡拉张应力区在不断扩展,其深度也在不断增加。并且随着坡度变陡,拉张区越靠近坡面。
|
| 图 5 不同坡角下边坡内部拉应力区分布(单位:N/m2) Fig. 5 Distributions of tension stresses in slopes with different slope angles(unit:N/m2) |
| |
基于有限元计算结果,量取边坡拉应力的发展深度H和旋转倾倒土坯的宽度Δ,量取方式参照图 2,其结果见表 2所示。并根据所量取的土坯宽度Δ,带入前面边坡极限高度上限解公式,求出旋转土坯的稳定高度[H],并将H和[H]进行比较分析,H=[H]时的坡角,则是该条件下边坡发生倾倒崩塌破坏的最小坡角。
| 坡角β/° | Δ/m | 拉应力发展深度H/m | 稳定张拉高度[H]/m |
| 50 | 3.71 | 7.68 | — |
| 55 | 3.9 | 9.21 | — |
| 60 | 5.45 | 10.71 | 41.1 |
| 65 | 4.54 | 13.98 | 12.5 |
| 70 | 4.31 | 15.04 | 7.83 |
| 75 | 3.15 | 18.76 | 5.69 |
| 80 | 2.62 | 23.55 | 4.79 |
| 85 | 1.36 | 29 | 4.11 |
| 90 | 0 | 30 | 3.56 |
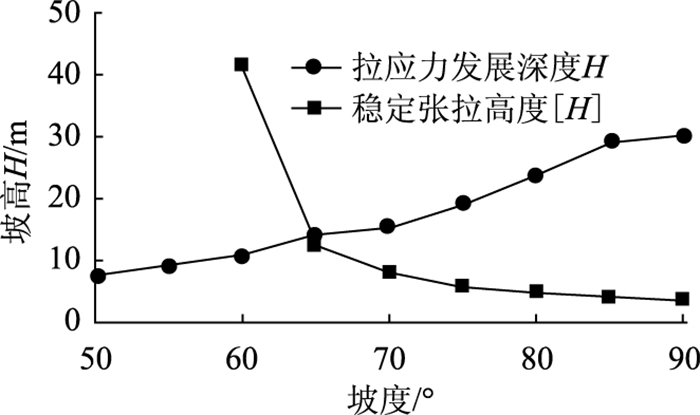
图 6给出了不同坡角时边坡内部拉应力发展深度曲线和边坡稳定张拉高度曲线。由图 6可见,在给定条件下,此土-岩二元结构边坡发生倾倒崩塌破坏的临界坡角应在65°左右。当坡角小于65°时,边坡的稳定张拉高度[H]远大于拉应力发展深度H,此时边坡最有可能发生因为抗剪强度不足而引发滑坡破坏,具体的滑动类型可进一步通过计算分析;而当边坡坡度大于65°时,边坡会因为拉张区扩展而发生崩塌破坏。当然坡角在65°左右时,两种模式的破坏均有可能发生。
|
| 图 6 不同坡角下边坡内拉应力发展深度与稳定张拉高度对比 Fig. 6 Tensile depth vs. stable height for slopes with different slope angles |
| |
2.2 坡高对破坏模式的影响
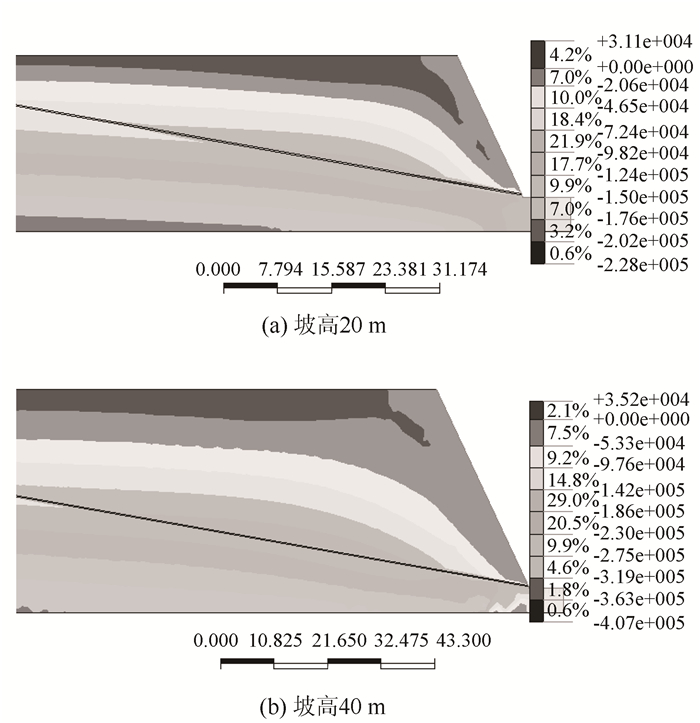
取坡角β图 6中的65°,岩土体的材料参数与前文表 1相同,研究坡高在20~45 m范围变化时,边坡拉应力区的分布及变化。以坡高为20 m和40 m为例,边坡内拉张区的分布如图 7所示。表 3给出了不同坡高时土坯宽度、拉应力发展深度H和边坡稳定高度[H],由结果可见,坡高变化对拉应力深度H的大小及分布的影响很小,且坡高在20~45 m范围内时,H始终稍大于[H]。所以根据稳定性判别结果,对于本文给定条件下65°坡角的土-岩二元结构边坡,在坡高小于45 m时,其破坏模式应属于滑坡破坏与崩塌破坏的临界点附近,两种破坏模式均有可能发生,且发生崩塌破坏的概率理论上会稍大一些。
|
| 图 7 不同坡高下边坡内部拉应力区分布(单位:N/m2) Fig. 7 Distribution of tension stresses in slopes with different slope heights(unit:N/m2) |
| |
| 坡高/m | Δ/m | 拉应力发展深度H/m | 稳定张拉高度[H]/m |
| 20 | 3.84 | 13.38 | 12.7 |
| 25 | 3.37 | 13.59 | 12.82 |
| 30 | 5.27 | 13.98 | 12.5 |
| 35 | 5.59 | 14.11 | 12.48 |
| 40 | 5.41 | 14.15 | 12.49 |
| 45 | 5.78 | 14.26 | 12.46 |
3 结论
本研究首先基于理论分析对边坡不同破坏形式的条件进行了探讨,以此为基础结合某土-岩二元结构边坡,就坡度、坡高对破坏模式的影响进行了研究,得到结论如下:
(1) 通过理论分析发现:相对于坡高而言坡角的变化对坡体内拉应力大小及分布影响显著,所以坡角是引起边坡破坏模式转变的主要因素,这符合实际规律。
(2) 对于本研究中30 m高的土-岩二元结构边坡而言,当坡度在65°左右时是其滑坡、崩塌破坏的理论界限:小于此坡角时可能的破坏模式以滑坡为主;大于此坡角时崩塌破坏概率增加;当然在界限值附近,可能会存在崩塌、滑坡破坏形式共存的情况。保持坡度在65°左右,坡高在20~45 m范围变化时,对破坏模式几乎不产生影响。
(3) 本研究可为类似边坡破坏模式及稳定性研究提供一定参考,但对于具体边坡工程建议可参考本研究分析思路进行具体分析。
| [1] |
关振长, 廖重辉, 龚振峰, 等. 基于振动台模型试验的二元结构边坡地震动力响应研究[J]. 工程地质学报, 2017, 25(1): 139-146. GUAN Zhen-chang, LIAO Zhong-hui, GONG Zhen-feng, et al. Seismic Response of Dual Structure Slope Based on Shaking Table Model Test[J]. Journal of Engineering Geology, 2017, 25(1): 139-146. |
| [2] |
于斯滢, 邵龙潭, 刘士乙. 基于有限元极限平衡法的尾矿坝坝体稳定分析[J]. 岩土力学, 2013, 34(4): 1185-1190. YU Si-ying, SHAO Long-tan, LIU Shi-yi. Stability Analysis of Tailings Dam Based on Finite Element Limit Equilibrium Method[J]. Rock and Soil Mechanics, 2013, 34(4): 1185-1190. |
| [3] |
ZHANG J, HUANG H W, ZHANG L M, et al. Probabilistic Prediction of Rainfall-induced Slope Failure Using a Mechanics-based Model[J]. Engineering Geology, 2014, 168: 129-140. |
| [4] |
戴自航, 徐祥. 边坡抗滑桩设计计算的三维有限元法[J]. 岩石力学与工程学报, 2012, 31(12): 2572-2578. DAI Zi-hang, XU Xiang. 3D Finite Element Method for Design Computations of Anti-slide Piles[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(12): 2572-2578. |
| [5] |
李典庆, 肖特, 曹子君, 等. 基于极限平衡法和有限元法的边坡协同式可靠度分析[J]. 岩土工程学报, 2016, 38(6): 1004-1013. LI Dian-qing, XIAO Te, CAO Zi-jun, et al. Auxiliary Slope Reliability Analysis Using Limit Equilibrium Method and Finite Element Method[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(6): 1004-1013. |
| [6] |
吴谦, 毛雪松, 刘龙旗, 等. 某弃渣场边坡稳定性的可靠度分析[J]. 桂林理工大学学报, 2017, 37(3): 475-480. WU Qian, MAO Xue-song, LIU Long-qi, et al. Stability Reliability Analysis of an Abandoned Dreg Site Slope[J]. Journal of Guilin University of Technology, 2017, 37(3): 475-480. |
| [7] |
PETTERSON K E. The Early History of Circular Sliding Surfaces[J]. Geotechnique, 1955, 5(4): 275-296. |
| [8] |
蒋楚生. 土质边坡最不利圆弧滑面及稳定系数解析解法[J]. 铁道工程学报, 2008, 25(6): 24-27. JIANG Chu-sheng. A Theoretical Solution of the Most Disadvantageous Circular Sliding Surface and Its Stability Coefficient for Soil Slide Slope[J]. Journal of Railway Engineering Society, 2008, 25(6): 24-27. |
| [9] |
BENSON W N. Landslides and Their Relation to Engineering in the Dunedin District, New Zealand[J]. Economic Geology, 1946, 41(4): 328-347. |
| [10] |
SKEMPTON A W. Soil Mechanics in Relation to Geology[J]. Proceedings of the Yorkshire Geological Society, 1953, 29(1): 33-62. |
| [11] |
LEGGET R F, BARTLEY M W. An Engineering Study of Glacial Deposits at Steep Rock Lake, Ontario, Canada[J]. Economic Geology, 1953, 48(7): 513-540. |
| [12] |
DORREN L K A. A Review of Rockfall Mechanics and Modelling Approaches[J]. Progress in Physical Geography, 2003, 27(1): 69-87. |
| [13] |
罗国煜, 王培清, 吴浩. 火成岩地区露采边坡主要变形破坏类型和模式[J]. 岩土工程学报, 1986, 8(6): 26-36. LUO Guo-yu, WANG Pei-qing, WU Hao. MAIN Types and Models of the Deformation and the Failure of Rock Slopes in Area of Igneous Rock[J]. Chinese Journal of Geotechnical Engineering, 1986, 8(6): 26-36. |
| [14] |
孙新坡, 何思明, 刘恩龙, 等. 基于SPH法的岩崩碎屑流与防护结构相互作用分析[J]. 山地学报, 2016, 34(3): 331-336. SUN Xin-po, HE Si-ming, LIU En-long, et al. Analysis of Rockfall Debris-obstacle Interaction with SPH Method[J]. Mountain Research, 2016, 34(3): 331-336. |
| [15] |
NĚMCOK A, PAŠEK J, RYBÁR J. Classification of Landslides and Other Mass Movements[J]. Rock Mechanics, 1972, 4(2): 71-78. |
| [16] |
中国科学院地质研究所. 岩体工程地质力学问题(三)[M]. 北京: 科学出版社, 1987. Institute of Geology and Geophysics, Chinese Academy of Sciences. Mechanical Problems in Rock Geology Engineering (3)[M]. Beijing: Science Press, 1987. |
| [17] |
杨铭键, 余贤斌, 黎剑华. 基于ANSYS与FLAC的边坡稳定性对比分析[J]. 科学技术与工程, 2012(24): 6241-6244, 6251. YANG Ming-jian, YU Xian-bin, LI Jian-hua. Comparative Analysis for Slope Stability by ANSYS and FLAC[J]. Science Technology and Engineering, 2012(24): 6241-6244, 6251. |
| [18] |
刘蕾, 陈亮, 崔振华, 等. 逆层岩质边坡地震动力破坏过程FLAC/PFC~(2D)耦合数值模拟分析[J]. 工程地质学报, 2014(6): 1257-1262. LIU Lei, CHEN Liang, CUI Zhen-hua, et al. FLAC/PFC 2D Hybrid Simulation for Seismically Induced Failure Process of Toppling Rock Slope[J]. Journal of Engineering Geology, 2014(6): 1257-1262. |
| [19] |
张倬元, 王士天, 王兰生, 等. 工程地质分析原理[M]. 北京: 地质出版社, 2005. ZHANG Zhuo-yuan, WANG Shi-tian, WANG Lan-sheng, et al. Analysis of Engineering Geology[M]. Beijing: Geological Publishing House, 2005. |
| [20] |
LU Ning, LIKOS W J. 非饱和土力学[M]. 韦昌富, 侯龙, 简文星, 译. 北京: 高等教育出版社, 2012. LU Ning, LIKOS W J. Unsaturated Soil Mechanics[M]. WEI Chang-fu, HOU Long, JIAN Wen-xing, translated. Beijing: Higher Education Press, 2012. |
| [21] |
王根龙, 张军慧, 李巨文, 等. 公路岩质边坡稳定性评价的能量法研究[J]. 公路交通科技, 2009, 26(12): 1-6, 16. WANG Gen-long, ZHANG Jun-hui, LI Ju-wen, et al. Study on Energy Method for Estimation of Highway Rock Slope Stability[J]. Journal of Highway and Transportation Research and Development, 2009, 26(12): 1-6, 16. |
| [22] |
张茂省. 延安宝塔区滑坡崩塌地质灾害[M]. 北京: 地质出版社, 2008. ZXHANG Mao-sheng. Landslide and Collapse Disasters in Baota District, Yanan[M]. Beijing: Geological Publishing House, 2008. |
 2018, Vol. 35
2018, Vol. 35
