扩展功能
文章信息
- 柳伍生, 周向栋, 贺剑, 李甜甜, 谌兰兰
- LIU Wu-sheng, ZHOU Xiang-dong, HE Jian, LI Tian-tian, CHEN Lan-lan
- 基于多需求响应的定制公交绿色线网优化
- Optimization of Green Customized Public Transport Network Based on Multiple Demand Response
- 公路交通科技, 2018, 35(3): 132-142
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(3): 132-142
- 10.3969/j.issn.1002-0268.2018.03.018
-
文章历史
- 收稿日期: 2017-02-09
随着社会经济的发展,城市拥堵也越来越严重,城市公共交通是减缓拥堵的可行方法。作为替代私家车出行的高端公共交通服务的定制公交,主要为出行起讫点、出行时间和服务水平要求相似的人群提供量身定制的交通服务,也称商务班车[1-3]。定制公交根据乘客出行时间、地点和服务需求设定运行线路,采用一站直达的公交服务模式,具有“定点、定线、定车、定时、定价、定人”等特点[4-5]。目前定制公交发展迅速,作为影响定制公交服务质量重要指标的定制公交网络规划也引起了国内外诸多学者的研究。
目前国外对于定制公交系统理论的研究方面较早,K. An等[6]提出了区间不确定性随机理论对公交线网进行了优化研究,N. Nassir等[7]通过阻抗访问理论对定制公交网络进行了优化,K. Kerkma等[8]提出了多维空间结合的公交网络优化理论。国内学者对定制公交系统的理论研究还相对较迟,定制公交研究主要集中于空间结构优化[9]、定制公交车型研究[10]、定制公交线路研究[11-12]、定制公交调度研究[13-15]、定制公交站点布局选址研究[16-17]。对于系统层面的定制公交网络规划研究较少,程立勤[18]基于点线面层次分析法研究了定制公交线网布局。徐杨等[19]以大规模个性化定制模型为基础,从市场需求出发构建了不同的公交线路规划模型。国内外研究几乎没有从网络总体层次对定制公交进行规划研究,存在很多不足,本研究将主要对城市定制公交线网优化设计进行研究。
目前国内外学者多集中于定制公交车辆、线路及站点研究,但对于定制公交线网整体系统研究较少,对于定制公交服务的多种模式没有系统整理研究。鉴于此,我们系统研究了定制公交服务模式,在已知乘客需求的条件下,考虑定制公交需求服务率、平均上座率,结合绿色交通理论,以运营距离成本、运营时间成本、运营环保成本、运营固定成本定制公交总成本3方面最优为目标,建立多种需求响应机制下的绿色定制公交线网优化模型,并提出基于蚁群算法和精确数学算法的分层线网混合求解算法。
1 定制公交线网规划模型 1.1 问题描述定制公交线网优化问题一般可分为4类问题,即单出发地单目的地(以下称单对单), 单出发地多目的地(以下称单对多),多出发地单目的地(以下称多对单),多出发地多目的地(以下称多对多)这4类定制公交线网优化问题。单对单定制公交对应于城市应急车辆、商务班车、旅游班车、临时需求车辆、特殊需求车辆。单对多定制公交对应于单个大型区域至多个目的地的企业通勤车辆、中小学校校车。多对单定制公交对应于多个出发地至单个大型区域的企业、公务员通勤车辆、中小学校车。多对多定制公交对应于多个出发地至多个目的地的企业联合协同、校园联合协同、市政单位联合协同通勤车辆。以上4个问题中除单对单定制公交线网优化问题外,通过整合处理在同一模型下解决。
针对多需求响应的定制公交线网优化问题可描述为:已知若干交通出行小区和若干交通目的小区以及对应的上下车站点,每辆定制公交车从任意上车站点出发,经过若干上车站点,到达若干下车站点,每个下车站点有对应的时间窗要求,满足公交需求、服务率,形成定制公交线网,对其线网进行优化。
1.2 参数设置针对多需求响应定制公交线网优化问题,已知n个交通出行小区Ai, i=1, 2, …, n,m个交通目的小区Bj, j=1, 2, …, m,q(AiBj)为交通出行小区Ai到交通目的小区Bj的交通出行量,每个出行小区分别对应于上车站点Ai, i=1, 2, …, n,每个目的小区分别对应于下车站点Bj, j=1, 2, …, m,每个站点服务周边1 km范围内的交通出行量或交通吸引量、上车站点、下车站点位于道路路网上。上车站点Ai的坐标为(x1, y1), (x2, y2), …, (xi, yi), 下车站点Bj的坐标为(x11, y11), (x21, y21), …, (xj1, yj1), 点间距离为考虑城市交通组织和路网结构的车辆行驶距离和运行时间距离,相应的行驶距离矩阵和时间距离矩阵分别用L和T表示,L={l(Ai, Aj, Bp, Bq), i, j=1, 2, …, n, p, q=1, 2, …, m},T={t(Ai, Aj, Bp, Bq), i, j=1, 2, …, n, p, q=1, 2, …, m},各个站点间的时间距离和行驶距离已知,上车站点Ai至下车站点Bj的行驶距离、时间距离分别为l(Ai, Bj),t(Ai, Bj),定制公交线网的线路RL={Ai, …, Ak→Bj, …, Bq, i, k=1,2, …, n, j, q=1,2, …, m},即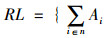
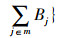
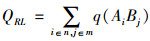

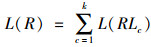
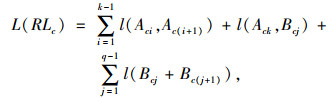
|
(1) |
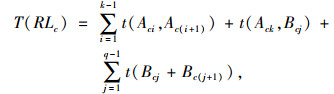
|
(2) |
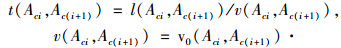
|
(3) |

|
(4) |
式中,l(Aci, Ac(i+1))为两个站点间的距离;l(Ack, Bcj)为上车站点和下车站点间的距离; l(Bcj+Bc(j+1))为两个下车站点间的距离;t(Aci, Ac(i+1))为两个上车站点间的时间距离;t(Ack, Bcj)为上车站点和下车站点间的时间距离;t(Bcj+Bc(j+1))为两个下车站点间的时间距离;v(Aci, Ac(i+1))为两个站点间道路的运行速度,v0(Aci, Ac(i+1))为两个站点间的设计运行速度;Q(Aci, Ac(i+1))为两个站点间的设计通行能力;q(Aci, Ac(i+1))为两个站点间的实际流量,可由百度、高德等地图实时得到。
线路c中定制公交到达下车站点Bj的距离为L(RLcBj),定制公交线网总里程时间T(R)=
由以上参数构建定制公交线网总模型,从公交企业、乘客、社会3方面综合考虑建立如下优化目标模型:
(1) 定制公交需求服务率最大,由于路网需求分布原因,定制公交线网规划不可能满足所有用户需求,但使需求服务覆盖率最大,剩余需求在后期解决。
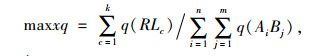
|
(5) |
式中,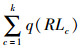
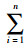
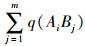
(2) 定制公交线网的平均上座率最高,即定制公交的资源利用率最大,节约社会成本,公交资源配置最优。
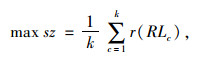
|
(6) |
式中r(RLc)为上座率。
(3) 定制公交总成本最小,即定制公交公司投入成本最小,使定制公交线网更加节约高效。
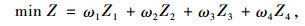
|
(7) |
式中,Z为总成本;Z1为运营距离成本;Z2为运营时间总成本;Z3为运营环保成本;Z4为运营固定成本;ω1,ω2,ω3,ω4分别为各成本的权重。
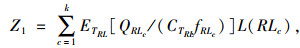
|
(8) |
式中,Z1为运营距离成本,可以用运输成本来表示,主要包括车辆固定成本、驾驶员费用、油耗成本等;ETRL为定制公交车型为TRL时每辆定制公交车每公里的油耗成本;QRLc为线路RLc的线路流量;CTRL为线路RLc所采用的定制公交车型容量;fRLc为线路RLc的线路发车频次;L(RLc)为线路RLc的实际运营距离。本研究对固定成本单独计算。运营距离成本通过油耗成本来简化计算,其他固定费用归入固定成本中计算。

|
(9) |
式中,Z2为运营时间成本,即运营时间成本与拥堵后产生的额外运营拥堵成本之和(即对社会造成的拥堵成本);FTRL为定制公交车型为TRL时每辆定制公交车单位时间的时间成本;QRLc为线路RLc的线路流量;CTRL为线路RLc所采用的定制公交车型容量;fRLc为线路RLc的发车频次;T(RLc)为线路RLc的实际运营时间;GTRL为定制公交车型为TRL时每辆定制公交车单位时间的拥堵时间成本;T(RLc)为线路RLc的正常道路情况下的行驶时间。
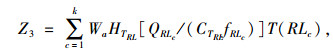
|
(10) |
式中,Z3为运营环保成本,即污染成本;Wa单位污染物排放量的环境污染成本;HTRL为定制公交车型为TRL时每辆定制公交车每小时排放的污染物排放量;QRLc为线路RLc的线路流量;CTRL为线路RLc所采用的定制公交车型容量;fRLc为线路RLc的线路发车频次;T(RLc)为线路RLc的实际运营时间。

|
(11) |
式中,Z4为运营固定成本,包含驾驶员工资、公交车日常维修费用、公交公司日常管理费用等;ITRL为定制公交车型为TRL时每辆定制公交车每天的固定运营成本;QRLc为线路RLc的线路流量;CTRL为线路RLc所采用的定制公交车型容量;fRLc为线路RLc的线路发车频次。
约束条件:
(1) 任意线路的上座率满足最低的定制公交上座率:
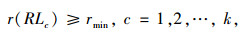
|
(12) |
式中rmin为考虑企业成本的最低上座率。
(2) 任意线路的定制公交到达任意下车站点符合任意下车站点的时间要求:

|
(13) |
式中,tcdBj为线路c中任意下车站点Bj规定到达的最迟时间;tc0为线路c定制公交的出发时间;T(RLcBj)为线路c中定制公交到达任意下车站点Bj的实际运行时间;tcbBj为线路c中任意下车站点Bj规定到达的最早时间。
(3) 任意线路的任意上车站点到达任意下车站点的距离不大于该上车站点直达下车站点距离的α倍,保证定制公交比普通公交的优越性:

|
(14) |
(4) 任意线路的任意上车站点到达任意下车站点的时间不大于该上车站点直达下车站点时间的β倍,保证定制公交比普通公交的优越性:

|
(15) |
从而构建定制公交线网优化的总模型(多对多):

|
(16) |

|
(17) |

|
(18) |

|
(19) |

|
(20) |
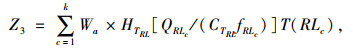
|
(21) |

|
(22) |

|
(23) |

|
(24) |

|
(25) |
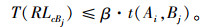
|
(26) |
若n=1,就转化为单对多定制公交线网优化问题,总模型即转化为单对多的定制公交线网优化模型。
1.3.3 多对单定制公交线网优化模型若m=1,就转化为多对单定制公交线网优化问题,总模型即转化为多对单的定制公交线网优化模型。
2 定制公交线网规划模型算法定制公交线网规划模型算法拆分为3个部分解决,即分为上车线网与下车线网连接、上车线网规划、下车线网规划3个部分。
2.1 上车线网与下车线网连接算法上车线网与下车线网连接算法,可得到上车点区域与下车点区域的两区域的最近两个站点,通过聚类分析得到上车点区域距离下车点区域的最近一个站点C和下车点区域距离上车点区域的最近一个站点D。
上车站点Ai的坐标为(x1, y1), (x2, y2), …, (xi, yi), 下车站点Bj的坐标为(x11, y11), (x21, y21), …, (xj1, yj1), 上车站点Ai到下车站点Bj的欧式距离
通过遍历每个点寻找两个区域之间最短的两个点。
2.2 上车线网规划算法上车线网规划算法,通过上车站点C、下车站点D、上车点区域A与下车站点D之间的上车线网规划问题,得到上车线网路径,同时满足车型容量约束和上座率约束,得到上车线网的成本。
对于上车线网规划问题,即为NP-hard问题,实质是为求解最优排列的问题,蚁群算法在求解路径寻优问题上有明显优势,本研究采用蚁群算法求解。
2.2.1 上车线网模型结构分析上车线网模型结构由定制公交线路数量、每条线路采用的车型、每条线路的行车路径、每个站点节点的上车人数4个部分构成。行车路径由节点路径表示,为定制公交车辆经上车站点的有序组合,如RLc={TRLc; Ac1, Ac2, …, Acn; q(Ac1), q(Ac2), …, q(Ack)}, 定制公交线路c选择定制公交车型TRLc,该上车线路的行驶路径选择为Ac1→Ac2→…→Ack→D, 在第i个上车点的上车人数为q(Aci),线路c的乘客数量为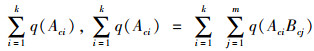
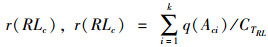
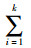


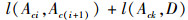

(1) 上车点排序。将所有上车点按与最近下车点D的距离远近排序,选择最远上车点为可行搜索的起始点,在最远点满足需求的情况下,以第2远点为起始点,以此类推。
(2) 禁忌表。作为蚁群算法核心的禁忌表决定蚁群搜索的原则和方向,本算法禁忌表包含距离、时间、容量3方面内容,分别对应上车线网的距离约束、时间约束、容量约束。
节点全集为TS,假设蚁群搜索当前线路记为RLc,当前服务节点为Aci,需求已被完全服务的节点集为DS,需求未被完全服务的节点集为NS,存在:DS+NS=TS。
蚁群当前已加入路径的节点集为SS,DS⊆SS。
禁忌表为Tabu,对于任意节点Ack,Ack∈NS,若

|
(27) |
则将Aci加入Tabu,加入该节点后路径超出长度约束,无法满足定制公交出行需求。
若节点Aci满足长度约束,若

|
(28) |
则将Aci加入Tabu,加入该节点后路径超出时间约束,无法满足定制公交出行需求。
若节点Aci满足长度约束与时间约束,同时Aci当前剩余未被服务的需求q(Aci),满足
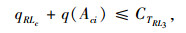
|
(29) |
式中,qRLc为线路RLc目前已服务的需求总量。节点Aci能被线路RLc服务的需求量必然小于该线路采用最大定制公交车型时的剩余容量,即其可被线路RLc服务的需求量为:
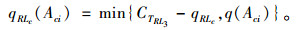
|
(30) |
若节点Aci被选择为下个服务点,则其剩余未被服务的需求量为:

|
(31) |
若q(Aci)=0,则将节点Aci置入节点集DS。线路RLc的服务需求总量更新为:
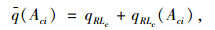
|
(32) |
同时,线路RLc的车型更改为最合适的车型,即:

|
(33) |
如此,蚁群搜索直至NS=Φ为空集时,迭代结束。
2.2.3 信息素更新为防止出现无效解,在蚁群搜索时,对于未满足线路开通条件的需求也以线路的形式服务,在进行解码的同时,剔除未满足上座率的需求点,再计算定制公交方案的服务率。
在搜索得到完整解后,需要进行模型目标函数值计算。按最优解的路径更新全局信息素。对多目标模型,通过归一化处理判断解优越性。
(1) 对于最大化目标。假定fb和fw分别为到目前为止搜索到的单个目标函数的最优解和最差解,评价任意解fi的适应性oi:

|
(34) |
(2) 对于最小化目标。假定fb和fw分别为到目前为止搜索到的单个目标函数的最优解和最差解,评价任意解fi的适应性oi:

|
(35) |
蚁群i搜索到的解的总适应性osi为:
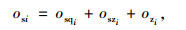
|
(36) |
式中,osqi为需求目标下的适应性;oszi为上座率目标下的适应性;ozi为成本目标下的适应性。
每次迭代完成,进行适应性从大到小排序,选择适应性排名前5位解进行路径信息素迭代。迭代方法:
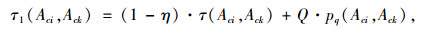
|
(37) |
式中,τ(Aci, Ack)为节点对(Aci, Ack)的信息素浓度;τ1(Aci, Ack)为更新后节点对(Aci, Ack)的信息素浓度;η为挥发系数;Q为迭代留下的信息量;pq(Aci, Ack)表示若路径Aci→Ack存在于解q中,则pq(Aci, Ack)=1,否则pq(Aci, Ack)=0。
2.2.4 上车线网算法步骤不固定蚁群数量,每次增加1只蚂蚁,直至该蚂蚁完成其路径搜索,若剩余总需求量不满足结束条件,则继续增加蚁群数量。迭代结束的条件为NS=Φ。从而得到蚁群算法求解定制公交上车线网规划模型的完整步骤为:
Step 1 初始化蚁群参数和全局信息素。设置蚁群总数G和算法总迭代次数N,当前迭代次数iter=1。
Step 2 当前蚁群序号ag=1。
Step 3 蚁群ag中蚂蚁数量as=1,蚁群置于最远的服务点。
Step 4 对于蚁群ag, 搜索所有需求点,并按式(28)更新该蚁群禁忌表Tabu。
Step 5 对于蚁群ag, 搜索所有需求点,再按式(29)更新该蚁群禁忌表Tabu。
Step 6 结合禁忌表Tabu,按节点间的信息素浓度选择下一需求服务点Ack,并按式(32)~(36)更新需求点状态和线路状态。
Step 7 若服务点Ack的剩余需求量为0,则将Ack加入DS节点集,并从NS节点集中删去Ack。
Step 8 若NS不为空,且第ag蚁群的禁忌表Tabu为空,则将该蚁群蚂蚁数量asag=asag+1, 返回Step 4。
Step 9 若NS为空,则蚁群ag的一次迭代结束,记录该蚁群的解,计算模型目标函数值;ag=ag+1。
Step 10 若ag≤G,转Step 3;否则,更新算法最优解,并更新全局信息素。
Step 11 若iter≤N,转Step 2;否则,输出算法最优解。
2.3 下车线网规划算法通过得到的上车线路,再依据乘客的上车出行需求,得到相应的下车站点及下车人数。对相应的下车站点组合优化得到下车线网路径、下车线网成本及相应下车站点的到达时间。
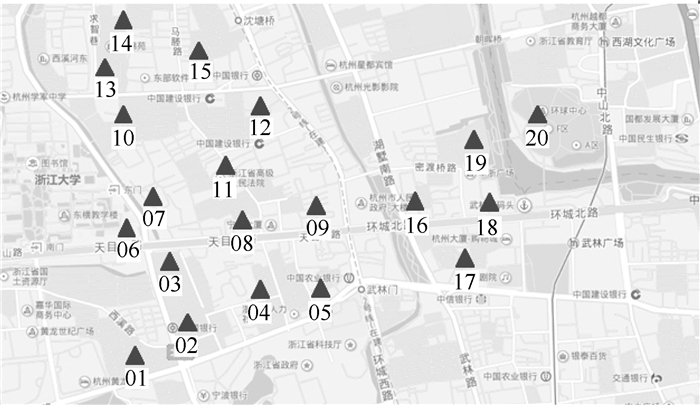
3 算例选择杭州市公交集团的定制公交班车客源需求数据为研究数据,本算例研究多对多定制公交问题,进行多对多定制公交线网优化模型及算法的研究。需求分布数据共包含15个交通出行小区和5个交通目的小区,交通出行小区编号为1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,交通目的小区编号为16, 17, 18, 19, 20。上、下车站点编号及需求数据如图 1,表 1,表 2所示,上、下车站点距离矩阵部分如表 3所示。
|
| 图 1 上下车站点需求分布图 Fig. 1 Demand distribution map of on-off stations |
| |
| 编号 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 |
| 上车点 | 友谊 | 松木场 | 松溪 | 金祝 | 胜利新村 | 浙大西溪 | 建华 | 武林花园 |
| 上车人数/人 | 16 | 21 | 10 | 30 | 26 | 8 | 13 | 26 |
| 编号 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 上车点 | 锦秀 | 文三新村 | 文天 | 武林门新村 | 文锦苑 | 崇文 | 沈塘新村 | |
| 上车人数/人 | 32 | 54 | 32 | 16 | 10 | 15 | 17 | |
| 编号 | 16 | 17 | 18 | 19 | 20 | |||
| 下车点 | 万豪 | 杭州剧院 | 杭州大厦 | 华浙广场 | 西湖文化广场 | |||
| 下车人数/人 | 99 | 70 | 49 | 53 | 55 |
| 需求矩阵 | 16 | 17 | 18 | 19 | 20 | 上车站点需求 |
| 01 | 10 | 5 | 0 | 0 | 1 | 16 |
| 02 | 8 | 5 | 5 | 0 | 3 | 21 |
| 03 | 2 | 5 | 0 | 3 | 0 | 10 |
| 04 | 10 | 8 | 2 | 10 | 0 | 30 |
| 05 | 7 | 5 | 3 | 6 | 5 | 26 |
| 06 | 3 | 2 | 3 | 0 | 0 | 8 |
| 07 | 5 | 0 | 3 | 3 | 2 | 13 |
| 08 | 8 | 3 | 0 | 5 | 10 | 26 |
| 09 | 7 | 10 | 5 | 7 | 3 | 32 |
| 10 | 15 | 10 | 12 | 4 | 13 | 54 |
| 11 | 6 | 5 | 11 | 2 | 8 | 32 |
| 12 | 5 | 4 | 0 | 4 | 3 | 16 |
| 13 | 3 | 2 | 3 | 2 | 0 | 10 |
| 14 | 6 | 3 | 0 | 4 | 2 | 15 |
| 15 | 4 | 3 | 2 | 3 | 5 | 17 |
| 下车站点需求 | 99 | 70 | 49 | 53 | 55 | 326 |
| 距离矩阵 | 01 | 02 | 03 | 04 | 05 | 06 | 07 |
| 01 | 0.00 | 5.39 | 10.77 | 11.18 | 17.00 | 15.03 | 20.62 |
| 02 | 5.39 | 0.00 | 8.06 | 5.83 | 11.66 | 13.60 | 18.00 |
| 03 | 10.77 | 8.06 | 0.00 | 7.81 | 11.18 | 5.83 | 10.05 |
| 04 | 11.18 | 5.83 | 7.81 | 0.00 | 5.83 | 13.45 | 15.81 |
| 05 | 17.00 | 11.66 | 11.18 | 5.83 | 0.00 | 15.65 | 15.62 |
| 06 | 15.03 | 13.60 | 5.83 | 13.45 | 15.65 | 0.00 | 6.40 |
| 07 | 20.62 | 18.00 | 10.05 | 15.81 | 15.62 | 6.40 | 0.00 |
通过上车线网与下车线网的连接算法,运用Matlab软件运算得到两区域最近两个上下车站点,编号分别为09, 16。结合专家经验法和实际路网调查数据情况,得到上车线网算法的各项参数:种群数G=10,迭代次数N=200,信息素留存系数η=0.9,信息素增量Q=0.1。上下车站点之间的距离矩阵由其坐标之间的距离得出,上下车站点之间的时间距离矩阵由距离矩阵和速度矩阵得出,速度矩阵由v=v0Q/q得到。由百度地图的路况信息分级为严重拥堵、拥挤、缓行、畅通,本算例分别简化为q=4.0Q, q=3.0Q, q=2.0Q, q=1.0Q。公交车型为3种,容量为(75, 50, 25)veh,线路运行的条件(企业要求的最低上座率)取0.75。上下车站点间的道路基本通行能力矩阵和实际交通量矩阵如表 4、表 5所示,速度矩阵和时间距离矩阵如表 6、表 7所示。各条定制公交线路流量QRLc可通过需求矩阵得出,线路RLc的线路发车频次fRLc在本算例中为方便计算定义早高峰1次,通过距离矩阵依据式(34)可得距离成本Z1,依据式(37)可得运营固定成本Z4,通过时间距离矩阵依据式(35)可得运营时间成本Z2,依据式(36)可得运营环保成本Z3,其中通过调查和专家经验得相应的权重ω1,ω2,ω3,ω4依次为0.3,0.4,0.2, 0.1,结合得到总成本矩阵,如表 8所示。
| 道路通行 能力矩阵 |
01 | 02 | 03 | 04 | 05 | 06 | 07 |
| 01 | 0 | 2 000 | 3 000 | 3 000 | 3 000 | 3 000 | 1 000 |
| 02 | 2 000 | 0 | 3 000 | 2 000 | 1 000 | 2 000 | 2 000 |
| 03 | 2 000 | 3 000 | 0 | 2 000 | 2 000 | 1 000 | 3 000 |
| 04 | 1 000 | 2 000 | 1 000 | 0 | 2 000 | 2 000 | 2 000 |
| 05 | 1 000 | 1 000 | 3 000 | 3 000 | 0 | 3 000 | 2 000 |
| 06 | 1 000 | 1 000 | 2 000 | 3 000 | 2 000 | 0 | 2 000 |
| 07 | 1 000 | 3 000 | 1 000 | 2 000 | 3 000 | 1 000 | 0 |
| 道路流量 矩阵 |
01 | 02 | 03 | 04 | 05 | 06 | 07 |
| 01 | 0 | 6 000 | 9 000 | 12 000 | 9 000 | 9 000 | 2 000 |
| 02 | 6 000 | 0 | 9 000 | 8 000 | 3 000 | 6 000 | 4 000 |
| 03 | 6 000 | 3 000 | 0 | 4 000 | 2 000 | 1 000 | 9 000 |
| 04 | 1 000 | 4 000 | 2 000 | 0 | 4 000 | 4 000 | 8 000 |
| 05 | 2 000 | 4 000 | 9 000 | 3 000 | 0 | 12 000 | 8 000 |
| 06 | 4 000 | 3 000 | 4 000 | 6 000 | 4 000 | 0 | 2 000 |
| 07 | 3 000 | 9 000 | 3 000 | 6 000 | 6 000 | 2 000 | 0 |
| 实际速度 矩阵 |
01 | 02 | 03 | 04 | 05 | 06 | 07 |
| 01 | 0.00 | 13.33 | 16.67 | 12.50 | 16.67 | 16.67 | 15.00 |
| 02 | 13.33 | 0.00 | 16.67 | 10.00 | 10.00 | 13.33 | 20.00 |
| 03 | 13.33 | 50.00 | 0.00 | 20.00 | 40.00 | 30.00 | 16.67 |
| 04 | 30.00 | 20.00 | 15.00 | 0.00 | 20.00 | 20.00 | 10.00 |
| 05 | 15.00 | 7.50 | 16.67 | 50.00 | 0.00 | 12.50 | 10.00 |
| 06 | 7.50 | 10.00 | 20.00 | 25.00 | 20.00 | 0.00 | 40.00 |
| 07 | 10.00 | 16.67 | 10.00 | 13.33 | 25.00 | 15.00 | 0.00 |
| 时间距离 矩阵 |
01 | 02 | 03 | 04 | 05 | 06 | 07 |
| 01 | 0.00 | 12.12 | 19.39 | 26.83 | 30.60 | 27.06 | 41.23 |
| 02 | 12.12 | 0.00 | 14.51 | 17.49 | 34.99 | 30.60 | 27.00 |
| 03 | 24.23 | 4.84 | 0.00 | 11.72 | 8.39 | 5.83 | 18.09 |
| 04 | 11.18 | 8.75 | 15.62 | 0.00 | 8.75 | 20.18 | 47.43 |
| 05 | 34.00 | 46.65 | 20.12 | 3.50 | 0.00 | 37.57 | 46.86 |
| 06 | 60.13 | 40.80 | 8.75 | 16.14 | 23.48 | 0.00 | 4.80 |
| 07 | 61.85 | 32.40 | 30.15 | 35.58 | 18.74 | 12.81 | 0.00 |
| 成本矩阵 | 01 | 02 | 03 | 04 | 05 | 06 | 07 |
| 01 | 0.00 | 64.62 | 109.86 | 140.87 | 173.40 | 153.34 | 226.77 |
| 02 | 64.62 | 0.00 | 82.24 | 87.47 | 174.93 | 163.22 | 162.00 |
| 03 | 129.24 | 43.54 | 0.00 | 70.29 | 67.08 | 40.82 | 102.51 |
| 04 | 78.26 | 52.48 | 85.91 | 0.00 | 52.48 | 121.08 | 237.17 |
| 05 | 187.00 | 221.58 | 114.04 | 31.49 | 0.00 | 197.22 | 234.31 |
| 06 | 285.63 | 204.02 | 52.48 | 104.94 | 140.87 | 0.00 | 38.42 |
| 07 | 309.23 | 183.60 | 150.75 | 189.74 | 121.84 | 70.43 | 0.00 |
通过蚁群算法优化定制公交线网线路,依据上下车站点的距离矩阵和时间距离矩阵,综合得到上下车站点间的综合总成本,再依据线路的最低上车率,搜索得到多需求响应下的城市定制公交绿色线网优化运行方案,如表 9~表 13所示。
| 序号 | 线路 | 各上下车站点服务乘客数 | 车型 | 上座率 | 平均上座率 | 里程/km | 总里程/km | 总体服务率 |
| 1 | (02, 04, 05, 16, 17, 18, 19, 20) | (20, 36, 19, 20, 16, 10, 16, 13) | 1 | 1 | 0.94 | 56.85 | 206.98 | 0.72 |
| 2 | (14, 15, 12, 16, 17, 18, 19, 20) | (15, 20, 15, 16, 10, 3, 11, 10) | 2 | 1 | 48.03 | |||
| 3 | (03, 08, 09, 16, 17, 18, 20) | (23, 20, 5, 9, 13, 14, 12) | 2 | 0.96 | 48.02 | |||
| 4 | (10, 11, 16, 17, 18, 19, 20) | (32, 27, 14, 13, 7, 8, 17) | 1 | 0.79 | 54.08 | |||
| 未来候补方案 | ||||||||
| 序号 | 线路 | 各上下车站点服务乘客数 | 车型 | 上座率 | 平均上座率 | 里程/km | 总里程/km | 总体服务率 |
| 1 | (01, 06, 07, 16, 17, 18, 19, 20) | (23, 27, 30, 20, 20, 13, 10, 17) | 1 | 1.07 | 71.00 | 125.63 | 0.28 | |
| 2 | (13, 16, 17, 18, 19, 20) | (10, 3, 2, 3, 2) | 3 | 0.4 | 54.63 | |||
| 序号 | 线路 | 各上下车站点服务乘客数 | 车型 | 上座率 | 平均上座率 | 时间/h | 总时间/h | 总体服务率 |
| 1 | (14, 15, 12, 16, 17, 18, 19, 20) | (15, 20, 15, 16, 10, 3, 11, 10) | 2 | 1 | 0.97 | 58.48 | 252.65 | 0.67 |
| 2 | (03, 05, 16, 17, 18, 19, 20) | (5, 20, 7, 7, 3, 3, 5) | 3 | 1 | 64.37 | |||
| 3 | (07, 08, 09, 16, 17, 18, 19, 20) | (23, 20, 30, 14, 21, 16, 3, 19) | 1 | 0.973 | 58.68 | |||
| 4 | (13, 10, 11, 16, 17, 18, 19, 20) | (10, 32, 27, 17, 15, 7, 11, 19) | 1 | 0.92 | 71.12 | |||
| 未来候补方案 | ||||||||
| 序号 | 线路 | 各上下车站点服务乘客数 | 车型 | 上座率 | 平均上座率 | 时间/h | 总时间/h | 总体服务率 |
| 1 | (01, 02, 04, 16, 17, 18, 19, 20) | (23, 19, 36, 23, 16, 10, 16, 13) | 1 | 1.04 | 53.38 | 130.28 | 0.33 | |
| 2 | (06, 16, 17, 18, 19, 20) | (27, 5, 5, 8, 4, 5) | 2 | 0.54 | 76.90 | |||
| 序号 | 线路 | 各上下车站点服务乘客数 | 车型 | 上座率 | 平均上座率 | 成本/元 | 总成本/元 | 总体服务率 |
| 1 | (02, 04, 05, 16, 17, 18, 19, 20) | (20, 36, 19, 20, 16, 10, 16, 13) | 1 | 1 | 0.97 | 505.09 | 1 771.98 | 0.83 |
| 2 | (14, 15, 12, 16, 17, 18, 19, 20) | (15, 20, 15, 16, 10, 3, 11, 10) | 2 | 1 | 356.62 | |||
| 3 | (07, 08, 09, 16, 17, 18, 19, 20) | (23, 20, 30, 14, 21, 16, 3, 19) | 1 | 0.97 | 428.44 | |||
| 4 | (13, 10, 11, 16, 17, 18, 19, 20) | (10, 32, 27, 17, 15, 7, 11, 19) | 1 | 0.92 | 481.83 | |||
| 未来候补方案 | ||||||||
| 序号 | 线路 | 各上下车站点服务乘客数 | 车型 | 上座率 | 平均上座率 | 成本/元 | 总成本/元 | 总体服务率 |
| 1 | (01, 03, 06, 16, 17, 18, 19, 20) | (23, 5, 27, 15, 12, 11, 7, 10) | 1 | 0.73 | 0.73 | 728.33 | 728.33 | 0.17 |
| 序号 | 线路 | 各上下站车点服务乘客数 | 车型 | 上座率 | 平均上座率 | 成本/元 | 总成本/元 | 总体服务率 |
| 1 | (02, 04, 05, 16, 17, 18, 19, 20) | (20, 36, 19, 20, 16, 10, 16, 13) | 1 | 1 | 0.94 | 505.09 | 1 694.20 | 0.80 |
| 2 | (14, 15, 12, 16, 17, 18, 19, 20) | (15, 20, 15, 16, 10, 3, 11, 10) | 2 | 1 | 356.62 | |||
| 3 | (07, 08, 09, 16, 17, 18, 19, 20) | (23, 20, 30, 14, 21, 16, 3, 19) | 1 | 0.973 | 428.44 | |||
| 4 | (10, 11, 16, 17, 18, 19, 20) | (32, 27, 14, 13, 7, 8, 17) | 1 | 0.787 | 404.05 | |||
| 未来候补方案 | ||||||||
| 序号 | 线路 | 各上下车站点服务乘客数 | 车型 | 上座率 | 平均上座率 | 成本/元 | 总成本/元 | 总体服务率 |
| 1 | (01, 03, 06, 16, 17, 18, 19, 20) | (23, 5, 27, 15, 12, 11, 7, 10) | 1 | 0.73 | 728.33 | 1 354.42 | 0.20 | |
| 2 | (13, 16, 17, 18, 19, 20) | (10, 3, 2, 3, 2) | 3 | 0.4 | 626.09 | |||
| 序号 | 线路 | 各上下车站点服务乘客数 | 车型 | 上座率 | 平均上座率 | 成本/元 | 总成本/元 | 总体服务率 |
| 1 | (02, 04, 05, 16, 17, 18, 19, 20) | (20, 36, 19, 20, 16, 10, 16, 13) | 1 | 1 | 0.97 | 505.09 | 1 771.98 | 0.83 |
| 2 | (14, 15, 12, 16, 17, 18, 19, 20) | (15, 20, 15, 16, 10, 3, 11, 10) | 2 | 1 | 356.62 | |||
| 3 | (07, 08, 09, 16, 17, 18, 19, 20) | (23, 20, 30, 14, 21, 16, 3, 19) | 1 | 0.97 | 428.44 | |||
| 4 | (13, 10, 11, 16, 17, 18, 19, 20) | (10, 32, 27, 17, 15, 7, 11, 19) | 1 | 0.92 | 481.83 | |||
| 未来候补方案 | ||||||||
| 序号 | 线路 | 各上下车站点服务乘客数 | 车型 | 上座率 | 平均上座率 | 成本/元 | 总成本/元 | 总体服务率 |
| 1 | (01, 03, 06, 16, 17, 18, 19, 20) | (23, 5, 27, 15, 12, 11, 7, 10) | 1 | 0.73 | 0.73 | 728.33 | 728.33 | 0.17 |
3.1 方案对比
从需求点的整体分布来看,可以分为3个大区域,区域内的需求比较集中,蚁群算法搜索的目标就是寻找出行需求集中度高的定制公交线路,实现定制公交尽可能高的服务率和高效的覆盖整体需求。
表 9为算法搜索到的总里程最短方案,其实质是挖掘出行需求最集中、聚集性最高的线路,其余较分散的出行需求用未来候补线路的形式解决。该方案中,开通线路的平均上座率为94%,50%的线路满员运行,可见已开通线路的运力得到较大的运用,线路里程最少,但72%的整体服务率表示存在较多的出行需求未被满足。
表 10为算法搜索到的总时间最少的方案,其实质是优化线路路径,寻求最短出行线路,尽可能提高定制公交的快速到达能力,缩短出行的时间,体现定制公交的快捷性、准时性。97%的平均上座率也充分运用了线路的运力,但67%的总体服务率需要有较大的提升,充分满足大众出行需求。
表 11为算法搜索到的服务率最高的方案,其实质是优化运力配置(线路路线、上车点服务量、线路车型选择)尽可能高地满足出行需求。97%的平均上座率,83%的总体服务率表明算法搜索到了较好的运力配置方案,但83%的整体服务率仍然有提升的空间。
表 12为算法搜索到的总成本最少的方案,其实质是挖掘出行需求、优化运力配置、充分考虑企业需求、乘客服务、社会效益的综合成本最低的方案,94%的平均上座率和80%的整体服务率表明了线路很好地满足了上座率、服务率,也同时满足了聚集较高的出行需求和企业的成本要求,剩余的出行需求在未来得以解决。
表 13为算法搜索到的最优方案,其实质是兼顾上座率和服务率,最大限度地发掘聚集性较高的线路,同时优化运力配置,使得服务覆盖尽可能广泛。线路平均上座率97%,总体服务率83%,综合成本仅次于总成本最少方案,总体服务率最高,平均上座率最高,兼顾社会、乘客、企业3方面权益,取得最优方案。剩余的出行需求分布太散,出行需求较少,需要未来候补方案进行解决。
从企业、社会、乘客3方面的权益考虑,同时考虑环境因素,依据实际线路方案中的平均上座率、总体服务率、总里程、总时间、总成本这5个因素,得到最佳方案。
3.2 车型选择从表 13可以看出,最优方案中实际线路中的平均上座率为0.97,选择车型1的线路共3条,平均服务量为72,选择车型2的线路为1条,服务量为50,总成本1 771.98元,总体服务率为83%,总体服务率居于首位,更好地满足乘客的需求,总成本仅次于总成本最低方案,满足了企业的收益要求,总里程位于所有方案中的第3位,总时间位于所有方案中的第3位,综合满足了社会、乘客、企业3方面因素,同时考虑了环境保护成本和绿色交通,作用显著。
3.3 车型分析从表 13可以看出,最优方案中未来候选线路只有1条,总体服务率为17%,服务量为55人。从表 12可以看出,未来候选线路选择车型1为1条线路,选择车型3为1条线路,总体服务率20%,服务量分别为55人和10人。从表 10可以看出,未来候选线路中选择车型1为1条线路,选择车型2为1条线路,总体服务率33%,服务量分别为78人和27人。从表 9可以看出,未来候选线路选择车型1为1条线路,车型3为1条线路,总体服务率28%,服务量分别为80人和10人。从中可以看出这些线路的服务量差别较大,采取线路达到开通要求不一定适合所有线路的情况。为提高线路的总体服务率,建议配置更多车型,使线路车型选择更具有灵活性,增强方案对于出行需求分布的适应性。
4 结论系统研究了针对多种需求响应下的城市绿色交通定制公交线网优化问题,通过案例研究分析确立了模型算法的有效性,得到以下结论:
(1) 针对整个定制公交网络,系统研究了定制公交模式,建立了针对各种需求下的定制公交网络,建立了相应的网络优化模型和多种响应机制,满足定制公交的多种乘客需求。
(2) 结合多种定制公交需求,对应地定制了公交网络优化模型,充分考虑了社会、企业、乘客3方面的因素,充分考虑了城市拥堵,使得定制公交更加准时、便捷。
(3) 引入绿色交通理论,在多种需求响应机制下的定制公交网络优化模型中充分考虑了环境保护成本,将绿色交通理论不断推广。
(4) 配置了多种定制公交车型,对于多种需求响应下的定制公交网络优化有直接的效果,更加灵活高效,同时可提升定制公交总体服务率。
| [1] |
徐康明, 李佳玲, 冯浚, 等. 定制公交服务初探[J]. 城市交通, 2013, 11(5): 30-33. XU Kang-ming, LI Jia-ling, FENG Jun, et al. Discussion on Subscription Bus Services[J]. Urban Transport of China, 2013, 11(5): 30-33. |
| [2] |
毕岩岩, 肖敏, 周溪召. 国外大中城市公交优先发展及启示[J]. 城市发展研究, 2013, 20(11): 87-94. BI Yan-yan, XIAO Min, ZHOU Xi-zhao. The Bus Priority Development and Revelation of Foreign Large and Medium Cities[J]. Urban Development Studies, 2013, 20(11): 87-94. |
| [3] |
付建广. 提高公交出行率关键技术研究[J]. 城市发展研究, 2014, 21(1): 79-83. FU Jian-guang. The Key Technologies Research to Improve Transit Trip Rate[J]. Urban Development Studies, 2014, 21(1): 79-83. |
| [4] |
VUCHIC V R. Urban Transit:Operations, Planning and Economics[M]. New Jersey: John Wiley & Sons, 2005.
|
| [5] |
CEDER A. Public Transit Planning and Operation:Theory, Modeling and Practice[M]. Amsterdam: Elsevier, 2007.
|
| [6] |
AN K, HONG K L. Two-phase Stochastic Program for Transit Network Design under Demand Uncertainty[J]. Transportation Research Part B:Methodological, 2016, 84: 157-181. |
| [7] |
NASSIR N, HICKMAN M, MALEKZADEH A, et al. A Utility-based Travel Impedance Measure for Public Transit Network Accessibility[J]. Transportation Research Part A:Policy & Practice, 2016, 88: 26-39. |
| [8] |
KERKMAN K, MARTENS K, MEURS H. A Multilevel Spatial Interaction Model of Transit Flows Incorporating Spatial and Network Autocorrelation[J]. Journal of Transport Geography, 2017, 60: 155-166. |
| [9] |
黄敏. 多层次公交线网拓扑结构分析[J]. 公路交通科技, 2010, 27(5): 93-99. HUANG Min. Analysis on Topology Frame of Multi-level Transit System Network[J]. Journal of Highway and Transportation Research and Development, 2010, 27(5): 93-99. |
| [10] |
李彬. 定制公交与定制公交客车的研究[D]. 西安: 长安大学, 2013. LI Bin. Research on Custom Bus and Custom Coach[D].Xi'an:Chang'an University, 2013. |
| [11] |
张敏捷, 冯偲, 吕晨曦, 等. 定制公交线路优化模型及求解算法[C]//第九届中国智能交通年会大会论文集. 北京: 电子工业出版社, 2014: 347-354. ZHANG Min-jie, FENG Si, LÜ Chen-xi, et al. An Optimized Model and Algorithm for Custom Bus Routing[C]//Proceedings of the 9th China Intelligent Transport Annual Conference. Beijing:Electronic Industry Press, 2014:347-354. |
| [12] |
潘述亮, 卢小林, 邹难. 灵活型接驳公交路径优化及协同调度模型[J]. 吉林大学学报:工学版, 2016, 46(6): 1827-1835. PAN Shu-liang, LU Xiao-lin, ZOU Nan. Route Planning and Coordinated Scheduling Model for Flexible Feeder Transit Service[J]. Journal of Jilin University:Engineering and Technology Edition, 2016, 46(6): 1827-1835. |
| [13] |
魏明, 靳文舟, 孙博. 随机旅行时间的区域公交车调度模型及算法[J]. 公路交通科技, 2011, 28(28): 124-129. WEI Ming, QIN Wen-zhou, SUN Bo. Model and Algorithm for Regional Bus Scheduling with Stochastic Travel Time[J]. Journal of Highway and Transportation Research and Development, 2011, 28(10): 124-129. |
| [14] |
魏明, 孙博, 靳文舟. 灰色旅行时间的区域公交车辆调度模型和算法[J]. 交通运输系统工程与信息, 2012, 12(6): 106-112. WEI Ming, SUN Bo, JIN Wen-zhou. Model and Algorithm of Regional Bus Scheduling with Grey Travel Time[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12(6): 106-112. |
| [15] |
卢小林, 张娴, 俞洁, 等. 灵活型定制公交系统综合评价方法研究[J]. 公路交通科技, 2015, 32(5): 135-140. LU Xiao-lin, ZHANG Xian, YU Jie, et al. Research of a Comprehensive Evaluation Method for Customized Flexible Transit System[J]. Journal of Highway and Transportation Research and Development, 2015, 32(5): 135-140. |
| [16] |
庞明宝, 张思林, 李春霞. 城市公交站设置双层规划[J]. 公路交通科技, 2013, 30(3): 118-124. PANG Ming-bao, ZHANG Si-lin, LI Chun-xia. Bi-level Programming of Urban Bus Stop Locating[J]. Journal of Highway and Transportation Research and Development, 2013, 30(3): 118-124. |
| [17] |
胡列格, 安桐, 王佳, 等. 城市定制公交合乘站点的布局研究[J]. 徐州工程学院学报:自然科学版, 2016, 3(1): 27-32. HU Lie-ge, AN Tong, WANG Jia, et al. The Layout of Rideshare Sites of Urban Customized Shuttle Bus[J]. Journal of Xuzhou Institute of Technology:Natural Science Edition, 2016, 3(1): 27-32. |
| [18] |
程立勤. 基于点线面层次分析法定制公交线网布局[J]. 大连交通大学学报, 2014, 35(3): 23-26. CHENG Li-qin. Study on the Line Network Layout of Customized Shuttle Bus Planning of the Level Analysis Method of Point, Line and Plane[J]. Journal of Dalian Jiaotong University, 2014, 35(3): 23-26. |
| [19] |
徐扬, 戴从蔚, 罗晶, 等. 大规模个性化公交定制研究[J]. 管理现代化, 2016, 36(1): 67-69. XU Yang, DAI Cong-wei, LUO Jing, et al. Research on Mass Personalized Bus Customization[J]. Modernization of Management, 2016, 36(1): 67-69. |
 2018, Vol. 35
2018, Vol. 35
