扩展功能
文章信息
- 李娟, 曲大义, 刘聪, 王五林, 刘冬梅
- LI Juan, QU Da-yi, LIU Cong, WANG Wu-lin, LIU Dong-mei
- 基于分子动力学的跟驰特性及其模型
- Car-following Characteristics and Its Models Based on Molecular Dynamics
- 公路交通科技, 2018, 35(3): 126-131
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(3): 126-131
- 10.3969/j.issn.1002-0268.2018.03.017
-
文章历史
- 收稿日期: 2016-12-07
跟驰行为是车辆驾驶中最基本的驾驶行为,跟驰模型是交通工程领域研究的重点和热点。跟驰行为受到驾驶员特性、道路情况、车辆动力性能、交通环境等一系列因素的影响,建模方法也涉及到物理、数学、心理学、动力学等理论方法。GM模型是跟驰理论研究中最经典的模型,模型的建立基于刺激-反应基本思想,驾驶人通常考虑当前车辆的速度、当前车与前车之间的距离以及当前车与前车之间的相对速度来调整车速[1-4]。后来衍生的生理-心理模型和人工智能(模糊推理、神经网络)跟驰模型也是基于刺激-反应思想。之后交通学者对GM模型进行改进,建立优化速度模型[5-6]、多速度差模型[7-8]、全速度差模型[9-10]等,模型的建立在不同程度上推进了经典GM模型的发展。在车辆跟驰建模领域,研究者利用分子动力学研究车辆跟驰特性,探索车辆跟驰的需求安全距离及其应用模型的构建,并利用分子动力学理论研究交通运行状态的稳定性,获得了一系列突破性进展[11-13]。
经典GM跟驰模型,将相对速度作为乘数置于模型结构中,导致模型存在缺陷,即当前后车的相对速度相同时,速度差为零,根据模型表述意味着不论车辆间距如何,目标车均不会进行速度调整,显然与实际交通状况不符。以往的分子跟驰模型建立时仅仅考虑需求安全距离的影响是不全面的。为解决此类问题,将相对速度这一影响因素剔除,在原有分子跟驰模型基础上,除考虑需求安全距离外,引入车辆期望速度因素的影响。根据此设想,本研究基于分子动力学特性,建立一维管道气体分子跟驰模型。通过构建车辆之间的相互作用势函数,分析车辆的受力情况,建立了基于相互作用势函数的分子跟驰模型。利用目前常用的视频检测技术,进行交通流状态拍摄,根据实测交通流数据对分子跟驰模型进行参数标定,通过与经典GM模型的对比,验证了模型的合理性。
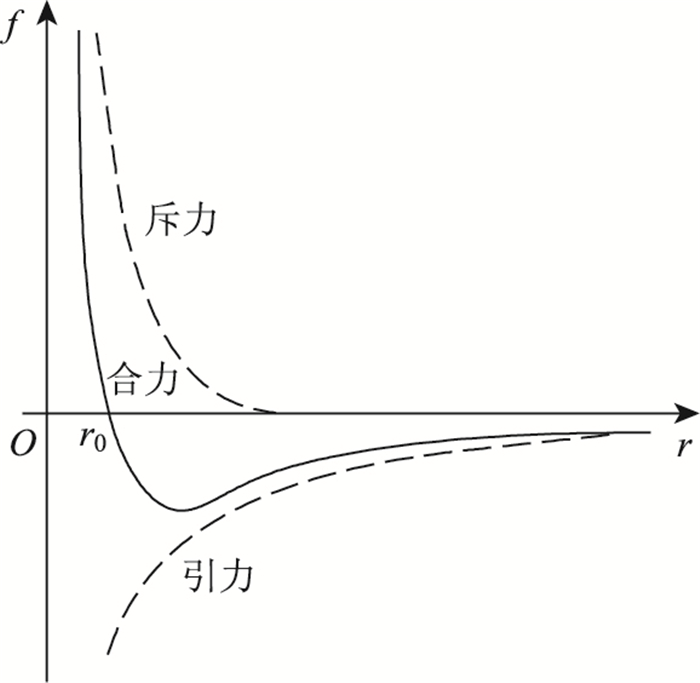
1 分子动力学分子间存在的分子力是指分子之间存在的吸引和排斥的相互作用,是分子呈现不同物理性质的主要原因。气体分子是由电子、质子等组成的复杂带电系统,试验证明当分子间距较大时,存在微弱的引力。随着间距的减小,引力逐渐加强,但当两分子靠近到r=r0 (称为平衡距离)以内时,相互间产生强烈的斥力作用而离开。分子间的引力和斥力总是同时存在,并且都随分子间的距离的增大而减小,只不过减小的规律不同,斥力减小得快。如图 1所示,当分子间距离等于平衡距离时,引力等于斥力,分子间作用力为零;当分子间距离小于平衡距离时,斥力、引力随分子间距离减小而增大,但斥力增加得快,所以表现出斥力;当分子间距离大于平衡距离时,斥力、引力随分子间距离增大而减小,但斥力减小得快,所以表现出引力[14]。
|
| 图 1 分子间力曲线图 Fig. 1 Curves of intermolecular force |
| |
图中虚线分别表示引力和斥力随距离变化的情况,实线表示合力随距离变化的情况。r>r0时,虽然引力和斥力都随着距离的增加而减小,但斥力减小得更快,因而分子间的作用力表现为引力;r < r0时,虽然引力和斥力都随着距离的减小而增加,但斥力增加得更快,因而分子间的作用力表现为斥力。
道路上跟驰车辆的运动状态如图 2所示。将车流的运动微化到粒子级别,就好比当前粒子被后面的粒子推着同时被前面的粒子拉着往前运动,车辆间不容易靠近也不容易远离,从动力学角度就是在引力与斥力共同作用下运动。道路上行驶车辆之间的跟驰交互关系与分子之间的力学关系有相似的特征,本研究将交通流看做自由流动的气体流,每一辆车看做是气体分子,单车道环境下车辆跟驰运动表现出的类似于分子的性质,称为车辆的分子跟驰特性。基于分子之间的相互作用关系,建立车辆之间的作用力模型,研究车辆跟驰驾驶行为特性。

|
| 图 2 单车道车辆跟驰运动示意图 Fig. 2 Schematic diagram of single lane car following |
| |
2 一维管道分子跟驰模型 2.1 分子跟驰模型
为了更加形象地模拟车道环境,建立一维管道气体分子跟驰模型,如图 3所示。

|
| 图 3 一维管道气体分子运动示意图 Fig. 3 Schematic diagram of 1D pipeline gas molecular motion |
| |
简化模型,将一维管道剖析为平板模型,即气体分子限制在2块间距非常小的平行的平板形成的狭缝中。假设平板由一层类气体分子构成,模拟气体分子除了自身相互作用外,还与壁面分子有相互作用,相互作用力如图 3所示。其中,f1和f2分别为气体分子之间的引力和斥力;f3为壁面分子对气体分子作用力的合力;r为气体分子间的间距。相互作用力由势能函数决定,分子在一维管道中运动,主要受到分子之间短程相互作用势和壁面势的影响。
类比单车道跟驰环境,一维管道分子跟驰模型中分子之间的相互作用,代表跟驰车与前导车之间的相互关系,壁面作用代表车道环境(本研究主要指道路限速)对跟驰车辆的制约。车辆在跟随驾驶时,跟随车不会长距离滞后前导车,也不会紧随前导车,为保证安全驾驶,跟随车会寻求一个安全距离,保证在前车紧急制动时,跟随车能避免与前车发生碰撞,这个安全距离定义为跟随车的需求安全距离。
2.2 相互作用势分析需求安全距离是一个即时状态参量,由车辆自身速度决定。当跟随车与前导车之间的距离过大或过小,都不是一个最优状态,只有当车间距满足跟随车的需求安全距离时,两车以相同速度快速安全的行驶是最有效率的跟驰状态。需求安全距离等同于分子动力学中的平衡距离r0,此时车辆之间的相互作用为零。
需求安全距离,是指车辆在一定速度下行驶,驾驶员需要的从开始反应到车辆制动停止的最小安全制动距离。
跟驰车辆速度-车头间距[15]表示为:
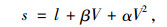
|
(1) |
速度-车间距[16]表示为:
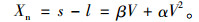
|
(2) |
式(1)、式(2)中,s为车头间距;Xn为需求安全距离;β为驾驶员反应时间;α为跟驰车辆最大减速度2倍的倒数;l为车辆长度;V为车辆即时速度。
平衡状态是一种理想状态,在实际交通环境中不存在。引入距离需求饱和系数C,即跟随车辆需求安全距离Xn与实际车间距L的比。
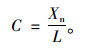
|
(3) |
当C < 1,即实际车间距大于需求安全距离时,维持现状可保证足够安全空间,跟随车为达到自己的期望速度(本研究以道路最大限速定义),会加速行驶;当C>1时,实际车间距小于需求安全距离,跟随车受前导车制约,会减速行驶。
所以,跟随车的加速度主要受到车辆需求安全距离和期望速度2方面因素的影响,基于分子跟驰模型中的车辆相互作用势和壁面势的存在,分析跟随车的受力关系,得到其加速度计算模型。
(1) 车辆间相互作用势函数在分子动力学中,分子间的对势认为分子间的相互作用是两两之间的作用,与其他分子无关。其中连续对势应用最为广泛的是Lennard-Jones势函数[17],一般用于描述流体和惰性气体之间的相互作用,实际应用当中常取:
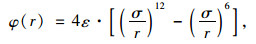
|
(4) |
式中,ε,σ分别为能量和长度尺度;r为分子间距离。式中第1项表示分子间的短程排斥力,第2项表示远程吸引力。
车辆间相互作用由斥力与引力共同保障,主要受到需求安全距离的影响,且呈指数型变化,建立车辆间相互作用势函数模型。
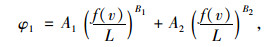
|
(5) |
式中,f(v)为速度函数;L为车辆之间的距离;A1,A2,B1,B2为相关参数或系数。
令A1=A2=4ε,B1=12,B2=6,f(v)=Xn,可以得到形如Lennard-Jones势函数如下:
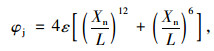
|
(6) |
式中,ε为势阱深度; Xn为需求安全距离,是车辆间相互作用势为零时的临界距离。
由势函数可推导出车辆间受力情况:
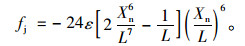
|
(7) |
加速度:
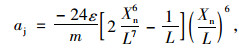
|
(8) |
式中m为车辆的质量。
为简化模型,令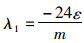
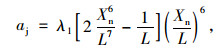
|
(9) |
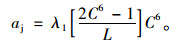
|
(10) |
(2) 车道环境“壁面势”
车道环境所产生的“壁面势”是一种虚拟势,只考虑车辆期望速度的影响,即车道的最大限速。在低速环境下车辆的速度较小,会产生较大加速度;在高速环境时,车辆速度较大,产生较小加速度,当车辆达到期望速度后就不会再继续加速。因此在自由流状态下,车辆的加速度随速度的增加而递减,当速度达到期望速度后,加速度为零。这对于车辆来说是一种引力的作用,在车道环境“壁面势”的作用下,车辆的加速度定义为:
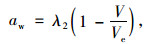
|
(11) |
式中,Ve为车辆期望速度; V为车辆实时速度; λ2为待定参数。
综上所述,一维管道分子跟驰的加速度模型为:
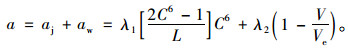
|
(12) |
本研究试验场地选择青岛市黄岛区的滨海大道,滨海大道是黄岛区的东西主干道,采集路段长2.1 km,包含4个交叉口,如图 4所示。
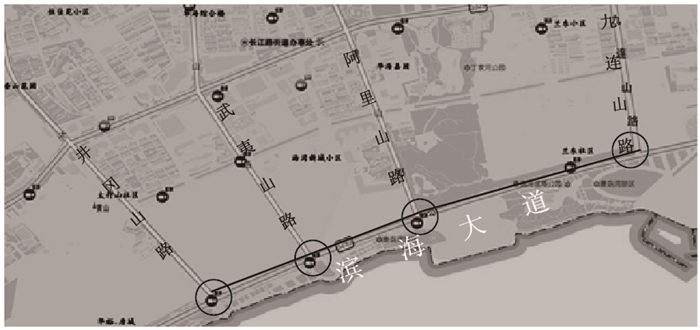
|
| 图 4 试验路段示意图 Fig. 4 Schematic diagram of test road section |
| |
交通流各参数主要采用高清交通视频分帧点录的方法获得。意思就是在滨海大道沿线选取高楼点位,使用全景高清摄像机拍摄试验车辆分别在路段和近交叉口的运动状态,对交通流进行几十分钟的连续拍摄,之后利用计算机软件对影像资料进行加工处理,通过人工干预逐帧步进,获得试验所需数据。试验数据主要包括车辆编号、颜色、车型等固定车辆特征,也包括车辆所在车道、速度、加速度、与前车间距、所处时间节点等。
3.2 参数标定为了保证数据的合理有效性,考察车流不同运行状态下的加速度变化规律,选取路段和临近交叉口两部分进行录像工作,根据采集到的数据,将交通流分为常态行驶、起动加速、减速停车3种状态。将数据分为两部分,一部分用来进行参数标定,一部分用来模型验证。在进行参数标定时,需按照不同状态下的数据进行处理,以保证模型的真实性。
选取每种状态下录像资料中呈现的完整跟驰过程各15组,反应时间取固定值0.5 s,数据采集路段限速为60 km/h。按照参考文献[18]所表述的遗传算法进行设置,选择方法为轮盘选择法,交叉率为0.85,交叉方法为均匀交叉法,变异率取0.01。分子跟驰模型参数标定结果如表 1所示。
| 车辆状态 | 样本数 | λ1 | λ2 | 相关系数 |
| 常态行驶 | 1 632 | 0.005 6 | 2.69 | 0.58 |
| 起动加速 | 1 450 | 0.003 7 | 2.95 | 0.63 |
| 减速停车 | 1 529 | 0.010 7 | 1.87 | 0.52 |
4 验证分析
为验证模型的有效性,用同样的实测数据对GM模型进行参数标定,参数标定方法与3.2节相同,参数标定结果如表 2所示。
| 车辆状态 | 样本数 | λ | m | l | 相关系数 |
| 常态行驶 | 1 632 | 9.25 | 0.39 | 1.31 | 0.69 |
| 起动加速 | 1 450 | 6.39 | 0.32 | 1.22 | 0.58 |
| 减速停车 | 1 529 | 11.23 | 0.68 | 1.47 | 0.67 |
选取未参与参数标定的数据代入本研究构建的分子跟驰模型和经典GM模型中,对比计算输出加速度与实测加速度的误差。为验证模型有效性,选取3种状态下交通流实测数据各3组进行误差分析,见表 3。其中MSE表示平均绝对误差,反映了2种跟驰模型与实测数据的偏差程度;σMSE是绝对误差的方差,反映误差值的变化程度,主要表征模型的稳定性。
| 车辆状态 | 样本 编号 |
数据 量 |
分子跟驰模型 | 经典GM模型 | |||
| MSE | σMSE | MSE | σMSE | ||||
| 常态行驶 | 1 | 134 | 0.79 | 0.28 | 0.83 | 0.44 | |
| 2 | 126 | 0.65 | 0.32 | 1.01 | 0.62 | ||
| 3 | 159 | 0.69 | 0.39 | 0.97 | 0.56 | ||
| 起动加速 | 4 | 96 | 0.72 | 0.23 | 1.87 | 1.03 | |
| 5 | 121 | 0.86 | 0.73 | 1.75 | 1.23 | ||
| 6 | 105 | 0.79 | 0.38 | 1.65 | 1.47 | ||
| 减速停车 | 7 | 183 | 0.95 | 0.61 | 1.44 | 1.01 | |
| 8 | 197 | 0.88 | 0.62 | 2.01 | 2.34 | ||
| 9 | 220 | 0.76 | 0.37 | 1.25 | 0.69 | ||
选取每种状态下的1组典型跟驰过程(样本3,6,9)进行数据绘图对比,如图 5所示。
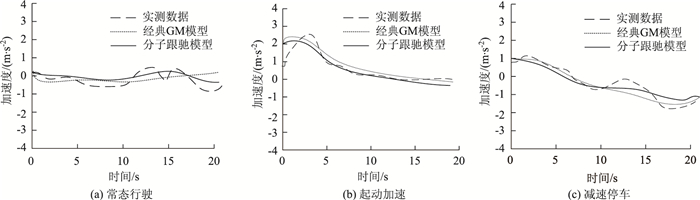
|
| 图 5 模型输出结果对比图 Fig. 5 Comparison of model output results |
| |
根据表 3可以看出,本研究构建的基于一维管道的分子跟驰模型,输出加速度与实测加速度之间的误差,总体上比经典GM模型要小,而且根据绝对误差方差显示,分子跟驰模型稳定性更高。根据图 5同样看出,分子跟驰模型输出加速度与实测数据变化趋势几乎一致,拟合效果比经典GM模型更好。
5 结论本研究利用分子动力学理论对跟驰车辆相互作用进行抽象化分析,将需求安全间距和期望速度作为主要影响因素,建立的跟驰加速度模型解决了传统跟驰模型的缺陷。参数标定后进行误差分析,其中分子跟驰模型的相对误差和绝对误差均相对较小。通过与实测数据的拟合分析,结果表明分子跟驰模型较传统GM模型稳定性更高,能更好地模拟实际交通驾驶行为。
| [1] |
PIPES L A. An Operational Analysis of Traffic Dynamics[J]. Journal of Applied Physics, 1953, 24(3): 274-281. |
| [2] |
HERMAN R, ROTHERY R W. Car Following and Steady-state Flow[C]//Proceedings of the 2nd International Symposium on the Theory of Traffic Flow. Paris:Organization for Economic Co-operation and Development, 1965:1-11.
|
| [3] |
彭光含. 交通流复杂耦合动态特性模拟研究[D]. 重庆: 重庆大学, 2009. PENG Guang-han. Research on Simulation of Complicated Coupling Dynamical Characteristic of Traffic Flow[D]. Chongqing:Chongqing University, 2009. |
| [4] |
赵康嘉, 陈淑燕. 基于元胞自动机的交通事件交通流仿真模型[J]. 公路交通科技, 2014, 31(3): 133-138. ZHAO Kang-jia, CHEN Shu-yan. Cellular Automaton Based Traffic Flow Simulation Model for Traffic Incidents[J]. Journal of Highway and Transportation Research and Development, 2014, 31(3): 133-138. |
| [5] |
赖林, 胡永红, 史忠科. 基于车头间距与前车速度的改进优化速度模型[J]. 西北工业大学学报, 2014, 32(1): 118-122. LAI Lin, HU Yong-hong, SHI Zhong-ke. An Improved Optimal Velocity Model Based on Space Headway and Speed of Front Vehicle[J]. Journal of Northwestern Polytechnical University, 2014, 32(1): 118-122. |
| [6] |
赵顺. 基于修正优化速度函数的多前车跟驰模型研究[D]. 哈尔滨: 哈尔滨工业大学, 2016. ZHAO Shun. Car-following Model Based on Modified Optimal Velocity Function and Multiple Proceeding Vehicles[D]. Harbin:Harbin Institute of Technology, 2016. |
| [7] |
王涛, 高自友, 赵小梅. 多速度差模型及稳定性分析[J]. 物理学报, 2006, 55(2): 634-640. WANG Tao, GAO Zi-you, ZHAO Xiao-mei. Multiple Velocity Difference Model and Its Stability Analysis[J]. Acta Physica Sinica, 2006, 55(2): 634-640. |
| [8] |
孙棣华, 李永福, 田川. 基于多前车位置及速度差信息的车辆跟驰模型[J]. 系统工程理论与实践, 2010, 30(7): 1326-1332. SUN Di-hua, LI Yong-fu, TIAN Chuan. Car-following Model Based on the Information of Multiple Ahead & Velocity Difference[J]. Systems Engineering-Theory & Practice, 2010, 30(7): 1326-1332. |
| [9] |
支梁, 史忠科, 刘通. 一种交叉路口全速度差改进模型[J]. 交通运输系统工程与信息, 2013, 13(6): 80-85. ZHI Liang, SHI Zhong-ke, LIU Tong. An Improved FVD Model for Intersection[J]. Journal of Transportation System Engineering and Information Technology, 2013, 13(6): 80-85. |
| [10] |
WILSON R E, BERG P, HOOPER S, et al. Many-neighbor Interaction and Non-locality in Traffic Module[J]. The European Physical Journal B, 2004, 39(3): 397-408. |
| [11] |
曲大义, 杨建, 陈秀锋, 等. 车辆跟驰的分子动力学特性及其模型[J]. 吉林大学学报:工学版, 2012, 42(5): 1198-1202. QU Da-yi, YANG Jian, CHEN Xiu-feng, et al. Molecular Kinetics Behavior of Car-following and Its Model[J]. Journal of Jilin University:Engineering and Technology Edition, 2012, 42(5): 1198-1202. |
| [12] |
郭涛, 曲大义, 郝杰, 等. 交通流稳定性的分子动力学分析[J]. 公路交通科技, 2014, 31(5): 129-134. GUO Tao, QU Da-yi, HAO Jie, et al. Analysis on Traffic Flow Stability by Molecular Kinetics[J]. Journal of Highway and Transportation Research and Development, 2014, 31(5): 129-134. |
| [13] |
陈文娇, 曲大义, 杨万三, 等. 基于分子动力学的车辆需求安全距离及模型[J]. 青岛理工大学学报, 2014, 35(1): 94-110. CHEN Wen-jiao, QU Da-yi, YANG Wan-san, et al. Molecular Kinetics Behavior of Car-following Required Safe Distance and Its Model[J]. Journal of Qingdao University of Technology, 2014, 35(1): 94-110. |
| [14] |
潘登, 郑应平. 基于双曲函数的车辆减速策略及安全跟驰车距的计算[J]. 交通信息与安全, 2007, 25(5): 54-58. PAN Deng, ZHENG Ying-ping. Deceleration Strategies of Vehicles Based on Hyperbolic Function and Calculation of Safe Following Distance between Two Cars[J]. Journal of Transport Information and Safety, 2007, 25(5): 54-58. |
| [15] |
AARTS L, VAN SCHAGEN I. Driving Speed and the Risk of Road Crashes:A Review[J]. Accident Analysis and Prevention, 2006, 38(2): 215-224. |
| [16] |
陈秀锋. 基于分子动力学的车辆运行安全特性研究[D]. 吉林: 吉林大学, 2013. CHEN Xiu-feng. A Study on Vehicle Operating Safety Characteristics Based on Molecular Dynamics[D].Jilin:Jilin University, 2013. |
| [17] |
李萌萌. 微通道气体流动的分子动力学模拟[D]. 西安: 西安电子科技大学, 2005. LI Meng-meng. Molecule Dynamics Simulation on Gas Flow in Microchannels[D]. Xi'an:Xidian University, 2005. |
| [18] |
罗亚中, 袁端才, 唐国金. 求解非线性方程组的混合遗传算法[J]. 计算机力学学报, 2005, 22(1): 109-114. LUO Ya-zhong, YUAN Duan-cai, TANG Guo-jin. Hybrid Genetic Algorithm for Solving Systems of Nonlinear Equations[J]. Chinese Journal of Computational Mechanics, 2005, 22(1): 109-114. |
 2018, Vol. 35
2018, Vol. 35
