扩展功能
文章信息
- 毕军, 王永兴, 赵小梅, 朱颖
- BI Jun, WANG Yong-xing, ZHAO Xiao-mei, ZHU Ying
- 考虑充电站效益的电动汽车充电分配优化模型
- An Optimization Model for Electric Vehicles Charging Assignment Considering Charging Station Benefits
- 公路交通科技, 2018, 35(3): 117-125
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(3): 117-125
- 10.3969/j.issn.1002-0268.2018.03.016
-
文章历史
- 收稿日期: 2017-01-03
2. 北京交通大学 城市交通复杂系统理论与技术教育部重点实验室, 北京 100044
2. Key Laboratory for Urban Transportation Complex Systems Theory and Technology of MOE, Beijing Jiaotong University, Beijing 100044, China
能源危机与环境污染已经成为人们日益关注的热点问题。在交通运输领域,利用电动汽车替代传统汽车被看成是解决能源和环境问题的有效手段。与传统汽车相比,电动汽车具有能源利用率高和尾气零排放的优点[1]。中国提出到2020年电动汽车保有量达到500万辆的发展规划[2]。然而,续驶里程较短和充电设施建设相对滞后等问题严重阻碍了电动汽车的使用和推广。当电动汽车的剩余电量所能行驶的距离不足以到达目的地时,用户需要寻找合适的充电站为电动汽车充电。合理的充电分配决策方案不仅需要考虑电动汽车用户的出行充电需求,而且需要考虑充电站效益。提高充电站效益可以提升服务水平,促进充电站建设,有利于电动汽车的使用和推广。
目前,针对电动汽车充电服务问题,国内外一些专家学者进行了相关研究。KEJUN等[3]在研究电动汽车充电问题时重点考虑充电行为对电网的影响,讨论了规模化电动汽车接入配电网对商业区、居民区以及工业区配电网的影响。王锡凡等[4]基于电动汽车充电负荷模型研究了电动汽车的有序充电。ERDOGAN和MILLER-HOOKS[5]从电动汽车用户的角度探讨电动汽车充电及路径规划问题,考虑时间窗约束,以总行驶距离最短为目标建立了电动汽车车队路径优化模型,并且运用2种启发式算法对模型进行求解。SAID等[6]以最小充电时间为目标,基于排队论建立电动汽车充电分配模型。苏舒等[7]依据交通信息探讨了单辆电动汽车和多辆电动汽车的充电导航,并提出智能充电导航系统。冯智泉等[8]考虑充电站分布约束,应用蚁群算法对电动汽车充电方案和行驶路径优化问题进行研究。另外,HE等[9]以出行时间最小为目标建立了3种网络均衡模型,从网络均衡的角度对电动汽车充电问题展开了研究。其中第1种模型为基本网络均衡模型,第2种模型在第1种模型基础上增加了充电时间约束,第3种模型在前2种基础上引入了能源消耗。最后整个网络达到平衡后为用户提供最优的路径选择。JIANG等[10]考虑停车场选择问题,提出了电动汽车和传统燃油车2种车辆类型的城市交通网络均衡问题。该研究假设电动汽车根据剩余里程选择停车场进行充电。但是,上述研究都没有充分考虑充电站效益,而充电站作为充电服务的主要提供方,其效益对于充电站运营商和电动汽车用户都具有重要意义。
鉴于上述相关研究,针对电动汽车充电分配决策问题,充分考虑路网中多个充电站的整体效益,在对充电站效益需求进行分析的基础上,建立以路网中多个充电站整体综合效益最大化为目标的多目标函数电动汽车充电分配模型,并将模型的多目标函数转化为考虑多个优化目标的单目标函数。针对模型设计了求解算法, 结合大量北京市充电站的静态数据设计算例对模型和算法进行了验证,并且对影响充电分配决策的主要因素进行了分析。研究成果旨在为充电站运营商进行充电分配时提供决策支持。
1 充电站效益需求分析充电站的效益需求主要体现在3个方面:(1)提高充电站经济收入;(2)提高充电站服务水平;(3)电动汽车充电分布均衡。
首先,提高经济收入是反映充电站效益需求的主要因素。充电站为用户提供电动汽车充电服务的同时会向用户收取充电服务费,该费用是充电站经济收入的主要来源。
其次,提高充电站服务水平也是体现充电站效益需求的主要因素。提高服务水平可以提升用户充电服务满意度。用户的充电服务满意度主要受电动汽车在充电站停留时间的影响,而停留时间主要包括排队时间和充电时间。目前,在相同充电模式下,充电桩的充电功率基本是统一的。因此充电时间对于用户充电服务满意度的影响很小,但是,当充电站内的车辆数大于充电桩数时,用户必须先排队,直到前面的用户完成充电后才可以进行充电。然而,用户一般都希望来到充电站后直接充电而不是排队等待。因此,排队时间是反映充电站服务水平的重要因素。
最后,电动汽车充电分布均衡也是反映充电站效益需求的主要因素。一般情况下,由于地理位置、充电价格等因素,部分充电站会受到用户的青睐而造成充电站拥挤,严重时会影响到充电站正常运营; 而另一部分充电站的充电设备却处于空闲状态,造成资源浪费,这就是充电分布不均衡现象。充电分布不均衡为充电站运营效益带来负面影响,尽量使电动汽车充电分布达到均衡是消除负面影响提高充电站效益的有效手段,充电分布均衡程度可以用充电站拥挤程度的方差来体现。由于用户排队时间和充电站拥挤程度都与充电站内的车辆数有关,因此两者具有一定的内在联系。但是,两者的侧重点和所希望达到的目标并不相同。用户排队时间主要侧重于从充电站服务满意度的角度进行考虑,并且希望当充电站内车辆数大于充电桩数时,站内车辆数越少越好。充电站拥挤程度则侧重于对充电站资源利用的合理性进行考虑,并没有明确地希望充电站内车辆数越多越好或者越少越好。因此,这2个因素会对最终的电动汽车分配结果产生不一样的影响。
综上所述,考虑充电站效益的电动汽车充电分配模型的优化目标主要从充电站运营商的经济收入、用户排队时间和充电站拥挤程度3个方面研究。
2 模型建立电动汽车充电分配方案中涉及的路径包括2条子路径,1条是从电动汽车用户产生充电需求的起点至充电站,另1条是从充电站至目的地。通常情况下,电动汽车从起点到目的地之间只需充电1次,充电次数多于1次的情况十分少见[11]。因此,假设电动汽车在1次出行中仅需充电1次即可顺利到达目的地。基于上述假设,建立考虑充电站效益的多目标函数电动汽车充电分配模型,同时,采用模糊规划法和模糊偏好关系将多目标函数转化为考虑多个优化目标的单目标函数。
2.1 目标函数为了实现建模,假设在路网中存在m辆待分配电动汽车和n个充电站(i=1, …, m; j=1, …, n)。模型的决策变量xij是一个0-1变量,具体含义如下:

|
(1) |
充电站向用户收取的充电服务费与充电量有关,同时希望收入最大。因此,针对提高充电站经济收入的目标函数为:
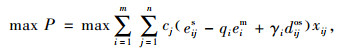
|
(2) |
式中,P为充电站的总经济收入;cj为充电站j的单位电量服务费;eijs为电动汽车i在充电站j完成充电后的电量;qi为电动汽车i发出充电请求时的初始SOC(State of Charge),SOC为电动汽车剩余电量与最大电量之间的比值[12];eim为电动汽车i的最大电量;γi为电动汽车i行驶单位距离所消耗的电量; dijos为电动汽车i从起点到充电站j之间的距离。
用户排队时间是体现充电站服务水平的重要因素,因此需要尽可能地减少用户在充电站的排队时间。针对提高充电站服务水平的目标函数如下:
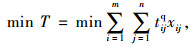
|
(3) |
其中:
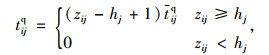
|
(4) |
式中,T为所有待分配电动汽车的总排队时间; tijq为电动汽车i在充电站j的排队时间; zij为当电动汽车i到达充电站j时充电站内车辆数;hj为充电站j内的充电桩个数(k=1, …, hj);tijq为当电动汽车i到达充电站j时车辆的平均排队时间。
式(4)中zij的计算方法如下:
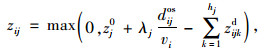
|
(5) |
式中,zj0为充电站j内初始时刻的车辆数;λj为平均每分钟到达充电站j的车辆数;vi为电动汽车i的平均行驶速度;zijkd为从电动汽车i到达充电站j的时间段内在充电桩k完成充电并且离开的车辆数。
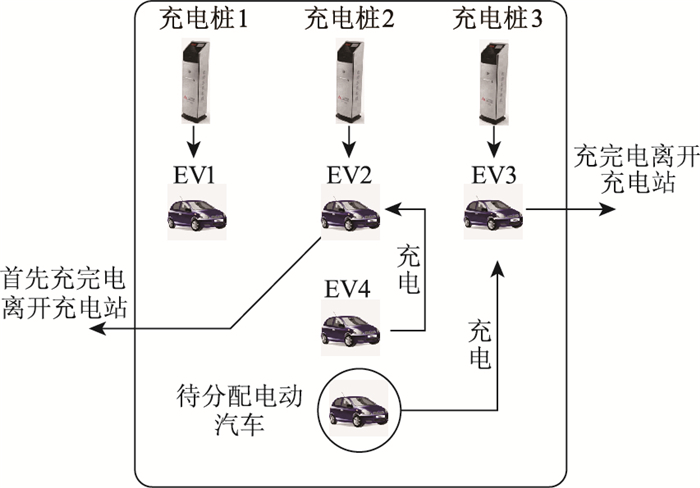
当待分配电动汽车到达充电站时,如果需要排队,则排队过程如图 1所示。图中所示充电站内有3个充电桩和5辆电动汽车,其中待分配电动汽车在图中用圆圈标注。在排队过程中,电动汽车EV2首先完成充电,排在待分配电动汽车前面的EV4开始充电,接着电动汽车EV3完成充电,待分配电动汽车才开始充电。
|
| 图 1 待分配电动汽车在充电站的排队过程 Fig. 1 Queuing process of EV to be assigned in charging station |
| |
充电站拥挤程度的方差可以表示电动汽车充电分布均衡情况,方差值越小表示电动汽车充电分布越均衡。针对电动汽车充电分布均衡的目标函数如下:
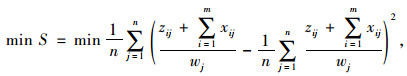
|
(6) |
式中,S为充电站拥挤程度的方差值;wj为充电站j所能容纳的最大车辆数。
2.2 约束条件为了保证电动汽车能够顺利完成出行同时保障车辆安全运行,针对模型提出了相应的约束条件。模型的约束条件如下:
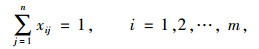
|
(7) |
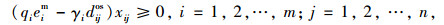
|
(8) |
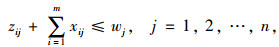
|
(9) |
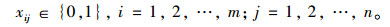
|
(10) |
上述各约束条件中:式(7)是充电站选择约束,保证每辆待分配电动汽车都可以充电且只可以选择1个充电站充电;式(8)是电动汽车运行电量约束,保证待分配电动汽车可以在电量耗尽之前到达充电站;式(9)是充电站最大可容纳车辆约束,保证充电站内的车辆数不能超过充电站可容纳的最大车辆数;式(10)是0-1变量约束,规定模型的决策变量xij只可以取0或者1。
2.3 模型转化所提出的考虑充电站效益的电动汽车充电分配模型存在3个目标函数。通常情况下,能够使3个目标函数全部达到最优的解是不存在的,但是,可以通过对3个目标函数的解进行折衷来得到考虑所有目标的解[13]。解决此类问题的基本思想是将多目标函数转化为单目标函数[14]。考虑到模型中3个目标函数的量纲不同,采用模糊规划法和模糊偏好关系对模型进行转化。模糊规划法主要基于模糊数学理论,采用从属函数表示目标函数的优化目标,同时保证求解结果的客观性。针对所提出的模型,采用线性从属函数[15]表示模型中目标函数的优化目标,以式(3)所示的目标函数为例,相应的线性从属函数为:
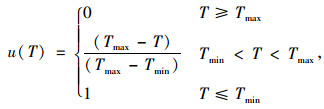
|
(11) |
式中,u(T)为目标函数min T对应的线性从属函数;Tmax和Tmin分别为T的最大值和最小值。需要注意的是,对于目标为求最大值的目标函数,需要将其转化为求最小值。
考虑到充电站运营商可能会对不同的优化目标采取不同的重视程度,采用模糊偏好关系[16]来客观地反映这种不同并且以此来为各优化目标赋予相应的权重值。在采用模糊偏好关系确定各目标权重值时,需要结合充电站运营商在实际运营过程中的效益需求,根据运营商在实际情况下对不同优化目标之间相对重视程度的差异性来计算各目标的权重值。以优化目标P和T为例,首先定义φPT为优化目标P对于T的相对重要系数,同时φTP为T对于P的相对重要系数。φPT和φTP的取值规则如下:如果优化目标P比T重要且重要程度较大时,则φPT =1-a, φTP=a;如果优化目标P比T重要且重要程度较小时,则φPT =1-b, φTP=b;如果优化目标P与T的重要性相同时,则φPT = φTP=0.5,其中0 < a < b < 0.5。然后,针对模型中的每个优化目标,将其对于其他优化目标的相对重要系数求和,以模型中优化目标T为例,求和结果为:
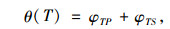
|
(12) |
式中,θ(T)为优化目标T对于其它优化目标的相对重要系数的求和结果;φTS为优化目标T对于S的相对重要系数。
最后,通过上述结果可以得到不同优化目标的权重,以优化目标T为例,权重为:
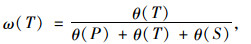
|
(13) |
式中,ω(T)为优化目标T的权重值。通过线性从属函数和优化目标的权重,可以将多目标函数模型转化为单目标函数模型,转化后的单目标函数为:
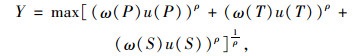
|
(14) |
式中ρ的取值可能为3种情况:ρ=1, ρ=2, ρ=∞,具体如下:
当ρ=1时,目标函数为:
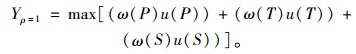
|
(15) |
当ρ=2时,目标函数为:
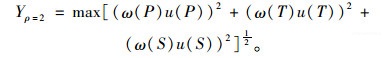
|
(16) |
当ρ=∞时,目标函数为:
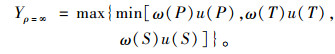
|
(17) |
考虑充电站效益的电动汽车充电分配模型是NP-Hard问题,遗传算法适合求解此类问题[17]。因此,设计遗传算法对模型进行求解。遗传算法是一类具有并行搜索特性的随机搜索算法。算法具体实现步骤包括相关参数设定、染色体编码、迭代进化,在每次迭代中根据种群中个体的适应度值进行选择、交叉和变异操作,产生新一代种群,直至算法结束求出最优解[18]。在遗传算法中,染色体编码是算法设计中的最基本内容,不同的问题所采取的编码方法也不同。针对所提出模型的特点,本研究算法采用整数排列编码方法。该方法是以问题中的待分配电动汽车的数量作为染色体的段数,同时每一段的数值代表为相应车辆所分配充电站的编号。例如,对于存在6辆待分配电动汽车和4个充电站的情况,相应的一条染色体如图 2所示。

|
| 图 2 染色体编码示例 Fig. 2 Example of chromosome coding |
| |
图 2染色体表示6辆待分配电动汽车分别被分配到编号为1,3,2,4,1和4的充电站。除了染色体编码之外,算法中其余步骤的设计思路类似于传统方法,因此对其不进行展开介绍。根据所设计的遗传算法可以实现对模型的求解。
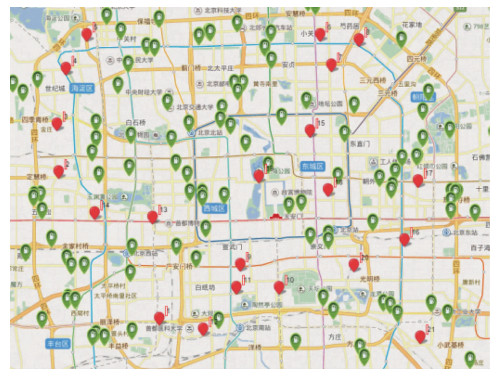
3.2 算例场景描述算例的数据包括充电站和待分配电动汽车的相关信息,其中充电站的位置、充电桩数量、单位充电服务费、最大可容纳车辆数等充电站静态数据来自实验室研发成果“电动汽车智能充电调度服务平台”的充电站数据库。数据库中包含全国的充电站数据,均是从各大充电站运营商网站以及相关平台上甄别提取出来的。试验选取北京市隶属于国家电网的充电站数据,其中包括可用公用充电站为168个。同时,在考虑到充电站数量和算例规模适当的前提下,试验假设在路网中存在21辆待分配电动汽车。此外,为保证试验结果具有代表性,待分配电动汽车的位置分布不宜过于集中。基于此,试验在路网中随机生成了21辆待分配电动汽车数据。待分配电动汽车及部分充电站的位置分布如图 3所示。
|
| 图 3 待分配电动汽车和部分充电站位置分布 Fig. 3 Location distributions of EVs to be assigned and part of charging stations |
| |
假设所有待分配电动汽车的最大电量是24 kW·h。通常情况下,电动汽车在充电过程中会以相对平稳且较快的速度使车辆SOC达到80%,当车辆SOC大于80%时,充电速度会相对变慢,因此用户一般会在SOC达到80%后停止充电,并且该电量在一般情况下也足以使电动汽车到达目的地[19]。基于此,试验假设电动汽车在充电站完成充电后的SOC为80%。算例中所涉及的21辆待分配电动汽车数据中的基本信息包括车辆初始位置的经度、纬度值和初始SOC。为了展示待分配电动汽车的数据信息,同时考虑到篇幅有限,将其中的5辆待分配汽车的基本信息以表格的形式列出,如表 1所示。
| 车辆编号 | 经度 | 纬度 | 初始SOC/% |
| 1 | 116.359131 | 39.867606 | 43 |
| 2 | 116.291866 | 39.929603 | 52 |
| 3 | 116.288417 | 39.94974 | 34 |
| 4 | 116.297903 | 39.969649 | 61 |
| 5 | 116.308539 | 39.984688 | 48 |
假设所有待分配电动汽车的平均行驶速度为40 km/h, 行驶单位距离所消耗的电量为0.15 (kW·h)/km, 部分电动汽车从起点到部分充电站的最短距离如表 2所示。
| 电动汽车 | 充电站 | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 46.40 | 42.55 | 55.20 | 36.92 | 6.90 | 9.15 |
| 2 | 48.12 | 53.67 | 18.58 | 17.25 | 25.19 | 12.67 |
| 3 | 12.84 | 57.64 | 45.92 | 39.94 | 17.07 | 15.92 |
| 4 | 30.41 | 33.74 | 45.72 | 41.97 | 48.40 | 26.20 |
| 5 | 27.84 | 10.04 | 24.07 | 45.39 | 27.02 | 4.88 |
通常情况下,充电桩的充电模式可以分为直流充和交流充,在实际充电站内可能存在充电模式不同的充电桩,由于不同充电模式下的充电桩相关参数不同,从而对充电站动态信息的假设以及仿真试验的结果造成影响。为了排除影响,需要对数据进行预处理,将充电站中具有相同充电模式的充电桩合并为一个新的虚拟充电站,且虚拟充电站的位置与原来的充电站相同,最大可容纳车辆数则按照充电桩数量占原充电站桩数量的比例重新划分。原数据中168个可用公用充电站中共有93个需要进行数据预处理,处理后的充电站共有261个,表 3列出了部分处理后充电站静态数据。
| 充电站 编号 |
纬度 | 经度 | 充电桩 数量/个 |
最大可容纳 车辆数/辆 |
单位服务费/ (元·kW·h-1) |
| 1 | 40.0365 2 | 116.354 6 | 2 | 3 | 0.8 |
| 2 | 40.048 54 | 116.363 3 | 3 | 5 | 0.8 |
| 3 | 39.997 04 | 116.203 2 | 2 | 3 | 1 |
| 4 | 39.987 | 116.339 7 | 2 | 3 | 0.8 |
| 5 | 39.985 5 | 116.366 9 | 5 | 8 | 0.8 |
由于包括充电站初始车辆数、车辆到达率和平均排队时间的充电站动态信息无法从充电站静态数据中直接获取,因此在算例中依据经验进行假设。所依据的经验是基于对某充电站运营商在运营过程中收集的充电站运营数据进行统计观察后所得。考虑到篇幅有限且充电站运营状态并非研究的重点,因此对数据分析内容不做具体描述。部分充电站动态信息如表 4所示。
| 充电站编号 | 初始车辆数/辆 | 车辆到达率/ (辆·min-1) |
平均排队 时间/min |
| 1 | 2 | 0.042 9 | 18 |
| 2 | 1 | 0.028 6 | 10 |
| 3 | 1 | 0.028 6 | 12 |
| 4 | 8 | 0.142 9 | 32 |
| 5 | 1 | 0.014 3 | 8 |
3.3 算例结果分析
首先根据算例场景中的数据和信息得出各条充电子路径的行驶时间和能耗等参数,然后用遗传算法对模型中3个单目标模型分别求解,其目标函数如式(2),(3)和(6)所示。遗传算法的参数如表 5所示,求解结果如表 6所示。
| 模型 | 运营商收入/元 | 排队时间/min | 拥挤程度方差 |
| max P | 545.4 | 2 307 | 0.64 |
| min T | 168.5 | 395 | 0.75 |
| min S | 354.8 | 1 647 | 0.45 |
通过观察表 6中单目标模型求解结果可知,以max P为目标的模型和以min S为目标的模型所得结果中的总排队时间过长,而排队时间过长会给用户的充电服务满意度造成极大的负面影响,同时,以min T为目标的模型所得结果中的运营商收入最低且拥挤程度方差最大,虽然缩短了用户的排队时间,但是却给运营商带来了收入的损失并且造成充电桩资源的浪费,因此,以单目标模型所得到的充电分配方案存在不合理性。
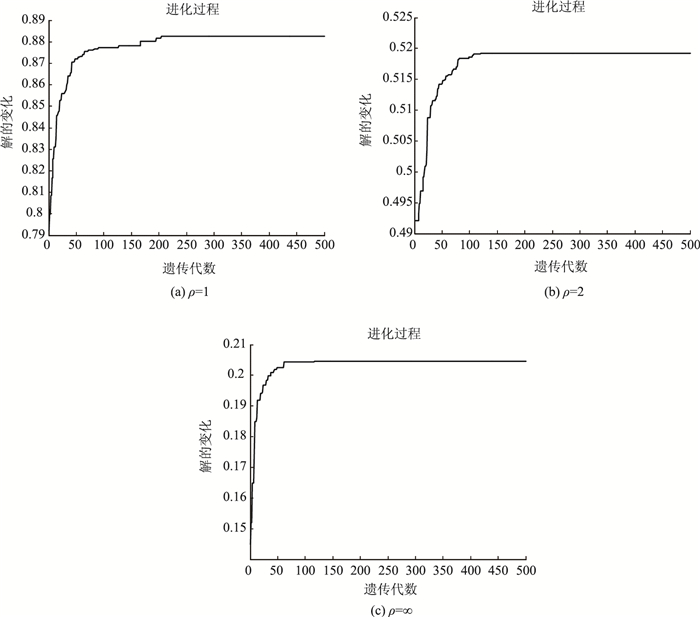
下面将3个单目标模型转化为多目标模型进行求解。假设运营商对于不同的优化目标采取相同的重视程度,根据式(12)和(13)可以得到各目标的权重值都为1/3,并且结合式(11)可以得到如式(14)所示的目标函数。针对ρ在不同取值下的目标函数,如式(15)~(17)所示,遗传算法的迭代过程如图 4所示。
|
| 图 4 多目标模型求解迭代过程 Fig. 4 Solution iteration process of multiple-objective model |
| |
如图 4所示,所有ρ取值下的多目标模型在求解迭代过程中都在最大迭代次数500以内达到平稳。表 7列出了多目标模型在不同ρ取值下的求解结果。
| ρ的取值 | Y | 充电站收入/元 | 排队时间/min | 拥挤程度方差 |
| 1 | 0.883 | 427.9 | 963 | 0.56 |
| 2 | 0.518 | 423.7 | 1 018 | 0.61 |
| ∞ | 0.204 | 467 | 1 136 | 0.49 |
将多目标模型的最优解与3个单目标模型的求解结果进行比较,比较方法如下:从最优解中充电站收入、排队时间、拥挤程度方差3个单优化目标值出发,求出不同ρ取值下多目标模型最优解中各目标值比单目标模型增加的百分比。然后,将各目标值增加的百分比进行加权求和,求出同时考虑3个优化目标的综合效益所增加的百分比,另外,由于优化目标中的排队时间和拥挤程度方差都是求最小值,因此为了表示效益的增加, 在加权求和时, 对优化目标中排队时间和拥挤程度方差的权重值取负数。表 8列出了多目标模型与单目标模型的比较结果。
| 比较项目 | ρ的取值 | 经济 收入/% |
排队 时间/% |
拥挤程度 方差/% |
综合 效益/% |
| 多目标模型与单目标模型max P比较 | ρ=1 | -21.5 | -58.3 | -12.5 | 16.2 |
| ρ=2 | -22.3 | -55.9 | -4.7 | 12.6 | |
| ρ=∞ | -14.4 | -50.8 | -23.4 | 19.7 | |
| 多目标模型与单目标模型min T比较 | ρ=1 | 153.9 | 143.8 | -25.3 | 11.7 |
| ρ=2 | 151.5 | 157.7 | -18.7 | 4.1 | |
| ρ=∞ | 177.2 | 187.6 | -34.7 | 8 | |
| 多目标模型与单目标模型min S比较 | ρ=1 | 20.6 | -41.5 | 24.4 | 12.4 |
| ρ=2 | 19.4 | -38.2 | 35.6 | 7.3 | |
| ρ=∞ | 31.6 | -31 | 8.9 | 17.7 |
表 8所示的比较结果表明,所有多目标模型所得分配方案下的综合效益都要大于单目标模型。同时,为了比较不同ρ取值下多目标模型的最优解,从而得到最终的电动汽车分配决策方案,将ρ取相同值下的综合效益所增加百分比进行求和,ρ=1,ρ=2和ρ=∞的求和结果分别为40.3%,24%和45.4%。最后将求和结果最大的ρ=∞时多目标模型的最优解所对应的分配方案作为最终的分配方案。如表 8所示,最终分配方案下的综合效益比单目标模型max P,min T,min S分别增加了19.7%,8%,17.7%。表 9列出了最优解中21辆待分配电动汽车的最终分配方案。
| 电动汽车 编号 |
充电站 编号 |
| 1 | 5 |
| 2 | 213 |
| 3 | 66 |
| 4 | 251 |
| 5 | 10 |
| 6 | 187 |
| 7 | 204 |
| 8 | 158 |
| 9 | 231 |
| 10 | 195 |
| 11 | 189 |
| 12 | 160 |
| 13 | 136 |
| 14 | 103 |
| 15 | 59 |
| 16 | 230 |
| 17 | 45 |
| 18 | 47 |
| 19 | 233 |
| 20 | 28 |
| 21 | 183 |
通过最优分配方案下各目标值对比单目标模型的变化情况进行观察分析可知,经济收入、排队时间和拥挤程度对充电分配决策都具有比较显著的影响,并且综合来看,排队时间的变化情况最为突出,说明排队时间对充电分配决策的影响相对较大。因此,在制订充电分配方案时要重视排队时间对最终方案确定的影响,同时,要增加充电站效益进而促进充电站的建设。
4 结论(1) 针对电动汽车用户在出行过程中所面临的车辆续驶里程较短和充电设施建设相对滞后的问题,考虑到充电站的效益需求,建立了一个考虑路网中多个充电站整体效益的多目标函数电动汽车充电分配模型。模型的目标函数包括充电站经济收入最大化、充电排队时间最小化和拥挤程度方差最小化。通过模糊规划法和模糊偏好关系,将模型的多目标函数转化为同时考虑多个优化目标的单目标函数,并且设计遗传算法对模型进行求解。
(2) 设计算例对模型和算法进行验证。算例场景的设计是基于北京市隶属于国家电网的可用公用充电站的静态数据。通过对试验结果进行比较分析后得出结论:多目标模型所得最优分配方案下的综合效益比以充电站经济收入最大化、充电排队时间最小化、充电站拥挤程度的方差最小化为目标的单目标模型分别增加了19.7%,8%,17.7%,并且通过分析可知由于充电设施建设滞后,排队时间对充电分配具有相对较大的影响。
(3) 为了简化建模,模型中的车辆到达率和平均排队时间都是基于经验的假设值,后续的工作将考虑充电站的实时动态信息变化,进一步结合真实的车辆到达率和平均排队时间,建立考虑动态变化下的车辆到达率和平均排队时间的电动汽车充电分配优化模型。同时,路网状况和交通出行条件等因素,对车辆行驶状态和充电分配的影响也会在今后的研究中加以考虑。并且,在此基础上,还会进一步将改进后的模型与工程实例相结合,对模型的实际应用效果与现状收益进行比较。另外,考虑到电动汽车充电分配决策结果可能会对个人用户、企业、社会所产生的影响,在今后的工作中,我们会进一步研究在不同优化目标下,电动汽车充电分配决策结果对个人、企业、社会的影响。
| [1] |
王健, 梁桂航. 纯电动出租汽车快速更换电池运营模式[J]. 公路交通科技, 2011, 28(11): 142-145. WANG Jian, LIANG Gui-hang. Battery-quick-replacement Operation Mode for Electric Taxi Vehicle[J]. Journal of Highway and Transportation Research and Development, 2011, 28(11): 142-145. |
| [2] |
刘志鹏, 文福拴, 薛禹胜, 等. 电动汽车充电站的最优选址和定容[J]. 电力系统自动化, 2012, 36(3): 54-59. LIU Zhi-peng, WEN Fu-shuan, XUE Yu-sheng, et al. Optimal Siting and Sizing of Electric Vehicle Charging Stations[J]. Automation of Electric Power Systems, 2012, 36(3): 54-59. |
| [3] |
KEJUN Q, CHENGKE Z, ALLAN M, et al. Modeling of Load Demand due to EV Battery Charging in Distribution Systems[J]. IEEE Transactions on Power Systems, 2011, 26(2): 802-810. |
| [4] |
王锡凡, 邵成成, 王秀丽, 等. 电动汽车充电负荷与调度控制策略综述[J]. 中国电机工程学报, 2013, 33(1): 1-10. WANG Xi-fan, SHAO Cheng-cheng, WANG Xiu-li, et al. Survey of Electric Vehicle Charging Load and Dispatch Control Strategies[J]. Proceedings of the CSEE, 2013, 33(1): 1-10. |
| [5] |
ERDOGAN S, MILLER-HOOKS E. A Green Vehicle Routing Problem[J]. Transportation Research Part E:Logistics & Transportation Review, 2012, 48(1): 100-114. |
| [6] |
SAID D, CHERKAOUI S, KHOUKHI L. Queuing Model for EVs Charging at Public Supply Stations[C]//20139th International Wireless Communications and Mobile Computing Conference (IWCMC). Sardinia, Italy:IEEE, 2013.
|
| [7] |
苏舒, 孙近文, 林湘宁, 等. 电动汽车智能充电导航[J]. 中国电机工程学报, 2013, 33(增1): 59-67. SU Shu, SUN Jin-wen, LIN Xiang-ning, et al. Electric Vehicle Smart Charging Navigation[J]. Proceedings of the CSEE, 2013, 33(S1): 59-67. |
| [8] |
冯智泉, 黄亦翔, 李杰, 等. 蚁群算法求电动汽车最优行驶路径与充电方案[J]. 机电一体化, 2013, 19(8): 43-48. FENG Zhi-quan, HUANG Yi-xiang, LI Jie, et al. Ant Colony Algorithm for EV Path and Charging Optimization[J]. Mechatronics, 2013, 19(8): 43-48. |
| [9] |
HE F, YIN Y, LAWPHONGPANICH S. Network Equilibrium Models with Battery Electric Vehicles[J]. Transportation Research Part B:Methodological, 2014, 67(3): 306-319. |
| [10] |
JIANG N, XIE C. Computing and Analyzing Mixed Equilibrium Network Flows with Gasoline and Electric Vehicles[J]. Computer-aided Civil & Infrastructure Engineering, 2014, 29(8): 626-641. |
| [11] |
SUN X H, YAMAMOTO T, MORIKAWA T. Fast-charging Station Choice Behavior among Battery Electric Vehicle Users[J]. Transportation Research Part D:Transport & Environment, 2016, 46: 26-39. |
| [12] |
ZHONG F, LI H, ZHONG S, et al. An SOC Estimation Approach Based on Adaptive Sliding Mode Observer and Fractional Order Equivalent Circuit Model for Lithium-ion Batteries[J]. Communications in Nonlinear Science & Numerical Simulation, 2015, 24(1-3): 127-144. |
| [13] |
卢冰原, 何力, 贾兆红. 模糊环境下的多目标非满载车辆调度问题[J]. 公路交通科技, 2011, 28(8): 147-153. LU Bing-yuan, HE Li, JIA Zhao-hong. Multi-objective Non-full Loaded Vehicle Scheduling Problemin Fuzzy Environment[J]. Journal of Highway and Transportation Research and Development, 2011, 28(8): 147-153. |
| [14] |
LIU H L, GU F, ZHANG Q. Decomposition of a Multiobjective Optimization Problem into a Number of Simple Multiobjective Subproblems[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(3): 450-455. |
| [15] |
WANG G, WANG X, WAN Z. A Fuzzy Interactive Decision Making Algorithm for Bilevel Multi-followers Programming with Partial Shared Variables among Followers[J]. Expert Systems with Applications, 2009, 36(7): 10471-10474. |
| [16] |
CHEN Y H, CHAO R J. Supplier Selection Using Consistent Fuzzy Preference Relations[J]. Expert Systems with Applications, 2012, 39(3): 3233-3240. |
| [17] |
彭怀军, 秦勇, 张尊栋, 等. 基于遗传算法的二元覆盖模型在交通警力部署中的应用[J]. 公路交通科技, 2016, 33(10): 125-130. PENG Huai-jun, QIN Yong, ZHANG Zun-dong, et al. Application of Dual Coverage Model Based on Genetic Algorithm in Traffic Police Deployment[J]. Journal of Highway and Transportation Research and Development, 2016, 33(10): 125-130. |
| [18] |
SHAFAHI Y, KHANI A. A Practical Model for Transfer Optimization in a Transit Network:Model Formulations and Solutions[J]. Transportation Research Part A:Policy & Practice, 2010, 44(6): 377-389. |
| [19] |
YONG J Y, RAMACHANDARAMURTHY V K, TAN K M, et al. Bi-directional Electric Vehicle Fast Charging Station with Novel Reactive Power Compensation for Voltage Regulation[J]. International Journal of Electrical Power & Energy Systems, 2015, 64: 300-310. |
 2018, Vol. 35
2018, Vol. 35
