扩展功能
文章信息
- 刘广龙, 刘江, 刘永健, 张宁
- LIU Guang-long, LIU Jiang, LIU Yong-jian, ZHANG Ning
- 西北极寒地区混凝土箱梁温度场实测与仿真分析
- Measurement and Simulation of Temperature Field of Concrete Box Girder in Northwest Severe Cold Area
- 公路交通科技, 2018, 35(3): 64-71
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(3): 64-71
- 10.3969/j.issn.1002-0268.2018.03.009
-
文章历史
- 收稿日期: 2016-11-22
2. 西北农林科技大学 水利与建筑工程学院, 陕西 杨凌 712100
2. School of Water Resources and Architectural Engineering, Northwest A & F University, Yangling Shaanxi 712100, China
混凝土材料导热性差,在太阳辐射、气温变化、风速等环境因素作用下,混凝土箱梁内部温度呈现非线性分布,引起较大的温度效应,甚至造成结构的开裂,其荷载效应甚至超过活载的作用[1-2]。混凝土箱梁温度场分布与地理位置、太阳辐射、气温变化、风速以及材料热工参数等因素有关,不同地区之间混凝土箱梁温度场分布会存在一定的差异。目前,中国公路桥涵设计规范(JTG D60—2015)关于温度梯度模式的规定借鉴了美国AASHTO规范中2区的温度模式及取值,规定我国各地的桥梁采用一致的温度梯度模式,并未考虑地域不同对温度梯度模式取值的影响,而我国幅员辽阔,横跨寒带、亚热带和热带,还需对规范条文进行相应补充[3-5]。
基于热传导理论和现场实测数据,国内外学者对混凝土箱梁温度场开展了很多研究。Kehlbeck[6]对太阳辐射、对流换热、气温变化、风速等气象因素对结构温度场的影响规律进行了分析,求得了以矩阵形式表示的温度函数;Priestley[7]基于Fourier热传导方程建立了一维热传导模型,得出5次抛物线函数温度分布模型;Elbadry等[8]综合考虑太阳辐射、气温变化、桥梁走向和材料物理特性等因素,采用二维有限元模型计算桥梁截面温度场;Miarmbell等[9]提出有限差分法和有限元法两种计算温度场分布的方法,并将计算结果和实测数据进行对比分析;汪剑等[10]基于热传导理论,对混凝土箱梁表面热流进行分析,建立箱梁温度场有限元模型;雷笑等[11]基于某预应力混凝土箱梁桥温度场观测数据,提出了观测桥梁的温度分布形式;吴六政[12]详细地分析了影响温度场变化的主要因素,建立了任意时刻桥梁结构的温度场模拟方法;Larsson等[13]通过对混凝土板的野外现场试验,论证了基于气象参数的有限元模型的可行性;顾斌等[14]建立了基于气象参数并考虑实际桥址和桥梁走向的混凝土箱梁日照温度场有限元模型,分析日平均风速和大气日温差对箱梁梯度温度的影响,并从概率统计角度,得出50年一遇气象参数条件下的梯度模式;还有其他学者对不同形式的混凝土箱梁温度场进行了分析。以上学者的研究者重点是箱梁温度场的数值模拟计算和基于实测数据的箱梁温度梯度的分析,而对于我国西北这种整体温度低、太阳辐射强的极寒地区的混凝土箱梁温度场分布的研究较少。
本研究以新疆小沙河中桥为背景,基于传热学分析理论和现场观测数据,建立二维温度场有限元模型,研究西北极寒地区混凝土箱梁在日照升温和寒潮降温作用下梁高、腹板以及底板壁厚方向的温度场分布特点及其变化规律,并对日照升温和寒潮降温作用下混凝土箱梁的温度效应进行分析,对同类地区的桥梁设计计算具有参考意义。
1 小沙河中桥温度场实测分析 1.1 观测截面与测点布置小沙河中桥位于新疆昌吉市,位于87.2°E、44.1°N,海拔高度0.5 km。跨径布置为3×25 m,如图 1所示,上部结构为装配式预应力箱梁,主梁采用等截面箱梁,上下行分幅布置,下部结构为柱式墩,桩基础。桥面铺装由10 cm厚C50混凝土桥面现浇层与12 cm厚沥青混凝土构成。

|
| 图 1 跨径布置示意图(单位:cm) Fig. 1 Schematic diagram of span arrangement (unit:cm) |
| |
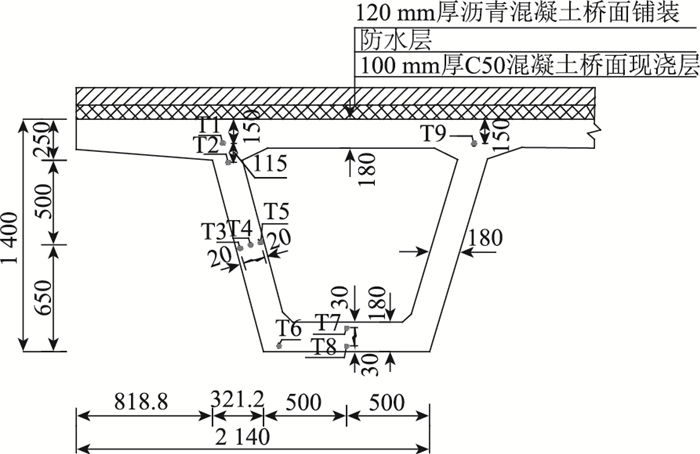
小沙河中桥温度场实测选取D1,D2两个断面作为观测截面,截面测点布置相同,截面位置与测点布置如图 1~2所示。
|
| 图 2 截面测点布置(单位:mm) Fig. 2 Layout of temperature sensors on cross-section (unit:mm) |
| |
1.2 数据分析
考虑到新疆地区气候特点以及温度场实测情况,选取2016年1月20日至2016年2月20日的混凝土箱梁温度场数据作为研究对象。
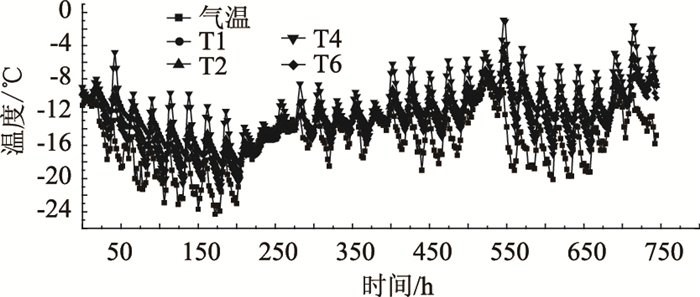
图 3所示为混凝土箱梁高度方向测点实测数据,可以看出,温度测点与环境温度变化趋势基本一致,但其变化与气温存在明显的滞后性;受太阳辐射的影响,梁高方向存在明显的温度梯度,测点T1,T4最大温差达到6.4 ℃,测点T4,T6最大温差达到5.6 ℃;由于桥面铺装层隔热作用,顶板测点T1波动较小,每天约有1.5 ℃的波动;腹板测点T4在一天内的波动较大,日最大温差达到14.2 ℃,主要原因是受太阳辐射和日落降温的影响较大。
|
| 图 3 梁高方向实测温度—时间曲线 Fig. 3 Curves of measured temperature-time in vertical direction |
| |
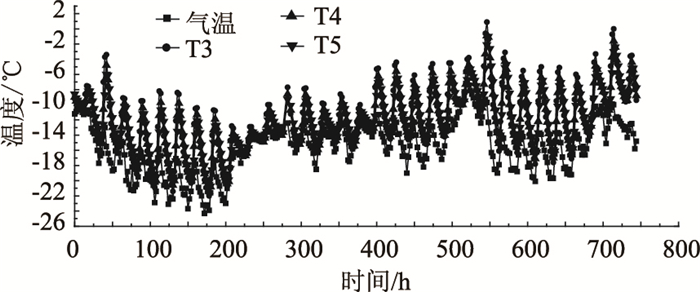
图 4所示为混凝土箱梁腹板壁厚方向温度实测数据,可以看出:在日照条件下,腹板外侧温度明显高于内侧,腹板壁厚方向存在明显的温度梯度,其中,测点T3,T5之间最大温差达到5.6 ℃,原因主要是混凝土材料的导热性差,腹板外侧吸收的热量传递到内侧的速度较慢;腹板温度测点在一天内波动较大,且温度变化趋势基本一致,其中,测点T3日最大温差达到17 ℃。
|
| 图 4 腹板壁厚实测温度-时间曲线 Fig. 4 Curves of measured temperature-time along web thickness |
| |
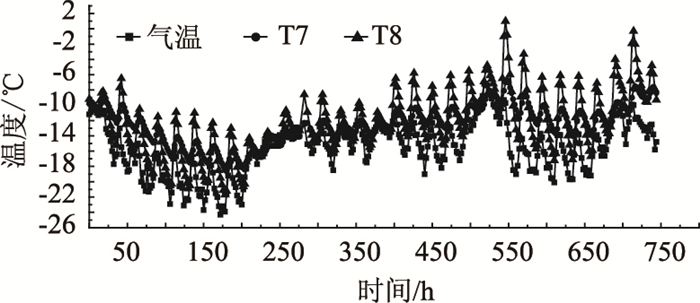
图 5所示为箱梁底板壁厚方向温度场实测数据,可以看出:底板沿壁厚方向存在明显的温度梯度,测点T7,T8之间最大温差达到8 ℃;测点T8在一天内的波动较大,日最大温差达到11 ℃左右,主要原因是底板受环境温度变化、地表辐射、遮挡等因素的影响较大。
|
| 图 5 底板壁厚实测温度-时间曲线 Fig. 5 Curves of measured temperature-time along bottom plate thickness |
| |
由于温度场测点布置有限,为了弄清高原极寒地区混凝土箱梁温度场的分布特点,有必要进行温度场的仿真分析,进一步了解混凝土箱梁的温度场分布规律。
2 箱梁温度场数值模拟 2.1 热传导理论桥梁结构温度场分析的理论基础为Fourier热传导微分方程[15],对于无内热源的桥梁结构温度场问题,热传导微分方程的如式(1):
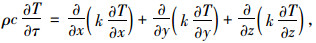
|
(1) |
式中,T为桥梁结构温度函数;τ,x,y,z分别为确定温度所对应的时间与坐标;ρ,c,k均为材料的热工参数,分别是密度、比热容和导热系数。
混凝土箱梁温度场为三维非线性瞬态温度场,在实际的计算中,近似地认为桥梁轴向没有热传导,温度只在箱梁截面上变化,将三维空间问题简化为二维平面问题,则热传导微分方程简化为式(2):
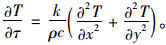
|
(2) |
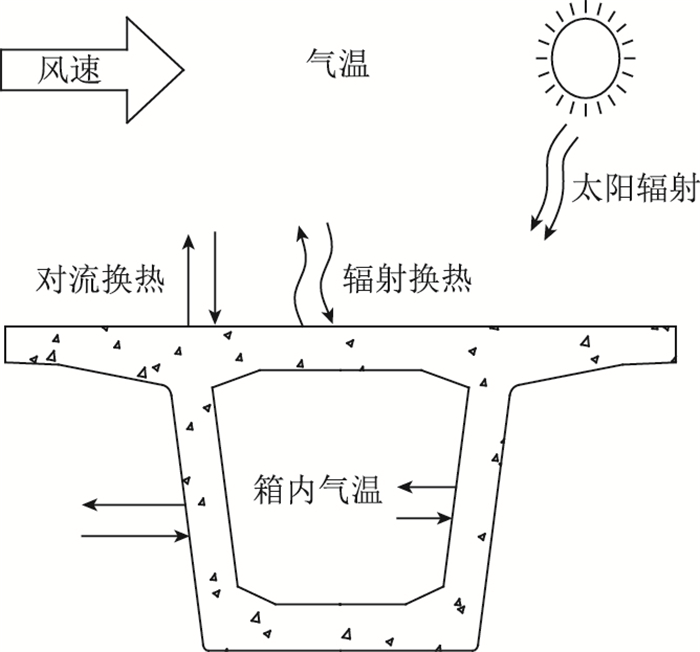
在太阳辐射条件下,混凝土箱梁与周围环境的热交换情况如图 6所示。混凝土桥梁结构表面热流密度包括3种类型,分别是太阳辐射、辐射换热与对流换热。
|
| 图 6 混凝土箱梁与环境热交换示意图 Fig. 6 Heat transfer between concrete box girder and environment |
| |
2.2.1 太阳辐射
在日照作用下,混凝土箱梁表面受到的太阳辐射包括直射辐射、天空散射辐射和地面反射辐射3部分。在本文中太阳辐射计算采用Hottel晴空模型[16]。
大气层外切平面上瞬时太阳辐射ION由式(3)计算:
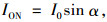
|
(3) |
式中, I0为太阳常数;α为太阳高度角。
晴朗天气太阳辐射直射透过比τb由式(4)计算:
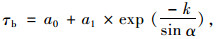
|
(4) |
式中, a0,a1和k是标准晴空大气的物理常数,由气候类型决定[17]。
晴朗天气太阳散射透过比τd 由式(5)计算:
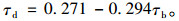
|
(5) |
水平面瞬时太阳直射辐射Icb由式(6)计算:
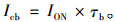
|
(6) |
水平面瞬时太阳散射辐射Icd由式(7)计算:
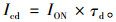
|
(7) |
水平面瞬时太阳总辐射Ic由式(8)计算:
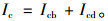
|
(8) |
任意表面实际吸收太阳辐射热流密度qt可按式(9)计算:
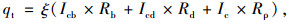
|
(9) |
式中,ζ为结构表面对太阳辐射的吸收率;Rb为直射辐射修正因子,按照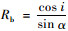
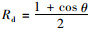
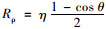
箱梁表面的对流换热服从牛顿冷却定律,由式(10)计算:
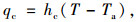
|
(10) |
式中,hc为对流换热系数,取值由环境风速v近似计算[6]:

|
(11) |
式中v为风速。
2.2.3 辐射换热箱梁表面辐射换热主要由大气辐射、地表辐射以及结构本身辐射3部分构成。箱梁表面吸收的大气辐射热流密度qa由式(12)计算:
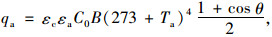
|
(12) |
式中,εc为结构表面长波辐射系数;εa为大气辐射系数,一般取值0.82;C0为Stefan-Boltzmann常数,其值为5.67×10-8W/(m2·k4);Ta为大气温度。
箱梁表面吸收的地表辐射热流密度qd由经验公式(13)计算:
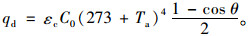
|
(13) |
箱梁表面向外界辐射的热辐射qR由式(14)计算:
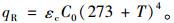
|
(14) |
在本研究中,采用Abaqus进行温度场的仿真分析,选用四节点线性传热四边形单元DC2D4,建立二维温度场有限元模型。其中,混凝土表面和沥青混凝土表面短波辐射吸收率分别为0.65和0.9,长波辐射吸收率分别为0.88和0.9,材料热工参数如表 1所示。
| 材料 | 密度/(kg·m-3) | 比热容/(J·kg-1·℃-1) | 导热系数/(W·m-1·℃-1) |
| 混凝土 | 2 500 | 880 | 2.5 |
| 沥青混凝土 | 2 100 | 1 680 | 1.05 |
2.4 模型验证
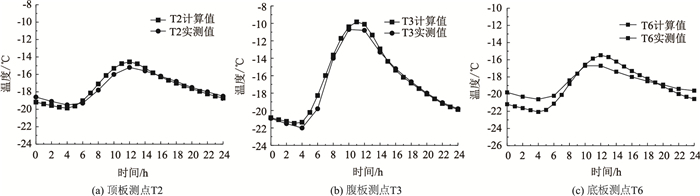
本研究选取天气较为晴朗的2016年1月27日06:00到2016年1月28日06:00作为温度场计算时间。箱梁顶板、腹板和底板等处测点计算温度和实测温度变化见图 7(a)~(c),日照作用下混凝土箱梁温度场影响因素较多,太阳辐射参数与材料热工参数的选取难以精确反映真实情况,故计算结果存在一定的偏差,但最大偏差为1.5 ℃,平均偏差近似为0,完全满足实际工程的精度要求。因此,本研究建立箱梁温度场的方法与参数的选取准确可行。
|
| 图 7 混凝土箱梁温度计算值与实测值对比 Fig. 7 Comparison of calculated and measured temperatures of concrete box girder |
| |
3 温度场分析
在本研究中,采用Abaqus对高原极寒地区混凝土箱梁在升温、降温作用下的温度场变化规律和特点进行研究,模型单元选择和参数取值不变,温度场分析包括梁高方向和板厚方向。通过对桥址历史气象数据(2011年1月至2016年5月)分析,选取2015年7月22日06:00至2015年7月22日22:00进行升温作用下温度场分析,日最高温度和最低温度分别43 ℃和23 ℃;选取2015年12月12日20:00至2015年12月13日8:00进行降温作用下温度场分析,受寒潮降温影响,温度骤降8 ℃左右。
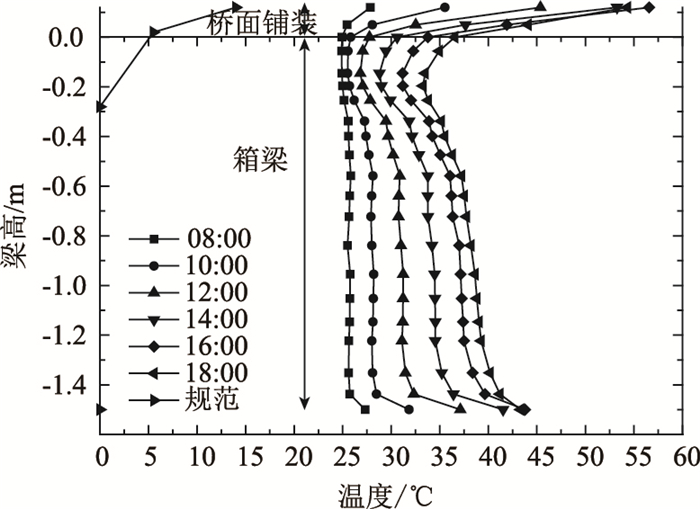
3.1 梁高方向图 8、图 9分别为日照升温和寒潮降温作用不同时刻梁高方向温度分布计算结果与《公路桥涵设计通用规范》(JTG D60—2015)中正、负温度梯度的对比。高原极寒地区混凝土箱梁温度梯度模式与规范温度梯度模式存在一定的差异,主要体现在以下几个方面:(1)箱梁顶板位置温度梯度较小,主要原因是沥青铺装层内温差非常明显,最高达23 ℃,在升温作用下起到明显的隔热作用,寒潮降温作用下起到明显的保温作用,与文献[19]的结果一致;(2)在日照升温作用下,腹板区的温度高于顶板温度,主要原因是新疆地区纬度较高,太阳高度角小,箱梁腹板遮挡较少,直接太阳辐射强度大;寒潮降温作用下,腹板及底板位置温度低于顶板温度,主要原因是腹板和底板直接与环境接触,受气温影响大;(3)在日照升温作用下,受地面反射作用的影响,底板存在明显的正温度梯度,最大温差在8 ℃左右,发生在14:00左右;受寒潮降温作用的影响,底板外侧温度明显低于内侧,最大达3 ℃。
|
| 图 8 升温作用主梁竖向温度分布 Fig. 8 Vertical temperature distribution of concrete box girder under effect of temperature rise |
| |
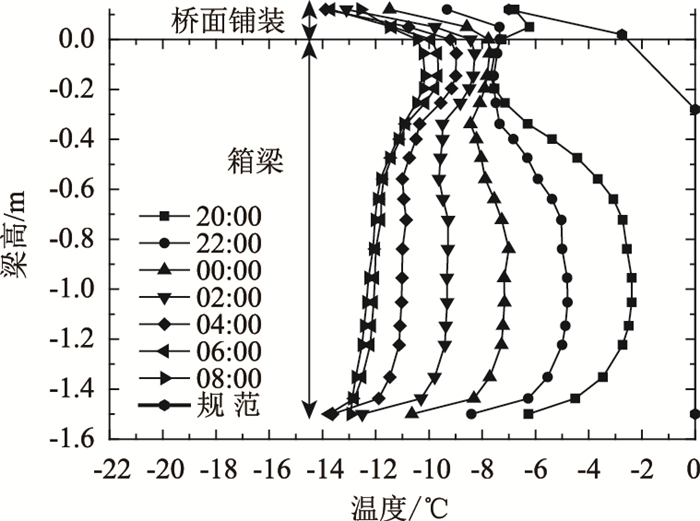
|
| 图 9 降温作用主梁竖向温度分布 Fig. 9 Vertical temperature distribution under effect of temperature drop |
| |
3.2 板厚方向
图 10(a)、(b)分别为日照升温和寒潮降温作用下不同时刻腹板壁厚方向温度场计算结果,在日照作用下,腹板壁厚方向存在明显的温度梯度,最大达7 ℃左右,发生在15:00左右,温度分布曲线近似按二次抛物线变化;受寒潮降温影响,在腹板壁厚方向存在明显的负温差,最大差值达到4 ℃左右,温度分布曲线近似按二次抛物线变化。

|
| 图 10 腹板壁厚方向温度分布 Fig. 10 Temperature distribution along web thickness |
| |
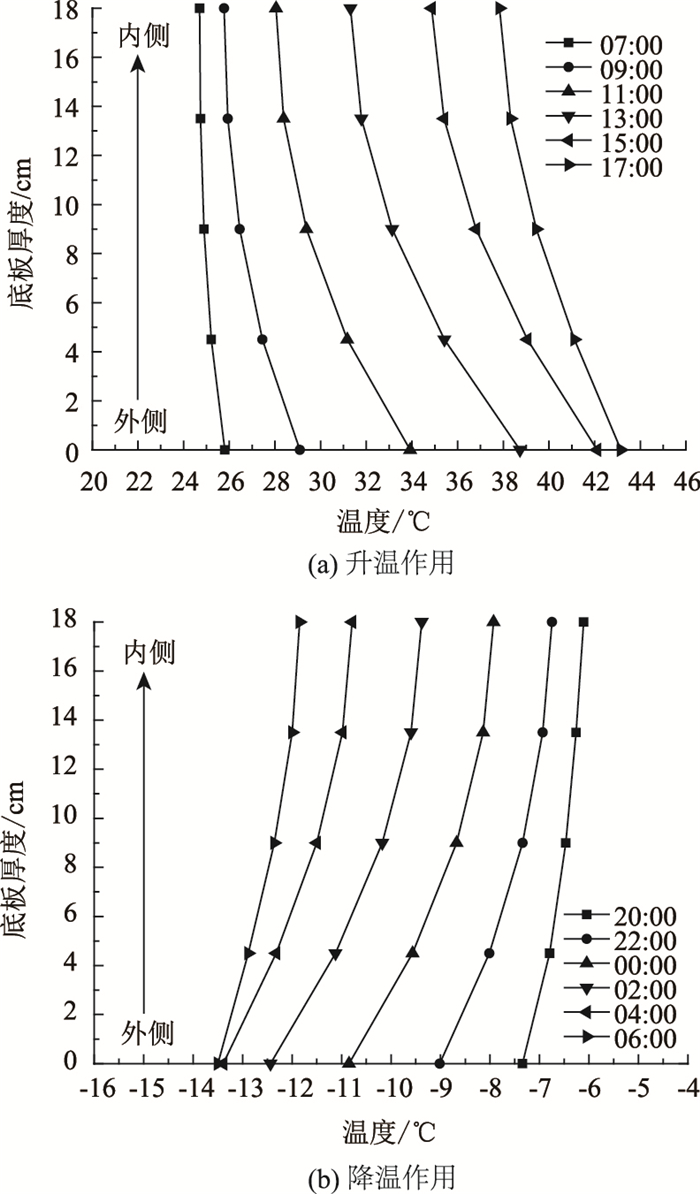
图 11(a)、(b)分别为日照升温和寒潮降温作用下不同时刻底板壁厚方向温度场计算结果。底板壁厚方向最大温差达到8 ℃左右,发生在13:00左右,温度分布曲线近似按二次抛物线变化,原因主要是新疆地区海拔较高,太阳辐射量大,地面反射强度高。寒潮降温作用下,底板壁厚方向负温差最大达到3 ℃左右,发生在02:00左右,温度分布曲线近似按二次抛物线变化。
|
| 图 11 底板壁厚方向温度分布 Fig. 11 Temperature distribution along bottom plate thickness |
| |
4 温度效应分析
建立混凝土简支箱梁实体单元模型,采用八结点线性六面体单元(C3D8R),主梁采用C50混凝土,弹性模量为34.5 N/m2,泊松比0.2,线膨胀系数为1×10-5,模型边界条件按照简支梁体系设定,其余模型参数取值与上文一致,分析计算温度梯度产生的温度效应与规范的差异,如图 12所示。在模型上分别施加两个工况:工况1:按照最不利时刻温度场进行加载;工况2:按照《公路桥规》中规定的温度梯度进行加载,计算结果如表 2所示。

|
| 图 12 温度效应计算模型 Fig. 12 Calculation model of temperature effect |
| |
| 计算结果 | 升温模式 | 降温模式 | ||||
| 工况1 | 工况2 | 工况1 | 工况3 | |||
| 跨中挠度 | 方向 | 向下 | 向上 | 向上 | 向下 | |
| 大小/mm | 3.4 | 4.5 | 0.4 | 2.2 | ||
| 顶板应力 | 正负 | - | - | + | + | |
| 大小/MPa | 2.3 | 2.4 | 1.9 | 1.2 | ||
| 底板应力 | 正负 | + | - | + | + | |
| 大小/MPa | 1.3 | 0.7 | 3.0 | 0.4 | ||
| 注:表中“+”表示拉应力;“-”表示压应力。 | ||||||
在升温模式下,工况1作用下主梁产生向下变形,跨中变形量为3.4 mm,底板受拉,大小为1.3 MPa,而工况2作用下产生向上的变形,跨中变形量为4.5 mm,底板受压,大小为0.7 MPa。主要原因是:沥青混凝土铺装层内温差大,起到明显的隔热作用,箱梁顶板温度较低,而箱梁底板受地面反射影响大,底板位置温度高。
在降温模式下,工况1作用下产生向上变形,与工况2相反;工况1、工况2作用下顶、底板位置都处于受拉状态,但工况1产生的拉应力明显高于工况2,在底板位置工况1为3.0 MPa,与其他荷载组合下可能发生开裂,而工况2作用下仅为0.4 MPa。主要原因是:沥青混凝土铺装起到保温作用,顶板温度高于腹板和底板温度;同时,底板收缩时受到边界条件的约束,出现拉应力。可以明显看出,西北地区混凝土箱梁的温度效应计算结果较规范更为不利,因此,在进行西北地区混凝土箱梁的设计计算时,建议根据桥位处气象数据对温度效应进行分析,而并非简单套用规范。
5 结论本研究以新疆小沙河中桥为背景,研究高原极寒地区混凝土箱梁的温度场分布特点及其温度效应。通过试验实测与有限元分析,分析混凝土箱梁在日照升温和寒潮降温作用下梁高、腹板以及底板壁厚方向的温度场分布特点及其温度效应,得出以下结论:
(1) 通过对箱梁温度实测数据分析,结果表明:在混凝土箱梁高度方向、腹板壁厚方向以及底板壁厚方向都存在明显的温差。
(2) 温度场有限元计算结果完全满足实际工程的精度要求,箱梁温度场建立方法与参数选取准确可行。
(3) 西北极寒地区混凝土箱梁高度方向温度梯度不同于规范中的规定,其主要特点为:箱梁顶板温度梯度较小;箱梁底板位置存在明显的温度梯度;升温作用下腹板温度高于顶板温度,但低于底板温度;降温作用下顶板温度高于腹板和底板温度。
(4) 西北极寒地区混凝土箱梁的温度效应计算结果较规范更为不利,因此,在进行西北地区混凝土箱梁的设计计算时,建议根据桥位处气象数据对温度效应进行分析,而并非简单套用规范。
| [1] |
PRIESTLEY M J N. Thermal Gradients in Bridges:Some Design Considerations[J]. New Zealand Engineering, 1972, 27(7): 228-233. |
| [2] |
KENNEDY J B, SOLIMAN M H. Temperature Distribution in Composite Bridges[J]. Journal of Structural Engineering, 1987, 113(3): 475-482. |
| [3] |
美国各州公路和运输工作者协会. 美国公路桥梁设计规范:荷载与抗力系数设计法[M]. 北京: 人民交通出版社, 1988, 95-97. AASHTO. Highway Bridge Design Specification:Load and Resistance Factor Design[M]. Beijing: China Communications Press, 1988, 95-97. |
| [4] |
JTG D60-2015, 公路桥涵设计通用规范[S]. JTG D60-2015, General Specifications for Design of Highway Bridges and Culverts[S]. |
| [5] |
TB 10002. 3-2005, 铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S]. TB 10002. 3-2005, Code for Design on Reinforced and Prestressed Concrete Structure of Railway Bridge and Culvert[S]. |
| [6] |
凯尔别克F. 太阳辐射对桥梁结构的影响[M]. 北京: 中国铁道出版社, 1981, 1-32. KEHLBECK F. Influence of Solar Radiation on Bridge Structure[M]. Beijing: China Railway Publishing House, 1981, 1-32. |
| [7] |
PRIESTLEY M J N. Design of Concrete Bridges for Temperature Gradients[J]. Journal of American Concrete Institute, 1978, 75(5): 209-217. |
| [8] |
ELBADRY M M, GHALI A. Temperature Variations in Concrete Bridges[J]. Journal of Structural Engineering, 1983, 109(109): 2355-2374. |
| [9] |
MIRAMBELL E, AGUADO A. Temperature and Stress Distributions in Concrete Box Girder Bridges[J]. Journal of Structural Engineering, 1990, 116(9): 2388-2409. |
| [10] |
汪剑, 方志. 混凝土箱梁桥的温度场分析[J]. 湖南大学学报:自然科学版, 2008, 35(4): 23-28. WANG Jian, FANG Zhi. Temperature Variation of Concrete Box Girder Bridge[J]. Journal of Hunan University:Natural Science Edition, 2008, 35(4): 23-28. |
| [11] |
雷笑, 叶见曙, 王毅, 等. 基于长期观测的混凝土箱梁温度与应变分析[J]. 江苏大学学报:自然科学版, 2010, 31(2): 230-234. LEI Xiao, YE Jian-shu, WANG Yi, et al. Analysis of Concrete Box-girder Temperature and Strain Based on Long Term Observation[J]. Journal of Jiangsu University:Natural Science Edition, 2010, 31(2): 230-234. |
| [12] |
吴六政. 混凝土箱梁桥温度场的模拟[J]. 公路交通科技, 2011, 28(10): 65-69. WU Liu-zheng. Simulation of Temperature Field of Concrete Box-girder Bridge[J]. Journal of Highway and Transportation Research and Development, 2011, 28(10): 65-69. |
| [13] |
LARSSON O, THELANDERSSON S. Estimating Extreme Values of Thermal Gradients in Concrete Structures[J]. Materials and Structures, 2011, 44(8): 1491-1500. |
| [14] |
顾斌, 陈志坚, 陈欣迪. 基于气象参数的混凝土箱梁日照温度场仿真分析[J]. 东南大学学报:自然科学版, 2012, 42(5): 950-955. GU Bin, CHEN Zhi-jian, CHEN Xin-di. Simulation Analysis for Solar Temperature Field of Concrete Box Girder Based on Meteorological Parameters[J]. Journal of Southeast University:Natural Science Edition, 2012, 42(5): 950-955. |
| [15] |
章熙民, 任泽霈, 梅飞鸣. 传热学[M]. 5版. 北京: 中国建筑工业出版社, 2007. ZHANG Xi-min, REN Ze-pei, MEI Fei-ming. Heat Transfer[M]. 5th ed. Beijing: China Architecture & Building Press, 2007. |
| [16] |
EVSEEV E G, KUDISH A I. The Assessment of Different Models to Predict the Global Solar Radiation on a Surface Tilted to the South[J]. Solar Energy, 2009, 83(3): 377-388. |
| [17] |
DUFFIE J A, BECKMAN W A. Solar Energy of Thermal Process[M]. New York: John Wiley and Sons, 1991.
|
| [18] |
向学建, 董军, 刘昊苏, 等. 高原冬季环境下桥梁温度场各参数的确定[J]. 公路交通科技, 2012, 29(3): 58-63. XIANG Xue-jian, DONG Jun, LIU Hao-su, et al. Determination of Parameters of Temperature Field of Box-girder Bridge in Winter Weather of Plateau[J]. Journal of Highway and Transportation Research and Development, 2012, 29(3): 58-63. |
| [19] |
刘文丽, 贡金鑫, 张秀芳. 铺装层对T形梁桥梁竖向温度梯度的影响[J]. 公路交通科技, 2014, 31(10): 45-50. LIU Wen-li, GONG Jin-xin, ZHANG Xiu-fang. Impact of Pavement Layer on Vertical Temperature Gradient of T-girder Bridge[J]. Journal of Highway and Transportation Research and Development, 2014, 31(10): 45-50. |
 2018, Vol. 35
2018, Vol. 35
