扩展功能
文章信息
- 陆云
- LU Yun
- 正交异性钢桥面U肋横梁相交处疲劳寿命的估算
- Prediction of Fatigue Life of U-rib to Cross Beam Weld Joints of Steel Orthotropic Deck
- 公路交通科技, 2018, 35(3): 52-57
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(3): 52-57
- 10.3969/j.issn.1002-0268.2018.03.007
-
文章历史
- 收稿日期: 2017-04-21
正交异性钢桥面(简称钢桥面)U肋与横梁相交处极易形成应力集中诱发疲劳裂纹[1-3],是控制正交异性钢桥面板疲劳性能的关键构造细节。
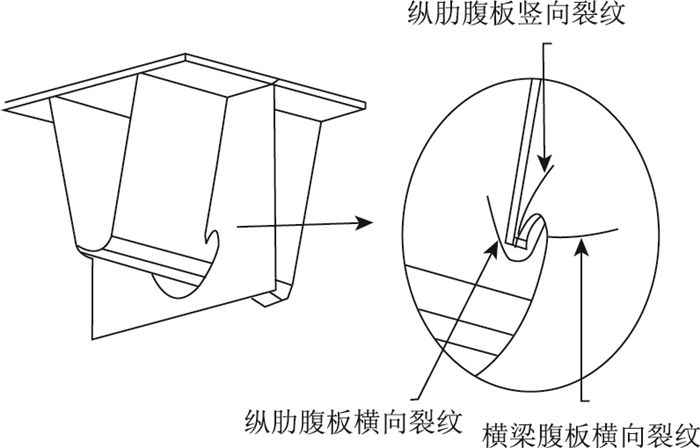
钢桥面U肋与横梁相交处常见有3类疲劳裂纹(见图 1)。其中,对纵肋腹板纵向裂纹(水平向裂纹)国内外的研究比较有限。Choi[4],Sim[5]和唐亮[6-7],李立峰[8]等采用足尺模型疲劳试验和有限元分析,对纵肋腹板纵向裂纹特性进行了相应的研究,研究者在对其进行疲劳寿命估算时,常采用传统的S-N曲线疲劳寿命评估方法。
|
| 图 1 纵肋与横梁相交处疲劳裂纹类型 Fig. 1 Fatigue crack patterns near U-rib to cross beam joints |
| |
传统的S-N方法假定材质为匀质连续的,没有考虑到在使用前钢材已经存在细微裂缝等情况,且随着裂纹开裂的深入,应力、应变场均会发生重分布,此时S-N曲线已经变得不太适用实际情况,不能保证疲劳设计的可靠性和经济性。
采用断裂力学理论研究钢结构的疲劳性能近年来取得很多进展,但用于钢桥面纵肋腹板纵向裂纹疲劳寿命评估较为少见。采用断裂力学方法进行疲劳评估是基于潜在裂纹尖端位置应力强度因子的正确计算,这在钢桥面计算分析中会遇到计算收敛困难、占用计算空间、计算时长等问题。本文针对某新建铁路桥节段钢桥面足尺试件,采用二阶段子结构模型技术,截取钢桥面整体模型中U肋与横梁相交处建立子模型,充分细化网格且用三维退化奇异单元模拟裂纹尖端应力场,通过腹板初始裂纹面的设置,有效模拟真实裂纹开裂。计算出含裂纹体的应力应变场强度的特征参数—应力强度因子K,结合Paris公式得到裂纹扩展曲线。计算结果与试验结果进行了比较。
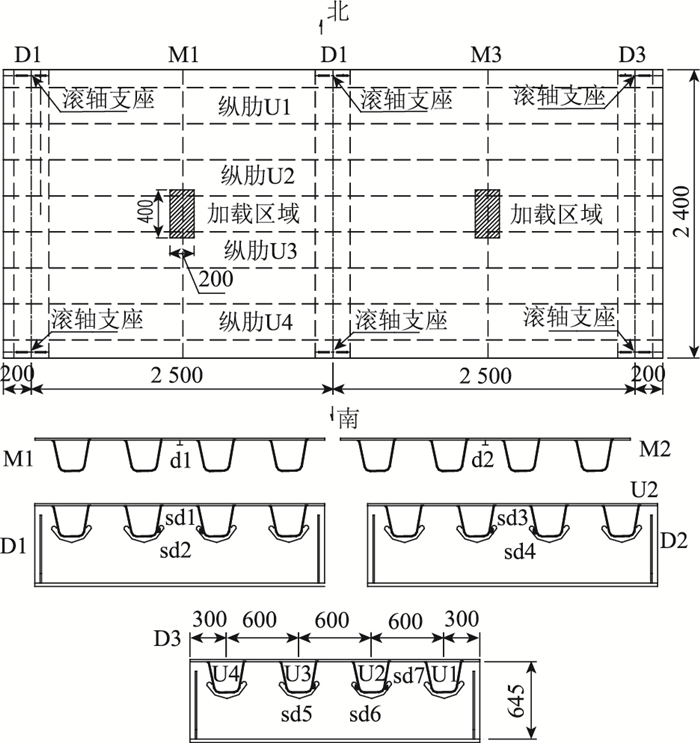
1 二阶段有限元模型钢桥面构造细节处受力具有很强的局部效应。本文针对某新建铁路桥节段钢桥面足尺试件[9],建立整体有限元模型,其尺寸、构件编号、加载示意、裂纹和有限元模型见图 2~图 4。表 1为试件疲劳试验前静载试验实测值及有限元计算值,表 1中d1和d2是跨中的位移测点,其余为应力测点。表 1表明:有限元模型计算值与试件的实测值基本吻合。
|
| 图 2 构件尺寸、编号与加载布置图(单位:mm) Fig. 2 Dimensions, numbers and load layout of specimens(unit: mm) |
| |

|
| 图 3 构件加载、裂纹示意图 Fig. 3 Loading and crack of specimen |
| |

|
| 图 4 两个阶段模型与裂纹前沿网格划分 Fig. 4 Two-stage analysis model and crack front meshing |
| |
| 测点 | 位移测点/mm | 应力测点/MPa | |||||
| d1 | d2 | sd1 | sd2 | sd3 | sd4 | ||
| 实测值 | -2.13 | -1.94 | 78.6 | 72.8 | 102.5 | 81.9 | |
| 计算值 | -2.02 | -2.02 | 76.3 | 76.3 | 91.0 | 76.3 | |
疲劳试验中,试件先后共出现了4条疲劳裂纹,均为U肋与横梁相交处的纵肋腹板纵向裂纹[7]。而有限元计算结果也同样显示:纵肋与横梁相交处,沿肋壁向的拉应力值最大。为精细分析上述部位的应力分布,在整体模型计算结果的基础上,进一步建立了纵肋与横梁相交处精细子模型,为便于区分,整体模型称为一阶段模型,子模型称为二阶段模型。鉴于分析方法和过程具有共性,下面以纵肋U2与中部横梁D2相交处为例进行子模型计算。
子模型裂纹尖端(裂纹前沿线)单元采用ANSYS中20节点的退化奇异单元solid45来有效地模拟裂纹尖端的应力场分布,见图 4。同时将一阶段整体模型切割边界的计算位移值作为子模型的边界条件进行约束。为便于与试验结果比较,采用Miner线性准则将疲劳试验加载一阶段的荷载幅对应的疲劳循环次数转换为二阶段荷载幅对应的循环次数,可得到U2与D2交叉处对应于应力幅172 MPa时,等效加载次数为156.9万次。
裂纹分析假设:(1)裂纹形状主要为表面半椭圆裂纹,裂纹深度为a,长度为2c,a和2c等裂纹参数以及裂纹前沿网格划分详见图 4;(2)纵肋腹板裂纹面沿着垂直于纵肋壁的方向由纵肋外侧向内部扩展,直至穿透;(3)裂纹类型为Ι型裂纹,其他两种裂纹模式的应力强度因子很小,故不在本文中阐述。
文献[10-11]表明:裂纹深度与裂纹长度比(a/2c,椭圆短边与椭圆长边比)不会引起应力强度因子很大的变化。例如:在疲劳试验中,出现在纵肋U2与横梁D2交叉位置裂纹的长度为20 mm (2c),已贯透纵肋板厚8 mm(a)[9],因此进行疲劳寿命估算时,取a/2c=0.4。
2 应力强度因子计算应力强度因子K是裂纹尖端应力-应变场强度的特征参数,是驱动裂纹扩展的最重要因素,简单受力状况下(平板张拉、T型搭接板等)可采用K的计算公式进行计算。
对于三维裂纹,裂纹尖端附近在图 5所示的局部坐标系的位移场可表示如式(1)~(3)[12]:
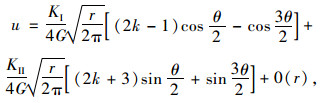
|
(1) |
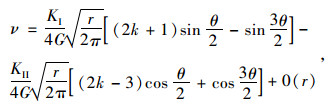
|
(2) |
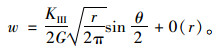
|
(3) |
|
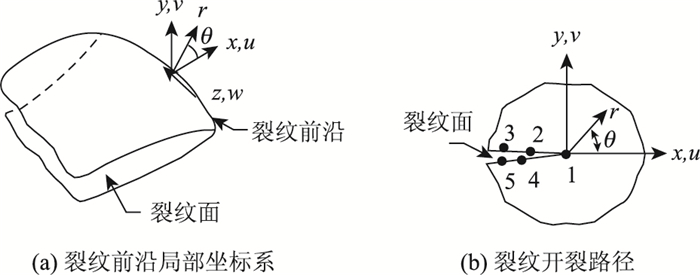
| 图 5 局部坐标系与裂纹面路径 Fig. 5 Local coordinate system and path of crack face |
| |
上述式中,当θ=±180°时,舍去公式右边高价无穷小项可以推得:
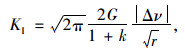
|
(4) |
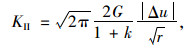
|
(5) |
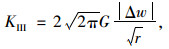
|
(6) |
其中u,ν,w为裂纹尖端直角坐标系下的位移分量,r,θ为裂纹尖端极坐标参量;G为剪切模量;μ为泊松比,k=3-4μ(平面应变);k=(3-μ)/(1+μ)(平面应力)。
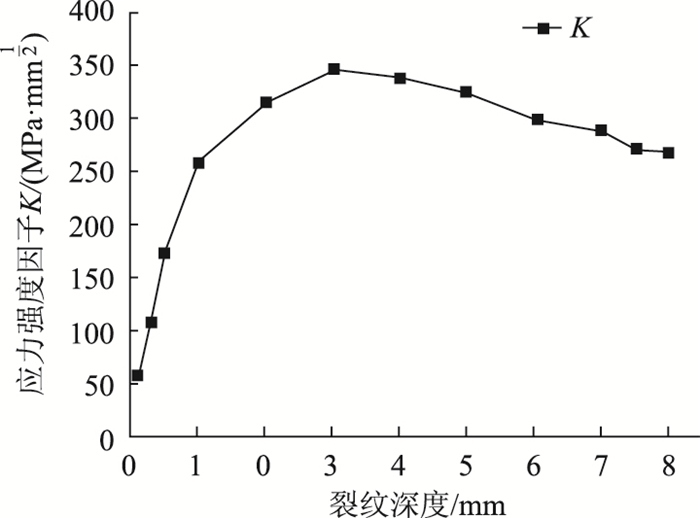
在验证子模型的合理性后,选择1-2-3-4-5节点来定义裂纹尖端位移路径(见图 5,且1必须在裂纹尖端。使用“位移外推法”[13]求得与不同裂纹深度所对应的K值,见表 2。根据表 2数据可绘制应力强度因子K和裂纹深度a的关系曲线见图 6。图 6显示:初期K值随着a增大而增大,K的增长速率随着a的增大则减小,裂纹深度扩展到3 mm时K值达到峰值。裂纹扩展至3 mm后,K值随着a增大而略有减小。
| a/mm | 0.1 | 0.3 | 0.5 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 8 |
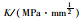 |
57.3 | 108.0 | 172.7 | 258.6 | 314.7 | 346.7 | 338.4 | 325.1 | 299.7 | 288.1 | 271.4 | 268.6 |
|
| 图 6 a/2c=0.4应力强度因子 Fig. 6 Stress intensity factors when a/2c=0.4 |
| |
3 疲劳寿命估算
断裂力学疲劳分析的基本思想是认为:疲劳开裂是一个裂纹的扩展过程。在循环应力作用下,裂纹尖端应力集中,裂纹尖端区域形成双向或三向同号应力场,引发裂纹扩展直至构件断裂。疲劳裂纹扩展模型有很多,采用Paris公式[14],疲劳寿命可表达为:
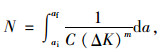
|
(7) |
式中, C, m为与材料有关的常数,可通过试验拟合得到;N为疲劳寿命;a为裂纹尺寸;ai和af分别为裂纹的初始和最终尺寸。
由于受检测手段所限,疲劳裂纹萌生和早期扩展的试验数据较少,Harris[15]提出以探伤设备的精度下限和疲劳试验数据来倒推得初始裂纹尺寸。Righiniotis[16]指出:桥梁焊接细节的初始裂纹尺寸的合理下限为0.1 mm。Nguyen和Chu[17]等利用试验数据倒推得到正交钢桥面构造细节处初始裂纹尺寸为0.1 mm。
裂纹尖端应力强度因子K还可以表达为[12]:
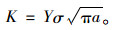
|
(8) |
将表 2中的Kmax和对应的a代入(8),可得到Y=0.7。假定Y是常数,将式(8)代入式(7),可得到:
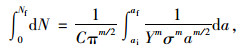
|
(9) |
在m≠2的情况下,可推导出:
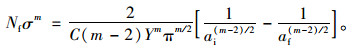
|
(10) |
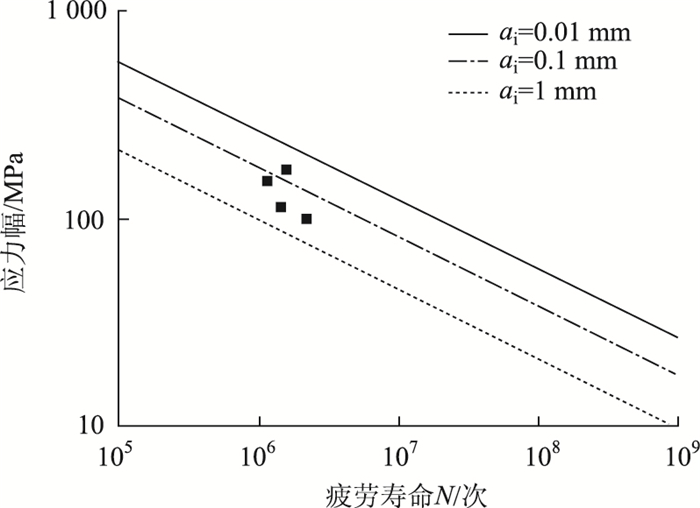
式(10)右端是含初始裂纹尺寸ai的函数,当ai为定值时,公式右端是一个常数,可得Nσm=C的表达式。当式(10)中ai分别为0.01,0.1,1 mm,可绘制成用双对数坐标表示的疲劳寿命曲线(见图 7),曲线绘制时,C和m值按规范BS7910[18]选取,分别为5.21×10-13和3。根据正交异性钢桥面足尺疲劳试验结果[9],将疲劳试验数据(表 1中4个应力测点)绘于图中,与初始裂纹尺寸分别为0.01,0.1, 1 mm的断裂力学疲劳曲线进行比较,可以发现:4个试验数据点分布在初始裂纹尺寸为0.1 mm计算曲线附近,其中有两个数据点相对另外两个数据点偏离度稍大些,鉴于疲劳问题的复杂性,采用试算倒推结果反映了疲劳强度与寿命的关系的趋势趋于一致,在工程疲劳裂纹寿命估算可接受的范围。
|
| 图 7 初始裂纹试算预测 Fig. 7 Trial assessing of initial crack depth |
| |
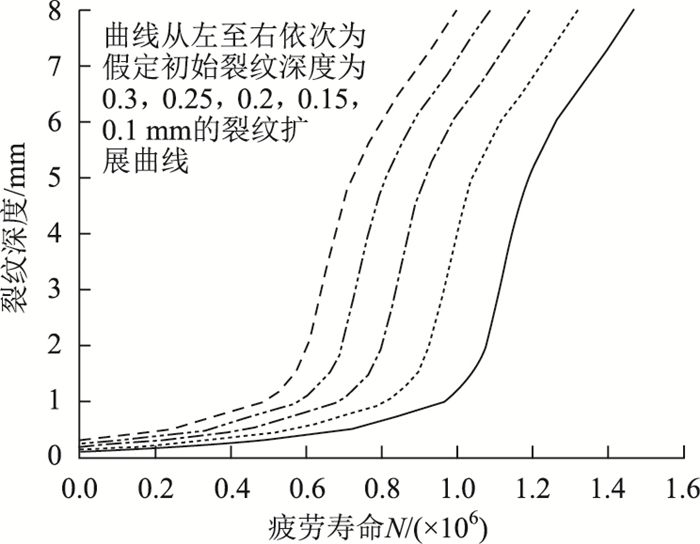
采用最小二乘法将图 6中应力强度因子K拟合成a的函数,并将此函数代入式(7),逐步数值积分可以得到疲劳寿命N与裂纹尺寸a的关系曲线(裂纹扩展曲线),见图 8。数值积分时,所选取初始裂纹尺寸分别为ai=0.1, 0.15, 0.2, 0.25和0.3 mm。
|
| 图 8 裂纹扩展曲线 Fig. 8 Crack propagation curves |
| |
图 8中,不同初始裂纹尺寸得到的裂纹扩张曲线形状和走势类似,仅在最终疲劳寿命的数值大小有所不同。随着初始裂纹尺寸的增大,裂纹贯穿板厚(af=8 mm)时对应的疲劳循环次数相应降低,降低的幅度也依次减小,分别为0.15,0.13,0.11和0.09百万次。表明初始裂纹尺寸对疲劳寿命有较大影响。
与试验结果相比较,假定初始裂纹尺寸为0.1 mm,其计算结果N=1.47×106最为接近。
从图 8不同裂纹扩展曲线(不同的ai)还可发现:在疲劳裂纹深度达到1 mm之前,疲劳裂纹扩展比较缓慢,当初始裂纹长度为0.1 mm,大致消耗掉总寿命的70%。在此之后裂纹扩展的速率相当快,在几十万次内裂纹迅速扩展直至穿透纵肋厚(8 mm)。这表明:位于U肋与横梁相交位置裂纹的疲劳寿命主要消耗在开裂初期,后期裂纹扩展寿命对疲劳寿命贡献不大,这可以解释试验中观察到疲劳裂纹萌生、发展的现象。试验初期,即在肉眼还无法观测到裂纹时,裂纹并非不存在,而是在缓慢地扩展,此时微小裂纹的存在对焊缝附近区域的受力性能影响很小,焊缝附近的测点应力幅值近似为直线[9]。当肉眼可观测到裂纹时,此时一般已是开裂的后期, 试验中在观测到裂纹之3~4万次前,4个测点应力幅已经发生变化,裂纹附近区域开裂,测点应力幅急剧下降。
4 结论(1) 进行了钢桥面整体和子结构有限元分析,计算结果表明:纵肋沿肋壁应力最大值发生在U肋与横梁连接处;可用退化奇异单元模拟该部位裂纹尖端应力场,通过位移外推求得裂纹尖端应力强度因子。
(2) 基于断裂力学理论,钢桥面的疲劳过程可模拟为钢桥面初始裂纹的扩展过程,通过裂纹尖端应力强度因子,可描述钢桥面构造细节位置开裂时应力应变的变化,跟踪裂纹发展过程。
(3) 初始裂纹尺寸对疲劳寿命有较大影响。初始裂纹尺寸ai=0.1 mm的裂纹扩展曲线中疲劳寿命与试验结果最为接近。
(4) 疲劳寿命主要消耗在疲劳裂纹扩展的初期,后期裂纹扩展寿命对疲劳寿命贡献不大。
| [1] |
BS EN 1993-2: 2006, Eurocode 3: Design of Steel Structures-Part 2: Steel Bridges[S].
|
| [2] |
DE JONG F B P. Overview Fatigue Phenomenon in Orthotropic Bridge Decks in the Netherlands[C]//2004 Orthotropic Bridge Conference. Sacramento: ASCE, 2004: 489-512.
|
| [3] |
WOLCHUK R. Lessons from Weld Cracks in Orthotropic Decks on Three European Bridges[J]. Journal of Structural Engineering, 1990, 116(1): 75-84. |
| [4] |
CHOI J H, KIM D H. Stress Characteristics and Fatigue Crack Behavior of the Longitudinal Rib-to-cross Beam Joints in an Orthotropic Steel Deck[J]. Advances in Structural Engineering, 2008, 11(2): 189-197. |
| [5] |
SIM H B. Fabrication Procedure Effects on Fatigue Resistance of Rib-to-deck Welded Joints of Steel Orthotropic Bridge Decks[D]. San Diego: University of California, 2010.
|
| [6] |
唐亮, 黄李骥, 王春生, 等. 正交异性钢桥面板足尺模型疲劳试验[J]. 土木工程学报, 2014, 47(3): 112-122. TANG Liang, HUAN Li-ji, WANG Chun-sheng, et al. Fatigue Experimental Study of a Full-scale Steel Orthotropic Deck Model[J]. China Civil Engineering Journal, 2014, 47(3): 112-122. |
| [7] |
唐亮, 黄李骥, 刘高. 正交异性钢桥面板横梁弧形切口周边应力分析[J]. 公路交通科技, 2011, 28(6): 83-90. TANG Liang, HUAN Li-ji, LIU Gao. FEA of Stress along Cope Hole Edge of Crossbeam in Orthotropic Steel Deck[J]. Journal of Highway and Transportation Research and Development, 2011, 28(6): 83-90. |
| [8] |
李立峰, 张东波, 袁卓亚, 等. 正交异性钢桥面板中弧形切口的应力分析[J]. 公路交通科技, 2012, 29(4): 55-61. LI Li-feng, ZHANG Dong-bo, YUAN Zhuo-ya, et al. Stress Analysis of Arc-shaped Cutouts in Steel Orthotropic Deck Plates[J]. Journal of Highway and Transportation Research and Development, 2012, 29(4): 55-61. |
| [9] |
顾萍, 裴辉腾, 盛博, 等. U肋带内隔板钢桥面疲劳性能研究[J]. 同济大学学报:自然科学版, 2014, 42(10): 1499-1504. GU Ping, PEI Hui-teng, SHENG Bo, et al. Fatigue Performance of Orthotropic Steel Bridge Decks with Inner Diaphragm in U-rib[J]. Journal of Tongji University:Natural Science Edition, 2014, 42(10): 1499-1504. |
| [10] |
XIAO Z G, YAMADA K, INOUE J, et al. Fatigue Crack in Longitudinal Ribs of Steel Orthotropic Deck[J]. International Journal of Fatigue, 2006, 28(4): 409-416. |
| [11] |
FISHER J W. Fatigue and Fracture in Steel Bridges[M]. New York: Wiley and Sons, Inc., 1984.
|
| [12] |
SURESH S. 材料的疲劳[M]. 王中光, 译. 北京: 国防工业出版社, 1999. SURESH S. Fatigue of Materials[M]. WANG Zhong-guang, translated. Beijing: National Defence Industry, 1999. |
| [13] |
张朝晖. ANSYS 16.1结构分析工程应用实例解析[M]. 北京: 机械工业出版社, 2015. ZHANG Chao-Hui. ANSYS 16.1 Example Analysis of Application of Structural Analysis Engineering Application[M]. Beijing: China Machine Press, 2015. |
| [14] |
张安哥, 朱成九, 陈梦成. 疲劳、断裂与损伤[M]. 西安: 西安交通大学出版社, 2006. ZHANG An-ge, ZHU Cheng-Jiu, CHEN Meng-cheng. Fatigue, Fracture and Loss[M]. Xi'an: Xi'an Jiaotong University Press, 2006. |
| [15] |
HARRIS D. Probabilistic Structural Mechanics Handbook[M]. New York: Chapman & Hall Ltd., 1995.
|
| [16] |
RIGHINIOTIS T D, CHRYSSANTHOPOULOS M K. Probabilistic Fatigue Analysis under Constant Amplitude Loading[J]. Journal of Constructional Steel Research, 2003, 59(7): 867-886. |
| [17] |
NGUYEN H T, CHU Q T, KIM S E. Fatigue Analysis of a Pre-fabricated Orthotropic Steel Deck for Light-weight Vehicles[J]. Journal of Constructional Steel Research, 2011, 67(4): 647-655. |
| [18] |
BS7910-2005. Guide to Methods for Assessing the Acceptability of Flaws in Metallic Structures[S].
|
 2018, Vol. 35
2018, Vol. 35
