扩展功能
文章信息
- 李琦, 李杰, 冷艳玲
- LI Qi, LI Jie, LENG Yan-ling
- 装配式混凝土空心板梁桥结构冗余性水平评估
- Assessment of Redundancy Level of Prefabricated Concrete Hollow Slab Bridge
- 公路交通科技, 2018, 35(3): 46-51, 57
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(3): 46-51, 57
- 10.3969/j.issn.1002-0268.2018.03.006
-
文章历史
- 收稿日期: 2016-11-01
2. 交通运输部公路科学研究院, 北京 100088
2. Research Institute of Highway, Ministry of Transport, Beijing 100088, China
装配式混凝土空心板梁桥具有以下优点: (1)建筑高度小, 不受填土高度限制; (2)构件尺寸易于设计成系列化和标准化, 可大批量工厂化集中预制; (3)体积小, 重量轻, 架设方便, 施工速度快; (4)装配式施工方法可以节约模板支架, 降低劳动强度, 减少施工工序, 缩短工期; (5)构造简单, 经济性好等。它是我国中小跨径桥梁的主要桥型, 在我国公路网中约有1/4的桥梁是装配式混凝土空心板梁桥[1]。装配式混凝土空心板梁桥在美国的应用也很广泛,据统计美国公共道路上每6座桥梁中就有一座装配式混凝土空心板梁桥[2]。
装配式混凝土空心板梁桥的各片板梁一般采用预制安装, 然后通过铰缝现浇混凝土加以横向连接, 再借助混凝土桥面铺装的整体化作用, 形成整体受力的桥跨结构。美国、日本的装配式混凝土空心板梁桥采用横向预应力钢绞线或螺纹钢筋将各片梁“绑”起来,其横向整体性相对较强。虽然横向联结构造存在差异,但铰缝开裂、渗水,桥面反射裂缝是中国、美国的装配式混凝土空心板梁桥普遍面对的问题[3-4]。20世纪90年代及之前所修建的装配式混凝土空心板梁桥大多采用的是“小企口”铰缝, 一般在投入使用3~5 a后, 铰缝就会出现不同程度的混凝土开裂、破损和脱落病害。严重者, 还会形成一条破碎带, 造成桥面铺装层局部纵向沟槽,甚至会出现“单板受力”现象。出现“单板受力”后,荷载不能有效传递给相邻梁,因此在重车过桥时,承载板会产生较大的竖向挠度,甚至引发局部板梁断裂、坍塌。2005年美国宾西佛利亚州华盛顿县的湖景路大桥(Lake View Drive Bridge)边梁断裂坍塌(见图 1)、2010年杭州钱塘三桥引桥边梁断裂,均与铰缝损伤有直接关系。美国的湖景路大桥(Lake View Drive Bridge)边梁断裂的主要原因是铰缝失效和预应力筋锈蚀。该事故发生后,在拆除桥梁的过程中,发现铰缝内有沥青,这反映该桥的铰缝开裂严重,在桥梁破坏之前,铰缝已经失效,各板不能有效联合受力,导致了“单板受力”现象。另外,板梁内2/3的预应力筋严重腐蚀,在此情况下,单梁的理论承载力低于板梁的自重效应。钱塘大桥引桥边梁在超重车通过时坍塌,铰缝损伤和超载是诱因。

|
| 图 1 美国湖景路桥边梁倒塌,2005 Fig. 1 Collapse of exterior beam of Lake View Drive Bridge, U.S., 2005 |
| |
由于铰缝开裂损伤这种具有通病性质的缺损, 其发展恶化的结果会直接影响到桥梁的安全性。目前的对铰缝开裂损伤问题的研究大多停留在铰缝病害识别、成因分析和处治措施方面。但在桥梁检查养护方面, 缺少对装配式空心板梁桥铰缝技术状况检查评定的定量化标准, 造成检查人员难以把握和判定“单板受力”问题, 导致桥梁运营安全事故时有发生。
当前,装配式混凝土空心板梁桥的承载能力评估方法是基于构件层次,即根据弹性分析的铰接板理论来确定最不利板(梁)的荷载横向分配系数,然后基于此荷载横向分配系数计算最不利板的荷载效应,忽略了铰缝损伤对桥梁荷载横向分配系数的影响。但是,在塑形变形阶段,铰缝损伤对桥梁的横向荷载分配系数影响较大,铰缝损伤严重时,按传统方法计算出的荷载横向分配系数偏于不安全,导致桥梁的实际承载力可能低于设计承载力,因此,我们推断在铰缝破损情况下,装配式混凝土空心板梁桥的冗余性较低。
桥梁结构系统冗余性反映的是桥梁结构的强度储备,指的是满足当前设计标准的桥梁结构,在关键构件达到承载力后,可将荷载分配给其他构件,从而能继续承受车辆荷载而不发生倒塌的能力。1968年伦敦罗兰公寓倒塌事故后,系统安全评估的概念被引入到结构工程领域。结构冗余性是结构系统安全性的一个评估。在过去30余年,学者们在此方向做了一些研究,有些成果已被纳入美国AASHTO LRFD桥梁设计规范[5]及AASHTO MBE LRFR荷载鉴定方法[6]。美国AASHTO LRFD桥梁设计规范是首个将冗余性水平纳入评估指标的公路桥梁规范,其在极限状态方程中的抗力中引入了一个冗余因子:非冗余性构件,冗余因子等于0.95;冗余性较高的桥梁,冗余因子等于1.05;其他情况,冗余因子取1.0。但是,由于该规范没有说明如何鉴定桥梁的冗余水平,设计人员只能依经验取值,主观性很强。Frangopol等人[7]研究了冗余因子的确定方法,该方法考虑了桥梁结构类型、构件抗力之间的关联度、系统中构件的数量以及材料的延性,将冗余性因子ηR定义为系统可靠度为3.5的桥梁系统中构件的平均抗力与构件可靠度为3.5的构件的平均抗力之比。该方法首先需要确定系统类型(并联,串联或者串并联)以及桥梁系统各部件之间的关联性,此外还需要进行可靠度计算,技术难度过高。因此,冗余因子的取值还有待进一步的研究。
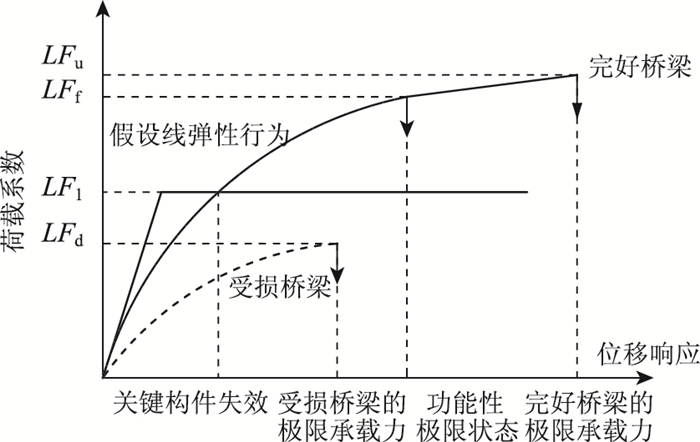
Ghosn研究团队[8-10]等提出的桥梁系统冗余性水平和鲁棒性水平评价方法,是目前桥梁工程届认可度最高的方法之一,典型桥梁结构在载荷作用下的响应如图 2所示,完好桥梁强度极限状态的冗余因子Ru、服务极限状态的冗余因子Rf,以及受损桥梁的鲁棒因子Rd的计算公式如下:
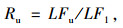
|
(1) |
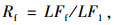
|
(2) |
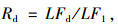
|
(3) |
|
| 图 2 典型桥梁系统的响应曲线 Fig. 2 Response curves of typical bridge system |
| |
式中, LF1为单梁的荷载系数;LFu为完好桥梁系统失效时对应的荷载系数; LFf为完好强度达到工作性能极限状态时对应的荷载系数; LFd为受损桥梁失效时对应的荷载系数。荷载系数指的是实际荷载与标准车辆荷载的比值。例如LF1=5表示当活载达到设计车辆荷载的5倍时,最不利梁达到其设计极限承载,AASHTO桥梁评估规范荷载鉴定的系统因子表,即由此方法确定。此方法也被成功应用于实际公路桥梁、铁路桥梁的安全鉴定。不同结构形式的桥梁,系统冗余水平不同,而AASHTO桥梁评估规范荷载鉴定的系统因子表只涵盖了有限的几种桥型,装配式混凝土空心板梁桥不在其中。
本研究利用Midas Civil有限元软件对一座装配式混凝土空心板桥的试验模型进行Pushover非线性分析,得到了桥梁在完好状态、铰缝开裂损伤状态的荷载位移响应关系曲线,并用模型桥破坏试验结果校准了有限元模型;然后利用有限元分析结果,计算了模型桥的冗余性水平。
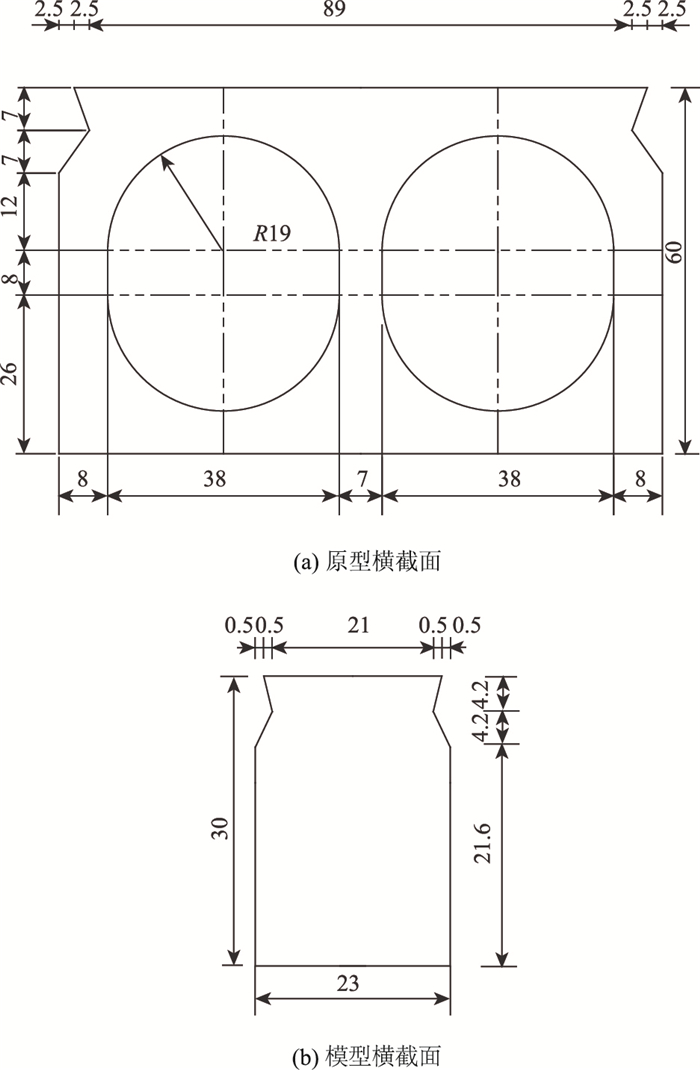
1 模型桥梁基本信息试验采用我国公路桥涵标准图之装配式预应力混凝土空心板(JT/GQB001—73)中跨径10 m(8块板)、荷载等级为汽-20级、挂车-100级的原型进行模型试验。考虑到截面模拟、量测方法和试验场地条件等因素,按照应力等效的原则,选择模型的几何相似常数为1/2。桥梁原型及缩尺模型的尺寸信息见图 3、表 1[11-12]。
|
| 图 3 主梁横截面(单位:cm) Fig. 3 Cross-section of main beam (unit:cm) |
| |
| 项目 | 跨径/m | 板梁/cm | 铰缝高度/cm | 桥面板厚度/cm | |
| 宽度 | 高度 | ||||
| 原桥 | 9.96 | 99 | 60 | 14 | 10 |
| 模型桥 | 4.98 | 23 | 30 | 8.4 | 5 |
试验模型桥建于2012年1月。2012年2月至7月在此模型桥上进行了一系列的试验研究,试验项目包括:(1)铰缝开裂扩展对荷载横向分布影响的研究;(2)板底横张预应力加固;(3)板底粘贴钢板加固[13]。
在进行本次试验之前,为了解模型桥的初始状况,对模型桥进行了检查,检查结果显示,板梁基本完好,但在之前的试验中,为了模拟铰缝开裂,铰缝均被锯开0.8L(L为桥梁跨径长度),试验结束后用环氧树脂胶封闭。而这次检查中发现,由于施工原因,4#铰缝未被封闭,在竖向活载作用下,模型桥的受力状态相当于1个双幅桥,即1#~4#板梁、5#~8#板梁各组成1个桥梁,这2个桥梁共用2个整体式支座和1个现浇桥面板,见图 4。

|
| 图 4 模型桥梁 Fig. 4 Model bridge |
| |
试验主梁设计时拟采用C40混凝土(150 mm×150 mm×150 mm的立方体抗压标准强度40 MPa),主筋为4ϕ16 HRB335螺纹钢(屈服强度335 MPa)。在破坏试验结果分析过程中,发现单梁的实测承载能力与理论承载能力相差较大。故在模型桥梁破坏试验结束之后,进行了混凝土取芯试验和钢筋拉伸试验。根据混凝土试块抗压结果得到:fc=60 MPa。此处试块采用的是100 mm×100 mm×100 mm的圆柱体试块,换算成150 mm×150 mm×150 mm的立方体试块的抗压标准强度为57 MPa。ft=4.45 MPa;根据钢筋拉伸曲线得到:fy=450 MPa,fu=580 MPa。
2 有限元模型本研究采用Midas Civil有限元程序,运用梁格法建立模型桥上部结构空间三维模型。钢筋混凝土空心板梁桥一般采用铰接理论设计,梁格纵向以各单板受力中心线建立纵梁,横向将现浇混凝土层划分为条状,模拟虚拟梁传递剪力,通过释放虚拟梁梁端约束来模拟纵梁间的铰缝传力行为。为了通过非线性有限元分析,得到结构体系的极限承载力,模型中纵梁单元在较大荷载作用下的非线性行为定义集中塑性铰的方式来反映,集中塑性铰的特性由截面的弯矩-曲率曲线得到,塑性铰长度取单元长度的1/2与单元截面高度的1/2两者中较小者。假设模型中横梁单元在整个加载分析过程中均处于线弹性阶段,且不考虑弯扭耦合效应。控制截面的弯矩-曲率曲线由Xtract程序计算得到。
板梁梁在竖向荷载作用下,主要失效模式之一为跨中抗弯失效形成塑性铰,结构变为机构,其次是距支座H/2截面处抗剪失效,发生脆性破坏。通过计算分析得到,边梁跨中抗弯失效起控制作用,故本报告仅分析该种失效模式。
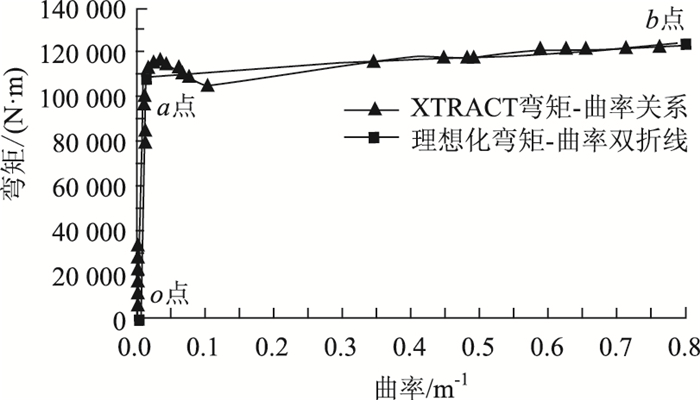
2.1 单梁模型通过XTRACT软件,计算得到的弯矩-曲率如图 5所示。
|
| 图 5 单梁截面M-C曲线 Fig. 5 M-C curve of single beam cross-section |
| |
近似地,采用等效准则得到理想线性化M-C曲线替代原M-C曲线,如图 5中双折线。折线oa段,表示截面处于线弹性阶段;转折处a点表示截面开裂;折线ab段表示截面开裂后的受力行为;末端b点表示截面达到极限状态失效。由双折线的o,a,b共3个控制点即可定义pushover分析中的塑性铰特性,Midas Civil塑形铰分配如图 6所示。将最大弯矩下降85%作为极限曲率评估条件。

|
| 图 6 Midas Civil塑性铰分配(单梁) Fig. 6 Allocation of Midas Civil plastic hinge joints (single beam) |
| |
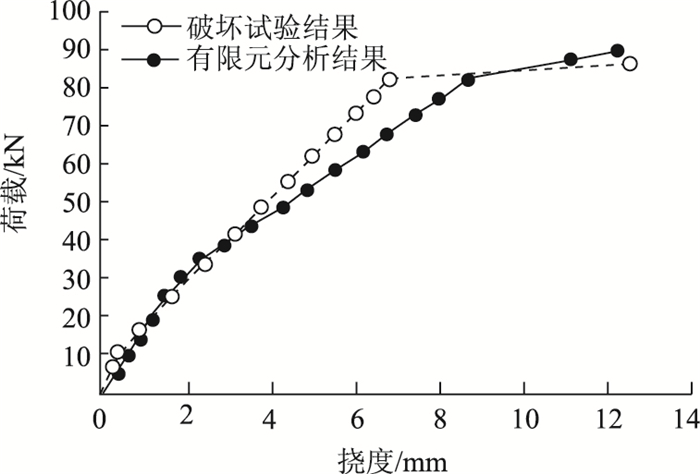
单梁在集中荷载作用下的荷载-跨中挠度响应如图 7所示,图 7中实线为有限元分析结果,虚线为破坏试验结果。有限元分析结果预测该梁的极限承载力为86.3 kN, 试验中施加的最大荷载值为89.4 kN。表 2比较了XTRACT, Midas Civil Pushover分析结果与试验结果,预测值与试验实测值的误差均比较小。
|
| 图 7 单梁集中荷载-跨中挠度响应 Fig. 7 Concentrated load vs. mid-span deflection response |
| |
| 极限荷载/kN | 误差 | |
| XTRACT分析 | 90.1 | < 1% |
| Midas Civil pushover分析 | 86.3 | 3.4% |
| 破坏试验数据 | 89.4 | — |
2.2 模型桥梁模型
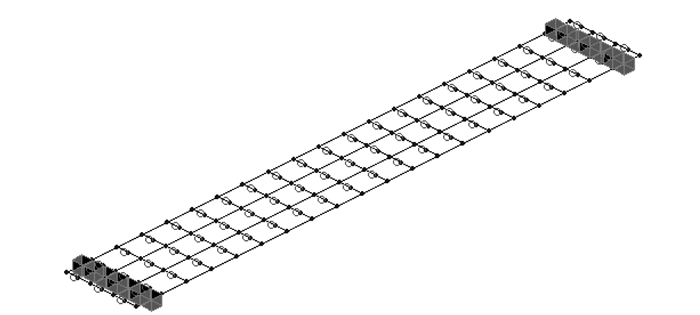
由于试验模型的4#铰缝在试验之前已经破坏,故运用Midas Civil进行Pushover分析的时候,模拟4片板桥梁模型(见图 8)进行pushover分析,混凝土抗剪强度与抗压强度比值在0.056~0.091。同时考虑到本试验模型铰缝沿接触面破坏,将该比值取为0.06。C30混凝土抗压强度设计值为20.1 MPa,则铰缝破坏抗剪强度取为1.2 MPa。同时,模型加载过程中铰缝剪力呈正弦波分布,有限元模拟按等效法则简化为剪力均匀分布,则虚拟梁抗剪强度取为0.5×1.2=0.6 MPa,故每根虚拟梁承受的最大剪力为0.6×0.25×0.05×103=7.5 kN,即当剪力超过7.5 kN,则铰缝破坏引起边梁单板受力。
|
| 图 8 模型桥梁梁格模型 Fig. 8 Grillage model of model bridge |
| |
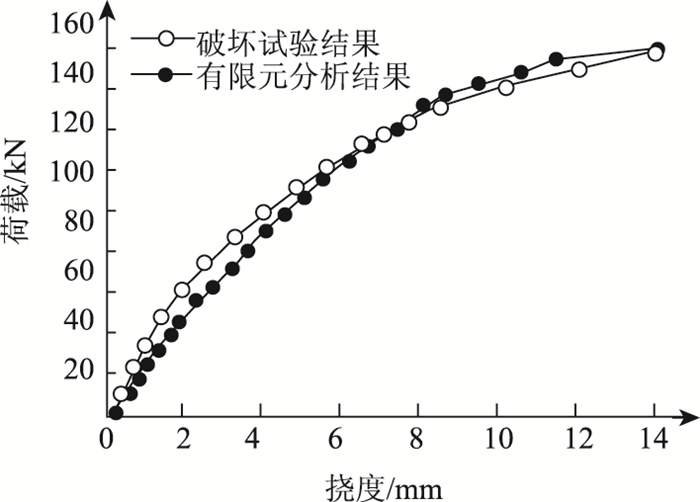
在模型桥梁的边梁跨中逐级加载,得到边梁跨中加载荷载-位移曲线见图 9。
|
| 图 9 边梁跨中荷载-位移曲线 Fig. 9 Curves of load vs. deflection of exterior beam mid-span |
| |
在模型桥梁破坏试验中,边铰缝完全断裂(失效)时的集中荷载值为147.50 kN,而有限元分析结果为146.2 kN,可见试验结果与有限元分析的差别在可接受范围内。下文将采用文献[8, 10]的方法对该桥的冗余性水平和鲁棒性水平进行评价。
3 桥梁系统冗余性水平评价对于4片板梁组成的铰接板桥,根据铰接板梁理论[14-15],荷载作用在1#板跨中时,1#板分配的荷载比例为0.4。根据《混凝土结构设计规范》(GB50010—2010)[16],单梁的承载力为88.6 kN,对应跨中弯矩为104.8 kN·m。模型桥的原型桥梁的设计荷载为汽-20,根据应力等效原则,原模型桥梁的最不利布载等效于在1#板跨中布置18.62 kN的集中荷载,其在1#梁跨中会产生23.18 kN·m的弯矩,板梁自重弯矩为5.77 kN·m[17]。根据文献[8]的方法:
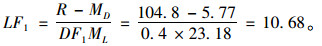
|
(4) |
根据有限元分析结果,模型桥梁的极限荷载为162.8 kN,则LFu=146.2 kN/18.62 kN=7.85。由式(1),冗余因子:
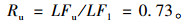
|
(5) |
目前对于桥梁结构冗余性,尚无阙值可参考。文献[8]给出的冗余因子Ru的阙值为1.30,这是目前唯一可找到的参考。本模型桥梁的冗余因子远低于1.30,可见其冗余性不足。此评价结果反映出该桥型的系统性较差,验证了本研究对该桥型冗余性水平偏低的预测。
4 结论与讨论目前对桥梁结构的安全评估仅停留在构件层次[18],在桥梁设计、评估中忽略桥梁结构系统行为的影响可能产生2种后果。对于冗余性高的结构,忽略其冗余性,容易造成不必要的或高于实际需要的维修、加固决策,造成养护资金的浪费;对于冗余性低的桥梁结构,考虑系统行为后,结构的可靠度会降低,表现在某个局部破坏可能会造成大范围的垮塌事故,装配式混凝土空心板梁桥的历史表现反映出该桥的系统性较差,有可能属于冗余性较差的桥梁结构。由于桥梁结构系统的受力情况复杂、荷载传输路径不易模拟且必须考虑几何非线性和材料非线性,需要进行精细化的有限元非线性分析,为了校准有限元模型,本研究利用Midas Civil有限元软件对一座铰接混凝土梁桥模型进行Pushover分析,得到了模型桥梁在集中荷载下的位移响应,对有限元分析结果与破坏试验结果进行了比较,校准了有限元模型,证明了利用Midas Civil梁格法进行pushover非线性分析计算桥梁结构体系承载能力可获得满意结果,保证了分析结果的可靠性。然后基于有限元分析结果,计算了模型桥梁的冗余性水平。计算结果表明,该模型桥梁的冗余因子为0.73,低于相关阙值1.30,验证了对该桥型冗余度低的推定。在下一步研究中,会采用本研究建立的分析方法,对装配式混凝土空心板桥进行冗余性和鲁棒性分析,得到规律性结果,并据此对旧桥承载能力评估规范提出修改建议。
| [1] |
LENG Yan-ling, ZHANG Jin-quan, JIANG Rui-nian, et al. Experimental Research on Strengthening Transverse Connections of Prefabricated Concrete Hollow Core Slab Beam Bridges[C]//Transportation Research Board 94th Annual Meeting. Washington, D. C. : Transportation Research Board, 2015: 2197-2206.
|
| [2] |
RUSSELL H G. Adjacent Precast Concrete Box-beam Bridges:State of the Practice[J]. PCI Journal, 2009, 56(1): 75-91. |
| [3] |
HUCKELBRIDGE A A, EL-ESNAWI H, MOSES F. Shear Key Performance in Multibeam Box Girder Bridges[J]. Journal of Performance of Constructed Facilities, 1995, 9(4): 271-285. |
| [4] |
RUSSELL H G. Adjacent Precast Concrete Box Beam Bridges: Connection Details, NCHRP Synthesis 393[R]. Washington, D. C. : Transportation Research Board, 2009.
|
| [5] |
AASHTO. AASHTO LRFD Bridge Design Specifications[S]. 6th ed. Washington, D. C. : AASHTO, 2012.
|
| [6] |
AASHTO. AASHTO Manual for Bridge Evaluation[S]. Washington, D. C. : AASHTO, 2012.
|
| [7] |
ZHU Bin. Redundancy, Reliability Updating, and Risk-based Maintenance Optimization of Aging Structures[D]. Bethlehem: Lehigh University, 2015
|
| [8] |
GHOSN M, MOSES F. Redundancy in Highway Bridge Superstructures, NCHRP Report 406[R]. Washington, D. C. : Transportation Research Board, 1998.
|
| [9] |
GHOSN M, MOSES F. Redundancy in Highway Bridge Substructures, NCHRP Report 458[R]. Washington, D. C: Transportation Research Board, 2001.
|
| [10] |
GHOSN M, YANG J. Bridge System Safety and Redundancy, NCHRP Report 776[R]. Washington, D. C. : NCHRP, 2014.
|
| [11] |
LENG Yan-ling, ZHANG Jin-quan, JIANG Rui-nian, et al. Experimental Research on Transverse Load Distribntion of Prefabricated Hollow Slab Concrete Bridges with Hinge Joint Cracks[C]//Transportation Research Board 94th Annual Meeting. Washington, D. C. : Transportation Research Board, 2015.
|
| [12] |
LENG Yan-ling. System Safety and Reliability Assessment for Adjacent Precast Concrete Box Beam Bridges[D]. Las Cruces, US: New Mexico State University, 2017.
|
| [13] |
冷艳玲, 张劲泉, 程寿山, 等. 装配式混凝土空心板梁桥单板受力问题的数值解析[J]. 公路交通科技, 2013, 30(5): 63-73. LENG Yan-ling, ZHANG Jin-quan, CHENG Shou-shan, et al. Numerical Analysis on Single Plate Loading Effect of Precast Hollow Plate Girder Bridge[J]. Journal of Highway and Transportation Research and Development, 2013, 30(5): 63-73. |
| [14] |
姚玲森. 桥梁工程[M]. 北京: 人民交通出版社, 2005. YAO Ling-sen. Bridge Engineering[M]. Beijing: China Communications Press, 2005. |
| [15] |
桂水荣, 刘律, 万水, 等. 简化建模方法对空心板桥力学性能的影响[J]. 公路交通科技, 2014, 31(12): 50-57. GUI Shui-rong, LIU Lü, WAN Shui, et al. Effect of Simplified Modeling Method on Mechanical Performance of Hollow Slab Bridge[J]. Journal of Highway and Transportation Research and Development, 2014, 31(12): 50-57. |
| [16] |
GB50010-2010, 混凝土结构设计规范[S]. GB50010-2010, Code for Design of Concrete Structures[S]. |
| [17] |
冷艳玲. 装配式空心板梁桥铰缝开裂及整体化加固研究[D]. 北京: 交通运输部公路科学研究所, 2012. LENG Yan-ling. Study on Crack Behaviors of Hinge Joints for Fabricated Hollow Slab Bridges and Transverse Integrity Reinforcement Technology[D]. Beijing: Research Institute of Highway of Ministry of Transport, 2012. |
| [18] |
张劲泉, 冷艳玲, 李万恒, 等. 中国公路桥梁承载能力评定规程的可靠性水准[J]. 公路交通科技, 2015, 32(4): 59-63. ZHANG Jin-quan, LENG Yan-ling, LI Wan-heng, et al. Reliability Level of Load-bearing Capacity Evaluation Specification of Highway Bridges in China[J]. Journal of Highway and Transportation Research and Development, 2015, 32(4): 59-63. |
 2018, Vol. 35
2018, Vol. 35
