扩展功能
文章信息
- 汪水银
- WANG Shui-yin
- 多年冻土地区填方路基温度场分布特征
- Temperature Field Distribution Characteristics of Filled Roadbed in Permafrost Region
- 公路交通科技, 2018, 35(3): 28-35
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(3): 28-35
- 10.3969/j.issn.1002-0268.2018.03.004
-
文章历史
- 收稿日期: 2017-12-20
2. 交通运输部科技司, 北京 100736
2. Department of Science and Technology, Ministry of Transport, Beijing 100736, China
多年冻土区特殊的气候、环境、地质条件,使该地区沥青路面不仅承受行车荷载作用,还受到气温、太阳辐射、冻土路基不均匀融沉变形等影响[1]。地表辐射热平衡状态的改变,加上行车荷载人为扰动增加,冻土路基不均匀融沉变形已成为该地区普遍的病害,严重影响了道路的正常运营与行驶安全[1-2]。针对冻土路基的稳定性,国内外已开展了广泛的研究,冻土的水热迁移与成冰过程本质上是多孔多相介质带相变的固、液、汽、热耦合问题,目前国内外的工作大多停留在试验探索阶段[1-3]。国外有研究从不同的角度对固-液-热三场耦合进行研究,以及对冻胀、水热迁移与水分冻结引起的孔隙吸力开展研究[4-6]。雷志栋等[7]采用Harlan模型模拟了水平、垂直土柱的冻结过程,并定性地分析了土中初始含水率对土冻胀量的影响。程国栋[8]等依据连续介质力学、热力学原理,提出了冻结过程中的三场耦合方程;樊贵盛等[9]采用包括汽态水迁移和热对流迁移的水热耦合数值模拟模型,模拟天然条件下土的季节性冻融过程以及其中的水热迁移规律,取得了较好的结果;李宁、陈波[10]等人在冻土多相介质静力平衡方程、能量守恒原理、土骨架与冰水之间的传力机制及相变机制的基础上,系统地推导了冻土中土、冰、水三相介质的温度场、变形场、水分场三场耦合问题的微分方程;毛雪松等[2, 11]在观测正冻土冻结过程中水分场和温度场随时间变化规律的基础上,建立冻土系统水、热耦合模型对所测的结果进行数值模拟。有研究针对多年冻土地区路面结构耐久性,利用有限元数值模拟方法分析了路面结构应力场与温度场变化[12-15]。综上可知,目前关于多年冻土地区沥青路面填方路基主要是针对冻土问题以及路面结构层的温度场开展研究,关于冻土地区填方路基温度分布特征的研究还不成熟,为此本文以共和至玉树公路G214为例,开展相关研究,为多年冻土地区公路工程建设提供参考。
1 路面结构计算模型与计算参数 1.1 公路沿线地质环境共和至玉树(G214)在海拔3 500~4 700 m,跨越黄河、长江两大流域,沿线不稳定路段多为富冰、饱冰或含土冰层路段,建模时需要参考高寒冰量路基地质结构。为适应地形需要,同时满足冻土地区路基设计“宁填勿挖”的设计理念,共玉路沿线以填方路基为主,路基最高填方高度达14.8 m。
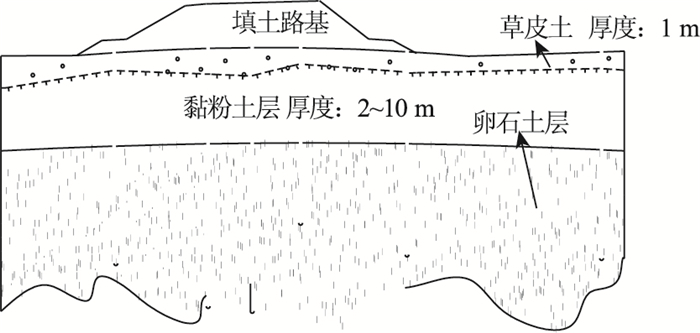
结合全线冻土专项勘察资料,根据现场地勘资料,地质结构图及钻孔取样,如图 1、图 2所示。
|
| 图 1 K562+468地质情况 Fig. 1 Geological condition of K562+468 |
| |

|
| 图 2 K562+468芯样 Fig. 2 Core samples of K562+468 |
| |
图 1、图 2表明,地表 1 m为含水量较高的草皮土,2~10 m为黏粉土,10 m以下至模型边界30 m处为卵石土。共玉公路沿线地温资料表明,沿线填方路段多年冻土年平均地温基本均在-0.2~-0.7 ℃,沿线多为高温、高退化速率冻土。考虑冻土后期退化影响,本文将温度计算边界条件简化为3类,即年平均地温分别为-0.2, -0.5, -0.8 ℃。
1.1 有限元计算模型与参数路面结构层的上边界受多种气象因素的综合作用,主要包括气温、地温、太阳辐射、对流换热、蒸发耗热、雪盖厚度等。本文采用附面层理论,将气温和地温的变化及对流换热简化为周期波动的函数,太阳辐射和蒸发耗热可以统一简化为温度边界[11-18]。
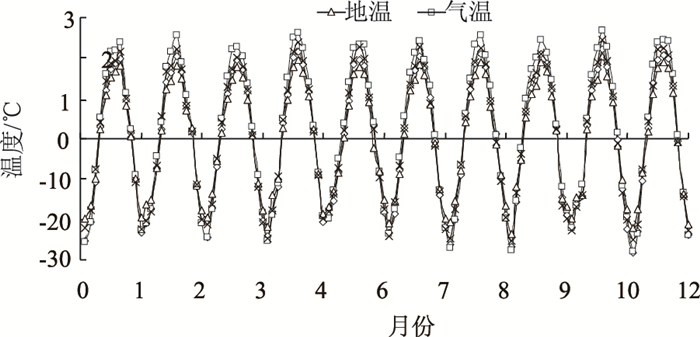
图 3为将低温边界拟合成周期函数的形式。本文将沥青路面、天然地表、阳坡坡面、阴坡坡面等处的温度观测值拟合为正弦形式的周期函数,来表征高原冻土地区四季温度变化规律。
|
| 图 3 气温与地温随时间的波动曲线 Fig. 3 Atmospheric temperature and ground temperature varying with time |
| |
路基温度场计算时,沥青路面、边坡、地表施加气温荷载按下式计算得到[2, 3, 13-14]。
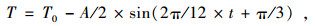
|
式中,T0为当地年平均气温;A为当地气温年较差;t为时间。
计算对应的边界条件方程参数取值如表 1所示,工况1、工况2、工况3分别对应年平均地温-0.2,-0.5,-0.8 ℃。
| 参数取值 | 工况1 | 工况2 | 工况3 | |||||
| T0 | A | T0 | A | T0 | A | |||
| 路面 | 6.5 | 37 | 5.5 | 33 | 4.5 | 29 | ||
| 天然地表 | -0.2 | 24 | -0.5 | 21 | -0.8 | 18 | ||
| 坡面 | 2.6 | 26 | 1.9 | 22 | 1.2 | 17 | ||
参考相关技术规范和研究成果[11-17],计算中各层材料参数和厚度如表 2所示。其中ρ为密度,Cu为融化状态的比热容; Cf为融合化过程中的潜热容; λu为融化状态的导热率; λf为冻结状态的导热率。
| 结构层 | Ρ/(kg·m-3) | Cu/(J·kg-1·℃-1) | Cf/(J·kg-1·℃-1) | λu/(W·m-1·℃-1) | λf/(W·m-1·℃-1) |
| 路基填料 | 2 000 | 980 | 210 | 1.48 | 1.64 |
| 黏土 | 800 | 1 040 | 7 150 | 1.72 | 1.85 |
| 碎石土 | 1 700 | 950 | 7 210 | 1.42 | 1.65 |
| 泥炭层 | 1 600 | 930 | 7 671 | 1.21 | 1.47 |
依托G214工程实际,建立了填方路基热传导计算有限元模型,见图 4,计算模型在X,Y方向,距离地表及坡脚距离均为30 m,试算结果可满足计算精度要求。路基模型底部及两侧认为热量流入与流出平衡,路面、天然地表、阴坡、阳坡等施加相应的周期函数,热传导单元采用DC2D4等参单元。

|
| 图 4 路基温度场计算模型 Fig. 4 Calculation model of roadbed temperature field |
| |
2 度场计算结果分析 2.1 填方高度对路基温度场影响
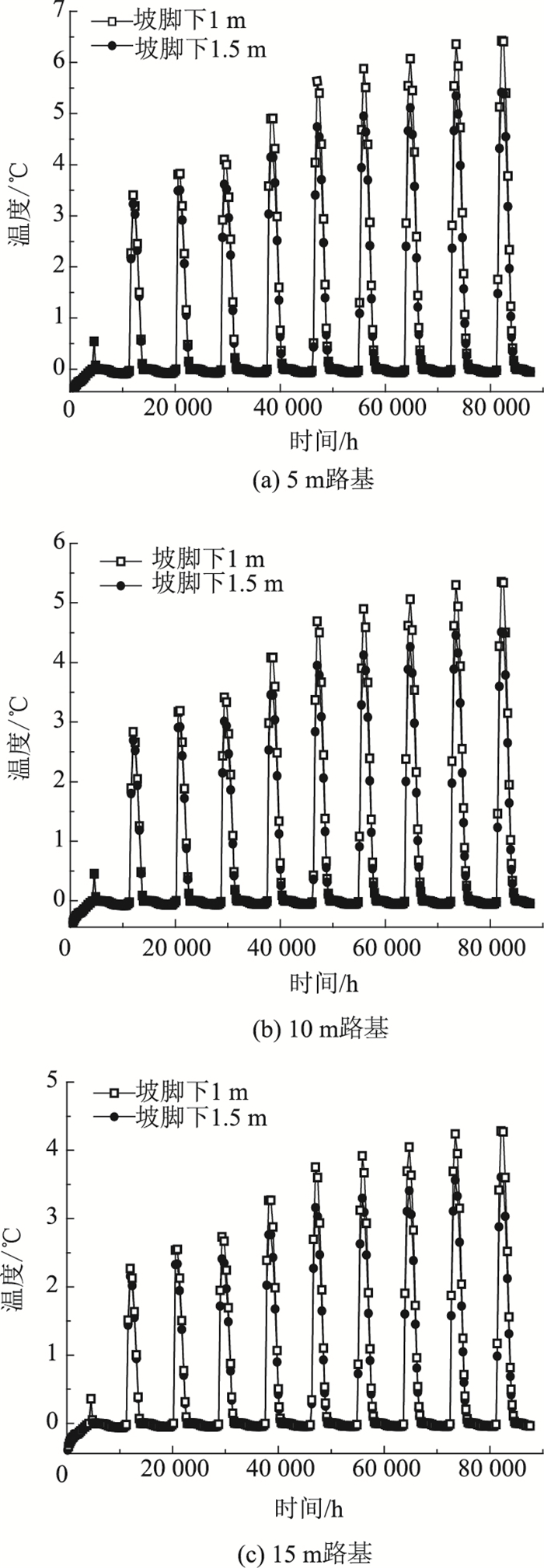
对5,10,15 m高度路基进行温度场计算,提取路基边坡下1 m深度处温度变化历史曲线进行分析,结果如图 5所示。
|
| 图 5 路基坡脚1 m深度温度历程 Fig. 5 Temperature history of roadbed slope at 1 m depth |
| |
由图 5可知:填土路基高度在5,10,15 m工况下,路基坡脚正下方温度历程均呈现震荡上升趋势,其中与原地面距离越近,温度振幅越高,振幅越大;随着填土路基高度的增大,坡脚下1,1.5 m处温度振幅最大值不断衰减,5,10,15 m填土高度时,1 m深度处的峰值分别为:6.42,5.35,4.28 ℃,温度降幅为:16.7%,33.3%;1.5 m处的峰值分别为:5.41,4.52,3.65 ℃,温度降幅为:16.4%,32.5%,即坡脚处距离原地表越深,温度变化越趋于平缓。
从温度变化时间历程来看,坡脚处不同深度位置温度均随时间增长而周期性增长,其中0~5年时间内温度增长速率较快,仅以峰值为例,前5年年均增长率约为3.2%~3.5%,第5年之后,温度增长变缓,增长速率约为0.8%~1%。
2.2 季节变化对路基温度场影响分别对5,10,15 m高度路基,第5年1月、4月、7月、10月温度场数据进行分析,对比不同填土高度路基融化状态差异。
在1月、4月寒冷季节,5,10,15 m高度填土路基均处于回冻过程状态。但两个季节内,路基回冻程度不同,其中1月左右时,外界气温虽然达到最低,但由于刚经过前一年暖季的路面吸热蓄热过程,路基体内融化夹层并未完全回冻,此时路基体内融化夹层形态较大,且填土路基越低,路基体内原储藏“冷量”越小,1月未完全回冻的融化夹层就越大;4月为外界气温拐点,1—4月份温度虽有回升,但总体气温仍在0 ℃以下,4月之后温度逐渐回暖,气温升至0 ℃以上,此时路基体处于最大回冻状态。此时5 m填方路基由于高度较小,已完全回冻,而10,15 m路基仍有少部分区域未完全回冻,这些区域主要分布在路面正下方及放坡台阶正下方。
在7月和10月,5,10,15 m高度填土路基均处于融化状态,但两个季节融沉状态却各有特点。对于天然地表而言:路基填土高度对路基以外的天然下限影响不大,路基坡脚10 m外的温度数据分析发现,7月最大融深均为1.9 m,10月份最大融深均为2.4 m;就路基体内而言,7月,各路基高度内均形成“凹”形融化盘,此外,7月份路基体内融化盘均为达到最大融深;7—10月,外界气温虽有所回落,但仍处于0 ℃以上,融化盘进一步发展,于10月份达到最大;10月份时,路基外天然地面达到最大融深,路基体内、坡脚处融深、路面下融化盘均达到最大,路基体处于最不利状态。
2.3 地温条件对路基温度场影响选取-0.2,-0.5,-0.8 ℃年平均地温条件,提取5,10,15 m高度4月份温度场数据进行分析,确定地温对不同高度填方路基温度场的影响。
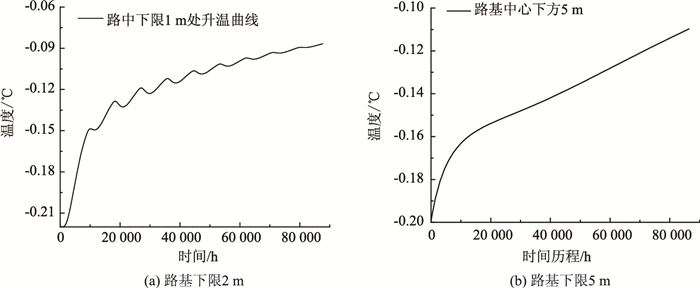
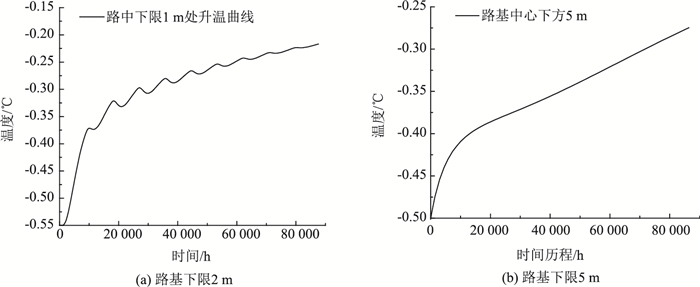
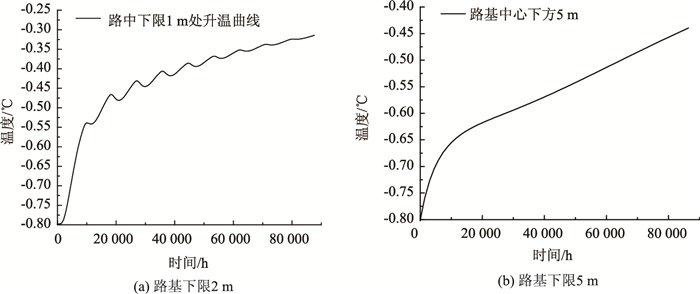
不同年平均地温条件下,路基中2,5 m深度处温度历程曲线如图 6~图 8所示。
|
| 图 6 年平均地温-0.2 ℃条件下路基温度变化 Fig. 6 Change of roadbed temperature at annual average temperature of -0.2 ℃ |
| |
|
| 图 7 年平均地温-0.5 ℃条件下路基温度变化 Fig. 7 Change of roadbed temperature at annual average temperature of -0.5 ℃ |
| |
|
| 图 8 年平均地温-0.8 ℃条件下路基温度变化 Fig. 8 Change of roadbed temperature at annual average temperature of -0.8 ℃ |
| |
由图 6~图 8可知:受路面吸热作用影响,年平均地温分别为-0.2,-0.5,-0.8 ℃工况下,路基中心下限2,5 m处温度均呈上升态势,且地温及外界气温越低,下限以下温度越低;下限深度2 m位置,受路面及边坡吸热作用影响,温度曲线呈周期震荡上升趋势,-0.2 ℃温度工况下,10年升温0.12 ℃;-0.5 ℃温度工况下,10年升温0.23, -0.8 ℃温度工况下,10年升温0.48 ℃。虽然地温越低,10年后2, 5 m深度处温度越低,但同时温度越低,相同路面吸热条件下,升温速率越快;下限深度5 m位置,与2 m位置相比,温度更低,升温模式基本为线性升温。同样外界温度条件下,5 m深度位置升温速率更低,-0.2 ℃温度工况下,10年升温0.09 ℃;-0.5 ℃温度工况下,10年升温0.22 ℃;-0.8 ℃温度工况下,10年升温0.36 ℃。
融化下限2 m处,受外界影响,温度呈现波动上升,而5 m位置外界气温波动已很难造成影响,只是随着时间累积,其增温效果才会慢慢显现,可认为下限5 m位置以下(下限为-2.5, 5 m以下为-7.5 m)材料属性不再随外界温度而波动。
2.4 “阴阳坡”效应对路基温度场影响路基走向将导致不同坡面接受太阳辐射不均衡,部分路段出现“阴阳坡”效应,冻土区路基稳定性与“阴阳坡”效应密切相关。
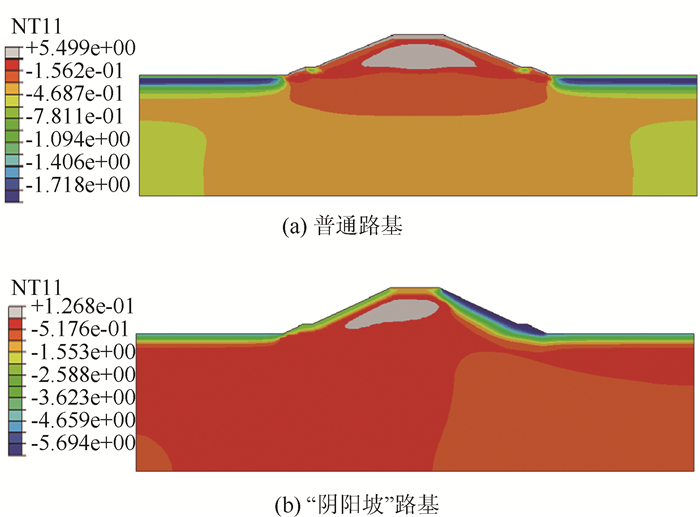
普通路基与“阴阳坡”路基第10年4月份温度场云图,如图 9所示。
|
| 图 9 第10年4月路基温度场(单位:℃) Fig. 9 Subgrade temperature field in April of the 10th year(unit:℃) |
| |
由计算结果和云图可知,4月份为冻土路基最大回冻季节,第1年无论普通路基还是“阴阳坡”路基均完全回冻;从第5年开始,普通路基与阴阳坡路基均出现未回冻融化夹层,其中普通路基未回冻融化夹层主要分布在路面正下方,放坡台阶正下方,而阴阳坡路基未回冻融化夹层仅存在于路面正下方;第10年融化夹层均进一步发展,其中阴阳坡路基融化夹层沿阳坡发育至放坡台阶附近,如图 9所示。
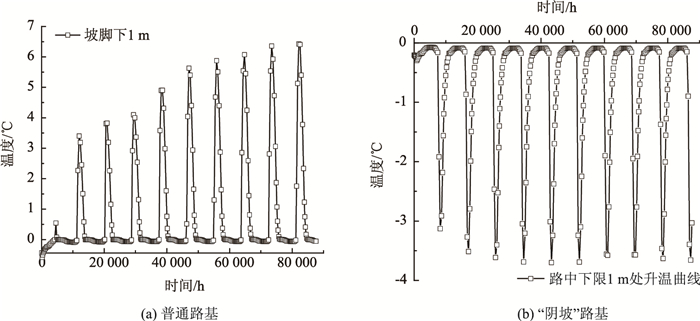
普通路基与“阴阳坡”路基坡脚1 m深度处温度数据比较,如图 10~图 12所示。
|
| 图 10 5 m路基坡脚处1 m温度变化 Fig. 10 Temperature change at 1 m height of slope foot of 5 m roadbed |
| |
|
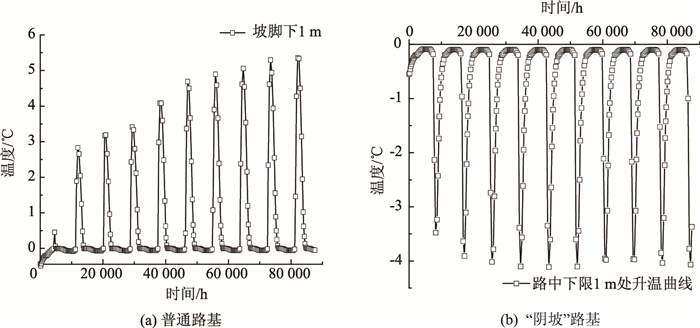
| 图 11 10 m路基坡脚处1 m温度变化 Fig. 11 Temperature change at 1 m height of slope foot of 10 m roadbed |
| |
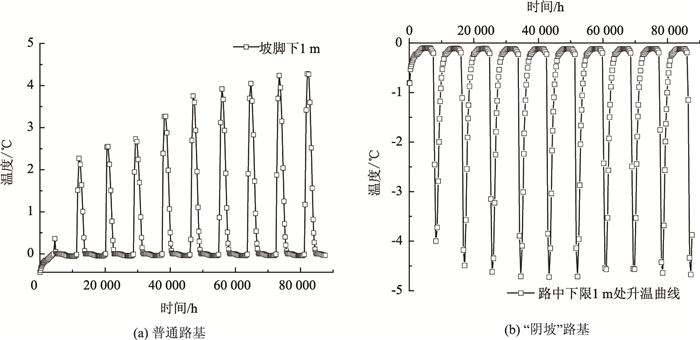
|
| 图 12 15 m路基坡脚处1 m温度变化 Fig. 12 Temperature change at 1 m height of slope foot of 15 m roadbed |
| |
由图 10~图 12可知:普通路基工况下,路基坡脚处温度呈周期性上升趋势,10 a内,温度普遍上升2~3 ℃,而“阴阳坡”路基阴坡侧由于温度较低,10 a内温度普遍下降0.3~0.8 ℃;路基高度越高,坡脚1 m处第10年温度峰值越低,以普通路基为例,5,10,15 m路基坡脚温度峰值分别为6.42,5.35,4.28 ℃,同比下降16.7%,33.3%;“阴阳坡”路基,阴坡侧温度峰值分别为:-3.66,-4.07,-4.67 ℃,同比下降:11.2%, 27.6%。在多年冻土地区路基选择和修筑时,应充分考虑温度场变化对路基及底部多年冻土的影响,填方路基高度要有合理控制区间,随着“阴阳坡”效应对路基稳定性的影响,要做好路基阳坡面的防护措施,减少外界热量向路基内部以及底部多年冻土侵入。
3 结论(1) 坡脚处不同深度位置温度均随时间增长而周期性增长,其中0~5年时间内温度增长速率较快,仅以峰值为例,前5年年均增长率约为3.2%~3.5%;第5年之后,温度增长变缓,增长速率约为0.8%~1%;10月份时,路基外天然地面达到最大融深,路基体内、坡脚处融深、路面下融化盘均达到最大,路基体处于最不利状态。
(2) 从融化夹层发育角度分析,第5年开始,未回冻融化夹层明显向阳坡侧偏移,从融化盘的形态上讲,普通路基融化盘呈扁平状,而阴阳坡路基融化夹层则沿阳坡方向呈长条形。
(3)“阴阳坡”路基由于路基两侧温差较大,彻底改变了传统“凸”型融化盘形态,导致融化峰面阴坡侧高、阳坡侧低,形成了天然滑动坡面,这个坡面自阴坡融化峰面起,止于阳坡坡脚融化盘,尤其是10月份,融化面处于最大季节,极大地威胁着路基稳定性。
| [1] |
汪双杰, 王佐, 袁堃, 等. 青藏公路多年冻土地区公路工程地质研究回顾与展望[J]. 中国公路学报, 2015, 28(12): 1-8. WANG Shuang-jie, WANG Zuo, YUAN Kun, et al. Qinghai-Tibet Highway Engineering Geology in Permafrost Regions:Review and Prospect[J]. China Journal of Highway and Transport, 2015, 28(12): 1-8. |
| [2] |
毛雪松, 杨锦凤, 张正波, 等. 温度-湿度-荷载综合作用下路基冻融过程试验研究[J]. 冰川冻土, 2012, 34(2): 427-434. MAO Xue-song, YANG Jin-feng, ZHANG Zheng-bo, et al. Experimental Study of Integrated Temperature-moisture-load Effect on Subgrade during Freeze-thaw Cycle[J]. Journal of Glaciology and Geocryology, 2012, 34(2): 427-434. |
| [3] |
马勤国, 赖远明, 吴道勇. 多年冻土区高等级公路路基温度场研究[J]. 中南大学学报:自然科学版, 2016, 47(7): 2415-2423. MA Qin-guo, LAI Yuan-ming, WU Dao-yong. Analysis of Temperature Field of High Grade Highway Embankment in Permafrost Regions[J]. Journal of Central South University:Science and Technology Edition, 2016, 47(7): 2415-2423. |
| [4] |
SCHIMPERNA G, SEGATTI A. Attractors for the Semiflow Associated with a Class of Doubly Nonlinear Parabolic Equations[J]. Mathematics, 2006, 56(2): 61-86. |
| [5] |
GATMIRI B, JABBARI E. Time-Domain Green's Functions for Unsaturated Soils[J]. International Journal of Solids & Structures, 2005, 42(23): 5991-6002. |
| [6] |
ALEXIADES V, SOLOMON A D, LUNARDINI V J. Mathematical Modeling of Melting and Freezing Processes[J]. Journal of Solar Energy Engineering, 1993, 115(2): 121. |
| [7] |
雷志栋, 杨诗秀, 许志荣, 等. 土壤特性空间变异性初步研究[J]. 水利学报, 1985(9): 12-23. LEI Zhi-dong, YANG Shi-xiu, XU Zhi-rong, et al. Preliminary Investigation of the Spatial Variability of Soil Properties[J]. Journal of Hydraulic Engineering, 1985(9): 12-23. |
| [8] |
程国栋, 何平. 多年冻土地区线性工程建设[J]. 冰川冻土, 2001, 23(3): 213-217. CHENG Guo-dong, HE Ping. Linearity Engineering in Permafrost Areas[J]. Journal of Glaciology and Geocryology, 2001, 23(3): 213-217. |
| [9] |
樊贵盛, 郑秀清, 潘光在. 地下水埋深对冻融土壤水分入渗特性影响的试验研究[J]. 水利学报, 1999, 30(3): 21-26. FAN Gui-sheng, ZHENG Xiu-qing, PAN Guang-zai. Experimental Study on the Influence of the Buried Depth of Ground Water Level on the Infiltration Characteristics of Freeze Thaw Soils[J]. Journal of Hydraulic Engineering, 1999, 30(3): 21-26. |
| [10] |
李宁, 陈波, 陈飞熊, 等. 奥地利岩土工程软件FINAL的应用与开发[J]. 西安公路交通大学学报, 2000, 20(1): 27-33. LI Ning, CHEN Bo, CHEN Fei-xiong, et al. Development and Application of the Austrian Software FINAL in China[J]. Journal of Xi'an Highway University, 2000, 20(1): 27-33. |
| [11] |
毛雪松, 胡长顺, 侯仲杰. 冻土路基温度场室内足尺模型试验[J]. 长安大学学报:自然科学版, 2004, 24(1): 20-33. MAO Xue-song, HU Chang-shun, HOU Zhong-jie. Laboratory Large-scale Test of Temperature Field in Permafrost Sub-grade[J]. Journal of Chang'an University:Natural Science Edition, 2004, 24(1): 20-33. |
| [12] |
樊凯, 俞祁浩, 李金平, 等. 典型冻土路基变形调控措施应用效能分析[J]. 公路交通科技, 2017, 34(10): 34-41. FAN Kai, YU Qi-hao, LI Jin-ping, et al. Analysis on Applied Efficiency of Deformation Control Measures for Typical Permafrost Subgrade[J]. Journal of Highway and Transportation Research and Development, 2017, 34(10): 34-41. |
| [13] |
易鑫, 胡达, 喻文兵, 等. 多年冻土区青藏公路路基边界温度及计算模型研究[J]. 冰川冻土, 2017, 39(2): 336-342. YI Xin, HU Da, YU Wen-bing, et al. Study on the Temperature Boundary of Embankment and Its Calculation Model of the Qinghai-Tibet Highway in Permafrost Area[J]. Journal of Glaciology and Geocryology, 2017, 39(2): 336-342. |
| [14] |
司伟, 马骉, 汪海年, 等. 基于路基顶面温度的多年冻土区沥青路面结构[J]. 长安大学学报:自然科学版, 2012, 32(6): 16-22, 32. SI Wei, MA Biao, WANG Hai-nian, et al. Subgrade Top Temperature of Asphalt Pavement Structure in Permafrost Areas[J]. Journal of Chang'an University:Natural Science Edition, 2012, 32(6): 16-22, 32. |
| [15] |
王威娜, 秦煜, 李小飞, 等. 季节冻土地区阴阳坡路基温度场及变形发育数值模拟[J]. 公路交通科技, 2017, 34(2): 20-28. WANG Wei-na, QIN Yu, LI Xiao-fei, et al. Numerical Simulation of Temperature Field and Deformation Development of Subgrade with Sunny-shady Slopes in Seasonal Frozen Region[J]. Journal of Highway and Transportation Research and Development, 2017, 34(2): 20-28. |
| [16] |
孙立军, 秦健. 沥青路面温度场的预估模型[J]. 同济大学学报:自然科学版, 2006, 34(4): 480-483. SUN Li-jun, QIN Jian. Prediction Model on Temperature Field in Asphalt Pavement[J]. Journal of Tongji University:Natural Science Edition, 2006, 34(4): 480-483. |
| [17] |
王铁行, 胡长顺. 多年冻土地区路基温度场和水分迁移场耦合问题研究[J]. 土木工程学报, 2003, 36(12): 93-97. WANG Tie-hang, HU Chang-shun. Study on the Problem of Coupled Temperature Field and Moisture Migration Field of Subgrade in Permafrost Region[J]. China Civil Engineering Journal, 2003, 36(12): 93-97. |
| [18] |
ZHANG Z, WU Q, XUN X. Radiation and Energy Balance Characteristics of Asphalt Pavement in Permafrost Regions[J]. Environmental Earth Sciences, 2016, 75(3): 221. |
 2018, Vol. 35
2018, Vol. 35
