扩展功能
文章信息
- 胡幼常, 陈晓鸣, 许爱华, 毛爱民, 刘杰
- HU You-chang, CHEN Xiao-ming, XU Ai-hua, MAO Ai-min, LIU Jie
- 加筋粗粒土坡稳定安全系数的简化计算方法
- A Simplified Method for Calculating Stability Factor of Reinforced Granular Soil Slope
- 公路交通科技, 2018, 35(3): 16-27
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(3): 16-27
- 10.3969/j.issn.1002-0268.2018.03.003
-
文章历史
- 收稿日期: 2017-04-17
2. 中国交通建设股份有限公司, 北京 100088;
3. 新疆维吾尔自治区 交通规划勘察设计研究院, 新疆 乌鲁木齐 830006
 =35°,36°,37°,重度γ=18,21,25 kN/m3,边坡高度H=4~50 m,坡率m=0.5,0.75或1,加筋层间距S=0.3~0.8 m组合出的一系列加筋粗粒土坡分别计算Fsg和对应的Fsj,发现Fsg和Fsj具有良好的相关性,并且当S在0.3~0.8 m内变化时,Fsg-Fsj关系曲线与S,H,
=35°,36°,37°,重度γ=18,21,25 kN/m3,边坡高度H=4~50 m,坡率m=0.5,0.75或1,加筋层间距S=0.3~0.8 m组合出的一系列加筋粗粒土坡分别计算Fsg和对应的Fsj,发现Fsg和Fsj具有良好的相关性,并且当S在0.3~0.8 m内变化时,Fsg-Fsj关系曲线与S,H, ,γ几乎无关,仅与m有关。当Fsg=1~2时,经曲线回归分析发现Fsg-Fsj关系与三次多项式几乎完全吻合,其相关系数达到1。于是,分别得到了坡率m=0.5,0.75,1这3种情况下的加筋粗粒土坡Fsg-Fsj回归公式,从而实现了以Fsj来计算Fsg的设想,使计算大为简化。而且,按这些回归公式计算出的Fsg,其绝对误差和相对误差在Fsg=1~2时分别不超过约±0.033和±1.6%,在Fsg=1~1.5时则分别不超过约±0.018和±1.2%,满足工程设计的要求。
,γ几乎无关,仅与m有关。当Fsg=1~2时,经曲线回归分析发现Fsg-Fsj关系与三次多项式几乎完全吻合,其相关系数达到1。于是,分别得到了坡率m=0.5,0.75,1这3种情况下的加筋粗粒土坡Fsg-Fsj回归公式,从而实现了以Fsj来计算Fsg的设想,使计算大为简化。而且,按这些回归公式计算出的Fsg,其绝对误差和相对误差在Fsg=1~2时分别不超过约±0.033和±1.6%,在Fsg=1~1.5时则分别不超过约±0.018和±1.2%,满足工程设计的要求。2. China Communications Construction Co., Ltd., Beijing 10083, China;
3. Xinjiang Transport Planning Survey and Design Institute, Urumqi Xinjiang 830006, China
加筋土坡的稳定性一般都采用极限平衡法进行分析,这种方法概念清晰,应用广泛,经验丰富,被各国规范所采用[1-3]。但由于其不能考虑土体及筋材的变形,也不能考虑筋-土间的相互作用,只能分析极限状态下的静力平衡关系,在理论上是不完善的。因此,人们一直在探寻其他更好的方法。包括有限元强度折减法在内的数值极限分析法[4],在分析时纳入了土的本构关系,从而可以考虑土体和筋材的变形因素,并且可以反映筋-土的相互作用[5],尽管其计算结果的准确性还依赖于土的本构关系和筋-土相互作用机理研究的进展,但在理论上比极限平衡法前进了一大步[4]。影响数值极限分析法推广应用的主要障碍是边坡失稳判据还没有取得共识[4, 6]。但可以预见,这类方法是非常具有发展前途的方法[4]。
无论是传统的极限平衡法,还是正在发展中的数值极限分析法,用于计算加筋土坡的安全系数时,都比较复杂。特别是在设计阶段,要进行多种方案的比较和试算工作,计算量很大,手工计算不现实,一般需要借助专业软件来完成,不便于在一般工程设计单位推广。陈祖煜等[7]将基于塑性力学上限解法的倾斜条块分析法[8]运用于加筋土坡的分析计算,指出在实际工程中采用的常规加筋间距下,直线滑动面的库仑滑移模式可能是唯一的破坏模式,运用上限解法经大量计算后绘制了均质加筋土坡的无量纲化参数安全系数图,对于给定的均质加筋土坡可方便地查出安全系数。这是值得继续广泛研究的新方法。笔者曾在试验的基础上提出了考虑加筋影响带的简化方法[9],但这个方法中有关加筋影响带范围的确定还有待进一步研究。
考虑到我国新疆等地区以砾石土为代表的粗粒土分布广泛,在公路建设中大量采用粗粒土填筑路基,同时现有的加筋土研究成果已表明,粗粒土采用土工格栅加筋能获得良好的加筋效果[10],且有良好的抗震性能[11],所以在像新疆这样的粗粒土分布广泛的地震高发区,非常适合于推广加筋路堤的应用。相对简单、实用且安全可靠的加筋粗粒土坡设计方法将有助于这一推广目标的实现。基于此,笔者借鉴李广信等[12]提出的关于加筋土应力应变计算的思路,将加筋粗粒土坡转化为无加筋的均质土坡,采用现行公路规范[1]推荐的简化Bishop法,经大量的对比计算,找出了加筋粗粒土坡安全系数Fsg和等代均质土坡安全系数Fsj的回归公式。根据该公式,只要求出了Fsj就可计算出相应的Fsg,于是就将复杂的加筋土坡安全系数的计算转化成了简单的均质土坡安全系数的计算,便于在工程中推广。
1 等代均质土坡在如图 1(a)所示的加筋土路堤边坡中,设筋材足够长,以致不会发生拔出破坏。根据Yang[13]关于加筋相当于增加了土体围压的观点,假设筋材所起的作用相当于对加筋区域的土体在边坡高度范围内附加了一个平均围压Δσ3,则Δσ3可按式(1)计算:
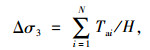
|
(1) |
|
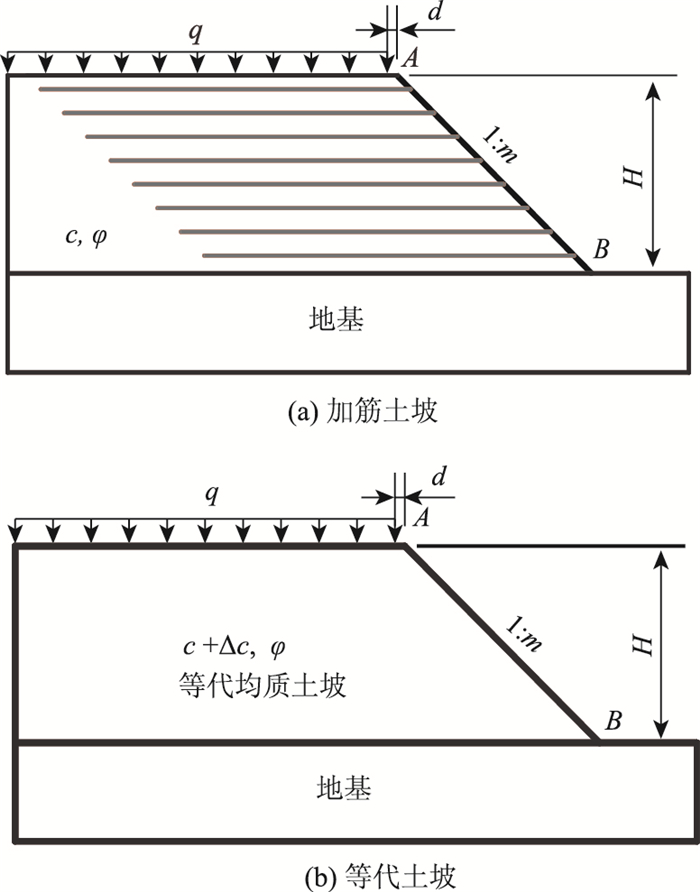
| 图 1 加筋土坡和等代土坡 Fig. 1 Reinforced soil slope and its equivalent soil slope |
| |
式中,N为加筋层数;Tai为第i层筋材设计抗拉强度;H为坡高;Δσ3为筋材施加于土体的平均围压。
根据准黏聚力理论[14],Δσ3的作用相当于使加筋区的土体黏聚力增加了Δc,而内摩擦角不变。Δc的大小由Δσ3确定,二者的关系可按以下方法推导出来。根据加筋区内土体的极限平衡条件,有:
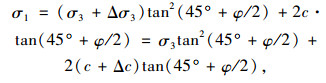
|
其中:
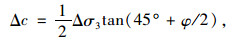
|
(2) |
将式(1)代入式(2)得:
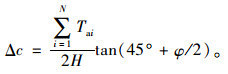
|
(3) |
这样,就把如图 1(a)所示的加筋土坡简化成了如图 1(b)所示的等代均质土坡。尽管均质土坡的稳定安全系数计算比加筋土坡简单得多,但计算结果表明,按黏聚力增加了由式(3)确定的Δc,内摩擦角不变的均质土坡计算出的安全系数Fsj与加筋土坡的实际安全系数Fsg有一定差别。所以,虽然如上所述的假黏聚力理论已提出许多年,但却一直没有在工程实践中得到推广应用。可以想象得到,Fsg与Fsj必然存在某种对应关系,而这一关系必定与加筋土坡中土的黏聚力c和内摩擦角





假定如图 1(a)所示的加筋土路堤边坡建在坚固的地基之上,其破坏滑动面不会伸入到地基中。路基填土为粗粒土,黏聚力c=0,内摩擦角
根据规范[1],加筋土坡的安全系数Fsg和等代均质土坡的安全系数Fsj都采用传统极限平衡法中的简化Bishop法计算。对土工格栅和土工织物等柔软满铺材料而言,极限平衡法在计算Fsg时,认为每层筋材的作用就相当于在该层筋材与圆弧滑动面相交处提供一个与滑面相切的拉力,其大小为该层筋材的设计抗拉强度Tai。于是,Fsg由式(4)计算[1]:
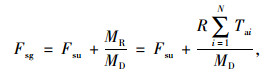
|
(4) |
式中,Fsg为加筋土坡的稳定安全系数;Fsu为不考虑筋材作用时土坡的稳定安全系数;MR为筋材提供的抗滑力矩;MD为不考虑筋材作用时土坡的滑动力矩;R为滑弧半径;N为加筋层数;Tai为第i层筋材的设计抗拉强度。
上述Fsg的计算方法实质上是将筋材和土的作用分开考虑的,没有从本质上考虑筋-土的相互作用,计算时与传统的圆弧条分法相同,需要事先假定滑动面形状和位置。由于纯土坡的极限平衡条分法在理论上可看成是塑性理论的下限解[18],其结果是偏于安全的,可靠性经受了几十年工程实践的检验,是趋于成熟的方法[4, 18],加之这种方法概念清晰,计算简单,也积累了较多的经验,所以仍是目前各国规范中普遍采用的方法[19]。
3 Fsg-Fsj关系的计算结果及分析 3.1 加筋层距S对Fsg-Fsj关系的影响加筋土坡筋层间距S的大小要从土坡的安全性和经济性两方面考虑[1]。从经济的角度,S不宜小于路基填土的分层压实厚度,粗粒土的分层压实厚度一般都在0.3 m以上;为保证加筋的有效性和加筋土坡的安全性,S不宜大于0.8 m[1],而要保证加筋土坡的抗震效果,S不宜超过0.6 m[11, 16]。所以,本文仅在S=0.3~0.8 m内进行讨论,并且从实际出发,排除设计中不可能采用的疏密悬殊的筋层布局,即认为在边坡高度范围内筋层间距基本是均匀的(筋层间距0.3~0.8 m范围内变化),以免滑动圆弧从坡面滑出的情况发生。
考虑到规范[20]规定正常工况下的容许安全系数为1.25~1.45,特殊工况为1.05~1.35[20-21],所以仅对Fsg∈[1,2]的Fsg-Fsj关系进行讨论。因为,如果Fsg < 1,则边坡在理论上都是不稳定的;如果Fsg>2,则安全系数过大,不经济,所以两种情况都没有实际意义。
为了寻找S对Fsg-Fsj关系的影响,对坡率m=0.5,0.75和1,坡高H=10 m,c=0,
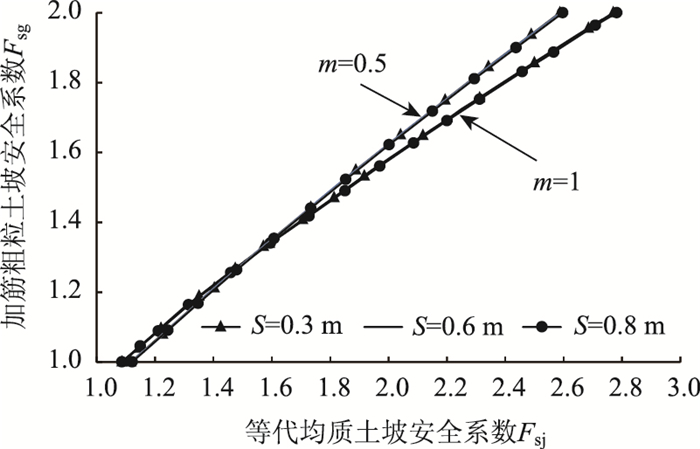
|
| 图 2 加筋层距S对Fsg-Fsj曲线的影响 Fig. 2 Effect of S on Fsg-Fsj curve |
| |
从图 2可知,在坡率m一定,S=0.3~0.8 m时,Fsg-Fsj关系曲线与S无关。不仅如此,计算还表明,当S在0.3~0.8 m范围内变化时,只要筋材的总拉力不变,Fsg和Fsj都与S无关。下面对此计算结果进行分析。
上述计算结果表明Fsg只与筋材的总拉力∑Tai有关,而与S无关。这说明,对于给定的边坡,当S在0.3~0.8 m范围内变化时,按简化Bishop条分法确定的最危险滑动圆弧的位置在∑Tai相等时是固定的,不随S的改变而变动。因为只有当滑弧半径R一定且滑弧位置相同时,Fsu和MD均为定值,由式(4)才能得出Fsg只与筋材的总拉力∑ Tai有关的结论。
也就是说,只要S=0.3~0.8 m,则不管筋层布局如何,也不管每层筋材的设计抗拉强度各为多少,只要筋材总拉力∑Tai是相等的,则安全系数Fsg就相等,即在S=0.3~0.8 m的前提下,如果每层筋材的设计抗拉强度都是一样的,则Fsg只与筋材层数N有关,而与筋层的布局无关,既与筋层是否等间距布设无关,也与筋层间距大小无关。
关于Fsg与S的关系,笔者还就S取较大值的情况做了计算,发现当∑Tai一定时,如果0.3 m≤S < 1.5 m,则最危险滑面的位置就几乎不受S的影响。这让我们更有理由假定S=0.3~0.8 m时,最危险滑面位置与S无关。
等代均质土坡中,均质土的黏聚力c=Δc,内摩擦角
由上述分析可知,当S=0.3~0.8 m时,对于坡高H、坡率m、内摩擦角
为了探寻坡高H对Fsg-Fsj关系的影响,先选取边坡坡率m=1、粗粒土的内摩擦角


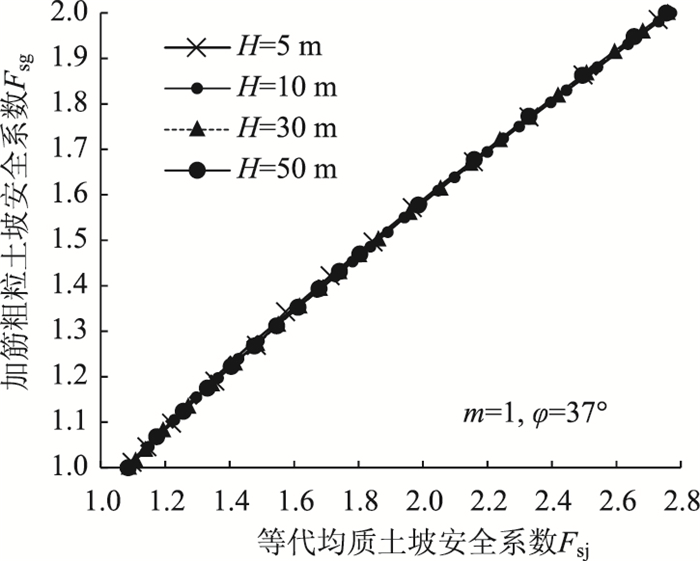
|
图 3 m=1,   |
| |
3.3 内摩擦角

图 4是几种不同坡高H和不同坡率m值时,粗粒土的内摩擦角


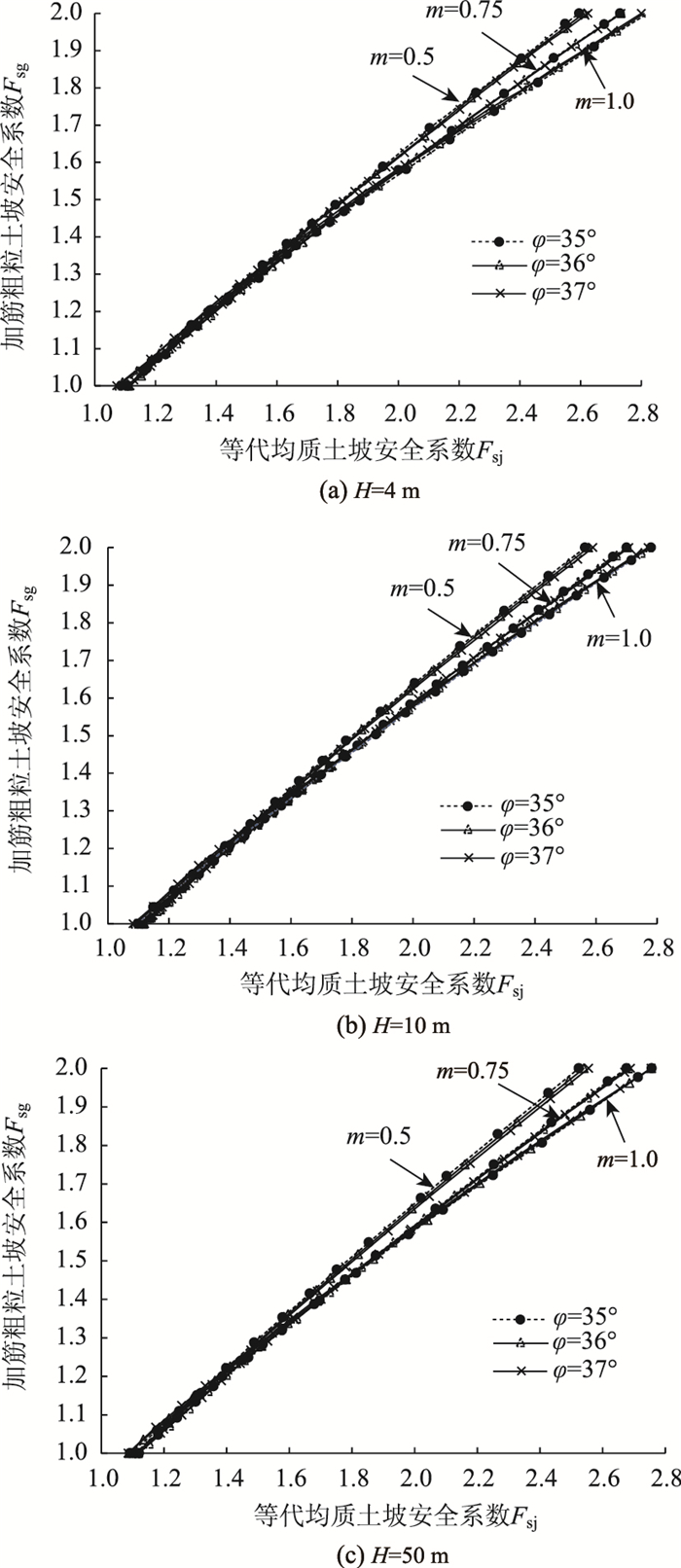
|
| 图 4 不同坡高H和坡率m时的Fsg-Fsj曲线 Fig. 4 Effect of H or m on Fsg-Fsj curve |
| |
3.4 重度γ对Fsg-Fsj关系的影响
为了研究粗粒土的重度γ对Fsg-Fsj关系的影响,对坡率m=0.5和1,坡高H=10 m,
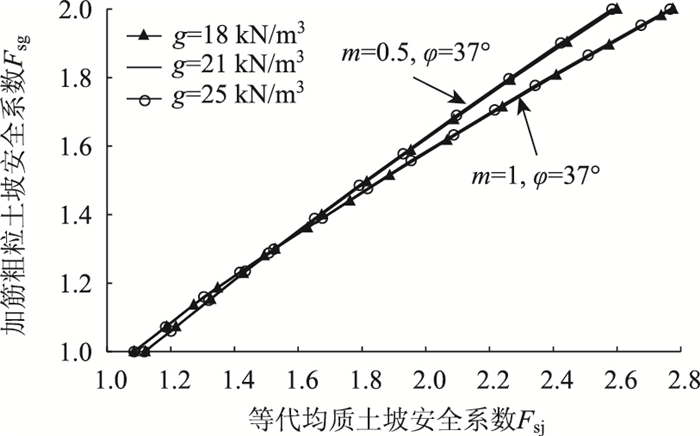
|
| 图 5 不同重度γ时的Fsg-Fsj曲线 Fig. 5 Effect of γ on Fsg-Fsj curve |
| |
从图 5可知,当粗粒土的重度γ分别为18,21,25 kN/m3时,Fsg-Fsj曲线是重合的,说明γ对Fsg-Fsj的关系没有影响。
4 加筋粗粒土坡的Fsg-Fsj回归公式上述分析已告诉我们,Fsg-Fsj关系与坡高H、粗粒土的内摩擦角
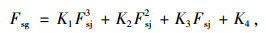
|
(5) |
式中,常数K1~K4的值见表 1,它们是以m=0.5,0.75或1,H=10 m,
| m | K1 | K2 | K3 | K4 |
| 0.5 | 0.01 | -0.102 9 | 0.957 | 0.046 5 |
| 0.75 | 0.020 2 | -0.167 6 | 1.038 3 | 0.018 8 |
| 1 | 0.017 | -0.152 4 | 0.978 7 | 0.094 2 |


| m=0.5 | m=0.75 | m=1 | ||||||||||||||
| Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | ||
| 10.09 | 1.116 | 1.000 | 1.000 | 0 | 6.11 | 1.120 | 1.000 | 1.000 | 0 | 2.75 | 1.090 | 1.000 | 1.002 | 2 | ||
| 11 | 1.161 | 1.033 | 1.035 | 2 | 6.5 | 1.144 | 1.017 | 1.018 | 1 | 3.5 | 1.154 | 1.045 | 1.047 | 2 | ||
| 12 | 1.205 | 1.069 | 1.068 | -1 | 7 | 1.174 | 1.037 | 1.039 | 2 | 5 | 1.259 | 1.121 | 1.119 | -2 | ||
| 13 | 1.252 | 1.103 | 1.103 | 0 | 7.5 | 1.203 | 1.058 | 1.060 | 2 | 6 | 1.321 | 1.164 | 1.160 | -4 | ||
| 14 | 1.297 | 1.137 | 1.136 | -1 | 8 | 1.231 | 1.079 | 1.081 | 2 | 7 | 1.385 | 1.204 | 1.203 | -1 | ||
| 15 | 1.341 | 1.169 | 1.169 | 0 | 8.5 | 1.257 | 1.102 | 1.099 | -3 | 8 | 1.447 | 1.244 | 1.243 | -1 | ||
| 16 | 1.383 | 1.201 | 1.200 | -1 | 9 | 1.284 | 1.122 | 1.118 | -4 | 9 | 1.503 | 1.280 | 1.279 | -1 | ||
| 17 | 1.427 | 1.232 | 1.232 | 0 | 10 | 1.339 | 1.160 | 1.157 | -3 | 10 | 1.562 | 1.315 | 1.316 | 1 | ||
| 18 | 1.470 | 1.262 | 1.263 | 1 | 11 | 1.392 | 1.195 | 1.194 | -1 | 11 | 1.619 | 1.350 | 1.351 | 1 | ||
| 19 | 1.510 | 1.292 | 1.291 | -1 | 12 | 1.440 | 1.229 | 1.227 | -2 | 12 | 1.672 | 1.384 | 1.384 | 0 | ||
| 20 | 1.552 | 1.321 | 1.321 | 0 | 13 | 1.493 | 1.263 | 1.263 | 0 | 13 | 1.727 | 1.416 | 1.417 | 1 | ||
| 21 | 1.594 | 1.350 | 1.351 | 1 | 14 | 1.542 | 1.295 | 1.295 | 0 | 14 | 1.782 | 1.449 | 1.450 | 1 | ||
| 22 | 1.633 | 1.379 | 1.378 | -1 | 15 | 1.592 | 1.327 | 1.329 | 2 | 15 | 1.835 | 1.481 | 1.482 | 1 | ||
| 23 | 1.674 | 1.407 | 1.407 | 0 | 16 | 1.638 | 1.356 | 1.359 | 3 | 16 | 1.884 | 1.512 | 1.511 | -1 | ||
| 24 | 1.715 | 1.435 | 1.436 | 1 | 17 | 1.686 | 1.388 | 1.390 | 2 | 17 | 1.937 | 1.541 | 1.542 | 1 | ||
| 25 | 1.755 | 1.462 | 1.463 | 1 | 18 | 1.735 | 1.419 | 1.421 | 2 | 18 | 1.988 | 1.570 | 1.571 | 1 | ||
| 27 | 1.832 | 1.516 | 1.516 | 0 | 19 | 1.778 | 1.449 | 1.449 | 0 | 19 | 2.036 | 1.599 | 1.599 | 0 | ||
| 29 | 1.909 | 1.569 | 1.568 | -1 | 20 | 1.825 | 1.478 | 1.478 | 0 | 20 | 2.087 | 1.628 | 1.627 | -1 | ||
| 31 | 1.987 | 1.620 | 1.620 | 0 | 21.5 | 1.895 | 1.521 | 1.522 | 1 | 21 | 2.137 | 1.656 | 1.656 | 0 | ||
| 33 | 2.062 | 1.671 | 1.670 | -1 | 23 | 1.961 | 1.564 | 1.563 | -1 | 22 | 2.183 | 1.684 | 1.681 | -3 | ||
| 35 | 2.140 | 1.721 | 1.721 | 0 | 24.5 | 2.029 | 1.604 | 1.604 | 0 | 24 | 2.282 | 1.737 | 1.736 | -1 | ||
| 37 | 2.214 | 1.770 | 1.769 | -1 | 26 | 2.093 | 1.644 | 1.643 | -1 | 26 | 2.376 | 1.789 | 1.787 | -2 | ||
| 39 | 2.287 | 1.818 | 1.817 | -1 | 29 | 2.224 | 1.722 | 1.721 | -1 | 28 | 2.472 | 1.839 | 1.839 | 0 | ||
| 41 | 2.363 | 1.865 | 1.865 | 0 | 32 | 2.352 | 1.797 | 1.797 | 0 | 30 | 2.564 | 1.889 | 1.888 | -1 | ||
| 43 | 2.437 | 1.912 | 1.912 | 0 | 35 | 2.482 | 1.871 | 1.872 | 1 | 32 | 2.656 | 1.938 | 1.937 | -1 | ||
| 45 | 2.511 | 1.959 | 1.959 | 0 | 38 | 2.607 | 1.944 | 1.944 | 0 | 34 | 2.749 | 1.986 | 1.986 | 0 | ||
| 46.78 | 2.575 | 2.000 | 1.999 | -1 | 40.4 | 2.705 | 2.000 | 2.001 | 1 | 34.58 | 2.775 | 2.000 | 2.000 | 0 | ||
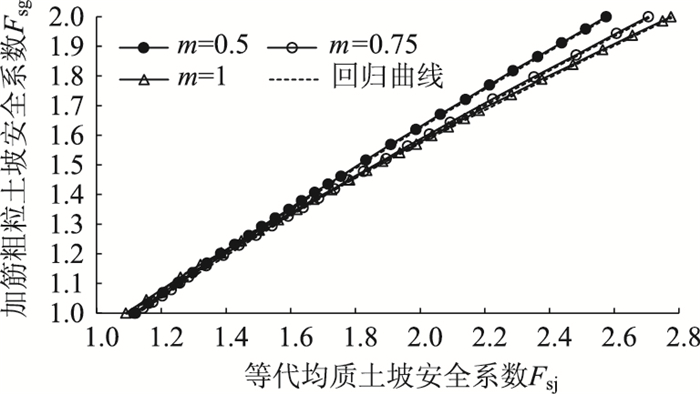
|
| 图 6 Fsg-Fsj回归曲线 Fig. 6 Regression curves of Fsg-Fsj |
| |
为了检验式(5)的计算精度,笔者对各种工况下按式(5)得到的加筋粗粒土坡安全系数拟合值Fsg1与规范法[1]计算的安全系数Fsg做了全面对比分析。由于数据量很大,不能一一列出,表 3~表 11中列出了误差相对较大的几种工况的对比结果。其中,δ为相对误差,δ=Δ/Fsg。未列入表 3~表 11的其他工况,其绝对误差Δ和相对误差δ均不超过表 3~表 11所列范围。
 =35° =35° |
 =37° =37° |
|||||||||||
| Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | |
| 4.96 | 1.109 | 1.000 | 0.995 | -5 | -0.5 | 4.32 | 1.116 | 1.000 | 1.000 | 0 | 0.0 | |
| 7 | 1.299 | 1.141 | 1.138 | -3 | -0.3 | 7 | 1.375 | 1.193 | 1.194 | 1 | 0.1 | |
| 9 | 1.472 | 1.264 | 1.264 | 0 | 0.0 | 8 | 1.466 | 1.257 | 1.260 | 3 | 0.2 | |
| 11 | 1.632 | 1.381 | 1.378 | -3 | -0.2 | 9 | 1.555 | 1.320 | 1.323 | 3 | 0.3 | |
| 13 | 1.792 | 1.486 | 1.489 | 3 | 0.2 | 10 | 1.642 | 1.379 | 1.385 | 6 | 0.4 | |
| 15 | 1.949 | 1.589 | 1.595 | 6 | 0.4 | 11 | 1.728 | 1.439 | 1.445 | 6 | 0.4 | |
| 17 | 2.103 | 1.692 | 1.697 | 5 | 0.3 | 13 | 1.900 | 1.549 | 1.562 | 13 | 0.8 | |
| 19 | 2.255 | 1.787 | 1.796 | 9 | 0.5 | 16 | 2.143 | 1.703 | 1.723 | 20 | 1.2 | |
| 21 | 2.405 | 1.879 | 1.892 | 13 | 0.7 | 19 | 2.380 | 1.855 | 1.876 | 21 | 1.1 | |
| 23.62 | 2.595 | 2.000 | 2.012 | 12 | 0.6 | 22.11 | 2.624 | 2.000 | 2.030 | 30 | 1.5 | |
 =35° =35° |
 =37° =37° |
|||||||||||
| Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | |
| 10.72 | 1.114 | 1.000 | 0.999 | -1 | -0.1 | 9.45 | 1.121 | 1.000 | 1.004 | 4 | 0.4 | |
| 13 | 1.216 | 1.079 | 1.076 | -3 | -0.3 | 13 | 1.291 | 1.127 | 1.132 | 5 | 0.4 | |
| 15 | 1.303 | 1.144 | 1.141 | -3 | -0.3 | 17 | 1.469 | 1.258 | 1.262 | 4 | 0.3 | |
| 19 | 1.468 | 1.265 | 1.261 | -4 | -0.3 | 20 | 1.597 | 1.348 | 1.353 | 5 | 0.4 | |
| 23 | 1.627 | 1.379 | 1.374 | -5 | -0.3 | 24 | 1.763 | 1.464 | 1.469 | 5 | 0.3 | |
| 27 | 1.781 | 1.487 | 1.481 | -6 | -0.4 | 28 | 1.923 | 1.572 | 1.577 | 5 | 0.3 | |
| 30 | 1.895 | 1.564 | 1.559 | -5 | -0.3 | 32 | 2.080 | 1.676 | 1.682 | 6 | 0.3 | |
| 37 | 2.155 | 1.738 | 1.731 | -7 | -0.4 | 36 | 2.238 | 1.777 | 1.785 | 8 | 0.4 | |
| 41 | 2.300 | 1.832 | 1.825 | -7 | -0.4 | 40 | 2.389 | 1.874 | 1.882 | 8 | 0.4 | |
| 48.32 | 2.564 | 2.000 | 1.992 | -8 | -0.4 | 45.31 | 2.590 | 2.000 | 2.009 | 9 | 0.4 | |
 =35° =35° |
 =37° =37° |
|||||||||||
| Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | |
| 48 | 1.109 | 1.000 | 0.995 | -5 | -0.5 | 42.42 | 1.117 | 1.000 | 1.001 | 1 | 0.1 | |
| 68 | 1.305 | 1.151 | 1.142 | -9 | -0.7 | 55 | 1.252 | 1.104 | 1.103 | -1 | -0.1 | |
| 78 | 1.398 | 1.221 | 1.211 | -10 | -0.9 | 65 | 1.353 | 1.179 | 1.178 | -1 | -0.1 | |
| 88 | 1.488 | 1.288 | 1.276 | -12 | -1.0 | 70 | 1.403 | 1.216 | 1.214 | -2 | -0.1 | |
| 98 | 1.578 | 1.353 | 1.340 | -13 | -1.0 | 90 | 1.595 | 1.355 | 1.352 | -3 | -0.2 | |
| 118 | 1.751 | 1.477 | 1.460 | -17 | -1.1 | 100 | 1.689 | 1.421 | 1.418 | -3 | -0.2 | |
| 130 | 1.853 | 1.548 | 1.530 | -18 | -1.2 | 125 | 1.915 | 1.577 | 1.572 | -4 | -0.3 | |
| 150 | 2.020 | 1.663 | 1.642 | -21 | -1.3 | 140 | 2.047 | 1.667 | 1.660 | -7 | -0.4 | |
| 160 | 2.102 | 1.720 | 1.696 | -24 | -1.4 | 155 | 2.177 | 1.753 | 1.745 | -8 | -0.4 | |
| 212.1 | 2.524 | 2.000 | 1.967 | -33 | -1.6 | 199.5 | 2.555 | 2.000 | 1.987 | -13 | -0.7 | |
 =35° =35° |
 =37° =37° |
|||||||||||
| Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | |
| 2.94 | 1.106 | 1.000 | 0.989 | -11 | -1.1 | 2.36 | 1.111 | 1.000 | 0.993 | -7 | -0.7 | |
| 4 | 1.233 | 1.084 | 1.082 | -2 | -0.2 | 3.5 | 1.254 | 1.103 | 1.097 | -6 | -0.5 | |
| 6 | 1.438 | 1.229 | 1.225 | -4 | -0.3 | 4.5 | 1.370 | 1.181 | 1.179 | -2 | -0.2 | |
| 8 | 1.633 | 1.353 | 1.355 | 2 | 0.2 | 5.5 | 1.479 | 1.254 | 1.253 | -1 | -0.1 | |
| 10 | 1.820 | 1.468 | 1.475 | 7 | 0.5 | 9 | 1.831 | 1.481 | 1.482 | 1 | 0.1 | |
| 12 | 2.000 | 1.579 | 1.587 | 8 | 0.5 | 11 | 2.021 | 1.593 | 1.599 | 6 | 0.4 | |
| 14 | 2.176 | 1.684 | 1.693 | 9 | 0.5 | 13 | 2.212 | 1.704 | 1.714 | 10 | 0.6 | |
| 18 | 2.511 | 1.880 | 1.889 | 9 | 0.5 | 16 | 2.482 | 1.860 | 1.872 | 12 | 0.7 | |
| 20.64 | 2.730 | 2.000 | 2.015 | 15 | 0.8 | 18.87 | 2.733 | 2.000 | 2.017 | 17 | 0.8 | |
 =35° =35° |
 =37° =37° |
|||||||||||
| Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | |
| 6.66 | 1.116 | 1.000 | 0.997 | -3 | -0.3 | 5.51 | 1.118 | 1.000 | 0.998 | -2 | -0.2 | |
| 8 | 1.192 | 1.055 | 1.053 | -2 | -0.2 | 8 | 1.268 | 1.107 | 1.107 | 0 | 0.0 | |
| 11 | 1.349 | 1.167 | 1.164 | -3 | -0.3 | 12 | 1.487 | 1.262 | 1.259 | -3 | -0.3 | |
| 14 | 1.495 | 1.265 | 1.264 | -1 | -0.1 | 15 | 1.639 | 1.359 | 1.359 | 0 | 0.0 | |
| 17 | 1.636 | 1.357 | 1.357 | 0 | 0.0 | 18 | 1.785 | 1.452 | 1.453 | 1 | 0.1 | |
| 20 | 1.772 | 1.445 | 1.445 | 0 | 0.0 | 20 | 1.879 | 1.511 | 1.512 | 1 | 0.1 | |
| 23 | 1.904 | 1.529 | 1.528 | -1 | -0.1 | 25 | 2.109 | 1.653 | 1.653 | 0 | 0.0 | |
| 29 | 2.164 | 1.686 | 1.686 | 0 | 0.0 | 29 | 2.287 | 1.759 | 1.758 | -1 | 0.0 | |
| 33 | 2.330 | 1.785 | 1.784 | -1 | -0.1 | 31 | 2.375 | 1.809 | 1.810 | 1 | 0.1 | |
| 37 | 2.495 | 1.883 | 1.880 | -3 | -0.2 | 35 | 2.551 | 1.908 | 1.912 | 4 | 0.2 | |
| 42.09 | 2.701 | 2.000 | 1.999 | -1 | -0.1 | 38.7 | 2.708 | 2.000 | 2.003 | 3 | 0.1 | |
 =35° =35° |
 =37° =37° |
|||||||||||
| Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | |
| 30.2 | 1.120 | 1.000 | 1.000 | 0 | 0.0 | 24.9 | 1.119 | 1.000 | 0.999 | -1 | -0.1 | |
| 40 | 1.242 | 1.092 | 1.089 | -3 | -0.3 | 35 | 1.257 | 1.099 | 1.099 | 0 | 0.0 | |
| 50 | 1.358 | 1.174 | 1.170 | -4 | -0.3 | 50 | 1.443 | 1.233 | 1.229 | -4 | -0.3 | |
| 60 | 1.469 | 1.249 | 1.246 | -3 | -0.2 | 65 | 1.617 | 1.347 | 1.345 | -2 | -0.2 | |
| 80 | 1.679 | 1.387 | 1.385 | -2 | -0.1 | 80 | 1.781 | 1.451 | 1.451 | 0 | 0.0 | |
| 90 | 1.778 | 1.451 | 1.449 | -2 | -0.2 | 90 | 1.885 | 1.517 | 1.516 | -1 | -0.1 | |
| 100 | 1.876 | 1.514 | 1.510 | -4 | -0.3 | 110 | 2.089 | 1.644 | 1.641 | -3 | -0.2 | |
| 120 | 2.067 | 1.635 | 1.627 | -8 | -0.5 | 130 | 2.286 | 1.764 | 1.758 | -6 | -0.4 | |
| 160 | 2.437 | 1.860 | 1.846 | -14 | -0.7 | 160 | 2.576 | 1.935 | 1.927 | -8 | -0.4 | |
| 186.5 | 2.676 | 2.000 | 1.984 | -16 | -0.8 | 171.9 | 2.689 | 2.000 | 1.992 | -8 | -0.4 | |
 =35° =35° |
 =37° =37° |
|||||||||||
| Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | |
| 1.4 | 1.086 | 1.000 | 0.999 | -1 | -0.1 | 0.93 | 1.072 | 1.000 | 0.989 | -11 | -1.1 | |
| 2.5 | 1.258 | 1.115 | 1.118 | 3 | 0.3 | 2 | 1.261 | 1.128 | 1.120 | -8 | -0.7 | |
| 4 | 1.444 | 1.239 | 1.241 | 2 | 0.1 | 3.5 | 1.476 | 1.273 | 1.261 | -12 | -0.9 | |
| 6 | 1.663 | 1.377 | 1.378 | 1 | 0.1 | 4.5 | 1.600 | 1.347 | 1.340 | -7 | -0.5 | |
| 8 | 1.873 | 1.497 | 1.504 | 7 | 0.5 | 6 | 1.770 | 1.451 | 1.443 | -8 | -0.5 | |
| 9.5 | 2.026 | 1.581 | 1.593 | 12 | 0.8 | 7 | 1.881 | 1.517 | 1.509 | -8 | -0.5 | |
| 11 | 2.169 | 1.661 | 1.673 | 12 | 0.8 | 9 | 2.095 | 1.634 | 1.632 | -2 | -0.1 | |
| 12.5 | 2.315 | 1.737 | 1.754 | 17 | 1.0 | 11 | 2.300 | 1.745 | 1.746 | 1 | 0.0 | |
| 14 | 2.459 | 1.814 | 1.832 | 18 | 1.0 | 13 | 2.500 | 1.846 | 1.854 | 8 | 0.4 | |
| 17.95 | 2.821 | 2.000 | 2.024 | 24 | 1.2 | 16.05 | 2.800 | 2.000 | 2.013 | 13 | 0.6 | |
 =35° =35° |
 =37° =37° |
|||||||||||
| Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | |
| 3.24 | 1.098 | 1.000 | 1.008 | 8 | 0.8 | 2.27 | 1.083 | 1.000 | 0.997 | -3 | -0.3 | |
| 6 | 1.279 | 1.131 | 1.132 | 1 | 0.1 | 4 | 1.229 | 1.105 | 1.098 | -7 | -0.6 | |
| 9 | 1.456 | 1.246 | 1.249 | 3 | 0.2 | 8 | 1.491 | 1.278 | 1.271 | -7 | -0.5 | |
| 12 | 1.621 | 1.348 | 1.353 | 5 | 0.3 | 10 | 1.610 | 1.352 | 1.346 | -6 | -0.5 | |
| 15 | 1.780 | 1.444 | 1.449 | 5 | 0.4 | 13 | 1.782 | 1.453 | 1.450 | -3 | -0.2 | |
| 19 | 1.977 | 1.561 | 1.565 | 4 | 0.2 | 15 | 1.891 | 1.518 | 1.515 | -3 | -0.2 | |
| 23 | 2.168 | 1.671 | 1.673 | 2 | 0.1 | 19 | 2.098 | 1.638 | 1.634 | -4 | -0.3 | |
| 27 | 2.356 | 1.773 | 1.776 | 3 | 0.2 | 23 | 2.299 | 1.750 | 1.745 | -5 | -0.3 | |
| 31 | 2.537 | 1.872 | 1.874 | 2 | 0.1 | 28 | 2.542 | 1.881 | 1.877 | -4 | -0.2 | |
| 36.47 | 2.781 | 2.000 | 2.003 | 3 | 0.1 | 32.8 | 2.771 | 2.000 | 1.998 | -2 | -0.1 | |
 =35° =35° |
 =37° =37° |
|||||||||||
| Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | Ta/(kN·m-1) | Fsj | Fsg | Fsg1 | Δ/(×10-3) | δ/% | |
| 14.6 | 1.091 | 1.000 | 1.003 | 3 | 0.3 | 10.3 | 1.085 | 1.000 | 0.998 | -2 | -0.2 | |
| 25 | 1.248 | 1.109 | 1.111 | 2 | 0.2 | 20 | 1.256 | 1.124 | 1.117 | -7 | -0.6 | |
| 40 | 1.452 | 1.243 | 1.246 | 3 | 0.2 | 35 | 1.477 | 1.268 | 1.262 | -6 | -0.5 | |
| 50 | 1.577 | 1.323 | 1.325 | 2 | 0.2 | 45 | 1.612 | 1.353 | 1.347 | -6 | -0.4 | |
| 70 | 1.813 | 1.468 | 1.469 | 1 | 0.1 | 60 | 1.804 | 1.470 | 1.464 | -6 | -0.4 | |
| 85 | 1.981 | 1.568 | 1.567 | -1 | -0.1 | 75 | 1.985 | 1.578 | 1.569 | -9 | -0.5 | |
| 95 | 2.090 | 1.632 | 1.629 | -3 | -0.2 | 90 | 2.159 | 1.678 | 1.668 | -10 | -0.6 | |
| 125 | 2.407 | 1.807 | 1.804 | -3 | -0.2 | 105 | 2.329 | 1.773 | 1.762 | -11 | -0.6 | |
| 140 | 2.560 | 1.892 | 1.886 | -6 | -0.3 | 120 | 2.495 | 1.863 | 1.851 | -12 | -0.6 | |
| 159.3 | 2.756 | 2.000 | 1.990 | -10 | -0.5 | 144.3 | 2.755 | 2.000 | 1.989 | -11 | -0.5 | |
分析表 3~表 11的数据可以得到如表 12所示的回归值Fsg1与规范法计算值Fsg的绝对误差Δ和相对误差δ的区间范围。此外,H=4 m的误差相对较大,且正误差较多,偏于危险;H=10 m的误差最小;H=50 m的误差大小居中,但基本都是负的,偏于安全。


| m | Fsg=1~2 | Fsg=1~1.5 | |||
| Δ/(×10-3) | δ/% | Δ/(×10-3) | δ/% | ||
| 0.5 | [-33, 30] | [-1.6, 1.5] | [-18, 13] | [-1.2, 0.8] | |
| 0.75 | [-16, 17] | [-1.1, 0.8] | [-11, 8] | [-1.1, 0.5] | |
| 1 | [-12, 24] | [-1.1, 1.2] | [-12, 12] | [-1.1, 0.8] | |
从表 12可知,当加筋粗粒土坡的简化Bishop法安全系数Fsg=1~2时,采用回归式(5)计算的安全系数Fsg1与Fsg的绝对误差Δ和相对误差δ的区间范围分别为Δ∈[-0.033, 0.03](近似地Δ≤±0.033),δ∈[-1.6%, 1.5%](近似地δ≤±1.6%),误差很小。考虑到现行公路规范[1, 18]规定的最高等级安全系数标准为Fsg≥1.45,对最高等级的加筋路堤边坡,设计的安全系数合理值应等于或略大于1.45,所以表 5中统计了Fsg=1~1.5范围内的Δ和δ,此时的Δ∈[-0.018, 0.013] (近似地Δ≤±0.018),δ∈[-1.2%, 0.8%](近似地,δ≤±1.2%),误差更小。所以采用式(5)计算加筋粗粒土坡的安全系数是可行的。
5 讨论工程中的粗粒土往往有较小的黏聚力c,根据笔者对新疆几种典型砾石土的大三轴试验结果,c≈0~10 kPa之间。现取c=10 kPa,分别计算了m=0.5,0.75,1且H=4 m(仅限m=0.5的边坡,m=0.75和1的边坡不加筋就能达到稳定要求), 10 m, 50 m,
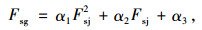
|
(6) |
式中,α1,α2,α3为拟合常数,见表 13。
| m=0.5 | m=0.75 | m=1 | ||||||||||||||||||
| H=4 m | H=10 m | H=50 m | H=10 m | H=50 m | H=10 m | H=50 m | ||||||||||||||
 =35° =35°
|
 =37° =37° |
 =35° =35° |
 =37° =37° |
 =35° =35° |
 =37° =37° |
 =35° =35° |
 =37° =37° |
 =35° =35° |
 =37° =37° |
 =35° =35° |
 =37° =37° |
 =35° =35° |
 =37° =37° |
|||||||
| α1 | -0.045 3 | -0.061 7 | -0.048 5 | -0.042 8 | -0.045 1 | -0.044 4 | -0.032 | -0.028 3 | -0.045 6 | -0.047 3 | -0.041 4 | -0.039 1 | -0.045 3 | -0.046 8 | ||||||
| α2 | 0.854 2 | 0.901 2 | 0.873 6 | 0.841 4 | 0.87 | 0.856 6 | 0.696 3 | 0.670 4 | 0.767 7 | 0.767 8 | 0.785 5 | 0.766 | 0.811 6 | 0.810 1 | ||||||
| α3 | 0.266 4 | 0.242 1 | 0.156 6 | 0.191 1 | 0.106 1 | 0.116 6 | 0.452 2 | 0.507 8 | 0.257 1 | 0.274 | 0.289 5 | 0.324 9 | 0.174 1 | 0.182 3 | ||||||
假定一个Fsj值,由式(6)计算出c=10 kPa的加筋边坡安全系数Fsg10,同时由式(5)计算出不考虑c的加筋边坡安全系数Fsg0,前者与后者之差β即为式(5)对安全系数的低估值。如此即可得到不同工况下的β-Fsg0曲线如图 7所示,图中β之后的4位数字中前两位表示坡高H,后两位表示土的内摩擦角 



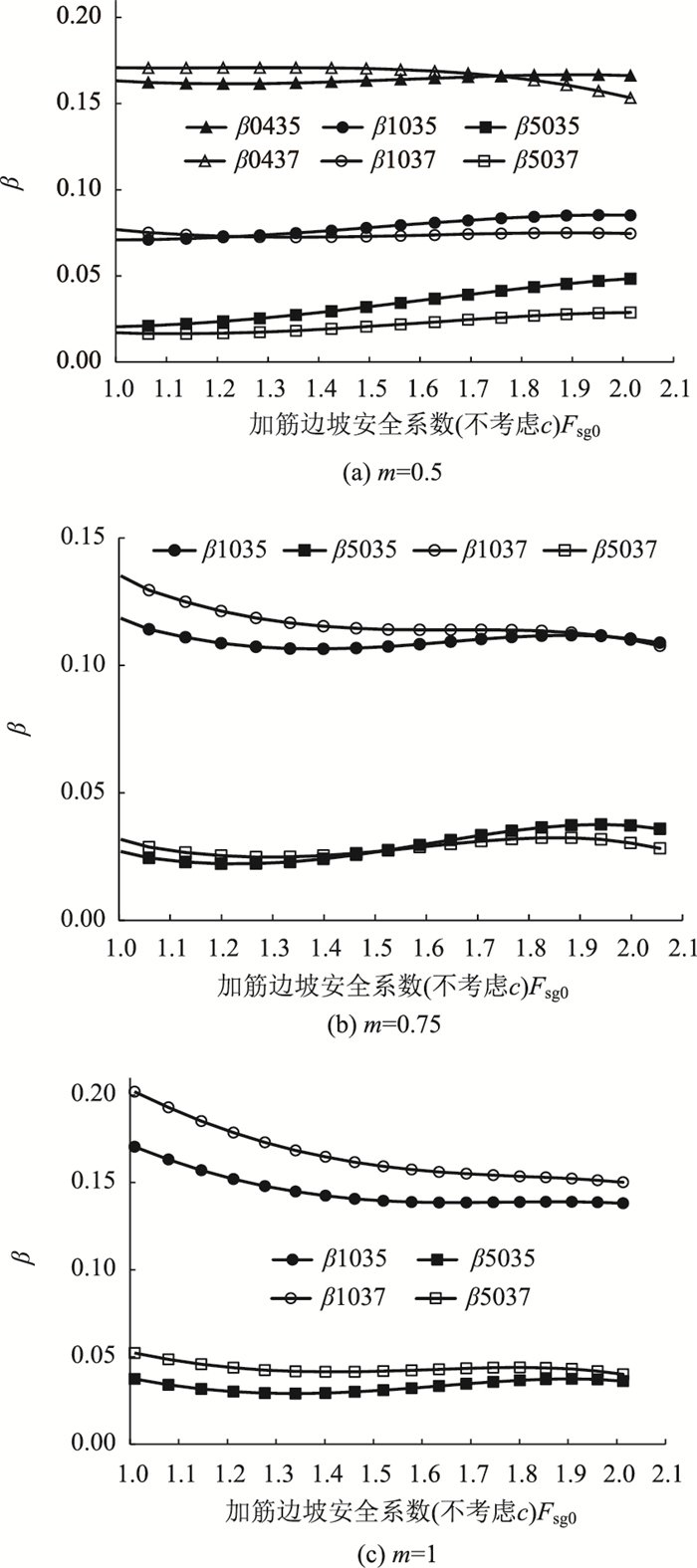
|
| 图 7 式(5)对安全系数Fsg的低估量β Fig. 7 Underestimation of Fsg by Eq. (5) |
| |
总之,由图 7可知,在Fsg=1~2, 
通过计算分析,有如下结论和建议:
(1) 土工合成材料加筋粗粒土坡安全系数Fsg与等代均质土坡的安全系数Fsj有良好的相关性,但二者在数值上有较大差别,不能直接用等代均质土坡的安全系数作为加筋粗粒土坡的安全系数。
(2) 提出的回归公式实现了将土工合成材料加筋粗粒土坡转化为等代均质土坡来计算稳定安全系数的目标,使计算工作大为简化。当简化Bishop法安全系数Fsg=1~2时,采用本文提出的回归公式计算的安全系数,其绝对误差Δ≤±0.033,相对误差δ≤±1.6%;当Fsg=1~1.5时,Δ≤±0.018,相对误差δ≤±1.2%,计算精度完全满足工程设计要求。
(3) 提出的土工合成材料加筋粗粒土坡安全系数计算方法适用于筋材发生拉断破坏而不是拔出破坏的情况,各层筋材必须有足够的锚固长度,这也正是设计时必须达到的要求,因此这并不影响该计算方法的适用性。但本文的方法没有涉及到每层筋材到底应取多长的问题,设计时可按现行国标[2]来确定各层筋材的设计长度。
| [1] |
JTG/T D32-2012, 公路土工合成材料应用技术规范[S]. JTG/T D32-2012, Technical Specifications for Applica-tions of Geosynthetics of Highway[S]. |
| [2] |
GB/T50290-2014, 土工合成材料应用技术规范[S]. GB/T50290-2014, Technical Code for Application of Geosynthetics[S]. |
| [3] |
FHWA NHI-10-024, Design and Construction of Mechanically Stabilized Earth Walls and Reinforced Soil Slopes[S].
|
| [4] |
郑颖人, 赵尚毅, 李安洪, 等. 有限元极限分析法及其在边坡工程中的应用[M]. 北京: 人民交通出版社, 2011, 2-6, 11-16. ZHENG Ying-ren, ZHAO Shang-yi, LI An-hong, et al. FEM Limit Analysis and Its Application in Slope Engineering[M]. Beijing: China Communications Press, 2011, 2-6, 11-16. |
| [5] |
介玉新, 李广信. 有限元法在加筋土结构设计中应用的必要性和可行性[J]. 长江科学院院报, 2014, 31(3): 34-38. JIE Yu-xin, LI Guang-xin. Necessity and Feasibility of FEM in the Design of Reinforced Soil Structure[J]. Journal of Yangtze River Scientific Research Institute, 2014, 31(3): 34-38. |
| [6] |
介玉新, 秦晓艳, 金鑫, 等. 加筋高边坡的稳定分析[J]. 岩土工程学报, 2012, 34(4): 660-666. JIE Yu-xin, QIN Xiao-yan, JIN Xin, et al. Stability of High Reinforced Soil Slopes[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(4): 660-666. |
| [7] |
陈祖煜, 宗露丹, 孙平, 等. 加筋土坡的可能滑移模式和基于库仑理论的稳定分析方法[J]. 土木工程学报, 2016, 49(6): 113-122. CHEN Zu-yu, ZONG Lu-dan, SUN Ping, et al. Investigation on Possible Failure Modes of Geotextile Reinforced Slopes and Stability Analysis Methods Based on Coulomb Theory[J]. China Civil Engineering Journal, 2016, 49(6): 113-122. |
| [8] |
DONALD I B, CHEN Z Y. Slope Stability Analysis by the Upper Bound Approach:Fundamentals and Methods[J]. Canadian Geotechnical Journal, 2011, 34(6): 853-862. |
| [9] |
胡幼常, 靳少卫, 宋亮, 等. 基于影响带观测的加筋土坡稳定性分析[J]. 岩土工程学报, 2017, 39(2): 228-234. HU You-chang, JIN Shao-wei, SONG Liang, et al. Stability Analysis of Reinforced Soil Slopes Based on Observation of Reinforcement-effected Strip[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(2): 228-234. |
| [10] |
ADAMS M T, SCHLATTER W, STABILE T. Geosynthetic Reinforced Soil Integrated Abutments at the Bowman Road Bridge in Defiance County, Ohio[C]//ASCE Geosynthetics in Reinforcement and Hydraulic Applications (GSP 165). Denver: ASCE, 2007: 119-129.
|
| [11] |
李广信. 地震与加筋土结构[J]. 土木工程学报, 2016, 49(7): 1-8. LI Guang-xin. Earthquake and Earth Reinforcement[J]. China Civil Engineering Journal, 2016, 49(7): 1-8. |
| [12] |
李广信, 陈轮, 蔡飞. 加筋土体应力变形计算的新途径[J]. 岩土工程学报, 1994, 16(3): 46-53. LI Guang-xin, CHEN Lun, CAI Fei. A New Approach to Analysis of Stress and Deformation of Reinforced Earth[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(3): 46-53. |
| [13] |
YANG Z. Strength and Deformation Characteristic of Reinforced Sand[D]. Los Angeles: University of California, 1972.
|
| [14] |
雷胜友. 现代加筋土理论与技术[M]. 北京: 人民交通出版社, 2006, 6-13. LEI Sheng-you. Theory and Technology of Modern Reinforced Soil[M]. Beijing: China Communications Press, 2006, 6-13. |
| [15] |
郭庆国. 粗粒土的工程特性及应用[M]. 郑州: 黄河水利出版社, 1998, 193-221. GUO Qing-guo. Engineering Properties and Applications of Coarse Grained Soil[M]. Zhengzhou: The Yellow River Water Conservancy Press, 1998, 193-221. |
| [16] |
唐善祥, 杜亮, 刘力, 等. 加筋土挡墙工程图集[M]. 2版. 北京: 人民交通出版社, 2015, 1-7. TANG Shan-xiang, DU Liang, LIU Li, et al. Drawings of Reinforced Soil Retaining Walls[M]. 2nd ed. Beijing: China Communications Press, 2015. |
| [17] |
JTG B01-2014, 公路工程技术标准[S]. JTG B01-2014, Technical Standard of Highway Engineering[S]. |
| [18] |
李广信. 高等土力学[M]. 北京: 清华大学出版社, 2004, 326-341. LI Guang-xin. Advanced Soil Mechanics[M]. Beijing: Tsinghua University Press, 2004, 326-341. |
| [19] |
包承纲, 丁金华, 汪明元. 极限平衡理论在加筋土结构设计中应用的评述[J]. 长江科学院院报, 2014, 31(3): 1-10. BAO Cheng-gang, DING Jin-hua, WANG Ming-yuan. Review on Limited Balance Theory Applied in the Design of Reinforced Soil Structures[J]. Journal of Yangtze River Scientific Research Institute, 2014, 31(3): 1-10. |
| [20] |
JTG D30-2015, 公路路基设计规范[S]. JTG D30-2015, Specifications for Design of Highway Subgrade[S]. |
| [21] |
JTG B02-2013, 公路工程抗震规范[S]. JTG B02-2013, Specification of Seismic Design for Highway Engineering[S]. |
 2018, Vol. 35
2018, Vol. 35
