扩展功能
文章信息
- 边超, 崔洪军, 刘召伟
- BIAN Chao, CUI Hong-jun, LIU Zhao-wei
- 收费公路费率与不同货类货车流量关系的灵敏度分析
- Analysis on Sensitivity of Relationship between Toll Rate and Traffic Volumes of Different Goods
- 公路交通科技, 2018, 35(2): 152-158
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(2): 152-158
- 10.3969/j.issn.1002-0268.2018.02.021
-
文章历史
- 收稿日期: 2017-07-28
2. 中国路桥工程有限责任公司, 北京 100011
2. China Road and Bridge Corporation, Beijing 100011, China
收费道路是公共产品,其收费费率的确定将影响货运者对路径进行选取,进一步影响该路径对应的各货类车的流量。合理的收费费率可优化社会资源配置、稳定市场秩序、促进交通流在路网内的均衡分布。因为运输货物种类具有多样性,且属性存在差异,所以它们对收费费率在灵敏程度上也存在差异,进而影响货运者对路径进行选择[1]。显然不同的收费费率影响各货类车流量在收费道路上的分配、货物的终端价格、鲜活程度、不同地区人群的消费习惯等,同时也是实施计重收费的关键。只有正确把握收费道路的收费费用与各货类车流量的相互关系,才能制订出合理的收费费率,并产生最大的运输效益,从而使产品生产者、运输企业、消费者、高速公路经营者等各利益相关方实现共赢局面,推进社会资源的合理利用[2]。
首先,针对目前已有货类展开聚类分析,获得大货类作为基础,提出货类属性的效用函数,再运用Logit模型得出同一OD对之间每条路径各货类货车的流量,建立其在各收费道路的均衡分布模型[3]。然后利用灵敏度分析法剖析收费公路费用与该路径上货类货车流量的关联性,提出建立在追求社会效益最大基础上分货类定费率的定价机制[4]。最后联系实际案例进行检验论证。
1 聚类分析聚类分析属于多元统计分类法,目标在于将聚类对象根据某一标准划分为几个类别,而这些类别主要根据数据特征进行区分[5]。由于聚类分析是对量化聚类对象的某种属性进行剖析和对获得数据进行分类的过程,因此,某一相同类里的对象非常类似,但是每个簇间的对象又有极大相异性[6]。本研究的目的是研究收费道路费率和各货类货车流量间的关系,因此选取的聚类变量指标应该反映两者之间的关系。以收费道路中每种货类货车的流量在收费费率变化后向不收费道路的转移率及费率重视程度(费率是货运人员选取路径时考虑的所有影响因素所占的比例)作为聚类变量指标[7]。接下来通过从天津到秦皇岛的唐津高速公路、沿海高速公路费率调整后,各货类货车流量是否会向与其平行的205国道转移的例子来解释聚类过程,在唐津高速的唐山主线收费站、沿海高速北戴河收费站和205国道设置调查点进行现场问卷调查。根据2010—2016年该高速公路交通流量统计数据和行业平时使用习惯及实际调查结果,运用Logit分离模型得到道路运输目前已有货类的转移率及费率重视程度,见表 1。
| 编号 | 货类名称 | 转移率/% | 费率重视程度/% | 编号 | 货类名称 | 转移率/% | 费率重视程度/% |
| 1 | 机械设备及电器 | 5 | 26 | 8 | 粮食 | 20 | 57 |
| 2 | 钢铁 | 10 | 29 | 9 | 有色金属 | 12 | 30 |
| 3 | 化工原料及制品 | 8 | 27 | 10 | 水泥 | 31 | 38 |
| 4 | 轻工、医药产品 | 18 | 50 | 11 | 木材 | 35 | 40 |
| 5 | 煤炭及制品 | 35 | 44 | 12 | 非金属矿 | 32 | 23 |
| 6 | 矿物性建筑材料 | 29 | 40 | 13 | 盐 | 22 | 49 |
| 7 | 农林牧渔业产品 | 15 | 53 | 14 | 其他 | 23 | 45 |
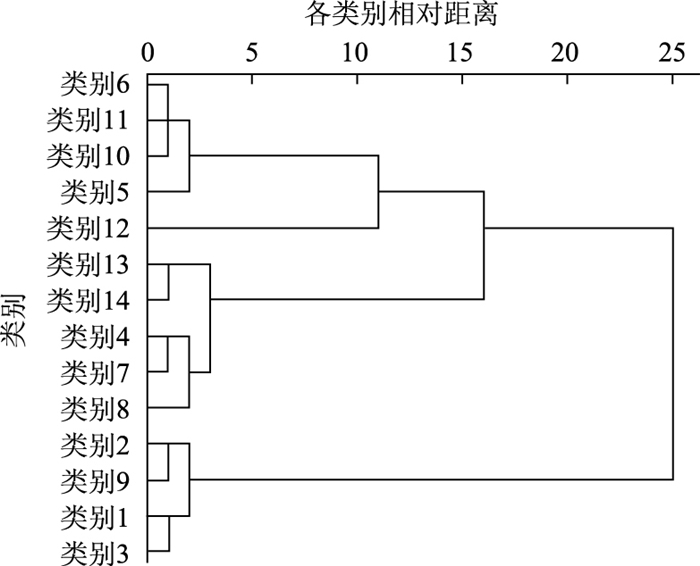
通过SPSS软件,使用系统聚类法中Q型聚类方法,通过聚类分析获得如图 1所示的聚类结果。
|
| 图 1 基于转移率和费率重视度的聚类结果 Fig. 1 Clustering result based on transfer rate and importance degree of toll rate |
| |
若划分为3类,那么以上聚类结果便可以调整成表 2。
| 聚类后货类代码 | A类 | B类 | C类 |
| 货类前货类代码 | 5, 6, 10, 11, 12 | 4, 7, 8, 13, 14 | 1, 2, 3, 9 |
2 考虑货物属性的均衡配流模型
货运人员对道路途径的选取属于决策规划的过程,也就是货运人员在整个货运过程中怎样对道路途径进行选取。他们所做的决定并非是任意而为,而是根据利益最大化准则,选取获益最高的那种路径作为第1路径[8]。换言之,每种不同的路径对他们的吸引程度或效用值都具有差异性[9]。吸引程度及效用值可根据量化来呈现,现实中影响效用值的因素很多且比较繁杂,主要通过确定以及随机两种效用值组成[10]。所以,如果在始发地和终点间存在n条路径,则第n条路径效用值Xn可表示为:

|
(1) |
式中,Xn为第n条路径效用值;αni为待定参数;kni为第n条路径的第i项路径属性值、费率、行程耗时、道路情况、安全性能等;δn为随机误差项。
在所有因素里,对货类车辆车流量处于各不相同路径分布起关键作用的就是通行费用。建立效用函数时应该基于分析每种类型货物属性来明确每个因素在其中的权重,这样方可更科学地阐述出行费用改变与每种货类车辆流量改变之间的关联性[11]。根据参考文献[8]里的效用函数定义方式,同时本研究核心目标在于依据货物属性来研究货类货车流量与通行费用间的关联性,另外因为每种路径在可靠程度、舒适程度及安全性能方面难以量化,所以这里着重分析通行费用及行程时间这2个因素。选用kn(A)和hn(A)代表通行费用及行程时间两个权重参变量,其值由货类经济特征及商品属性所决定,另外还可以体现货运人员基于货类特征时对这两个参变量的重视度,详细标定应结合统计数据采用Matlab进行迭代计算或试算法并参照文献[12]。所以考虑货物属性这类效用函数可以通过如下函数来表达:
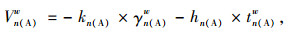
|
(2) |
式中γn(A)w,tn(A)w,kn(A),hn(A)依次为OD对w第n条路径针对A货类货车的收费、平均运行时间、对收费及时间的敏感参数。
根据以上对效用值的阐述,能够得出每条路径对每种货类效用值具有随机性。因此可以说货运人员对路径选取其实体现的是概率问题[13]。Logit分离模型在交通探索领域得到普遍运用,假设OD对已经存在的几条路径并且达到均衡状态货运流量时满足如下Logit分离模型[7]:
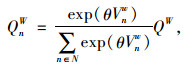
|
(3) |
式中,QnW为OD对w的第n条路径的货车流量;θ为待定参数;QW为OD对w的货车总流量; W为OD对之间的所有道路的集合。
货运人员选取路径过程中始终青睐普遍所说的费用最低这种路径,所以处于相同OD对间每条路径的货车流量能够实现均衡。根据参考文献[7]制定出如下数学规划模型(A):
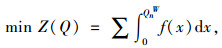
|
(4) |
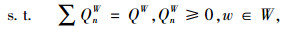
|
(5) |
式中f(x)为OD对w第n条路径货车运输广义费用函数,它存在幂数及对数两种形式,所以能够获得每类货车流量处于相同OD对间每条路径的不同分离模式。
3 灵敏度分析法灵敏度分析是指对系统或事物因周围条件改变所呈现出的敏感度展开的剖析。这种方法通常被运用于变分不等式里,利用此分析能够计算出不等式里扰动参变量的导数[14]。
因为本研究将重点放在每类货车流量与通行费用两者之间的关联性上,加之其他影响因素如舒适程度及安全性能等变量不能具体化,所以,在这里把相同OD对间每条路径的费率设置成扰动参数,而其余因素没有变化,并且每条路径每个特性指标持续改变[15]。
上述均衡配流模型(A)能够利用如下变分不等式来呈现:
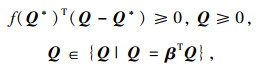
|
(6) |
式中Q*为模型(A)的均衡解,所有变量都通过列向量呈现,Q*=(Q1*, Q2*, …, QN*)T, Q=(Q1, Q2,…, QN)T, f(Q*)=(f(Q1*), f(Q2*),…,f(QN*))T, β=(β1, β2, …, βN)T,其中β=(1, 1,…,1)T代表维数是N元素都是1的列向量。由于f(Q)包含扰动参数γ=(γ1, γ2,…,γN)T的通常情况,所以f(Q, γ)将变成如下形式:
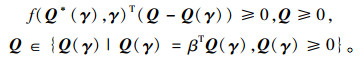
|
(7) |
假设已知上式在γ=γ0的解为Q*(γ0)(γ0为模型(A)均衡解Q*对应的变量),并且这个解唯一。根据文献[8],上式在γ=γ0时有解的必要条件为:
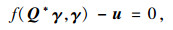
|
(8) |
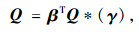
|
(9) |
式中u为有N个相同元素的拉格朗日乘子列向量。
设y(γ)=[Q(γ), u(γ)]T通过Jy(γ)来代表式(11)~(12)对于[Q, u]的雅克比矩阵,通过Jγ(γ)来代表式(8)~(9)对于γ的雅克比矩阵,参照文献[16]得出下面结论:
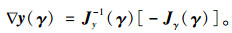
|
(10) |
按泰勒展开公式获得每个路径计重费率及对应货车流量间的近似关系如下:
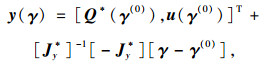
|
(11) |
式中Jy*,Jγ*分别为Jy(γ)(和Jγ(γ)在γ=γ(0)时的值。
根据以上计算,便能够获得每条路径计重费率及对应的货类货车流量间存在的近似关系。对γ进行调整便能够获得路径上的货车流量,然后进一步获得整个路网的收益值及车辆出行的整体耗时等指标。把所有指标值比较,根据“社会效益最大,分货类定费率”的准则定价便能够获得合理费率[17]。
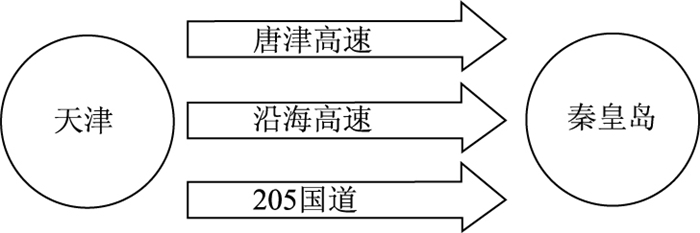
4 实例分析从天津到秦皇岛之间的主要公路有3条,其中一条是唐津高速,一条是沿海高速,另一条是205国道,图 2呈现的便是两地间3条收费路径简略图。结合本研究的实际调查,得到3条道路的A类运输货类中煤炭类占比例较大,且煤炭类货车有明显向国道转移的趋势。
|
| 图 2 天津到秦皇岛两地路径图 Fig. 2 Path between Tianjin and Qinhuangdao |
| |
3条路径对于煤炭类货车的效用函数如下:
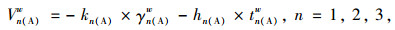
|
(12) |
式中,Vn(A)w为3条道路对A类煤炭类货车的效用值;tn(A)w为A类煤炭类货车处于3条高速时的行程时间;γn(A)w为3条道路对A类煤炭类货车的收费因素。
由于不同道路的通行费用不同,此时对应的A类煤炭货车广义费用函数使用幂函数形式,即:
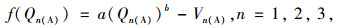
|
(13) |
式中Vn(A)为3条高速公路对于A类煤炭类货车的效用值;a, b为待定参数。
经交通调查得到天津-秦皇岛之间的A类煤炭类货车流量是23 000 veh/h,主要由以上3条道路分担,出行参数如表 3所示。
| 序号 | 路径名称 | 收费价格/元 | 行程时间/h |
| G1 | 唐津高速 | 105 | 3.5 |
| G2 | 沿海高速 | 90 | 4 |
| G3 | 205国道 | 40 | 6 |
结合参考文献[18],把效用函数和Logit分离模型里的待定参数进行假设,具体如表 4所示。
| 参数 | θ | k1 | k2 | k3 | h | a | b |
| 值 | 0.08 | 0.03 | 0.03 | 0.03 | 0.2 | 0.5 | 0.6 |
利用Logit分离模型获得煤炭类货车位于G1,G2,G3时流量比例依次是66.25%,8.32%,25.43%。通过灵敏度分析法获得煤炭货车流量对通行费用的变化率是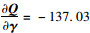
由此得到在这3条收费公路中A类煤炭类货车的不同流量的雅克比矩阵Jy(γ),Jγ(γ):
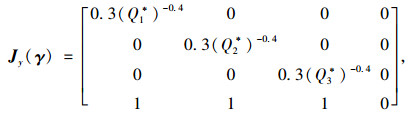
|
(14) |
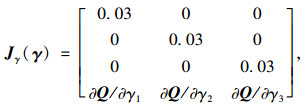
|
(15) |
式中γ1,γ2,γ3分别为唐津高速公路、沿海高速级205国道对A类煤炭类货车收费因素,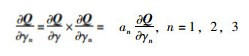
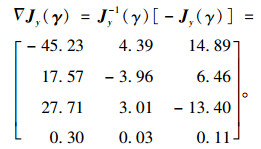
|
(16) |
通过上述关联式能够获得A类煤炭类货车流量与天津—秦皇岛两地间3条收费道路费率之间的近似关系为:
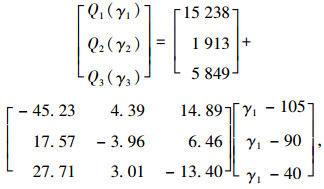
|
(17) |
式中Q1(γ1), Q2(γ2),Q3(γ3)分别为3条收费公路在考虑γ1,γ2,γ3取值时A类煤炭类货车的流量。
天津—秦皇岛之间3条收费道路对A类煤炭类货车的费率依次为-20,-10,0, 10, 20时,该类货车流量变化如表 5~表 7所示。
| 调整额 | γ1/元 | γ2/元 | γ3/元 | Q1/(veh·h-1) | Q2/(veh·h-1) | Q3/(veh·h-1) | 3条道路总收益/元 | 货车行程总耗时/h |
| -20 | 95 | 90 | 40 | 16 142.68 | 1 561.51 | 5 294.71 | 6 407 527 | 106 576.8 |
| -10 | 105 | 90 | 40 | 15 690.34 | 1 737.25 | 5 571.85 | 6 613 101 | 105 950.9 |
| 0 | 105 | 90 | 40 | 15 238.00 | 1 913.00 | 5 849.00 | 6 809 630 | 105 325 |
| 10 | 115 | 90 | 40 | 14 785.66 | 2 088.75 | 6 076.15 | 6 980 612 | 104 499.1 |
| 20 | 125 | 90 | 40 | 14 333.32 | 2 264.49 | 6 403.29 | 7 175 546 | 104 073.2 |
| 调整额 | γ1/元 | γ2/元 | γ3/元 | Q1/(veh·h-1) | Q2/(veh·h-1) | Q3/(veh·h-1) | 3条道路总收益/元 | 货车行程总耗时/h |
| -20 | 105 | 70 | 40 | 15 150.13 | 1 992.164 | 5 788.87 | 6 858 207 | 104 882.7 |
| -10 | 105 | 80 | 40 | 15 194.07 | 1 952.58 | 5 818.94 | 6 834 314 | 105 103.8 |
| 0 | 105 | 90 | 40 | 15 238.00 | 1 913.00 | 5 849.00 | 6 809 630 | 105 325 |
| 10 | 105 | 100 | 40 | 15 281.93 | 1 843.42 | 5 879.06 | 6 784 154 | 105 546.2 |
| 20 | 105 | 110 | 40 | 15 325.87 | 1 783.84 | 5 909.13 | 6 757 887 | 105 767.3 |
| 调整额 | γ1/元 | γ2/元 | γ3/元 | Q1/(veh·h-1) | Q2/(veh·h-1) | Q3/(veh·h-1) | 3条道路总收益/元 | 货车行程总耗时/h |
| -20 | 105 | 90 | 20 | 14 940.13 | 1 783.843 | 6 117.00 | 6 643 642 | 104 520.2 |
| -10 | 105 | 90 | 30 | 15 089.06 | 1 848.42 | 5 983.00 | 6 727 976 | 104 922.6 |
| 0 | 105 | 90 | 40 | 15 238.00 | 1 913.00 | 5 849.00 | 6 809 630 | 105 325 |
| 10 | 105 | 90 | 50 | 15 386.94 | 1 977.58 | 5 483.00 | 6 979 724 | 106 799.4 |
| 20 | 105 | 90 | 60 | 15 535.87 | 2 142.16 | 5 117.00 | 7 152 499 | 108 273.8 |
从表 5~表 7中能够发现,煤炭类货车总流量保持平稳,同一OD对中平行收费道路费率的升降会对其路径的选取造成影响。费率提高(降低),该路径的车流量会减少(增多),相应的其他平行道路的车流量会增多(减少)。费率调整越大,车流量变化越明显,进一步干扰货流量在整体路网的流量分配、收益值及货车行程总耗时等指标[19]。通过以上费率的调整范围能够计算出γ1=105,γ2=90,γ3=40时路网收益值最大、货车行程总耗时最小,社会效益最大。
5 结论(1) 对现有货类进行聚类分析得到大货类,提出了基于货类属性的效用函数,得到了基于货类属性的Logit模型。
(2) 通过灵敏度分析的方法分析了收费公路费率与该路径上各大货类货车流量的关系,提出了在社会效益最大化基础上分货类定费率的定价机制。
(3) 研究是从货类属性和车流量分配的角度建立模型得到最优费率的。随着货运市场的不断发展,货运定价机制也在不断完善。计重、各货类的经济车型、运输里程也应在优化费率中重点考虑。
| [1] |
潘艳荣, 邓卫. 不同交通方式服务可靠度与客流量间的灵敏度分析[J]. 武汉理工大学学报:交通科学与工程版, 2007, 31(5): 765-768. PAN Yan-rong, DENG Wei. Sensitivity Analysis for the Relationship between Reliability of Different Traffic Modes and Passenger Flow Volume[J]. Journal of Wuhan University of Technology:Transportation Science Engineer-ing Edition, 2007, 31(5): 765-768. |
| [2] |
冯妍, 李得伟. 基于Logit模型的城际运输通道客运量分担率计算研究[J]. 铁道运输与经济, 2016, 38(4): 46-49. FENG Yan, LI De-wei. Research on Passenger Traffic Volume Sharing Rate of Inter-city Transport Corridor Based on Logit Model[J]. Railway Transport and Economy, 2016, 38(4): 46-49. |
| [3] |
孙燕. 随机效应半参数Logit模型的惩罚似然估计研究[J]. 统计研究, 2013, 30(4): 10-15. SUN Yan. Penalized Likelihood Estimation for Semi-parametric Logit Model with Random Effects[J]. Statistical Research, 2013, 30(4): 10-15. |
| [4] |
熊文涛, 刘三阳, 李卫华. 一种基于灵敏度分析的多属性权值确定方法[J]. 武汉理工大学学报, 2004, 26(12): 92-95. XIONG Wen-tao, LIU San-yang, LI Wei-hua. A Method to Determine Multi-attribute Weights Based on Sensitivity Analysis[J]. Journal of Wuhan University of Technology, 2004, 26(12): 92-95. |
| [5] |
周嘉男, 何丹恒, 罗霞. 基于Logit模型的路径选择及交通流分配[J]. 大连交通大学学报, 2013, 34(2): 31-34. ZHOU Jia-nan, HE Dan-heng, LUO Xia. Research on Route Selection Survey Methodology and Traffic Assignment Based on Logit Model[J]. J ournal of Dalian Jiaotong University, 2013, 34(2): 31-34. |
| [6] |
姚丽亚, 孙立山, 关宏志. 基于分层Logit模型的交通方式选择行为研究[J]. 武汉理工大学学报:交通科学与工程版, 2010, 34(4): 738-741. YAO Li-ya, SUN Li-shan, GUAN Hong-zhi. Study on Modal Split Method Based on Nested Logit Model[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition, 2010, 34(4): 738-741. |
| [7] |
罗朝晖, 韦增欣, 王松华. 出行量预测不确定下基于灵敏度分析的拥挤收费定价模型[J]. 数学的实践与认识, 2013, 43(4): 17-25. LUO Chao-hui, WEI Zeng-xin, WANG Song-hua. Congestion Pricing Model Based on the Sensitivity Analysis under Uncertainty in the Travel Volume Forecast[J]. Mathematics in Practice and Theory, 2013, 43(4): 17-25. |
| [8] |
王丽, 朱吉双. 运量分布与交通配流组合问题灵敏度分析方法[J]. 数学的实践与认识, 2012, 42(8): 126-133. WANG Li, ZHU Ji-shuang. Sensitivity Analysis Approach for Combination Problem of Trip Distribution and Traffic Assignment[J]. Mathematics in Practice and Theory, 2012, 42(8): 126-133. |
| [9] |
李艳红, 袁振洲, 靳雄焕. 基于自由流时间的交通拥挤收费费率研究[J]. 公路交通科技, 2009, 26(6): 109-113. LI Yan-hong, YUAN Zhen-zhou, JIN Xiong-huan. Research on Traffic Congestion Tolling Rate Based on Free Flow Time[J]. |
| [10] |
曹毅, 魏连雨, 马士宾, 等. 基于Mixed Logit模型的土木系统可靠性检测[J]. 科技导报, 2013, 31(21): 26-29. CAO Yi, WEI Lian-yu, MA Shi-bin, et al. Reliability Analysis of Civil Systems Engineering Based on Mixed Logit Model[J]. Science & Technology Review, 2013, 31(21): 26-29. |
| [11] |
蔚欣欣, 陆化普, 李悦. 考虑用户风险态度的不确定离散交通网络设计模型[J]. 北京工业大学学报, 2013, 39(4): 582-586, 593. WEI Xin-xin, LU Hua-pu, LI Yue. Model and Algorithm of Discrete Network Design Problem Considering Risk Attitude of Users Under Uncertainty[J]. Journal of Beijing University of Technology, 2013, 39(4): 582-586, 593. |
| [12] |
周嘉男, 何丹恒, 罗霞. 基于Logit模型的路径选择及交通流分配[J]. 大连交通大学学报, 2013, 34(1): 31-34. ZHOU Jia-nan, HE Dan-heng, LUO Xia. Research on Route Selection Survey Methodology and Traffic Assignment Based on Logit Model[J]. Journal of Dalian Jiaotong University, 2013, 34(1): 31-34. |
| [13] |
陆化普, 李悦, 蔚欣欣. 供给与需求不确定的离散交通网络设计模型[J]. 东南大学学报:自然科学版, 2012, 42(6): 27-32. LU Hua-pu, LI Yue, WEI Xin-xin. Discrete Traffic Network Design Model under Supply and Demand Uncertainty[J]. Journal of Southeast University:Natural Science Edition, 2012, 42(6): 27-32. |
| [14] |
沈强. 基于高速公路收费数据的路网运行状态评价[J]. 公路交通科技, 2012, 29(8): 118-126. SHEN Qiang. Road Network Mobility Performance Evaluation Based on Freeway Toll Data[J]. Journal of Highway and Transportation Research and Development, 2012, 29(8): 118-126. |
| [15] |
徐婷, 陈志建, 程琳. 高速公路交通运行状态分类方法研究[J]. 中国科技论文在线, 2010, 5(10): 744-746. XU Ting, CHEN Zhi-jian, CHENG Lin. Research on Methods of Highway Traffic State Classification[J[J]. Sciencepaper Online, 2010, 5(10): 744-746. |
| [16] |
杨兆升, 王伟, 刘雪杰, 等. 公路网分车型收费费率优化算法研究[J]. 公路交通科技, 2008, 25(3): 119-123. YANG Zhao-sheng, WANG Wei, LIU Xue-jie, et al. Research on Optimal Algorithm of Toll Rate for Different Vehicle Types in Highway Network[J]. Journal of Highway and Transportation Research and Development, 2008, 25(3): 119-123. |
| [17] |
王芳, 吴群琪, 郭慧婷. 应对财务危机的收费公路费率优化方法[J]. 公路交通科技, 2017, 34(8): 152-158. WANG Fang, WU Qun-qi, GUO Hui-ting. A Highwsy Toll Rste Optimizstion Method sgsinst Finsncisl Crisis[J]. Journal of Highway and Transportation Research and Development, 2017, 34(8): 152-158. |
| [18] |
王建伟, 付鑫, 马暕. 复杂路网条件下高速公路收费费率计算方法[J]. 中国公路学报, 2010, 23(1): 105-110. WANG Jian-wei, FU Xin, MA Jian. Calculated Method of Expressway Toll Rate Under Condition of Complex Road Network[J]. China Journal of Highway and Transport, 2010, 23(1): 105-110. |
| [19] |
刘飞. 基于多因素分析的竞争性高速公路费率优化模型与方法改进研究[D]. 西安: 长安大学, 2010. LIU Fei. Research on Improvement of Competitive Expressway Toll-setting Optimization Model Based on Multi-factor Analysis[D]. Xi'an: Chang'an University, 2010. |
 2018, Vol. 35
2018, Vol. 35
