扩展功能
文章信息
- 李珣, 赵征凡, 刘瑶, 南恺恺
- LI Xun, ZHAO Zheng-fan, LIU Yao, NAN Kai-kai
- 车路协同下带诱导车速的单车道改进NS模型
- An Improved NS Model for Single Lane with Induce Speed under Situation of Cooperative Vehicle Infrastructure System
- 公路交通科技, 2018, 35(2): 101-108
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(2): 101-108
- 10.3969/j.issn.1002-0268.2018.02.014
-
文章历史
- 收稿日期: 2017-03-17
2. 西北工业大学 自动化学院, 陕西 西安 710068;
3. 解放军63961部队九室, 北京 100012
2. School of Automation, Northwestern Polytechnical University, Xi'an Shaanxi 710068, China;
3. Ninth Room of PLA 63961 Unit, Beijing 100012, China
城市交通信息的共享已在保证城市交通畅通、安全等方面做出了极大的贡献,出行者可以依靠各种交通软件获取城市道路流量情况,并进行出行规划[1]。出行者这种依靠动态信息进行自身车辆诱导控制的行为对减少城市交通拥堵、改善交通环境和提高道路使用率做出了一定的贡献。可以预见,随着交通信息网络的发展,基于信息共享的车路协同系统(Cooperative Vehicle Infrastructure System, CVIS)[2]将在未来服务城市交通。
交通信息共享环境发展中,车辆间信息的交互对交通流的影响是诸多机构研究的重点内容,近年来随着科学技术的快速发展,特别是计算机通讯、信息网络及自动控制装备等,个体车辆已经开始装备越来越多的车载智能信息和车辆自动控制设备,如:车载导航、自动巡航及自适应巡航设备等[3]。因此,作为交通组成的基础单元,厘清未来交通环境中车辆在诱导控制下所表现出的运行特点,根据可共享的基础车辆信息进行交通流模型研究,能够洞察未来城市交通路网中交通状态的微观变化。
交通流模型主要分为宏观和微观模型两大类[4],其中微观交通流模型主要用于描述微观交通现象[5],例如车辆的跟随、超车、换道等。交通流元胞自动机模型是一种经典的微观交通流模型,由于其描述微观交通现象能够使用简单的模型再现复杂的各种微观交通现象,同时精确地反映出微观交通流特性而被广泛作为基础模型,以进行各种特殊条件下微观交通流的研究, 其中NS模型是较为成功的元胞自动机模型。Nagel和Schreckenberg改进了Wolfram命名的184号基本TCA模型,增加了体现车辆运动存在的随机特性,在位置、速度更新规则上,扩展了车辆的速度值域。此后因不同交通环境特征,众多学者利用元胞自动机模型设计了反映微观交通现象的交通流模型,近年来主要集中于应对突发交通瓶颈的元胞自动机模型、偶发拥堵的传播规律[6]、瓶颈口拥堵消散的控制策略[7]等方面。根据不同道路结构特征的模型,分别有以多车道换道合理策略为目标的[8-9]、以快速路匝道分流、合流控制为研究对象的元胞自动机模型[10-12]。除了以交通环境和交通参与者本身作为特征对象进行研究外,许多学者将天气因素也纳入影响因素,进行了雨、雪等特征天气情况下的微观交通流建模[13]。
综上所述,利用元胞自动机基本模型进行特征环境条件下的改进,已经成为微观交通流模型研究的主流方法之一,并且形成了卓有成效的研究成果。但是,上述研究均以当前实际交通环境中面临的问题作为研究对象进行特征分析和建立模型,为数不多的车路协同条件下的交通流模型研究多集中于交叉口协同控制问题[14-15]、多车道换道规则研究[16-17]等。因此对于车路协同交通环境下单车道车辆CA模型的研究尚为一个较新的研究点,构成具有合理性、可靠性的微观交通流模型是未来交通智能控制所需的基础模型。所以,本研究基于车路协同条件,根据车辆交互基本信息,分析在此环境中的车辆诱导车速获取方式及其交通流规律,建立车路协同条件下带诱导车速的单车道微观交通流模型,并进行数值模拟和分析。
1 NS模型及跟车改进模型 1.1 单车道环境建模将目标单车道路段分为若干个等长度的小格子,每小格代表 1个元胞。左上角的序号作为当前占据该位置的车辆编号,右下角序号为该小格中车辆的速度,每个元胞在t时刻具有空置或被车辆占据两种状态,如图 1所示。

|
| 图 1 单车道车辆位置、速度示意图 Fig. 1 Schematic diagram of single lane vehicle locations and speeds |
| |
以vi(t)和xi(t)表示第i辆车Ci(车流方向由左向右,车辆编号依次增大)在t时刻的速度、位置,di, i-1(t)表示车辆Ci车头与Ci-1的车尾的间距,vmax为路段限制的最大速度,则速度取值vi∈[0, vmax],同时引入参数pdec来表示车辆的随机减速概率,随时间步长得出每一时刻路段中车辆的速度分布,根据速度与当前时刻位置对下一时刻车辆的位置进行推导。
1.2 基于跟车行为的改进NS模型NS模型全称Nagel-Schreckenberg模型,于1992年提出。当以vmax作为某路段车辆最大速度时,车辆速度取值范围为[0, vmax],同时NS模型中还引入了表征车辆运行具有随机性的随机慢化规则,更为真实地还原交通流特征,使其成为元胞自动机模型具有突破性研究的成果之一。虽然NS模型能够更好地描述实际交通现象,但是由于数值模拟中获得的平均车头间距大于实际值,且安全间距条件采用较为严格的防碰撞条件,所以仿真结果中获得的最大交通量不能与实测数据相匹配,同时未能描述出临界点位置的亚稳态性质。针对这些问题,改进的单车道交通流模型中,基于跟车行为的单车道元胞自动机模型是一种更能反映现实中交通流的特征元胞自动机模型[17]。
本研究将基于跟车行为的元胞自动机模型简称为NS-F模型。在NS-F模型规则描述中,在前述描述符号基础上,增加车辆Ci在t时刻时的加速度为acci,减速度为deci,以及安全驾驶参数k。以选定车流队列中第i辆车为例,NS-F模型的更新规则如下。
(1) 加速规则:
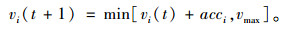
|
(1) |
(2) 减速规则:
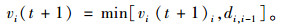
|
(2) |
(3) 随机慢化:
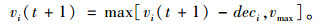
|
(3) |
(4) 位置更新:
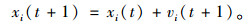
|
(4) |
(5) 行驶空间更新规则:
继续向后搜索到Ci+1辆车,如果Ci+1编号i+1不为设定车辆数a,则对车辆Ci+1前的行驶空间进行更新,如式(5)所示,然后对车辆Ci+1进行状态更新。
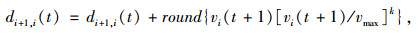
|
(5) |
式中,round表示对括号内数字的取整操作,体现了跟车行为中相对运动的影响,通过调节安全驾驶参数k值改变驾驶员的保守程度和主观安全距离的大小。
当Ci+1的编号就是设定车辆数a时,则代表本次迭代更新过程的结束,需要对每辆车的行驶空间进行更新,如式(6)所示,然后进入t+1时刻的更新进程:
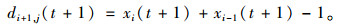
|
(6) |
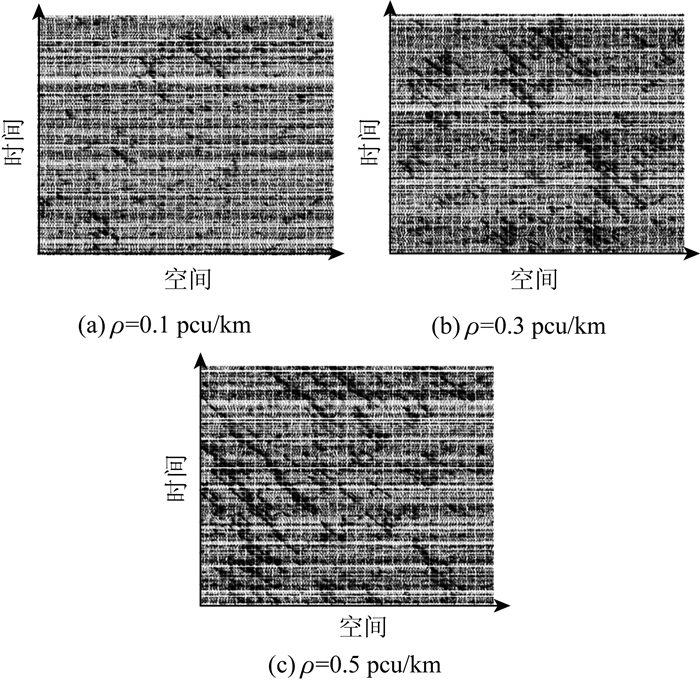
通过增加行驶更新规则,NS-F模型结合了实际跟车行为中车辆的相对运动和安全驾驶条件,得出更加符合实际数据的仿真流量,并能够描述系统在临界密度附近的亚稳态性质。本研究对NS-F模型进行了仿真复现,设置单个元胞长度为cell=5 m,单车道长度n=400 cell=2.0 km,最大速度vmax=4 cell/s=72 km/h;随机慢化概率pdec=0.2。分别设置道路车流密度ρ为0.1,0.3,0.5 pcu/km,获得单车道交通流模型时空图,如图 2所示。
|
| 图 2 NS-F交通流模型时空图 Fig. 2 Space-time diagram of NS-F traffic flow model |
| |
图 2中标出了时间和空间演化方向,深色部分表现出当前区域车辆密度较大,称为阻塞相;浅色区域则表示该位置车流密度较小,称为自由相。从图 2中可以看出,阻塞相随车流密度的增大而增多,同时在图 2(a)中,仅在0.1 pcu/km的车流密度条件下仍然存在阻塞相,说明NS-F模型中随机慢化很好地表征了实际道路中阻塞相发生的随机性,具有更加优良的微观交通流特性描述能力。
2 基于诱导车速的改进NS模型由当前车路协同系统发展及车载智能设备现状可知,当存在车辆运行诱导信息时,机动车行驶过程中,在摆脱前向视野约束的同时,速度控制过程中包含了道路远端车辆对本车的扰动。因此,车路协同下诱导信息的引入对车辆运行主要存在以下影响:可获知前向车辆下一时刻信号传递周期内的运动趋势;可获知上一时刻后方车辆保持运动趋势下的状态;除能够根据前后车辆对本车速度进行诱导控制外,还能根据道路远端车辆运行状态对本车状态进行控制。所以,该方法能够根据全局车辆运行状态减少车辆盲目加速和紧急刹车的频次,从而保障道路的顺畅及车辆运行的安全和高效性。
2.1 车路协同下基本交互信息及条件假设在车路协同的条件下,车辆可交互的车辆运动基本信息至少包括车辆速度、加速度,以及获取当前行驶路段的局部信息,如路段当前车辆密度、运行前方阻塞状况和局部路段的平均速度等。本研究以城市道路为交通流研究环境,因此车辆模型以中、小型车辆为主,此类车型存在以下外形及运动特征:
车辆外形(长、宽):Clength≤5 m, Cwidth≤2 m;
加速度:0.4g≤a≤0.8g, g=9.8 m/s;
减速度:-1.2g≤a≤-0.8g, g=9.8 m/s。
因此,在假设信息交互频率为1 Hz的条件下可知,在车辆加、减速度信息更新频率和时间内,位置变化范围如下。
加速过程位置变化范围:2 m≤xi(t+1)-xi(t)≤4 m;
减速过程位置变化范围:4 m≤xi(t+1)-xi(t)≤5 m。
由上述假设条件可知,在极端加减速过程中,若设定元胞格表征5 m的道路距离,车辆位置变化均小于等于1个元胞格,因此,与复现NS模型中元胞表征道路长度相同,本研究设置单个元胞长度cell=5 m。
2.2 车路协同下诱导车速根据NS模型中的位置更新规则可知x(t+1)=xi(t)+vi(t),即t+1时刻的车辆位置与其t时刻的位置和速度相关,所以当存在车路协同条件时,t时刻的车辆速度与前后车辆和全局路况相关。设vg(t)为t时刻第i辆车的诱导车速,加速度acci与NS-F模型设定相同,且包含加速度分量,具体获得方式和对应路况如下。
(1) 基于前向车辆运动趋势的诱导车速
在当前车路协同技术尚未实现的路况条件下,前车的运动仅仅依靠驾驶员的经验判断,因此会造成一定的加速延迟,这对于道路的高效利用存在提升的空间。本研究基于车辆速度信息可交互假设,得到在前车运动趋势可知条件下观察车Ci的诱导速度公式:
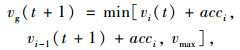
|
(7) |
即观察车的车速与前车下时刻加速趋势相关联,达到同步加速的效果。
(2) 基于后向车辆运动趋势的诱导车速
在可获得车辆交互信息的条件下,车辆运行过程中可采取主动加速的运动规则,在保证运动同步的同时避免追尾事故的发生,在获得后向车辆运行趋势的条件下诱导车速需满足:
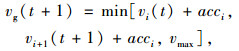
|
(8) |
即观察车在车路协同条件下,同样可以做到与后车加速趋势相关联。
(3) 基于临近阻塞点的诱导车速
当车流密度高于临界值后,道路阻塞点的产生不可避免,即使在自由流密度的状况下,阻塞点依然有可能产生。这使得车辆在道路中处于走走停停的状态,如果能够对前往阻塞点位置的车辆给予早期的速度指导,那么,均匀的减速和加速过程使道路畅通性、车辆燃油经济性和环保都将得到提高。所以在车路协同条件下,提出基于临近阻塞点的车速调节规则。
借鉴文献[18]中搜索阻塞点的方法,若满足式(9)条件,且阻塞车辆数m≥3,则判定该处存在阻塞点,并设置阻塞点中最后的车辆为阻塞点参考位置处vjam_i(t)=vi(t)。
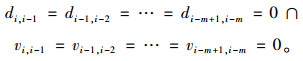
|
(9) |
统计阻塞点包含的车辆数m,按照符合实际情况的慢启动原则[19],处于阻塞点位置的首车启动速度及阻塞点内的启动速度均应为1个元胞距离,阻塞点消散时间为tjam=m-1个仿真步长,所以对应未到达阻塞点的后续车辆,给予的诱导车速值为:
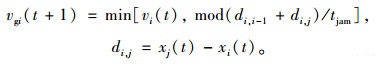
|
(10) |
在车路协同条件下进行诱导车速的获取,通过式(7)(10)能够将车辆速度的变化与前车、后车速度及前方道路的拥堵状况相关联,有效减少道路中走走停停的车辆状态,提高路段中的同步相。与NS-F模型中采用同样的行驶空间更新规则,本研究带诱导车速的改进NS模型NS-S的更新规则如下。
(1) 基于前后车速度的加速规则:
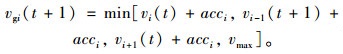
|
(11) |
(2) 基于临近阻塞点的减速规则:
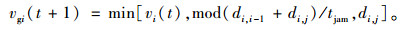
|
(12) |
(3) 随机慢化:
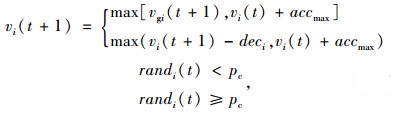
|
(13) |
式中,pc为遵守诱导车速的概率;randi(t)为车辆Ci在随机慢化迭代步产生随机数,取值[0, 1]。
(4) 位置更新:
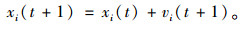
|
(14) |
在Matlab仿真环境建立的单车道试验环境中,对NS模型、基于跟车行为的模型及本研究车路协同下的单车道模型进行对比分析。在模拟中,车辆密度ρ=n/L,n为仿真车道长度为L的道路中车辆数,仿真道路长度为L=2 km,由400个格点组成。最大车速按照我国城市道路同方向只有1条机动车道的道路限速50 km/h进行近似取值,且为了简化数值模拟的计算,选取vmax=3 cell/s=54 km/h,其余参数说明如上文所述。模拟时间为10 000个仿真步长,初始车速按照0-vmax随机分布于道路中。为减少初始分布的影响,模拟结果的数据统计范围为5 000~10 000个步长范围内。
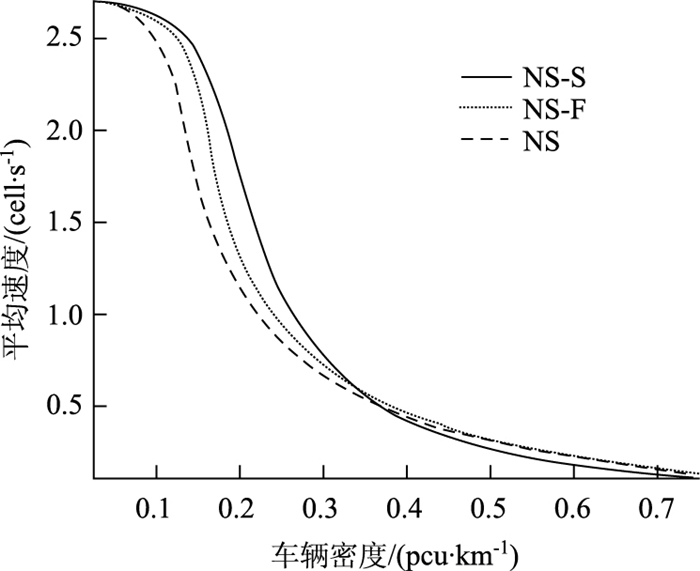
3.1 速度与流量在数值模拟中,将本研究提出的NS-S模型与NS模型和文献[15]中提出的基于跟车行为的改进模型NS-F进行不同密度下车流平均速度和车流量的比较,获得速度基本图(图 3)和流量基本图(图 4)。
|
| 图 3 单车道速度基本曲线 Fig. 3 Basic curves of single lane speed |
| |
|
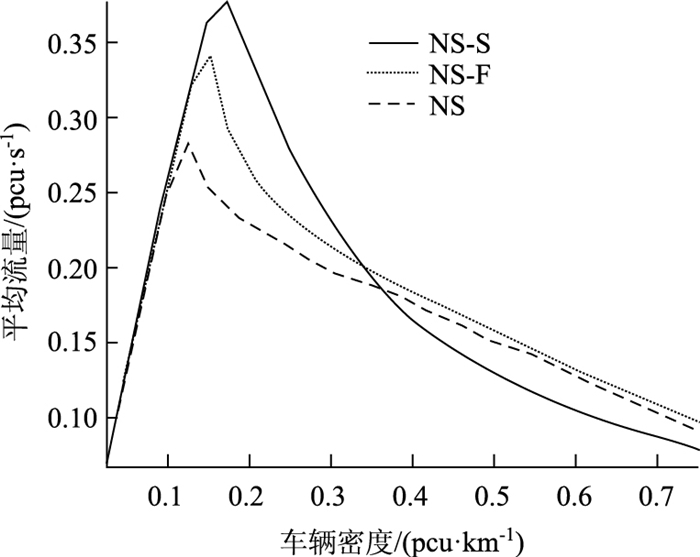
| 图 4 单车道流量基本曲线 Fig. 4 Basic curves of single lane traffic volume |
| |
在图 3中,当车流密度增加时,在密度值约为0.325 pcu/km之前,提出的改进NS模型速度平均值优于其他两种模型。这是因为,在较低的车流密度下,NS-S模型中车辆按照诱导车速行驶易于趋于同步,减少了随机慢化过程中的停车起步次数,同时阻塞点消散时间小于上游车辆到达所需时间,减少了上游车辆因阻塞点而产生的减速、启停行为,所以道路车辆趋于一个较优的平均速度。而当车流密度值大于0.325 pcu/km时,由于阻塞点的增多,造成阻塞点车辆消散时间大于上游车辆到达时间,NS-S模型中较多的同步相产生,上游车辆为符合临近阻塞点所供给的诱导车速,导致车辆平均速度随阻塞点的增多而急剧下降,使得对应中高密度的平均车速小于NS-F模型值,当密度值大于0.375 pcu/km时,改进NS模型获得的平均车速甚至小于NS经典模型。对应流量基本图(图 4)表现出同样变化趋势。
3.2 时空图分析根据道路流量图中3种模型的基本曲线,取差别最大位置的车流密度0.175,观察其时空图,如图 5所示。

|
| 图 5 三种元胞自动机时空图对比 Fig. 5 Comparison of space-time diagrams under 3 cellular automata |
| |
从图 5可明显看出,在密度值为0.175时,改进的NS-S模型在随机进入车辆的情况下,车辆慢慢趋于同步,比较图 2中NS-F严重的阻塞相,本研究模型表现出良好的车辆同步特征,说明在信息交互的条件下,对车辆进行有效的引导可以改变道路车辆运行的方式,保证车辆随道路密度同步加减速,有效减少启停状态的产生。
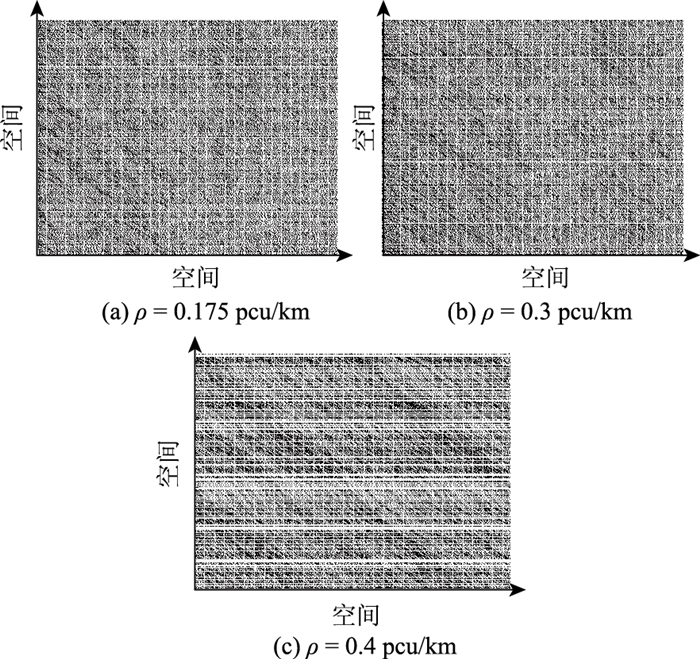
从图 6可以看出,当车流密度增至0.4 pcu/km时,由于阻塞点的增加,迫使每个阻塞点上游车辆进行早期减速造成路段平均速度和流量的下降,且出现较为规律的阻塞相,所以造成当车流密度增加时,平均速度和车流量表现出劣于NS和NS-F两种模型的情况。
|
| 图 6 不同车流密度下时空图对比 Fig. 6 Comparison of space-time diagrams under different traffic flow densities |
| |
3.3 诱导车速遵守率分析
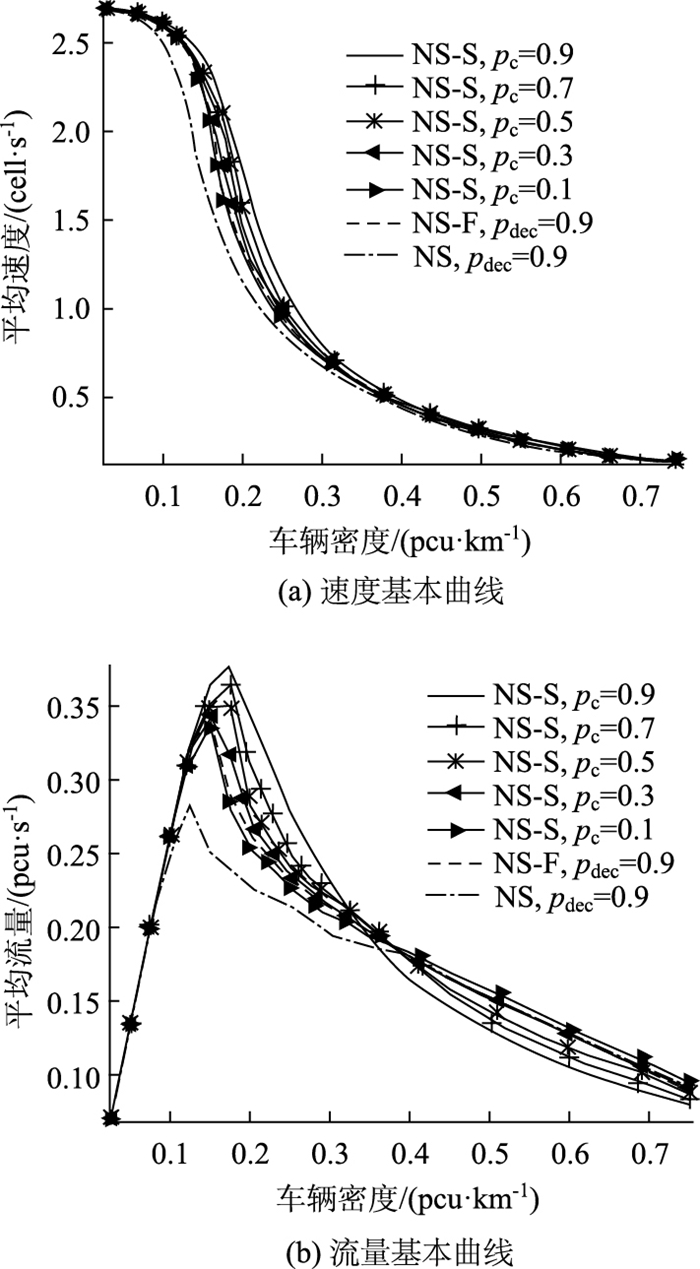
在当前交通环境中,车辆的控制主要依靠人工手段,因此在车路协同信息共享初期,诱导车速的遵守在一段时期内同样是依靠驾驶员来完成的,因此本研究根据不同的遵守情况对不同遵守率下的速度、流量与车辆密度关系进行了分析。诱导车速遵守率取值pc=0.9, 0.7, 0.5, 0.3, 0.1获得不同遵守率下平均车速和平均流量与车辆密度的关系,如图 7所示,设NS模型和NS-F模型随机慢化概率pdec=0.9。
|
| 图 7 不同诱导车速遵守率下单车道速度、流量基本曲线 Fig. 7 Basic curves of single lane speed, traffic volume under different induce speed compliance rates |
| |
观察图 7(a)可以发现,在诱导车速的高遵守率(0.9, 0.7),且在车辆密度小于0.4 pcu/km时,带诱导的车辆平均车速和平均流量是优于NS-F模型中描述的当前微观交通流状况的。对比不同遵守率所对应的平均速度基本图,遵守率越低则微观交通流表现出的状态越接近于NS-F模型。当遵守率为0.3时,平均车速趋于NS-F模型,在车辆密度大于0.4 pcu/km时,其平均速度劣于NS-F模型。分析可知,当驾驶员自主判断和车速诱导混乱使用时,在车辆密度较大的道路中会造成更为严重的拥堵状况。当遵守率仅为0.1时,这种混乱造成的附加拥堵更甚,因此NS-S微观交通流模型表现出更差的平均车速和平均流量。
除图 7(a)中不同遵守率所表现出的不同交通流状态外,从图 7(b)可以看出,随着遵守率的下降,最大流量对应的车辆密度区间也在遵守率为0.5时发生变化。因此,当诱导车速遵守率低时,车路协同所提供的共享信息将失去其改善交通状态的能力。在过低的遵守率(0.3)情况下,共享信息反而会加剧路段拥堵情况的产生。
4 结论车路协同下的车辆信息共享将会是改进城市交通拥堵状况的有力手段,因此本研究从影响车辆运行的基本运动信息出发,分析了单车道交通环境中车辆之间相互影响所必须的基本交互信息。根据当前实际道路中影响车辆运行的前后车、阻塞点与车辆位置等影响特征,基于元胞自动机模型建立了不同车辆影响状态的诱导车速模型。通过引入诱导车速,改进了NS模型中的速度更新规则,对车路协同下的单车微观交通流环境进行了建模。数值模拟结果表明,在小于0.4 pcu/km的车辆密度和较高的诱导车速遵守率条件下,车路协同环境能够提高单车道的平均车速和平均流量。当车辆密度大于0.425 pcu/km时,单车道路况下NS-S模型中的微观交通流状态将劣于描述当前交通流的NS-F模型。上述结论说明,本研究提出的NS-S车路协同下的单车道微观交通流模型,能够较好地解析未来信息交互交通环境中交通流的变化情况,能够为交通智能化建设提供一定的理论基础。
| [1] |
段宗涛, 康军, 唐蕾, 等. 车联网大数据环境下的交通信息服务协同体系[J]. 长安大学学报:自然科学版, 2014, 34(2): 108-114. DUAN Zong-tao, KANG Jun, TANG Lei, et al. Traffic Information Service Cooperation Architecture Based on Vehicular Network Big Data[J]. Journal of Chang'an University:Natural Science Edition, 2014, 34(2): 108-114. |
| [2] |
杨澜, 马佳荣, 赵祥模, 等. 基于车路协同的高速公路车辆碰撞预警模型[J]. 公路交通科技, 2017, 34(9): 123-129. YANG Lan, MA Jia-rong, ZHAO Xiang-mo, et al. A Vehicle Collision Warning Model in Expressway Scenario Based on Vehicle-infrastructure Cooperation[J]. Journal of Highway and Transportation Research and Development, 2017, 34(9): 123-129. |
| [3] |
华雪东, 王玮, 王昊. 考虑车与车互联通讯技术的交通流跟驰模型[J]. 物理学报, 2016, 65(1): 44-55. HUA Xue-dong, WANG Wei, WANG Hao. A Car-following Model with the Consideration of Vehicle-to-vehicle Communication Technology[J]. Acta Physica Sinica, 2016, 65(1): 44-55. |
| [4] |
李志林, 邱红桐, 封春房, 等. 基于路网分层的协同诱导路径搜索算法[J]. 公路交通科技, 2017, 34(1): 143-148. LI Zhi-lin, QIU Hong-tong, FENG Chun-fang, et al. A Cooperative Guidance Path Searching Algorithm Based on Hierarchical Road Network[J]. Journal of Highway and Transportation Research and Development, 2017, 34(1): 143-148. |
| [5] |
TANG T Q, SHI W F, SHANG H Y, et al. An Extended Car-following Model with Consideration of the Reliability of Inter-vehicle Communication[J]. Measurement, 2014, 58(11): 286-293. |
| [6] |
龙建成. 城市道路交通拥堵传播规律及消散控制策略研究[D]. 北京: 北京交通大学, 2009. LONG Jian-cheng. Research on Traffic Congestion Propagation and Dissipation Control Strategies in Urban Roads[D]. Beijing: Beijing Jiaotong University, 2009. |
| [7] |
张敖木翰, 高自友, 任华玲. 突发事故下交通拥堵控制策略[J]. 中国科学:技术科学, 2011(7): 955-961. ZHANG Ao-mu-han, GAO Zi-you, REN Hua-ling. Incident-based Traffic Congestion Control Strategies[J]. Scientia Sinica:Technologica, 2011(7): 955-961. |
| [8] |
李珣, 曲仕茹, 夏余, 等. 车路协同环境下多车道车辆的协同换道规则[J]. 中国公路学报, 2014, 27(8): 97-104. LI Xun, QU Shi-ru, XIA Yu, et al. Cooperative Lane-changing Rules on Multilane under Condition of Cooperative Vehicle and Infrastructure System[J]. China Journal of Highway and Transport, 2014, 27(8): 97-104. |
| [9] |
MARZOUG R, EZZAHRAOUY H, BENYOUSSEF A. Cellular Automata Traffic Flow Behavior at the Intersection of Two Roads[J]. Physica Scripta, 2014, 89(6): 065002. |
| [10] |
熊胜辉, 李星毅, 施化吉. 基于元胞自动机的快速路交织区交通流仿真建模[J]. 计算机应用, 2010, 30(2): 551-554. XIONG Sheng-hui, LI Xing-yi, YI Hua-ji. Traffic Modeling and Simulation of Expressway Weaving Area Based on Cellular Automata[J]. Journal of Computer Applications, 2010, 30(2): 551-554. |
| [11] |
张存保, 冉斌, 梅朝辉, 等. 车路协同下道路交叉口信号控制优化方法[J]. 交通运输系统工程与信息, 2013, 13(3): 40-45. ZHANG Cun-bao, RAN Bin, MEI Zhao-hui, et al. An Optimization Method of Traffic Signal Control Based on Cooperative Vehicle Infrastructure System[J]. Journal of Transportation Systems Engineering and Information Technology, 2013, 13(3): 40-45. |
| [12] |
梅超群, 黄海军, 唐铁桥. 城市快速路系统的元胞自动机模型与分析[J]. 物理学报, 2009, 58(5): 3014-3021. MEI Chao-qun, HUANG Hai-jun, TANG Tie-qiao. Modeling Urban Expressway Systems with Ramps and Accessory Roads by Cellular Automaton Model[J]. Acta Physica Sinica, 2009, 58(5): 3014-3021. |
| [13] |
GOODALL N J, SMITH B L, PARK B. Traffic Signal Control with Connected Vehicles[J]. Transportation Research Record, 2013, 2381: 65-72. |
| [14] |
赵韩涛, 聂涔, 李静茹. 冰雪条件下的交通流元胞自动机模型[J]. 交通运输系统工程与信息, 2015, 15(1): 87-92. ZHAO Han-tao, NIE Cen, LI Jing-ru. Cellular Automaton Model for Traffic Flow under Ice and Snowfall Conditions[J]. Journal of Transportation System Engineering and Information Technology, 2015, 15(1): 87-92. |
| [15] |
江金胜, 董力耘. 基于元胞自动机模型的C型交织区交通流特性[J]. 力学学报, 2012, 44(6): 996-1004. JIANG Jin-sheng, DONG Li-yun. Investigation on Traffic Flow Characteristics around a Type C Weaving Section Based on Cellular Automaton Model[J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(6): 996-1004. |
| [16] |
常浩. 车路协同下的车辆换道驾驶辅助方法研究[D]. 北京: 北京交通大学, 2015. CHANG Hao. Research on Vehicle Lane Changing Driving Assistant Method under Vehicle-road Coordination[D]. Beijing: Beijing Jiaotong University, 2015. |
| [17] |
敬明, 邓卫, 王昊, 等. 基于跟车行为的双车道交通流元胞自动机模型[J]. 物理学报, 2012, 61(24): 323-331. JING Ming, DENG Wei, WANG Hao, et al. Two-lane Cellular Automaton Traffic Model Based on Car Following Behavior[J]. Acta Physica Sinica, 2012, 61(24): 323-331. |
| [18] |
王永明. 基于元胞自动机的道路交通堵塞仿真研究[J]. 系统仿真学报, 2010(9): 2149-2154. WANG Yong-ming. Study of Traffic Congestion's Simulation Based on Cellular Automaton Model[J]. Journal of System Simulation, 2010(9): 2149-2154. |
| [19] |
JIA Ning, MA Shou-feng, ZHONG Shi-quan. Analytical Investigation of the Boundary-triggered Phase Transition Dynamics in a Cellular Automata Model with a Slow-to-start Rule[J]. Chinese Physics B, 2012, 21(10): 38-43. |
 2018, Vol. 35
2018, Vol. 35
