扩展功能
文章信息
- 郑来, 陈永胜, 孙金玮
- ZHENG Lai, CHEN Yong-sheng, SUN Jin-wei
- 基于计算机视觉的信号交叉口排队车辆静态间距研究
- Study on Static Spacing of Queuing Vehicles at Signalized Intersection Based on Computer Vision
- 公路交通科技, 2018, 35(2): 95-100, 108
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(2): 95-100, 108
- 10.3969/j.issn.1002-0268.2018.02.013
-
文章历史
- 收稿日期: 2017-03-14
2. 哈尔滨工业大学 电气工程及自动化学院, 黑龙江 哈尔滨 150010
2. School of Electrical Engineering and Automation, Harbin Institute of Technology, Harbin Heilongjiang 150010, China
信号交叉口是典型的间断流设施,其范围内的车辆始终包含停止和运行2种状态。信号交叉口排队车辆静态间距是指当前车辆停止等候红灯时与前车保持的空间间隔,本研究特指前车车尾至当前车车头的距离。静态间距在一定程度上反映了停止之前车辆间的相互作用,对信号交叉口的通行效率和安全状况均有重要的影响。
现阶段对信号交叉口车辆间隔的研究主要以车辆动态运行过程中的间距分析为主。比如,赵星和任刚分析了信号交叉口排队车辆通过停车线的车头时距特征,建立了饱和车头时距与其影响因素间的关系模型[1];邵长桥等人分析了信号交叉口排队离散车头时距的统计特征,发现车头时距可以用Log-normal分布来拟合[2];Murat和Gedizlioglu分析了低交通量条件下信号交叉口的车头时距分布,发现负指数分布和Weibull分布是较好的拟合选择[3];李爱增等人探讨了信号交叉口下游车头时距的分布特征,结果表明随高平峰时段的不同车头时距分布在移位负指数分布和M3分布之间过渡[4];苏岳龙等人研究了信号交叉口放行时不同车型组成的混合机动车流车头时距的分布[5];也有较多研究涉及到其他道路的车头时距分布[6-8]。部分研究探讨了车头时距的影响因素。比如,刘明君等人分析了交叉口布局、车辆特性等对停车线处车头时距的影响[9];邵长桥和荣建则对比分析了信号交叉口内外侧专用左转车道的车头时距特征[10]。此外,杨东援等人探讨了利用感应线圈检测器动态提取车头时距的方法[11]。
相比较而言,学者们对信号交叉口排队车辆的静态间距则较少予以关注。对静态间距的研究较早地出现于路侧停车时的车辆间距分析,所采用的方法包括无规则吸附模型和随机矩阵理论等[12-15]。JIN等人则将复杂的随机矩阵理论引入到信号交叉口排队车辆静态间距分布研究中,发现高斯辛系统能够较好地描述此类静态间距的分布。他们认为不同城市里静态间距的分布可能相同但均值不同,却未对影响静态间距的因素进行具体分析[16]。吴潜蛟等人则分析了车辆静态间距对信号交叉口通行能力的影响,发现间距在4~8 m时能最大提升交叉口通行能力[17]。
停车状态是信号交叉口交通运行状态中不可或缺的一部分。深入分析停车状态下的车辆分布特性,对全面掌握和理解信号交叉口的交通运行规律具有重要意义。本研究将结合行车记录仪记录的视频数据,详细分析信号交叉口排队车辆静态间距的分布特性和主要影响因素。
1 数据描述共收集到哈尔滨市26辆出租车及其对应驾驶员的基本数据,主要包括出租车行车记录仪视频和出租车驾驶员基本信息。其中,出租车行车记录仪视频主要记录了出租车运行时前方的道路、交通和环境条件,记录时间均为白天,视频总时长为236.7 h,平均每辆出租车约为8.4 h;驾驶员基本信息包括驾驶员的性别、年龄和出租车驾龄。
采用人工观测方法,从行车记录仪视频中截取出租车在信号交叉口红灯排队等候时的前车图像,共1 896个,平均每辆出租车约73个。此外,记录了每一次信号交叉口停车图像所对应的交通条件信息,具体包括:前车车型信息,分为小型车和非小型车;是否高峰时段信息,主要是根据校正后的行车记录仪记录时间确定每一个图像所在时段是否为高峰时段,其中早高峰时段为06: 30—08: 30,晚高峰时段为16: 30—18: 30;所在车道信息,主要是当前车辆所处车道的类型,分为直行车道、直左车道、直右车道、左转车道和右转车道,相关数据的统计情况见表 1。
| 最小值 | 均值 | 最大值 | ||
| 驾驶员信息 | 年龄/a | 25 | 39 | 54 |
| 出租车驾龄/a | 1 | 8 | 22 | |
| 视频图像信息 | 视频时长/h | 5.4 | 8.4 | 13.0 |
| 图像数量/个 | 39 | 127 | 76 |
2 排队车辆静态间距测算
排队车辆的静态间距测算主要是利用计算机单目视觉技术,通过对图像中车牌的识别和定位,结合针孔模型计算实现。
2.1 图像预处理与车牌定位测距的先决条件是定位图像中车牌的位置。为了提高车牌定位的效率和保证定位的准确性,需要对截取的图像进行预处理。
图像预处理的流程见图 1。首先,通过图像裁剪删除与研究不相关区域的图像信息,从而提高车牌定位的效率;其次,对图像进行灰度化处理和灰度化校正,增强图像的可检测性;再次,对灰度图像进行中值滤波处理,消除噪声干扰;进而,采用canny算子进行边缘检测,勾勒和加强车牌边缘区域;然后,对边缘图像进行腐蚀、膨胀和开闭运算等形态滤波处理,形成完整的车牌填充区域;最后,结合车牌颜色的先验知识,对车牌进行切割,以验证车牌定位的准确性。

|
| 图 1 图像预处理流程示意图 Fig. 1 Procedures of image pre-processing |
| |
2.2 静态间距测算模型
基于计算机单目视觉技术及针孔模型的间距测量实际上是利用图像空间I={u, v}中的数据,结合一定的先验知识(如车牌底边距地面高度和行车记录仪距地面高度)计算现实空间R={x, y, z}中一个平面S={(x, y, o)∈I}上的数据。
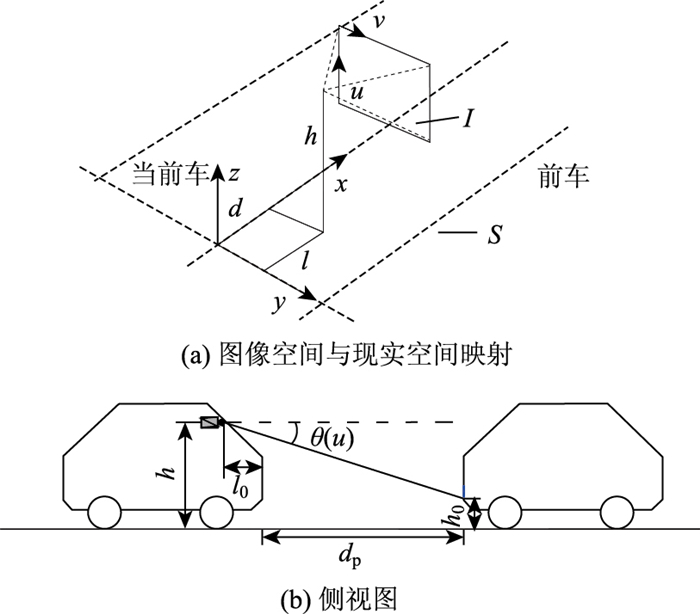
参照文献[18],构建了基于车牌高度的静态间距测算模型,测距模型计算原理和主要相关参数见图 2。由图 2可知,车辆之间的间距为:
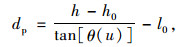
|
(1) |
|
| 图 2 测距模型主要参数示意图 Fig. 2 Illustration of parameters of distance measuring model |
| |
式中,dp为前车尾部与当前车头部之间的距离;h为行车记录仪距地面高度;h0为车牌底边距地面高度;θ(u)为图像中的点(u, v)的射线在现实空间中与标准轴线形成的垂直夹角;l0为行车记录仪摄像头距其所在车(当前车)车头的距离。根据三维现实空间和二维图像空间的映射关系可知:
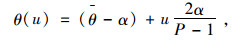
|
(2) |
式中,θ摄像机中心轴与标准轴的垂直夹角;2α为摄像机的孔径张角;u为目标车牌在图像空间中的纵坐标;P为截取图像的分辨率(P=m×n)。将式(2)代入式(1),即可得到静态间距测算模型:
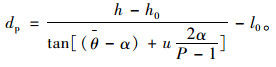
|
(3) |
测距模型的部分参数,如行车记录仪距地面高度和行车记录仪距车头距离,是通过对行车记录仪所在车辆的实际测量获得;摄像机的孔径张角等参数是通过标定试验获得;而前车车牌距地面高度,则是通过在观看视频时记录前车品牌、型号等信息,后期在停车场寻找相同类型车辆进行测量获得。
为了检验测距模型的精度及可靠性,在无干扰的平直路段环境下开展测距检验试验,试验所涉及到的模型基本参数见表 2。考虑到实际视频中行车记录仪摄像头距其所在车车头之间有一定的距离,测距试验在2.0~6.5 m范围内每隔0.5 m拍摄取样。根据试验图像所得到的测量结果对比见表 3。
| 参数名 | 参数值 |
| 与标准轴线形成的垂直夹角θ/rad | 0 |
| 摄像机的孔径张角2α/rad | 0.61 |
| 摄像机清晰度m×n/像素 | 1 280×720 |
| 摄像机与地面距离h/m | 1.30 |
| 车牌底边到地面的高度h0/m | 0.78 |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 实际值/m | 2.00 | 2.50 | 3.00 | 3.50 | 4.00 | 4.50 | 5.00 | 5.50 | 6.00 | 6.50 |
| 测量值/m | 1.95 | 2.38 | 2.96 | 3.40 | 3.70 | 4.08 | 4.54 | 5.40 | 5.90 | 5.83 |
| 绝对误差/m | 0.05 | 0.12 | 0.04 | 0.10 | 0.30 | 0.42 | 0.46 | 0.20 | 0.10 | 0.67 |
| 相对误差/% | 2.50 | 4.80 | 1.33 | 2.86 | 7.50 | 9.33 | 9.20 | 3.64 | 1.67 | 10.3 |
由表 3可知,测距模型的总体精度较高,平均相对误差仅为5.31%。但是,随着距离的增加,测量误差会逐渐增大,当距离≤ 4 m时,平均绝对误差仅为0.12 m;当距离>4 m时,平均绝对误差增大至0.37 m。因此,本模型主要适用于短距离条件下间距测量,而信号交叉口排队车辆的静态间距一般都位于该模型可测范围内。
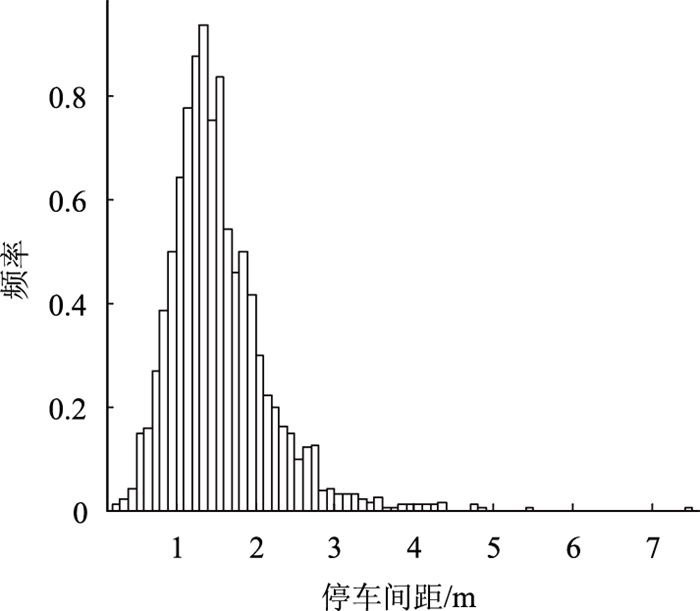
3 静态间距分布特性分析利用构建的静态间距测算模型,计算得到了所截取的1 896个图像所对应的静态间距。其中,静态间距最小值为0.23 m,最大值为7.43 m,平均值为1.54 m。静态间距的分布直方图见图 3。
|
| 图 3 静态间距分布直方图 Fig. 3 Histogram of distribution of static spacings |
| |
考虑到静态间距为非负的连续型变量,因此选择常用的描述非负变量的连续型分布进行静态间距样本的拟合,具体的候选分布包括Gamma分布、Exponential分布、Erlang分布、Weibull分布、Log-normal分布和Log-logistic分布。利用Kolmogorov-Smirnov(K-S)检验进行拟合优度检验和分布比选。静态间距分布拟合结果见表 4。
| 分布类型 | 概率密度函数 | 参数估计 | K-S值 |
| Gamma | 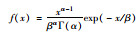
|
α=6.03 β=0.25 |
0.049 |
| Erlang | 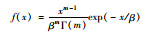
|
m=6 β=0.25 |
0.053 |
| Weibull | 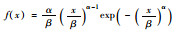
|
α=3.22 β=1.70 |
0.084 |
| Log -normal | 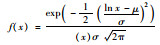
|
σ=0.39 μ=0.35 |
0.036 |
| Log -logistic | 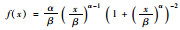
|
α=4.65 β=1.42 |
0.017 |
由表 4可知,在0.05的显著性水平上,Gamma分布、Log-normal分布和Log-logistic分布均达到统计显著性要求,其中Log-logistic分布对静态间距样本的拟合优度最好。因此,所采集的信号交叉口排队车辆静态间距更适合用Log-logistic分布描述。
4 静态间距影响因素分析 4.1 驾驶员因素影响分析以每一个出租车驾驶员为主体,分析驾驶员年龄和出租车驾龄因素对静态间距的影响。其中,每一个驾驶员所对应的静态间距为其所驾驶车辆的所有静态间距的平均值,即期望静态间距。
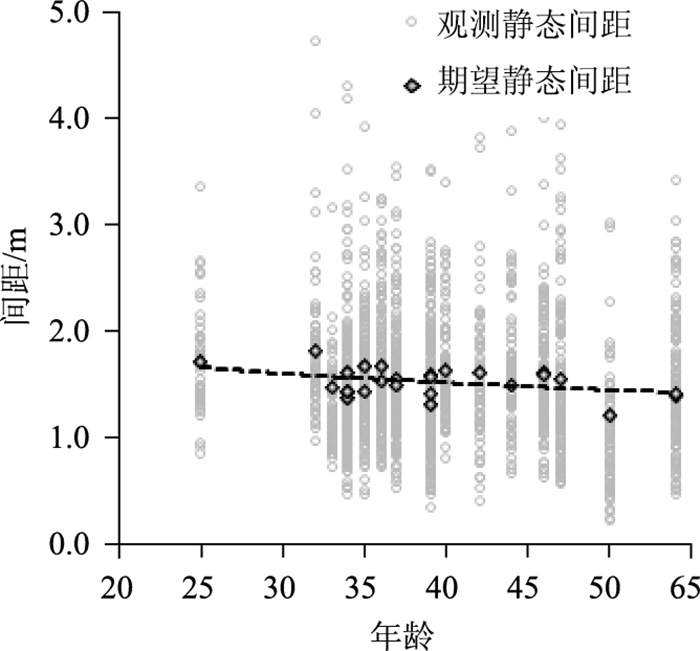
计算得到26个驾驶员所对应的期望静态间距在1.33~1.83 m之间。期望静态间距与驾驶员年龄的关系见图 4。随着年龄的增加,出租车驾驶员倾向于与前车保持更小的停车间距。同样地,随着驾龄的增加,静态间距也逐渐减小,如图 5所示。这说明随着阅历的增加和驾驶经验的积累,出租车驾驶员相信自己在较小的间距情况下也能保证在启动时不与前车发生追尾,因而会在一定程度上减小与前车的停车间距。
|
| 图 4 静态间距与驾驶员年龄关系 Fig. 4 Relationship between static spacings and age of driver |
| |
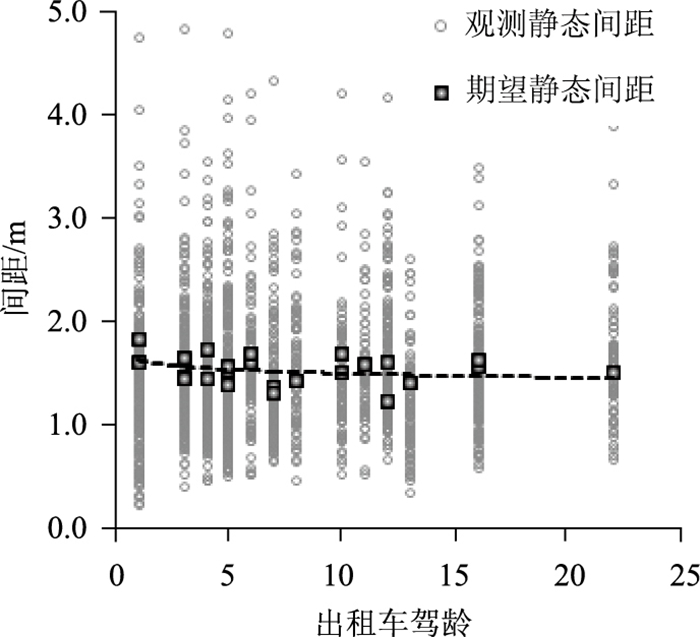
|
| 图 5 静态间距与出租车驾龄关系 Fig. 5 Relationship between static spacings and taxi driving years |
| |
此外,期望静态间距与驾驶员年龄、出租车驾龄之间并不是线性的单调递减关系。由图中的趋势线可以看出,随着年龄或驾龄的增加,静态间距的减小幅度将逐渐变小并最终将趋向于一个最小值,即临界安全静态间距。
4.2 道路交通条件因素影响分析以每一个静态间距为主体,分析前车车型、是否高峰时段以及所在车道类型等交通条件因素对静态间距的影响。采用差异性分析方法,进行不同组别样本的T检验或F检验(其中,两组别样本采用T检验,多组别样本采用F检验),判定不同组别均值之间的差异是否显著。各变量的差异性分析结果见表 5。
| 变量 | 组别 | 样本量 | 均值 | 标准差 | T/F值 | 显著性水平 |
| 前车车型 | 小型车 | 1 761 | 1.52 | 0.59 | -2.587 | 0.005 |
| 非小型车 | 135 | 1.76 | 0.96 | |||
| 是否高峰 | 否 | 1 313 | 1.55 | 0.61 | 3.343 | 0.001 |
| 是 | 583 | 1.43 | 0.61 | |||
| 所在车道类型 | 直 | 1 183 | 1.55 | 0.02 | 1.045 | 0.382 |
| 直右 | 278 | 1.50 | 0.04 | |||
| 直左 | 83 | 1.59 | 0.07 | |||
| 右 | 43 | 1.60 | 0.11 | |||
| 左 | 309 | 1.49 | 0.04 |
在前车车型方面,小型车所对应的静态间距与非小型车所对应的静态间距之间存在显著性差异(p=0.005<0.05)。其中,小型车所对应的平均静态间距为1.52 m,非小型车所对应的平均静态间距为1.76 m,表明相较于小型车而言,出租车倾向于与前方的大中型车保持更大的间距。这可能是由于两方面原因引起:一是大中型车的启动速度较慢,为了避免与其发生追尾,启动速度较快的小型车会适当加大其与大型车的距离;二是在信号交叉口,前方的大中型车辆(比如公交车)会对后方的小型车驾驶员产生视线遮挡,为了能够有较好的视野和较为充足的反应时间,后方的小型车驾驶员也会适当增加其与前方大中型车的距离。
在是否高峰方面,高峰时段的平均静态间距小于非高峰时段的平均静态间距,并且两者的差异具有统计显著性(p=0.001<0.05)。在高峰时段,交通拥堵现象一般比较明显,因此车辆希望通过尽可能地缩小与前车的距离来更快地通过信号交叉口。这也导致了实际视频处理过程中,在高峰时段观察到较多的二次调整现象,即在信号交叉口已完全停止的车辆会再次启动并低速前进一段距离,其目的是缩短与前车的间距、提高通过效率。
在所在车道类型方面,直行车道、直右车道、直左车道、右转车道和左转车道所对应的平均静态间距依次为1.55,1.50,1.59,1.60,1.49 m。虽然5者各不相同,但F检验表明它们之间并没有显著性差异(p=0.382>0.05)。因此,所在车道类型对静态间距没有显著性影响。
5 结论以行车记录仪视频数据为基础,结合计算机单目视觉技术和统计分析方法,研究了信号交叉口排队车辆静态间距的分布特性和影响因素,取得了以下研究成果:
(1) 构建了基于计算机单目视觉的静态间距测算模型,借助车牌定位和车牌距地面高度等关键参数的标定,测算得到了具有较高精度的信号交叉口排队车辆静态间距数据。
(2) 探讨了信号交叉口排队车辆静态间距的分布特征,明确了所采集的出租车静态间距样本服从Log-logistic分布。
(3) 分析了驾驶员因素和交通条件因素对静态间距的影响,发现驾驶员年龄、出租车驾龄与静态间距呈负相关关系,而非高峰时段、大中型车出现等因素则会导致静态间距的增加。
| [1] |
赵星, 任刚. 信号交叉口车头时距特性分析[J]. 交通运输工程与信息学报, 2010, 8(1): 103-108. ZHAO Xing, REN Gang. Analysis of Vehicle Headway Characters at a Signalized Intersection[J]. Journal of Transportation Engineering and Information, 2010, 8(1): 103-108. |
| [2] |
邵长桥, 杜晓辉, 李光芹. 信号交叉口排队离散车头时距统计分析[J]. 公路交通科技, 2003, 20(4): 76-79. SHAO Chang-qiao, DU Xiao-hui, LI Guang-qin. Queuing Vehicle Headway Statistic Analysis at Signalized Intersection[J]. Journal of Highway and Transportation Research and Development, 2003, 20(4): 76-79. |
| [3] |
MURAT Y S, GEDIZLIOGLU E. Investigation of Vehicle Time Headways in Turkey[J]. Transport, 2007, 160(2): 73-78. |
| [4] |
李爱增, 宋向红, 马志博, 等. 信号交叉口下游车头时距分布特征[J]. 交通运输系统工程与信息, 2013, 13(4): 66-75. LI Ai-zeng, SONG Xiang-hong, MA Zhi-bo, et al. Time Headway Distribution on Downstream Section of Signalized Intersection[J]. Journal of Transportation Systems Engineering and Information Technology, 2013, 13(4): 66-75. |
| [5] |
苏岳龙, 魏铮, 姚丹亚, 等. 混合交通状态下交叉口排队机动车流启动车头时距研究和应用[J]. 公路交通科技, 2008, 25(7): 113-117, 140. SU Yue-long, WEI Zheng, YAO Dan-ya, et al. Model of Start-up Lost Time and Headway of Queuing Motor Vehicles under Mixed Traffic Condition[J]. Journal of Highway and Transportation Research and Development, 2008, 25(7): 113-117, 140. |
| [6] |
李文权, 王炜, 周荣贵. 高速公路合流区1车道车头时距分布特征[J]. 公路交通科技, 2003, 20(1): 114-117. LI Wen-quan, WANG Wei, ZHOU Rong-gui. Headway Characteristics of Lane 1 on Expressway Merge Area[J]. Journal of Highway and Transportation Research and Development, 2003, 20(1): 114-117. |
| [7] |
赵晓翠, 杨峰, 邓宝. 高速公路互通立交分流区车头时距分布[J]. 公路交通科技, 2012, 29(2): 136-139. ZHAO Xiao-cui, YANG Feng, DENG Bao. Headway Distribution Characteristics of Diverging Area on Expressway Interchanges[J]. Journal of Highway and Transportation Research and Development, 2012, 29(2): 136-139. |
| [8] |
陶鹏飞, 王殿海, 金盛. 车头时距混合分布模型[J]. 西南交通大学学报, 2011, 46(4): 633-637, 644. TAO Peng-fei, WANG Dian-hai, JIN Sheng. Mixed Distribution Model of Vehicle Headway[J]. Journal of Southeast Jiaotong University, 2011, 46(4): 633-637, 644. |
| [9] |
刘明君, 孙全欣, 高利平, 等. 基于风险分析方法的首车疏解车头时距[J]. 吉林大学学报:工学版, 2011, 41(5): 1262-1267. LIU Ming-jun, SUN Quan-xin, GAO Li-ping, et al. Modeling First Discharge Headway Based on Hazard Analysis[J]. Journal of Jilin University:Engineering and Technology Edition, 2011, 41(5): 1262-1267. |
| [10] |
邵长桥, 荣建. 信号交叉口专用双左转车道通行能力[J]. 交通运输工程学报, 2010, 10(4): 79-84. SHAO Chang-qiao, RONG Jian. Capacity of Exclusive Dual Left-turn Lanes at Signalized Intersection[J]. Journal of Traffic and Transportation Engineering, 2010, 10(4): 79-84. |
| [11] |
杨东援, 罗江邻, 刘翀, 等. 信号交叉口饱和流率动态提取方法[J]. 交通运输工程学报, 2013, 13(1): 98-103. YANG Dong-yuan, LUO Jiang-lin, LIU Chong, et al. Dynamic Extraction Method of Saturation Flow Rate at Signalized Intersection[J]. Journal of Traffic and Transportation Engineering, 2013, 13(1): 98-103. |
| [12] |
RAWAL S, RODGERS G J. Modelling the Gap Size Distribution of Parked Cars[J]. Physica A:Statistical Mechanics and Its Applications, 2005, 346(3): 621-630. |
| [13] |
ABUL-MAGD A Y. Modelling Gap-size Distribution of Parked Cars Using Random-matrix Theory[J]. Physica A:Statistical Mechanics and Its Applications, 2005, 368(2): 536-540. |
| [14] |
LEE J W. Reversible Random Sequential Absorption on a One-dimensional Lattice[J]. Physica A:Statistical Mechanics and Its Applications, 2004, 331(3): 531-537. |
| [15] |
TALBOT J, TARJUS G, TASSEL P V, et al. From Car Parking to Protein Adsorption:An Overview of Sequential Adsorption Processes[J]. Colloids and Surfaces A:Physicochemical and Engineering Aspects, 1999, 165(1): 287-324. |
| [16] |
JIN Xue-xiang, SU Yue-long, ZHANG Yi, et al. Modeling of Spacing Distribution of Queuing Vehicles at Signalized Junctions Using Random-matrix Theory[J]. Tsinghua Science and Technology, 2009, 14(2): 252-254. |
| [17] |
吴潜蛟, 罗向龙, 武奇生, 等. 基于车间距的交叉口通行能力分析[J]. 长安大学学报:自然科学版, 2009, 29(6): 88-92. WU Qian-jiao, LUO Xiang-long, WU Qi-sheng, et al. Passing Capacity of Signal Intersection Based on Vehicles' Parking Space[J]. Journal of Chang'an University:Natural Science Edition, 2009, 29(6): 88-92. |
| [18] |
刘茜. 基于MATLAB的单目视觉车辆测距技术研究[D]. 西安: 长安大学, 2008. LIU Qian. Study on MATLAB-based Single-vision Vehicles Ranging Technology[D]. Xi'an: Chang'an University, 2008. |
 2018, Vol. 35
2018, Vol. 35
