扩展功能
文章信息
- 曹峰, 凌同华, 刘家澍, 张亮, 谷淡平
- CAO Feng, LING Tong-hua, LIU Jia-shu, ZHANG Liang, GU Dan-ping
- 分岔隧道浅埋连拱段的爆破振动效应分析
- Analysis on Blasting Vibration Effect of Shallow Multi-arch Section of Bifurcated Tunnel
- 公路交通科技, 2018, 35(2): 86-94
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(2): 86-94
- 10.3969/j.issn.1002-0268.2018.02.012
-
文章历史
- 收稿日期: 2017-03-03
2. 长沙理工大学桥梁工程高校重点实验室, 湖南 长沙 410114;
3. 中国电建集团中南勘测设计研究院有限公司, 湖南 长沙 410014
2. Key Laboratory of Bridge Engineering of Universities, Changsha University of Science and Technology, Changsha Hunan 410114, China;
3. PowerChina Zhongnan Engineering Co., Ltd., Changsha Hunan 410014, China
近年来,分岔隧道已经逐渐成为交通工程领域关注的重点[1]。它兼具连拱隧道和小净距隧道的特点,一般由洞口的连拱隧道逐渐过渡到小净距隧道,最后变为常规的分离式隧道。由于分岔隧道涉及了多种隧道结构形式,受力结构复杂,使得各过渡段应力较为集中,特别是分岔隧道的连拱段,常常多为浅埋段,承载能力低,围岩稳定性较差。而隧道开挖产生的爆破荷载对围岩和相邻洞室受力结构进行冲击和反复扰动,加剧了隧道的变形,极易造成塌方事故。因此,有必要开展分岔隧道浅埋连拱段的爆破振动效应研究,探索地质条件、隧道特征与爆源特性之间的相互关系和相互作用,降低爆破振动对隧道上覆浅层岩体及受力结构的冲击危害。许多学者在隧道洞口浅埋段的爆破振动危害控制和稳定性方面作了研究[2-10],但对分岔隧道浅埋连拱段的围岩、支护及受力结构在爆破地震波作用下的力学特性仍缺乏系统研究。
在此,本研究以湘西六月田公路隧道为工程背景,对洞口分岔段爆破开挖引起的振动进行监测,探讨后行隧道爆破振动对中隔墙的影响。同时,采用数值模拟方法,分析后行隧道爆破荷载作用下覆盖层围岩的振动传播规律,研究受力结构的破坏机理,从而制定科学合理的安全控制标准,为隧道的后续开挖提供指导。
1 现场爆破试验 1.1 工程概况六月田隧道地处湘西自治州永顺县芙蓉镇境内,隧道左线桩号为K10+445~K11+449,右线桩号为YK10+440~YK11+449。分岔段隧道设置在出口(吉首端),出口端洞口地处猛洞河岸边的陡坡上,山体自然坡度为30°~35°。坡面上局部散落滚石,微风化灰岩广泛出露,坡体自稳能力差。出口前方与猛洞河大桥相连。六月田隧道由连拱段、小净距段隧道逐渐过渡到分离式隧道。其中,连拱段隧道为Ⅴ级围岩,最小埋深仅8 m,最大开挖跨度12.24 m,开挖高度9.96 m,开挖断面100.4 m2。
浅埋连拱段采用三导洞法开挖,掏槽眼采用楔形方式布置,孔底间距10~20 cm。周边眼采用光面爆破,孔间距为50 cm。炸药选用2#岩石乳化炸药,最大段装药量为7.2 kg,循环进尺1.2~1.5 m。
1.2 振动监测系统爆破振动测试系统由四川某测控科技有限公司生产的NUBOX—8016爆破振动智能监测仪、TP3V—4.5三维速度型传感器等组成。NUBOX—8016是一款采用全新技术设计的新一代智能爆破测振仪,测振过程中实时显示被测波形。图 1为隧道现场测试时的爆破振动监测系统。

|
| 图 1 爆破振动监测系统 Fig. 1 Test system of blasting vibration |
| |
1.3 振动监测方案
已有研究成果表明[11],后行隧道爆破振动对中隔墙的影响较大。鉴于此,本工程的爆破振动监测点将布置在先行隧道(右洞)中隔墙的拱腰和拱脚处,纵向长度上沿YK11+447~YK11+431每隔4 m布置1个断面,如图 2所示。
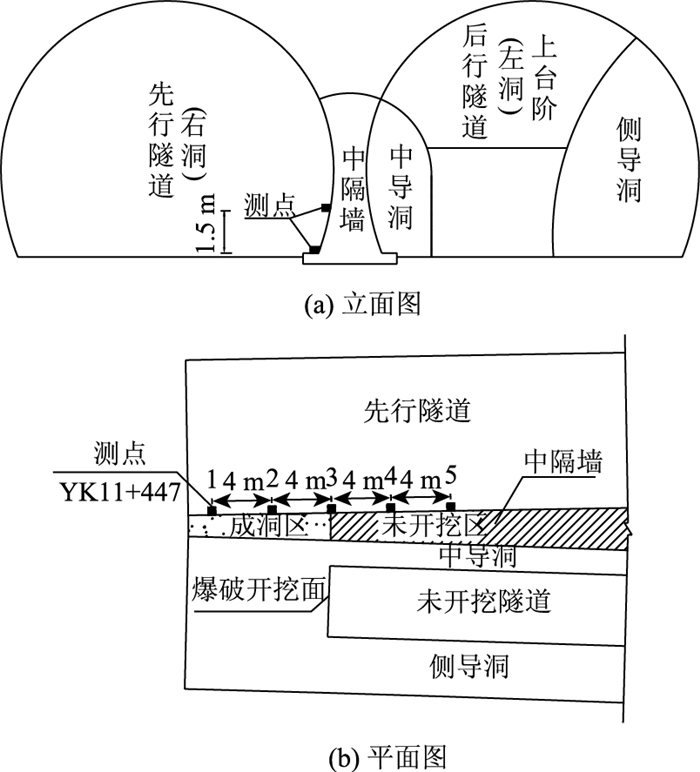
|
| 图 2 爆破振动测点布置图(单位:m) Fig. 2 Layout of measuring points of blasting vibration(unit:m) |
| |
2 数值模拟试验 2.1 数值计算模型
根据分岔隧道浅埋连拱段的开挖状况,采用LS-DYNA显式有限元程序建立三维模型,模型计算尺寸为:左右两侧宽度各取60 m,上边界到地表,下边界取36 m,隧道纵向长度取20 m。模型左右两侧施加X方向位移约束,底部施加Y方向位移约束,顶部为自由边界,前后方向施加Z方向位移约束。除模型顶部和前部外,其他部位都施加无反射边界,这样可以避免应力波反射对模型计算结果的影响。模型由炸药、岩石、喷射混凝土、衬砌混凝土和空气5部分组成。隧道洞口桩号为YK11+449,见图 3。
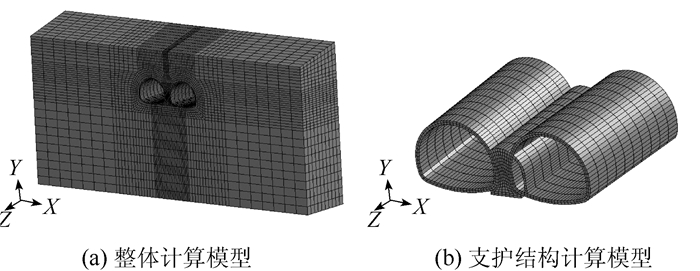
|
| 图 3 计算模型及网格划分 Fig. 3 Computational model and meshing |
| |
2.2 材料参数
由于集中装药模式并不影响振动波对隧道影响规律的研究[12],为便于计算,6个段的炮孔均采用集中装药模式进行模拟,即将同段炮孔简化为一个炮孔,布置在后行隧道左侧上台阶部位。
炸药的爆炸过程采用JWL(Jones-Wilkens-Lee)状态方程进行模拟。炸药起爆后,炸药单元体内的压力P由状态方程求得,表现形式为:
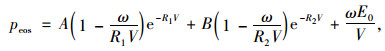
|
(1) |
式中, A, B为材料常数;R1, R2, ω为状态方程的常数;V为相对体积;E0为初始内能密度。
单元内的压力为:
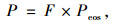
|
(2) |
式中F为单元的燃烧反应率。
炸药采用MAT_HIGH_EXPLOSIVE_BURN模型模拟,定义EOS_JWL为炸药的状态方程。炸药材料及状态方程参数见表 1。
| 密度/(g·cm-3) | 爆速/(m·s-1) | A/(×104 GPa) | B/GPa | R1 | R2 | ω | E0/GPa |
| 1.1 | 4 200 | 5.24 | 76.9 | 4.2 | 1 | 0.3 | 8.5 |
根据六月田工程地质勘查报告对岩石的物理力学参数的描述,经现场勘查,隧道出口段围岩为黏土和顶板厚度小的微风化灰岩。洞内初期支护采用C20喷射混凝土,衬砌采用C25混凝土。岩石和混凝土的物理力学参数见表 2。
| 材料 | 密度ρ/(g·cm-3) | 弹性模量E/GPa | 泊松比v | 内摩擦角φ/(°) | 黏聚力/MPa |
| Ⅴ级围岩 | 1.8 | 1 | 0.37 | 27 | 1 |
| C20混凝土 | 2.4 | 26 | 0.22 | — | — |
| C25混凝土 | 2.5 | 30 | 0.18 | — | — |
3 试验结果及分析 3.1 测试结果分析
现场爆破振动监测以采集后行隧道(左洞)上台阶的爆破振动速度为主。试验共进行了3次,爆破开挖面桩号分别为YK11+443,YK11+440,YK11+435。开挖面对应的中隔墙厚度为3.0~3.4 m。中隔墙的实测振动波形如图 4所示。爆破振动测试部分数据见表 3。
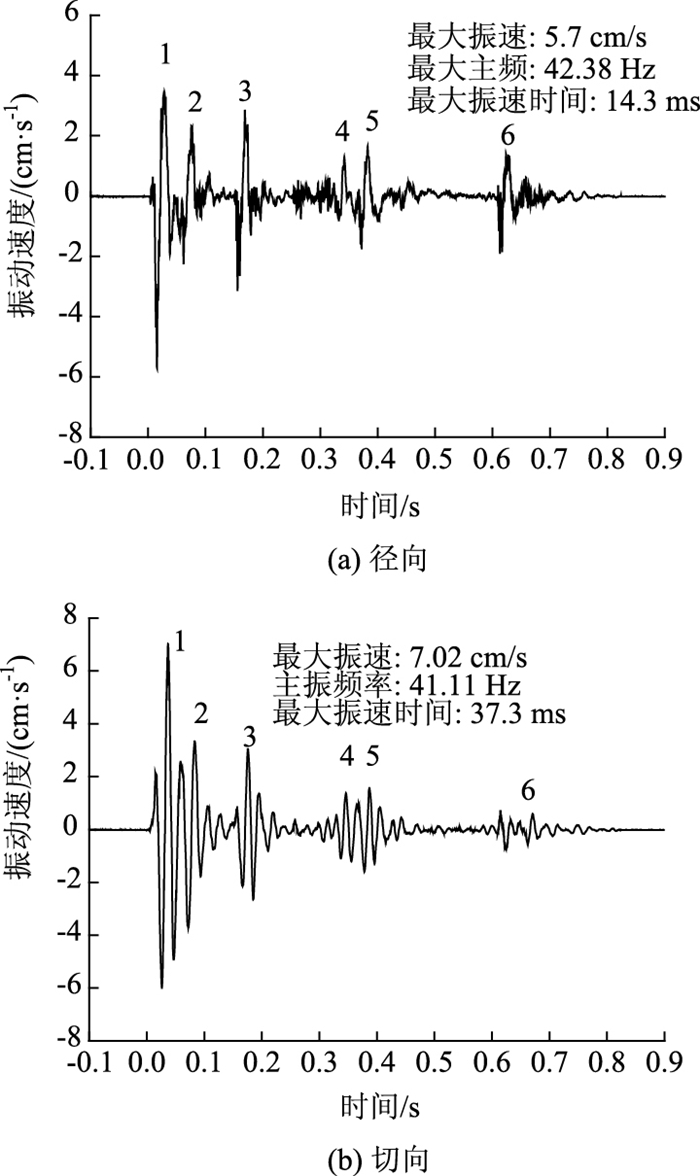
|
| 图 4 中隔墙实测振动波形 Fig. 4 Vibration waveform measured at mid-partition wall |
| |
| 桩号及测点部位 | 监测点 | 单段最大药量/kg | 爆心距/m | 振动速度峰值/(cm·s-1) | ||
| 径向 | 垂直向 | 切向 | ||||
| YK11+443拱腰 | 1 | 7.2 | 8.91 | 6.93 | 4.56 | 7.86 |
| 2 | 7.2 | 8.07 | 7.08 | 3.86 | 7.93 | |
| 3 | 7.2 | 9.11 | 5.86 | 4.01 | 7.05 | |
| 4 | 7.2 | 11.52 | 5.43 | 1.86 | 6.33 | |
| 5 | 7.2 | 14.65 | 5.40 | 3.01 | 5.23 | |
| YK11+443拱脚 | 1 | 7.2 | 9.30 | 5.26 | 4.75 | 6.5 |
| 2 | 7.2 | 8.47 | 6.42 | 5.07 | 6.33 | |
| 3 | 7.2 | 9.44 | 5.03 | 3.43 | 6.81 | |
| 4 | 7.2 | 11.77 | 3.9 | 3.42 | 6.70 | |
| 5 | 7.2 | 14.84 | 3.19 | 3.00 | 4.29 | |
| YK11+439拱腰 | 1 | 7.2 | 12.38 | 4.51 | 2.96 | 5.86 |
| 2 | 7.2 | 10.36 | 5.7 | 3.34 | 7.02 | |
| 3 | 7.2 | 9.66 | 6.6 | 3.51 | 6.35 | |
| 4 | 7.2 | 10.56 | 5.15 | 2.91 | 5.33 | |
| 5 | 7.2 | 12.71 | 2.92 | 1.96 | 3.31 | |
由图 4可知,爆破振动典型波形分为6段,其中,第1段和第2段、第4段和第5段振动波形之间出现了叠加,表明段与段之间的延时时间过短。为了减弱爆炸过程中的干涉效应,避免爆炸冲击波的叠加作用对振速的影响,建议各分段的爆破延时时差大于100 ms。从各分段的振速大小来看,掏槽孔爆破产生的振速最大,其径向振速和切向振速分别为其他炮孔振速的1.80~4.38倍和2.32~10.00倍。显然,掏槽孔爆破对隧道的危害更大。究其原因,掏槽孔爆破时,自由面较少导致围岩的夹制作用较大,振速显著增大。因此,隧道内的爆破振动控制主要以降低掏槽眼的爆破振速为主。
由表 3可以看出,相同爆破开挖面条件下,拱腰的爆破振动要大于拱脚。因此,后述的研究对象主要以拱腰为主。从3个方向上看,径向和切向振动较大,垂直向较小。
3次测试中,以爆破开挖面为分界面,将两侧等距离测点的振速进行对比可知,成洞区的振速要大于未开挖区的振速。其径向放大倍数分别为1.18, 1.33和2.35;垂直向放大倍数分别为1.13, 1.33, 2.01;切向放大倍数分别为1.11, 1.54, 2.87。可以看出,成洞区长度越长,放大系数越大,放大效应越明显。同时,随着中隔墙厚度的不断增大,测试区的最大振速不断降低。经结果分析,径向振速分别降低了12.17%和30.29%;垂直向振速分别降低了21.45%和39.66%;切向振速分别降低了18.13%,32.00%。
目前,爆破振动的传播和衰减规律主要采用萨道夫斯基经验公式[13],其表达式为:
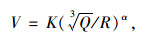
|
(3) |
式中, V为质点振速;R为测点与爆源距离;K,α分别为场地因素和衰减系数;Q为段最大装药量。
通过对现场拱腰处的径向、切向和垂直向实测数据进行回归分析,得到传播和衰减经验公式为:

|
(4) |
该拟合公式可对未开挖区的爆破振速进行预测。而成洞区受到空洞的影响,振速无法直接采用萨道夫斯基公式进行预测。为了获得成洞区中隔墙处爆破振动的传播规律,可采用式(5)表示为:
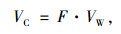
|
(5) |
式中,VC为成洞区的爆破振速;F为成洞区相比未开挖区的放大倍数;VW为未开挖区的爆破振速。
根据相关实测数据,可建立未开挖洞段长度与放大倍数的函数关系,通过曲线拟合方程得到3个方向的拟合公式为:
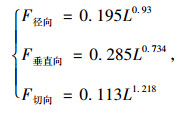
|
(6) |
式中L为未开挖洞段的长度。
由式(6)可知,放大系数为未开挖洞段长度的幂函数。
联立式(4)~(6),可得:
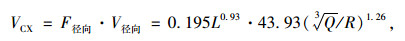
|
(7) |
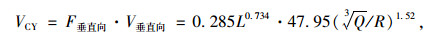
|
(8) |
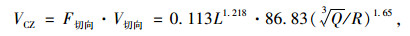
|
(9) |
式中,VCX,VCY,VCZ分别为成洞区径向、垂直向和切向的振速。
式(7)~(9)可对成洞区中隔墙的爆破振速进行预测。
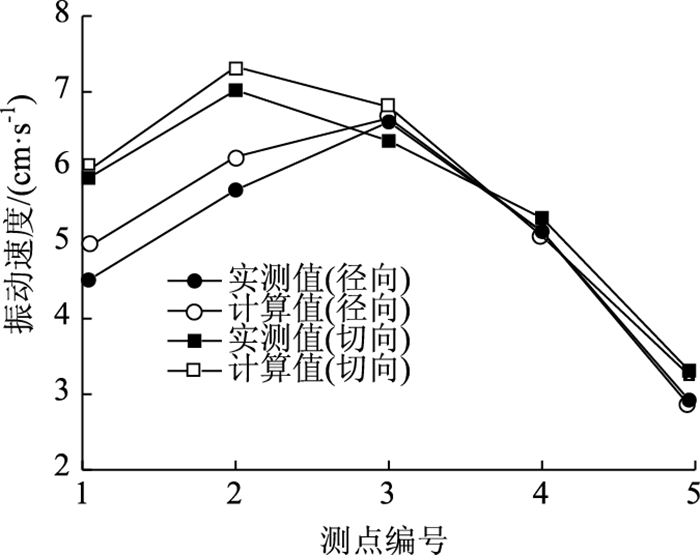
3.2 数值模拟结果分析 3.2.1 计算模拟值与实测值对比选取实测径向和切向振速与数值计算结果进行对比,如图 5所示。
|
| 图 5 实测值与计算值的比较图 Fig. 5 Comparison of measured values and calculated values |
| |
可以看出,实测波形与数值计算波形的变化规律基本一致。径向和切向振速的相对误差分别为0~9.76%和1.71~7.09%,计算结果略大于实测结果,但两者相差不大,验证了数值模拟计算结果的准确性。
3.2.2 中隔墙的振动效应分析中隔墙作为连拱段隧道的关键受力构件,不仅距离后行隧道(左洞)的爆源距离较近,而且受到爆破振动波的多次冲击,易产生损伤开裂甚至破坏,影响隧道的结构安全。
图 6为左洞爆破时,中隔墙的最大振速云图。爆破开挖面桩号设为K11+439。
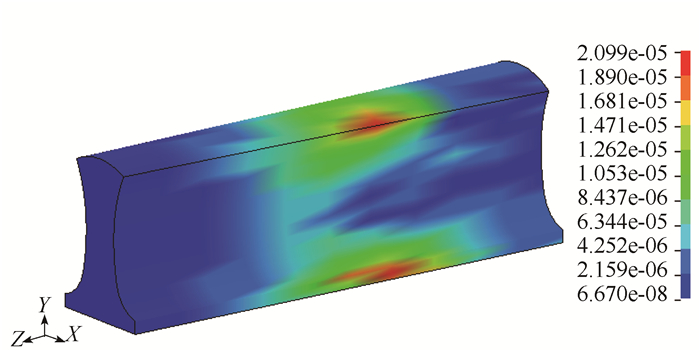
|
| 图 6 中隔墙最大振速对应时刻的云图(单位:×10-6cm/s) Fig. 6 Nephogram at moment of maximum vibration speed at mid-partition wall (unit:×10-6cm/s) |
| |
可以看出,左洞爆破时,振速较大值主要分布在靠近左洞侧的中隔墙墙顶和墙脚处,最大值为20.99 cm/s。这是由于左洞侧墙顶和墙脚均位于截面变化处,应力较为集中。同时,混凝土与岩石的阻抗不一致,造成交界面上的冲击波和应力波发生折射和反射,对振速和应力有放大作用。因此,在施工过程中,应适当控制药量,采用预裂爆破等方式减弱振动对中隔墙的影响,同时确保中隔墙特别是墙顶和墙脚的施工质量。
为了考察不同中隔墙厚度处的爆破振动规律,在YK11+447~YK11+431每隔4 m依次布置1个爆源,爆源编号为1~5,节点位置设在左洞侧中隔墙墙顶处,提取X方向上的振速如图 7所示。相对距离0 m为爆破开挖面,正方向为隧道开挖方向。后述相对距离的含义均与此相同。
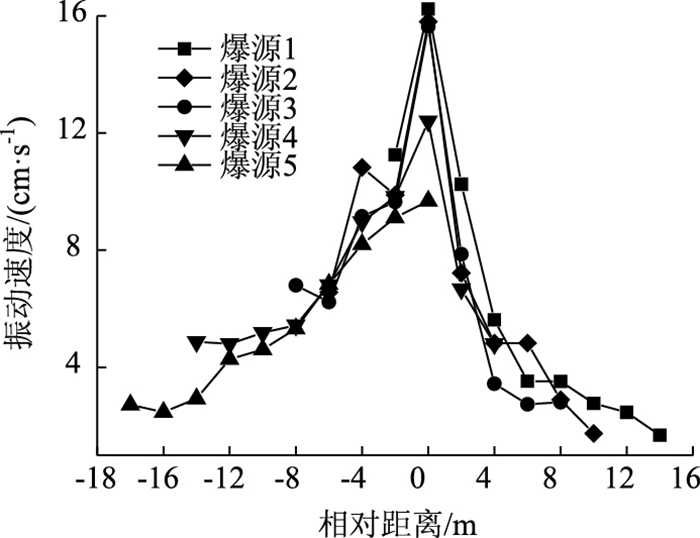
|
| 图 7 不同距离处爆源的振速 Fig. 7 Vibration velocities at different distance from explosive source |
| |
由图 7可知,成洞段中隔墙的振速大于未开挖段。相对距离-12~8 m范围内,爆破振速急剧减小,之后振速衰减较慢,并逐渐趋于平缓。因此,后行隧道爆破产生的振动对中隔墙成洞段12 m至未开挖段8 m范围内的影响较大。
3.2.3 爆破振动对岩石覆盖层的影响浅埋是分岔隧道洞口段的又一特征,研究爆破开挖对隧道覆盖层的影响,有利于及时调整支护和爆破参数,确保上覆围岩的稳定性。
在计算模型纵向方向YK11+445~YK11+433段每隔2 m设置一个爆源,选取隧道洞顶纵轴线上覆盖层厚度1~14.5 m范围内的节点,得到Y方向振速与覆盖层厚度的拟合关系曲线如图 8所示。曲线的拟合方程为y=31.794x-0.65,即振速为覆盖层厚度的幂函数。可以看出,洞顶覆盖层4 m范围内爆破近区的振速衰减较快,随着覆盖层厚度的增加,振速衰减趋于平缓。
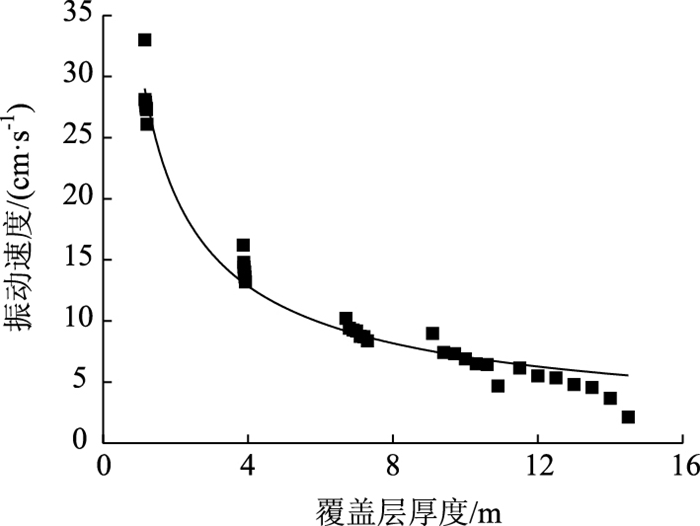
|
| 图 8 覆盖层厚度与振速的关系曲线 Fig. 8 Curves of relation between overburden thickness and vibration velocity |
| |
爆破荷载作用下,岩石的破坏准则取决于岩体的性质和受力状况。考虑到岩石一般为脆性材料,抗压强度明显高于抗拉强度。炸药爆炸时,岩石的裂隙区主要是拉伸破坏造成的[14]。
为了研究隧道洞顶覆盖层的爆破振动损伤范围,本研究采用Von Mises屈服准则[14-16]来分析岩石的爆破破碎特性。Von mises屈服理论为形状改变比能理论。当岩体内某点的应力状态对应的畸变能达到极限值k时,该点发生屈服,即:
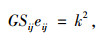
|
(10) |
式中,Sij=σij-σmδij,δij为Kronecker符号,σij为应力张量, σm为平均应力;eij=Sij/2G;G为剪切模量;k为屈服特性参数。
则单向应力状态下材料的应力可表示为:
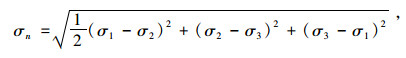
|
(11) |
于是Mises屈服条件为:
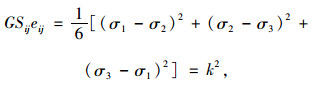
|
(12) |
则由上述两式,当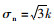
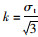
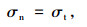
|
(13) |
式中σt为抗拉强度, 即当材料的应力达到或大于抗拉强度时,材料发生破坏。数值计算时,可用自由面上单元的Von Mises有效应力峰值与岩石的抗拉强度进行比较。当有效应力峰值大于岩石抗拉强度时,该单元处岩石发生拉伸破坏。
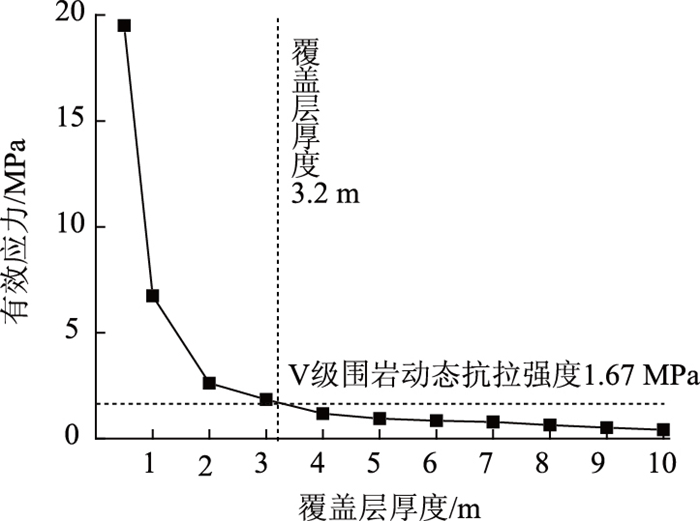
覆盖层厚度与有效应力的关系见图 9。可以看出,覆盖层厚度2 m范围内有效应力衰减较快,当覆盖层厚度超过4 m后,有效应力曲线趋于平缓。
|
| 图 9 覆盖层厚度与有效应力的关系曲线 Fig. 9 Curves of relation between overburden thickness and effective stress |
| |
根据六月田隧道地质勘查报告的试验结果,Ⅴ级围岩的抗拉强度取1.5 MPa,参考相关文献[17],岩石的动力抗拉强度提高系数为1.24。考虑到隧道内岩体存在节理、裂隙、断层等地质构造,取岩体的抗拉强度为岩石抗拉强度的0.9倍,则隧道岩体的动力抗拉强度提高系数为1.116倍。取Ⅴ级围岩的动态抗拉强度为1.67 MPa,由图 9可知,洞顶围岩发生损伤破坏的临界覆盖层厚度约为3.20 m。在现场施工过程中,建议对洞顶覆盖层4 m范围内的围岩进行注浆补强加固,并增设长管棚,使洞顶覆盖层形成约4 m厚的围岩加固圈。
3.2.4 爆破振动对开挖面后方喷射混凝土的影响隧道爆破产生的振动易引起岩石掉块及塌方,造成喷射混凝土等初期支护的损伤破坏,形成较大安全隐患。因此,有必要分析爆破振动对开挖面后方喷射混凝土的影响。将K11+431设为爆破开挖面,喷射混凝土的最大振速时刻云图如图 10所示。

|
| 图 10 最大振速对应时刻的云图(单位:10-6cm/s) Fig. 10 Nephogram at moment of maximum vibration speed (unit: 10-6cm/s) |
| |
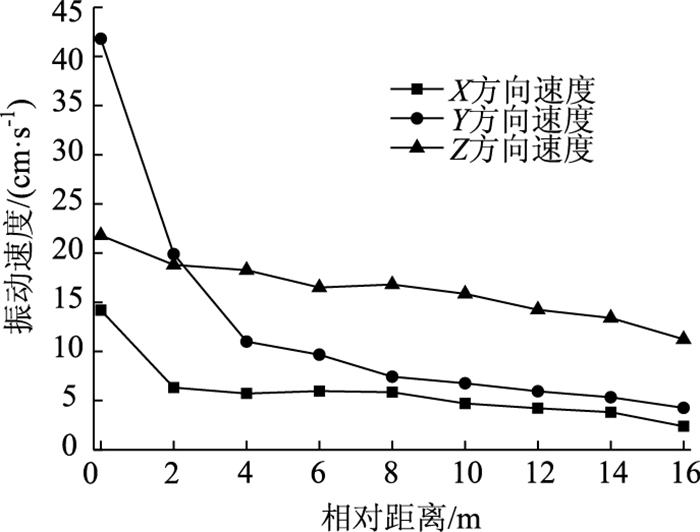
由图 10可知,振速较大值发生在拱顶和拱肩。其中,最大值为48.57 cm/s,出现在拱顶。该值超过了安全质点振动控制标准[13]。图 11为喷射混凝土拱顶节点沿纵轴线方向的振速曲线。
|
| 图 11 沿纵向方向的最大振速曲线 Fig. 11 Curves of longitudinal maximum vibration speed |
| |
可以看出,相对距离2 m范围内,Y方向振动最大,Z方向次之,X方向最小。随着应力波的传播扩大,Y方向振速迅速衰减,而Z方向和X方向衰减较慢。究其原因,距离掌子面2 m范围内,节点位于爆源的上方,波的传播以垂向纵波为主。随着相对距离的增加,波的传播转变为切向纵波为主。
由于喷射混凝土是脆性材料,其抗拉强度远小于抗压强度。当爆炸应力波产生的拉应力超过混凝土的抗拉强度时,喷射混凝土将产生拉裂直至破坏。因此,可以采用拉应力与抗拉强度进行对比,判断混凝土是否屈服破坏。
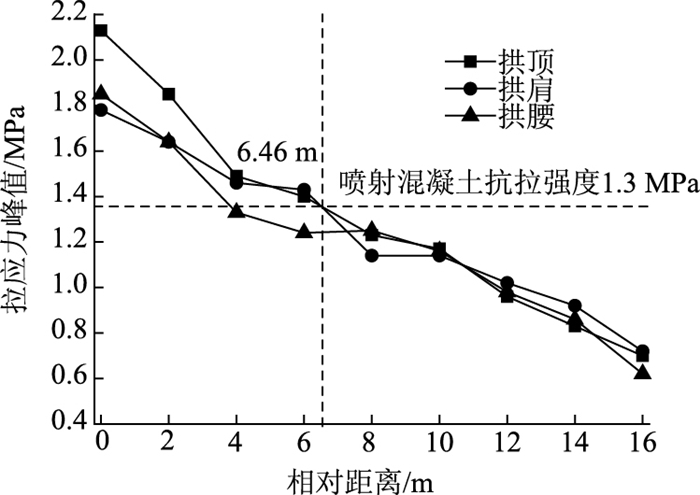
图 12为喷射混凝土关键点沿隧道纵轴线方向的最大拉应力曲线。
|
| 图 12 纵轴线方向的最大拉应力曲线 Fig. 12 Curves of longitudinal maximum tension stress |
| |
可以看出,随着相对距离的增加,拉应力逐渐降低。其中,拱顶的拉应力最大,为2.13 MPa,拱肩次之,拱腰最小。根据文献[18],喷射混凝土的静抗拉强度取1.13 MPa,取动力抗拉极限强度为1.2倍静抗拉强度[17],即1.36 MPa,则拱顶、拱肩和拱腰处喷射混凝土沿隧道纵轴线方向发生开裂破坏的距离依次为6.46,6.40,3.76 m。当相对距离超过10 m时,三者的拉应力值基本趋于一致。
由图 11和图 12可知,最大振速和最大拉应力具有相似的变化规律。因此,可取混凝土拉裂破坏处的最大振速作为安全临界值,即混凝土拉裂破坏时的临界振速为16.5 cm/s。考虑到频繁的爆破振动对喷射混凝土造成的累计损伤,喷射混凝土的安全振速控制标准取10 cm/s。
4 结论(1) 测试结果表明,先行隧道侧中隔墙的切向和径向振速较大,垂直向振速最小。考虑到成洞区的爆破振速具有放大作用,施工过程中应重点监测成洞区侧中隔墙振速,同时防止中隔墙沿切向方向产生破坏。
(2) 探讨了成洞区振速放大倍数与未开挖洞段长度之间的关系,通过曲线拟合方程建立了两者之间的计算公式,通过推导得到了成洞区爆破振速的传播与衰减规律。
(3) 对不同覆盖层厚度的振速进行了拟合,拟合函数为y=31.794x-0.65,即振速为覆盖层厚度的幂函数。在地质情况、炸药量类似的情况下,可作为振速预测公式。
(4) 采用Von Mises屈服准则分析了岩石的爆破破碎特性,得到了隧道洞顶覆盖层的爆破振动损伤范围为3.20 m。因此,在进行隧道的拱部支护时,可对拱顶覆盖层4 m范围内进行注浆加固,增设超前小导管,提高围岩强度。同时尽早施作二次衬砌,确保上覆围岩的稳定性。
(5) 后行隧道喷射混凝土的最大振速发生在拱顶,其次是拱肩。在爆破荷载作用下,喷射混凝土沿纵轴线方向产生拉裂破坏的距离为6.46 m,混凝土产生拉裂破坏处的临界振速为16.5 cm/s。在施工过程中应加强隧道开挖面附近拱顶和两侧拱肩的支护,确保隧道开挖安全。
| [1] |
张庆松, 李术才, 李利平. 分岔隧道大拱段围岩稳定性监控与爆破振动效应分析[J]. 岩石力学与工程学报, 2008, 27(7): 1462-1468. ZHANG Qing-song, LI Shu-cai, LI Li-ping. Study of Blasting Dynamic Effect and Site Monitoring of Large-span Shallow Part of Bifurcated Tunnel[J]. Journal of Rock Mechanics and Engineering, 2008, 27(7): 1462-1468. |
| [2] |
喻军, 刘松玉, 童立元. 浅埋隧道爆破振动空洞效应[J]. 东南大学学报:自然科学版, 2010, 40(1): 176-179. YU Jun, LIU Song-yu, TONG Li-yuan. Hollow Effect Induced by Blasting Vibration in Shallow Tunnels[J]. Journal of Southeast University:Natural Science Edition, 2010, 40(1): 176-179. |
| [3] |
SHIN J H, MOON H G, CHAE S E. Effect of Blast-induced Vibration on Existing Tunnels in Soft Rocks[J]. Tunnelling and Underground Space Technology, 2011, 26(1): 51-61. |
| [4] |
DEY K, MURTHY V. Prediction of Blast-induced Overbreak from Uncontrolled Burn-cut Blasting in Tunnels Driven through Medium Rock Class[J]. Tunnelling and Underground Space Technology, 2012, 28: 49-56. |
| [5] |
李利平, 李术才, 张庆松, 等. 小间距隧道爆破动力响应分析[J]. 公路交通科技, 2008, 25(7): 100-106. LI Li-ping, LI Shu-cai, ZHANG Qing-song, et al. Analysis of Dynamic Response on Blasting Excavation of Close-spaced Tunnel[J]. Journal of Highway and Transportation Research and Development, 2008, 25(7): 100-106. |
| [6] |
赵新涛, 黄海龙. 影响岩体爆破质量的垂直炮孔堵塞长度研究[J]. 公路交通科技, 2010, 27(7): 94-99. ZHAO Xin-tao, HUANG Hai-long. Study on Vertical Hole Stemming Length Affecting Rock Blasting Quality[J]. Journal of Highway and Transportation Research and Development, 2010, 27(7): 94-99. |
| [7] |
凌同华, 张胜, 陈倩倩, 等. 模式自适应小波构造与添加及其在爆破振动信号分析中的应用[J]. 振动与冲击, 2014, 33(12): 53-57, 120. LING Tong-hua, ZHANG Sheng, CHEN Qian-qian, et al. Pattern Adapted Wavelet Construction and Addition and Its Application in Blast Vibration Signal Analysis[J]. Journal of Vibration and Shock, 2014, 33(12): 53-57, 120. |
| [8] |
高照帅, 王德胜, 尹作明, 等. 城市地铁浅埋隧道掘进爆破地表振动试验研究[J]. 山东科技大学学报:自然科学版, 2016, 35(1): 79-85. GAO Zhao-shuai, WANG De-sheng, YIN Zuo-ming, et al. Experimental Study of Ground Vibration Induced by Shallow Urban Subway Tunnel Excavation Blasting[J]. Journal of Shandong University of Science and Technology:Natural Science Edition, 2016, 35(1): 79-85. |
| [9] |
李育枢, 李天斌. 高烈度地震区山岭隧道洞口减震问题的数值模拟研究[J]. 公路交通科技, 2009, 26(10): 100-104. LI Yu-shu, LI Tian-bin. Numerical Simulation of Shock Absorption of Mountainous Tunnel Portal in Highly Seismic Region[J]. Journal of Highway and Transportation Research and Development, 2009, 26(10): 100-104. |
| [10] |
凌同华, 曹峰, 李洁. 断层隧道爆破开挖的动力响应分析[J]. 现代隧道技术, 2016, 53(2): 107-113. LING Tong-hua, CAO Feng, LI Jie. Dynamic Response Analysis of Blasting Excavation for a Tunnel Passing through Faults[J]. Modern Tunnelling Technology, 2016, 53(2): 107-113. |
| [11] |
时亚昕, 王明年, 李强. 爆破振动对双连拱隧道中墙的影响分析[J]. 岩土力学, 2007, 28(6): 1275-1279. SHI Ya-xin, WANG Ming-nian, LI Qiang. Analysis of Influence of Blasting Vibration on Middle Wall of a Double-arch Tunnel[J]. |
| [12] |
林从谋, 陈礼彪, 蒋丽丽, 等. 高速公路扩建大断面特小净距隧道爆破稳定控制技术研究[J]. 岩石力学与工程学报, 2010, 29(7): 1371-1378. LIN Cong-mou, CHEN Li-biao, JIANG Li-li, et al. Research on Blasting Stability Control Technology of Large-span Highway Tunnel with Super-small Clear Spacing at Highway Expansion Project[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(7): 1371-1378. |
| [13] |
GB6722-2014, 爆破安全规程[S]. GB6722-2014, Safety Regulations for Blasting[S]. |
| [14] |
戴俊. 岩石动力学特性与爆破理论[M]. 北京: 冶金工业出版社, 2013. DAI Jun. Dynamic Behaviors and Blasting Theory of Rock[M]. Beijing: Metallurgical Industry Press, 2013. |
| [15] |
周传波. 深孔爆破一次成井模拟优化与应用研究[D]. 武汉: 中国地质大学, 2004. ZHOU Chuan-bo. Study on Simulation Optimization and Application of Shaft Formation by One Deep-hole Blasting[D]. Wuhan: China University of Geosciences, 2004. |
| [16] |
刘优平, 龚敏, 黄刚海. 深孔爆破装药结构优选数值分析方法及其应用[J]. 岩土力学, 2012, 33(6): 1883-1888. LIU You-ping, GONG Min, HUANG Gang-hai. Numerical Analysis Method for Optimizing Charging Structure of Deep-hole Blasting and Its Application[J]. Rock and Soil Mechanics, 2012, 33(6): 1883-1888. |
| [17] |
蒋楠, 周传波, 罗钢, 等. 铁路隧道混凝土衬砌爆破振动安全判据[J]. 中南大学学报:自然科学版, 2012, 43(7): 2746-2750. JIANG Nan, ZHOU Chuan-bo, LUO Gang, et al. Blasting Vibration Safety Criterion of Railway Tunnel Concrete Lining[J]. Journal of Central South University:Science and Technology Edition, 2012, 43(7): 2746-2750. |
| [18] |
JTGD70-2004, 公路隧道设计规范[S]. JTGD70-2004, Code for Design of Road Tunnel[S]. |
 2018, Vol. 35
2018, Vol. 35
