扩展功能
文章信息
- 马驰, 刘世忠, 冀伟, 李爱军
- MA Chi, LIU Shi-zhong, JI Wei, LI Ai-jun
- 单箱多室波形钢腹板PC组合箱梁剪力滞效应研究
- Study on Shear Lag Effect of Single-box Multi-cell PC Composite Box Girder with Corrugated Steel Webs
- 公路交通科技, 2018, 35(2): 62-71, 78
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(2): 62-71, 78
- 10.3969/j.issn.1002-0268.2018.02.009
-
文章历史
- 收稿日期: 2016-10-17
波形钢腹板PC组合箱梁与普通混凝土腹板箱梁的受力特性相似,在这种结构中剪力主要由钢腹板承担,弯矩主要由混凝土顶底板承担,箱梁翼板也存在弯曲应力分布不均匀的现象,称为剪力滞效应[1]。冀伟等[2]基于势能驻值原理,导出了单箱单室波形钢腹板简支梁在集中荷载作用下的剪力滞系数表达式。李立峰等[3]导出了单箱单室波形钢腹板PC组合箱梁在不同载荷作用下的剪力滞效应计算式,还分析了在这种组合结构波高区混凝土的合理计算宽度取值问题。吴文清等[4]在对称荷载作用下研究了翼板弯曲正应力分布规律。周茂定等[5]运用三杆比拟法导出了波形钢腹板简支梁在横向力作用下的弯曲正应力计算表达式。陈水生等[6]采用余弦函数定义了单箱多室波形钢腹板组合箱梁结构的剪滞翘曲位移差函数,推导了此类箱梁结构的控制微分方程,对此类箱梁结构在荷载作用下的剪滞效应结果作了对比。王静[7]利用有限元软件对单箱多室波形钢腹板PC组合箱梁建模分析,得到挠度及应力的一般分布规律。马磊[8]对单箱三室波形钢腹板PC组合箱梁剪力滞效应进行试验研究。李丽园[9]对单箱单室连续波形钢腹板箱梁剪力滞效应进行理论和试验研究。
从文献的检索可以看出,对混凝土箱梁[10-11]和单箱单室波形钢腹板PC组合箱梁的剪力滞效应研究很多,而对于单箱多室的波形钢腹板PC组合箱梁的剪力滞效应研究偏少。由于波[12-18]形钢腹板PC组合箱梁相比混凝土箱梁,波形钢腹板几乎承担截面的全部剪力,需考虑对波形钢腹板剪切模量的修正,并未考虑波形钢腹板本身的面外刚度、剪力连接部位影响。目前,单箱多室波形钢腹板PC组合箱梁在斜拉桥、连续梁(刚构)中的应用越来越多,那么对该结构的剪力滞效应的研究更有必要。所以为研究单箱多室波形钢腹板PC组合箱梁的剪力滞效应的影响,本文采用二次、三次抛物线定义了单箱双室、单箱三室波形钢腹板箱梁的纵向位移差函数,以满足剪力滞翘曲应力的轴向平衡条件,建立了考虑剪切变形影响的波形钢腹板组合箱梁剪力滞效应的控制微分方程组,推导出了简支梁、悬臂梁、连续梁在集中荷载、均布荷载作用下的解析解,并通过算例得出剪力滞效应在不同荷载作用下的分布规律。
1 单箱多室波形钢腹板PC组合箱梁剪力滞翘曲位移模式采用势能驻值原理分析单箱双室和单箱三室波形钢腹板剪力滞效应的时候,引入两个广义位移即竖向挠度ω(x)与纵向位移ui(x, y, z),表达式为:
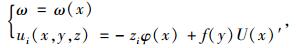
|
(1) |
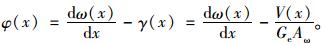
|
(2) |
式中, f(y)为剪力滞翘曲位移差函数; γ(x)为波形钢腹板组合箱梁的剪切应变平均值; Aω为波形钢腹板的横截面面积; Ge为波形钢腹板的有效剪切模量。
Samanta在文献[19]中给出波形钢腹板的剪切模量Ge应按式(3)进行修正计算:
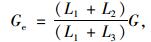
|
(3) |
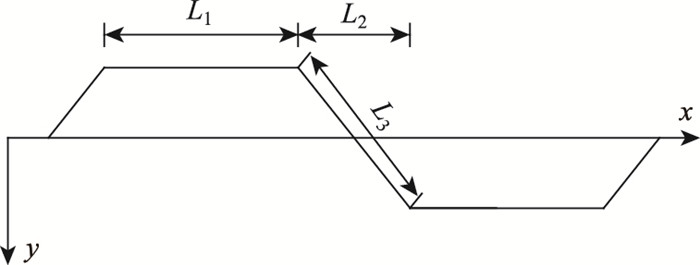
式中, G分别为钢板的剪切模量; L1,L2,L3为波形钢腹板的几何尺寸,如图 1所示。
|
| 图 1 波形钢腹板几何形状示意图 Fig. 1 Geometry of corrugated steel web |
| |
当波形钢腹板PC组合箱梁截面为单箱双室时,剪力滞翘曲位移函数f(y)(取二次抛物线为例)可以表示为:
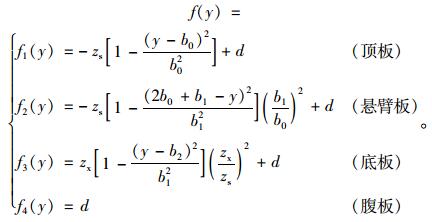
|
(4) |
d为满足全截面的轴力自平衡的附加轴力位移,b0,b1,b2如图 2所示。根据截面轴力为零的平衡条件∫A f(y)dA=0,得:
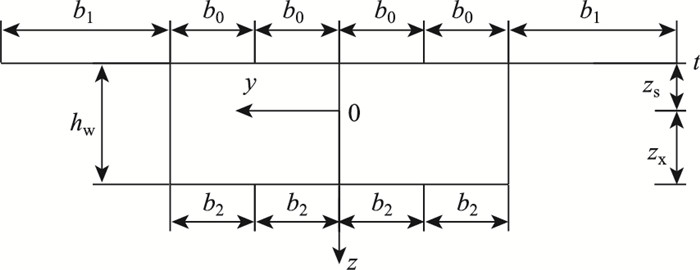
|
| 图 2 单箱双室波形钢腹板箱梁横截面图 Fig. 2 Cross-section of single-box double-cell box girder with corrugated steel webs |
| |
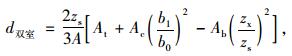
|
(5) |
式中, At=t×2b0,Ac=tb1,Ab=t×2b2。
当波形钢腹板PC组合箱梁截面为单箱三室时,如图 3所示,剪力滞翘曲位移函数f(y) (同样取二次抛物线为例)可以表示为:
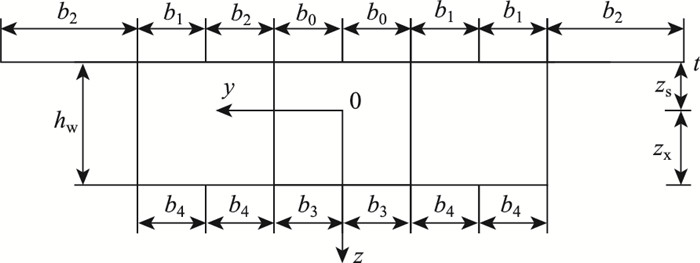
|
| 图 3 单箱三室波形钢腹板箱梁横截面图 Fig. 3 Cross-section of single-box three-cell box girder with corrugated steel webs |
| |
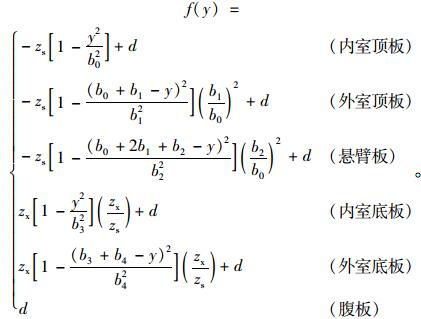
|
(6) |
同理得到:
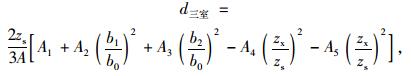
|
(7) |
式中,A1=tb0,A2=2tb1,A3=tb2,A4=tb3,A5=2tb4,A6=Aw。
当剪力滞翘曲位移函数取三次抛物线时,式(5)和式(7)中的2/3变为3/4,当取n次抛物线时,两式中2/3变为n/n+1。
2 建立控制微分方程组单箱双室波形钢腹板箱梁截面的外力势能为:
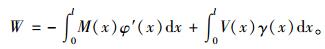
|
(8) |
剪力滞的腹板剪切应变能:
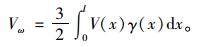
|
(9) |
顶底板的应变能:
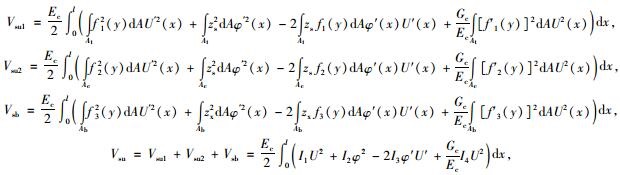
|
(10) |
式中, Ec,Gc分别为混凝土的弹性模量和剪切模量;
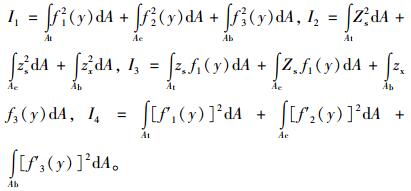
|
体系的总势能为:
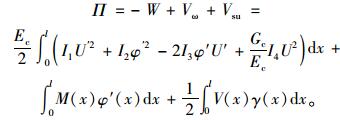
|
(11) |
令: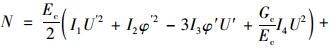
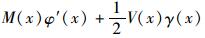
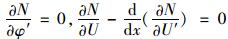
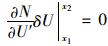
由上列各式得出的微分方程和边界条件为:
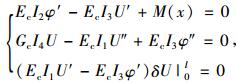
|
(12) |
得剪力滞微分方程:
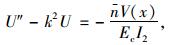
|
(13) |
式中,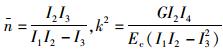
微分方程解的一般表达式:
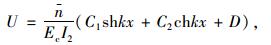
|
(14) |
式中,D为与剪力V(x)分布有关的特解;C1,C2由边界条件确定。
得到弯曲正应力:
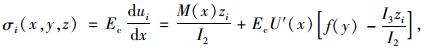
|
(15) |
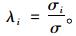
|
(16) |
同理得到与式(11)和式(15)一样的单箱三室箱梁的总势能表达式和弯曲正应力表达式。
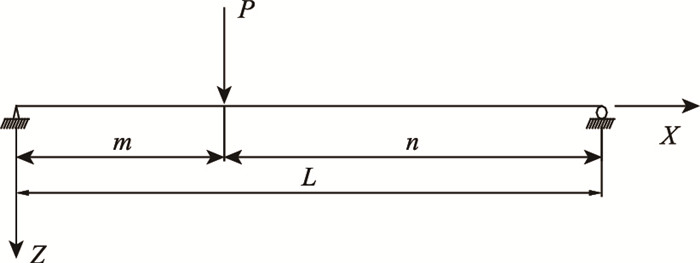
3 单箱多室波形钢腹板箱梁在不同荷载作用下的解析解 3.1 波形钢腹板简支梁在集中荷载作用下的剪力滞系数波形钢腹板简支梁在集中荷载作用下的剪力滞系数(见图 4)。
|
| 图 4 单箱多室波形钢腹板简支梁受集中荷载作用示意图 Fig. 4 Schematic diagram of single-box multi-cell simply supported beam with corrugated steel webs under concentrated load |
| |
当0≤x≤m时,M1(x)=ξPx V1(x)=ξP,其中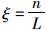
当m < x < l时,M2(x)=(m-ηx)P V2(x)=-ηP,其中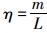
以上两种情况分别代入式(13),得

|
边界条件:(1)u′1|x=0=0;(2)u′2|x=l=0;(3)x=m, u1=u2;(4)从变分条件要求x=m时,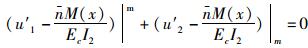
根据以上4个边界条件,代入得4个方程并求解得:
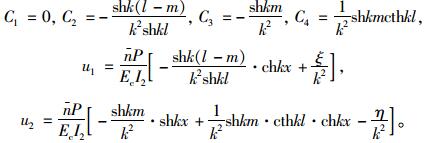
|
当0≤x≤m时,u1代入式(15),得:
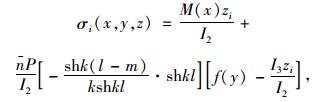
|
(17) |
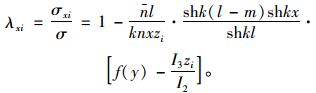
|
(18) |
当m < x < l时,u2代入式(15),得:
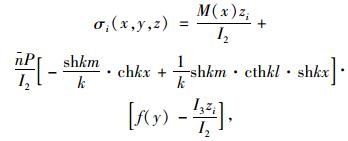
|
(19) |
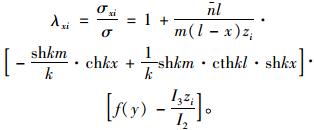
|
(20) |
波形钢腹板简支梁在均布荷载作用下的剪力滞系数(见图 5)。
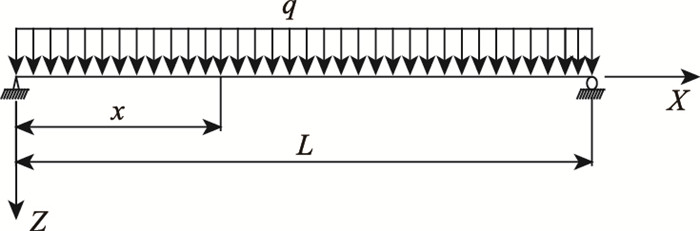
|
| 图 5 单箱多室波形钢腹板简支梁受均布荷载作用示意图 Fig. 5 Schematic diagram of single-box multi-cell simply supported beam with corrugated steel webs under uniformly distributed load |
| |
弯矩与剪力函数为: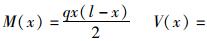
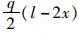
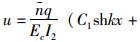
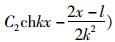
由边界条件u′1|x=0=0,u′1|x=l=0(弯矩为零)得,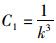
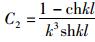
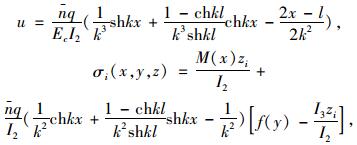
|
(21) |
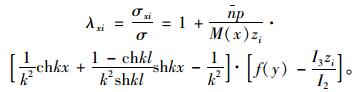
|
(22) |
波形钢腹板悬臂箱梁在集中荷载作用下的剪力滞系数(见图 6)。
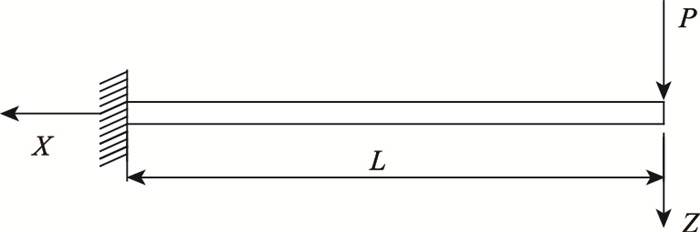
|
| 图 6 单箱多室波形钢腹板悬臂箱梁受集中荷载作用示意图 Fig. 6 Schematic diagram of single-box multi-cell cantilever beam with corrugated steel webs under concentrated load |
| |
弯矩与剪力函数为:M(x)=-Px V(x)=-P,代入(13)式求解得,
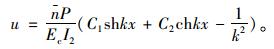
|
由边界条件u′|x=0=0,u|x=l=0(弯矩为零),得C1=0,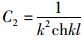
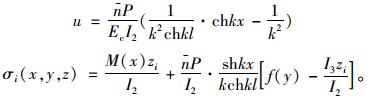
|
(23) |
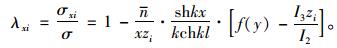
|
(24) |
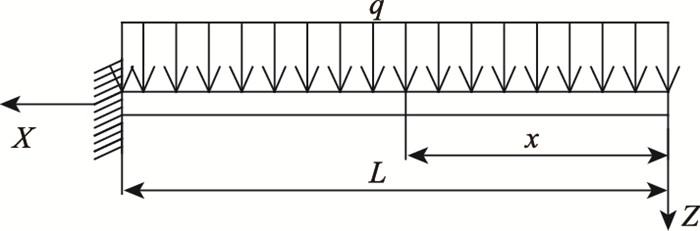
波形钢腹板悬臂箱梁在均布荷载作用下的剪力滞系数(见图 7)。
|
| 图 7 单箱多室波形钢腹板悬臂箱梁受均布荷载作用示意图 Fig. 7 Schematic diagram of single-box multi-cell cantilever beam with corrugated steel webs under uniformly distributed load |
| |
弯矩与剪力函数为: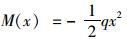
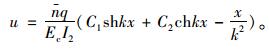
|
由边界条件u′|x=0=0,u|x=l=0(弯矩为零)得,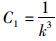
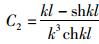
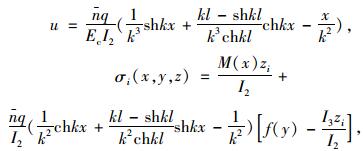
|
(25) |
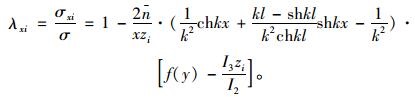
|
(26) |
波形腹板腹板连续梁在集中荷载作用下的剪力滞系数(见图 8)。
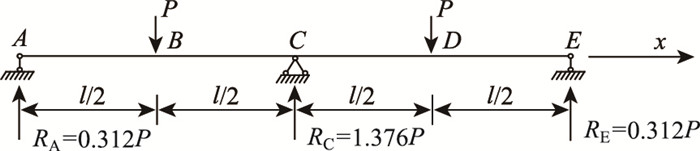
|
| 图 8 单箱多室波形钢腹板连续箱梁受集中荷载作用示意图 Fig. 8 Schematic diagram of single-box multi-cell continuous beam with corrugated steel webs under concentrated load |
| |
取一跨为研究对象(另一跨可根据对称性求得),其弯矩与剪力方程为分段函数:
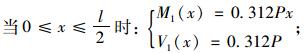
|
(27) |
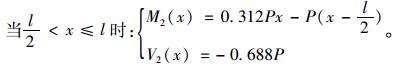
|
(28) |
剪力滞控制微分方程为:
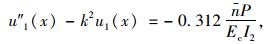
|
(29) |
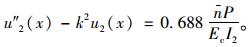
|
(30) |
上两式的通解分别为:
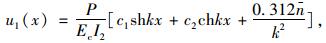
|
(31) |
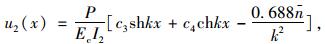
|
(32) |
式中,c1,c2,c3和c4为由边界条件确定的常数。
则边界条件为:
(1) u′1(x)|x=0=0;(2)u2(x)|x=l=0;
(3) 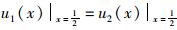
(4) 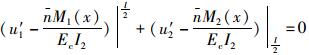
由边界条件可得c1,c2,c3和c4,代入式(31)及式(32)可得:
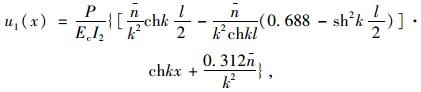
|
(33) |
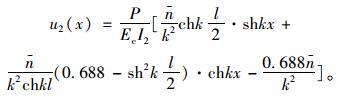
|
(34) |
将u1(x),u2(x)代入式(15)和式(16)可得该工况下各截面的弯曲正应力和剪力滞系数。
3.6 波形钢腹板连续箱梁在均布荷载作用下的剪力滞效应波形钢腹板连续箱梁在均布荷载作用下的剪力滞效应(见图 9)
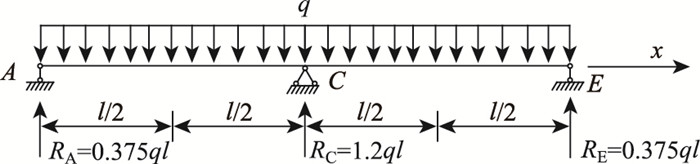
|
| 图 9 单箱多室波形钢腹板连续箱梁受均布荷载作用示意图 Fig. 9 Schematic diagram of single-box multi-cell continuous beam with corrugated steel webs under uniformly distributed load |
| |
图 9所示的为两跨受均布荷载作用下等截面波形钢腹板连续箱梁,以左跨为研究对象:
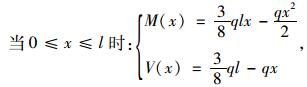
|
(35) |
微分方程为:
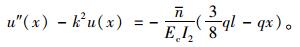
|
(36) |
式(36)的通解为:
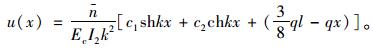
|
(37) |
边界条件为:u′(x)|x=0=0 u(x)|x=l=0。
将u(x)代入边界条件可得c1,c2并代入式(37)可得:
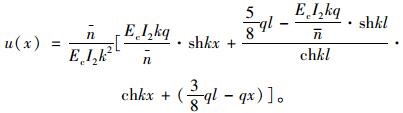
|
(38) |
同理,将u(x)代入式(15)和式(16)可得该工况下各截面的弯曲正应力和剪力滞系数。
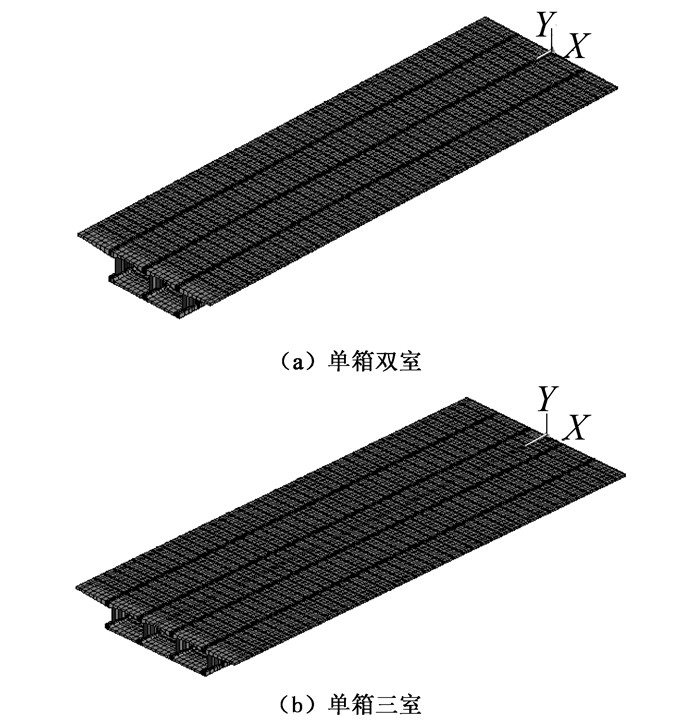
4 算例分析以文献[6]中的波形钢腹板PC组合箱梁桥为例,分别取跨径为30 m等截面的单箱双室和单箱三室简支梁进行计算,单箱双室和单箱三室横截面的结构计算具体尺寸参考文献[6],混凝土强度等级采用C50,波形钢腹板采用1200型的Q235钢材,分别建立ANSYS实体模型进行计算,箱梁的顶底板采用solid65实体单元,波形钢腹板采用shell63壳体单元,有限元模型如图 10所示。单箱双室箱梁分别在跨中作用集中荷载P=90kN如图 11(a)所示和均布荷载q=30 kN/m如图 12(a);单箱三室箱梁分别在跨中作用集中荷载P=90 kN,如图 11(b)所示,和均布荷载q=30 kN/m作用在横截面腹板对应的箱梁顶板部位如图 12(b)所示。本文通过建立各个工况下单箱多室的midas梁单元模型,已验证ANSYS模型[20]的计算值是可靠的。
|
| 图 10 实桥有限元模型 Fig. 10 Real bridge finite element model |
| |
|
| 图 11 集中荷载作用示意图 Fig. 11 Concentrated loads |
| |

|
| 图 12 均布荷载作用示意图 Fig. 12 Uniformly distributed loads |
| |
4.1 集中荷载作用于简支梁跨中截面剪力滞的效应
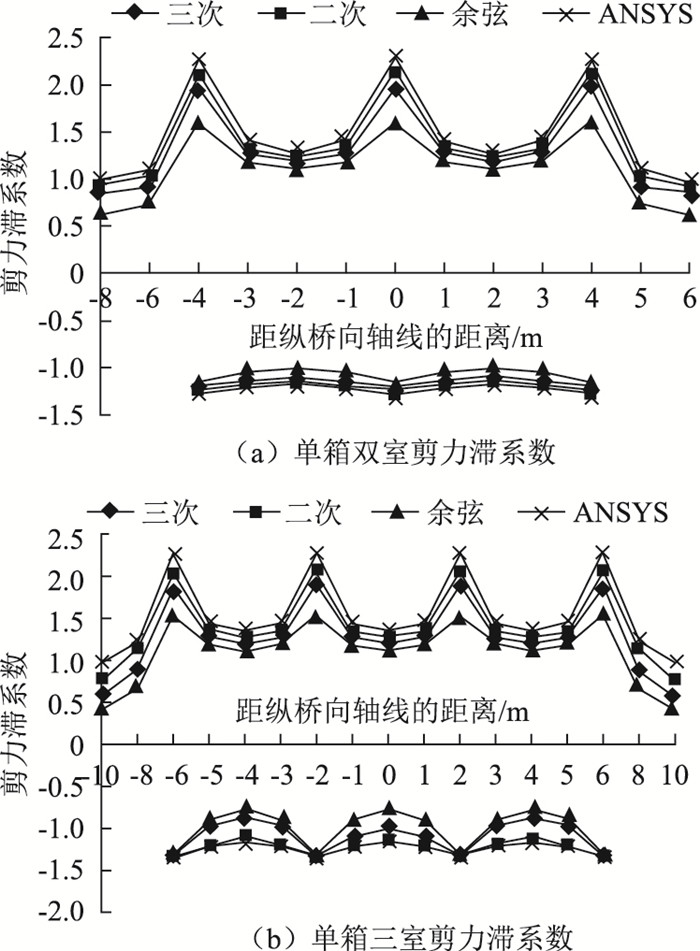
当简支梁在跨中作用集中荷载和满跨均布荷载时,其跨中的弯矩和变形是最大的部位,跨中的弯矩在集中荷载作用时为1/4Pl,在均布荷载作用时为1/4Pl2;利用本文的解析解和ANSYS的数值解得到单箱双室和单箱三室跨中截面的剪力滞系数,如图 13所示。
|
| 图 13 集中荷载作用时跨中截面的剪力滞系数 Fig. 13 Shear lag coefficients of midspan cross-section under concentrated load |
| |
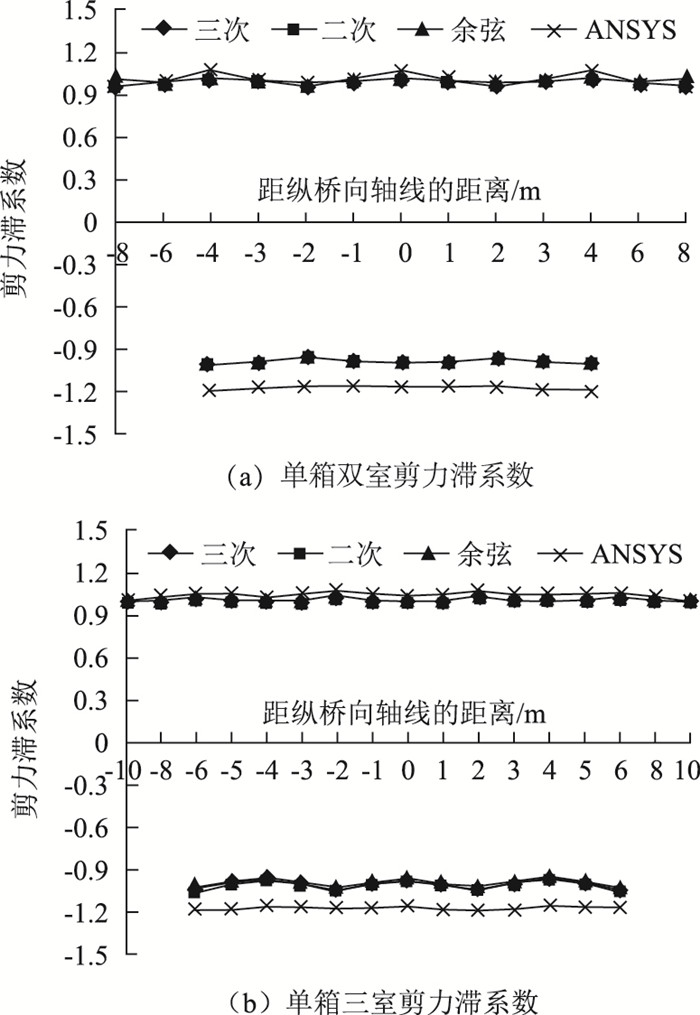
本文中剪力滞翘曲位移采用余弦函数时的值采用文献[6]中的理论进行计算,从图 13和图 14中看出,剪力滞翘曲位移采用二次、三次抛物线、余弦函数时和ANSYS数值解,在跨中集中荷载和均布荷载作用时都表现出同样的规律,波形钢腹板和顶底板交界处的剪力滞系数最大,随离腹板和顶底板交界处距离的增大而减小。在集中荷载作用工况下,翘曲位移函数采用二次抛物线时,与ANSYS计算值最接近,采用三次抛物线时次之,采用余弦函数时与ANSYS计算值相差最大,且两者在波形钢腹板与顶底板交接处和箱梁截面悬臂板边缘处的剪力滞系数相差最大。通过ANSYS计算值和理论值的比较,翘曲位移函数取二次抛物线更为合理,因为从波形钢腹板组合箱梁各翼缘板的面内剪切变形与纵向位移关系出发,可以推导出波形钢腹板PC组合箱梁各板面内剪切变形的翘曲位移函数是二次抛物线的形式,具体见另篇文章。
|
| 图 14 均布荷载作用时跨中截面的剪力滞系数 Fig. 14 Shear lag coefficients of midspan cross-section under uniformly distributed load |
| |
4.2 均布荷载作用于简支梁跨中截面剪力滞的效应
由图 14可以看出,在均布荷载作用下,翘曲位移函数采用二次、三次抛物线、余弦函数和ANSYS计算值在顶板处吻合程度良好,几乎完全重合;在底板处翘曲位移函数采用二次、三次抛物线、余弦函数的剪力滞系数要大于ANSYS的计算值。
在集中荷载和均布荷载作用下,翘曲位移函数取二次抛物线时,单箱双室箱梁剪力滞系数最大相差0.211,单箱三室箱梁剪力滞系数最大相差0.209,约为ANSYS计算值得1.13~1.22倍。由于未考虑波形钢腹板本身的面外刚度、剪力连接部位影响等,采用不同的连接方式,必然会使腹板对于顶底板的约束作用会有比较大的差别,对于整体框架体系的强弱会有影响,剪力滞后的效应等都会有差别,导致分析计算值和模拟值存在一定的差异。所以可引入修正系数1.2对结果进行调整,得到更为精确的结果。
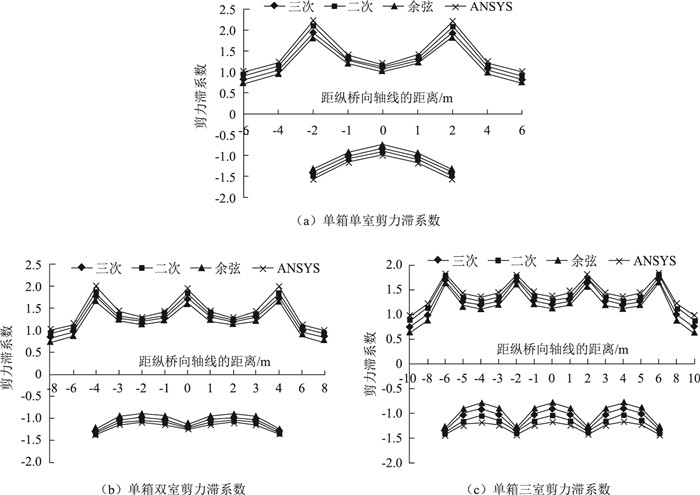
4.3 集中荷载作用于等跨连续梁跨中截面剪力滞的效应等跨连续箱梁在跨径为30 m简支梁的基础上,跨中増加一个支座,使简支梁变成连续梁;并在单箱双室截面的基础上减少一个室,桥面宽度也减少一个室的宽度,使单箱双室变成单箱单室截面,在单箱单室的跨中截面腹板与顶板交接处加载一对45 kN的集中力。由于简支梁在集中荷载作用下的剪力滞效应明显,所以本文只对连续梁在集中荷载作用下的剪力滞效应进行分析计算。单箱双室箱梁左右各跨分别在跨中加载图 11(a)所示集中荷载,单箱三室箱梁左右各跨分别在跨中加载图 11(b)所示集中荷载。
由图 15可以看出,等跨连续箱梁在受集中荷载作用时,翘曲位移函数采用二次、三次抛物线、余弦函数和ANSYS计算值在顶底板处变化趋势一致,吻合程度良好;同集中荷载作用于简支梁时一致,翘曲位移函数采用二次抛物线时,与ANSYS计算值最接近,采用余弦函数时与ANSYS计算值相差最大。且在相同荷载相同跨径的作用下,随着室数的增多,剪力滞系数在峰值上明显减少,单箱双室比单箱单室减少12%,单箱三室比单箱双室减少9%左右。从得到的剪力滞系数的数学表达式考虑,基本方程与室数并没有关系,但是随着箱梁室数的增多,腹板对于顶底板的约束作用变大,形成的整体框架体系强,整个箱梁的纵向抗弯刚度也随着得到了提高,导致剪力滞后的效应小。其次,随着箱梁室数的增加,顶、底板受力变得越来越均匀。
|
| 图 15 波形钢腹板连续箱梁受集中荷载作用跨中截面的剪力滞系数 Fig. 15 Shear lag coefficients of midspan cross-section of continuous box girder with corrugated steel webs under concentrated load |
| |
5 结论
本文以满足剪力滞翘曲应力的轴向平衡条件,定义了单箱双室、单箱三室波形钢腹板箱梁的纵向位移差函数,通过势能驻值原理的能量变分法建立了考虑剪力滞、剪切变形效应波形钢腹板PC组合箱梁的控制微分方程组,并推导出了简支梁、悬臂梁、连续梁在集中荷载、均布荷载作用下的解析解。通过解析法和有限元法分析了简支梁、连续梁在集中荷载和满跨均布荷载作用下的单箱多室的剪力滞效应的分布规律,结果表明:
(1) 本文采用二次、三次抛物线剪力滞翘曲位移函数推导的剪力滞系数解析解与余弦函数和ANSYS数值解,在跨中截面上集中荷载和均布荷载作用时都表现出同样的规律,在集中荷载作用下,翘曲位移函数采用二次抛物线时,与ANSYS计算值最接近,采用三次抛物线时次之,采用余弦函数时与ANSYS计算值相差最大,且两者在波形钢腹板与顶底板交界处和箱梁截面悬臂板边缘处的剪力滞系数偏差最大,所以翘曲位移函数取二次抛物线更为合理。
(2) 在集中和均布荷载作用下,翘曲位移函数采用二次、三次抛物线、余弦函数时,和ANSYS模拟值在顶板处吻合程度良好,在底板处解析解要大于ANSYS的模拟值,可引入修正系数1.2对结果进行调整,得到更为精确的结果。
(3) 在集中荷载作用于等跨连续梁时,同集中荷载作用于简支梁时变化趋势一致,吻合程度良好;翘曲位移函数采用二次抛物线时,与ANSYS计算值相差最小。且在相同荷载相同跨径的作用下,从单箱单室、单箱双室和单箱三室波形钢腹板PC组合箱梁的剪力滞系数的对比,得到随组合箱梁室数的增加,剪力滞系数减少。
(4) 在集中荷载和均布荷载作用下得到的剪力滞系数不同,当单箱双室和单箱三室箱梁在跨中作用集中荷载时,波形钢腹板与混凝土顶底板交接处的剪力滞效应尤为突出,应对此位置附近进行钢筋加密、相交部位的截面尺寸调整等措施,以减小弯曲应力,并应考虑此部位开裂情况,以避免桥梁的局部破坏。
| [1] |
郭金琼, 房贞政, 郑振. 箱形梁设计理论[M]. 北京: 人民交通出版社, 2008, 1-50. GUO Jin-qiong, FANG Zhen-zheng, ZHENG Zhen. Design Theory of Box Girder[M]. Beijing: China Communications Press, 2008, 1-50. |
| [2] |
冀伟, 蔺鹏臻, 刘世忠, 等. 波形钢腹板箱梁剪力滞效应的变分法求解[J]. 兰州交通大学学报, 2010, 29(6): 16-19. JI Wei, LIN Peng-zhen, LIU Shi-zhong, et al. Variational Principle of Shear Lag Effect of Composite Box Girders with Corrugated Steel Webs[J]. Journal of Lanzhou Jiaotong University, 2010, 29(6): 16-19. |
| [3] |
李立峰, 彭鲲, 王文. 波形钢腹板组合箱梁剪力滞效应的理论与试验研究[J]. 公路交通科技, 2009, 26(4): 78-83. LI Li-feng, PENG Kun, WANG Wen. Theoretical and Experimental Study on Shear Lag Effect of Composite Box Girder with Corrugated Steel Webs[J]. Journal of Highway and Transportation Research and Development, 2009, 26(4): 78-83. |
| [4] |
吴文清, 万水, 叶见曙, 等. 波形钢腹板组合箱梁剪力滞效应的空间有限元分析[J]. 土木工程学报, 2004, 37(9): 31-36. WU Wen-qing, WAN Shui, YE Jian-shu, et al. 3-D Finite Element Analysis on Shear Lag Effect in Composite Box Girder with Corrugated Steel Web[J]. |
| [5] |
周茂定, 刘世忠, 杨子江. 波形钢腹板组合箱梁剪力滞效应的比拟杆法求解[J]. 兰州交通大学学报, 2012, 31(4): 41-44. ZHOU Mao-ding, LIU Shi-zhong, YANG Zi-jiang. Bar Simulation Method on Shear Lag Effect of Composite Box Girder with Corrugated Steel Web[J]. Journal of Lanzhou Jiaotong University, 2012, 31(4): 41-44. |
| [6] |
陈水生, 田正龙, 桂水荣, 等. 单箱多室波形钢腹板箱梁剪力滞研究[J]. 公路交通科技, 2015, 32(7): 69-75. CHEN Shui-sheng, TIAN Zheng-long, GUI Shui-rong, et al. Research on Shear Lag of Single-box Multi-cell Girder with Corrugated Steel Webs[J]. Journal of Highway and Transportation Research and Development, 2015, 32(7): 69-75. |
| [7] |
王静. 单箱多室波形钢腹板箱梁的受力特性分析[D]. 西安: 长安大学, 2011. WANG Jing. Analysis on Mechanical Characteristics of Single-box Multi-cell Box Girder with Corrugated Steel Webs[D]. Xi'an: Chang'an University, 2011. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1947099 |
| [8] |
马磊, 周林云, 万水, 等. 单箱三室波形钢腹板箱梁剪力滞效应研究[J]. 中外公路, 2013, 33(3): 95-99. MA Lei, ZHOU Lin-yun, WAN Shui, et al. Research on Shear Lag Effect of 3-cell Single Box Girder with Corrugated Steel Webs[J]. Journal of China & Foreign Highway, 2013, 33(3): 95-99. |
| [9] |
李丽园. 波形钢腹板组合连续箱梁剪力滞效应的理论与试验研究[D]. 兰州: 兰州交通大学, 2012. LI Li-yuan. Theoretical and Experimental Research on Shear-lag Effect in Continuous Box Girder with Corrugated Steel Webs[D]. Lanzhou: Lanzhou Jiaotong University, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2155645 |
| [10] |
刘勇, 张丽, 张元海, 等. 单箱双室箱梁剪力滞效应的差分解[J]. 兰州交通大学学报, 2012, 31(3): 31-34. LIU Yong, ZHANG Li, ZHANG Yuan-hai, et al. Difference Solution for Shear Lag Effect of Twin-cell Box Girder[J]. Journal of Lanzhou Jiaotong University, 2012, 31(3): 31-34. |
| [11] |
雒敏, 蔺鹏臻, 孙理想. 单箱双室箱梁剪力滞效应分析[J]. 力学与实践, 2013, 35(6): 70-74. LUO Min, LIN Peng-zhen, SUN Li-xiang. Application of the Bar Simulation Method in the Study of Shear Lag Effect of Single Box Double Cell Box Girder[J]. Mechanics in Engineering, 2013, 35(6): 70-74. |
| [12] |
EVANS H R, AHMAD M K, KRISTEK H V. Shear Lag in Composite Box Girders of Complex Cross-sections[J]. Journal of Constructional Steel Research, 1993(24): 183-204. |
| [13] |
马磊, 万水, 蒋正文. 单箱多室波形钢腹板简支箱梁偏载系数简化计算方法[J]. 公路交通科技, 2017, 34(2): 62-67. MA Lei, WAN Shui, JIANG Zheng-wen. A Simplified Calculation Method for Eccentric Load Coefficient of Simply Supported Single-box Multi-cell Girder with Corrugated Steel Webs[J]. Journal of Highway and Transportation Research and Development, 2017, 34(2): 62-67. |
| [14] |
JIANG R J, AU F T K, XIAO Y F. Prestressed Concrete Girder Bridges with Corrugated Steel Webs:Review[J]. Journal of Structural Engineering, 2014, 141(2): 04014108. |
| [15] |
HASSANEIN M F, KHAROOB O F. Shear Buckling Behavior of Tapered Bridge Girders with Steel Corrugated Webs[J]. Engineering Structures, 2014, 74: 157-169. |
| [16] |
聂建国, 李法雄, 樊建生. 波形钢腹板变形计算的有效刚度法[J]. 工程力学, 2012(8): 71-79. NIE Jian-guo, LI Fa-xiong, FAN Jian-sheng. Effective Stiffness Method for Calculating Deflection of Corrugated Web Girder[J]. Engineering Mechanics, 2012(8): 71-79. |
| [17] |
刘保东, 任红伟, 李鹏飞, 等. 波纹钢腹板组合箱梁偏心增大系数计算方法[J]. 公路交通科技, 2012, 29(3): 80-85. LIU Bao-dong, REN Hong-wei, LI Peng-fei, et al. Calculation Methods of Eccentric Magnified Factor of Concrete Box Girder with Corrugated Steel Webs[J]. Journal of Highway and Transportation Research and Development, 2012, 29(3): 80-85. |
| [18] |
卫星, 杨世玉. 单箱双室波形钢腹板PC箱梁剪力滞效应分析[J]. 铁道工程学报, 2017, 3(3): 29-33. WEI Xing, YANG Shi-yu. Research on the Shear-lag Effect in Twin-cell PC Box-girder with Corrugated Steel Web[J]. Journal of Railway Engineering Society, 2017, 3(3): 29-33. |
| [19] |
SAMANTA A, MUKHOPADHYAY M. Finite Element Static and Dynamic Analyses of Folded Plates[J]. Engineering Structures, 1999, 21(3): 277-287. |
| [20] |
王新敏. ANSYS工程结构数值分析[M]. 北京: 人民交通出版社, 2007. WANG Xin-min. ANSYS Numerical Analysis of Engineering Structures[M]. Beijing: China Communi-cations Press, 2007. |
 2018, Vol. 35
2018, Vol. 35
