扩展功能
文章信息
- 韩州斌, 李东升, 杨洋
- HAN Zhou-bin, LI Dong-sheng, YANG Yang
- 等值张拉时基于振动法的平行钢绞线索索力测试分析
- Measurement and Analysis of Cable Tension of Parallel Strands under Equivalent Tension Based on Vibration Method
- 公路交通科技, 2018, 35(2): 55-61
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(2): 55-61
- 10.3969/j.issn.1002-0268.2018.02.008
-
文章历史
- 收稿日期: 2016-12-29
2. 安徽省交通规划设计研究总院股份有限公司, 安徽 合肥 230088
2. Anhui Transport Consulting & Design Institute Co., Ltd., Hefei Anhui 230088, China
索力是斜拉桥施工过程控制及运营期结构安全评估的重要指标[1-5]。由于受到张拉设备、材料参数的不确定性、外界环境及拉索自身的损伤与松弛等因素影响[6-8],索力会出现不同程度的损失,使斜拉桥出现安全隐患。索力测试能够及时掌握斜拉索的受力状态,是评估结构运营期安全性的重要途径。振动法因其操作简便、仪器可重复使用等优点,已成为索力测试中使用最广泛的方法[9-11]。
近年来,诸多学者对振动法测索力做了大量而深入的研究。徐霞飞等[12]从Bernoulli-Euler理论出发,推导了吊索在一般边界条件下的自由振动频率方程和索力的解析表达式。苏成等[13]通过有限元法及样条拟合方法成功地描述了索力与频率之间的关系。Kangas等[14]讨论了拉索垂度、拉索倾斜度、测试环境等因素对振动频率的影响。王荣辉等[15]通过试验标定法得出了索力张拉过程中拉索与频率回归线方程,证明了拉索与频率成二次比例关系。何伟等[16]建立了复杂边界条件下吊杆张力与其横向振动频率之间关系的隐式解析表达式,并给出表达式中各参数的确定方法。李枝军等[17]采用振动法对索力进行了测试,分析并讨论了索力测试的影响因素以及模型修正方法。孙增寿[18]等基于振动法对平行钢绞线索索力进行了测试并进行了有限元模拟。本文以杭埠河大桥为工程背景,对拉索-HDPE套管的区域性接触、垂度效应、索力不均匀等影响平行钢绞线索索力的因素进行讨论,建立拉索有限元模型来考虑各影响因素,并与现场实测索力进行对比。
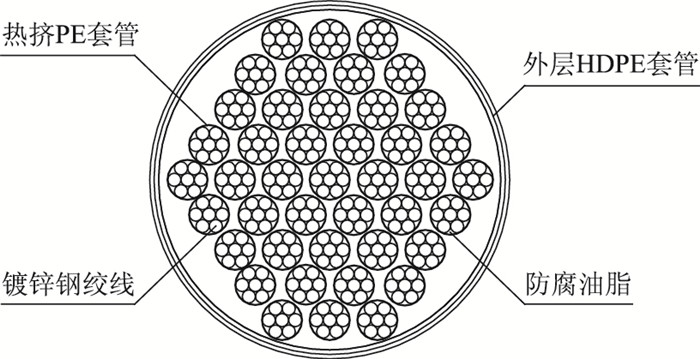
1 索力影响因素分析杭埠河大桥主桥为(130+130)m预应力混凝土独塔斜拉桥,主塔采用钢-混组合体系,主塔与主梁采用塔梁固结体系,全桥共设38对斜拉索。平行钢绞线索在外界激励作用下的振动十分复杂,由于拉索的垂度效应,各钢绞线既独立振动,又相互影响。在中间部位各拉索相互接触,在锚固端又相互离散,要准确量化这种关系是比较困难的。且在施工过程中,由于逐根张拉及人为操作等因素影响,各根钢绞线中索力并不是相同的。本文选取主桥南侧(S侧)第10号索下游侧(X侧)拉索作为研究对象,物理参数见表 1,钢绞线分布如图 1所示。
| 索号 | 规格 | 索长/m | 倾角/(°) | 初拉力/kN | 弹性模量/GPa | 换算直径/mm |
| S10X | 43-ϕ15.2 | 92.57 | 42.918 3 | 3 255 | 1.95 | 87.236 |
|
| 图 1 S10X钢绞线横断面图 Fig. 1 Cross section of cable S10X |
| |
1.1 斜拉索垂度
许多学者在考虑垂度效应时,都是将斜拉索作为一个整体,其线形用二次抛物线或者悬链线来代替,在假定的边界条件下,推导出拉索的索力计算公式。然而在实际工程中,一束钢绞线中各根拉索中实际拉力并不均匀,其线形也不尽相同。随着斜拉桥跨径的不断增大,单束拉索中拉索根数不断增加,索力计算和拉索数值模拟中采用固定的抛物线或者悬链线代替实际拉索的线形并不准确,且工作量繁重。因此本文采用修正拉索弹性模量的方法考虑拉索垂度效应。其Ernst公式见式(1):
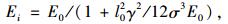
|
(1) |
式中,Ei为修正弹性模量;E0为不考虑拉索垂度时的弹性模量;γ为拉索重度;l0为拉索水平投影长度;σ为拉索中的应力。
1.2 钢绞线及套管间区域性接触在重力作用下,钢绞线会产生垂度效应,使其在部分区域里相互接触。平行钢绞线索采用多层防腐体系,一般由防腐油脂、热挤PE套管以及耐腐蚀的HDPE套管组成。HDPE套管抗弯刚度较小,外包在钢绞线上时,在拉索中间区域会搭在最上层索体上,拉索振动也会引起套管振动。因索长及拉索拉力的不同,拉索自身以及与套管之间的实际接触区域无法准确测量。因此,在建立模型时,采用逐步扩大接触区域的方法去修正所建立的初始平行钢绞线索模型,使得接触区域能够较为真实地反映实际接触情况。
1.3 索力的不均匀性由于逐根张拉以及人为控制误差,钢绞线中拉力并不均匀,且后张拉的钢绞线对先张拉的钢绞线有卸载作用。由于张拉一根钢绞线,结构变位很难准确测量和计算,工程中是将张拉力平均分配到每根钢绞线上。《公路斜拉桥设计细则》中规定:拉索张拉完成后,索力值与设计值误差不能大于5%。本文假定:拉索之间的卸载作用是线性的,且最大值与最小值之间误差为5%。因此,可认为最后张拉的一根钢绞线索力没有损失,取总张拉力的平均值,其余钢绞线索力可通过差值得到。如图 1所示,从左至右,从上至下依次对钢绞线进行编号,各根钢绞线索力的取值见表 2。
| 编号 | 索值/kN |
| 1 | 72.752 |
| 2 | 72.843 |
| 3 | 72.935 |
| 4 | 73.026 |
| 5 | 73.117 |
| 6 | 73.208 |
| 7 | 73.299 |
| 8 | 73.391 |
| 9 | 73.482 |
| 10 | 73.573 |
| 11 | 73.664 |
| 12 | 73.755 |
| 13 | 73.846 |
| 14 | 73.938 |
| 15 | 74.029 |
| 16 | 74.120 |
| 17 | 74.211 |
| 18 | 74.302 |
| 19 | 74.393 |
| 20 | 74.485 |
| 21 | 74.576 |
| 22 | 74.667 |
| 23 | 74.758 |
| 24 | 74.849 |
| 25 | 74.940 |
| 26 | 75.032 |
| 27 | 75.123 |
| 28 | 75.214 |
| 29 | 75.305 |
| 30 | 75.396 |
| 31 | 75.487 |
| 32 | 75.579 |
| 33 | 75.670 |
| 34 | 75.761 |
| 35 | 75.852 |
| 36 | 75.943 |
| 37 | 76.034 |
| 38 | 76.126 |
| 39 | 76.217 |
| 40 | 76.308 |
| 41 | 76.399 |
| 42 | 76.490 |
| 43 | 76.581 |
2 平行钢绞线索有限元模拟
平行钢绞线分布的离散性、接触区域的未知性及索力的不均匀性导致了实际索力测试中存在诸多困难,因此准确合理地考虑各影响因素是索力测试与分析的关键。本文选取杭埠河大桥S10号下游侧索,分别建立拉索和拉索-HDPE套管接触耦合有限元模型。采用beam188单元模拟斜拉索。shell63弹性壳单元模拟HDPE套管,弹性模量取155 MPa。对于拉索上的索夹以及HDPE套管上的钢导管均采用mass21单元模拟,并按实际质量取值,且索夹的位置附近30 cm范围内的钢绞线按全部耦合处理。钢绞线与HDPE套管之间的接触用耦合自由度方式处理。为了真实反映平行钢绞线索的空间振动行为,按照实际尺寸对拉索进行细化离散,不考虑HDPE套管时拉索模型如图 2所示。

|
| 图 2 S10X拉索有限元模型 Fig. 2 Finite element model of cable S10X |
| |
2.1 钢绞线间离散性与索力不均匀影响
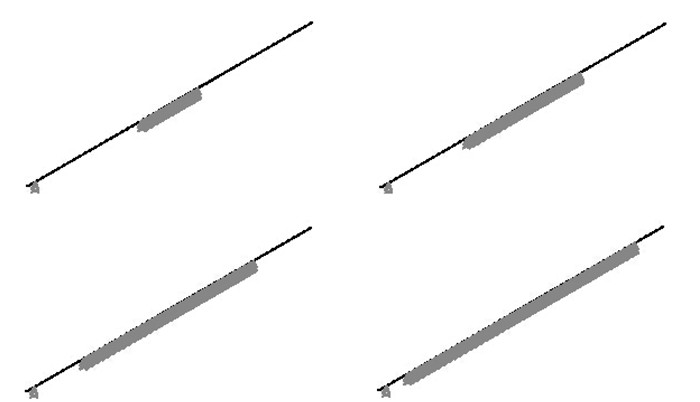
平行钢绞线索接触区域主要集中在中间部位,并向两边逐步延伸,且并没有全部接触。为合理考虑平行钢绞线的离散性对索力测试的影响,本文采用耦合中间一点、耦合中间1/5区域、耦合中间2/5区域、耦合中间3/5区域以及耦合中间4/5区域逐步考虑钢绞线间的相互影响。其接触区域如图 3所示。采用耦合竖向自由度模拟索中各根钢绞线之间的接触,对应输入表 2中给出的不均匀索力值,并在索夹位置30 cm范围内耦合拉索所有自由度时,拉索的前五阶竖向振动频率见表 3。可以看出:
|
| 图 3 S10X拉索接触区域图 Fig. 3 Contact area of cable S10X |
| |
| 竖弯阶数 | 整索频率f0 | 单根钢绞线频率f1 | 钢绞线区域性接触 | |||||||||
| 中间一点f2 | f2/f1 | 1/5区域f3 | f3/f1 | 2/5区域f4 | f4/f1 | 3/5区域f5 | f5/f1 | 4/5区域f6 | f6/f1 | |||
| 1 | 1.422 | 1.426 | 1.422 | 0.997 | 1.423 | 0.998 | 1.422 | 0.997 | 1.422 | 0.997 | 1.422 | 0.997 |
| 2 | 2.844 | 2.853 | 2.835 | 0.994 | 2.843 | 0.996 | 2.844 | 0.997 | 2.845 | 0.997 | 2.843 | 0.996 |
| 3 | 4.268 | 4.279 | 4.263 | 0.996 | 4.266 | 0.997 | 4.264 | 0.996 | 4.262 | 0.996 | 4.267 | 0.997 |
| 4 | 5.695 | 5.706 | 5.674 | 0.994 | 5.693 | 0.998 | 5.654 | 0.991 | 5.682 | 0.996 | 5.688 | 0.997 |
| 5 | 7.127 | 7.133 | 7.125 | 0.999 | 7.122 | 0.998 | 7.118 | 0.998 | 7.122 | 0.998 | 7.124 | 0.999 |
(1) 随着接触区域的增大,钢绞线不同接触区域同阶次振动频率变化较小,且越来越接近整体索的振动频率。
(2) 单根钢绞线与整体索振动频率基本一致,随着阶数增加,其差值变大,但一阶振动频率相差较小。
(3) 只有中间一点接触时,钢绞线间接触区域较小,在正对称振型时,各根钢绞线可以同时起振,其振动频率相差不大。反对称振型时,由于各根钢绞线间既独立振动又相互干扰,振动频率存在误差。
以钢绞线中间3/5接触区域为例,其前四阶振型如图 4所示。可以看出,各根钢绞线振型较为规整,切向滑移可以忽略,在反对称振型时也没出现较大的相互干扰。由上述分析可知,钢绞线间的离散性以及索力的不均匀性对索力测试的影响较小,可以采用振动法对平行钢绞线索索力进行测试。

|
| 图 4 5接触区域时S10X索前四阶振型 Fig. 4 The first 4 vibration modes of cable S10X with intermediate 3/5 contact area |
| |
2.2 HDPE套管影响
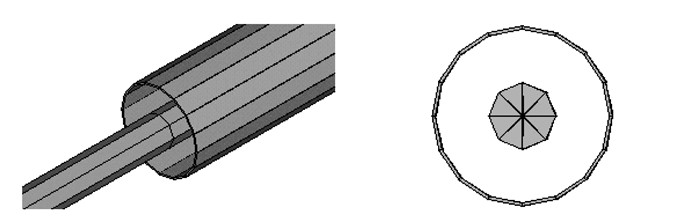
HDPE套管属于柔性结构,在自重作用下,直接搭在最上层索体上,并随拉索一起振动,其振动形式属于受迫振动。在索力测试时,尤其是成桥以后,一般是将拾振器固定在套管上拾取拉索的振动加速度,因此,有必要对HDPE套管对拉索振动的影响进行研究。本文采用耦合中间2/5区域、中间3/5区域、中间4/5区域以及全部接触来模拟索体与套管之间的相互作用,并与修正拉索线密度的方法进行对比。拉索与套管接触模型如图 5所示,不同接触区域下,拉索与套管整体振动频率见表 4。可以看出,随着接触区域的增大,拉索不同接触区域同阶次振动频率逐渐减小,HDPE套管对拉索振动影响逐渐增大。对于中间4/5接触区域,其基频与整索振动基频相差1.4%。但相同接触区域各阶次振动频率差值基本与对应基频一致。因此,在索力测试时,应考虑HDPE套管的影响以减小索力测试的误差。
|
| 图 5 S10X索与HDPE套管接触模型 Fig. 5 Model of contact between cable S10X and HDPE casing |
| |
| 索号 | 竖弯阶数 | 整索频率f0 | 钢绞线-HDPE套管区域性接触 | |||||
| 2/5区域f7 | f7/f0 | 3/5区域f8 | f8/f0 | 4/5区域f9 | f9/f0 | |||
| S10X | 1 | 1.422 | 1.416 | 0.996 | 1.408 | 0.990 | 1.402 | 0.986 |
| 2 | 2.844 | 2.834 | 0.996 | 2.823 | 0.993 | 2.811 | 0.988 | |
| 3 | 4.268 | 4.258 | 0.998 | 4.249 | 0.996 | 4.223 | 0.989 | |
| 4 | 5.695 | 5.685 | 0.998 | 5.653 | 0.993 | 5.627 | 0.988 | |
| 5 | 7.127 | 7.114 | 0.998 | 7.105 | 0.997 | 7.004 | 0.983 | |
以钢绞线-套管中间耦合3/5区域为例,前四阶振型如图 6所示。可以看出,拉索振型较为规整,但随着阶次的增加,在拉索非接触区域,套管的振动愈加明显,但对拉索整体振型影响较小。

|
| 图 6 钢绞线-套管中间耦合3/5区域时系统前四阶振型 Fig. 6 The first 4 vibration modes of strand-casting coupling with 3/5 contact area |
| |
随着接触区域的增加,套管对拉索的振动频率影响逐渐增大。根据实际工程经验,拉索与套管之间的接触区域在一半以上,由表 4可知,套管对拉索振动频率的影响较大。拉索在自重作用下直接搭在最上层索体上,可采用修正拉索线密度方法考虑套管对拉索振动特性的影响,换算后的拉索线密度为49.093 kg/m。修正后的计算频率以及耦合计算频率见表 5。可以看出:修正拉索线密度后计算的索体振动频率与钢绞线-套管全部耦合时各阶次振动频率基本一致,在索力测试中可以考虑修正拉索线密度。
| 索号 | 竖弯阶数 | 整索频率f0 | HDPE重量计入索线密度f11 | 钢绞线-HDPE套管区域性接触 | |||||
| 4/5区域f9 | f9/f0 | f9/f11 | 全部接触f10 | f10/f0 | f10/f11 | ||||
| S10X | 1 | 1.422 | 1.396 | 1.402 | 0.986 | 1.004 | 1.397 | 0.982 | 1.001 |
| 2 | 2.844 | 2.793 | 2.811 | 0.988 | 1.006 | 2.796 | 0.983 | 1.001 | |
| 3 | 4.268 | 4.192 | 4.223 | 0.989 | 1.007 | 4.194 | 0.983 | 1.000 | |
| 4 | 5.695 | 5.593 | 5.627 | 0.988 | 1.006 | 5.591 | 0.982 | 1.000 | |
| 5 | 7.127 | 6.998 | 7.004 | 0.983 | 1.001 | 6.995 | 0.981 | 1.000 | |
3 斜拉索测试试验
于所有斜拉索二次张拉完成后,对全桥进行了索力测试。索力计算采用式(2):
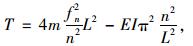
|
(2) |
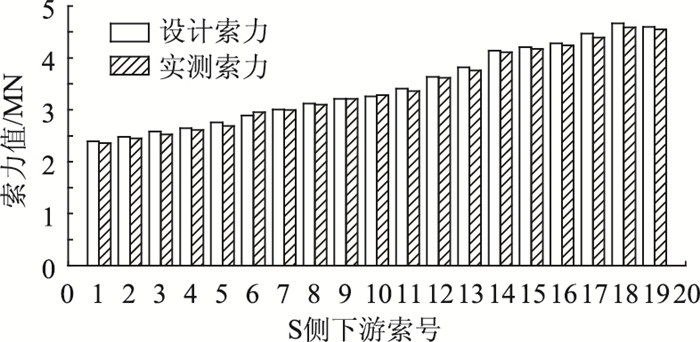
式中,T为拉索所受的轴向力;m为拉索单位长度的质量;EI为拉索的弯曲刚度;fn为拉索的第n阶振动频率;n为振动阶次;L为拉索的长度。考虑HDPE套管质量,索力计算过程中采用修正拉索线密度。结果显示,修正后的实测索力更接近设计索力,且随着索长的增加,套管的影响也越明显。S10X索力计算结果见表 6,S侧下游索力测试结果如图 7。
| 拉索编号 | 设计索力/kN | 实测索力 | |||
| 不考虑套管/kN | 误差 | 考虑套管/kN | 误差 | ||
| S10X | 3 255 | 3 157 | -3.01% | 3 286 | 0.95% |
|
| 图 7 S侧下游索修正拉索线密度后实测索力与设计索力对比 Fig. 7 Comparison between measured cable force and designed cable force of downstream cable of S side after modifying line density |
| |
4 索力测试中的几个问题讨论 4.1 自振频率的确定
索力计算过程中,最关键的步骤就是根据实测振动数据确定拉索的振动频率fn及其对应的阶数n。在环境激励下,拉索做多个模态的复合运动,实测数据频谱显示,拉索振动的低阶自振分量较少,高阶自振分量较多。索力测试中拾振器一般是放置在拉索靠近梁端的位置,此位置是拉索的低阶频率对应振幅较小的位置,在频谱图上,拉索的低阶振动频率和基频很难分辨。
根据弦理论,拉索各阶自振频率是其基频的整数倍,即fn/n是基频,反映在频谱上是各相邻阶次频率之差。由于索力测试的局限性及拉索振动的独特性,在频谱上很难分辨各阶次自振频率对应的阶次。因此本次测试选取频谱上峰值最高点作为基准频率,选出清晰可辨的振动频率,相邻的频率值两两作差后求其均值,以基准频率与此均值的比值作为基准频率的阶次。由于频率选取对索力计算精度影响较大,应尽量选取低阶自振频率计算索力。
4.2 面内、面外振动的计算精度拉索-主塔-主梁之间的耦合振动是十分复杂的,尤其在主梁施工过程中,实测数据显示:
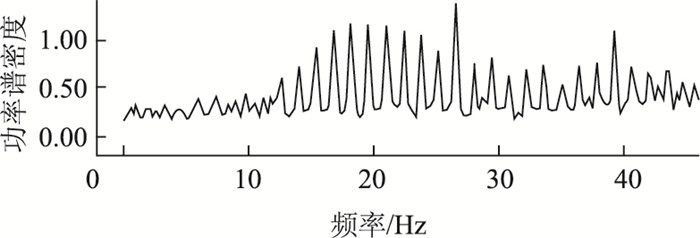
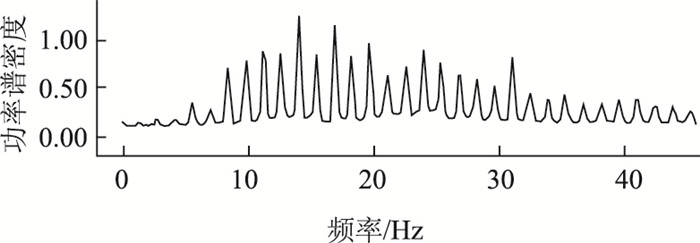
(1) 单根钢绞线频谱如图 8与图 9所示,可以看出:拉索面外振动的低阶分量和高阶分量都较为明显,面内振动高阶分量较多,低阶分量较少。
|
| 图 8 单根钢绞线面内振动频谱 Fig. 8 In-plane vibration spectrum of single steel strand |
| |
|
| 图 9 单根钢绞线面外振动频谱 Fig. 9 Out-plane vibration spectrum of single steel strand |
| |
(2) 拉索面内振动受主梁振动影响较大,不利情况下,主梁振动会引起实测拉索频率的失真。面外振动与主梁振动相关性很小,此时,拉索主要以自身频率振动,受主梁振动影响较小。
(3) 施工过程中引起主梁较大振动时,面内振动受其影响较大,面外振动受影响较小。因此,可以根据拉索面外振动数据,确定振动频率以计算出正确合理的索力值。
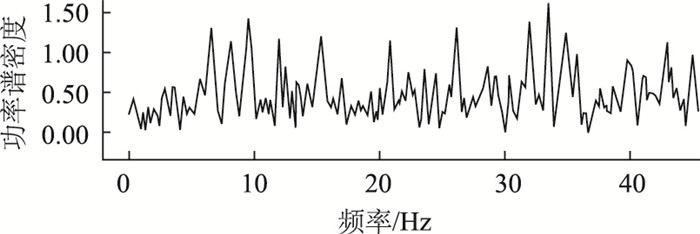
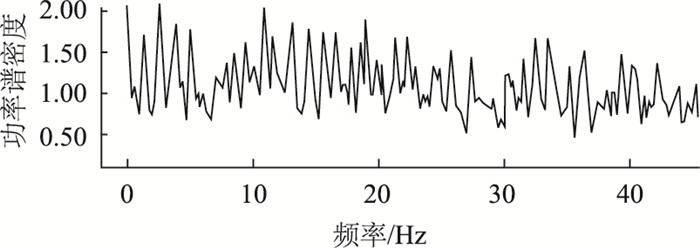
4.3 拾振器不同放置位置影响本次索力测试将拾振器固定在HDPE套管及拉索索夹(距拉索锚固端约4 m)上分别拾取了拉索的振动数据,实测数据频谱如图 10与图 11所示。可以看出,将拾振器放置在套管上,拉索低阶振动分量较为明显且易分辨。将其放置在索夹上,拉索振动分量不明显且不易分辨。因此,在索力测试过程中,可将拾振器固定在套管上,应多次测量来测量消除误差,且在条件容许的情况下,应尽量将拾振器布置在远离拉索锚固端位置以得到更为明显的拉索低阶振动特性。
|
| 图 10 拾振器在索夹时面外振动频谱 Fig. 10 Out-plane vibration spectrum with sensor at cable clamp |
| |
|
| 图 11 拾振器在HDPE套管时面外振动频谱 Fig. 11 Out-plane vibration spectrum with sensor at HDPE casing |
| |
5 结论
(1) 振动法可以用于平行钢绞线索索力测试,索力计算时应尽量采用低阶频率。
(2) HDPE套管对拉索振动影响较大,索力计算时根据套管质量修正拉索线密度,可以提高索力计算精度。
(3) 钢绞线间的离散性和索力不均匀性对拉索振动影响较小,相对于面内振动,钢绞线面外振动频谱特征更为明显,低阶振动分量较多且易识别,索力计算中可以根据面外振动确定钢绞线振动频率。
| [1] |
罗勋. 频率法测定斜拉索索力若干问题的研究[D]. 成都: 西南交通大学, 2009: 44-51. LUO Xun. Study on Measurement of Cable Tension by Frequency Method[D]. Chengdu: Southwest Jiaotong University, 2009: 44-51. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1573042 |
| [2] |
李凤臣. 大跨度桥梁斜拉索的参数振动及索力识别研究[D]. 哈尔滨: 哈尔滨工业大学, 2009: 139-162. LI Feng-chen. Parametric Vibration and Cable Force Identification of Staying Cable of Large-span Bridges[D]. Harbin: Harbin Institute of Technology, 2009: 139-162. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D269208 |
| [3] |
程检廷, 张俊平, 张力文. 猎德大桥吊索张拉施上方案分析与优化[J]. 中外公路, 2011, 31(6): 172-175. CHENG Jian-ting, ZHANG Jun-ping, ZHANG Li-wen. Analysis and Optimization of Hanger Tensioning Construction Scheme of Liede Bridge[J]. Journal of China & Foreign Highway, 2011, 31(6): 172-175. |
| [4] |
冉志红, 李乔. 提高斜拉索索力估算精度的一种新方法[J]. 公路交通科技, 2007, 24(8): 96-98. RAN Zhi-hong, LI Qiao. A New Method to Enhance the Estimation Accuracy of Stay Cable Tension[J]. Journal of Highway and Transportation Research and Development, 2007, 24(8): 96-98. |
| [5] |
张志伟. 自锚式悬索桥索鞍无预偏施工吊杆张拉的优化研究[J]. 世界桥梁, 2011(2): 34-37. ZHANG Zhi-wei. Optimization Research of Construction of Hanger Tensioning for Self-anchored Suspension Bridge with No Pre-offsetting of Cable Saddles[J]. World Bridges, 2011(2): 34-37. |
| [6] |
柯红军, 李传习, 刘建. 平胜大桥自锚式悬索桥静载试验与评价[J]. 公路交通科技, 2009, 26(2): 53-59. KE Hong-jun, LI Chuan-xi, LIU Jian. Static Loading Test and Assessment of Pingsheng Self-anchored Suspension Bridge[J]. Journal of Highway and Transportation Research and Development, 2009, 26(2): 53-59. |
| [7] |
闫维明, 许晓建, 李勇, 等. 基于振动频率法和优化功能的斜拉索索力测试研究[J]. 公路交通科技, 2015, 32(11): 61-67. YAN Wei-ming, XU Xiao-jian, LI Yong, et al. Cable Force Measurement Based on Vibration Frequency Method and Optimization Function[J]. Journal of Highway and Transportation Research and Development, 2015, 32(11): 61-67. |
| [8] |
吉伯海, 陈苗, 傅中秋, 等. 基于振动频率法的斜拉桥索力测试影响因素[J]. 中南大学学报:自然科学版, 2015, 46(7): 2620-2625. JI Bo-hai, CHEN Miao, FU Zhong-qiu, et al. Influential Factors in Cable Force Measurement of Cable-stayed Bridges Based on Vibration Frequency Method[J]. Journal of Central South University:Science and Technology Edition, 2015, 46(7): 2620-2625. |
| [9] |
张卓杰, 王荣辉, 甄晓霞, 等. 平行钢绞线斜拉索索力测试方法评价[J]. 桥梁建设, 2016, 46(2): 42-47. ZHANG Zhuo-jie, WANG Rong-hui, ZHEN Xiao-xia, et al. Evaluation of Measurement Methods for Tension of Parallel Steel Strand Stay Cables[J]. Bridge Construction, 2016, 46(2): 42-47. |
| [10] |
FANG Z, WANG J Q. Practical Formula for Cable Tension Estimation by Vibration Method[J]. Journal of Bridge Engineering, 2012, 17(1): 161-164. |
| [11] |
ZUI H, SHINKE T, HAMAZAKI Y. Improved Practical Formulas for Estimation of Cable Tension by Vibration Method[J]. Journal of Structural Engineering, 1996, 122(6): 651-656. |
| [12] |
徐霞飞, 任伟新. 边界条件对吊索索力估算的影响[J]. 铁道科学与工程学报, 2008, 5(6): 26-31. XU Xia-fei, REN Wei-xin. Effect of Boundary Conditions on the Estimation of Suspender Tension[J]. Journal of Railway Science and Engineering, 2008, 5(6): 26-31. |
| [13] |
苏成, 徐郁峰, 韩大建. 频率法测量索力中的参数分析与索抗弯刚度的识别[J]. 公路交通科技, 2005, 22(5): 75-78. SU Cheng, XU Yu-feng, HAN Da-jian. Parameter Analysis and Identification of Bending Stiffness of Cables During Tension Measurements by Frequency Method[J]. Journal of Highway and Transportation Research and Development, 2005, 22(5): 75-78. |
| [14] |
KANGAS S, HCLMICKI A, HUNT V, et al. Cable-Stayed Bridges:Case Study for Ambient Vibration-Based Cable Tension Estimation[J]. Journal of Bridge Engineering, 2012, 17(6): 839-846. |
| [15] |
王荣辉, 薛礼建. 矮塔斜拉桥索力测试方法研究[J]. 中外公路, 2011, 31(2): 116-120. WANG Rong-hui, XUE Li-jian. Study on Test Method of Cable Tension of Low Tower Cable-stayed Bridge[J]. Journal of China & Foreign Highway, 2011, 31(2): 116-120. |
| [16] |
何伟, 陈淮, 王博, 等. 复杂边界条件下基于频率法的吊杆张力测定研究[J]. 土木工程学报, 2012, 45(3): 93-98. HE Wei, CHEN Huai, WANG Bo, et al. Study of Suspender Tension Measurement Based on Frequency Method with Complex Boundary Conditions[J]. China Civil Engineering Journal, 2012, 45(3): 93-98. |
| [17] |
李枝军, 李爱群, 缪长青, 等. 运营状态下南京长江二桥拉索索力测试与分析[J]. 东南大学学报:自然科学版, 2007, 37(6): 1057-1060. LI Zhi-Jun, LI Ai-qun, MIAO Chang-qing, et al. Measurement and Analysis of Cable Tension in the Second Nanjing Yangtze River Bridge under Running Condition[J]. Journal of Southeast University:Natural Science Edition, 2007, 37(6): 1057-1060. |
| [18] |
孙增寿, 赵云鹏, 秦磊. 基于频率法的平行钢绞线索索力测试研究[J]. 铁道科学与工程学报, 2014, 11(3): 17-22. SUN Zeng-shou, ZHAO Yun-peng, QIN Lei. Research of Tension Measurement of Parallel Steel Stranded Wire Cable Based on Frequency Method[J]. Journal of Railway Science and Engineering, 2014, 11(3): 17-22. |
 2018, Vol. 35
2018, Vol. 35
