扩展功能
文章信息
- 郝丽, 胡大伟, 李晨
- HAO Li, HU Da-wei, LI Chen
- T-JIT环境下企业供应链中采购管理供应商选择和订单分配
- Supplier Selection and Order Allocation of Purchasing Management for Enterprise Supply Chain in T-JIT Environment
- 公路交通科技, 2018, 35(1): 149-158
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(1): 149-158
- 10.3969/j.issn.1002-0268.2018.01.020
-
文章历史
- 收稿日期: 2016-10-12
2. 山东公路技师学院, 山东 济南 250104
2. Shandong Institute of Highway Technician, Jinan Shandong 250104, China
随着时代的变迁,高效率、绿色化、可持续成为当代社会发展的标签。汽车制造业从20世纪早期的粗放型生产转变为后期的精益生产,可以达到降低库存、节约成本、灵活可靠的目的。多样化精益生产对质量、人的作用和客户个性化的要求很高,适应多品种小批量的生产模式。日本丰田公司在1973年针对精益生产提出丰田生产方式——准时化(JIT)和自动化是主要精髓。文献[1]将丰田生产方式命名为精益生产, 以零库存为目标不断优化生产量。JIT管理思想已经扩展到JIT生产、JIT采购、JIT运输、JIT存储、JIT预测等领域。美国几乎所有企业早已采用JIT管理模式,并带来巨大效益,而在我国,JIT管理思想已被个别大型供应链企业采用并取得良好效果。Total Just In Time (T-JIT)是近年来最新的研究领域,文献[2]首次提出并定义为JIT生产、JIT采购、JIT销售,新增加了带JIT信息的一种集成供应链管理策略,研究了T-JIT对整个供应链管理策略的影响。T-JIT是高度综合性的概念,符合系统工程整体性、目的性与最优化的特点,可以更全面准确地反应供应链管理优化问题。这个新增加的概念对整个企业的竞争力、供应链能力和组织绩效有影响。文献[3]提出了考虑运输成本对多样化库存系统中的供应商选择和订单数量分配问题进行研究。文献[4]为使企业提高订货周期、增强客户服务水平、减小库存并创新供应链管理策略,提出了精益生产的制造技术,如JIT和SMED。文献[5]用两阶段模糊综合方法对供应商选择和订单分配问题研究,主要考虑了产品数量折扣、交货期因素的影响。文献[6]在随机性、多方利益相关者和多标准环境下,采用AHP-QFD的组合优化算法对供应商选择和订单分配问题的决策支持系统进行了研究。文献[7]研究了在逆向物流系统中的供应和需求不确定情况下采用模糊多目标模型法选择供应商和订单分配优化的问题。文献[8]对某汽车公司和相关供应商实地进行了调查,以推进JIT环境下供应商和制造商之间的合作。文献[9]创建了JIT环境下单周期的订购和配送模型, 研究了制造商与供应商在信息不完全共享和完全共享合作下双方的决策行为。文献[10-11]参考模糊理论和数理统计方法,采用两阶段混合整数规划方法,研究了多目标的供应商选择和订单分配问题。
国内对T-JIT还没有深入研究,但对供应商选择和订单分配问题有些成果。阳燕[12]使用改进的遗传算法对供应链中供应商选择进行了研究。胡艳春[13]从质量、产能、采购周期3方面研究了JIT采购中供应商的选择策略与战略合作的重要性。郭婷婷[14]在JIT环境下对供应商选择和采购量分配进行了研究,以完善供应链采购管理。徐艳飞[15]考虑到顾客需求和供应商供应能力的随机不确定性,研究了在批量折扣环境下企业采购量分配优化问题,建立了多产品情形下选择供应商并建立订单分配的多目标优化模型。张翠华等[16]对JIT采购的订单分配问题进行了模型及仿真研究。
目前我国对JIT采购管理模块研究很少,考虑T-JIT策略对采购管理的影响和信息共享条件下的供应商选择和订单分配问题还没有研究。本研究从全新的T-JIT角度(如图 1所示)考虑信息共享成本、交货成本、采购成本、库存成本和质量成本等因素,采用两阶段多目标混合整数规划模型,用matlab与lingo软件计算,以达到总成本最低、方便灵活地适应多品种小批量生产模式的目的。研究重点突出T-JIT环境下信息共享成本对采购管理的影响,可提升供应链管理方法的理论价值,提高企业供应链管理水平和企业的核心竞争力。
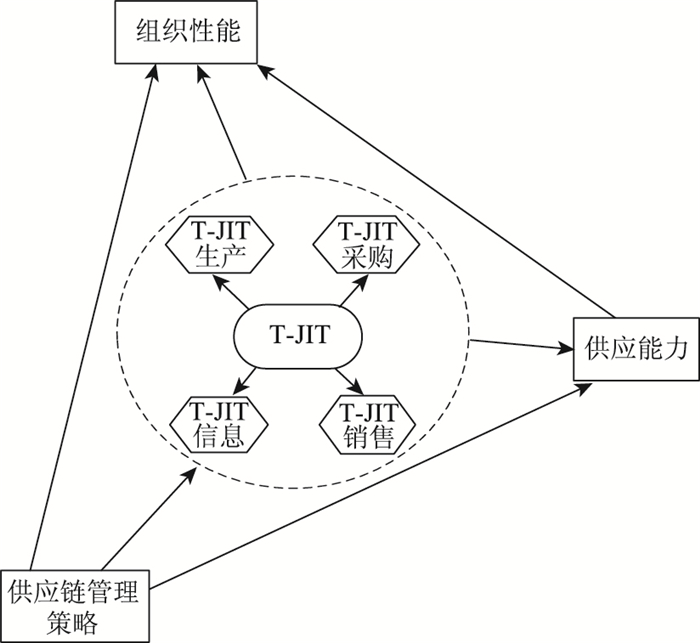
|
| 图 1 T-JIT理论模型 Fig. 1 T-JIT theoretical model |
| |
1 供应商选择和订单分配研究方法
面对复杂的市场格局,信息共享条件下采购管理供应商选择和订单分配研究成为供应链管理的主流。图 2为两阶段多目标混合整数规划流程图。
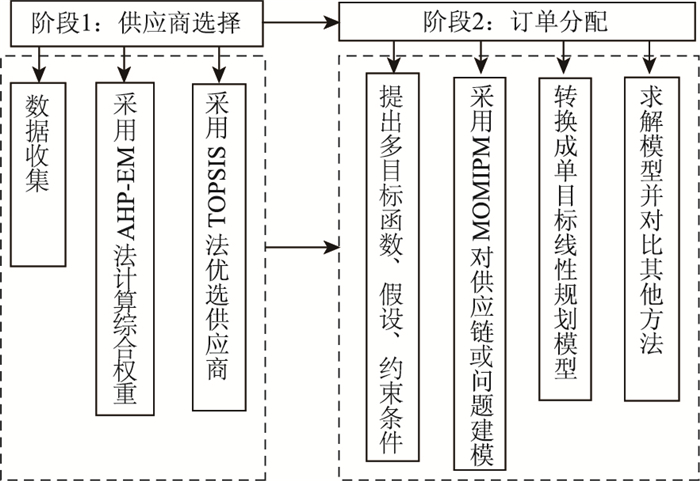
|
| 图 2 两阶段法流程图 Fig. 2 Flowchart of two-stage method |
| |
1.1 采用AHP-EM和TOPSIS组合方法选出供应商数量
由于多目标函数对于不同供应商选择的订单分配都有各自需求的侧重点,不同的目标权重会给企业决策带来很大差异,因此准确选择目标权重问题至关重要。结合主观和客观赋权的优势,采用层次分析法(AHP)和熵值法(EM),可以更准确客观地确定目标函数的综合权重[17]。
假设目标函数中权重为Wi,i=1, 2, …, n,且满足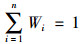
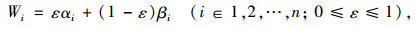
|
(1) |
根据风险偏好程度,取ε=0.3。
TOPSIS法于1981年由Hwang和Yoon提出,它适用于多项指标,可进行多方案目标择优选取,也叫做逼近理想点排序方法[18]。基本原理:假设模型有n个目标,每个目标都有m个属性,多属性决策目标函数为:Z=max/min{Zij|i=1, 2, …, m;j=1, 2, …, n},其中Zij代表每个目标函数。假设每个变量为xij,首先为了去除量纲的影响,可按式(2)标准化初始矩阵得到矩阵A:
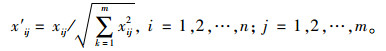
|
(2) |
根据各因素的权重计算出加权判断矩阵B:
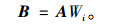
|
(3) |
根据加权判断矩阵,得出正负理想解C+和C-:
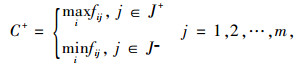
|
(4) |
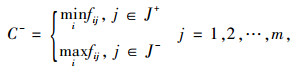
|
(5) |
式中,fij为加权决策标准化矩阵B中的每项数据;C+属于效益指标;J+属于效益属性;C-属于损耗性指标;J-属于成本性属性。C+越大,表示在第i个指标上的最优值越有利;C-越大,表示第i个指标上的最劣值越大,越不利。
计算各评价对象与正负理想值之间的距离,目标到正负理想解的距离S+和S-分别为:
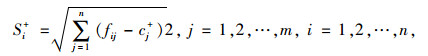
|
(6) |
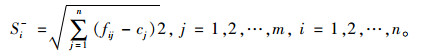
|
(7) |
计算各个目标的相对相近度:
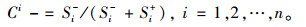
|
(8) |
通过相对贴近度对目标进行排序,从而为供应商最优选择做出决策。
1.2 采用整数线性规划模型(MOMIPM)对供应商订单分配问题(OR)求解设定生产商按如下供应链管理策略进行采购:
(1) 为了达到长期合作的战略伙伴关系,每种产品必须从能够提供该种产品的每个供应商处采购此种产品需求总量的至少10%。所以该产品的供应商数量不能超过10个[15]。
(2) 每种产品的信息共享率至少要达到80%。
(3) 运输成本由生产商承担总的45%。
(4) 每种产品从每个供应商的采购量不能超过该供应商所提供该种产品总量的65%。
(5) 根据以上要求生产商的总采购成本最小[15]。
为了描述数学模型,引入如下数学模型符号,如表 1所示。
| 符号集合 | 数学表示 |
| 供应商的集合I | I∈(1, 2, …, i, …, I) |
| 采购的产品集J | J∈(1, 2, …, j, …, J) |
| 设定的目标函数S | S∈(1, 2, …, s, …, S) |
| 决策变量 | 含义 |
| xij | 从供应商i订购产品j的数量 |
| xijm | 从供应商i订购产品j在信息流覆盖区间m上的数量 |
| yij | 供应商选择变量,yij=1表示从供应商i处采购产品j;反之yij=0表示没有从供应商i处采购到产品j |
| yi | 供应商选择变量,yi=1表示供应商i至少为企业供应1种产品;反之yi=0表示供应商i不为企业供应任何产品 |
| Zijm | 供应商i采购的产品j在信息流覆盖区间下的选择变量 |
| 参数 | 含义 |
| Dj | 表示产品j的需求量,服从正态分布Dj~N(μDj, ∂Dj2),其中μDj和∂Dj分别代表产品j需求的均值和标准差 |
| Vij | 供应商i提供产品j的能力限制,服从正态随机分布Vij~(μVij, ∂2Vij), μVij和∂Vij分别代表供应商i提供产品j的能力限制的均值和标准差 |
| uvij | 供应商i提供产品j的单位生产能力 |
| Kij | 第i个供应商在生产商生产产品j的总产量 |
| pij | 产品j从供应商i处的采购价格 |
| rij | 生产商从供应商i处采购产品j的单位运输成本 |
| Aij | 供应商i中能提供产品j的所有供应商 |
| Aj | 能提供产品j的所有供应商,Aj∈(0,1)变量 |
| Tj | 产品j的信息共享率(maxTj=1.0) |
| Qij | 从供应商i采购的数量占总的j采购量的百分比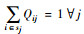 |
| qij | 从供应商i交货的产品j中废品数所占的比率 |
| invj | 产品j的单位库存持有成本比率 |
| lij | 供应商i处产品j的信息共享程度(0≤lij≤1) |
| glij | 信息共享条件下从供应商i处采购产品j的交货提前期 |
| ηd | 企业自身设置的需求数量满意度下限 |
| ηl | 企业自身设置的初始信息共享满意水平下限 |
| ηv | 企业预先给定的供应商供应能力满意水平下限 |
| Ei | 在信息共享环境下企业对供应商i的交易成本 |
| μijm | 从供应商i中采购产品j在信息流覆盖m区间的上限值 |
| βijm | 从供应商i中采购产品j在信息流覆盖区间m上的信息共享率 |
| αijm | 从供应商i中采购产品j在信息流覆盖区间m上的总金额 |
| αβijh | 产品i在供应商j中的评估值由第h个决策者决定 |
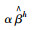 |
平均的模糊权重 |
| α*βijh | 平均的模糊权重进行的归一化处理 |
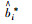 |
转化后的模糊量量刚值 |
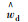 |
三角模糊数中平均的权重分布值 |
目标函数:
总成本目标[18]:主要以生产商的质量成本、交货成本、采购成本、库存成本和信息共享成本为衡量供应商选择和订单分配问题的标准,因此建立多目标整数规划模型。
质量成本:用废品率来衡量,即总的废品数量最小化:
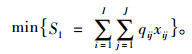
|
(9) |
交货成本:用延迟交货产品数量来衡量,即总的交货延迟产品数量最小化:
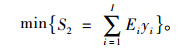
|
(10) |
采购成本:
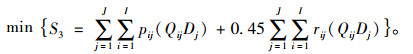
|
(11) |
库存成本:产品j在T-JIT环境下的库存持有成本最小:
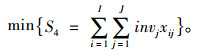
|
(12) |
信息共享成本:
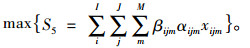
|
(13) |
供应链企业中信息化水平的高低一般以企业信息共享率作为衡量产品j的采购情况。信息共享程度高,则采购成本相应降低,反之信息共享水平过低,采购费用就会相对增加。信息共享可减少企业间的不确定性与随机性,可弱化库存的牛鞭效应,同时可协调供应链的目标冲突。
约束条件:
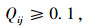
|
(14) |
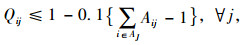
|
(15) |
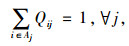
|
(16) |
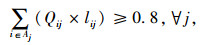
|
(17) |
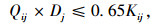
|
(18) |
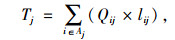
|
(19) |
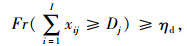
|
(20) |
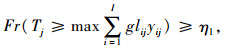
|
(21) |
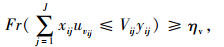
|
(22) |
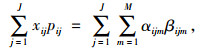
|
(23) |
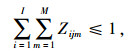
|
(24) |
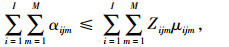
|
(25) |
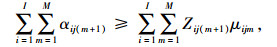
|
(26) |
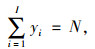
|
(27) |
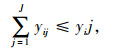
|
(28) |
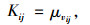
|
(29) |
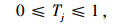
|
(30) |
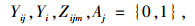
|
(31) |
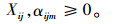
|
(32) |
式(14)满足采购策略(1)的要求;式(15)为每种产品占供应商供货量百分比的上限;式(16)为每种产品j占各个供应商供货量的百分比之和为1;式(17)满足采购策略(2)的要求;式(18)满足采购策略(4)的要求;式(19)为产品j的送货及时率;式(20)和式(21)分别为供应商i提供产品j的数量和交货期满足企业对订单数量和时间要求的概率要在企业自身设置的各个满意水平之上,可用函数Fr{h(x)≥ε}≥a表示,其中ε为正态随机变量,a为满意度水平,h(x)为供应商i提供产品j的数量或者交货期的概率函数, 则机会约束的确定性为μ+εQ-1(1-a),表示在满意度水平下最高订单数量和交货期的值, 其中μ为订单数量交货期的均值,Q-1(1-a)为满意度水平下的置信度;式(22)为供应商i的供应能力满足企业需求的概率要大于企业自身设置的满意水平;式(23)为选择某个供应商i供应产品的总价值;式(24)为企业从某个供应商i处采购的产品j必须在信息共享范围内购买;式(25)为某个供应商提供信息覆盖率区间的下限;式(26)为某个供应商提供信息覆盖率区间的上限;式(27)为供应商选择数目的约束, N为最大选择供应商的数量;式(28)为供应商选择的约束;式(29)为供应商i对产品j的产量等同于产品j单位生产能力;式(30)为产品j的送货及时率的范围;式(31)为选择变量取值是0-1约束;式(32)为决策变量取值为非负约束。
2 模型求解 2.1 供应商选择模型求解T-JIT环境下企业供应链的多目标因素[10]如表 2所示,熵权法计算权重步骤参考文献[19-20]。
| 目标A | 供应链成本最小 | |||||||
| 子目标B | 质量成本B1 | 交货成本B2 | 采购成本B3 | |||||
| 指标C | 供应产品完好率C1 | 生产过程可靠性C2 | 交货能力C3 | 满载率C4 | 订单完成率C5 | 订单完成及时性C6 | 总的物流管理成本C7 | 员工增加工作效率价值C8 |
| 子目标B | 库存成本B4 | 信息共享成本B5 | ||||||
| 指标C | 流动产品率C9 | 固定产品管理成本C10 | T-JIT环境成本C11 | 绿色化信息处理成本C12 | 信息管理系统C13 | 售后处理能力C14 | ||
表 2中创新性地提出了信息共享成本对总成本的影响,指标选取也融入T-JIT概念,可准确反映信息成本对供应商选择和分配的敏感程度。对评价因素进行问卷调查, 量化专家打分法,采用matlab编程软件计算得出:层次分析法权重系数α=(0.162 4, 0.297 2, 0.215 3, 0.143 1, 0.182),熵权法权重系数β=(0.190, 0, 348 2, 0.148 8, 0.146 9, 0.165 2),由式(1)得出评价指标的综合权重W=(0.181 7, 0.332 9, 0.168 8, 0.145 8, 0.170 8)。
2.2 订单分配模型求解转化随机变量的约束条件,式(14)~式(16)已经限定了未知量的区间范围, 即Qij∈[0.1,1-0.1(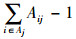
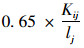
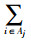
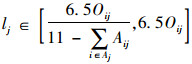
利用机会约束规划理论对供应商中含随机变量的式(20)~式(22)进行转换,得到:
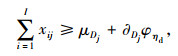
|
(33) |
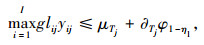
|
(34) |
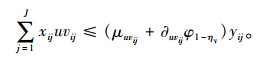
|
(35) |
式(33)~式(35)中, φηd,φ1-ηl,φ1-ηv分别为标准正态分布函数在累积概率ηd,1-ηl,1-ηv条件下的随机变量值;μTj, ∂Tj分别为产品j在信息共享环境下的均值和标准差。
(3) 多目标规划模型转化为单目标规划模型
由阶段1中各指标权重系数Wi可知:

|
(36) |
约束条件:
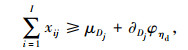
|
(37) |
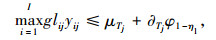
|
(38) |
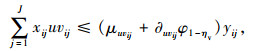
|
(39) |
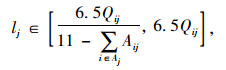
|
(40) |
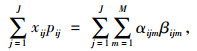
|
(41) |
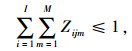
|
(42) |
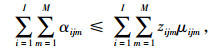
|
(43) |
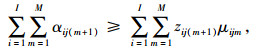
|
(44) |
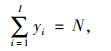
|
(45) |
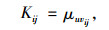
|
(46) |
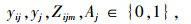
|
(47) |
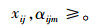
|
(48) |
(4) JIT信息共享成本与总成本二律背反,影响整体优化效果。采用模糊多目标线性规划方法,用最大最小切比雪夫不等式[21]进行转换,把最大需求的信息共享率表示成不精确的模糊系数,并用三角型分布表示,即:
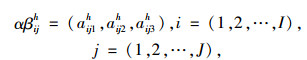
|
(49) |
式中,αβijh表示产品i在供应商j中的评估值由第h个决策者决定。
求出平均的模糊权重:
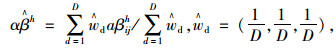
|
(50) |
同时对αβijh进行归一化处理,得到:
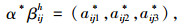
|
(51) |
式中aij1*, aij2*, aij3*分别为三角型分布表示的模糊权重归一化处理值。
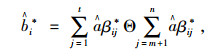
|
(52) |
即:
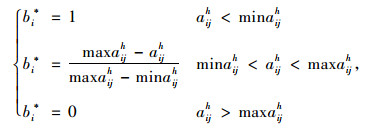
|
(53) |
式中,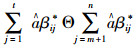
利用非模糊性能式(BNPj)来求解模糊量bi*的量钢值为:
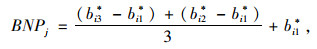
|
(54) |
式中bi1*,bi2*,bi3*分别为三角型分布所表示的模糊量量纲值。
BNPj可以利用最大最小值转换法对原始数据进行替换,这样就能与目标函数的意义想符合,即BNPj值越小,总的采购成本值也越小,两者呈现正相关。此方法可使混合整数规划模型更加精确,可行性和有效性得到很好的诠释。
3 实证研究 3.1 T-JIT环境下供应商优化选择问题参考文献[15]中的算例中的数据,加入信息共享率数据,针对某中小型汽车企业中关键产品橡胶圈和密封圈采购来研究供应商选择和订单分配量。原始数据表如表 3~表 5所示。
| 因素 | 供应商 | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 交易成本Ei | |||||
| 产品1 | 1 200 | 1 000 | 1 200 | 2 000 | 1 500 |
| 产品2 | |||||
| 价格Pij | |||||
| 产品1 | 5 | 7 | 6 | 3 | 4 |
| 产品2 | 4 | 8 | 5 | 4 | 5 |
| 单位运输成本rij | |||||
| 产品1 | 0.2 | 0.1 | 0.3 | 0.1 | 0.2 |
| 产品2 | 0.3 | 0.2 | 0.2 | 0.2 | 0.3 |
| 次品率qij | |||||
| 产品1 | 5 | 2 | 3 | 5 | 4 |
| 产品2 | 4 | 2 | 4 | 6 | 5 |
| 延迟交货率dij | |||||
| 产品1 | 7 | 4 | 4 | 4 | 5 |
| 产品2 | 8 | 3 | 5 | 5 | 6 |
| 单位库存成本率invj | |||||
| 产品1 | 3 | 2 | 4 | 5 | 2.6 |
| 产品2 | 4.2 | 2.5 | 4.8 | 4.4 | 2 |
| 交货提前期glij | |||||
| 产品1 | 8 | 9 | 8 | 10 | 9 |
| 产品2 | 10 | 13 | 12 | 11 | 13 |
| 生产能力uvij | |||||
| 产品1 | 7 500 (300) |
6 500 (300) |
7 000 (300) |
6 800 (300) |
7 200 (300) |
| 产品2 | 13 000 (300) |
10 000 (300) |
15 000 (300) |
12 000 (300) |
11 000 (300) |
| 信息共享率lij | |||||
| 产品1 | 0.85 | 0.8 | 0.9 | 0.88 | 0.88 |
| 产品2 | 0.9 | 0.84 | 0.82 | 0.85 | 0.95 |
| 产品 | 需求量Dj | 信息率需求时机 | 满意水平ε | 标准正态分布分位数点Zε | 标准正态分布分位数点Z1-ε |
| 1 | 6 000(120) | 15(1.4) | 0.95 | 1.644 9 | -1.644 9 |
| 2 | 9 000(200) | 18(1.4) | 0.95 | 1.644 9 | -1.644 9 |
| 供应商 | M | aijm | M | aijm |
| 1 | 0.9 | 4 000 | 1 | 8 000 |
| 2 | 0.9 | 5 800 | 1 | 11 600 |
| 3 | 0.85 | 6 000 | 1 | 10 000 |
| 4 | 0.9 | 8 000 | 1 | 16 000 |
| 5 | 0.8 | 7 500 | 1 | 15 000 |
| 注:M为各供应商给某公司的信息率折扣值;aijm为各供应商给某公司折扣区间的上限值。 | ||||
为了尽力满足顾客和供应商的需求,假设ηd,ηl,ηv的满意度下限水平均为0.95,则标准正态分布分位数点为1.644 9。
根据阶段1求解方法,采用matlab编程软件对TOPSIS法进行计算,得出表 6所示结果。
| 指标供应商 | 1 | 2 | 3 | 4 | 5 |
| S+ | 0.092 6 | 0.104 6 | 0 | 0 | 0 |
| S- | 0.056 5 | 0.209 2 | 0 | 0 | 0 |
| C+ | 0.100 4 | 0.097 3 | 0.149 8 | 0.156 8 | 0.168 9 |
从表 6可看出,可供选择的供应商优先排序顺序是S5>S4>S3>S1>S2,因此商家可以考虑选择供应商5,4,3为优选合作伙伴,供应商5的库存成本较低,信息共享率较高,其余指标均处于中上等。供应商4的优势主要在于运输成本较低,交货提前期较高。供应商3的优势在于延迟交货率较低,企业可以根据具体情况做出决策。
3.2 采用lingo18.0软件进行编程计算(1) 先用lingo计算出采购成本的值,采购成本对应式(14)~式(19)的约束条件,计算出Qij的可行解,如Q11=0.1,Q21=0.1,Q31=0.1,Q41=0.1,Q51=0.6,Q12=0.62,Q22=0.1,Q32=0.1,Q42=0,Q52=0.18.可计算出总的采购成本为:S3=707 69。
(2) S6中信息共享率转换,如表 7所示。
| 信息共享多目标 | 参数值 |
| FMA | aβ1=(0.875, 0.88, 0.81, 0.84, 0.915) |
| aβ2=(0.85, 0.825, 0.815, 0.835, 0.925) | |
| aβ3=(0.815, 0.865, 0.81, 0.89, 0.93) | |
| aβij*h | aβ1*=(0.263, 0.264, 0.243, 0.252, 0.275) |
| aβ2*=(0.255, 0.248, 0.245, 0.25, 0.278) | |
| aβ3*=(0.245, 0.26, 0.243, 0.267, 0.279) | |
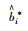 |
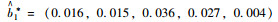 |
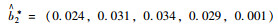 |
|
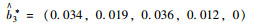 |
|
| BNPj | (0.025, 0.022, 0.035, 0.023, 0.002) |
采用BNPi的值作为呈正相关的信息贡献率值。
(3) 用LINGO18.0计算多目标混合整数规划模型,整理得到表 8所示结果。
| 采购数量 | 供应商 | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 产品1 | 0 | 0 | 0 | 573 | 5 625 |
| 产品2 | 0 | 0 | 9 329 | 0 | 0 |
| 总数 | 0 | 0 | 9 329 | 573 | 5 625 |
可以看出,产品1主要在供应商4和供应商5两处采购,采购量分别为573件和5 625件;产品2主要在供应商3处采购,采购量为9 329件。
由LINGO计算结果可知,4种目标函数下总的最小成本为2 515.54元。由式(1)可知,总的采购成本为2 515.54+0.168 8×70 769=14 461.35元。同时可知该公司可选供应商3, 4, 5作为采购对象,采购总金额分别为46 644.90,1 717.164,22 500元,其中供应商5选择产品1金额为7 500元,产品2金额为15 000元。从表 3可以看出,供应商5选择产品2时,可以享受更高的信息覆盖率,而供应商4则信息覆盖率较小,对比表 5可以看出,供应商3的总金额超出了范围,则可以任意享受最高的信息覆盖率。总之,信息覆盖率范围越大,总的成本就越小,对总成本的敏感度就越高。
表 9对两种环境的优劣对比分析。一般环境下侧重点主要考虑生产能力和交易成本,但价格水平、运输成本、延迟交货率较高,且交货提前期变短,总成本较高,可以看出一般环境下的结果不是最优解。而在T-JIT环境下,综合考虑多种目标的影响,总成本较低,信息覆盖率、交货提前期高,价格、运输成本均相对较低,优势远远大于一般环境下供应商的选择,可以更全面准确地反映实际情况。
| 项目 | 供应商选择 | |
| 总成本/元 | 一般环境(1, 3, 5) | T-JIT环境(3, 4, 5) |
| 信息覆盖率/% | 92 185.18 | 14 461.35 |
| 生产能力/交货提前期/ (piece·d-1) |
0 | 0.88 |
| 价格/元 | 10 116.7/(8, 10),(8, 12),(9, 13) | 9 833.3/(8, 12),(10, 11),(9, 13) |
| 运输成本/(元·km-1) | (5, 4),(6, 5),(4, 5) | (6, 5),(3, 4),(4, 5) |
| 交易成本/元 | (0.2, 0.3),(0.3, 0.2),(0.2, 0.3) | (0.3, 0.2),(0.1, 0.2),(0.2, 0.3) |
| 延迟交货率/ % | 1 200 | 2 000 |
| 总成本/元 | (7, 8) | (4, 5) |
4 结论
本研究结合系统工程的理念,讨论了在T-JIT环境下的供应商选择和OR问题,创新性地提出了信息共享环境下如何分配和选择供应商,达到精益物流生产,节约总的成本效益。构建了两阶段模型并利用AHP-EM和TOPSIS法进行供应商选择,应用权重采用多目标混合整数规划模型进行订单分配研究,提出了信息共享成本对总成本的影响,并用最大最小化法转换信息共享率使计算更准确,并用文献算例验证,对比出使用信息共享率对供应商选择、分配和总成本的影响。与已有的方法相比,该方法对供应商合理选择和订单分配的准确性有显著的提高,同时扩展了供应链系统管理理论,以提高企业供应链管理水平,增强企业核心竞争力。
| [1] |
WOMACK J R. 改变世界的机器[M]. 沈希瑾, 译. 北京: 商务印书馆, 1999: 17-54. WOMACK J R. The Machine That Changed the World[M]. SHEN Xi-jin, translated. Beijing:The Commercial Press, 1999:17-54. |
| [2] |
GREEN K W Jr, INMAN R A, BIROU L M, et al. Total JIT(T-JIT) and Its Impact on Supply Chain Competency and Organizational Performance[J]. International Journal of Production Economics, 2014, 147: 125-135. |
| [3] |
MENDOZA A, VENTURAB J A. A Serial Inventory System with Supplier Selection and Order Quantity Allocation[J]. European Journal of Operational Research, 2010, 207(3): 1304-1315. |
| [4] |
RODRÍGUEZ-MÉNDEZ R, SÁNCHEZ-PARTIDA D, MARTÍNEZ-FLORES J L, et al. A Case Study:SMED & JIT Methodologies to Develop Continuous Flow of Stamped Parts into AC Disconnect Assembly Line in Schneider Electric Tlaxcala Plant[J]. IFAC-Papersonline, 2015, 48(3): 1399-1404. |
| [5] |
CEBI F, OTAY Í. A Two-stage Fuzzy Approach for Supplier Evaluation and Order Allocation Problem with Quantity Discounts and Lead Time[J]. Information Sciences, 2016, 339: 143-157. |
| [6] |
SCOTT J, HO W, DEY P K, et al. A Decision Support System for Supplier Selection and Order Allocation in Stochastic, Multi-stakeholder and Multi-criteria Environments[J]. International Journal of Production Economics, 2015, 166: 226-237. |
| [7] |
MOGHADDAM K S. Fuzzy Multi-objective Model for Supplier Selection and Order Allocation in Reverse Logistics Systems under Supply and Demand Uncertainty[J]. Expert Systems with Applications, 2015, 42(15/16): 6237-6254. |
| [8] |
CHEN S Y, CHEN R Q. Relationship between Supplier and Manufacturer under the Condition of JIT Purchase[J]. Journal of Management Engineering, 1998, 12(3): 46-52. |
| [9] |
ZIMMER K. Supply Chain Coordination with Uncertain Just-in-time Delivery[J]. International Journal of Production Economics, 2002, 77(1): 1-15. |
| [10] |
ÖGEN D, ÖNÜT S, GÜLSÜN B, et al. A Two-phase Possibilistic Linear Programming Methodology for Multi-objective Supplier Evaluation and Order Allocation Problems[J]. Information Sciences, 2008, 178: 485-500. |
| [11] |
ÖZGEN D, GÜLSÜNN B. Combining Possibilistic Linear Programming and Fuzzy AHP for Solving the Multi-objective Capacitated Multi-facility Location Problem[J]. Information Sciences, 2014, 268: 185-201. |
| [12] |
阳燕. 基于遗传算法的供应商选择问题研究[D]. 成都: 西南交通大学, 2009. YANG Yan. Study of Supplier Selection Based on Genetic Algorithm[D]. Chengdu:Southwest Jiaotong University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10613-2010142079.htm |
| [13] |
胡艳春. JIT采购中的供应商选择策略研究[J]. 中国管理信息化, 2008, 10(11): 82-83. HU Yan-chun. Research on Supplier Selection Strategy in JIT Purchasing[J]. China Management Informationization, 2008, 10(11): 82-83. |
| [14] |
郭婷婷. JIT采购中的供应商选择及采购量分配模型研究[D]. 沈阳: 东北大学, 2008. GUO Ting-ting. Research on Model of Vendor Selection and Purchasing Quantity Allocation in JIT Purchase Environments[D]. Shenyang:Northeastern University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10145-2010258840.htm |
| [15] |
徐艳飞. 不确定性环境下最优供应商数量和订单分配问题研究[D]. 秦皇岛: 燕山大学, 2013. XU Yan-fei. Research on Optimal Number of Suppliers and Order Allocation Problem in Uncertainty Environment[D]. Qinhuangdao:Yanshan University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10216-1014033404.htm |
| [16] |
张翠华, 朱宏, 马林. 基于JIT采购的订单分配问题模型及仿真应用[J]. 东北大学学报:自然科学版, 2006, 11(27): 1291-1294. ZHANG Cui-hua, ZHU Hong, MA Lin. The Model of Order Allocation for JIT Purchasing and Its Simulative Application[J]. Journal of Northeastern University:Natural Science Editon, 2006, 11(27): 1291-1294. |
| [17] |
姜燕宁, 郝书池. 基于部分跨级和集中存储模式的库存配置与选址决策模型[J]. 公路交通科技, 2016, 33(11): 152-158. JIANG Yan-ning, HAO Shu-chi. Inventory Allocation and Location Decision Model Based on Partial Cross-level and Centralized Storage[J]. Journal of Highway and Transportation Research and Development, 2016, 33(11): 152-158. |
| [18] |
熊云峰, 陈章兰, 袁红莉. 基于复合权重TOPSIS的船舶性能综合评价法[J]. 船舶工程, 2012, 34(3): 28-31. XIONG Yun-feng, CHEN Zhang-lan, YUAN Hong-li. Comprehensive Evaluation of Ship Performance Based on Synthesized Weight and TOPSIS[J]. Ship Engineering, 2012, 34(3): 28-31. |
| [19] |
魏书堤, 姜小奇. 一种利用信息熵确定属性权重的模糊单因素评价方法[J]. 计算机工程与科学, 2010, 32(7): 93-94, 107. WEI Shu-di, JIANG Xiao-qi. A Single-factor Fuzzy Evaluation Method of Using Information Entropy to Determine the Property Weights[J]. Computer Engineering and Science, 2010, 32(7): 93-94, 107. |
| [20] |
孔峰, 刘鸿雁. 基于理想点的改进AHP综合排序算法[J]. 系统工程, 2007, 25(4): 98-103. KONG Feng, LIU Hong-yan. Improvement on Algorithm for Final Priorities of AHP Based on Ideal Solution[J]. Systems Engineering, 2007, 25(4): 98-103. |
| [21] |
刘奎, 张琨, 王翠荣. 利用切比雪夫不等式的背景建模算法[J]. 计算机应用与软件, 2012, 29(4): 53-56. LIU Kui, ZHANG Kun, WANG Cui-rong. Background Modeling Algorithm That Uses Chebyshev Inequality[J]. Computer Applications and Software, 2012, 29(4): 53-56. |
 2018, Vol. 35
2018, Vol. 35

 ,
,