扩展功能
文章信息
- 周茂定, 张元海, 李丽园
- ZHOU Mao-ding, ZHANG Yuan-hai, LI Li-yuan
- 薄壁简支箱梁的弯曲振动频率研究
- Study on Bending Vibration Frequency of Thin-walled Simply-supported Box Girder
- 公路交通科技, 2018, 35(1): 72-78
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(1): 72-78
- 10.3969/j.issn.1002-0268.2018.01.010
-
文章历史
- 收稿日期: 2016-10-18
目前大跨度桥梁常用的截面形式为箱形截面,而箱形梁截面在弯曲荷载作用下由于存在翼板及腹板的剪切变形,使其弯曲纵向位移不再符合平截面假定而出现纵向翘曲的现象。众所周知,当箱梁翼板出现上述不均匀翘曲变形时称之为箱梁的剪力滞效应,而关于上述剪切变形对箱梁静力影响的分析已有不少文献[1-5]。薄壁箱梁的动力特性因受上述作用的影响也变得十分复杂。薄壁箱梁的弯曲振动频率对计算桥梁的冲击系数、判断桥梁刚度等有重要意义[6-7]。张永建等[8]利用能量变分原理分析了考虑剪力滞效应的箱梁自振特性。刘世忠等[9]在同时考虑箱梁剪力滞效应及腹板剪切变形的双重影响下,采用梁段有限元法分析了薄壁箱梁的自振特性,其对腹板的剪切变形是通过引入剪切修正系数(铁木辛柯梁理论)的方式解决。也有文献[10-12]分别取用多个未知量来考虑箱梁翼板的剪力滞和腹板剪切变形,同时考虑梁挠曲时截面的转角转动惯量,从而分析箱梁的自振特性。冀伟等[13-14]将薄壁箱梁理论引入波形钢腹板箱梁中并结合波形钢腹板的特点,导出适用于波形钢腹板箱梁的自振频率。以上文献对于箱梁的剪切变形都是将翼板和腹板分开来分析,对于翼板的纵向位移均以拟合的剪力滞翘曲位移函数为基础分析。
本文将统一用一个未知量来综合考虑截面翼板和腹板的剪切变形,运用能量变分法及Hamilton原理,导出薄壁箱梁自振特性的控制微分方程及相应边界条件。采用伽辽金法求解简支薄壁箱梁的自振频率,并通过数值算例来分析剪切效应对薄壁箱梁弯曲振动频率的影响。
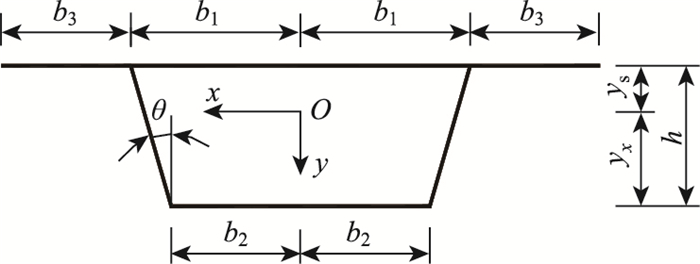
1 考虑面内剪切效应时总弯曲势能薄壁杆件一般指截面厚度较薄的杆件,通常截面厚度小于其宽或高的0.1倍[15]。如图 1所示薄壁箱梁截面,图中采用正交笛卡尔坐标系Oxyz,坐标原点O位于截面形心处。
|
| 图 1 梯形截面箱梁示意图 Fig. 1 Schematic diagram of box girder with trapezoidal cross-section |
| |
针对简支单室薄壁箱梁在弯曲荷载作用下,将产生竖向挠曲,其纵向位移模式除符合平截面假定外,尚有翼板及腹板的面内剪切翘曲纵向位移,其纵向总位移表达式可表示为:
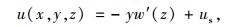
|
(1) |
式中w表示薄壁箱梁的竖向挠度。us表示全截面剪切的翘曲纵向位移,文献[16]中已对此项进行了系统推导分析,在此不再赘述,其表达式为:
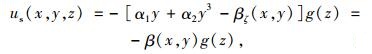
|
(2) |
式中, g(z)为反映截面剪切变形影响的纵向函数;α1和α2为箱梁腹板剪切翘曲系数;βζ(x, y)为箱梁各个翼板剪切横向翘曲位移分布函数;β(x, y)为全截面广义剪切翘曲位移函数。考虑薄壁箱梁截面各板剪切翘曲应力的轴向平衡条件,对其纵向翘曲位移进行修正后,可得横向翘曲位移分布函数βζ(x, y)为:
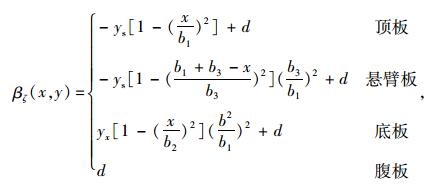
|
(3) |
式中,d为考虑截面轴向平衡条件后的附加项,其表达式见文献[16]。
由式(1)~(3)可求得薄壁箱梁截面各点的纵向应变表达式为:
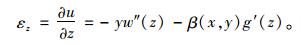
|
(4) |
薄壁箱梁各板的剪切应变为:
翼板
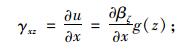
|
(5) |
腹板:
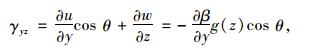
|
(6) |
对于直腹板箱梁θ为0。根据能量原理[17],可得薄壁箱梁的弯曲应变能为:
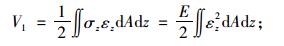
|
(7) |
剪切应变能为:
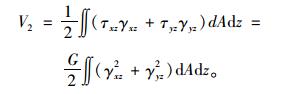
|
(8) |
从而可求得薄壁箱梁总的弯曲剪切应变能为:
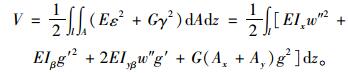
|
(9) |
式中,E和G分别为材料的弹性模量和剪切模量;Ix为平截面假定下的弯曲惯性距;Iβ为截面剪切翘曲惯性距;Iyβ为截面翘曲惯性积;Ax,Ay分别为翼板、腹板剪切翘曲面积。本文定义的剪切翘曲截面参数的表达式如下:
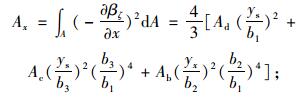
|
(10) |
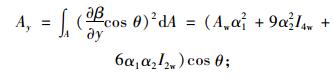
|
(11) |
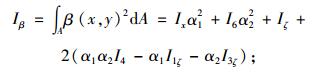
|
(12) |
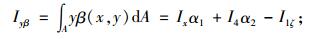
|
(13) |
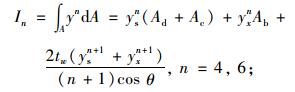
|
(14) |
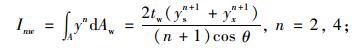
|
(15) |
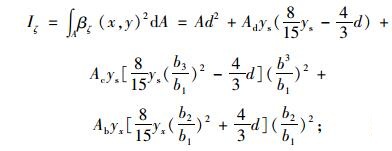
|
(16) |
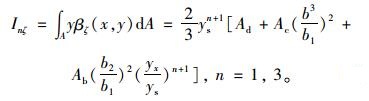
|
(17) |
以上截面参数式中Ad,Ab,Ac,Aw,A分别为箱梁顶板、底板、悬臂板、腹板和全截面面积,tw为腹板厚度。
2 控制微分方程的建立薄壁箱梁的动能主要包括竖向弯曲动能和梁的转动动能两项[12],对于转动动能有文献忽略,也有文献考虑此项,本文将以考虑和忽略此项作对比分析。
竖向弯曲动能:
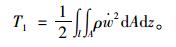
|
(18) |
转动动能:
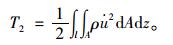
|
(19) |
箱梁总动能:
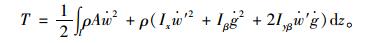
|
(20) |
式中“点”和“撇”分别表示对时间t和对坐标轴z的偏导数;ρ为材料的密度。
由式(9)和式(20)可得(忽略扭转等其他变形影响):

|
(21) |
由Hamilton原理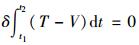
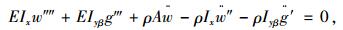
|
(22) |
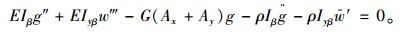
|
(23) |
所得自然边界条件为:
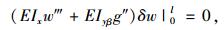
|
(24) |
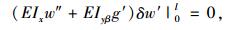
|
(25) |
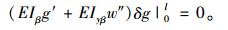
|
(26) |
若忽略箱梁转动动能,则控制微分方程为:
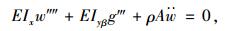
|
(27) |
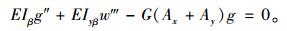
|
(28) |
其自然边界条件仍为式(24)~(26)。对于不同的边界条件,式(24)~(26)可转化为:
对于简支端:w=0, w″=0, g′=0;
对于固定端:w=0, g=0, g′=-w″(Ix/Iyβ);
对于自由端:w″=0, g′=0, g″=-w″′(Ix/Iyβ)。
3 伽辽金数值解法对于建立的薄壁箱梁弯曲振动控制微分方程,较多文献采用消除变量方法求得一个高次微分方程,再求解高次微分方程后得出弯曲振动频率计算式。显然上述计算较为复杂,对于简支薄壁箱梁,本文将采用伽辽金分离变量的方法求解。根据简支端边界条件可设w(z, t),g(z, t)分别为:
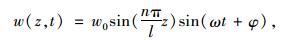
|
(29) |
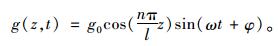
|
(30) |
其满足边界边界条件w0, l=0,w″0, l=0,g′0, l=0,n为自然数。
若忽略梁的转动动能时,将式(29)~式(30)代入式(27)~式(28)化简后可得:
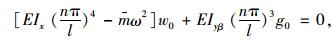
|
(31) |
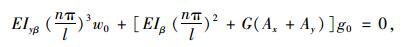
|
(32) |
式中m=ρA。
式(31)和式(32)是关于w0,g0的二元一次方程组,若方程组有非零解,则需系数矩阵行列式为0,即
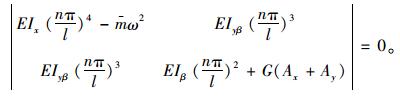
|
(33) |
根据式(33)可求得圆频率ω的表达式如下:
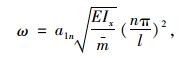
|
(34) |
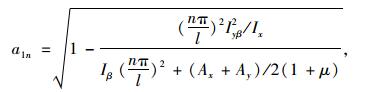
|
(35) |
式中μ为材料的泊松比。
若考虑梁的转动动能影响时,同样将式(29)~(30)代入式(22)~(23)化简后可得:
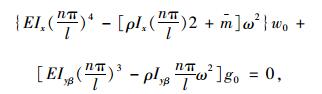
|
(36) |
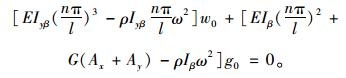
|
(37) |
同样,式(36)和式(37)是关于w0,g0的二元一次方程组,若方程组有非零解,则需系数矩阵行列式为0,在此不再详述求解过程,可求得考虑箱梁转动动能时的圆频率ω表达式为:
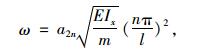
|
(38) |
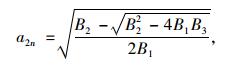
|
(39) |
式中B1,B2,B3的表达式如下:
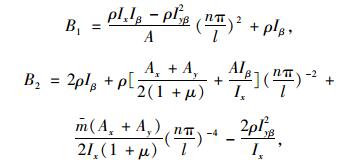
|
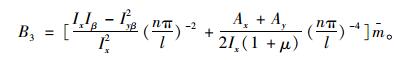
|
结构振动频率f与圆频率ω的关系式为:
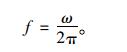
|
(40) |
由于本文是以薄壁结构弯曲理论为基础,故式(34)和式(38)较为适用于忽略面外剪切变形的薄壁箱梁结构。通过计算求得的弯曲振动频率回代入式(31)~(32)或式(36)~(37)中可求得w0,g0,于是便可求得相对应频率的振型。
4 数值算例 4.1 算例验证某简支直腹板箱形截面梁[10],其材料特性及截面几何参数分别为:弹性模量E=3.5×104MPa,密度ρ=2 500 kg/m3,泊松比μ=0.2,各翼板厚均为0.25 m,腹板厚为0.40 m,顶板半宽b1=3.55 m,梁高h=3.75 m,悬臂板宽b3=2.5 m,计算跨度l=40 m。
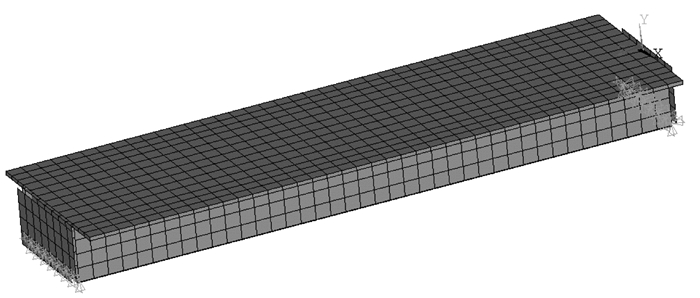
分别运用ANSYS的beam189(考虑截面剪切效应)梁单元及shell 63壳单元(空间有限元)建立上述简支梁有限元模型如图 2所示。分别采用笔者所推导的两种公式计算上述箱梁前5阶竖向弯曲振动频率,并将其与ANSYS有限元计算值对比,如表 1所示。
|
| 图 2 简支箱梁有限元模型 Fig. 2 Finite element model of simply supported box girder |
| |
| 频率阶数 | 忽略梁转动 | 计入梁转动 | ANSYS梁结果 | ANSYS壳结果 |
| 1 | 5.482 | 5.449 | 5.487 | 5.212 |
| 2 | 18.878 | 18.627 | 18.831 | 14.212 |
| 3 | 35.614 | 35.067 | 35.315 | 35.463 |
| 4 | 53.455 | 52.660 | 52.548 | — |
| 5 | 71.769 | 70.758 | 69.766 | — |
由于ANSYS壳单元计算的竖向弯曲频率中会参杂扭转、畸变以及箱梁横向变形等因素,故本文只挑选其前三阶竖向弯曲振动频率(其他因素影响相对较小,高阶振动的结果差异较大)列于表中。由表 1可知:(1)本文的解析解与考虑剪切效应的ANSYS梁单元及空间壳单元计算值吻合良好,从而验证了本文解析解的正确性;(2)梁转动动能对其自振频率的影响较小。
4.2 对比分析《公路桥涵设计通用规范》(JTG D60—2015)[18]中给出的简支梁竖向基频的估算公式为:
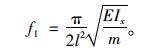
|
(41) |
将式(34)或式(38)代入式(40)后,令n=1与式(41)对比可知,式(34)或式(38)仅多系数a11或a21。显然,规范所给的简支梁竖向基频计算式是不考虑薄壁箱梁的剪切变形影响的。
若要单独计算腹板剪切变形对箱梁竖向弯曲振动频率的影响大小,只需在计算截面剪切翘曲参数式(10)~(17)时,忽略关于翼板的翘曲函数βζ(x, y)的积分项,同时去掉a1n或a2n中的Ax即可,在此不再赘述。为对比分析剪切变形的影响,仍以上述模型梁为例,表 2中分别列出①考虑剪切变形影响,②忽略箱梁剪切变形影响,③仅考虑腹板剪切变形影响的弯曲振动频率。
| 频率阶数 | ①频率/Hz | ②频率/Hz | ③频率/Hz | ②差比/% | ③差比/% |
| 1 | 5.482 | 5.836 | 5.570 | 6.5 | 1.6 |
| 2 | 18.878 | 23.345 | 19.792 | 23.7 | 4.8 |
| 3 | 35.614 | 52.526 | 38.305 | 47.5 | 7.6 |
| 4 | 53.455 | 93.380 | 58.308 | 74.7 | 9.1 |
| 5 | 71.769 | 145.907 | 78.616 | 103.3 | 9.5 |
| 注:②差比=(②-①)/①;③差比=(③-①)/①。 | |||||
通过表 2可得:(1)在计算箱梁2阶以上弯曲振动频率时,考虑剪切变形的影响与不考虑的计算结果差值较大,竖向弯曲3阶以上时差值已超过50%;(2)考虑箱梁全截面剪切变形影响与仅考虑腹板剪切变形影响的计算结果差值比较小,即③差比远小于②差比,说明箱梁翼板的剪切变形对其竖向弯曲振动频率影响较小。
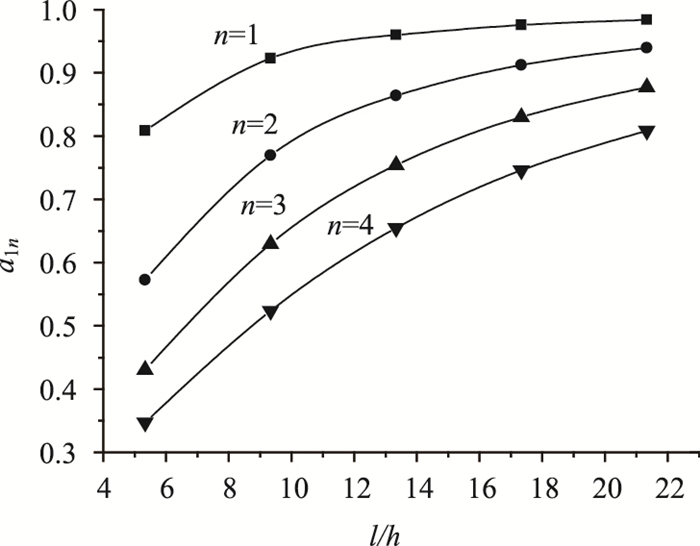
通过上述分析可知,箱梁腹板剪切变形对箱梁竖向弯曲振动频率影响较大。由于本文是以薄壁箱梁的弯曲理论为基础来分析组成箱梁各板的面内剪切变形,故对箱梁腹板面内剪切影响较大的因素为梁高。为分析不同跨高比(l/h)时剪切变形对箱梁弯曲振动频率的影响,仍以上述箱梁截面为例,计算不同跨高比时,考虑剪切变形影响的竖向弯曲振动频率fs与忽略剪切变形时的竖向弯曲振动频率fc的比a1n,如图 3所示。
|
| 图 3 不同跨高比下的剪切影响参数 Fig. 3 Influence parameters of shear effect with different span-height ratios |
| |
通过观察图 3可知,(1)当n确定时,随着跨高比的不断增大,a1n将不断接近于1,说明随着跨高比的增加,剪切变形对箱梁竖向弯曲振动频率的影响将减小;(2)在相同的跨高比区段范围内,a1n各条曲线的斜率随着n的增加而增大,这说明剪切变形对竖向弯曲振动频率的影响,随着阶数的增加而变得更为明显。
5 结论(1) 与已有文献不同,以薄壁箱梁的弯曲理论为基础将翼板、腹板剪切变形综合为一个剪切参数,再运用能量法及Hamilton原理推导控制微分方程,不但减少了未知量个数,同时降低了分析的工作量。
(2) 对于简支箱梁,通过分析控制微分方程的自然边界条件,运用伽辽金数值解法,在不求解控制微分方程的情况下,导出箱梁的自振频率计算式,省去了求解高次微分方程的复杂计算。
(3) 数值算例结果表明,在计算薄壁箱梁弯曲振动频率时,梁的转动动能对其影响较小,可忽略。翼板的剪切变形对箱梁的弯曲振动频率影响小于腹板剪切变形的影响。剪切变形对箱梁竖向弯曲振动频率的影响,随着跨高比的增加而减小,随着频率阶数的增加而增大。
| [1] |
张士铎, 邓小华, 王文州. 箱形薄壁梁剪力滞效应[M]. 北京: 人民交通出版社, 1998. ZHANG Shi-duo, DENG Xiao-hua, WANG Wen-zhou. Shear Lag Effect in Thin-walled Box Girder[M]. Beijing: China Communications Press, 1998. |
| [2] |
LUO Q Z, WU Y M, LI Q S, et al. A Finite Segment Model for Shear Lag Analysis[J]. Engineering Structures, 2004, 26(14): 2113-2124. |
| [3] |
ZHOU S J. Shear Lag Analysis in Prestressed Concrete Box Girders[J]. Journal of Bridge Engineering, 2011, 16(4): 500-512. |
| [4] |
冀伟, 刘世忠, 蔺鹏臻. 均布荷载作用下波形钢腹板简支箱梁的挠度[J]. 公路交通科技, 2012, 29(12): 69-73. JI Wei, LIU Shi-zhong, LIN Peng-zhen. Deflection of Simple-supported Box Girder with Corrugated Steel Webs under Uniform Load[J]. Journal of Highway and Transportation Research and Development, 2012, 29(12): 69-73. |
| [5] |
ZHANG Y H. Improved Finite-segment Method for Analyzing Shear Lag Effect in Thin-walled Box Girders[J]. Journal of Structural Engineering, 2014, 138(10): 1279-1284. |
| [6] |
JI W, DENG L, LIU S Z, et al. Study of Vertical Bending Vibration Behavior of Continuous Prestressed Concrete Box Girders with Corrugated Steel Webs[J]. Advances in Structural Engineering, 2016, 19(6): 953-965. |
| [7] |
GAO Q, WANG Z, LIU Y, et al. Modified Formula of Estimating Fundamental Frequency of Girder Bridge with Uniform Cross-section[J]. Advanced Engineering Forum, 2012, 5: 177-182. |
| [8] |
张永建, 黄平明. 考虑剪力滞效应的简支梁自振特性[J]. 建筑科学与工程学报, 2005, 22(2): 40-42. ZHANG Yong-jian, HUANG Ping-ming. Free Vibration Characteristics of Simply Supported Box Girder with Effect of Shear Lag[J]. Journal of Architecture and Civil Engineering, 2005, 22(2): 40-42. |
| [9] |
刘世忠, 吴亚平, 夏旻, 等. 薄壁箱梁剪力滞剪切变形双重效应分析的矩阵方法[J]. 工程力学, 2001, 18(4): 140-144. LIU Shi-zhong, WU Ya-ping, XIA Min, et al. Matrix Analysis of Thin-walled Box Girders with Both Shear Lag and Shear Deformation[J]. Engineering Mechanics, 2001, 18(4): 140-144. |
| [10] |
甘亚南, 周广春. 基于能量变分原理的薄壁箱梁自振特性分析[J]. 中国公路学报, 2007, 22(1): 73-78. GAN Ya-nan, ZHOU Guang-chun. Analysis of Analysis of Free Vibration Characteristics of Thin-walled Box Girder Based on Energy Variation Principle[J]. China Journal of Highway and Transport, 2007, 22(1): 73-78. |
| [11] |
甘亚南, 周广春. 薄壁箱梁自振频率分析的多参数翘曲位移函数法[J]. 铁道学报, 2007, 29(5): 93-98. GAN Ya-nan, ZHOU Guang-chun. An Approach of Multi-parameter Warping Displacement Function for Natural Frequency Analysis of Thin-walled Box Girders[J]. Journal of the China Railway Society, 2007, 29(5): 93-98. |
| [12] |
周旺保, 蒋丽忠, 戚菁菁. 考虑剪力滞和剪切变形的薄壁箱梁自振特性分析[J]. 计算力学学报, 2013, 30(6): 802-806. ZHOU Wang-bao, JIANG Li-zhong, QI Jing-jing. Analysis of Free Vibration Characteristic of Thin-wall Box-girder Considering Shear Lag and Shear Deformation[J]. Chinese Journal of Computational Mechanics, 2013, 30(6): 802-806. |
| [13] |
冀伟, 刘世忠, 蔺鹏臻. 波形钢腹板连续梁的动力特性[J]. 公路交通科技, 2011, 28(11): 55-59. JI Wei, LIU Shi-zhong, LIN Peng-zhen. Dynamic Characteristics of Composite Box Girder with Corrugated Steel Webs[J]. Journal of Highway and Transportation Research and Development, 2011, 28(11): 55-59. |
| [14] |
冀伟, 刘世忠, 蔺鹏臻. 波形钢腹板组合箱梁振动频率分析与试验[J]. 中国公路学报, 2013, 26(5): 102-107. JI Wei, LIU Shi-zhong, LIN Peng-zhen. Experiment and Analysis for Vibration Frequency of Composite Box Girder with Corrugated Steel Webs[J]. China Journal of Highway and Transport, 2013, 26(5): 102-107. |
| [15] |
包世华, 周坚. 薄壁杆件结构力学[M]. 北京: 中国建筑工业出版社, 2005, 1-20. BAO Shi-hua, ZHOU Jian. Structural Mechanics of Thinwalled Bar[M]. Beijing: China Architecture & Building Press, 2005, 1-20. |
| [16] |
周茂定, 李丽园, 张元海. 考虑剪切变形时薄壁箱梁的挠曲分析[J]. 工程力学, 2015, 32(10): 138-144. ZHOU Mao-ding, LI Li-yuan, ZHANG Yan-hai. Flexural Analysis of Thin-walled Box Girders with Shear Deformation[J]. Engineering Mechanics, 2015, 32(10): 138-144. |
| [17] |
徐芝纶. 弹性力学(上册)[M]. 北京: 高等教育出版社, 2006, 257-286. XU Zhi-lun. Elasticity Mechanics (Volume One)[M]. Beijing: Higher Education Press, 2006, 257-286. |
| [18] |
JTG D60-2015, 公路桥涵设计通用规范[S]. JTG D60-2015, General Specifications for Design of Highway Bridges and Culverts[S]. |
 2018, Vol. 35
2018, Vol. 35
