扩展功能
文章信息
- 黄海新, 安帅锟, 程寿山
- HUANG Hai-xin, AN Shuai-kun, CHENG Shou-shan
- 基于反拱行为的空心板桥横向体外预应力加固模型
- A Lateral External Prestress Reinforcement Model for Hollow Slab Bridge Based on Arching Behavior
- 公路交通科技, 2018, 35(1): 55-63
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(1): 55-63
- 10.3969/j.issn.1002-0268.2018.01.008
-
文章历史
- 收稿日期: 2017-01-20
2. 交通运输部公路科学研究院, 北京 100088
2. Research Institute of Highway, Ministry of Transport, Beijing 100088, China
装配式混凝土空心板梁桥因其预制方便、施工简便,在我国中小跨径桥梁中占有很大比重[1]。但随着服役年限增加、车辆超载、养护管理不到位等原因[2-3],出现了诸如铰缝损伤等病害[4-5],急待维修加固。横向体外预应力加固[6-8]是近年来出现的一种新型加固方法,其以经济成本低、加固工期短、成效良好等优势在桥梁维护中被逐步采用,但现有的工程应用中均出现了不同程度的“反拱”现象[9-10]。“反拱”在一定程度上对桥梁线形、桥下净空及桥面铺装等带来了影响,严重的甚至加剧了铰缝病害,不利于各板梁间的协调工作,与加固初衷相违背。可惜该现象目前还未引起足够的重视,对其机理也未加以深入剖析。“反拱”虽是梁体边梁下挠中梁上拱的外在直观表现,但其实质应是横向体外预应力使装配式板梁体系横向受力行为发生变化所致,而且应与预应力大小、铰缝损伤程度等诸多因素有关。
针对上述问题,选取各板梁端支座反力作为切入点,通过分析其变化间接反馈各板梁的载荷横向分布,从而揭示“反拱”现象的本质。同时,基于铰接板理论建立横向体外预应力下的各板梁反力分布解析式,列出影响横向加固的诸多影响因素,并利用数值仿真手段对各因素进行量化分析,探讨横向预应力下空心板梁桥的受力行为,明确加固方法中的注意事项并给出设计建议,为今后类似工程实践提供参考。
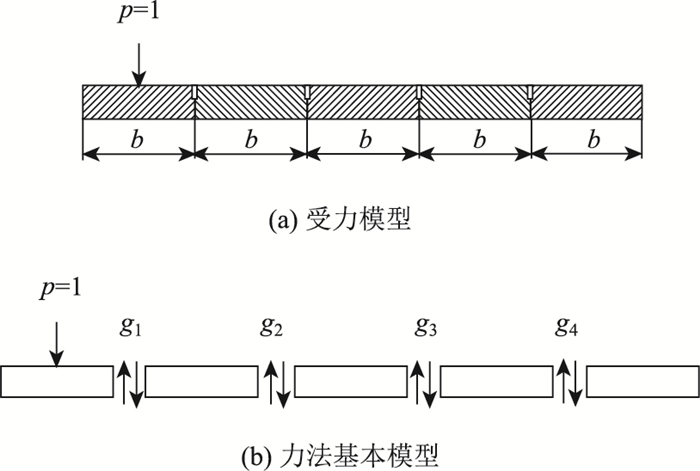
1 理论分析 1.1 铰接板法简介装配式混凝土空心板桥荷载横向分布的铰接板法[11-12]计算模型如图 1所示。
|
| 图 1 铰接板计算图式 Fig. 1 Computation patterns of hinge slab |
| |
根据变形协调原理,建立正则方程:
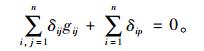
|
(1) |
对于5片梁,引入刚度系数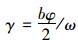
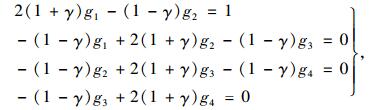
|
(2) |
解得边板铰缝竖向剪力为:
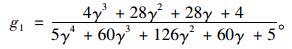
|
(3) |
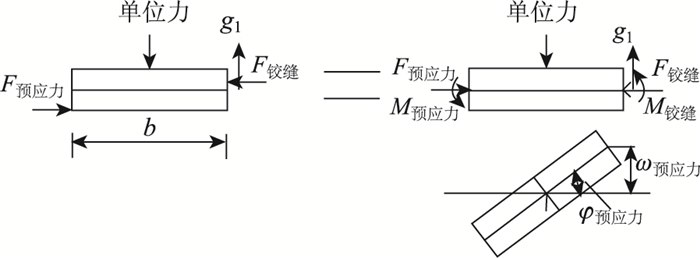
横向加固用体外预应力改变了桥梁原有的受力状态,边板受力如图 2所示。
|
| 图 2 横向预应力下边板受力模型 Fig. 2 Mechanical model of transverse prestressed lower slab |
| |
可以看出,横向预应力并未直接对板梁竖向受力产生影响,但附加扭矩对其边板产生了一个转角φ预应力。根据变形协调原理知,边板与次边板发生了相对位移ω预应力。设未施加横向预应力前,原桥面系结构在单位偏心荷载下单板产生位移和转角分别为ω和φ,板内对应的偏心扭矩为M。为体现横向加固前后偏心力矩的变化,这里引入一个比例系数k,设
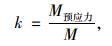
|
(4) |
则由材料力学,可知:
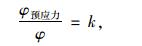
|
(5) |
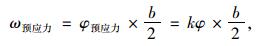
|
(6) |
正则方程(2)变换后有:
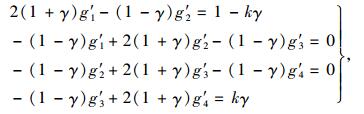
|
(7) |
解得边板铰缝竖向剪力为:
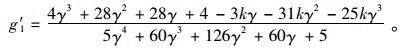
|
(8) |
对于边板,依据铰缝竖向剪力和支座反力的关系,求得施加预应力后其支座反力变化为:
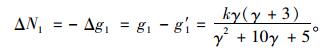
|
(9) |
对于γ的取值,一般中小板桥在[0, 1]区间[13]内,所以分母:
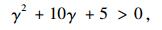
|
(10) |
而:
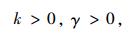
|
(11) |
故:
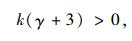
|
(12) |
可知:
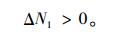
|
(13) |
式(13)说明,横向预应力的施加使边板支座反力增大。
同理有:
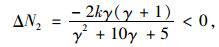
|
(14) |
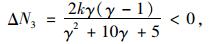
|
(15) |
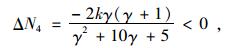
|
(16) |
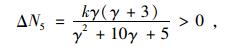
|
(17) |
则各板实际受力方向为如图 3所示。

|
| 图 3 横向加固预应力下各板受力状态 Fig. 3 Force state of each slab under transverse prestressing |
| |
图 3可以清晰表明,横向预应力的附加扭矩对各板产生附加内力,使得边板支反力增大,非边板支反力减小。也正是如此,在竖向外载不变的情况下,支反力减小的板,向下的竖向作用效应自然减小,向下的竖向挠曲变形亦减小,形成“反拱”现象。由此可见,板受力状态的变化是产生“反拱”现象的根本原因。
2 数值模拟由前述理论分析可知,横向预应力作用下各板支反力的变化是加固系数k和主梁刚度系数γ的函数,其中k和γ除受预应力筋张拉力大小、作用位置、板的片数等因素影响外,势必还与铰缝损伤程度、预应力筋沿纵向的布置间距等因素相关,而后者在解析的理论公式中难以直接体现,故这里引入有限元数值模拟手段,旨在检验理论解析式合理性的同时,对各影响因素进行量化分析,明确主次,找出影响规律,进一步深入剖析“反拱”现象,为横向预应力加固实践提供指导。
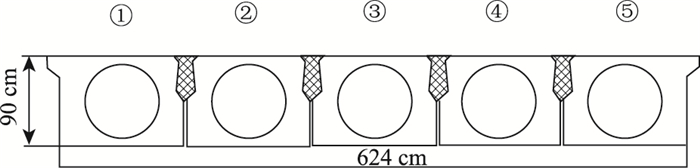
2.1 有限元模型建立数值模拟以天津某实桥为背景。桥梁跨径10 m,计算跨径9.66 m,横向由5块宽1.24 m,高0.9 m的空心板拼装而成,板间预留1 cm宽的施工缝,横向由企口混凝土铰缝连接,如图 4所示。
|
| 图 4 主梁构造图 Fig. 4 Main girder structure |
| |
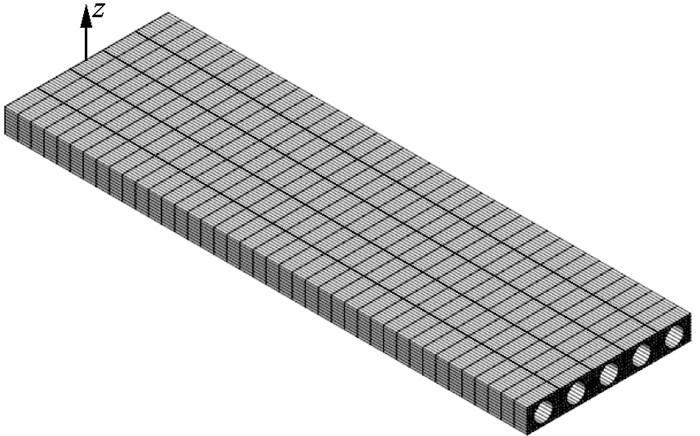
利用FEA有限元软件建立精确的空间有限元实体模型[14],由于实桥混凝土桥面铺装层已破损,与空心板连接的整体性较为弱化,故建模时忽略铺装层的刚度,仅计入主梁刚度,如图 5所示。
|
| 图 5 主梁有限元模型 Fig. 5 Finite element model of main girder |
| |
2.2 模型有效性检验
为了验证模型的有效性,这里将理论值与有限元模拟值进行对比。将实桥加固中k和γ值代入式(13)~(17)求得理论值,利用式(18):

|
(18) |
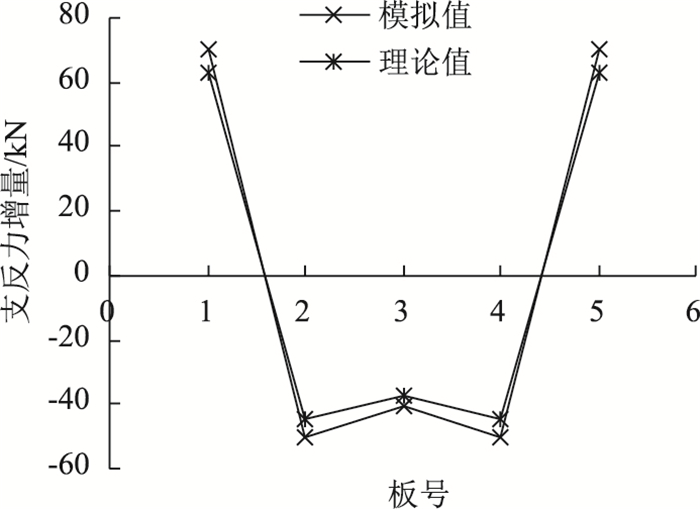
求得模拟值,对比结果见图 6。
|
| 图 6 理论值与模拟值对比 Fig. 6 Comparison of theoretical value and simulation value |
| |
可以看出,支座反力增量理论值与有限元模拟值均呈现边板增大、非边板反力减小的相同趋势,说明所建立的有限元模型可较好反映支反力增量的变化。从数值上看,在M预应力锚点作用边板处支反力模拟结果比理论稍大,意味着边板承受更多的荷载。究其原因,一方面边板锚固处预应力较为集中,数值模拟能较好体现该种现象;同时,由于铰接板理论分析采用的是简化方法,认为荷载仅在跨中加载截面先行横向传递,而实际空间分析中荷载是以加载位置为源头向周边多个截面位置同时传递。
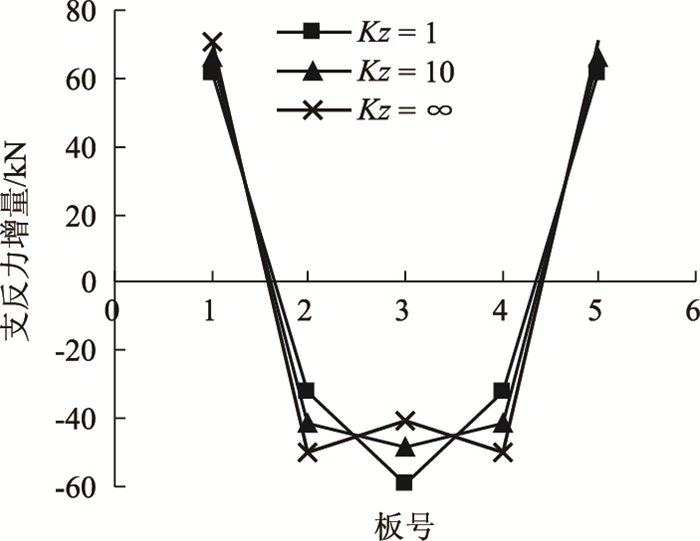
此外,需要说明的是,实际工程中在求解支座反力增量ΔN时,梁体需要与支座实际物理力学特性相协调,然而理论计算中为简化起见将支座竖向刚度视为无穷大。为了更加贴合实际情况,有必要对上述有限元模型做出修正,观察支座刚度变化对结构带来的影响。这里设无量纲参数Kz=模型支座刚度/支座真实刚度,尝试选取3种参数值,即①Kz=∞;②Kz=10;③Kz=1,计算当Kz由无穷大理论值向实际刚度过渡时各片板梁支座反力增量的变化,计算结果见图 7。
|
| 图 7 支座刚度对各板支反力影响 Fig. 7 Influence of bearing stiffness on support reaction of each slab |
| |
由图 7可知,随着支座刚度的减小,各板支反力呈现不同的变化,其中边板支反力逐渐减小,非边板支反力曲线由开始的“上凹”到逐渐平缓再到“下凸”,说明在有限元模拟中,支座竖向刚度这一边界条件对支反力数值以及趋势均有较大的影响。考虑到工程实际中支座刚度的有限性,加固有限元模型中支座刚度应尽可能与实际状况相符。因此,这里以Kz=1模型为基本加固用模型,对后继支反力影响因素进行探究。
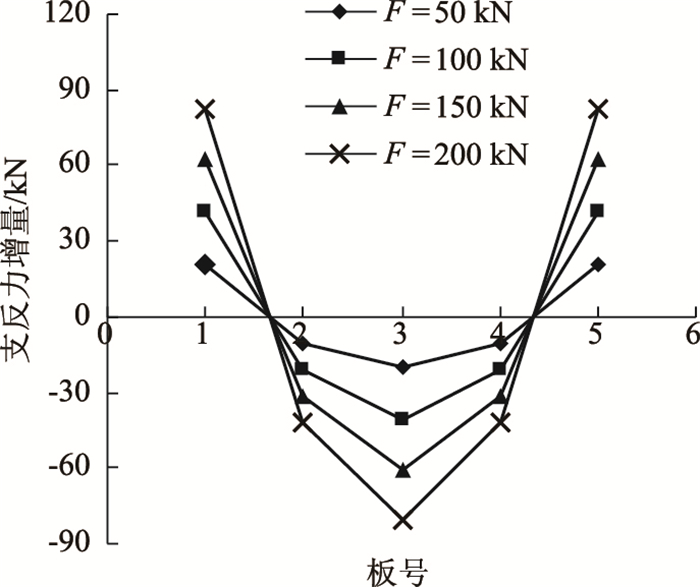
2.3 预应力大小影响分析为研究施加预应力大小对支座反力的影响,在计算模型中的顺桥方向布置5根间距均为1 m的预应力筋。张拉力逐级分4次张拉,每级增量为50 kN,即4次张拉力分别为F=50 kN/根、F=100 kN/根、F=150 kN/根和F=200 kN/根。图 8、图 9给出了各片板梁支座反力的增量变化。
|
| 图 8 预应力大小对各板支反力影响 Fig. 8 Influence of prestress on support reaction of each slab |
| |
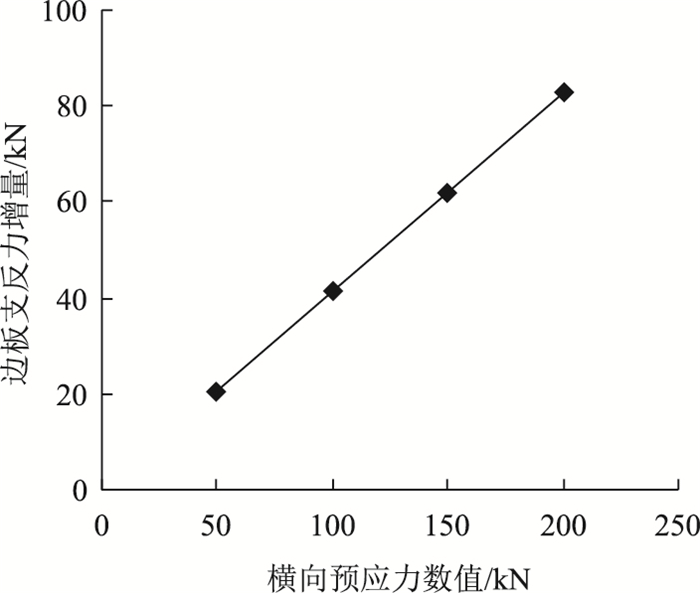
|
| 图 9 预应力大小对边板支反力影响 Fig. 9 Influence of prestress on support reaction of side slab |
| |
由图 8可知,施加横向预应力后各板梁支座反力呈不同程度的变化,其中边板支座反力增大明显,且左右对称;中板支座反力减小,减小趋势从次边板到中板逐渐增强。
为进一步探究不同预应力大小对支反力的影响,提取不同预应力数值下具有代表性的边板反力增量(见图 9),可见边板支反力增量与预应力大小正相关,且增势大致为线性,这是因为在预应力筋布置高度一定的情况下,预应力大小与附加扭矩M预应力线性正相关,进而与k和ΔN成线性关系,与式(13)趋势相符。
本工程实例中,边板反力增量占横向加固预应力数值总和比约为8.27%,5根预应力筋各150 kN张拉力[15-16]下对应的边板反力增量62.03 kN,中板支反力减少60.74 kN,可见横向预应力对各板支反力影响较大,支反力的不均匀性较为突出,实际发现这也与活载作用在边板有关。计算发现,当活载作用在中板时,各个支座在横向预应力和活载的共同作用下反力则较为均匀,有利于各板协同工作[17]。因此,横向预应力加固方式对外载经常位于非边板的活载类型较为合适。
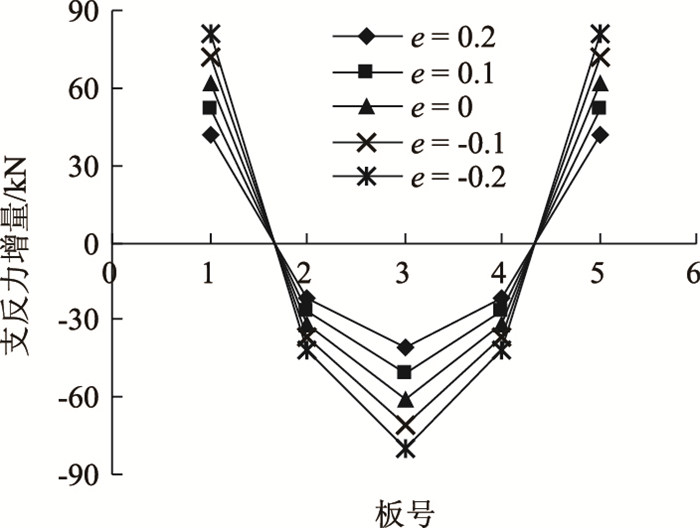
2.4 预应力筋布置高度影响分析为研究预应力筋位于梁底缘高度e对边板支反力增量的影响,进行如下建模分析:(1)预应力筋位于板梁底缘上0.2 m;(2)预应力筋位于板梁底缘上0.1 m;(3)预应力筋位于板梁底缘;(4)预应力筋位于板梁底缘下0.1 m;(5)预应力筋位于板梁底缘下0.2 m。横向预应力张拉力大小150 kN, 预应力间距1 m。这里规定预应力筋在梁底缘以上为正,梁底缘以下为负,分析得各板支反力,如图 10、图 11所示。
|
| 图 10 预应力筋高度对各板支反力影响 Fig. 10 Influence of height of prestressing tendon on support reaction of each slab |
| |
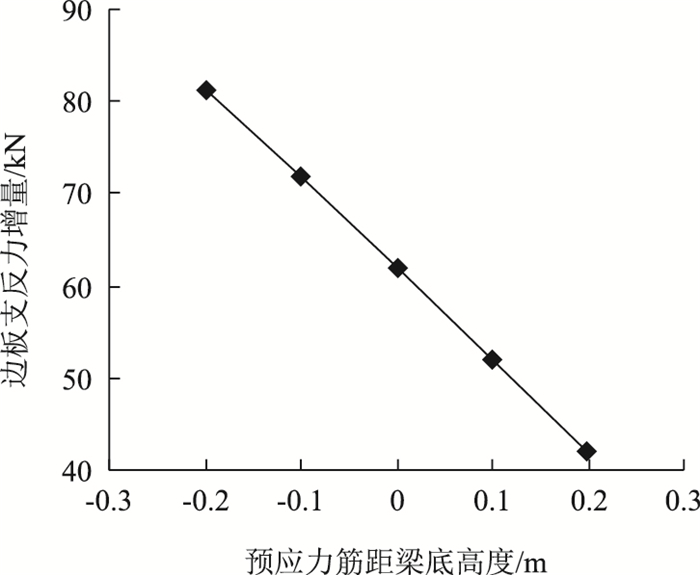
|
| 图 11 预应力筋高度对边板支反力影响 Fig. 11 Influence of height of prestressed tendons on support reaction of side slab |
| |
由图 10可知,横向预应力使边板支反力增加,且随着预应力筋高度的降低,各板支反力增量数值越来越大,这说明预应力筋越靠下,预应力与板形心距离越长,对支反力的影响越大。由图 11可知,边板支反力增量随预应力筋高度呈线性变化,其原因在于附加扭矩M预应力随着预应力作用点与板形心间距呈线性变化,导致k线性变化,最终反馈到边板支反力ΔN1亦成线性变化,这与式(13)相符。对该工程实例,边板线性增加比例系数(边支反力增量/预应力高度)为100.95 kN/m。
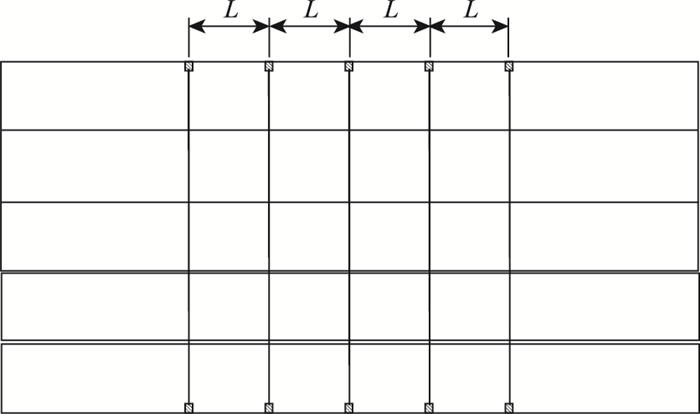
2.5 预应力筋布置间距影响分析为研究预应力筋间距对支座反力增量的影响,选择如下4种方式进行建模分析:(1)预应力筋间距L=0.5 m;(2)预应力筋间距L=1 m;(3)预应力筋间距L=1.5 m;(4)预应力筋间距L=2 m,预应力布置如图 12所示。
|
| 图 12 预应力筋布置图 Fig. 12 Layout of prestressing tendons |
| |
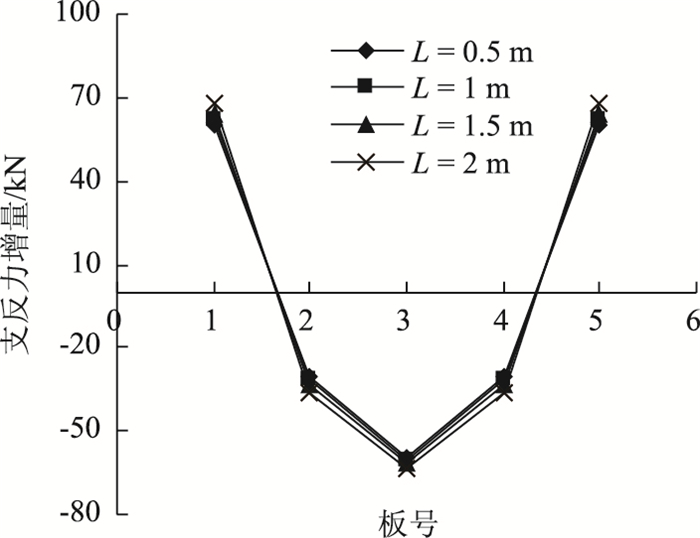
计算得各板支反力增量见图 13。
|
| 图 13 预应力筋间距对各板支反力影响 Fig. 13 Influence of spacing of prestressed tendons on support reaction of each slab |
| |
由图 13可以得知,预应力筋间距布置的不同对各板支反力影响并不显著,说明在附加扭矩M预应力总和一定的条件下,作用点的纵向位置虽影响横向传力但效果并不明显,即可认为横向体外预应力筋纵向布置间距对总附加扭矩M预应力影响甚微,对各板支反力增量ΔN的影响可忽略不计。
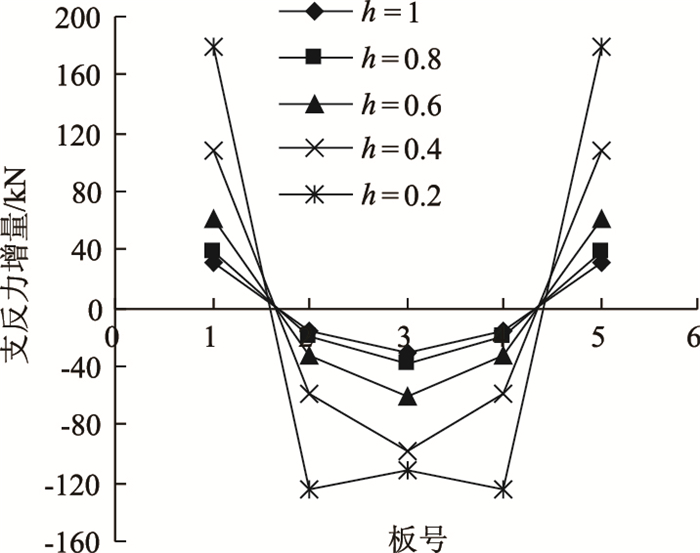
2.6 铰缝深度影响分析为研究铰缝深度对支反力的影响,将模型中铰缝单元的竖向高度进行增减,为消除梁高与铰缝深度间的相互影响,这里设定铰缝深度参数h=铰缝深度/梁高,选择如下5种参数值进行建模分析:(1)h=1(全铰缝);(2)h=0.8;(3)h=0.6;(4)h=0.4;(5)h=0.2,计算得各板支反力增量见图 14、图 15。
|
| 图 14 铰缝深度对各板支反力影响 Fig. 14 Influence of hinge joint depth on support reaction of each slab |
| |
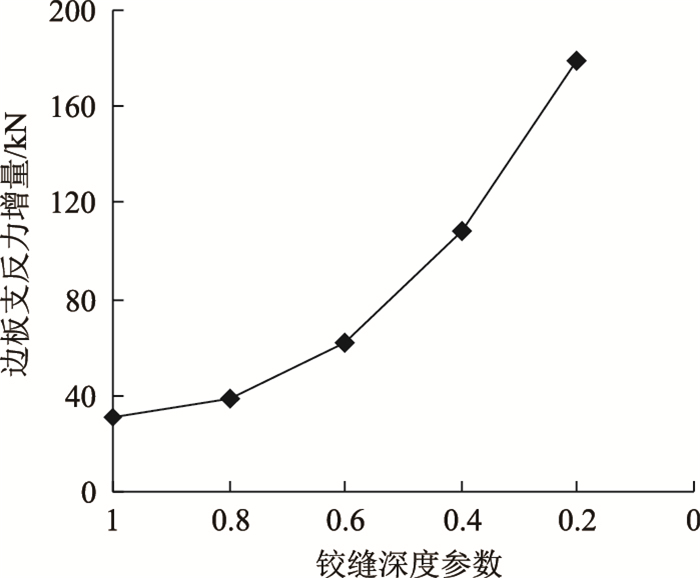
|
| 图 15 铰缝深度对边板支反力影响 Fig. 15 Influence of hinge joint depth on support reaction of side slab |
| |
由图 14可知,随着铰缝深度的减小,各板支反力增量越来越大,且支座反力增量的离散程度要强于前面分析的3种影响因素,这说明铰缝深度对支反力影响更为显著。由图 15进一步可知,边板支反力增量与铰缝深度负相关且不再呈线性趋势,这可能是由于一方面铰缝深度减小增大了铰心与横向预应力作用点的距离,增加了M预应力的大小,提升了ΔN1;另一方面铰缝深度的减小导致板间传力减弱,桥梁横向整体抵抗变形的能力被削弱,最终导致各板支反力呈现较大的离散性。考虑到工程加固中,产生的过大支反力对梁体和支座均会带来不利的影响,可见横向体外预应力加固对大铰缝梁桥更具安全性和适用性,对小铰缝梁桥应慎重。
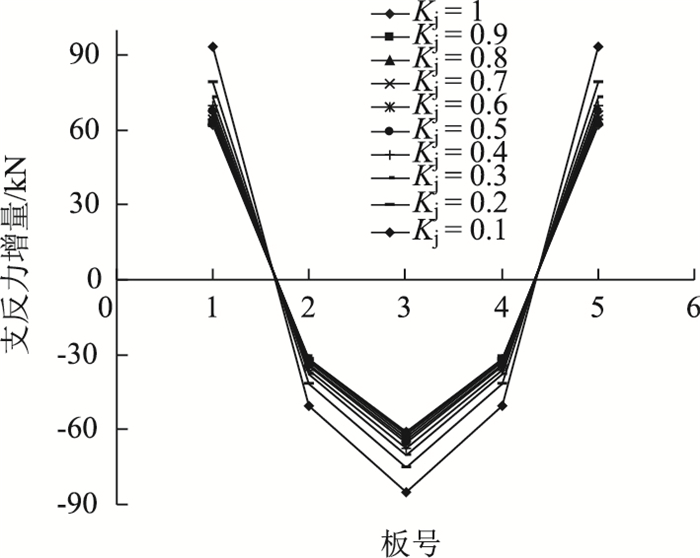
2.7 铰缝损伤程度影响分析为研究铰缝不同破坏状况下,横向预应力对支反力的影响,这里对铰缝剪切刚度进行折减[18],建立了不同损伤程度的模型,引入铰缝损伤参数Kj=旧桥铰缝刚度/初始铰缝刚度。计算得各板支反力增量见图 16、图 17。
|
| 图 16 铰缝损伤程度对各板支反力影响 Fig. 16 Influence of hinge joint damage degree on support reaction of each slab |
| |
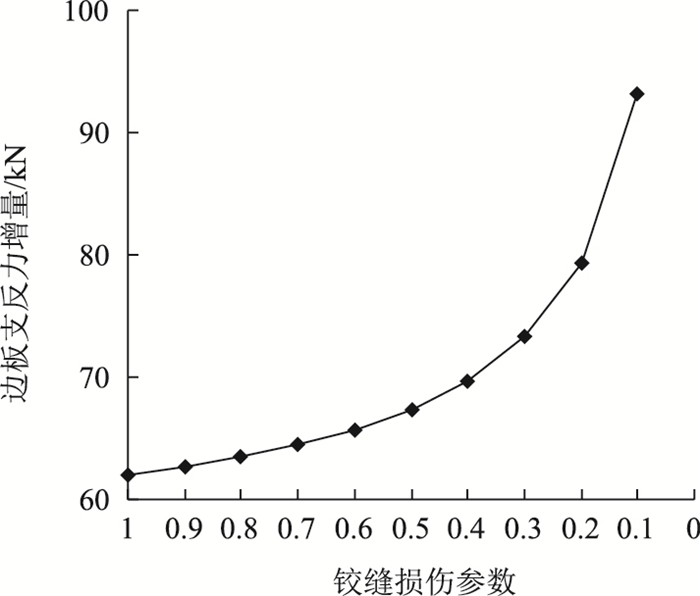
|
| 图 17 铰缝损伤程度对边板支反力影响 Fig. 17 Influence of hinge joint damage degree on support reaction of side slab |
| |
由图 16可知,随着铰缝刚度的减小,各支座反力增量越来越大,说明铰缝破坏程度对支座反力正相关。由图 17进一步得知,在Kj从1变化到0.5过程中,边板支反力增量变化值增长缓慢,说明在铰缝破损不严重时,各板支反力平稳变化;Kj大于0.5后,ΔN1增长较快且呈非线性,此时梁体已经发生严重的破坏,而横向预应力加固方式进一步加剧了铰缝的病害。所以在工程实践中,横向体外预应力加固方法对损伤程度严重的桥梁会产生负面影响,加固方案选取时要慎重对待。
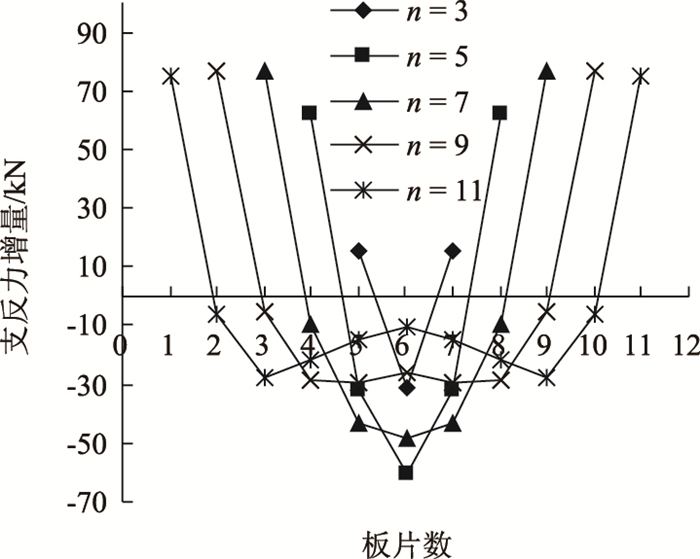
2.8 板梁片数影响分析为探究不同数量空心板梁对支反力的影响,建立了如下5种不同数量的板梁模型并进行分析:(1)3片板梁;(2)5片板梁;(3)7片板梁;(4)9片板梁;(5)11片板梁,计算得各板支反力增量,如图 18、图 19所示。
|
| 图 18 梁片数对各板支反力影响 Fig. 18 Influence of number of beams on support reaction of each slab |
| |
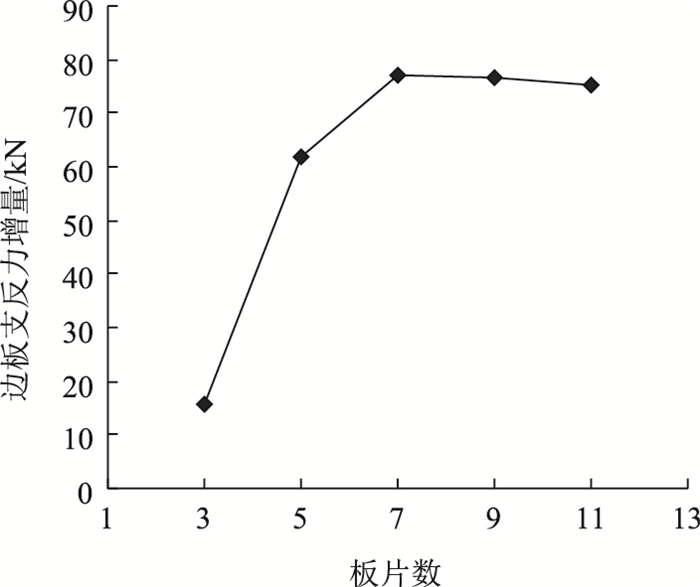
|
| 图 19 梁片数对边板支反力影响 Fig. 19 Influence of number of beams on support reaction of edge slab |
| |
由图 18可知,随着横桥向空心板梁片数的增多,各板支反力增量大体呈增加趋势。对整体线形而言,n=3到n=7各板支反力始终保持着从边板到中板依次减小的“V”形,在n=9时则变化成相对平缓的“U”形,n=11时又变成更加离散的“W”形。分析其原因,发现这是由于支座刚度的存在对各板的变形起到了调和作用,导致附加扭矩直接作用板(即边板)附近有更大的变形,与其临近的几片次边板支反力增量差值更为明显,而中板反力增量数值的大小则完全受边板距离的影响,随着n的增加,中板距离边板越来越远,受到的影响越来越弱,中板附近支反力增量越发趋向于0,故线形呈“V”形到“W”形变化。对于边板支反力增加量(如图 19所示),由n=3到n=7各板支反力增量较为明显,n=7到n=11时增量趋于稳定,可以认为在临界数量点7片板的空心板梁桥中,各板变形协调性出现拐点,横向预应力作用下支座反力得到充分释放。
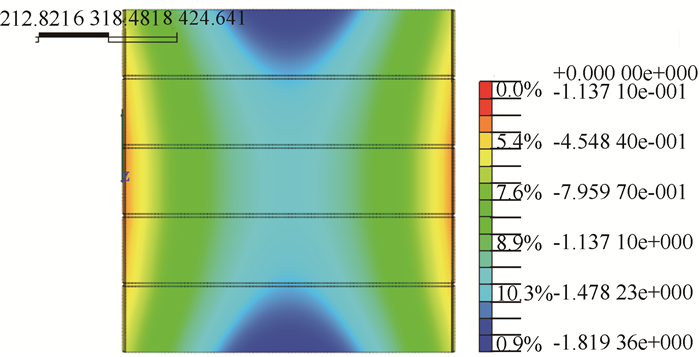
2.9 活载效应分析为研究横向预应力加固后桥梁结构在运营阶段结构的反拱行为,有必要对加固后结构进行恒载和恒载+活载作用下对空心板挠度和支反力的影响分析。这里选取在有限元模型中板跨中施加100 kN集中力来模拟活载,竖向位移云图如图 20、图 21所示。
|
| 图 20 恒载作用下主梁位移云图(单位:mm) Fig. 20 Nephogram of girder displacement under dead load(unit:mm) |
| |
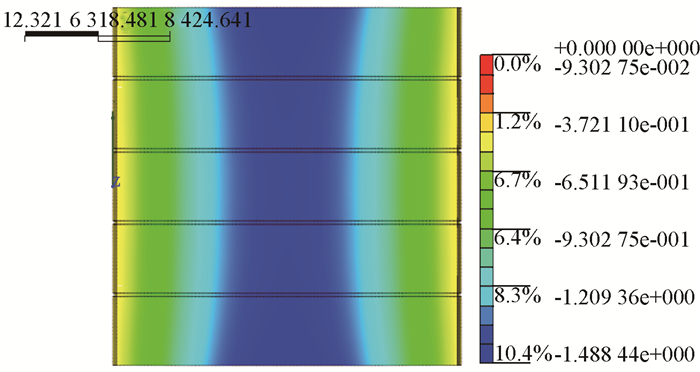
|
| 图 21 恒载+活载作用下主梁位移云图(单位:mm) Fig. 21 Nephogram of girder displacement under dead load and live load(unit:mm) |
| |
由图 20可以看出,桥梁在施加横向预应力后,边板挠度变大、中板挠度变小,形成两端下挠中间顶起的“反拱”现象。如图 21所示,当施加活载后,位移云图趋于缓和,说明在跨中活载作用下反拱现象受到削弱。两种工况下各板支反力如图 22所示。
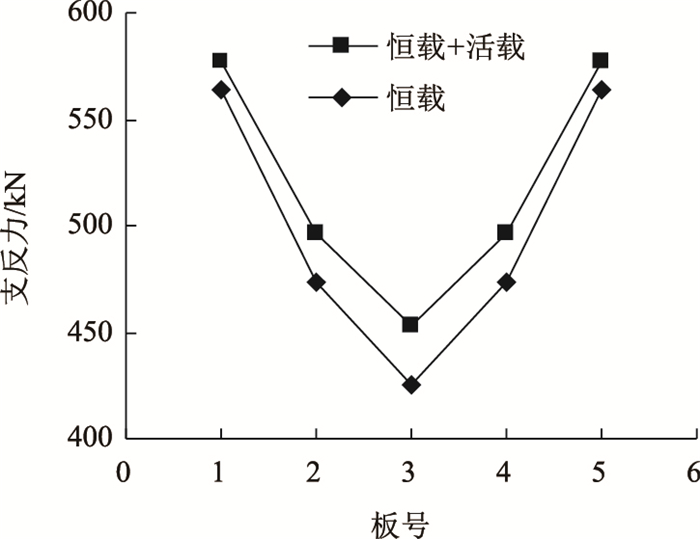
|
| 图 22 恒活载作用对各板支反力影响 Fig. 22 Influence of dead load and live load on support reaction of each slab |
| |
由图 22可以看出,活载作用下,各板支反力均增大,但以活载作用位置处的中板增加最为明显,边板增量最小,其他各板支反力增量逐渐过渡,说明横向预应力加固后的桥梁在活载作用下的反拱现象得到了一定程度的改善,各板受力更为均衡。
3 结论(1) 考虑加固中横向体外预应力的作用,基于铰结板理论,建立了各片板支反力的解析表达式,明确了横向施加预应力对各片板支反力的影响,揭示了“反拱”现象的内在原因,为结构的加固设计提供了理论指导。
(2) 对活载经常作用于边板的空心板梁桥,横向预应力加固方法使边板受力过大,且显著增加边板支座压力,对结构不利;但对活荷载主要作用于中板的情况,预应力和活载的叠加效应将使各板受力较为均匀,故横向体外预应力加固方法对活载长期偏中板作用的窄梁桥,具有更好的适用性。
(3) 预应力具体加固方式影响各板支反力的大小,其中预应力筋的大小、预应力筋布置高度与支座反力大小呈线性相关,而预应力布置间距影响甚微。在各板支反力的影响因素中,梁桥铰缝的深度影响最大,铰缝破坏程度次之,这就要求工程人员在对空心板梁桥进行加固方案比选时要“因桥制宜”,即将加固方式与加固对象的当前状态相结合。
(4) 空心板梁桥片数影响各板支反力的大小,总体趋势是片数越多,支反力增量越大;但当板梁片数增大到7片以上时,边板支反力基本不再变化,非边板支反力呈现中间小两边大的趋势。
(5) 相比于横向预应力的加固方式(含张拉力大小和布置位置),空心板梁桥自身的状态(如铰缝大小、损伤程度)对加固效果影响更为明显。对损伤严重、小铰缝板梁桥进行横向预应力加固时应慎重,否则可能会加剧梁体破坏。
| [1] |
姚玲森. 桥梁工程[M]. 北京: 人民交通出版社, 2003. YAO Ling-sen. Bridge Engineering[M]. Beijing: China Communications Press, 2003. |
| [2] |
刘能文. 铰接板桥梁病害分析及优化设计方法研究[J]. 公路交通科技, 2016, 33(2): 73-81. LIU Neng-wen. Analysis and Optimization Design Method of Diseases of Hinged Plate Bridge[J]. Journal of Highway and Transportation Research and Development, 2016, 33(2): 73-81. |
| [3] |
乔学礼. 空心板铰缝破坏机理及防治措施研究[D]. 西安: 长安大学, 2008. QIAO Xue-li. Study on Destruction Mechanism and Prevention Measures of Hollow Plate Hinge Joint[D]. Xi'an: Chang'an University, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=shanxjz200902201 |
| [4] |
霍航鹰. 高等级公路中"单板受力"现象及原因[J]. 交通世界:运输车辆, 2012(11): 186-187. HUO Hang-ying. Phenomenon of Single Slab Bearing in High-grade Highway and Analysis of Its Reasons[J]. Transpo World, 2012(11): 186-187. |
| [5] |
于长久. 空心板简支梁桥横向铰接缝病害分析[D]. 哈尔滨: 哈尔滨工业大学, 2009. YU Chang-jiu. Disease Analysis of Transverse Hinge Joint of Hollow Plate Simply Supported Beam Bridge[D]. Harbin: Harbin Institute of Technology, 2009. |
| [6] |
王同卫. 浅析简支空心板梁桥横向体外预应力加固[J]. 山西建筑, 2008, 34(31): 30-31. WANG Tong-wei. Brief Analysis on Consolidation of Crosswise Out-body Prestressed of Simple Support Hollow Board Beam Bridge[J]. Shanxi Architecture, 2008, 34(31): 30-31. |
| [7] |
梁全富. 体外横向预应力加固简支空心板梁桥工艺研究[J]. 福建建筑, 2007, 111(9): 43-44. LIANG Quan-fu. A Technical Study of External Transverse Prestress for Hollow-plate to Strengthen and Support Girder Bridges[J]. Fujian Architecture and Construction, 2007, 111(9): 43-44. |
| [8] |
张雷. 预应力混凝土空心板桥横向体外预应力加固方法[J]. 内蒙古公路与运输, 2015, 150(6): 13-15. ZHANG Lei. Lateral External Prestressed Strengthening Method of the Prestressed Concrete Hollow Slab Bridge[J]. Highways and Transportation in Inner Mongolia, 2015, 150(6): 13-15. |
| [9] |
康叶铭. 体外预应力加固机理及应用[D]. 南京: 河海大学, 2006. KANG Ye-ming. External Prestressed Reinforcement Mechanism and Application[D]. Nanjing: Hohai University, 2006. |
| [10] |
刘凤山, 杨琪. 装配式简支空心板梁桥体外横向预应力加固效果分析[J]. 筑路机械与施工机械化, 2014, 31(9): 79-82. LIU Feng-shan, YANG Qi. Analysis on Reinforcement Effect of External Transverse Prestress on Fabricated Simply-supported Hollow-slab Bridge[J]. Road Machinery and Construction Mechanization, 2014, 31(9): 79-82. |
| [11] |
李国豪. 公路桥梁荷载横向分布计算[M]. 北京: 人民交通出版社, 1984. LI Guo-hao. Calculation of Lateral Load Distribution of Highway Bridges[M]. Beijing: China Communications Press, 1984. |
| [12] |
贺拴海. 公路桥梁荷载横向分布计算方法[M]. 北京: 人民交通出版社, 1996. HE Shuan-hai. Highway Bridge Load Transverse Distribution Calculation Method[M]. Beijing: China Communications Press, 1996. |
| [13] |
赵兴中. 预制装配式小箱梁桥横向分布计算方法的研究分析[D]. 西安: 长安大学, 2007. ZHAO Xing-zhong. Study on Transverse Distribution Calculation Method of Prefabricated Box Girder Bridge[D]. Xi'an: Chang'an University, 2007. http://d.wanfangdata.com.cn/Thesis/Y1528668 |
| [14] |
桂水荣. 简化建模方法对空心板桥力学性能的影响[J]. 公路交通科技, 2014, 31(12): 50-57. GUI Shui-rong. Effect of Simplified Modeling Method on Mechanical Performance of Hollow Slab Bridge[J]. Journal of Highway and Transportation Research and Development, 2014, 31(12): 50-57. |
| [15] |
陈淮, 孙云娜. 施加横向预应力加固装配式空心板桥研究[J]. 公路交通科技, 2008, 10(25): 58-62. CHEN Huai, SUN Yun-na. Research on Strengthening Fabricated Hollow Slab Bridge by Applying Transverse Prestress[J]. Technology of Highway and Transport, 2008, 10(25): 58-62. |
| [16] |
JTG D62-2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG D62-2004, Code for Design of Highway Reinforced Concrete and Presstressed Concrete Bridges and Culverts[S]. |
| [17] |
刘平. 空心板横向预应力加固分析[J]. 郑州大学学报, 2014, 35(4): 24-28. LIU Ping. Hollow Slab Transverse Prestressing Reinforcement Analysis[J]. Journal of Zhengzhou University, 2014, 35(4): 24-28. |
| [18] |
杜红静. 装配式空心板桥横向加固结构分析方法研究[D]. 西安: 长安大学, 2012. DU Hong-jing. Assembled Hollow Slab Bridge Transverse Reinforcement Structure Analysis Method[D]. Xi'an: Chang'an University, 2012. |
 2018, Vol. 35
2018, Vol. 35
