扩展功能
文章信息
- 李微哲, 娄平
- LI Wei-zhe, LOU Ping
- 计入水平力剪切变形和轴力影响的柱单元及其在支座基桩共同作用分析中的应用
- Beam Element Considering Lateral Shear Deformation and Axial Force Effect and Its Application in Analysis of Bearing and Pile Combined Action
- 公路交通科技, 2018, 35(1): 46-54, 78
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(1): 46-54, 78
- 10.3969/j.issn.1002-0268.2018.01.007
-
文章历史
- 收稿日期: 2016-11-22
2. 中煤科工集团重庆设计研究院有限公司, 重庆 400016
2. Chongqing Design and Research Institute, Co., Ltd., China Coal International Engineering Group, Chongqing 400016, China
工程实际进行结构线弹性分析时因其剪切变形影响较小而常忽略不计。但进行抗震分析时,轴力构件的剪切变形的影响则需考虑。此外,桥梁支座作为一种大剪切变形的轴力构件,其偏心弯矩效应极显著,目前对其动力黏弹性模型研究较多,但对其静力大剪切变形和轴力共同作用下的力学模型研究则尚似未见报道。因此提出一种同时考虑水平力剪切变形和轴力P-Δ效应的柱单元,以模拟支座的大偏心工作特性和其他轴力构件抗震分析时的剪切效应,具有实际意义。
柱剪切效应和轴力P-Δ效应研究广泛。忽略剪切变形并计入轴力P-Δ效应影响的柱单元刚度矩阵,由弹性刚度矩阵和几何刚度矩阵构成,有限元分析时无需迭代计算。1985年,王用中等基于三次Hermite插值函数和最小势能原理和能量法提出了一致几何刚度矩阵[1]。1987年Wilson E.L.提出了线性近似的几何刚度矩阵[2]。2006年赵明华等提出了另一种形式的线性近似的几何刚度矩阵[3-4]。1993年舒兴平等基于非线性连续介质力学一般原理及拉格朗日列式法,分析了剪切变形对结构轴力P-Δ效应的影响,认为剪切变形不应忽略[5]。1998年李国强提出了计入剪切变形和轴力P-Δ效应影响的柱单元刚度方程,但其刚度矩阵中系数为级数形式,表现形式复杂,应用不便[6]。随后,孙飞飞等提出了考虑滑移剪力滞后和剪切变形的组合梁单元,但忽略了轴力P-Δ效应[7]。聂国隽等提出了微分求积单元法计算轴力P-Δ效应,亦忽略了剪切变形影响[8]。李国强提出了一种考虑初始缺陷、剪切变形和轴力P-Δ效应的非线性柱单元,其形式极复杂,通用性不足[9]。夏拥军等先构造三节点Euler-Bernoulli梁单元位移模式,推导其弹性刚度矩阵和几何刚度矩阵后,用静力凝聚方法消除三节点梁单元中间节点的自由度,得到了一种考虑轴力P-Δ效应的柱单元,但忽略了剪切变形影响[10]。孟凡涛等综合考虑剪切变形和梁柱节点连接半刚性影响的基础上,给出了框架柱的抗侧移刚度公式,认为剪切变形对框架结构的轴力P-Δ效应影响显著,已超出工程上可接受的5%的误差范围[11]。传光红基于Timoshenko梁理论,提出了计入剪切变形和轴力P-Δ效应影响的变截面Timoshenko梁柱单元,并指出在一定范围内具有足够的精度[12]。王强等基于ABAQUS的纤维梁单元模拟钢筋混凝土柱受力破坏全过程[13]。孙治国等利用OpenSees分析平台,用纤维梁单元模拟分析RC桥墩抗震工作时非线性剪切效应[14]。朱绩超等结合模型试验提出了考虑粘结-滑移与剪切作用的钢筋混凝土柱侧向变形的宏单元模型[15]。丁然等在传统纤维截面模型的分布塑性铰梁单元基础上引入截面剪力-剪切变形关系和剪力-剪切滑移关系,通过MSC.MARC程序二次开发,实现了一种适用于普通配筋RC连梁非线性地震反应分析的纤维梁单元[16]。赵明华等基于有限杆单元法进行了陡坡桩计算分析,但忽略了桩身剪切变形,亦未进行基桩和支座共同作用分析[17-18]。
本文将基于王用中、Wilson E. L.和赵明华等分别提出的柱单元弹性刚度矩阵和几何刚度矩阵,推导了3种计入水平力剪切变形和轴力P-Δ效应影响的柱单元刚度矩阵方程,并应用到支座基桩共同作用分析中。此外还推导外两种新的忽略剪切变形但考虑了轴力P-Δ效应的柱单元刚度矩阵方程。
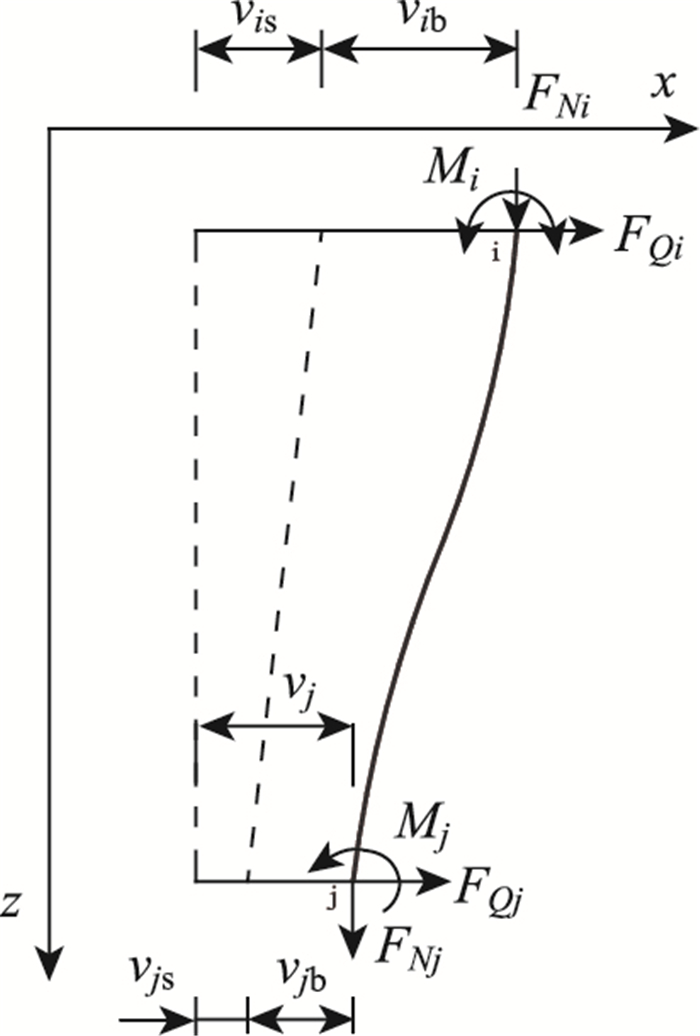
1 不计剪切变形的柱单元刚度矩阵方程柱单元受力如图 1,忽略剪切变形但考虑了轴力的P-Δ效应时,柱单元刚度矩阵方程如下:
|
| 图 1 柱单元受力图 Fig. 1 Force diagram of pile element |
| |
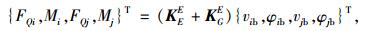
|
(1) |
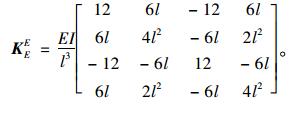
|
(2) |
式中,FNi,FQi,Mi,FNj,FQj,Mj为单元节点内力;vib,vjb,φib,φjb为仅考虑弯曲变形时单元节点i和j的水平位移和转角;KEE为忽略剪切变形的柱单元弹性刚度矩阵; KGE为忽略剪切变形的几何刚度矩阵; E为柱单元弹性模量; I为单元截面惯性矩; l为单元长度。
本文假定轴力拉为负,压为正。则按文献[1],一致几何刚度矩阵KGE如下:
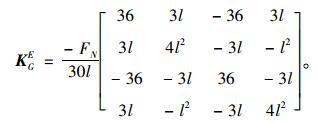
|
(3) |
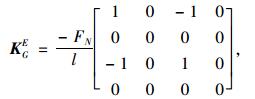
|
(4) |
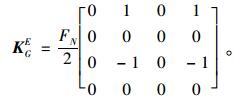
|
(5) |
设柱单元水平位移由弯曲变形和水平力剪切变形组成:
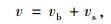
|
(6) |
式中,v为单元总水平位移;vb弯曲变形引起的水平位移;vs为水平力剪切变形引起的水平位移。
因剪切变形引起的转角在节点处因集中剪力而表现非连续,因此柱单元刚度矩阵方程中的转角位移依旧采用仅考虑弯曲变形影响的转角。
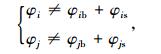
|
(7) |
式中φis,φjs分别为水平力剪切变形在单元i,j节点产生的转角,其余符号意义同前。
剪切变形将进一步增加P-Δ效应,按文献[2],单元节点轴力因水平力剪切变形产生的附加水平力计算如下:
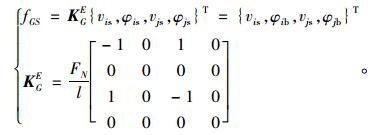
|
(8) |
联立由式(3)~(5)和式(7)可知,计入水平力剪切变形后,柱单元刚度矩阵方程如下:
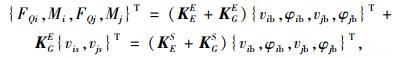
|
(9) |
式中, KES为计入水平力剪切变形的柱单元弹性刚度矩阵;KGS为计入水平力剪切变形的几何刚度矩阵;本章余下章节将给出解答;其余符号意义同前。
联立式(9)、式(8)、式(3),可得计入水平力剪切变形和轴力P-Δ效应的柱单元刚度方程如下:

|
(10) |
联立式(8)、式(9)、式(4),可得计入水平力剪切变形和轴力P-Δ效应的柱单元刚度方程另一种形式如下:

|
(11) |
联立式(8)、式(9)、式(5),可得计入水平力剪切变形和轴力P-Δ效应的柱单元刚度方程第3种形式如下:

|
(12) |
由式(10)、(11)、(12)可知,式中含有节点弯曲位移和剪切位移,则需通过其他方法将其消除,并表现为节点总位移的形式。
依材料力学水平力产生的剪切变形计算如下:
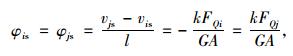
|
(13) |
式中,FQi,FQj为单元节点水平剪力; k为形状剪切系数,对矩形截面取1.2,对圆形截面取10/9;G为计算剪切模量; vis,vjs,φis,φjs分别为水平力剪切变形在单元i,j节点产生的水平位移和转角。
联立式(6)和式(13),可得水平力剪切变形节点位移、弯曲变形节点位移、总位移关系如下:
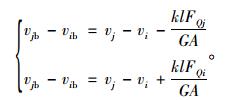
|
(14) |
由式(10)可得FQi,FQj,Mi,Mj,Mi表达式如下:
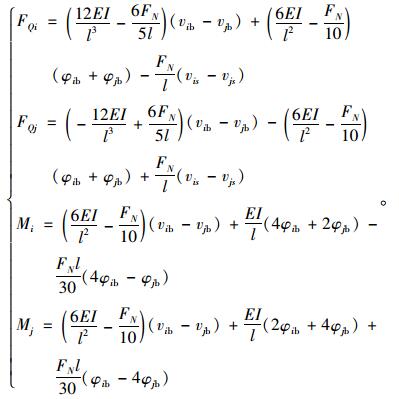
|
(15) |
将式(14)代入式(15)并消去vib,vjb,vis,vjs重新整理可得FQi,Mi表达式如下:
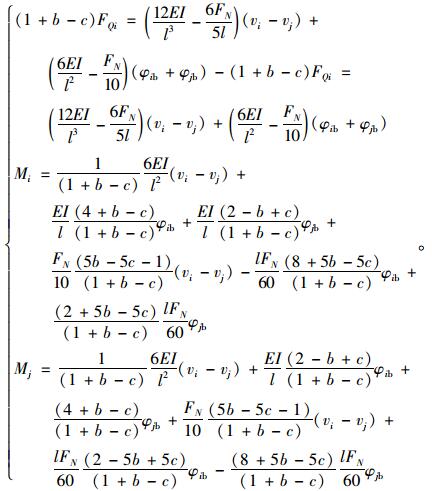
|
(16) |
重新整理式(16)即可得计入水平力剪切变形和轴力P-Δ效应的柱单元刚度方程如下:
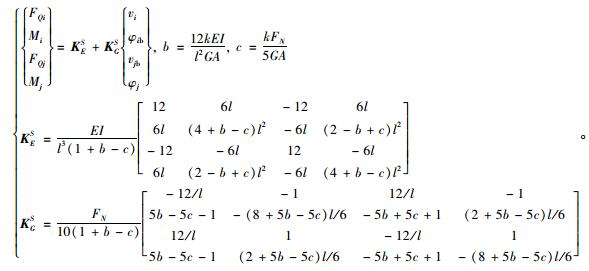
|
(17) |
将式(14)代入式(12)中消去vib,vjb,vis,vjs重新整理可得计入水平力剪切变形和轴力P-Δ效应的柱单元刚度方程第2种形式如下:
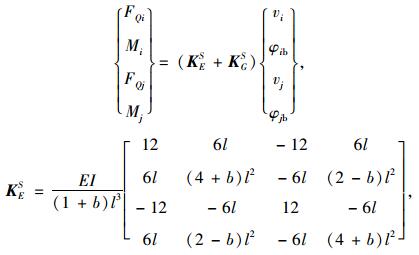
|
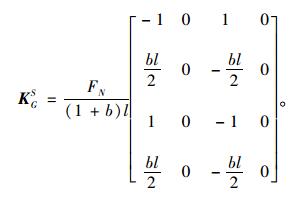
|
(18) |
将式(14)代入式(12)中消去vib,vjb,vis,vjs重新整理可得计入水平力剪切变形和轴力P-Δ效应的柱单元刚度方程第3种形式如下:
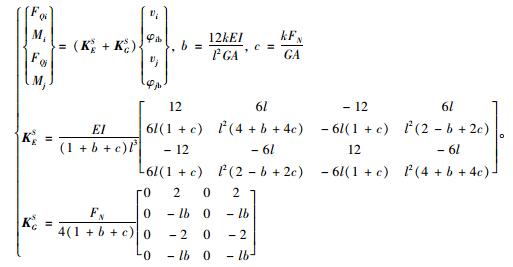
|
(19) |
式(18)形式最简洁,其KES即忽略轴力影响并计入水平力剪切变形的弹性刚度矩阵,因此KGS即为计入剪切变形影响的几何刚度矩阵。如竖向力不等于0,则式(17)和式(19)的单元刚度矩阵每一项均含有竖向力。其中式(18)的运算效率最高,在进行基桩非线性、动力、屈曲稳定分析中更有优势,本文推荐优先推荐式(18)。
2.3 单元刚度矩阵中轴力的求解按忽略剪切变形和P-Δ效应的一般梁单元有限元分析,即求解得各单元节点的轴力FN(压为正、拉为负)。
2.4 单元节点转角位移求解计入剪切变形后,柱单元刚度矩阵方程中的转角位移为弯曲变形引起的,而忽略了剪切变形引起的转角。因此计入剪切变形后的转角需根据节点位移和单元长度反算而得。
2.5 单元节点剪力已知单元节点位移后,按式(17)~(19)刚度矩阵方程中求解所得的剪力未包含竖向力径向剪切分力。如需考虑,则需对剪力结果进行修正。修正剪力可按式(20)计算。
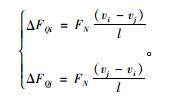
|
(20) |
当竖向力等于0时,式(17)~(19)均退化到式(14)的形式,即计入水平力剪切变形的梁单元刚度矩阵方程。理论上验证了本文推导过程。
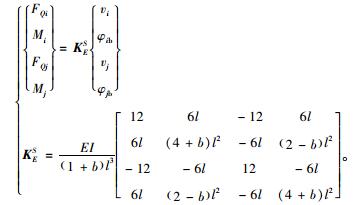
|
(21) |
当剪切刚度G→∞时,即剪切变形就没有了,此时剪切系数b=0。则式(17)~(19)分别退化到式(22)~(24)。其中式(23), 即文献[2]Wilson E L提出的忽略剪切变形时计入P-Δ效应的柱单元刚度矩阵方程。而式(22)、式(23)则是忽略剪切变形时计入P-Δ效应的柱单元刚度矩阵方程的另外两种新形式。

|
(22) |

|
(23) |

|
(24) |
式(22)、式(24)则是忽略剪切变形时计入P-Δ效应的柱单元刚度矩阵方程的两种新形式,需经算例验证其正确。
某桥梁基桩[1],冲刷线以上桩长30.212 m,其中l1=8.012 m,d1=1.8 m,E1=1.933 3×104 MPa;l2=22.2 m,d2=2.2 m,E2=1.8×104 MPa;局部冲刷线以下桩长l3=42.8 m,d3=2.2 m,E3=1.8×104 MPa;地基比例系数m=10 000 kN/m3,竖向荷载Fz=9 102.2 kN,水平荷载Fx=165 kN。
将桩划分为731个单元,单元长度为0.1 m。按本文式(22)~(24)有限元法计算基桩内力位移主要结果见表 1,其中按式(23)计算即为按文献[2]方法计算结果。由表 1可知,本文计算结果与文献[1, 3]计算结果基本一致,验证了本文忽略剪切变形时计入P-Δ效应的柱单元刚度矩阵方程。
| 项目 | 文献[1] | 按式(22) | 按式(23)即文献[2]法 | 按式(24) | 文献[3] | |
| 不计P-Δ效应 | xp/mm | 133.949 | 133.955 | 133.955 | 133.955 | 133.96 |
| x0/mm | 6.418 | 6.419 | 6.419 | 6.419 | 6.419 | |
| 考虑P-Δ效应 | xp/mm | 182.17 | 182.160 | 182.160 | 182.159 | 182.15 |
| φp/(×10-3) | -7.785 | -7.784 7 | -7.784 7 | -7.784 6 | -7.784 | |
| x0/mm | 8.417 7 | 8.418 3 | 8.418 3 | 8.418 2 | 8.418 | |
| φ0/(×10-3) | / | -2.319 3 | -2.319 3 | -2.319 3 | -2.319 | |
| Mmax/(kN·m) | 6 914.5 | 6 914.8 | 6 914.8 | 6 914.7 | 6 915.7 | |
| Qmax/kN | / | -922.884 | -922.881 | -922.871 | -923.3 | |
| σmax/kPa | / | 91.349 2 | 91.348 9 | 91.347 8 | 91.35 | |
| Qp/kN | / | 235.857 4 | 235.857 3 | 235.856 5 | \ | |
| 注:表中xz为z支座顶水平位移; xp为桩顶水平位移; φp为桩顶转角; x0为地面处桩身位移; φ0为地面处桩身转角; Mmax为桩身最大弯矩; Qp为桩顶修正剪力(计入了竖向力剪切分力); Qmax为桩身最大剪力σmax为最大计算土压力。 | ||||||
4 支座基桩共同作用分析
桥梁支座为大偏心大变形工作构件,水平力作用下水平位移极为显著,竖向力因大水平位移产生的偏心弯矩亦极为显著,不容忽略。本文剪切变形、弯曲变形假定独立而不关联,计入剪切变形的柱单元刚度矩阵方程式(17)~(19)均可良好地模拟支座等大剪切变形构件偏心工作。基于m法的线弹性地基土约束则可按节点弹簧模拟。
某桥梁基桩,冲刷线以上桩长30.2 m,冲刷线以下桩长42.8 m,桩径d=2.2 m;桩身混凝土弹性模量E=1.8×104 MPa;地基比例系数m=10 MN/m4,竖向荷载Fz=9 102.2 kN,水平荷载Fx=165 kN。设墩顶支座GPZ(Ⅱ)9DX,H=160 mm,计算直径D=725 mm,剪切模量G=2 MPa,弹性模量E=2×104 MPa。
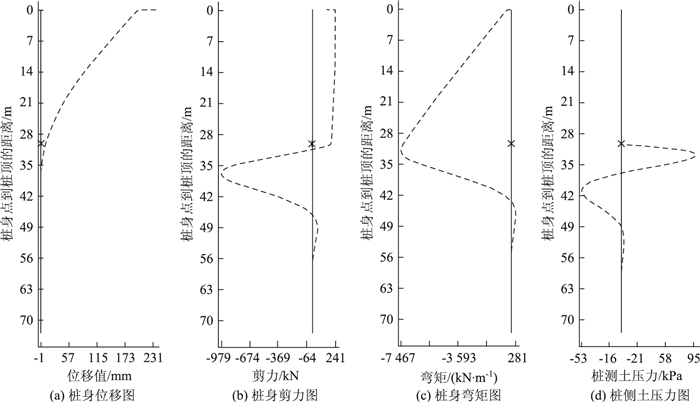
本文建立了支座和桩柱共同作用的有限元模型,支座划分了2个单元,局部冲刷线以上基桩柱划分302个单元,冲刷线以下2.2 m的桩划分428个单元。支座单元和桩单元刚度矩阵方程均采用本文式(17)、式(18)或式(19)。采取MATLAB自编有限元程序计算,其结果如表 2和图 2所示。由表 2可知,计入剪切变形的基桩支座共同作用分析与单纯忽略剪切变形的基桩P-Δ分析相比,桩顶位移和转角分别增加了9.9%和11.89%,地面处桩身位移和转角分别增加了7.74%和8.69%,桩身最大弯矩和最大剪力分别增加了7.71%和6.25%,桩侧最大土压力增加了6.37%,桩顶修正剪力增加了3.47%,基桩等效计算长度增加了3.2%,基桩支座等效计算长度增加了3.45%。
| 项目 | ①基桩水平力计算 | ②基桩P-Δ计算 | ③基桩支座共同作用分析 |
| xz/mm | / | / | 234.948 |
| xp/mm | 132.353 | 180.248 | 198.086 |
| φp/(×10-3) | -5.382 | -7.394 | -8.273 |
| x0/mm | 6.417 | 8.438 | 9.091 |
| p0/(×10-3) | -1.747 | -2.325 | -2.527 |
| Mmax/(kN·m) | 5 146.9 | 6 931.4 | 7 466.1 |
| Qmax/kN | -685.482 | -921.15 | -978.75 |
| σmax/kPa | 70.454 | 91.554 | 97.383 |
| Qp/kN | 165 | 232.302 | 240.370 |
| 基桩l0 | 73.586 | 81.566 | 84.173 |
| Xz1/mm | 31.97 | 31.97 | / |
| 基桩支座l0 | 79.090 | 86.129 | 89.100 |
| 注:表中xz为z支座顶水平位移; xp为桩顶水平位移; φp为桩顶转角; x0为地面处桩身位移; φ0为地面处桩身转角; Mmax为桩身最大弯矩; Qp为桩顶修正剪力(计入了竖向力剪切分力); Qmax为桩身最大剪力σmax为最大计算土压力; l0为等效计算长度; xz1为水平力下支座顶水平剪切位移。解答①为忽略竖向力和剪切变形的基桩计算,解答②为忽略剪切变形时基桩P-Δ计算;解答③为则考虑支座影响同时也计入了桩身水平力剪切变形影响。 | |||
|
| 图 2 支座和基桩共同作用分析结果 Fig. 2 Analysis result of combined action of pile and bearing |
| |
5 结论
(1) 推导了3种计入水平力剪切变形和轴力P-Δ效应的柱单元刚度方程,即式(17)、式(18)和式(19),可模拟支座大剪切变形下的偏性工作特性,也可用于地震力作用下计入水平力剪切变形的柱P-Δ效应分析,从技术效率角度出发本文优先推荐采用式(18)。
(2) 推导了另外2种仅计入P-Δ效应而忽略剪切变形的柱单元刚度方程,即式(22)和式(24)。
(3) 支座基桩共同作用案例分析表明,竖向力因支座大水平剪切位移产生的偏心弯矩极为显著,对基桩受力特性影响较大,有效增大了基桩内力和其等效计算长度,减小了支座基桩的整体水平抗推刚度,不容忽略。
(4) 最后,本文建议进行基桩设计计算以及制动力等水平力在墩台间分配计算时采用支座基桩共同作用有限元模型。
| [1] |
王用中, 张河水. 弹性地基梁的压弯计算及其应用[J]. 桥梁建设, 1985, 14(4): 30-52. WANG Yong-zhong, ZHANG He-shui. Bending Calculation of Elastic Foundation Beam and Its Application[J]. Bridge Construction, 1985, 14(4): 30-52. |
| [2] |
WILSON E L, EERI M, HABIBULLAH A. Static and Dynamic Analysis of Multi-story Buildings Including P-Delta Effects[J]. Earthquake Spectra, 1987, 3(2): 289-298. |
| [3] |
赵明华, 李微哲, 曹文贵. 复杂荷载及边界条件下基桩有限杆单元方法研究[J]. 岩土工程学报, 2006, 28(9): 1059-1064. ZHAO Ming-hua, LI Wei-zhe, CAO Wen-gui. Study on Applying Finite Pole Element Method to Analysis of Piles under Complex Loads with Different Boundary Restraints[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1059-1064. |
| [4] |
赵明华, 李微哲, 单远铭, 等. 成层地基中倾斜荷载桩改进有限杆单元法研究[J]. 工程力学, 2008, 28(05): 79-85. ZHAO Ming-hua, LI Wei-zhe, SHAN Yuan-ming, et al. Behavior Analysis of Piles in Layered Clays under Eccentrjc and Inclined Loads by Improved Finite Pole Element Method[J]. Engineering Mechanics, 2008, 28(05): 79-85. |
| [5] |
舒兴平, 沈浦生. 剪切变形对钢框架结构P-Δ效应的影响研究[J]. 湖南大学学报, 1993, 20(2): 89-94. SHU Xing-ping, SHEN Pu-sheng. Study of the Influence of Shear Deformation on the P-Δ Effect of Plane Seel Frames[J]. Journal of Hunan University, 1993, 20(2): 89-94. |
| [6] |
李国强. 考虑轴力和剪切变形影响的梁单元刚度方程及其级数展开[C]//材料科学与工程技术-中国科协第三届青年学术年会论文集. 北京: 中国科学技术出版社, 1998: 453-457. LI Guo-qiang. A Series-style Stiffness Equation of Beam Element Considering Shear Deformation and Effect of Axial Force[C]//Proceedings of the Third Youth Academic Annual Conference of China Association for Science and Technology: Materials Science and Engineering Technology. Beijing, China Science and Technology Press, 1998: 453-457. |
| [7] |
孙飞飞, 李国强. 考虑滑移剪力滞后和剪切变形的组合梁单元[J]. 同济大学学报, 2004, 32(4): 436-440. SUN Fei-fei, LI Guo-qiang. Beam Formulation for Composite Beams with Slip, Shear Lag and Shear Deformation[J]. |
| [8] |
聂国隽, 仲政. 框架结构P-Δ效应分析的微分求积单元法[J]. 力学季刊, 2004, 25(2): 195-200. NIE Guo-jun, ZHONG Zheng. Second Order Analysis of Frames by Differential Quadrature Element Method[J]. Chinese Quarterly of Mechanics, 2004, 25(2): 195-200. |
| [9] |
李国强, 刘玉姝. 一种考虑初始缺陷影响的非线性梁单元[J]. 计算力学学报, 2005, 22(1): 69-72. LI Guo-qiang, LIU Yu-shu. A Nonlinear Beam Element Considering Initial Imperfection[J]. Chinese Journal of Computational Mechanics, 2005, 22(1): 69-72. |
| [10] |
夏拥军, 陆念力. 梁杆结构二阶效应分析的一种新型梁单元[J]. 工程力学, 2007, 24(7): 39-43. XIA Yong-jun, LU Nian-li. A New Beam Element for Second-order Effect Analysis of Beam Structures[J]. Engineering Mechanics, 2007, 24(7): 39-43. |
| [11] |
孟凡涛, 张玉明, 阮兴群. 考虑剪切变形的半刚性连接钢框架P-Δ效应研究[J]. 应用力学学报, 2013, 30(1): 136-140. MENG Fan-tao, ZHANG Yu-ming, RUAN Xing-qun. P-Δ Effects Analysis of Steel Frame with Semi-rigid Connection and Shear Deformation[J]. Chinese Journal of Applied Mechanics, 2013, 30(1): 136-140. |
| [12] |
传光红, 陈以一, 童根树. 变截面Timoshenko梁的单元刚度矩阵[J]. 计算力学学报, 2014, 31(2): 265-272. CHUAN Guang-hong, CHEN Yi-yi, TONG Gen-shu. Element Stiffness Matrix for Timoshenko Beam with Variable Cross-section[J]. Chinese Journal of Computational Mechanics, 2014, 31(2): 265-272. |
| [13] |
王强, 宋雪迪, 郝中华, 等. 基于ABAQUS纤维梁单元的钢筋混凝土柱受力破坏全过程数值模拟[J]. 土木工程学报, 2014, 47(12): 16-81. WANG Qiang, SONG Xue-di, HAO Zhong-hua, et al. Numerical Simulation of Failure Process of RC Columns Based on Fiber Beam Element in ABAQUS[J]. China Civil Engineering Journal, 2014, 47(12): 16-81. |
| [14] |
孙治国, 陈灿, 司炳君, 等. 考虑非线性剪切效应的RC桥墩抗震分析模型[J]. 工程力学, 2015, 32(5): 28-36. SUN Zhi-guo, CHEN Can, SI Bing-jun, et al. Seismic Analysis Model Considering Nonlinear Shear Effect for RC Bridge Piers[J]. Engineering Mechanics, 2015, 32(5): 28-36. |
| [15] |
朱绩超, 王响, 张勤. 考虑粘结-滑移与剪切作用的钢筋混凝土柱侧向变形分析[J]. 工程力学, 2015, 32(7): 128-135. ZHU Ji-chao, WANG Xiang, ZHANG Qin. Lateral Deformations Analysis of Reinforced Concrete Columns Incoparating Bond-slip and Shear Effects[J]. Engineering Mechanics, 2015, 32(7): 128-135. |
| [16] |
丁然, 聂建国, 陶慕轩. 用于钢筋混凝土连梁地震反应的考虑非线性剪切的纤维梁单元Ⅰ:原理与开发[J]. 土木工程学报, 2016, 49(3): 31-42. DING Ran, NIE Jian-guo, TAO Mu-xuan. A Fiber Beam-column Element Considering Nonlinear Shear Effects for Seismic Response of Reinforced Concrete Coupling Beams Ⅰ:Theory and Implementation[J]. China Civil Engineering Journal, 2016, 49(3): 31-42. |
| [17] |
赵明华, 杨超炜, 杨明辉. 基于有限杆单元法的陡坡段桥梁基桩受力分析[J]. 中国公路学报, 2014, 27(6): 51-58. ZHAO Ming-hua, YANG Chao-wei, YANG Ming-hui. Mechanical Analysis of Bridge Pile Foundation in High and Steep Slopes Based on Finite Bar Element Method[J]. China Journal of Highway and Transport, 2014, 27(6): 51-58. |
| [18] |
杨超炜, 赵明华, 尹平保. 基于综合刚度原理的陡坡基桩有限杆单元分析[J]. 地质工程学报, 2015, 37(增1): 46-51. YANG Chao-wei, ZHAO Ming-hua, YIN Ping-bao. Finite Bar Element Analysis of Bridge Pile Foundation in Steep Slopes Based on Composite Stiffness Principle[J]. China Earthquake Engineering Journal, 2015, 37(S1): 46-51. |
 2018, Vol. 35
2018, Vol. 35
