扩展功能
文章信息
- 于泉, 郭增增, 梁锐
- YU Quan, GUO Zeng-zeng, LIANG Rui
- 基于马尔科夫链的高速公路机电设备寿命预测研究模型
- A Prediction Model of Expressway Electromechanical Equipment Life Based on Markov Chain
- 公路交通科技, 2018, 35(1): 28-35
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(1): 28-35
- 10.3969/j.issn.1002-0268.2018.01.005
-
文章历史
- 收稿日期: 2016-07-01
高速公路机电设备的运行状况是一个动态时变过程,存在大量的不确定性和随机性。如何准确地预测机电设备的运行状况,合理安排预防性维修工作,是高速公路养护管理部门面临的严重课题。机电设备在运行过程中会由于多种原因产生故障,也会由于自身的性能原因导致无法应对出现的偶发性事故。再者,机电设备也往往容易受到环境因素的影响,不稳定的外界环境给机电设备维护管理工作带来了很多突发性故障。由于设备在其运行过程中,必然要达到寿命的极限,在寿命期中会发生偶发性故障,造成生产过程的中断,给设备的运行和管理带来不必要的困难。因此,研究高速公路机电设备寿命的预测和判断,为设备的维修和更换提供依据就显得越来越重要。
目前,已经有很多方法从不同角度对不同领域的设备寿命进行了研究。例如,在机械零件方面,Gebraeel[1]针对轴承传感信号提出各种假设先验下的寿命预测方法,利用贝叶斯理论对每个时刻的剩余寿命进行迭代估计。潘冬等[2]提出一种对机械齿轮磨损寿命的预测方法。在电气领域中,周建宝等[3]提出基于RVM的锂离子电池剩余寿命预测方法。Tang[4]利用基于维纳过程的方法预测锂电子电池剩余寿命预测。在工程领域中,Wang等[5]利用失效数据计算相似度进而获取工程系统的剩余寿命。唐圣金[6]等对卫星用的光纤陀螺也用维纳过程预测剩余寿命。在航空领域中,郝旭东[7]提出基于RVM-PF的卫星关键部件寿命预测方法。王安东[8]等人研究飞机结构件的腐蚀随时间的变化规律,将灰色GM(1, 1)模型与马尔科夫链模型相结合,建立起能预测蚀坑深度的灰色马尔科夫模型。崔建国[9]等基于遗传算法和ARMA模型来预测航空发电机寿命。
对于高速公路机电设备的使用寿命的研究多是针对设备的故障率,提出了一系列对设备进行维修维护的策略[10-13],从设备的使用年限方面开展研究尚处于进展阶段。饶永波等[14]在用Delphi法预测高速公路机电设备的物理寿命,用最小年平均费用法和低劣化数值法计算高速公路机电设备的经济寿命的基础上,提出了基于设备的物理寿命和经济寿命的综合预测新模型。
近年来,很多研究者将马尔科夫链方法应用于寿命预测的研究,从而建立一种寿命预测方法。张继军等[15]针对机载设备剩余使用寿命预测中存在的不确定性因素,建立了基于状态条件概率分布的机载设备剩余寿命模型,从而提高了设备使用寿命的预测精度。何兆民等[16]提出了具有时变状态转移概率矩阵的隐半马尔科夫模型,相比传统的隐半马尔科夫模型,可显著提高剩余寿命预测的准确性。李洪儒等[17]将灰色马尔科夫模型应用到滚动轴承剩余寿命预测中,从而建立一种基于广义数学形态颗粒与灰色马尔科夫模型的剩余寿命预测方法。赵飞等[18]基于变压器的历年健康指数,在传统马尔科夫预测模型的基础上,建立了改进的马尔科夫预测模型。冯隽等[19]将灰色GM(1, 1)模型与马尔科夫链有机地结合起来,利用各自优点并充分考虑大型结构整体变化趋势和局部波动的情况。通过对某桥梁结构的损伤系数进行预测分析并与GM(1, 1)预测结果进行对比,该方法解决了GM(1, 1)模型对波动性较大数据拟合较差,预测精度较低的缺陷。严野等[20]针对潜油泵振动状态数据具有波动性的问题,建立了基于马尔科夫方法对灰色预测结果修正的预测模型。沈鑫等[21]提出了基于领结模型和半马尔科夫的变压器故障率预测模型,采用经验公式获得威布尔分布的参数,然后得到与实际统计结果趋势一致的故障率曲线,可较好地反映实际变压器的故障机制。
马尔科夫链方法是通过对系统已有信息的获取, 建立系统的状态分类以及转移概率矩阵, 来预测在现有状态下, 经由一段时间系统将会达到的状态, 该方法对设备管理和决策有重要的意义。本研究根据高速公路机电设备的相关维修资料统计,发现高速公路机电设备存在各种状态转移的现象,运用马尔科夫链能够对高速公路机电设备进行故障预测分析,并根据机电设备故障率变化曲线判断设备的有效寿命和使用寿命,对高速公路机电设备的维修管理工作能够起到预防事故发生,减少故障损失,延长设备寿命的作用。
1 马尔科夫链模型马尔科夫链模型在各领域都有着非常广泛的应用,是一种在预测研究中非常有用的数学工具。马尔科夫链模型可以分为:系统状态空间(E), 系统状态之间的转换概率矩阵(P)。
(1) 现用分布函数来表述马尔科夫性。
P{X(tn)≤xn|X(ti)=xi, X(t2)=x2, …,X(tN-1)=xN-1}=P{X(tn)≤xn|X(tN-1)=xN-1}, Xn∈R,则称过程{X(t), t∈T}具有马尔科夫性或无后效性,并称此过程为马尔可夫过程。
(2) 条件概率
Pij(m, m+n)=P{Xm+n=aj|Xm=ai}为马氏链在时刻m处于状态ai条件下,在时刻m+n转移到状态aj的转移概率。设马尔科夫链的状态空间为E={S1, S2, …, Sn}, 根据系统的历史情况计算出一步状态转移矩阵P1:
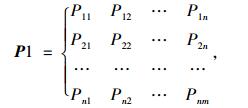
|
(1) |
其中Pij为一步转移概率, 表示系统由状态Si只经过一步就转移到Sj的概率, i, j=1, 2, …, n, 且:
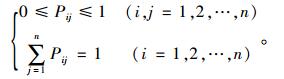
|
(2) |
P中的所有元素都是非负的,且每一行元素之和等于1。
(3) 设齐次马氏链{Xn, n≥1}的状态空间为I={a1, a2, …, an}, P是它的一步转移概率矩阵,如果存在正整数m,使对任意ai, aj∈I, 都有Pij(m)>0, i, j=1, 2, …, N, 则此链具有遍历性,具有极限分布π=(π1,π2,…,πN), 它是方程组π=πP或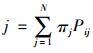
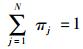
在高速公路机电设备维修中,根据维修特点和机电设备工作状况可以分为3种状态,即正常状态,一般故障状态和严重故障状态。相对应地将3个状态分为3个等级:S0,S1,S2。其中,S0表示正常状态,机电设备能够正常工作。S1表示一般故障状态,在这种情况下,因为某个功能无法工作造成,由维修人员简单处理后便可正常工作。S2表示严重故障状态,在这种情况下,机电设备无法完成工作,需要更换某关键部件后才能正常工作。当设备出现S1或S2状态时,维修人员会进行维修,维修后设备会达到正常状态S0。这3种状态可以相互转化,而且将来运行状况的等级在现在的等级已知的条件下与过去的等级无关。因而我们可以得到3个状态的马尔科夫链{Sn, n∈T}。则可建立状态空间为S={S0,S1,S2}。当样本量足够大时,1步转移概率可以近似地用状态相互转移的频率描述。
根据2007—2013年京藏高速公路的八达岭高速路段清河主站进京出收费站的机电设备的维修记录,将7 a所调查的设备故障状态划分3个等级S0,S1,S2, 对其运用马尔科夫链进行故障分析,进而对其有效寿命和使用寿命进行判断。以车辆检测器为例来说明运用马尔科夫链进行故障分析的过程。根据车辆检测器设备维修记录档案,提取出该收费站全部车道7 a中每天的设备状态记录情况,以月为时间滚动窗口,计算每月车辆检测器的极限概率,得到各种状态在每月的状态概率。根据每月的状态极限概率画出状态趋势图,从而为预测和判断设备故障状态和设备的有效寿命和使用寿命服务。
本研究选择2007-01-01到2013-12-31,7 a共2 555 d的车辆检测器的维修统计数据作为样本数据。以每月为一个分析时段计算其极限概率,得出趋势图。以2007年1月的车辆检测器设备状态记录为例,见表 1。
| 时间 | 状态编号 |
| 2011-01-01 | S0 |
| 2011-01-02 | S0 |
| 2011-01-03 | S0 |
| 2011-01-04 | S0 |
| 2011-01-05 | S0 |
| 2011-01-06 | S0 |
| 2011-01-07 | S0 |
| 2011-01-08 | S0 |
| 2011-01-09 | S0 |
| 2011-01-10 | S0 |
| 2011-01-11 | S0 |
| 2011-01-12 | S0 |
| 2011-01-13 | S0 |
| 2011-01-14 | S0 |
| 2011-01-15 | S0 |
| 2011-01-16 | S0 |
| 2011-01-17 | S0 |
| 2011-01-18 | S0 |
| 2011-01-19 | S0 |
| 2011-01-20 | S1 |
| 2011-01-21 | S0 |
| 2011-01-22 | S0 |
| 2011-01-23 | S0 |
| 2011-01-24 | S0 |
| 2011-01-25 | S0 |
| 2011-01-26 | S0 |
| 2011-01-27 | S0 |
| 2011-01-28 | S0 |
| 2011-01-29 | S0 |
| 2011-01-30 | S0 |
| 2011-01-31 | S1 |
运用一阶转移矩阵即Pij=Mij/Mi, i, j∈S, 其中Mi为处于状态i的原始状态样本数;Mij为样本中由状态i一步转移到状态j的样本数。从而得到一步转移概率矩阵P1:
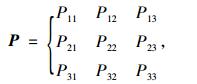
|
(3) |
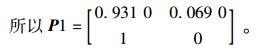
|
(4) |
根据平衡分布的方程组得:
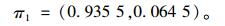
|
(5) |
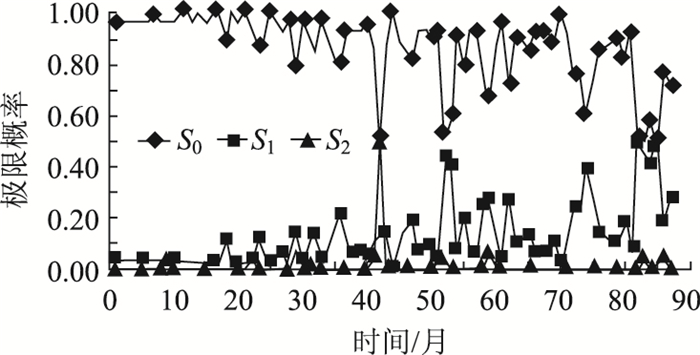
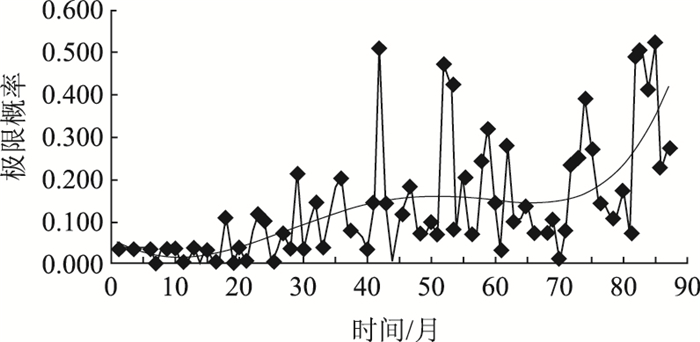
因为在1月份并没有出现S2状态,所以在状态转移概率中不考虑,S2吸收态为0。从S1状态到S0状态,设备经过了维修恢复到了正常状态。那么在2011年1月的车辆检测器状态的转移概率: S0为0.935 5,S1为0.064 5,S2为0。依次计算每月的状态概率,得到状态极限概率趋势图,如图 1所示。
|
| 图 1 车辆检测器极限概率分布图(以2007-01为第1个月) Fig. 1 Limit probability distribution of vehicle detectors (taking January, 2007 as the first month) |
| |
极限概率分布图说明了各种状态的存在状态,根据图 1可知S0正常状态的故障概率呈现波动曲线,整体上正常状态极限概率是下降的趋势。S1一般故障的故障概率也呈波动曲线,整体上一般故障状态的极限概率是上升的趋势。S2严重故障的极限概率低,说明设备出现更换关键部件的情况较少。
根据车辆检测器故障极限概率得到该设备的故障概率图,如图 2所示,随着时间的推移,车辆检测器的故障概率呈现上升的趋势。
|
| 图 2 车辆检测器故障概率图 Fig. 2 Fault probability curves of vehicle detector |
| |
3 高速公路机电设备有效寿命和使用寿命判断
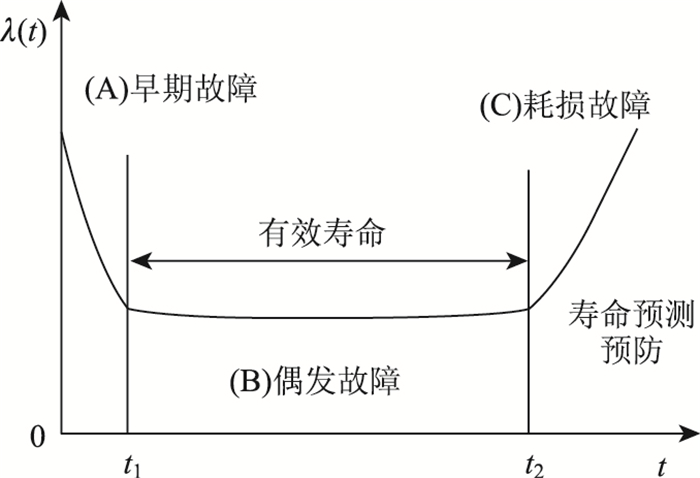
由第2节得到了车辆检测器的极限概率图(图 1)和车辆检测器故障概率图(图 2)。研究设备的故障率变化情况,一般符合浴盆曲线理论。运用马尔科夫链的方法得到的设备故障极限概率曲线图是否也符合浴盆曲线理论,要根据设备的维修记录来判断,如图 3所示。
|
| 图 3 浴盆曲线 Fig. 3 Bathtub curve |
| |
本研究引入浴盆曲线理论,结合基于马尔科夫链模型的设备故障概率曲线,判断设备的有效寿命和使用寿命。
根据清河主站收费站的车辆检测器安装时的设备资料,该设备在缺陷责任期外进行维护维修记录登记(资料显示设备缺陷责任期为3 a,即在该3 a内,设备维护维修由设备供应商负责,3 a后设备维护维修由高速公路管理部门负责),因此对应图 3浴盆曲线,车辆检测器故障概率曲线图 2是从t1开始,设备使用进入偶发故障期。根据马尔科夫极限概率图可知,设备开始故障率保持一定的概率没有大的变化,这是设备的偶发故障期,在第22个月后,设备故障率开始升高,这时设备进行耗损故障,由于维修和维护的投入设备的故障率在今后的时间里呈现波动趋势,总体上故障率趋势呈现上升趋势,在第81个月后故障率明显升高,设备已经严重影响到正常使用,维修次数显著增加,不仅影响设备工作效率,还要使管理部门增加人力和费用投入,不管是经济方面还是使用方面都已经说明设备进入报废待更换的时期,该点可以作为设备使用寿命的临界点。那么在马尔科夫链方法下,利用浴盆曲线我们可以判断设备在这样的状态下使用寿命终止。超过该使用寿命临界点的车辆检测器尽管经过维修后还能继续使用,但是其故障率明显升高,可以考虑更换设备,以减少管理和维护成本。
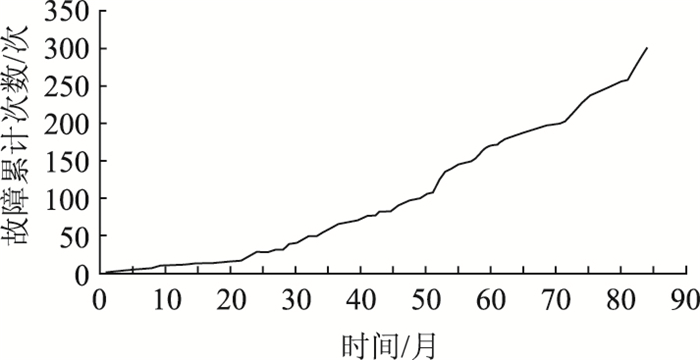
为了说明故障概率曲线判断的有效性和合理性,本研究根据车辆检测器故障累计次数曲线对分界点补充说明,如图 4、图 5所示。
|
| 图 4 车辆检测器故障累计次数曲线图 Fig. 4 Cumulative frequency curve of vehicle detector faults |
| |
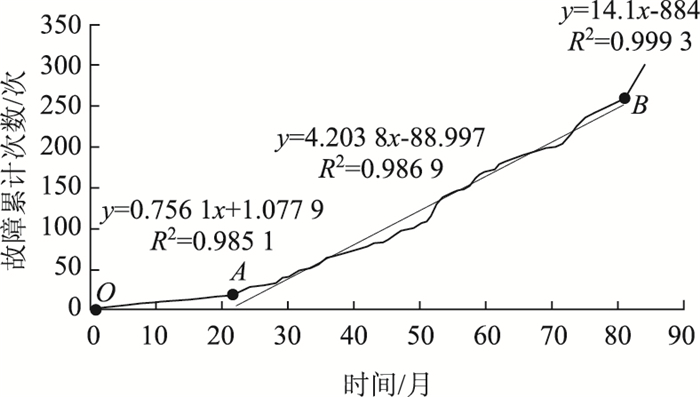
|
| 图 5 车辆检测器寿命分界点分析图 Fig. 5 Analytical curve of vehicle detector's life demarcation point |
| |
根据故障累计次数曲线的斜率(图 4、图 5)以及突变点处的故障次数的明显增加,判断A,B两点为分界点。曲线从O点开始到A点(第22个月)故障次数累计曲线斜率平稳,从A点到B点(第81个月)曲线斜率明显上升,B点之后的曲线斜率明显继续增大,判断B点后设备投入维修次数增加,设备超出使用寿命值。从设备投入使用到A点,设备在正常使用的状态下有效寿命为22个月,即在马尔科夫链方法下根据故障累计曲线在这段时期的平稳性状态,判断这段时期是设备的有效寿命, A点后故障累计曲线斜率上升,判断设备到达时期A状态时设备有效寿命终止。A点后设备处于磨损故障期,这时故障次数增加,故障率有所波动,整体上故障率曲线逐步升高。到B点出现拐点,故障次数和故障率显著提高,设备从投入到B点为使用寿命期,设备的使用寿命期为81个月。B点后故障率升高,但未达到设备的极限寿命,设备经过维修虽然可以继续使用,但经济效益严重下滑,可考虑更换设备。车辆检测器的有效寿命为22个月,约2 a。考虑设备故障记录在3 a缺陷责任期外开始,因此八达岭高速车辆检测器使用寿命约为10 a(81个月+36个月)与车辆检测器的实际寿命相一致,说明了利用马尔科夫链模型判断设备寿命的合理性和有效性。
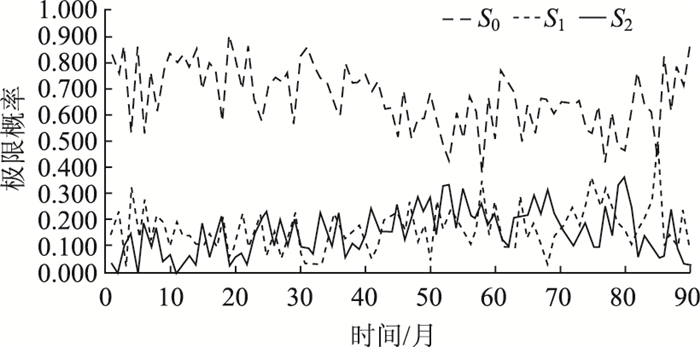
利用同样的方法,来判断高速公路的其他机电设备的有效寿命和使用寿命。选择清河主站收费站的全部自动栏杆机设备,利用马尔科夫链的方法得到设备的极限概率分布图。根据自动栏杆机的的设备维修资料和极限概率转移法得到概率分布图和设备故障概率曲线图,如图 6、图 7所示。
|
| 图 6 自动栏杆机极限概率分布图(以2007-01为第1个月) Fig. 6 Limit probability distribution curve of automatic rail machine (taking January, 2007 as the first month) |
| |
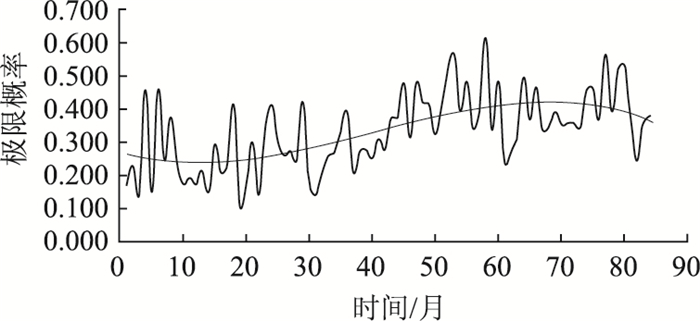
|
| 图 7 自动栏杆机故障概率曲线图 Fig. 7 Fault probability curves of automatic rail machine |
| |
由于自动栏杆机设备同样是在设备缺陷责任期外投入使用,所以根据浴盆曲线,设备安装完成后使用进入偶发故障期(t1开始),设备在早期故障期结束后安装投入使用,第1个月到第25个月的故障概率都低于0.27,第25个月后故障概率明显增加,设备进入耗损故障期,根据浴盆曲线判断前25个月,大约2 a,是设备的有效寿命,到第65个月,设备故障率平均曲线图达到峰点,第65个月后设备故障率下降,这是由于设备老化严重、化学腐蚀等原因不得不对设备进行更换主要部件或进行大修,这时设备的故障率就会降低。但是设备未达到极限寿命,还能继续使用,但会造成维护人员和维护费用的投入,可考虑更换新的设备。根据浴盆曲线判断大约8 a,共(65+36)个月,是设备的使用寿命。我们可以看到利用马尔科夫链的方法预测自动栏杆机设备的有效寿命和使用寿命有效性。
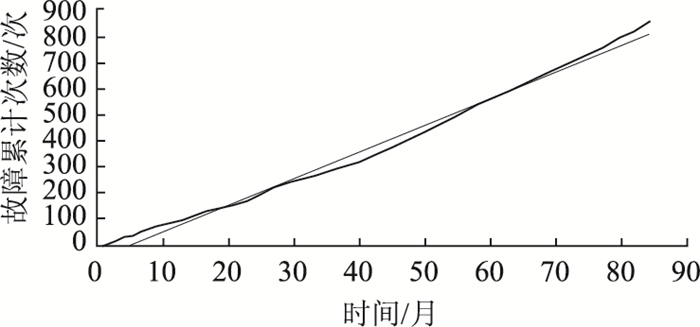
根据自动栏杆机故障累计次数曲线对浴盆曲线的拐点进行验证,如图 8、图 9所示。
|
| 图 8 自动栏杆机故障累计次数曲线图 Fig. 8 Cumulative frequency curves of faults of automatic rail machine |
| |
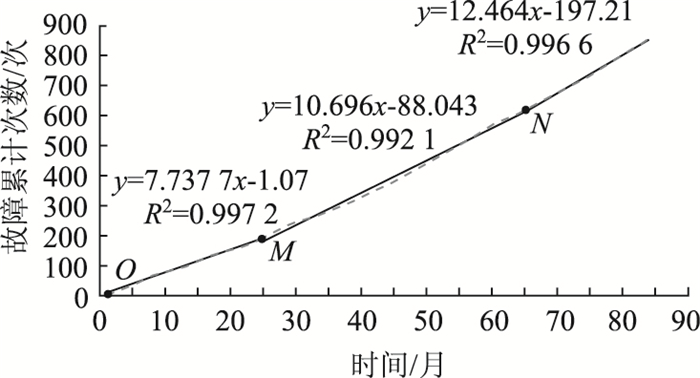
|
| 图 9 自动栏杆机寿命分界点分析图 Fig. 9 Analytical curve of automatic railing machine's life demarcation point |
| |
根据自动栏杆机的故障累计次数曲线斜率,判断M和N点为分界点。从O点到M点(第25个月)的曲线斜率相对平稳,M点后曲线斜率升高,维修故障次数上升。到达N(第65个月)点后曲线斜率再次升高,故障维修次数明显增多。由故障累计次数曲线分界点M和N。判断在M点和N点是故障维修次数突变点,由设备寿命和设备健康状态的关系,说明M点(第25个月)前是设备的正常工作状态,故障概率稳定,由浴盆曲线确定是设备的偶发故障期,也就是说该设备的有效寿命为25个月(大约2 a)。M点到N点的曲线段为设备的耗损故障期,这是由于设备零件老化、磨损等造成设备故障维修和故障概率升高。N点后曲线斜率增大,设备故障累计次数有明显增加,说明N点(第65个月)前故障维修是设备在使用寿命期的正常维护,N点后增加了对设备的维修和维护次数,说明设备故障频繁,接近报废阶段,设备在极限寿命期还能继续使用一段时间。虽然经过大修后设备的故障率呈现波动曲线,这个时期设备的经济效益和使用效益已经下滑,继续使用会增加维护费用和人员的投入,这时可以考虑更换新的设备。设备的使用寿命为(65+36)个月,大约8 a,与马尔科夫链模型极限概率预测的一致。
根据对2种高速公路机电设备的故障概率研究,研究结果表明,利用马尔科夫链的方法能够判断高速公路机电设备的有效寿命和使用寿命,为高速公路管理部门对机电设备进行有效的维护提供帮助,同时能够预测设备的健康情况,及时处理设备在运行期间的各种偶发故障,保障高速公路交通流的高效通行。
4 结论本研究将马尔科夫链的方法应用于高速公路收费设备上进行有效寿命和使用寿命的判断,基于历史数据计算出转移概率、极限概率和时间滚动窗口的设备状态之间的关系,预测设备未来发生各类故障的概率,结合浴盆曲线理论,判断设备的有效寿命;根据极限概率和故障累计次数预测设备的使用寿命。同时建立了基于马尔科夫链的故障预测模型,该预测模型能够反映出设备随着运行时间变化的健康状态情况。以八达岭高速公路车辆检测器和自动栏杆机为例,通过对历史维修数据运用马尔科夫链的方法,再根据浴盆曲线理论判断设备的有效寿命和使用寿命,验证了该模型的可行性。根据对此方法的研究,应用于其他高速公路机电设备的寿命预测;结果表明该方法也能够判断高速公路其他机电设备的寿命。通过对有效寿命和使用寿命的预测研究,可以掌握设备的实际性能,科学指导未来维修工作的重点,进而在高速公路机电设备的维护中,实现有限的人力、技术和资金条件下,预防和维护当中抓住重点,避免设备的突发性故障和设备老化给高速公路的正常运行带来困难,同时也为高速公路机电设备的寿命管理提供理论支撑。
| [1] |
GEBRAEEL N Z, LAWLEY M A. A Neural Network Degradation Model for Computing and Updating Residual Life Distributions[J]. IEEE Transactions on Automation Science and Engineering, 2008, 5(1): 154-163. |
| [2] |
潘冬, 赵阳, 李娜, 等. 齿轮磨损寿命预测方法[J]. 哈尔滨工业大学学报, 2012, 44(9): 29-33. PAN Dong, ZHAO Yang, LI Na, et al. The Wear Life Prediction Method of Gear System[J]. Journal of Harbin Institute of Technology, 2012, 44(9): 29-33. |
| [3] |
周建宝. 基于RVM的锂离子电池剩余寿命预测方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2013. ZHOU Jian-bao. Research on Residual Life Prediction Method of Lithium Ion Battery Based on RVM[D]. Harbin: Harbin Institute of Technology, 2013. |
| [4] |
TANG S, YU C, WANG X, et al. Remaining Useful Life Prediction of Lithium-ion Batteries Based on the Wiener Process with Measurement Error[J]. Energies, 2014, 7(2): 520-547. |
| [5] |
WANG Tian-yi, YU Jian-bo. A Similarity Based Prognostics Approach for Remaining Useful Life Estimation of Engineered Systems[C]//Proceedings of 2008 International Conference on Prognostics and Health Management. Washington, D. C: IEEE, 2008: 6-9.
|
| [6] |
唐圣金, 郭晓松, 司小胜, 等. 基于维纳过程的卫星用光纤陀螺剩余寿命预测[J]. 红外与激光工程, 2013, 42(12): 3347-3352. TANG Sheng-jin, GUO Xiao-song, SI Xiao-sheng, et al. Remaining Useful Life Prediction of FOGs Used for Satellite Based on Wiener Process[J]. Infrared and Laser Engineering, 2013, 42(12): 3347-3352. |
| [7] |
郝旭东. 基于RVM-PF的卫星关键部件寿命预测[D]. 长沙: 国防科学技术大学, 2011. HAO Xu-dong. Life Prediction of Key Components of Satellite Based on RVM-PF[D]. Changsha: National University of Defense Technology, 2011. |
| [8] |
王安东, 陈跃良, 张勇, 等. 基于灰色马尔科夫模型的2A12铝合金腐蚀预测方法研究[J]. 装备环境工程, 2014(6): 22-28. WANG An-dong, CHEN Yue-liang, ZHANG Yong, et al. The Research on 2A12 Aluminum Corrosion Prediction Method Based on Gray Markov Model[J]. Equipment Environmental Engineering, 2014(6): 22-28. |
| [9] |
崔建国, 赵云龙, 董世良, 等. 基于遗传算法和ARMA模型的航空发电机寿命预测[J]. 航空学报, 2011, 32(8): 1506-1511. CUI Jian-guo, ZHAO Yun-long, DONG Shi-liang, et al. Life Prognostics for Aero-generator Based on Genetic Algorithm and ARMA Model[J]. Acta Aeronautica ET Astronautica Sinica, 2011, 32(8): 1506-1511. |
| [10] |
SI X S, WANG W, HU C H, et al. Remaining Seful Life Estimation-A Eview on the Statistical Data Driven Approaches[J]. European Journal of Operational Research, 2011, 213(1): 1-14. |
| [11] |
杨帅. 机电产品寿命预测方法研究[D]. 成都: 电子科技大学, 2013. YANG Shuai. Research on Life Prediction Method of Mechanical and Electrical Products[D]. Chengdu: University of Electronic Science and Technology of China, 2013. |
| [12] |
刘文彬, 徐微, 王庆锋. 基于威布尔概率统计分析方法的设备可靠性预测研究[J]. 机械科学与技术, 2012, 31(4): 154-158, 163. LIU Wen-bin, XU Wei, WANG Qing-feng. Equipment Reliability Prediction Research Based on Weibull Probability and Statistical Analysis Method[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(4): 154-158, 163. |
| [13] |
徐宇亮, 孙际哲, 陈西宏, 等. 电子设备健康状态评估与故障预测方法[J]. 系统工程与电子技术, 2012, 34(5): 1068-1072. XU Yu-liang, SUN Ji-zhe, CHEN Xi-hong, et al. Method of Health Performance Evaluation and Fault Prognostics for Electronic Equipment[J]. Systems Engineering and Electronics, 2012, 34(5): 1068-1072. |
| [14] |
饶永波, 常治元, 杨宗霄, 等. 高速公路机电设备使用寿命预测模型[J]. 河南科技大学学报:自然科学版, 2011, 32(2): 12-15. RAO Yong-bo, CHANG Zhi-yuan, YANG Zong-xiao, et al. Service Lifetime Prediction Modeling for Expressway Electromechanical Equipments[J]. Journal of Henan University of Science and Technology:Natural Science Edition, 2011, 32(2): 12-15. |
| [15] |
张继军, 邓力, 马登武, 等. 基于状态条件概率的设备剩余寿命预测[J]. 北京航空航天大学学报, 2014, 40(5): 602-607. ZHANG Ji-jun, DENG Li, MA Deng-wu, et al. Remaining Useful Life Prediction for Equipment Based on Conditional Probability of States[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(5): 602-607. |
| [16] |
何兆民, 王少萍. 基于时变状态转移隐半马尔科夫模型的寿命预测[J]. 湖南大学学报:自然科学版, 2014, 41(8): 47-53. HE Zhao-min, WANG Shao-ping. Life Remaining Lifetime Prediction Based on Time-varying State Transition Probabilities of Hidden Semi-Markov Model[J]. Journal of Hunan University:Natural Science Edition, 2014, 41(8): 47-53. |
| [17] |
李洪儒, 王余奎, 王冰, 等. 面向广义数学形态颗粒特征的灰色马尔科夫剩余寿命预测方法[J]. 振动工程学报, 2015(2): 316-323. LI Hong-ru, WANG Yu-kui, WANG Bing, et al. The Method of Grey Markov Remaining Service Life Prediction Specific to Generalized Mathematical Morphological particle[J]. Journal of Vibration Engineering, 2015(2): 316-323. |
| [18] |
赵飞, 眭欢然, 戴岩, 等. 基于随机模糊理论和改进马尔科夫法的变压器寿命评估[J]. 电力系统保护与控制, 2014(15): 39-44. ZHAO Fei, SUI Huan-ran, DAI Yan, et al. Power Transformers Life Assessment Based on Random Fuzzy Theory and Improved Markov Method[J]. Power System Protection and Control, 2014(15): 39-44. |
| [19] |
冯隽, 王岩, 边军. 灰色马尔科夫组合模型对结构剩余寿命预测的研究[J]. 港工技术, 2014(6): 27-29. FENG Jun, WANG Yan, BIAN Jun. Structure Residual Life Forecast by Using Grey Markov Combination Model[J]. |
| [20] |
严野, 李建兰, 康乐, 等. 基于马尔科夫修正的潜油泵灰色振动预测模型[J]. 石油机械, 2013, 41(3): 84-88. YAN Ye, LI Jian-lan, KANG Le, et al. Markov Correction-based Grey Prediction Model for Submersible Pump Vibration[J]. China Petroleum Machinery, 2013, 41(3): 84-88. |
| [21] |
沈鑫, 曹敏, 高文胜, 等. 基于领结模型和半马尔科夫的变压器故障率预测及研究[J]. 电子器件, 2015(6): 1421-1427. SHEN Xin, CAO Min, GAO Wen-sheng, et al. Prediction and Research on Transformer Fault Based on the Bow Tie and Semi-Markov Model[J]. Chinese Journal of Electronic Devices, 2015(6): 1421-1427. |
 2018, Vol. 35
2018, Vol. 35
