扩展功能
文章信息
- 张名芳, 付锐, 石涌泉, 程文冬
- ZHANG Ming-fang, FU Rui, SHI Yong-quan, CHENG Wen-dong
- 基于激光雷达的远距离运动车辆位姿估计
- Estimation of Long Distance Moving Vehicle Pose Based on LIDAR
- 公路交通科技, 2017, 34(12): 131-139
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(12): 131-139
- 10.3969/j.issn.1002-0268.2017.12.019
-
文章历史
- 收稿日期: 2016-08-24
2. 西安工业大学 机电工程学院, 陕西 西安 710032
2. School of Mechatronic Engineering, Xi'an Technological University, Xi'an Shaanxi 710032, China
自主驾驶是当前智能车辆领域的研究热点之一。为了保证在未知的环境中安全行驶,实现周围车辆运动状态的准确估计是自主驾驶车辆需要解决的首要任务之一。运动车辆位姿(Moving Vehicle Pose, MVP)的准确估计能为目标车辆的速度估计和自主车辆自身的运动路径规划提供可靠依据[1-5]。激光雷达(LIght Detection And Ranging,LIDAR)能精确获取周围环境物体的深度信息,且不受光照和天气状况的干扰,可有效感知周围物体位置和状态变化。
目前,国内外学者主要基于点云分布特征和测量模型两种方法估计运动车辆位姿。在基于点云分布特征方面,通常是利用点云的几何分布进行最小二乘拟合,得到最小外接矩形实现目标车辆中心位姿提取,并用于后续的车辆跟踪过程[6-7]和路径规划[8-9]。同时,有学者采用随机采样一致性(RANdom Sample Consensus,RANSAC)算法在水平面上拟合离散点云类簇得到分段的主方向,作为车辆可见面投影的长线段方向,再根据角特征拟合估计车辆位姿[10-11]。C. Mertz等[12]对每个类簇提取线特征和角特征,初步拟合后滤除20%最差的异常点,对保留的扫描点进行再次拟合以提高鲁棒性。D. Morris等[13]利用近距离采样密度较高的三维点云对给定的目标车辆表面建模,通过多个边缘的信息推断目标车辆位置实现位姿估计。这类基于点云分布特征的MVP估计方法的结果受局部遮挡和扫描距离变化的影响较大。基于测量模型的位姿估计方面,一些学者利用矩形或立方体盒子模型表示车辆,采用优化算法从分段的扫描点中找到最可能的车辆位姿[14-16]。N. Wojke等[14]基于RANSAC算法进行直线特征和角特征拟合,整合拟合出矩形盒的时空几何特征变化,缩小了采样范围以提高位姿估计的效率。M. Himmelsbach等[15]利用物体水平的标量特征和点水平的特征直方图提取包含点云类簇的车辆立方体盒子模型,计算出目标车辆位姿。上述方法提出的测量模型在实际应用上更侧重于检测最接近于车辆的目标物,而在目标车辆位姿估计方面仍存在提升的空间。
综上所述,基于点云分布特征和基于测量模型的位姿估计方法在点云密集、分布特征显著时是可行的。但在实际道路交通环境下,目标车辆与车载LIDAR间距时远时近,而LIDAR进行远距离扫描时分辨率受限,生成稀疏的采样点,得到的物体表面变化较大,甚至只有单层扫描线投射到目标表面。这将导致难以对远距离粗采样的目标车辆进行准确的位姿估计。针对以上不足,本研究通过对矩形拟合模块进行改进,结合连续帧拟合优化,实现远距离MVP的准确估计。
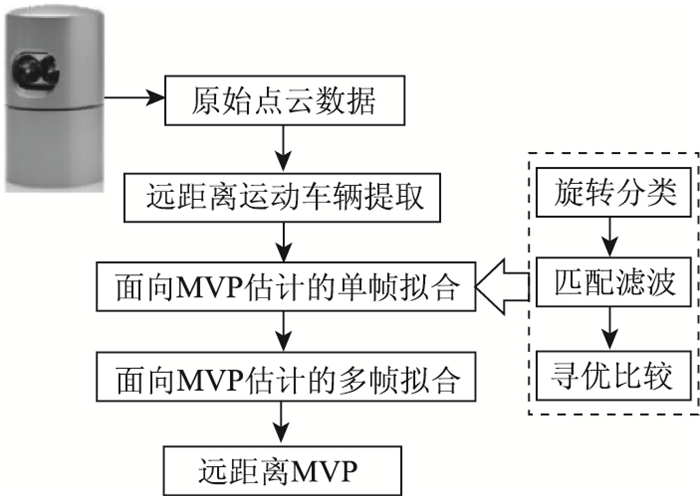
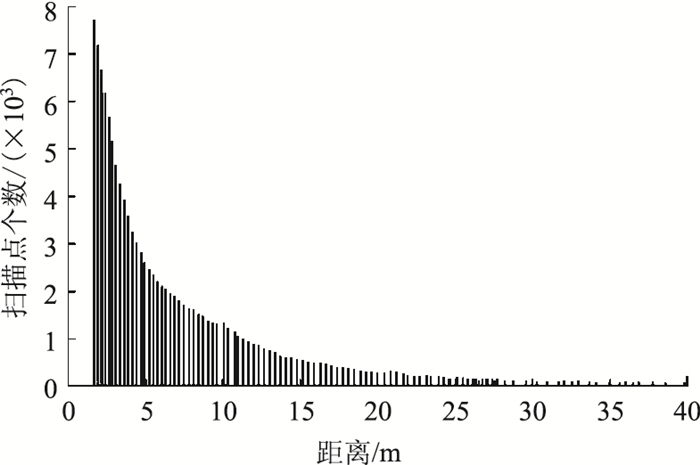
1 算法概述远距离MVP估计方法的处理流程(见图 1)如下:从三维点云场景中提取远距离运动车辆,对点云二维投影做旋转分类和匹配滤波,利用单帧拟合初步提取最优矩形位姿,再通过多帧拟合优化拟合矩形位姿,实现远距离MVP的准确估计。LIDAR选用Velodyne HDL-32E,能实现360°全方位扫描周围环境,每秒钟生成约70万个点,设置扫描频率为10 Hz,实物见图 1。随着目标车辆与LIDAR间距离的增加,其反射回的扫描点个数逐渐下降,如图 2所示。当间距超过30 m时,返回的扫描点个数低于100个,因此选取分布在LIDAR周围距离大于30 m的区域为远距离区域。在运动车辆提取阶段,首先将场景中的静态背景与运动目标车辆分离,结合时间线索与几何线索从目标物体中剔除静态扫描点;然后采用盒子模型作为滑动窗口划分远距离近似车辆点云簇的有效兴趣区域,避免一般空间聚类方法占用较高计算内存。
|
| 图 1 算法流程图 Fig. 1 Flowchart of algorithm |
| |
|
| 图 2 目标车辆扫描点个数随距离变化分布直方图 Fig. 2 Histogram of number of scanning points on target vehicle varying with distance |
| |
2 面向MVP估计的单帧拟合 2.1 旋转分类
针对远距离MVP估计,将LIDAR所在位置作为世界坐标系W的原点,目标车辆位姿记为状态向量(x0w, y0w, θ0w),由原始三维点云数据获得最接近真实位姿的最优状态估计值。为更好地基于稀疏点云提取运动车辆位姿,忽略纵向高度,只考虑点云在水平面上的二维投影。利用最小二乘拟合得到稀疏点云水平面二维投影近似拟合直线的斜率,作为经过二维投影平均值点的垂直正交直线对L1和L2的初始斜率。将世界坐标系内的二维投影点云坐标变换成以直线对L1和L2为坐标轴的坐标系C内的点坐标:
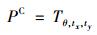
|
(1) |
式中, P=(p1, …, pn)为运动点云在世界坐标系内俯视图水平面上的二维投影坐标,n为点云数目;Tθ, tx, ty为点云由世界坐标系到坐标系C的转换过程,θ为转换过程的角度参数,tx和ty分别为转换过程x轴和y轴的转换系数。
通过在两个坐标轴的有效投影区间内等间隔划分固定宽度的容器,绘制各容器的投影点数直方图。利用线性插值建立一维向量估计的装箱模型对每个运动点进行更精确的位置估计:
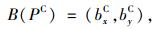
|
(2) |
式中, B(PC)表示对转换坐标后的点云PC进行装箱运算; bxC和byC分别为二维水平投影转换到坐标系C后划分到两坐标轴各容器内的装箱向量。
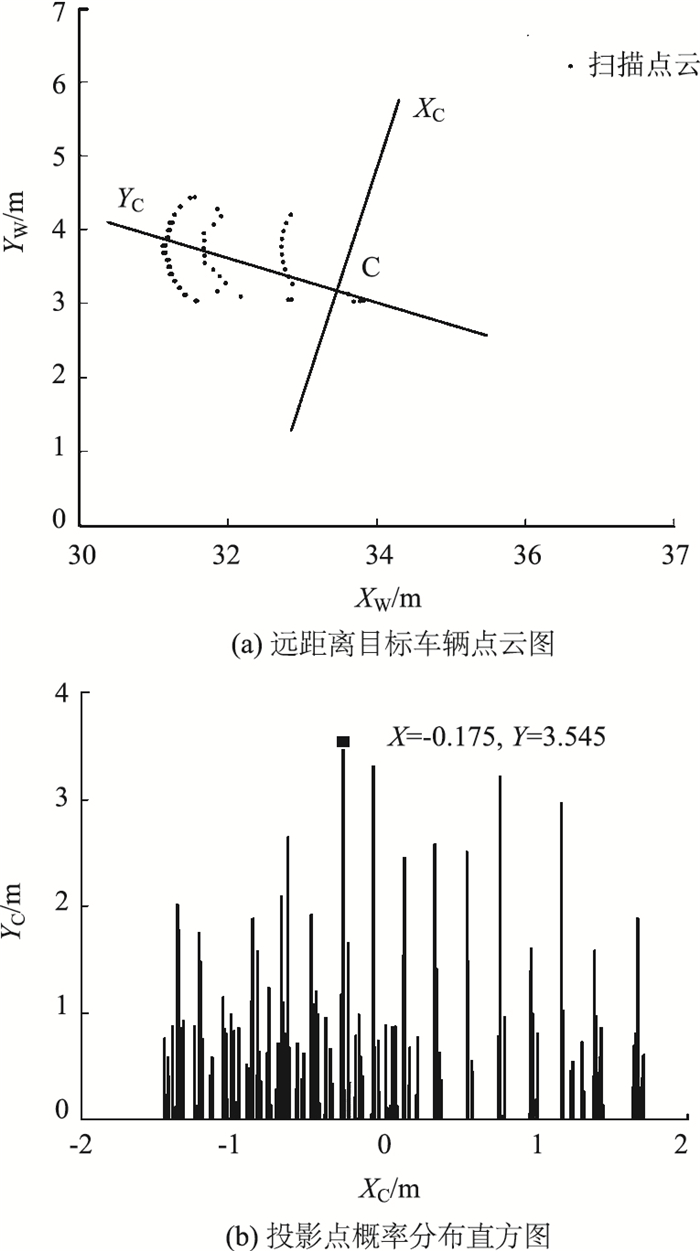
该装箱模型中的每个点在投影区间内最多有可能对应于两个容器,具体取决于它与每个容器区间的重合度。将较低容器和较高容器之间的距离分数赋予每个投影点,再利用稀疏矩阵获取坐标系C中两坐标轴上有效区间内各容器的投影点概率分布。选取某帧扫描点云,得到某组正交直线对构成的坐标系C中XC轴上的投影点概率分布,如图 3所示。可见,中心坐标为X=-0.175的容器所包含的投影点数概率最大。
|
| 图 3 坐标系C的XC轴上投影点概率分布 Fig. 3 Projective point probability distribution on XC axis in coordinate system C |
| |
2.2 匹配滤波
匹配滤波常用于信号处理和雷达跟踪,通过滤波匹配目标信号的特征并与噪声信号做卷积,利用信噪比最大化从带噪声信号的背景聚类中识别目标和估计目标位置[17-18]。由于扫描场景中目标车辆的大部分面积是自我遮挡的,表面采样点的变化受目标车辆与LIDAR间相对位置的影响。综合考虑自我遮挡和采样变化,本研究自适应估计滤波大小,将滤波响应设定为基于目标车辆与LIDAR间相对位置的观测角函数,通过最大化匹配滤波响应实现车辆位姿估计。
将车辆的俯视图投影看作矩形,投射到非遮挡表面区域的扫描点数与目标车辆和LIDAR间的相对位置相关。设LIDAR和目标车辆的连线与目标车辆中心线的相对角为β,扫描点分布的权重受β影响。设定原始信号x,给定带噪声的信号p(x)和等价于理想信号的滤波s(x),利用一维匹配滤波计算偏移量t:
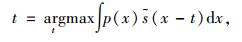
|
(3) |
式中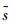
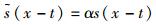
分别对各直线对两轴容器内投影点概率分布进行一维匹配滤波,定义每个容器内点数为高斯信号:
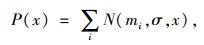
|
(4) |
式中,mi为均值;σ为标准差。
坐标系C中两坐标轴上有效区间内各容器的投影点数值为Np,信号均值为xNp和yNp,滤波信号定义为与理想矩形拟合对应的投影点分布相关的阶跃函数s(Np, x),取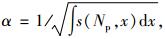
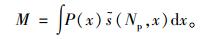
|
(5) |
设定每组直线对两轴上的理想信号阶跃函数突变点分别发生在容器xa和ya处,则匹配滤波后在两轴上各产生一个离散的代价函数Ixβ和Iyβ,注意匹配滤波生成的离散代价函数与投影点概率分布必须具有相同的宽度值。两轴对应的离散代价函数Ixβ和Iyβ的计算公式分别为:
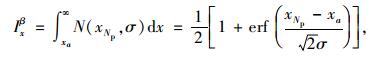
|
(6) |
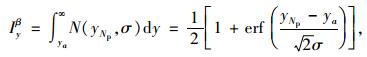
|
(7) |
式中erf表示误差函数,是高斯概率密度函数的积分。
2.3 寻优比较将经过二维投影平均值点的直线对旋转90°,每隔Δα(Δα为相邻直线对的角度差)计算1次,得到90/Δα组直线对。Δα取值越小,最优矩形拟合的位姿精度越高。原坐标系依次旋转到不同角度的直线对上,建立新的坐标系。然后将原始二维水平投影点云相应地变换到旋转后的坐标系中,并投影到当前角度的直线对上,获取1组新的点云坐标。对投影点概率分布与上述一维匹配滤波运算得到的代价函数作离散卷积,获得每组直线对的综合卷积分数值S:
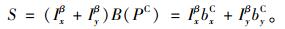
|
(8) |
利用全局最优算法快速求解两轴上综合卷积分数最大值Smax对应的直线对:
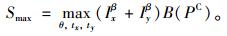
|
(9) |
为使正交直线对与车辆矩形长宽边的一维拟合效果最佳,取两轴卷积分数值之和最大时的直线对为最优直线对,即得到最优单帧拟合矩形两边方向的斜率,其所在平面为坐标系L。将Ix和Iy取最小值时所在的容器中心点旋转变换到原坐标系,换算得到拟合矩形的中心点,选取长边倾斜角作为目标车辆单帧拟合矩形位姿角度,确定远距离车辆的单帧拟合最优矩形位姿(xL, yL, θL),其中xL和yL为矩形中心坐标,θL为矩形位姿角度。
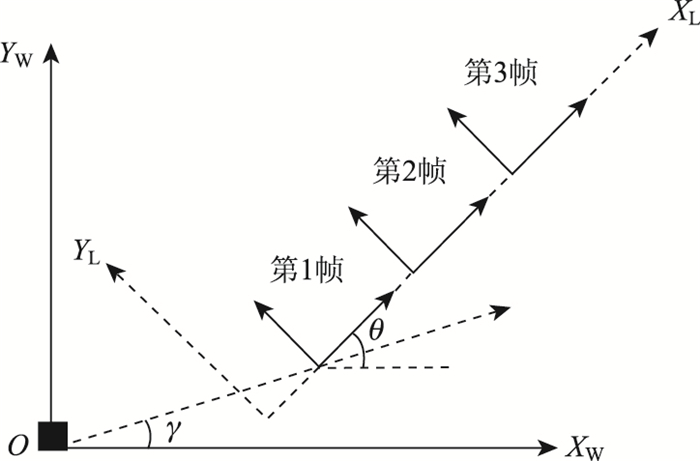
3 面向MVP估计的多帧拟合远距离车辆运动时,不断变化的稀疏点云分布容易造成位姿估计结果鲁棒性较差。因此,选取连续3帧扫描点云对中间帧的单帧拟合最优位姿进行多帧拟合优化。以L为参考坐标系,以单帧拟合最优矩形的长边为XL轴。考虑到相邻两帧时间间隔非常短,进行如下假设:连续3帧的拟合矩形位姿方向在XL轴上发生平移,但在YL轴上保持不变。构造水平的平移模型约束,定义位置变量x2=x1+Δx,y2=y1,其中Δx为未知变量,其值大小不影响假设,见图 4。
|
| 图 4 三帧拟合的平移模型约束示意图 Fig. 4 Schematic diagram of 3-frame fitted translation model constraint |
| |
利用全局最优算法求解拟合矩形两边方向上连续3帧扫描的最优直线对的位姿,连续3帧点云综合卷积分数和最大值S的计算公式为:
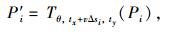
|
(10) |
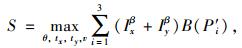
|
(1) |
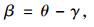
|
(12) |
式中,Pi为第i帧扫描点云;v为目标车辆运动速度;对应连续帧的时间差记为Δs1, …, Δsn;vΔsi为连续帧间沿XL方向的水平位移差;Tθ, tx+vΔsi, ty表示连续帧中世界坐标系内的点云坐标转换到当前帧点云坐标系沿XL轴方向平移vΔsi后的坐标系内;P′i为第i帧点云转换后的点云坐标;γ为当前帧目标车辆位姿中心和LIDAR的连线与XW轴正方向的夹角。
4 仿真结果分析为证实所提方法的有效性,采用MATLAB编程进行仿真分析。考虑到RANSAC算法作为目标位姿估计的常用方法,能对包含大量误差的数据做迭代拟合,有效估计出模型参数[5-6],因此,本研究将提出的面向远距离MVP的单帧拟合、多帧拟合方法与RANSAC算法[10]进行对比,分析拟合估计得到的几何位姿测量值与真实位姿值间的误差。
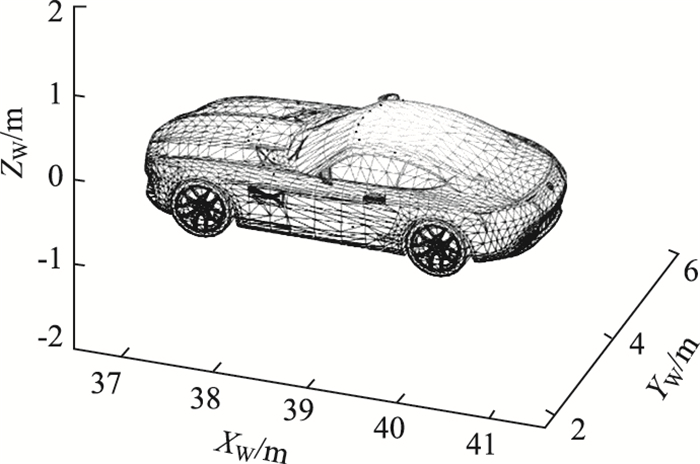
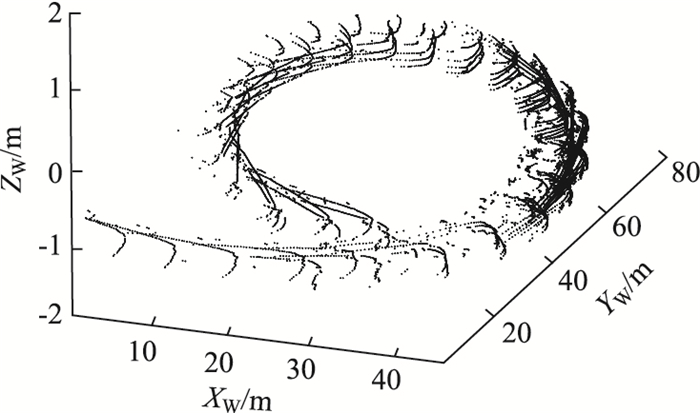
采用福特Fusion的网格模型作为远距离目标车辆,见图 5。这里仅考虑LIDAR静止时扫描远距离运动车辆的情况。设定目标车辆的运动状态,生成连续帧扫描时不同位姿下的所有可能的扫描点云,见图 6。
|
| 图 5 福特轿车Fusion的网格模型 Fig. 5 Grid model of Ford Fusion car |
| |
|
| 图 6 目标车辆运动时LIDAR连续帧扫描点云场景 Fig. 6 Scanning point cloud scene of LIDAR in consecutive frames when target vehicle is moving |
| |
4.1 直线运动仿真
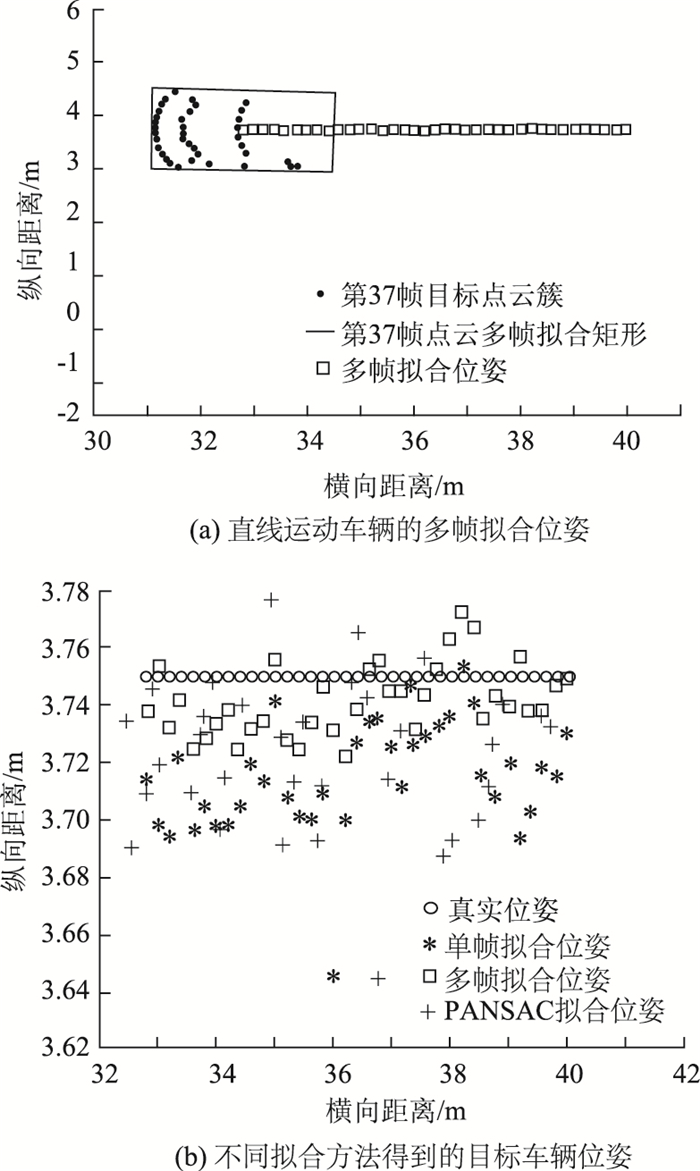
当远距离目标车辆做直线运动时,设定初始位姿为[40, 3.75, -π],速度恒定为2 m/帧,选取连续37帧扫描点云数据,以车载LIDAR为世界坐标系原点,对比3种方法得到的目标车辆位姿估计值与真实值,见图 7。
|
| 图 7 目标车辆直线运动时LIDAR连续帧扫描得到的位姿变化 Fig. 7 Pose change from LIDAR scanning in consecutive frames when target vehicle is moving in straight line |
| |
由图 7可知,多帧拟合方法得到的位姿估计值最为接近真实值。而单帧拟合和RANSAC拟合结果均较为明显地偏离真实位姿,尤其是RANSAC拟合结果离散程度最高。
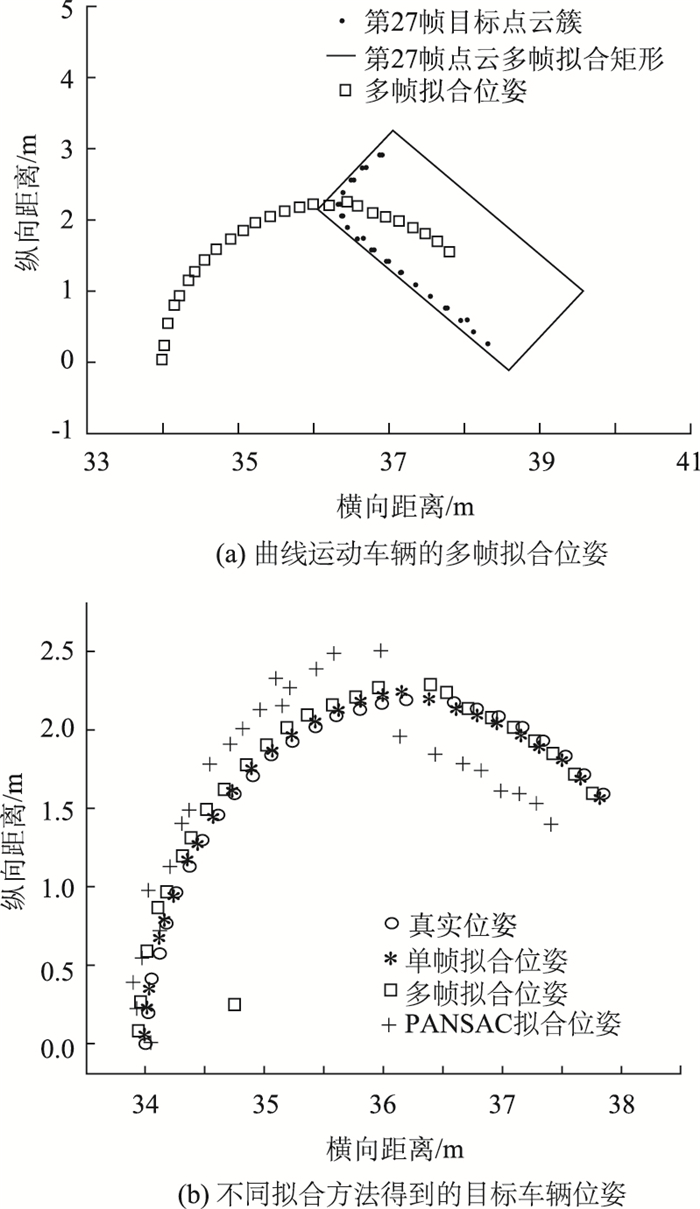
4.2 曲线运动仿真当远距离目标车辆做曲线运动时,设定初始位姿为[34, 0, π/2],角速度大小为-π/36,线速度大小为2 m/帧。选取连续27帧扫描点云数据,以车载LIDAR为世界坐标系的原点,对比3种方法得到的目标车辆位姿估计值与真实值,见图 8。
|
| 图 8 目标车辆曲线运动时LIDAR连续帧扫描得到的位姿变化 Fig. 8 Pose change from LIDAR scanning in consecutive frames when target vehicle is moving in curved line |
| |
由图 8可知,目标车辆位姿均逐帧变化。随着目标车辆与LIDAR的距离越来越远,RANSAC拟合的结果偏离真实位姿的幅度逐渐增大,表现出明显差异。而多帧拟合和单帧拟合方法得到的结果较为接近,且与真实位姿的变化一致。
4.3 结果分析均方根误差(Root Mean Square Error,RMSE)常用来衡量观测值偏离真实值的程度。RMSE越小,测量精度越高。因此,选用RMSE进一步比较3种方法的位姿估计测量精度。
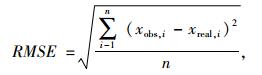
|
(13) |
式中,xobs, i为第i帧扫描点云计算得到的目标车辆位姿估计值;xreal, i为第i帧扫描时目标车辆位姿真实值。
远距离目标车辆直线运动和曲线运动时的位姿估计RMSE结果分别见表 1和表 2。
由表 1可知,直线运动时,多帧拟合方法计算得到的横向位姿、纵向位姿、位姿角度和位置估计的RMSE均小于单帧拟合和RANSAC拟合。因此,直线运动中多帧拟合的位姿估计结果优于单帧拟合和RANSAC拟合,对目标车辆的位姿估计效果良好,多帧拟合利用卷积滤波实现的离散和多帧平移约束使得直线运动的车辆位姿能够进行准确估计,而不受点云稀疏的局限。
由表 2可知,曲线运动时,单帧拟合与多帧拟合的位姿估计RMSE较为近似,而RANSAC拟合的RMSE明显大于单帧拟合和多帧拟合。曲线运动造成目标车辆方向角变化较大,相邻帧的车辆位姿在横向和纵向上均发生改变,多帧拟合过程中的连续帧平移约束并未对单帧拟合的最优位姿实现较为理想的优化。综合表 2和表 3,当远距离目标车辆以恒定速度大小运动时,3种方法在曲线运动中位姿估计各参数的RMSE均大于直线运动中的结果。这是因为曲线运动导致目标车辆横向位姿、纵向位姿和位姿角度的变化幅度均大于直线运动。曲线运动中随着目标车辆与LIDAR的距离增大,点云稀疏程度增加,RANSAC拟合的输入参数个数降低,即使增加迭代次数,也难以估计出最优模型参数,导致RANSAC拟合偏离真实位姿的幅度逐渐增大。
5 真实试验结果分析
为进一步验证提出算法的可靠性,同时确保交通安全,将Velodyne HDL-32E LIDAR固定在Husky机器人顶部(见图 9(a)),LIDAR 360°扫描周围环境,帧率为10帧/s,在校园试验场真实道路场景中进行试验。试验过程中,在Husky机器人身上安装GPS,并选用实验室中载有高精度差分GPS系统的测试车辆作为远距离运动目标车辆,以对比GPS获取的目标车辆真实位姿与不同算法计算出的位姿。考虑到实际场景中LIDAR也可能处于运动状态,目标车辆与LIDAR间的距离时远时近,因此为检验不同距离条件下算法的适应性,共进行5次试验,每次试验均设定该机器人以恒定速度3 m/s沿图 9(b)标记的路线行驶,目标车辆与LIDAR间的相对距离分别保持在10,20,30,40,50 m,相对距离偏差在3 m范围内均可接受。图 9(c)为试验采集的三维点云场景,其中矩形框A表示当前帧扫描提取的目标车辆。

|
| 图 9 真实试验场景设计 Fig. 9 Real test scene design |
| |
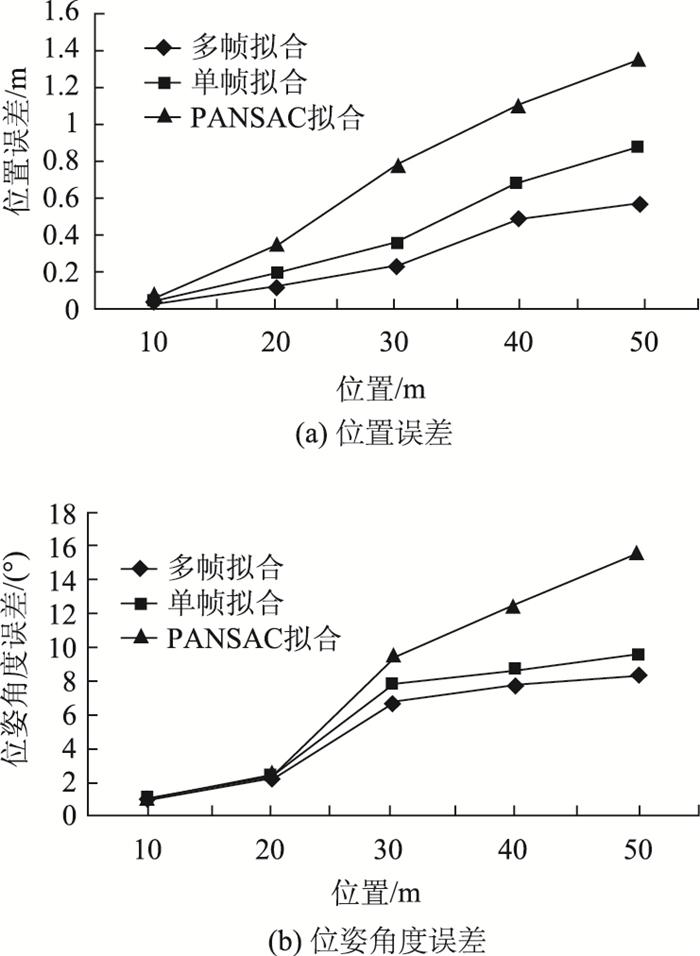
试验选取上述5种不同相对距离条件下采集的目标车辆点云各500帧,分别运用RANSAC拟合和本研究提出的单帧拟合与多帧拟合算法估计目标车辆位姿,统计出位置和位姿角度RMSE,结果见图 10。由统计结果可知,当相对距离较近,保持在10 m和20 m时,3种拟合方法得到的位置和位姿角度RMSE较为接近,而当相对距离增大到30 m甚至更远时,RANSAC拟合得到的RMSE不断增加,明显大于本研究提出的单帧拟合和多帧拟合方法,其对距离变化的适应性较差。这是由于距离远近对采集的点云个数影响较大,RANSAC拟合在点云稀少时较难估计出最优解,而所提方法利用旋转直线对的投影点概率分布进行匹配滤波扩大了车辆位姿分布的可能性。对于远距离条件下采集的目标车辆点云,多帧拟合方法计算出的位置和位姿角度RMSE小于单帧拟合,原因在于连续帧拟合约束优化了单帧拟合位姿估计结果。综合分析试验结果可知,相比于RANSAC拟合方法,本研究提出的单帧拟合和多帧拟合方法对不同相对距离下采集的车辆点云的适应性更高,对远距离目标车辆位置和位姿角度的估计结果更为准确。
|
| 图 10 目标车辆与LIDAR处于不同相对距离时位姿估计RMSE比较 Fig. 10 Comparison of RMSEs for pose estimation when distance between target vehicle and LIDAR changes |
| |
为测试算法的实时性,选取真实道路场景下采集的目标车辆点云(共计5 000帧)进行算法耗时测试,统计结果见表 3。由于本研究提出的单帧拟合和多帧拟合算法需要进行平面维度的旋转分类数据统计和匹配滤波,因此计算量较大,运算效率略低于RANSAC拟合。多帧拟合算法在单帧拟合的基础上,基于连续帧平移约束求解全局最优,导致数据计算量大于单帧拟合。整体而言,本研究提出的多帧拟合算法已能够实现高于8帧/s的处理速度。若植入具备较高硬件配置的专用计算处理系统,算法的实时性可进一步提高,能够满足实时的位姿估计需求。
6 结论针对LIDAR扫描远距离车辆获取的点云稀疏导致不易估计车辆位姿的问题,本研究提出了一种远距离车辆位姿估计方法。首先对稀疏点云在正交旋转直线对上的二维水平投影点进行一维向量估计的装箱过程,再用一维匹配滤波生成两正交直线方向上的离散代价函数,寻优比较得到单帧拟合最优的矩形位姿。结合连续帧平移模型约束,实现了多帧拟合最优位姿估计。利用仿真和真实场景下采集的目标车辆点云数据集对所提出的算法进行了验证,并与常用的RANSAC拟合算法进行了对比。试验结果表明:多帧拟合方法对远距离直线运动车辆的位姿估计具有较高的准确性,能克服点云稀疏性;远距离车辆做曲线运动时,多帧拟合方法与单帧拟合方法的位姿估计效果较为接近,不需要进一步的多帧拟合优化;对于不同相对距离下采集的目标车辆点云,所提出的单帧拟合和多帧拟合位姿参数估计结果准确性高于RANSAC拟合,算法适应性更好。总体而言,面向MVP估计的单帧拟合和多帧拟合方法均优于RANSAC算法。所提方法能够为基于LIDAR的运动车辆跟踪提供技术支撑。
| [1] |
周俊静, 段建民, 杨光祖. 基于雷达测距的车辆识别与跟踪方法[J]. 汽车工程, 2014(11): 1415-1420. ZHOU Jun-jing, DUAN Jian-min, YANG Guang-zu. A Vehicle Identification and Tracking Method Based on Radar Ranging[J]. Automotive Engineering, 2014(11): 1415-1420. |
| [2] |
彭军, 王江锋, 王娜. 基于机器视觉的智能车辆避撞预警算法[J]. 公路交通科技, 2011, 28(增1): 124-128. PENG Jun, WANG Jiang-feng, WANG Na. Intelligent Vehicle Collision Warning Algorithm Based on Machine Vision[J]. Journal of Highway and Transportation Research and Development, 2011, 28(S1): 124-128. |
| [3] |
葛艳, 王健, 孟友新, 等. 车辆导航动态路径规划的研究进展[J]. 公路交通科技, 2010, 27(11): 113-117. GE Yan, WANG Jian, MENG You-xin, et al. Research Progress on Dynamic Route Planning of Vehicle Navigation[J]. Journal of Highway and Transportation Research and Development, 2010, 27(11): 113-117. |
| [4] |
姜岩, 王琦, 龚建伟, 等. 无人驾驶车辆局部路径规划的时间一致性与鲁棒性研究[J]. 自动化学报, 2015, 41(3): 518-527. JIANG Yan, WANG Qi, GONG Jian-wei, et al. Research on Temporal Consistency and Robustness in Local Planning of Intelligent Vehicles[J]. Acta Automatica Sinica, 2015, 41(3): 518-527. |
| [5] |
胡永仕, 张阳. 基于遗传模糊算法的智能车辆避障路径规划研究[J]. 福州大学学报:自然科学版, 2015, 43(2): 219-224. HU Yong-shi, ZHANG Yang. Path Planning of Intelligent Vehicle Based on Genetic Fuzzy Algorithm[J]. Journal of Fuzhou University:Natural Science Edition, 2015, 43(2): 219-224. |
| [6] |
甘志梅, 王春香, 杨明. 基于激光雷达的车辆跟踪与识别方法[J]. 上海交通大学学报, 2009(6): 923-926. GAN Zhi-mei, WANG Chun-xiang, YANG Ming. A Method for Vehicle Tracking and Recognition Based on Scanning Laser Radar[J]. Journal of Shanghai Jiaotong University, 2009(6): 923-926. |
| [7] |
方彦军, 周亭亭, 谭磊. 基于交互式多模型算法的无人车车辆跟踪预测技术[J]. 武汉大学学报:工学版, 2013, 46(4): 540-544. FANG Yan-jun, ZHOU Ting-ting, TAN Lei. Unmanned Vehicle Tracking Prediction Technology Based on Interacting Multiple Model Method[J]. Engineering Journal of Wuhan University, 2013, 46(4): 540-544. |
| [8] |
梁栋, 史忠科. 半结构化道路下智能车辆路径规划与控制算法研究[J]. 交通运输系统工程与信息, 2011, 11(2): 44-51. LIANG Dong, SHI Zhong-ke. Path Planning and Control Algorithm for Intelligent Vehicles under Semi-structured Road Condition[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(2): 44-51. |
| [9] |
肖已达, 王冰, 杨明, 等. 基于激光雷达的道路可通行区域检测[J]. 机电一体化, 2013, 19(2): 62-66. XIAO Yi-da, WANG Bing, YANG Ming, et al. Road Available Area Detecting Based on Laser Scanner[J]. Mechatronics, 2013, 19(2): 62-66. |
| [10] |
MORRIS D, HALEY P, ZACHAR W, et al. Ladar-based Vehicle Tracking and Trajectory Estimation for Urban Driving[C]//Proceedings of Association for Unmanned Vehicle Systems International Conference. San Diego:AUVSI, 2008:535-550. http://arxiv.org/abs/1709.08517
|
| [11] |
TEICHMAN A, LEVINSON J, THRUN S. Towards 3D Object Recognition via Classification of Arbitrary Object Tracks[C]//Proceedings of International Conference on Robotics and Automation. Shanghai:IEEE, 2011:598-603. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5979636
|
| [12] |
MERTZ C, NAVARRO E, MACLACHLAN R, et al. Moving Object Detection with Laser Scanners[J]. Journal of Field Robotics, 2013, 30(1): 17-43. |
| [13] |
MORRIS D, HOFFMAN R, MCLEAN S. Ladar-based Vehicle Detection and Tracking in Cluttered Environments[C]//Proceedings of 26th Army Science Conference. Orlando:Defense Technical Information Center, 2008:416-424. http://www.mendeley.com/catalog/ladarbased-vehicle-detection-tracking-cluttered-environments/
|
| [14] |
WOJKE N, HASELICH M. Moving Vehicle Detection and Tracking in Unstructured Environments[C]//Proceedings of 2012 IEEE International Conference on Robotics and Automation. St Paul:IEEE, 2012:3082-3087. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6224636
|
| [15] |
HIMMELSBACH M, WUENSCHE J. Tracking and Classification of Arbitrary Objects with Bottom-up/Top-down Detection[C]//Proceedings of 2012 IEEE Intelligent Vehicles Symposium. Madrid:IEEE, 2012:577-582. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6232181
|
| [16] |
杨飞, 朱株, 龚小谨, 等. 基于三维激光雷达的动态障碍实时检测与跟踪[J]. 浙江大学学报:工学版, 2012, 46(9): 1565-1571. YANG Fei, ZHU Zhu, GONG Xiao-jin, et al. Real-time Dynamic Obstacle Detection and Tracking Using 3D Lidar[J]. Journal of Zhejiang University:Engineering Science Edition, 2012, 46(9): 1565-1571. |
| [17] |
董华安, 王建国, 陆军, 等. 基于匹配滤波器设计的粒子滤波检测前跟踪算法研究[J]. 电光与控制, 2016(9): 44-48. DONG Hua-an, WANG Jian-guo, LU Jun, et al. Particle Filter for Track-before-detect Based on Matched Filter Design[J]. Electronics Optics and Control, 2016(9): 44-48. |
| [18] |
罗飞腾, 王东进, 陈卫东. 基于雷达原始幅度数据的目标跟踪性能分析与实现[J]. 中国科学技术大学学报, 2010, 40(11): 1159-1165. LUO Fei-teng, WANG Dong-jin, CHEN Wei-dong. Performance Analysis and Implementation of Radar Tracking Based on Raw Amplitude Data[J]. Journal of University of Science and Technology of China, 2010, 40(11): 1159-1165. |
 2017, Vol. 34
2017, Vol. 34
