扩展功能
文章信息
- 钱蕾, 韩印, 姚佼
- QIAN Lei, HAN Yin, YAO Jiao
- 基于改进K-Means算法的交叉口影响路段行程速度估计
- Estimation of Travel Speed on Intersection Influenced Link Based on Improved K-Means Algorithm
- 公路交通科技, 2017, 34(12): 115-122
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(12): 115-122
- 10.3969/j.issn.1002-0268.2017.12.017
-
文章历史
- 收稿日期: 2017-04-24
GPS技术在交通领域的应用一直是智能交通系统中的研究热点。其中,低频浮动车数据分析是在交通大数据背景下重要的微观小样本机理分析,与交通大数据态势分析相互嵌套[1]。虽然采样频率较低,但是由于浮动车数量大和不间断运营,能在满足对车辆安全监控、对数据存储成本降低的同时,进行城市路网中全天时天候的信息采集。在交通信息中,路段平均行程速度是路段交通状态判定的重要指标,更是整个智能交通系统中重要的基础参数。
基于浮动车数据,在道路参数估计方面如路段平均行程速度的估计一直不乏研究者探讨。传统的对浮动车数据的处理研究多针对理想的高频采样数据,或仅对单列数据进行处理[2-10],运用的方法有:均值法、积分模型法、神经网络、模糊推理等方法。积分模型法研究较多,分为速度-时间积分模型和坐标-时间内插模型[5-6]。随着人工智能算法的应用,对单一浮动车交通参数估计出现了利用BP神经网络、模糊推理[9]等方法。但是,高频数据不易得到;而且尽管为高频数据,但在单列数据点中仍存在着需要分类讨论匹配后的数据点个数、位置与不同交叉口路段的几何关系,需要考虑的情形多且易疏漏。
近些年,随着大数据的研究与应用,聚类分析在决策精细化中越来越重要。短时交通流通常研究在5~30 min内交通流状态的变化情况[11],应用聚类方法对短时交通流中的浮动车数据提取交通参数,更为贴近实际交通情况[12-15],而且浮动车的数据点数量大大增加更有利于聚类分析:把杂乱的数据点集分组为由类似的对象组成的多个类,可以使数据更具代表性,更好地利用数据特征,更及时准确地表征短时交通状态。但目前研究中处理浮动车数据时较少考虑不同聚类算法存在的弊端,较少把路段交通特征和数据点特征结合起来。
因此本研究沿用短时交通流背景下的聚类分析处理,并加以改进。以短时间(5 min)为研究单位,对短时内所有有效数据点进行累积曲线拟合后聚类处理,成为能快速准确计算出实时路段行程速度的方法。在聚类分析时,考虑初始聚类中心重要性、聚类有效性评价、聚类个数的最优选取等问题进行研究。最后,以杭州城市交通为例,利用低频采样(≥30 s)的混合车辆(能采集到GPS数据的所有车辆,以出租车为主,包括公交车、客货运车以及部分私人小汽车)浮动车数据进行试验验证。
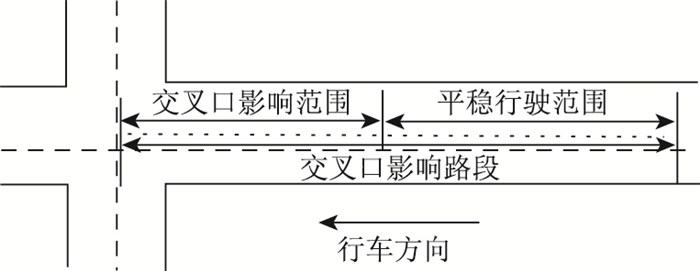
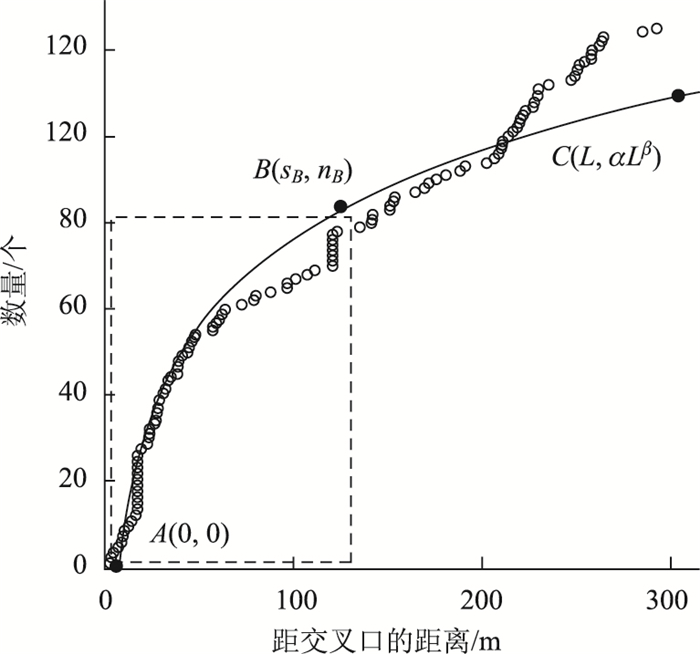
1 交叉口影响路段中交叉口影响范围交叉口影响路段,如图 1所示,通过路段划分和子路段划分后[16],大多数路段都受到交叉口上游的影响,车辆行驶过程中表现出来“平稳行驶-交叉口排队”节律,故把交叉口影响路段划分为交叉口影响范围和平稳行驶范围。并对5 min内所有数据点进行地图匹配。从中不难看出,对于数据点的数量和密度,在交叉口影响范围内明显大于不受影响的车辆平稳行驶范围。以距交叉口的距离为x轴,自交叉口附近第一个数据点算起的数据点累积数量为y轴建立路段数据累积图(如图 2所示),更为直观体现该规律。另外,通过观察数据集瞬时速度发现,在车辆平稳行驶范围内数据点较少但是相对稳定,但在交叉口影响范围内,受交叉口信控的影响,GPS返回的瞬时速度变化很大,经常出现速度为0的情况,数据点多而复杂,需要对其进行聚类处理。
|
| 图 1 交叉口上游影响范围示意图图 Fig. 1 Influencing range of intersection upstream |
| |
|
| 图 2 数据累积图及曲线拟合结果 Fig. 2 Data cumulative and fitting curves |
| |
在聚类处理之前,首先要确定交叉口影响的具体范围长度:利用样本数据特性,通过浮动车数据量随距离的累积过程,用IBM SPSS 22.0数据分析软件中几种常用拟合模型[17]分别拟合后发现拟合效果最好的模型。经过多个交叉口影响路段试验拟合,对比拟合优度R2,发现幂函数的拟合效果较好,R2∈(0.85, 0.98),而且在数据点密集区域,曲线能更好地反映交叉口影响范围内的数据点变化,见图 2。由此,设交叉口影响路段5 min内样本数据量为N, 路段长度为L,则计算具体步骤如下:
(1) 对交叉口路段上所有GPS数据点计算距交叉口的距离,并升序排列,得到si,si∈[0, L],i=1, 2, …, N,i为按距离升序处理后的数据点编码。
(2) 记第i个点对应的浮动车数据累积量为ni(在数值上i=ni)。
(3) 以浮动车数据累积量ni对距路段起始点距离si构建函数模型,见式(1):
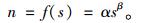
|
(1) |
(4) 计算得出累积速度的“减速点”B,即为交叉口影响的终点。
在式(1)所确定曲线上,有2个点的坐标是已知的,即A[0, 0],C[L, αLβ];记点B(sB, nB)。由此,将交叉口影响路段数据累积过程划分为两个范围:交叉口影响范围(AB段),平稳行驶范围(BC段)。求点B坐标:连接点A,C得到曲线的割线AC,向下作AC的平行线,交曲线于点B,则根据拉格朗日(lagrange)中值定理,可建立方程:
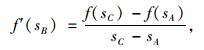
|
(2) |
将式(1)代入有:
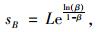
|
(3) |
则有:
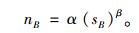
|
(4) |
对于α,β的确定,用最优拟合的对数函数得到。那么从路段起点到SB点之间路段为交叉口影响范围。由于nB不为整数,nB前面的点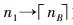
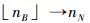
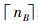
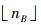
本研究以5 min为状态分析时段。在该路段、该时间段的时空范围内,接收到的所有车辆返回数据点的瞬时速度整体均值表征路段此时的行程速度。由于单车GPS数据采集受很多因素影响,如出租车上下客、交叉口延误等因素。尤其是当浮动车频率较低时,这些因素干扰可能被放大,不能代表整体。本方法不局限于单辆浮动车,随着研究时间段延长,就固定的路段,采集到的样本量增大;另外研究区域内平均信号周期180 s,最长200 s,5 min完全可以覆盖一个周期。这些因素产生的影响会反映在数据点的整体属性值上,采集频率较低等缺点也随之弥补。所以本研究不一一挖掘速度影响因素形成机理,而是以整体数据情况表征整个路段的交通状态。而交叉口影响范围内的数据点多而复杂,需要对其进行聚类处理,然后结合平稳行驶范围的数据点得到整个路段的行程速度。
GPS数据原始属性值为位置(经纬度)、瞬时速度、返回时刻、方向角等,经过第一节的处理,将位置信息转化为距路段起点距离的“距离”属性si。为方便表示,将数据的时刻转化为在该5 min内距时间起点的“时间”属性ti(单位s)。故而我们的数据拥有了瞬时速度vi、距离si、时间ti、方向角dai(direction angle)这些属性。对瞬时速度进行聚类分析需要利用这些数据作为聚类的依据。
2.1 聚类流程本研究的主要目的是对交叉口影响范围内数据点进行聚类分析。采用的K-Means聚类算法,基于初始聚类中心新算法和聚类有效性函数来改进。
K-Means聚类算法的聚类效果很大程度上依赖于K值和初始聚类中心的选定,但是传统的K-Means算法只能从纯数学角度聚类[18],K值给定较为粗略,而且初始聚类中心是随机给定的,二者一旦选择不好,可能无法得到有效的聚类结果。针对以上缺点,首先,在K-Means聚类之前先进行初始聚类中心的设定算法;其次,利用一种新的聚类有效性评价函数对聚类结果进行判断,从而实现结构参数K的优化。该算法的具体流程如图 3所示。
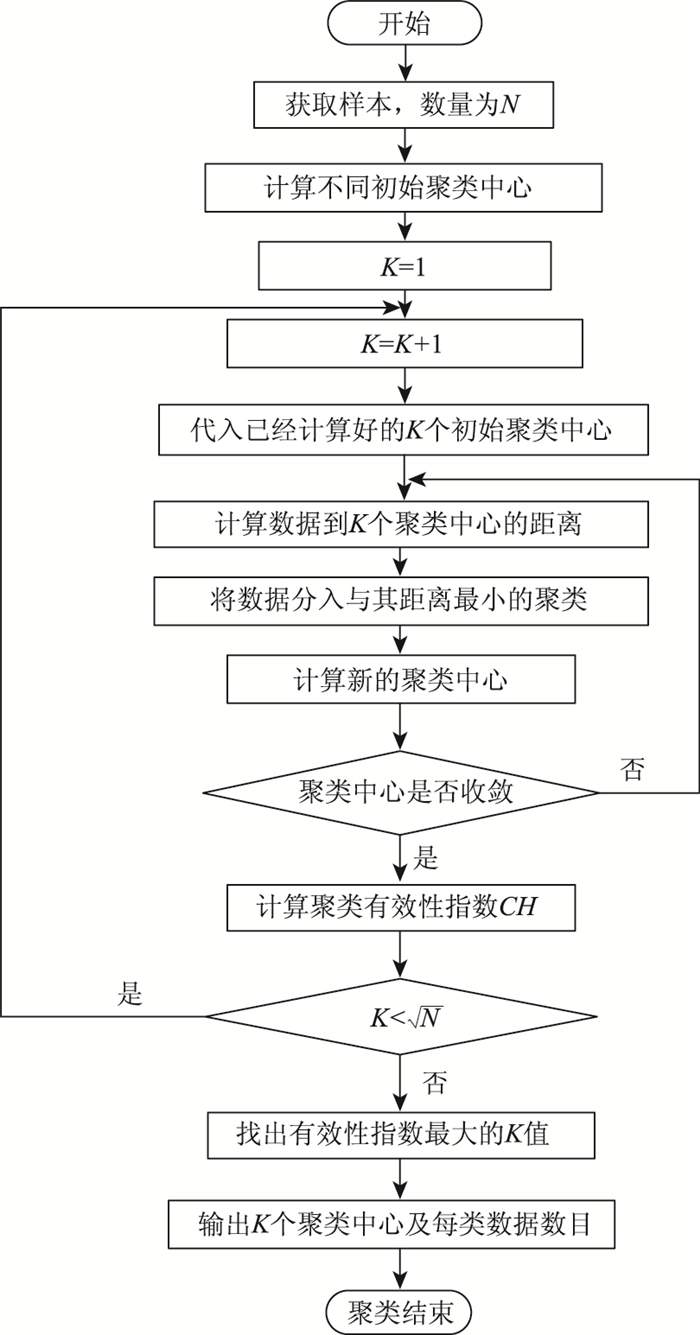
|
| 图 3 改进K-Means聚类流程 Fig. 3 Clustering process of modified K-Means algorithm |
| |
2.2 改进的K-Means聚类
K-Means是聚类算法中的一种,其中K表示类别数,Means表示均值。顾名思义K-Means是一种通过均值对数据点进行聚类的算法。K-Means算法通过预先设定的K值及每个类别的初始聚类中心对相似的数据点进行划分。并通过划分后的均值迭代优化获得最优的聚类结果。具体算法过程详见参考文献[19-20]。针对算法本身缺点,本研究作如下改进。
2.2.1 初始聚类中心的计算该算法利用GPS数据多维属性作为聚类依据,对瞬时速度进行处理。由于GPS数据属性较多(设共有p个属性),需要在其中挑选出两个属性,用于最好地描述数据特征。
首先,如式(5),用于计算最主要的属性作为主轴。设t为某一属性:
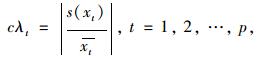
|
(5) |
式中,s(xt)为t属性下数值的标准差,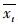
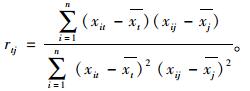
|
(6) |
在决定了主轴后,式(6)中的相关系数rtj,表示某一属性t和主轴属性j之间的相关性,rtj的最小值对应的属性确定为第二轴xⅡ。第二轴应垂直于主轴。在大数据中依据数据特征,选取该两轴是容易做到的。经过多次试验测算,距离属性si和速度属性vi的相关性最强。那么得到新的GPS数据集X,拥有两个属性瞬时速度vi和距离si,分别作为坐标轴。
然后,依据选取出的两个坐标轴,找到数据集的中心:主次轴xⅠ,xⅡ各自均值构成的中心m,m的坐标: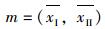
由欧式距离计算在主次轴环境下数据集中每个数据点与中心点m的距离:
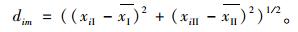
|
(7) |
确定第一个初始聚类中心c1:把式(7)中,所有数据点中距离中心点m距离最远的点作为第1个初始聚类中心c1;再确定第2个初始聚类中心c2:把式(8)中,所有数据点中距离第1个初始聚类中心c1距离最远的点作为第2个初始聚类中心c2。
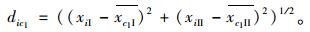
|
(8) |
若要确定第3个及以后的初始聚类中心:如式(9),计算第3个初始聚类中心,把距离前两个初始聚类中心c1,c2距离之和Sdi3最大的点作为第3个初始聚类中心c3。以此类推,直到聚类中心个数满足预先设定值(K)。
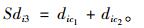
|
(9) |
式(9)可以避免距离上一个聚类中心最近的点被选作下一个初始聚类中心,所以该式挑选出来的初始聚类中心与上一个中心距离甚远[21]。
2.2.2 聚类有效性指数CalinskiHarabasz(CH) Index,简称CH指数。它是计算基于簇内距离和簇外距离的比例的一种聚类有效性评价函数[22]。对于N个数据点和K个聚类数,计算如下:
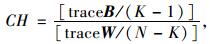
|
(10) |
式中,B和W是簇间和簇内散布矩阵。CH指数最大代表着最佳聚类数。
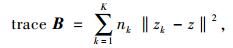
|
(11) |
式中,nk是聚类k中的对象数目,z是整个样本数据集的聚类中心,即样本均值。
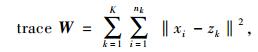
|
(12) |
因此,由式(10)~(12),CH指数能够写成:
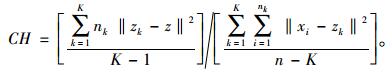
|
(13) |
CH指标值越大表示聚类效果越好,其最大值对应的类数为最佳聚类数Kopt,即本研究中改进K-Means算法的终止条件。步骤如下:
(1) 首先选择聚类数的搜索范围[Kmin, Kmax],取Kmin=2,即对样本数据集至少分为两类;Kmax= 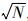
(2) 对聚类个数K从Kmin到Kmax进行遍历
从Kmin开始,聚类个数为K,对聚类结果求CH指数,直到计算出Kmax对应的CH指数。找出CH指数最大值CHmax,CHmax对应的K值为最佳聚类数Kopt。
(3) 输出Kopt个簇的簇内对象个数η(η1, η2, …, ηKopt)、聚类中心C(c1, c2, …, cKopt)。
2.2.3 聚类后的融合分析由聚类算法得到的结果,能计算出交叉口影响范围的平均行程速度V1见式(14);对平稳行驶范围,数据点个数记为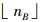
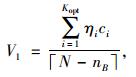
|
(14) |
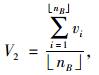
|
(15) |
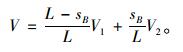
|
(16) |
为了验证本研究所提出的计算方法,选取了杭州市西湖区主干路组成的某路网区域,如图 4所示。该区域经度范围为[120.106, 120.127],纬度范围为[30.271, 30.283]。该路网主要信息见表 1。根据杭州市车辆出行历史数据分析结果显示,工作日早晚高峰出行量大、行程速度波动大、不同路段速度差别大,早高峰尤甚,但总体上工作日呈现一定的规律性。因此于2016年10月17日(工作日周一)对该区域进行实地交通调查。利用车辆牌照法抽样获取通过该路网的各路段行程时间(抽样牌照尾号为2,4,6,8,调查得到进入路网的机动车8 500辆,推算出实际进入路网车辆有21 250辆)。进而用路段长度除以行程时间计算出行程速度,作为试验的精确数据,即真实值。之后获取该路网区域早高峰时期2 600辆浮动车产生的12 000条浮动车数据(获取的浮动车数据属性包括车牌、道路编号、车种、经纬度、瞬时速度、返回时刻、方向角),得到在路网内浮动车覆盖率为12.2%,覆盖率较高,能够表征整体交通流特征[24]。经过数据点地图匹配、路段划分等数据预处理工作后,选择具有代表意义的主、次干路交叉口影响路段进行对比分析,比较估计值和真实值的接近程度。
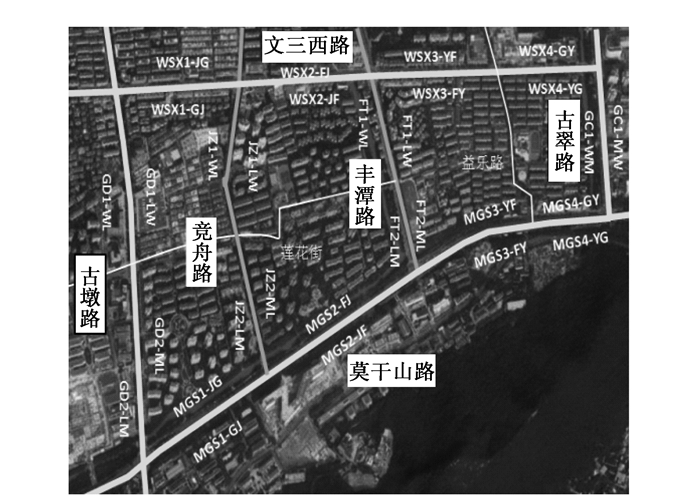
|
| 图 4 验证研究区域 Fig. 4 Study area for verification |
| |
| 主干路 | 次干路 | |||||
| 路名 | 路段 | 方向 | 路名 | 路段 | 方向 | |
| 文三西路 | WSX1 | GJ | 竞舟路 | JZ1 | WL | |
| JG | ||||||
| WSX2 | JF | LW | ||||
| FJ | ||||||
| WSX3 | FY | JZ2 | LM | |||
| YF | ||||||
| WSX4 | YG | ML | ||||
| GY | ||||||
| 莫干山路 | MGS1 | GJ | 丰潭路 | FT1 | WL | |
| JG | ||||||
| MGS2 | JF | LW | ||||
| FJ | ||||||
| MGS3 | FY | FT2 | LM | |||
| YF | ||||||
| MGS4 | YG | ML | ||||
| GY | ||||||
| 注:路段符号——以所在道路(莫干山路MoGanShan)名称拼音简写(MGS)命名,数字表示为其中的某段(MGS1);方向符号——该路段(MGS1)相交两条道路名称(古墩路、竞舟路)首字母命名(G,J),字母顺序表示了行车方向(GJ表示在莫干山路上从古墩路口开往竞舟路口) | ||||||
3.1 单组数据处理
以8:25—8:30丰潭路由南向北的路段FT1-LW作为算法示例试验路段。该路段全长约为386.5 m,终点为“十”字信控交叉口。符合本研究的研究对象,数据较为完整。通过数据预处理和曲线拟合,线拟合,得到sB=142.0,nB=18.2,即B点坐标为(142.0, 18.2)。那么,交叉口影响范围为距交叉口距离[0, 142.0]的区域;需要对第1至19个数据的瞬时速度进行聚类处理。在进行改进聚类后,得到:K取值2, 3, 4,对应CH指数为60.21,228.76,126.5。可以看出,CHmax=228.757 1,对应的Kopt=3,故而把交叉口影响区域部分的数据分为3类。得到结果见表 2,数据均有效,没有缺失。由式(14)知,交叉口上游影响段的平均行程速度为V1=20.26 km/h,由式(15)得到平稳行驶段的平均速度为V2=25.29 km/h,由式(16)得到路段最终的行程速度V=23.44 km/h。
| 聚类个数 | |||
| 簇1 | 簇2 | 簇3 | |
| 瞬时速度/(km·h-1) | 5.44 | 22.29 | 60.00 |
| 距离/m | 210.90 | 333.75 | 281.58 |
| 聚类中案例个数 | 9.00 | 7.00 | 3.00 |
3.2 主次路段各时段估计值与真实值对比
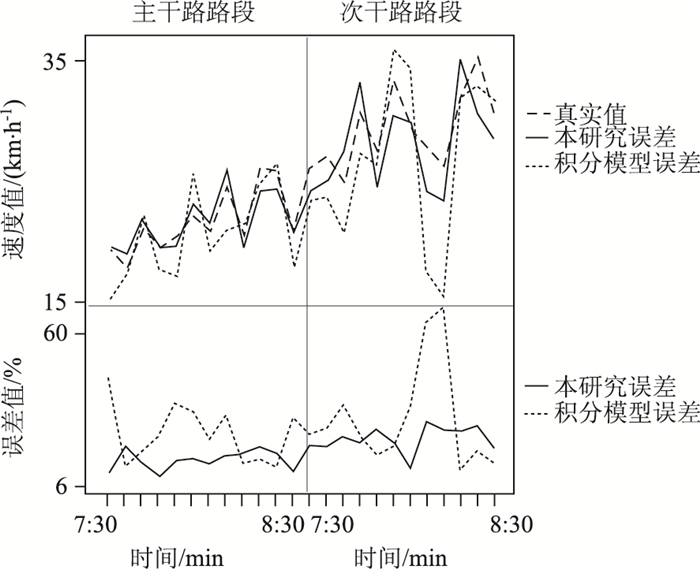
选取路网中具有代表性的主次干路路段,在主次干路段各时段计算平均行程速度,对比本研究算法和经典积分模型法[8]在5 min内所有轨迹计算结果均值与真实值的试验误差。由于数据较多,在表 3仅展示部分路段数据。两种算法估计值与真实值的比对、二者估计误差比对见图 5。由图 5可知,不论对于主次干路,本研究方法和经典方法都接近真实值,可以较好地得到交通参数。但是本研究的方法更接近真实值,误差更小,计算结果更为稳定。
| 时段 | 主干路路段MGS1-GJ | 次干路路段FT1-LW | |||||||||||
| 真实值/ (km·h-1) |
本研究方法 | 积分模型法 | 真实值/ (km·h-1) |
本研究方法 | 积分模型法 | ||||||||
| 估计值/ (km·h-1) |
误差% | 估计值/ (km·h-1) |
误差/% | 估计值/ (km·h-1) |
误差% | 估计值/ (km·h-1) |
误差/% | ||||||
| 7:30—7:35 | 14.49 | 14.61 | 0.83 | 10.21 | 29.54 | 21.10 | 19.07 | 9.62 | 18.41 | 12.75 | |||
| 7:35—7:40 | 12.69 | 13.90 | 9.54 | 12.28 | 3.23 | 22.09 | 20.03 | 9.37 | 18.84 | 14.71 | |||
| 7:40—7:45 | 16.10 | 16.76 | 4.10 | 17.33 | 7.64 | 19.83 | 22.26 | 12.21 | 15.55 | 21.58 | |||
| 7:45—7:50 | 14.44 | 14.42 | 0.14 | 12.59 | 12.81 | 25.72 | 28.33 | 10.15 | 22.53 | 12.40 | |||
| 7:50—7:55 | 15.37 | 14.61 | 4.94 | 11.94 | 22.32 | 22.56 | 19.32 | 14.36 | 21.09 | 6.51 | |||
| 7:55—8:00 | 17.20 | 18.18 | 5.70 | 20.64 | 20.00 | 28.48 | 25.45 | 10.64 | 31.00 | 8.85 | |||
| 8:00—8:05 | 15.74 | 16.39 | 4.13 | 14.01 | 11.05 | 24.36 | 24.92 | 2.30 | 29.38 | 20.61 | |||
| 8:05—8:10 | 19.59 | 20.84 | 6.33 | 15.93 | 18.68 | 22.98 | 19.10 | 16.88 | 12.34 | 46.30 | |||
| 8:10—8:15 | 15.37 | 14.27 | 7.16 | 16.22 | 4.10 | 21.20 | 18.21 | 14.10 | 10.33 | 51.27 | |||
| 8:15—8:20 | 21.10 | 19.16 | 9.19 | 20.00 | 5.50 | 26.49 | 30.18 | 13.89 | 26.93 | 1.66 | |||
| 8:20—8:25 | 20.88 | 19.35 | 7.33 | 21.47 | 2.75 | 30.38 | 25.73 | 15.30 | 28.00 | 7.83 | |||
| 8:25—8:30 | 15.45 | 15.71 | 1.68 | 12.68 | 17.92 | 25.60 | 23.44 | 8.437 5 | 26.69 | 4.23 | |||
|
| 图 5 估计结果比对 Fig. 5 Comparison of estimated and true values |
| |
以主干路路段MGS1-GJ为例,除误差外,估计值与真实值的比对:(1)Sig < 0.05,表明无显著性差异;(2)相关性检验中,Pearson相关值为0.94,为极强相关。对其余主次干路路段,每个路段的对比分析结果进行汇总分析,得到的结果见表 4。从中可看出,该算法估计无显著性差异,平均误差为5.3%,误差较小,精确度较高,所以估计效果较好;主次干路误差为4.1%和9.5%,该算法均适用。在主次干路对比中,主干路相关性更高、误差范围从1.0%~19.4%减少到0.1%~10.2%,误差均值降低了5.4%,且误差更稳定,所以主干路估计效果更好。
| 统计描述 | 显著性 | Pearson相关 | 相对误差% | ||||||
| 最小值 | 25%分位数 | 75%分位数 | 最大值 | 均值 | 标准差 | ||||
| 主干路 | 0.00 | 0.8-0.9 | 极强相关 | 0.1 | 0.9 | 7.0 | 10.2 | 4.1 | 2.9 |
| 次干路 | 0.00 | 0.6-0.8 | 强相关 | 1.0 | 6.4 | 13.3 | 19.4 | 9.5 | 4.5 |
| 整体分析 | 无显著性差异 | 0.6-0.9 | 强相关 | 0.1 | 2.2 | 8.5 | 19.4 | 5.3 | 3.6 |
4 结论
对于浮动车数据估计路段行程速度因其直接来源于数据库中的属性值,提取方便,更是为路段交通状态的判定、先进的出行者信息系统等智能交通模块中奠定了基础。本研究在聚类计算的基础上考虑了交叉口影响范围界定,计算更优的初始聚类中心,以CH有效性评价指数作为聚类个数择优条件。通过研究得出以下结论:
(1) 本方法对主干路路段行程速度估计精度要高于次干路路段。
(2) 把交叉口影响范围和平稳行驶范围分开考虑比经典算法估计更有效。因速度低对应行程时间长,返回低速数据点概率更大,造成计算结果偏低;利用聚类分析及权重分配结合运算,能解决数据点复杂多变的问题;其次选取5 min内所有车辆数据点比选取单列数据更具有代表性,避免偶发性影响。
(3) 通过有效性选择最优聚类个数能避免仅仅把数据点分为快、中、慢3类进行聚类分析的主观性带来的误差。
需要指出的是,交通环境比想象中更多变,浮动车GPS设备不同,设定值也不同,尤其是出现偶发性交通堵塞时,都可能会出现计算结果有所偏离,针对不同应用环境可能需要进一步研究和改进该算法。
| [1] |
杨东援. 通过大数据促进城市交通规划理论的变革[J]. 城市交通, 2016(3): 72-80. YANG Dong-yuan. Promoting Urban Transportation Planning Theory Innovation Using Big Data[J]. Urban Transportation of China, 2016(3): 72-80. |
| [2] |
FAGHRI A, HAMAD K. Travel Time, Speed, and Delay Analysis Using an Integrated GIS/GPS System[J]. Canadian Journal of Civil Engineering, 2002, 29(2): 325-328. |
| [3] |
FABRITⅡS C D, RAGONA R, VALENTI G. Traffic Estimation and Prediction Based on Real Time Floating Car Data[C]//11th International IEEE Conference on Intelligent Transportation Systems. Beijing:IEEE, 2008:197-203. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4732534
|
| [4] |
翁剑成, 荣建, 于泉, 等. 基于浮动车数据的行程速度估计算法及优化[J]. 北京工业大学学报, 2007, 33(5): 459-464. WENG Jian-cheng, RONG Jian, YU Quan, et al. Optimization on Estimation Algorithms of Travel Speed Based on the Real-time Floating Car Data[J]. Journal of Beijing University of Technology, 2007, 33(5): 459-464. |
| [5] |
QUIROGA, AUGUSTO C. An Integrated GPS-GIS Methodology for Performing Travel Time Studies[D].Baton Rouge:Louisiana State University, 1997. https://www.researchgate.net/publication/35521354_An_integrated_GPS-GIS_methodology_for_performing_travel_time_studies?ev=auth_pub
|
| [6] |
李筱菁, 孟庆春, 魏振钢, 等. GPS技术在城市交通状况实时检测技术中的应用[J]. 青岛海洋大学学报:自然科学版, 2002, 32(3): 475-481. LI Xiao-jing, MENG Qing-chun, WEI Zhen-gang, et al. The Applications of GPS Technology in the Real-time Detection of City Traffic Condition to GPS[J]. Journal of Ocean University of Qingdao:Natural Science Edition, 2002, 32(3): 475-481. |
| [7] |
姜桂艳, 常安德, 李琦, 等. 基于出租车GPS数据的路段平均速度估计模型[J]. 西南交通大学学报, 2011, 46(4): 638-644. JIANG Gui-yan, CHANG An-de, LI Qi, et al. Estimation Models for Average Speed of Traffic Flow Based on GPS Data of Taxi[J]. |
| [8] |
沙云飞, 曹瑾鑫, 史其信. 基于GPS的路段旅行时间和速度估计算法研究[J]. ITS通讯, 2006(1): 46-48. SHA Yun-fei, CAO Jin-xin, SHI Qi-xin. The Estimation of Vehicle Speed and Travel Time Based on GPS[J]. Intelligent Transportation Systems, 2006(1): 46-48. |
| [9] |
LI Y, MCDONALD M. Link Travel Time Estimation Using Single GPS Equipped Probe Vehicle[C]//IEEE 5th International Conference on Intelligent Transportation Systems. Singapore:IEEE, 2002, 932-937.
|
| [10] |
曲鑫, 林赐云, 杨兆升, 等. 采用低频浮动车数据的行程时间估计[J]. 哈尔滨工业大学学报, 2016, 48(9): 30-34. QU Xin, LIN Ci-yun, YANG Zhao-sheng, et al. Travel Time Estimation Using Low-frequency Floating Car Data[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 30-34. |
| [11] |
VLAHOGIANNI E I, GOLIAS J C, KARLAFTIS M G. Short-term Traffic Forecasting:Overview of Objectives and Methods[J]. Transport Reviews, 2003, 24(5): 533-557. |
| [12] |
SOHR A, WAGNER P. Short Term Traffic Prediction Using Cluster Analysis Based on Floating Car Data[J]. Neurosurgery, 2008, 60(4): 649-656. |
| [13] |
董红召, 吴方国. 基于FCM的路段平均行程时间估计[J]. 科技通报, 2011, 27(3): 426-430. DONG Hong-zhao, WU Fang-guo. Estimation of Average Link Travel Time Using Fuzzy C-mean[J]. Bulletin of Science and Technology, 2011, 27(3): 426-430. |
| [14] |
PASCALE A, DEFLORIO F, NICOLI M, et al. Motorway Speed Pattern Identification from Floating Vehicle Data for Freight Applications[J]. Transportation Research Part C:Emerging Technologies, 2015, 51(51): 104-119. |
| [15] |
朱鲤, 杨东援. 基于低采样频率浮动车的行程车速信息实时采集技术[J]. 交通运输系统工程与信息, 2008, 8(4): 42-48. ZHU Li, YANG Dong-yuan. Dynamic Travel Speed Collection Technology Based on Low Frequence FCD[J]. Journal of Transportation Systems Engineering and Information Technology, 2008, 8(4): 42-48. |
| [16] |
姜桂艳, 常安德, 张玮. 基于GPS浮动车采集交通信息的路段划分方法[J]. 武汉大学学报:信息科学版, 2010, 35(1): 42-45. JIANG Gui-yan, CHANG An-de, ZHANG Wei. Link Dividing Method for Traffic Information Collecting Based on GPS Equipped Floating Car[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1): 42-45. |
| [17] |
申德拉C F G. SPSS回归分析[M]. 宋武, 译. 北京: 电子工业出版社, 2015. SCHENDERA C F G. Regressions Analysis of SPSS[M]. SONG Wu, Translated. Beijing:Publishing House of Electronics Industry, 2015. |
| [18] |
杨珍珍, 郭胜敏, 李平, 等. 基于浮动车数据的交通流变化趋势提取方法[J]. 公路交通科技, 2013, 30(12): 125-131. YANG Zhen-zhen, GUO Sheng-min, LI Ping, et al. An Extraction Method for Traffic Flow Trend Based on Floating Car Data[J]. Journal of Highway and Transportation Research and Development, 2013, 30(12): 125-131. |
| [19] |
卓金武. MATLAB在数学建模中的应用[M]. 2版. 北京: 北京航空航天大学出版社, 2014. ZHUO Jin-wu. Application of MATLAB in Mathematical Modeling[M]. 2nd ed. Beijing: Beijing University of Aeronautics and Astronautics Press, 2014. |
| [20] |
张润楚. 多元统计分析[M]. 北京: 科学出版社, 2006. ZHANG Run-chu. Multivariate Statistical Analysis[M]. Beijing: Science Press, 2006. |
| [21] |
ERISOGLU M, CALIS N, SAKALLIOGLU S. A New Algorithm for Initial Cluster Centers in k-means Algorithm[J]. Pattern Recognition Letters, 2011, 32(14): 1701-1705. |
| [22] |
MAULIK U, BANDYOPADHYAY S. Performance Evaluation of Some Clustering Algorithms and Validity Indices[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2002, 24(12): 1650-1654. |
| [23] |
杨善林, 李永森, 胡笑旋, 等. K-means算法中的K值优化问题研究[J]. 系统工程理论与实践, 2006, 26(2): 97-101. YANG Shan-lin, LI Yong-sen, HU Xiao-xuan, et al. Optimization Study on K Value of K-means Algorithm[J]. Systems Engineering-Theory & Practice, 2006, 26(2): 97-101. |
| [24] |
张永强. 浮动车覆盖率问题初探[C]//中国智能交通年会论文集. 北京: 人民交通出版社, 2006: 162-166. ZHANG Yong-qiang. Research on Area Coverage of FCD[C]//Proceedings of the Annual Conference of ITS. Beijing:China Communications Press, 2006:162-166. |
 2017, Vol. 34
2017, Vol. 34
