扩展功能
文章信息
- 李素兰, 张谢东, 施俊庆, 张莉
- LI Su-lan, ZHANG Xie-dong, SHI Jun-qing, ZHANG Li
- 信号控制交叉口交通流建模与通行能力分析
- Traffic Flow Modeling and Capacity Analysis of Signalized Intersection
- 公路交通科技, 2017, 34(12): 108-114
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(12): 108-114
- 10.3969/j.issn.1002-0268.2017.12.016
-
文章历史
- 收稿日期: 2017-06-01
2. 武汉市桥梁维修管理处, 湖北 武汉 430015;
3. 浙江师范大学 工学院, 浙江 金华 321004;
4. 武汉市交通科学研究所, 湖北 武汉 430015
2. Wuhan Bridge Maintenance Management Office, Wuhan Hubei 430015, China;
3. School of Engineering, Zhejiang Normal University, Jinhua Zhejiang 321004, China;
4. Wuhan Transportation Science Research Institute, Wuhan Hubei 430015, China
道路和交叉口的通行能力决定了城市交通网络的承载能力[1]。平面十字信号控制交叉口是城市交叉口的常见形式,研究交叉口的车流运行规律,建立更加符合实际的交通流模型,正确分析信号控制交叉口的通行能力,对于合理进行交叉口规划,提高交通管理科学水平具有积极意义。
国内外学者对信号控制交叉口通行能力进行了广泛的研究,取得了一系列的研究成果,主要包括德国的“HBS”[2]、芬兰的“信号控制交叉口通行能力”[3]、加拿大的“CCG”[4]、澳大利亚的“Traffic Signals:Capacity and Timing Analysis”[5]、瑞典的“Swedish Capacity Manual”[6],以及我国学者提出的停止线法[7]、停车线法[8]、冲突点法[9]等。上述方法通常需要制定比较严格的假设条件并对现实的交通条件进行大量简化,这可能导致计算结果与实际情况不相符合。
随着交通流模型的发展,利用计算机仿真的方法对交叉口通行能力进行模拟和分析是一个比较有前途的方法[10]。其中,元胞自动机(Cellular Automata,简称CA)模型在交叉口建模与通行能力分析中得到了广泛应用[11-12]。陈军华等建立了基于CA模型的无信号控制交叉口仿真平台,研究了不同冲突流率下的交叉口通行能力[13]。Li等建立了无信号控制T型交叉口的CA模型,研究了T型交叉口的通行能力[14]。刘琳等提出了一种基于CA模型的可变车道控制技术,模拟可变车道对交叉口通行能力的影响[15]。杨庆芳等提出了一种基于改进间隙接受理论的CA模型,用于分析环形交叉口交织区的通行能力[16]。上述模型对不同交叉口转向比例下的通行能力研究较少,且在模型的可靠性上缺乏实际数据的支撑。
基于此,本研究考虑了平面十字信号控制交叉口各向冲突车流的相互影响,建立了交叉口交通流微观仿真模型,利用实际交叉口验证了模型的有效性,研究了车辆转向比例对交叉口通行能力的影响。
1 模型如图 1所示,交叉口包含4条双向行驶的四车道道路,采用固定信号周期控制。假设车辆按照均匀分布到达,车辆从进口道始端进入,行驶至交叉口后可以直行、左转或右转,沿出口道行驶至终端后离开。
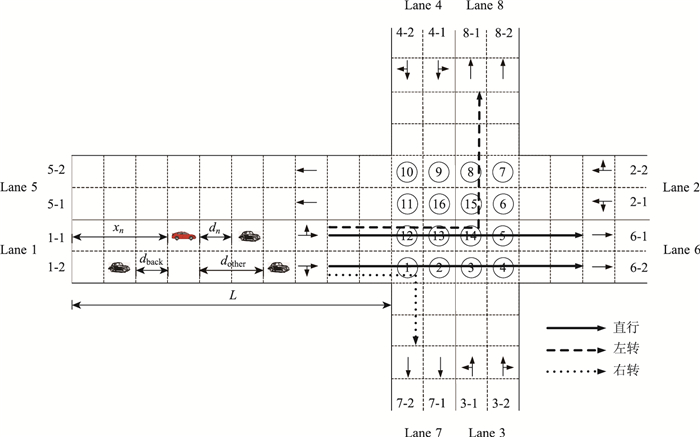
|
| 图 1 交叉口和路段示意图 Fig. 1 Schematic diagram of intersection and roads |
| |
1.1 路段上的车辆更新规则
如图 1所示,每条道路包含2个相向行驶的路段,每个路段包含2条车道,每条车道被分割成L个元胞,每个元胞长度为7.5 m,假设所有车辆均为小汽车,每辆车占据1个元胞,每个时间步对应于1 s。设xn、vn表示第vmax辆车在某个路段中的位置与速度。vn可以取0到vmax之间的任意一个整数,其中vmax(≥1)为最大速度。dn表示第n辆车与前车之间的距离。sn=L-xn表示第n辆车与前方交叉口之间的距离。dback表示第n辆车与相邻车道后方车辆的间距,dother表示第n辆车与相邻车道前方车辆的间距。xn, other表示第n辆车在旁边车道中的位置。Kn表示第n辆车在路段中所处的车道(Kn∈[1, 2],Kn=1表示车辆位于内侧车道,Kn=2表示车辆位于外侧车道)。Fn表示第n辆车在下一个交叉口的转向(Fn∈[1, 3],Fn=1表示左转,Fn=2表示右转,Fn=3表示直行)。Di表示i进口的车辆到达率(i∈[1, 4],i=1表示西进口,i=2表示南进口,i=3表示东进口,i=4表示北进口)。Ri, Fn表示i进口Fn方向的车辆比例。车辆的更新过程由两个步骤来完成,第一步,车辆按照换道规则进行换道;第二步,换道后,各条车道上的车辆按照单车道的NaSch模型[17]规则前进。
1.1.1 换道(1)(min(vn+1, vmax)>dn且dother>dn)或者(Kn≠Fn且Kn≠3),表示车辆按照当前速度行驶至下一个时间步时,行驶过的距离大于与前车的间距,且旁边车道具有更好的行驶条件,或者车辆所处的车道方向与其在下游交叉口的转向不一致,从而产生换道意愿。
(2) dback>dsafe,表示车辆与相邻车道后车距离大于安全距离。
当满足上述两个条件时,车辆向旁边车道换道,xn→xn, other。
1.1.2 前进(1) Step 1:加速,若vn < vmax,则vn+1;若vn=vmax,则vn不变,即vn→min(vn+1, vmax),表示驾驶员都有以尽量快的速度行驶的一般趋势,但不能超过最高车速。
(2) Step 2:减速,当前方交叉口内存在车辆试图占用前方停车线内第一个元胞时,vn→min(vn, dn, sn),表示车辆受前车影响和为了避让交叉口内的冲突车流而减速。这种规则设定是基于这样的背景:如果交叉口内有另一方向的车在绿灯时已进入交叉口,则车辆要停车避让,让交叉口内的冲突车流先通过交叉口。当前方交叉口内不存在车辆试图占用前方停车线内第一个元胞时,分红灯和绿灯两种情况:
Case Ⅰ:绿灯时
vn→min(vn, dn, sn+1),表示车辆要减速通过交叉口,交叉口内最高速度为1 cell/s,即车辆从路段驶入交叉口时第一步最多只能前进至交叉口内第一个元胞。
Case Ⅱ:红灯时
① 直行和左转车辆:vn→min(vn, dn, sn),表示直行和左转车辆受红灯影响而停车。
② 右转车辆:当右转车辆受信号控制时,vn→min(vn, dn, sn);当右转车辆不受信号控制时,vn→min(vn, dn, sn+1)。
(3) Step 3:随机慢化,若vn>0,以随机慢化概率p,vn→max(vn-1, 0)。
(4) Step 4:运动,车辆按照Step 1~3中更新好的速度向前行驶,xn→xn+vn。
1.2 交叉口处的车辆更新规则交叉口处元胞划分及车辆运行轨迹如图 1所示。交叉口处的元胞被分为两种类型:(1)交叉口外层元胞(即元胞1~12);(2)交叉口内层元胞(即元胞13~16)。直行、左转和右转的车辆沿着不同的轨迹穿过交叉口。例如,Lane 1上的左转车辆沿着元胞12~15和8进入Lane 8;直行车辆可以沿着元胞12~14和5进入Lane 6,也可以沿着元胞1~3和4进入Lane 6;右转车辆经过元胞1进入Lane 7。其余的3个方向遵循同样的运动模式。假设车辆在交叉口内的速度可以取0或者1。因此,车辆在交叉口处必须逐一经过上述元胞,不能跨越。交叉口处的车辆按照下述两条规则进行更新:
(1) 交叉口内层元胞上的车辆更新规则
如果车辆前方的元胞是空的,则车辆在当前时间步结束时向前移动一个元胞,否则,车辆将停车等待。此规则适用于元胞13~16上面的所有车辆。
(2) 交叉口外层元胞上的车辆更新规则
如果车辆的前方元胞是空的,且交叉口内层元胞上不存在车辆试图占用该元胞,则车辆向前移动一个元胞,否则,车辆将停车等待。例如,如果元胞16被一个从Lane 2到Lane 7的左转车,或者从Lane 4到Lane 7的直行车,或者从Lane 4到Lane 6的左转车占据的话,元胞12上的车辆禁止驶入元胞13。如果元胞13被一个从Lane 2到Lane 7的左转车,或者从Lane 4到Lane 7的直行车占据的话,元胞1上的车辆禁止驶入元胞2。此规则适用于元胞1~12上面的所有车辆。
2 模型验证为了验证本模型的有效性,选取了武汉市某交叉口,进行基础数据调查,标定模型参数,仿真分析其通行能力,并将仿真结果与停止线法计算结果进行对比。
2.1 基础数据调查该交叉口位于武汉市中心城区,高峰时段非常繁忙,排队现象比较严重。交叉口包含4个进口道,每个进口道包含两条车道,分别为直左车道和直右车道,交叉口车辆构成以小汽车为主,东、南、西、北4个方向小汽车比例分别为90%,85%,87%,95%,根据规范,将高峰小时流量转换为标准小客车[8]。交叉口平面布置与高峰时段流量如图 2所示。交叉口采用如图 3所示的两相位设置,信号周期时长为84 s,其中第一相位38 s、第二相位46 s(含黄灯时间)。
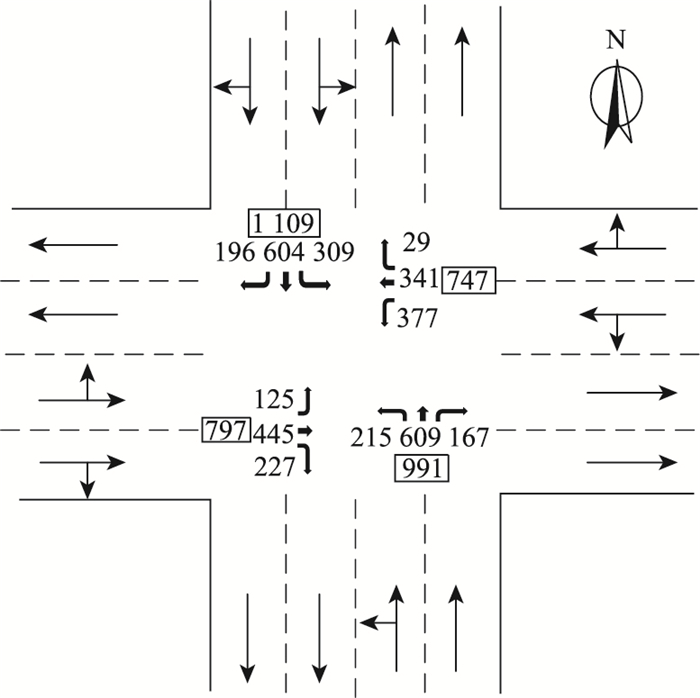
|
| 图 2 交叉口平面布置与流量示意图 Fig. 2 Schematic diagram of intersection plane layout and traffic flow |
| |
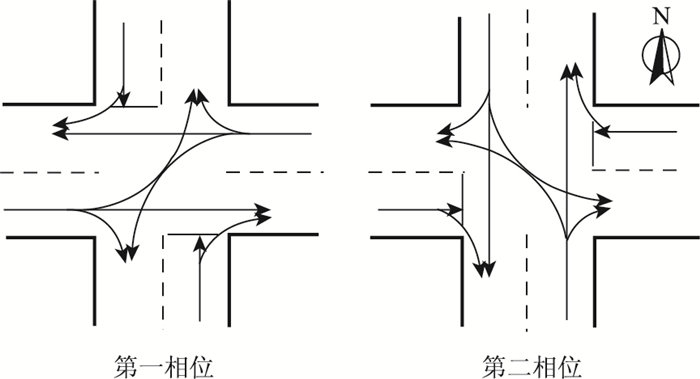
|
| 图 3 交叉口相位图 Fig. 3 Intersection phases |
| |
2.2 通行能力计算
停止线法是中国《城市道路工程设计规范》(CJJ37—2012)中推荐的方法,该方法首先确定直行车道设计通行能力,其余各种功能车道的通行能力以此为基础修正后得到。该方法可表示为:
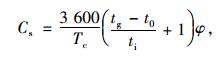
|
(1) |
式中,Cs为一条直行车道的设计通行能力;Tc为信号周期;tg为信号周期内的绿灯时间;t0为绿灯变亮后第1辆车启动并通过停止线的时间;ti为直行车通过停止线的平均间隔时间;φ为折减系数。
直右车道和直左车道的设计通行能力分别可以按照下述公示计算得到:
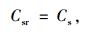
|
(2) |
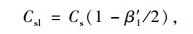
|
(3) |
式中,Csr为一条直右车道的设计通行能力;Csl为一条直左车道的设计通行能力;β′1为直左车道中左转车所占的比例。
根据交通实测结果,Tc为84 s,东西向tg为38 s,南北向tg为46 s,t0,ti和φ分别取规范中的推荐值2.3,2.5 s和0.9,经过计算,得到该交叉口通行能力为4 564 pcu/h。
停车线法计算得到的通行能力一般高于实测通行能力,袁晶矜等利用一个典型的交叉口将停车线法、冲突点法和停止线法计算得到的通行能力与实测值进行了比较,发现停止线法计算结果比实测值高10.4%[18]。
2.3 通行能力仿真根据交通调查情况,标定模型参数,元胞数L为100,即每个路段长度为750 m,最高车速vmax取3 cell/s,随机慢化概率p取0.03。根据4个方向的车辆比例定义车辆到达率,总到达率为4个方向到达率之和,通行能力定义为单位时间(3 600 s)内通过交叉口的车辆数。
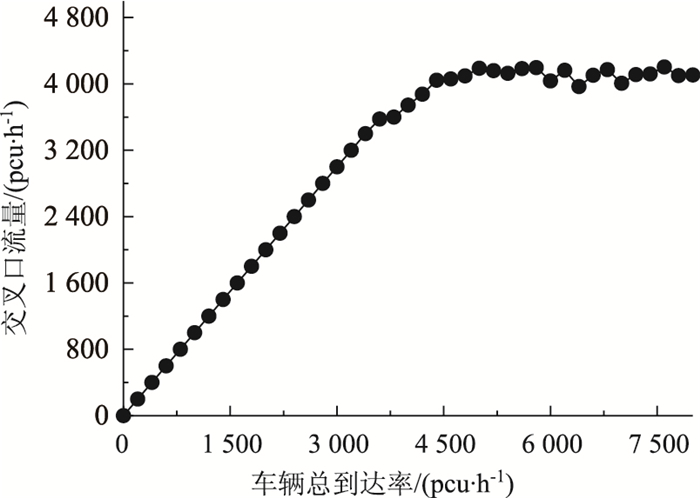
通行能力的仿真结果如图 4所示。单位时间内通过交叉口的车辆数随着车辆到达率的增加而增加,趋向于某一固定值(4 000 pcu/h),当车辆到达率进一步增加时,交叉口流量不再发生变化。这是因为当车辆到达率较低时,所有的车辆都能够顺利通过交叉口,当车辆到达率增加至一定程度时,开始出现车辆排队现象,随着车辆到达率的增加,排队长度越来越长,此时,该固定值即为当前交通条件和道路条件下的交叉口通过能力。通过比较, 发现停止线法计算得到的设计通过能力比仿真结果高14%,与文献[18]中的结论基本吻合,说明交通仿真的结果更接近于实测值,达到了预期目标,证明了模型的可靠性。
|
| 图 4 交叉口流量与车辆到达率的关系 Fig. 4 Relationship between intersection traffic volume and vehicle arrival rate |
| |
3 交叉口转向比例对通行能力的影响 3.1 左转车比例对通行能力的影响
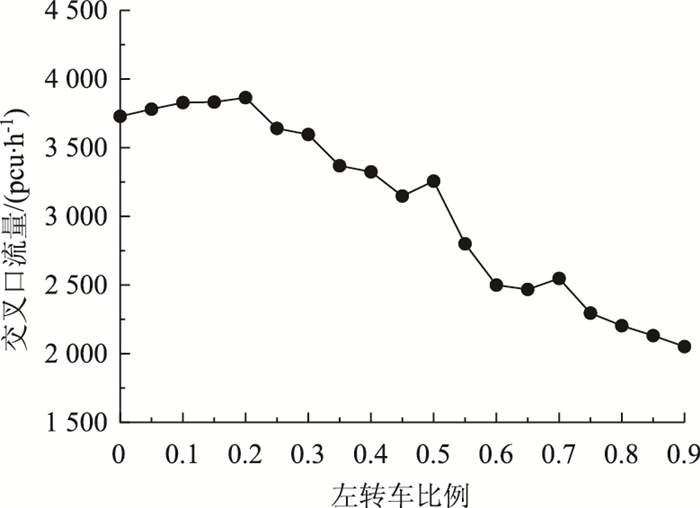
假设右转车转向比例保持0.1不变,改变左转车和直行车的比例(左转车和直行车比例之和为0.9),交叉口流量与车辆转向比例的关系如图 5所示。交叉口通行能力先随着左转车比例增加而增加,当左转车比例为0.2时,交叉口通行能力达到最大值,当左转车比例进一步增加时,交叉口通行能力逐渐下降。这是因为交叉口流量与冲突点密切相关,当左转车比例小于0.2时,冲突点车流数量随着左转车比例增加而减少,当左转车比例大于0.2时,冲突车流数量随着左转车比例增加而增加,导致车辆排队增加,而降低了交叉口通行能力。
|
| 图 5 左转车比例对交叉口通行能力的影响 Fig. 5 Influence of proportion of left-turning vehicles on intersection capacity |
| |
3.2 右转车比例对通行能力的影响
假设存在2种相位设置方案,第1种方案,右转车受信号控制,第2种方案,右转车不受信号控制。假设左转车和直行车比例相同,随着右转车比例的增加而相应减少,不同条件下右转车比例对交叉口通行能力的影响如图 6所示,当右转车不受信号控制时,交叉口通过能力随着右转车比例的增加而增加,这是因为右转车不受信号控制,任意时刻都可以通过交叉口,并且与其他车流冲突较少,因此右转车比例越高,交叉口通过能力越大。
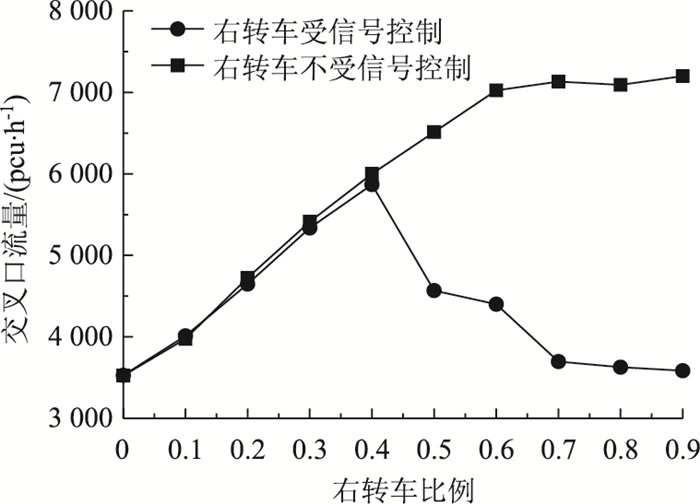
|
| 图 6 右转车比例对交叉口通行能力的影响 Fig. 6 Influence of proportion of right-turning vehicles on intersection capacity |
| |
当右转车受信号控制时,交叉口通过能力首先随着右转车比例增加而增加,当右转车比例为0.4时,交叉口通过能力达到最大值; 当右转车比例进一步增加时,交叉口通过能力随着右转车比例增加而下降。这是因为当右转车比例高于0.4时,右转车越来越多,意味着直行车的数量越来越少,直行车数量的减少意味着直左车道和直右车道的直行功能得不到充分利用,导致交叉口通行能力减少。
4 结论本研究建立了由信号控制交叉口和双向四车道道路(直左+直右)组成的城市路网交通流元胞自动机模型,该模型的交叉口优先权规则能够保证冲突车流有序前进,提高了交叉口仿真的真实性,得到了车辆到达率与交叉口流量的关系,探讨了车辆转向比例和右转车是否受信号控制对交叉口通行能力的影响,仿真结果显示:
(1) 交叉口流量随着车辆到达率的增加而增加,仿真结果与停止线法计算结果误差为14%,验证了模型的可靠性。
(2) 当道路条件确定时,即该交叉口的车道功能确定时,车辆转向比例和信号配时方案对交叉口通行能力具有较大影响,存在一个最佳的车辆转向比例,使得交叉口通行能力达到最大。
(3) 交叉口通行能力随着左转车比例的增加先上升后下降。
(4) 当右转车不受信号控制时,交叉口通行能力随着右转车比例的增加而上升;当右转车受信号控制时,交叉口通行能力随着右转车比例的增加先上升后下降。
对于十字信号控制交叉口交通流建模与通行能力分析的进一步研究可以考虑混合交通、绿信比、左转专用道、车辆到达规律等因素,构建更加符合实际的城市道路交叉口元胞自动机模型,提高交通仿真的真实性,为交通工程实践提供决策支持。
| [1] |
杨晓光, 赵婧, 马万经, 等. 信号控制交叉口通行能力计算方法研究综述[J]. 中国公路学报, 2014, 27(5): 148-157. YANG Xiao-guang, ZHAO Jing, MA Wan-jing, et al. Review on Calculation Method for Signalized Intersection Capacity[J]. China Journal of Highway and Transport, 2014, 27(5): 148-157. |
| [2] |
LEMKE K. The New German Highway Capacity Manual (HBS 2015)[J]. Transportation Research Procedia, 2016, 15: 26-35. |
| [3] |
LUTTINEN R T, NEVALA R. Capacity and Level of Service of Finnish Signalized Intersections[M]. Helsinki: Finnish Road Administration, 2002.
|
| [4] |
TEPLY S, ALLINGHAM D I, RICHARDSON D B, et al. Canadian Capacity Guide for Signalized Intersections[M]. 3rd ed. Ottawa: Institute of Transportation Engineers, 2008.
|
| [5] |
AKCELIK R. Traffic Signals:Capacity and Timing Analysis[M]. Melbourne: Road Research Board, 1981.
|
| [6] |
PETERSON B E, HANSSON A, BANG K, et al. Swedish Capacity Manual[M]. Borlange: National Swedish Road Administration, 1977.
|
| [7] |
CJJ37-2012, 城市道路工程设计规范[S]. CJJ37-2012, Code for Design of Urban Road Engineering[S]. |
| [8] |
徐吉谦, 陈学武. 交通工程总论[M]. 3版. 北京: 人民交通出版社, 2008. XU Ji-qian, CHEN Xue-wu. Fundamentals of Traffic Engineering[M]. 3rd ed. Beijing: China Communications Press, 2008. |
| [9] |
张亚平. 道路通行能力理论[M]. 哈尔滨: 哈尔滨工业大学出版社, 2007. ZHANG Ya-ping. Road Traffic Capacity Theory[M]. Harbin: Harbin Institute of Technology Press, 2007. |
| [10] |
施俊庆, 程琳, 褚昭明, 等. 城市路网交通流元胞自动机模型研究[J]. 公路交通科技, 2015, 32(4): 143-149. SHI Jun-qing, CHENG Lin, CHU Zhao-ming, et al. Cellular Automata Model of Urban Road Network Traffic Flow[J]. |
| [11] |
庞明宝, 吴淑香, 蔡章辉. 基于CAM的港口道路交叉口设计参数优化[J]. 公路交通科技, 2016, 33(1): 103-111. PANG Ming-bao, WU Shu-xiang, CAI Zhang-hui. Optimization of Design Parameters for Intersection of Port Road Based on CAM[J]. Journal of Highway and Transportation Research and Development, 2016, 33(1): 103-111. |
| [12] |
刘应东, 牛惠民, 王建强. 短连线信号交叉口的元胞自动机模型[J]. 公路交通科技, 2015, 32(2): 140-146, 153. LIU Ying-dong, NIU Hui-min, WANG Jian-qiang. Cellular Automata Model of Short-link Grouped Intersections[J]. Journal of Highway and Transportation Research and Development, 2015, 32(2): 140-146, 153. |
| [13] |
陈军华, 张星臣, 赵凛, 等. 基于元胞自动机的交叉口仿真平台研究[J]. 交通运输系统工程与信息, 2009, 9(1): 68-73. CHEN Jun-hua, ZHANG Xing-chen, ZHAO Lin, et al. Simulation Platform for Non-signalized Intersection Based on Cellular Automation[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 9(1): 68-73. |
| [14] |
LI X G, GAO Z Y, JIA B, et al. Cellular Automata Model for Unsignalized T-shaped Intersection[J]. International Journal of Modern Physics C, 2009, 20(4): 501-512. |
| [15] |
刘琳, 王武宏, 郭伟伟, 等. 基于元胞自动机仿真的可变车道控制技术[J]. 长安大学学报:自然科学版, 2015(增1): 250-253, 264. LIU Lin, WANG Wu-hong, GUO Wei-wei, et al. Control Technique for Variable Lane Based on Cellular Automaton[J]. Journal of Chang'an University:Natural Science Edition, 2015(S1): 250-253, 264. |
| [16] |
杨庆芳, 韦学武, 李志林, 等. 基于元胞自动机的环形交叉口通行能力分析[J]. 北京工业大学学报, 2016, 42(4): 561-568. YANG Qing-fang, WEI Xue-wu, LI Zhi-lin, et al. Analysis of Roundabout Capacity Based on Cellular Automat[J]. Journal of Beijing University of Technology, 2016, 42(4): 561-568. |
| [17] |
KAI N, SCHRECKENBERG M. A Cellular Automaton Model for Freeway Traffic[J]. Journal de Physique I, 1992, 2(12): 2221-2229. |
| [18] |
袁晶矜, 袁振洲. 信号交叉口通行能力计算方法的比较分析[J]. 公路交通技术, 2006(5): 123-128, 132. YUAN Jing-jin, YUAN Zhen-zhou. Comparison Analysis of Calculation Methods for Traffic Capacity at Signal Junction[J]. |
 2017, Vol. 34
2017, Vol. 34
