扩展功能
文章信息
- 孙可朝
- SUN Ke-chao
- 基于规划求解的组合预测模型在道路客运量预测中的应用
- Application of Combination Forecasting Model Based on Planning Solving in Road Passenger Transport Volume
- 公路交通科技, 2017, 34(12): 103-107, 114
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(12): 103-107, 114
- 10.3969/j.issn.1002-0268.2017.12.015
-
文章历史
- 收稿日期: 2017-03-18
近几年来,随着乘客对出行服务水平的不断提高,在高铁、民航和私家车等运输方式的冲击下,以及长途班线和卧铺客车逐步退出情况下,我国道路旅客运输客运量逐步下降,客运量是各级道路运输管理部门和企业进行资源配置的重要依据,准确的对道路旅客运输客运量预测有十分重要的意义。
在道路客运量预测方法方面,传统预测方法有:四阶段法、回归分析[1]、灰色理论[2]、神经网络、弹性系数、遗传算法[3]等,国内外许多学者进行了研究,目前很多学者通过运用组合预测模型[4-8]或改进相关模型[9-10]提高预测的精度。同时,在港口和铁路客运量等相关行业的预测方法也有很好的借鉴价值[11-13]。从方便操作和提高预测精度的角度,通过建立基于灰色模型、回归模型和指数平滑的组合预测模型。在规划求解过程中,定义了目标函数变化值确定迭代次数确定方法,目前查阅到的文献中并未有对规划求解中迭代次数的确定方法。利用Excel中的规划求解模块,计算了组合预测模型的权重,以提高预测准确性。
1 基于规划求解的组合预测模型介绍 1.1 灰色模型灰色模型不是基于原始数据进行建立规律,而是通过对历史数据累加,消除原始数据波动较大的弊端。灰色模型一般用于规律性不强,通过历史数据累加,对累加数据进行分析,并对累加数据建立相应的微分方程模型,利用微分方程模型对已知数据的发展趋势情况进行预测,最后利用累加结果计算出源数据。
灰色预测一般情况下是建立灰色模型GM(1, 1)来进行定量分析。
令X(0)为GM(1, 1)建模序列:
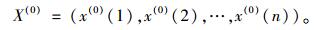
|
(1) |
X(1)为X(0)1-AGO序列:
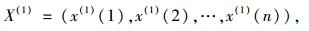
|
(2) |
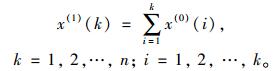
|
(3) |
令Z(1)为X(1)的紧邻均值(MEAN)生成序列:
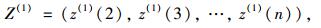
|
(4) |
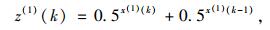
|
(5) |
则GM(1, 1)的定义型,即GM(1, 1)的灰色微分方程模型为:
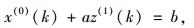
|
(6) |
式中,a称为发展系数;b为灰色作用量。
灰色微分方程的最小二乘估计参数列满足:
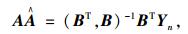
|
(7) |
式中,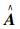
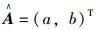
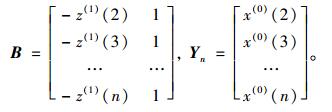
|
称:
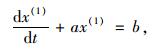
|
(8) |
式(8)为灰色微分方程式(6)的白化方程, 则有:
(1) 白化方程式(8)的解也称时间响应函数为:
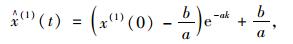
|
(9) |
式中e=2.718 28…, k=1, 2, …, n。
(2) GM(1, 1)灰色微分方程式(6)的时间响应序列为:
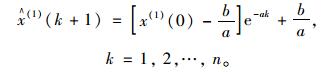
|
(10) |
(3) 取x(1)(0)=x(0)(1),则:
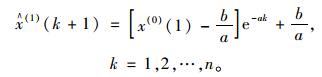
|
(11) |
(4) 还原值:
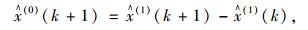
|
(12) |
式(12)即为可以计算出预测数值。
1.2 一元回归模型回归分析模型是基于客运量历史统计数据与自变量函数的关系,建立相应的函数模型,其中回归分析的目标就是要确定函数f(·)的具体形式:
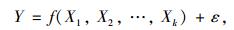
|
(13) |
式中,X1, X2, …, Xk分别代表k个自变量的观测值;ε服从正态分布的误差。
对于某一变量或指标的观测值按照间隔相等的时间先后次序排列起来的时间序列,并利用变量和时间序列的规律,建立基于时间序列的一元或多元回归模型,找到相应的规律,并建立相应模型:
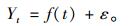
|
(14) |
通过计算最小化估计误差的平方和(Error Sum of Squares, ESS),找到函数参数的值。
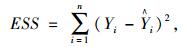
|
(15) |
式中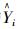
利用已知的观测值来求出ESS,在计算ESS过程中,根据ESS的性质其最小值为0,计算的原理也就是平时所用的最小二乘法。
1.3 指数平滑预测模型指数平滑预测主要特点是近期数据权重较大,远期数据权重较小,并呈现逐步变化的特征。指数平滑预测分为一次指数平滑预测、二次指数平滑预测、三次指数平滑预测等多种类型。结合道路旅客客运量特点,采用三次指数平滑预测方法。
指数平滑法的基本公式是:
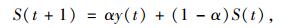
|
(16) |
式中,S(t)为t期的平滑值;y(t)为t期的实际值;α为平滑系数,0≤α≤1。
三次指数平滑预测是结合一次指数平滑,利用模型参数分配不同的指数平滑权重,其预测公式是:
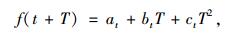
|
(17) |
式中,T为预测期数;at, bt, ct为模型参数。
计算如下:
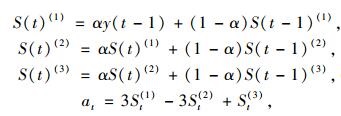
|
(18) |
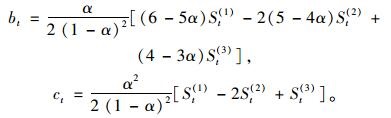
|
(19) |
平滑初始值的确定,可以取前3年的平均值即: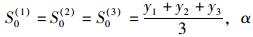
上述3种方法在对道路客运量进行预测中,由于各种方法的特点,其预测的精确度不尽相同,为提高预测精度,需要将3种单独的预测方法组合起来,其中比较重要的一个环节就是组合权重的确定,组合模型克服上述不足的同时,也提高了预测精度及预测可信度。
假设灰色预测、一元回归和三次指数平滑三种预测模型的预测结果分别为yt(1), yt(2), yt(3),t为时间序列1≤t≤n,则组合预测结果为:
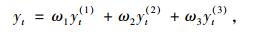
|
(20) |
式中,ω1, ω2, ω3为单个预测模型在组合预测模型中所占权重。
3个权重的确定采用规划求解,规划求解模型如下:
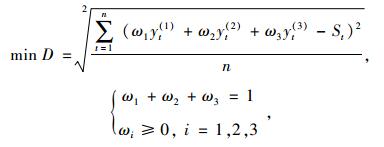
|
(21) |
式中,St为实际客运量;D为3种方法历年预测值加权之和与实际值的差值的绝对值之和。通过规划求解,即可求出权重ω1, ω2, ω3。
3种预测方法分别有自己的检验模型,当客运量预测值不适合某种预测方法时,在确定权重时,规划求解可强制此预测模型的权重为零,这样就排除了这种预测对组合预测的影响,得到合适的组合预测权重。
2 道路旅客运输客运量预测实例分析考虑数据的准确性方面,根据中国道路运输发展报告(2011—2015)[14-18],选取交通运输部实施百城百站以来的旅客发送量进行分析。全国“百城百站”2011—2015年旅客发送量见表 1。
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 旅客发送量/万人 | 53 951.3 | 55 585.0 | 54 366.8 | 51 697.4 | 48 080.8 |
根据3种预测方法的预测模型和算法,对旅客发送量的预测结果见表 2。
| 年份 | 实际发送量/万人 | 灰色模型 | 一元回归 | 指数平滑 | |||||
| 预测值/万人 | 绝对误差/% | 预测值/万人 | 绝对误差/% | 预测值/万人 | 绝对误差/% | ||||
| 2012 | 55 585.0 | 56 222.7 | 1.15 | 55 152.2 | (0.78) | 53 951.3 | (2.94) | ||
| 2013 | 54 366.8 | 53 610.9 | (1.39) | 54 442.7 | 0.14 | 57 784.8 | 6.29 | ||
| 2014 | 51 697.4 | 51 120.4 | (1.12) | 52 025.8 | 0.64 | 52 762.9 | 2.06 | ||
| 2015 | 48 080.8 | 48 745.6 | 1.38 | 47 901.5 | (0.37) | 47 769.6 | (0.65) | ||
| 误差平均值 | 1.26 | 0.48 | 2.98 | ||||||
| 注:绝对误差中带括号表示为负数 | |||||||||
由于指数平滑不能对初始年度的数据进行预测,通过规划求解计算组合权重时仅选取2012—2015年预测数据进行计算。结合Excel选项中规划求解模块的功能,建立规划求解模型。在计算权重过程中,随着迭代次数的增加,目标函数逐渐减小(如表 3所示),如何确定迭代次数是创新点之一。
| 迭代次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 目标函数 | 397.185 6 | 277.003 0 | 249.134 9 | 246.927 6 | 246.442 6 | 246.344 3 | 246.344 0 | 246.343 3 |
| 目标函数变化值 | — | 120.182 6 | 27.868 1 | 2.207 3 | 0.485 0 | 0.098 3 | 0.000 4 | 0.000 7 |
以目标函数的变化值为参考,经过多次迭代计算,当式(21)中目标函数D的变化值出现拐点时,确定了组合预测的权重系数,见表 4。
| 单元格 | 名字 | 单元格值 | 公式 | 状态 | 型数值 |
| $F$65 | 约束条件 | 1 | $F$65=1 | 未到限制值 | 0 |
| $E$65 | W3 | 0.084 732 041 | $E$65>=0 | 未到限制值 | 0.084 7 |
| $D$65 | W2 | 0.483 585 25 | $D$65>=0 | 未到限制值 | 0.483 6 |
| $C$65 | W1 | 0.431 682 71 | $C$65>=0 | 未到限制值 | 0.431 77 |
根据组合权重,计算出组合预测的预测结果及预测误差,如表 5所示。
| 年份 | 实际发送量/万人 | 组合模型 | |
| 预测值/万人 | 绝对误差/% | ||
| 2012 | 55 585.0 | 55 512.6 | (0.13) |
| 2013 | 54 366.8 | 54 366.8 | (0.00) |
| 2014 | 51 697.4 | 51 697.4 | 0.00 |
| 2015 | 48 080.8 | 48 254.7 | 0.36 |
| 误差平均值 | 0.12 | ||
| 注:绝对误差中带括号表示为负数 | |||
从预测结果来看,预测精度明显提高,并可避免一种预测方法对模型预测的经验缺陷。根据以上预测模型,可根据上述模型对未来道路旅客发送量进行预测。
3 结论基于灰色模型、一元回归和指数平滑3种预测方法,建立了基于规划求解的组合预测方法,应用Excel中的“规划求解”功能,确定组合预测模型的权重,从而得到基于规划求解的道路旅客运输组合预测模型。以选取交通运输部实施“百城百站”以来的旅客发送量进行分析,分析结果与灰色模型、一元回归和指数平滑的预测结果进行对比,验证了基于规划求解的组合预测模型的预测精度更高、误差更小。在参数改进方面,结合Excel选项中规划求解模块的功能,建立规划求解模型。规划求解过程中,定义了目标函数变化值确定迭代次数确定方法。同时,组合预测模型可减少单个模型预测的不确定性,也说明基于规划求解的组合预测模型是有效的,具有一定的实际应用价值。
| [1] |
鲁亚. 基于多元回归模型的公路客运量预测分析[J]. 重庆理工大学学报:自然科学, 2016, 30(8): 152-155. LU Ya. Prediction of Traffic Volume Based on Multiple Regression Model[J]. Journal of Chongqing University of Technology:Natural Science Edition, 2016, 30(8): 152-155. |
| [2] |
刘昱岗, 董道建. 灰色关联弹性模型在公路客运量预测中的运用[J]. 公路工程, 2015, 40(1): 253-256. LIU Yu-gang, DONG Dao-jian. The Application of Grey Correlation-elastic Model in the Prediction of Road Passenger Transport Volume[J]. |
| [3] |
甘秋明. 基于遗传算法优化支持向量机的公路客运量预测[J]. 公路工程, 2012, 37(6): 192-195. GAN Qiu-ming. Passenger Traffic Volume Forecasting Based on Support Vector Machine Optimized by Genetic Algorithm[J]. Highway Engineering, 2012, 37(6): 192-195. |
| [4] |
王晓静, 胡郁葱, 朱信山, 等. 基于灰色Verhulst_马尔可夫链组合预测方法的公路客运量预测研究[J]. 公路工程, 2009, 34(2): 169-171. WANG Xiao-Jing, HU Yu-cong, ZHU Xin-shan, et al. Highway Passenger Volume Forecasting Based on Verhulst-Markov Chain Combination Forecast Model[J]. Highway Engineering, 2009, 34(2): 169-171. |
| [5] |
徐月圆, 谢金宝, 匡荣杰, 等. 基于组合模型的公路客运量预测研究[J]. 西部交通科技, 2014, 81(4): 63-66. XU Yue-yuan, XIE Jin-bao, KUANG Rong-jie, et al. Research on Highway Passenger Volume Forecast Based on Combined Model[J]. Western China Communications Science & Technology, 2014, 81(4): 63-66. |
| [6] |
杨文华. 加权几何平均组合预测方法在公路客运量预测中的应用研究[J]. 合肥学院学报:自然科学, 2014, 24(4): 32-36. YANG Wen-hua. The Application in the Highway Passenger Quantity Based on the Method of Weighted Geometric Means Combination Forecasting Model[J]. Journal of Hefei University:Nature Science Edition, 2014, 24(4): 32-36. |
| [7] |
郑海云. 道路旅游客运运力预测混合模型构建[D]. 西安: 长安大学, 2016. ZHENG Hai-yun. Establishment of Forecast Mixture Models on Tourist Transportation Capacity[D]. Xi'an:Chang'an University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10710-1016920791.htm |
| [8] |
芮海田, 吴群琪, 袁华智, 等. 基于指数平滑法和马尔科夫模型的公路客运量预测方法[J]. 交通运输工程学报, 2013, 13(4): 87-93. RUI Hai-tian, WU Qun-qi, YUAN Hua-zhi, et al. Prediction Method of Highway Passenger Transportation Volume Based on Exponential Smoothing Method and Markov Model[J]. Journal of Traffic and Transportation Engineering, 2013, 13(4): 87-93. |
| [9] |
何南. 考虑诱增交通量的四阶段交通需求预测模型研究[D]. 大连: 大连理工大学, 2014. HE Nan. A Study on Four-step Travel Demand Model Incorporating Induced Traffic[D]. Dalian:Dalian University of Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10141-1015573833.htm |
| [10] |
王浩, 郭瑞军. 改进PCA-BP神经网络模型在公路客运量预测的应用[J]. 大连交通大学学报, 2016, 37(2): 1-5. WANG Hao, GUO Rui-jun. Forecasting of Highway Passenger Transportation Volume Based on Improved PCA-BP Neural Network Model[J]. Journal of Dalian Jiaotong University, 2016, 37(2): 1-5. |
| [11] |
刘驰. 我国沿海港口吞吐量预测方法和模型研究[D]. 武汉: 武汉理工大学, 2012. LIU Chi. Study on Forecasting Methods and Models of Coastal Throughput in China[D]. Wuhan:Wuhan University of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10497-1012403821.htm |
| [12] |
冯冰玉, 鲍学英, 王起才, 等. 基于灰色和神经网络的铁路客运量预测研究[J]. 铁道科学与工程学报, 2015, 12(5): 1227-1231. FENG Bing-yu, BAO Xue-ying, WANG Qi-cai, et al. Research of Railway Passenger Volume Forecast Based on Grey and Neural Network[J]. Journal of Railway Science and Engineering, 2015, 12(5): 1227-1231. |
| [13] |
于俊, 陈国华. 基于傅里叶级数的铁路客运量预测研究[J]. 铁路运输与经济, 2016, 33(2): 92-94. YU Jun, CHEN Guo-hua. Forecast of Railway Passenger Traffic Volume Based on Fourier Series[J]. Railway Transport and Economy, 2016, 33(2): 92-94. |
| [14] |
中华人民共和国交通运输部. 中国道路运输发展报告(2011)[R]. 北京: 人民交通出版社, 2011. Ministry of Transport of PRC. National Report on Road Transport Development(2011)[R].Beijing:China Communications Press, 2011. |
| [15] |
中华人民共和国交通运输部. 中国道路运输发展报告(2012)[R]. 北京: 人民交通出版社, 2012. Ministry of Transport of PRC. National Report on Road Transport Development(2012)[R].Beijing:China Communications Press, 2012. |
| [16] |
中华人民共和国交通运输部. 中国道路运输发展报告(2013)[R]. 北京: 人民交通出版社, 2013. Ministry of Transport of PRC. National Report on Road Transport Development(2013)[R].Beijing:China Communications Press, 2013. |
| [17] |
中华人民共和国交通运输部. 中国道路运输发展报告(2014)[R]. 北京: 人民交通出版社, 2014. Ministry of Transport of PRC. National Report on Road Transport Development(2014)[R].Beijing:China Communications Press, 2014. |
| [18] |
中华人民共和国交通运输部. 中国道路运输发展报告(2015)[R]. 北京: 人民交通出版社, 2015. Ministry of Transport of PRC. National Report on Road Transport Development(2015)[R].Beijing:China Communications Press, 2015. |
 2017, Vol. 34
2017, Vol. 34
