扩展功能
文章信息
- 肖大海, 谢全敏, 杨文东
- XIAO Da-hai, XIE Quan-min, YANG Wen-dong
- 基于多变量的集成预测模型在隧道拱顶沉降变形预测中的应用
- Application of Integrated Forecasting Model Based on Multivariable in Tunnel Vault Settlement Forecasting
- 公路交通科技, 2017, 34(12): 90-96
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(12): 90-96
- 10.3969/j.issn.1002-0268.2017.12.013
-
文章历史
- 收稿日期: 2016-12-26
隧道工程稳定性影响因素较多,如地质条件、施工方法、人为因素等,这些因素造成的影响通常难以准确估测,并且相互制约,相互影响,这大大增加了数值模拟的难度。位移是隧道围岩在施工过程中变形所反映出的重要信息,是多种影响因素相互作用下的直观体现[1],通过现场监测围岩位移的变化,可以及时了解围岩所处状态,正确掌握围岩位移变化规律,以选择合适时机进行衬砌支护。因此,掌握隧道围岩拱顶变形的动态规律,随着施工进度准确预测其变形发展趋势,对隧道的开挖、支护及其安全稳定性都有重要的意义[2-3]。目前,国内外学者主要利用围岩变形实测数据建立回归模型,多根据数据分布情况采用对数、指数函数以及差分求解模型,但是这些都无法体现岩体结构内部复杂的物理力学性质和施工方法等因素带来的影响。杨伟超等[4]利用非平稳时序分析法对隧道施工变形进行了预测;齐甦[2]、高文华[5]等利用优化的GM(1, 1)模型对围岩变形预测等方面的问题进行了研究;龙浩等[6]提出了基于BP神经网络-马尔科夫模型,结合BP神经网络和滚动预测方法对隧道围岩变形进行了预测,但以上都只是根据拱顶变形的前期监测数据进行拟合建模,即利用以前的监测值对后期进行预测,由于隧道变形速率在前后期明显不同,故单一变量模型很难达到较高精度预测。
时序分析法可根据输入输出数据自行调整模型参数, 并随着数据更迭, 自动更新参数, 使其接近最佳值;灰色模型建模不需要数据具有平稳性,且即使训练数据较少也能达到较高的预测精度;BP神经网络具有拓扑结构简单、学习速率快等优点,且具有可以逼近任意非线性映射的能力。本研究首先分别构建带输入变量的3种模型,再根据TEI@I理论[7]将3个模型进行非线性结合,构建集成预测模型,从而提高预测精度,为隧道施工提供依据。最后将其用于宝汉铁路连拱隧道台阶法施工过程中拱顶变形位移预测中,论证了模型的可行性。
1 隧道拱顶沉降集成预测模型 1.1 ARIMA时序模型时间序列是按照时间顺序得到的一系列随机变量。构建时间序列模型首先要验证样本数据是否为平稳过程,若为非平稳序列,则需要对原数据进行处理,可采用差分处理,一般经过一次至两次差分即可平稳。目前,理论最成熟且应用最多的模型有移动平均模型MA(q)、自回归模型AR(p)、自回归移动平均模型ARMA(p, q), 其中,MA(q)和AR(p)是ARMA(p, q)的特殊情况,这类模型在极大近似地描述动态数据时,只需要根据其ACF图、PACF图即可总体确定模型形式,即便于分析数据的内部机理,也便于在最小方差意义下达到最大精度的预测。
ARMA(p, q)模型的一般表达式为[7]:
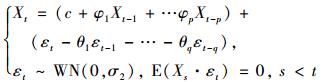
|
(1) |
其中,φ1, …, φp,为自回归系数,θ1,…,θq为移动平均模型;εt为白噪声序列;c为常数。
当φi=0时,则变为MA(q)模型;当θi=0时,则变为AR(p)模型。
时序模型的识别及确定(见表一)主要是利用样本的自相关系数{ρk}和偏自相关系数{γkk},根据ρk和γkk判断可能模型及可能存在的阶数,对每个模型及阶数进行对比,通过比较与选择,根据Q统计量、Adjusted R2值、DW值、AIC值,综合考虑各方面的因素,选择最优模型。
| 模型(序列) | AR(p) | MA(q) | ARMA(p, q) |
| 自相关系数(ACF) | 拖尾 | q阶截尾 | 拖尾 |
| 偏自相关系数(PACF) | q阶截尾 | 拖尾 | 拖尾 |
因为隧道位移变形大体呈现波动递减趋势,不符合平稳性要求,故构建带输入变量的ARIMA(p, d, q)模型,即通过d次差分构建平稳序列,再根据差分后的数据构建ARMA(p, q)模型。其模型构造思想是:假设输出变量序列(因变量序列){Yt}和输入变量序列(自变量序列){X1t},{X2t},…,{Xkt}均平稳,首先构建输出序列和输入序列的回归模型[8-9]:
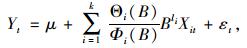
|
(2) |
式中,μ为自变量Xit的期望;Φi(B)为Xit的自回归系数多项式;Θi(B)为Xit的移动平均系数多项式;{εt}为回归残差序列;li为Xit的滞后阶数;B为一步延迟算子。
1.2 GM(1, 2)模型灰色预测理论是通过利用当前可知的信息建立一个具有解释和预测能力的灰色模型, 从而达到模型的预测目的[10, 11]。GM(1, n)模型是灰色预测理论中最基本的、最重要的模型, 这类模型不需要原数据属于平稳序列,且即使训练数据较少也能达到较高的预测精度,其原理是根据系统的已知信息,对原始数据累加求和,并建立一阶线性微分方程时序模型[12]。建模过程如下:设输出变量列为:x1(0)=x1(0)(1), x1(0)(2), …, x1(0)(n), 输出变量序列为x2(0)=x2(0)(1), x2(0)(2), …, x2(0)(n),将x1(0)和x2(0)分别累加一次可得到x1(1)和x2(1)。GM(1, 2)表示一阶且含有2个变量的微分方程,可以表示为[13]:
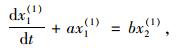
|
(3) |
式中,a为系统发展系数;b为驱动系数。
设
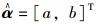
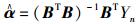
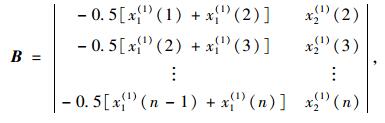
|
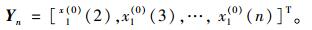
|
(4) |
该微分方程的解为:
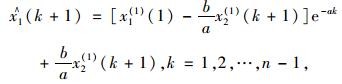
|
(5) |
从而得到相应的原始数据拟合值:
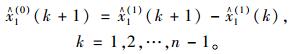
|
(6) |
隧道拱顶沉降常受到多种因素作用,且并非简单的线性变形过程,采用只含一个变量的预测模型常常难以达到较高精度的预测,以至于无法满足工程需要。神经网络是一种非常复杂的网络系统,层与层之间由通过神经元相互连接,它根据试验数据和输出结果类型等设定相关参数后进行学习训练,经过有限次迭代后建立数据之间的映射关系,对非线性变化过程的拟合精度较好。因此,可采用带输入变量的BP神经网络对隧道拱顶变形进行预测,相关理论介绍可参考文献[6, 14, 15]。
1.4 拱顶集成策略本文采用集成策略将带输入变量的时序模型、GM(1, 2)模型和BP模型进行加权集成,建立集成预测模型,模型中的加权系数采用熵值法计算,将3种模型的的综合集成输出作为最终预测结果[16]。
设xt表示第t时刻拱顶变形的实际值,xit°表示第i个单一模型在第t时刻的预测值,则eit = xt -xit°,表示第i个单一模型在第t时刻的预测偏差。令wi为第i个单一模型的加权系数,则集成模型可表示为[14]:
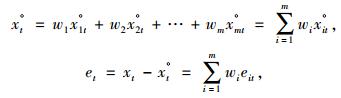
|
(7) |
式中,i=1,2,…,m;t=1,2,…,n,且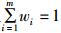
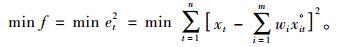
|
(8) |
设拱顶沉降的时间序列实际观察值为{xt,t =1,2,…,n},有m个模型对其进行预测,xit°为第i个模型在第t时刻的拱顶沉降预测值。令:
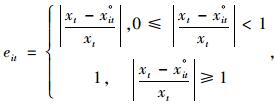
|
(9) |
式中,显然0≤|eit|≤1,{eit}为第i个预测模型在第t时刻的预测相对偏差序列,i = 1,2,…,m;t= 1,2,…,n。
集成模型的加权系数采用信息熵权法确定,建模思想即:第i个单一模型的变异度与其在集成模型中对应的权重成反比。文中的变异度采用信息论中的熵值法确定,并采用熵值法确定加权系数[17-18],其步骤如下:
Step 1:计算单一模型的预测值与实测值之差的权重,表示如下:
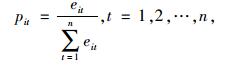
|
(10) |
式中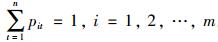
Step 2:计算单一模型预测相对偏差的熵值Ei。

|
(11) |
式中k>0为常数。
对于第i个单一预测模型而言,若pit= 1/n,t=1,2,…,n,则Ei取最大值,也就是Ei=kln n其中k=1/ln n,则有:0≤Ei≤1。
Step 3:计算{eit}的变异度系数di。
由信息论中熵权法思想知di可表示为:
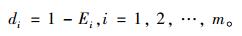
|
(12) |
Step 4:计算各单一预测模型加权系数wi。
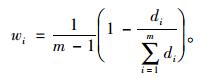
|
(13) |
Step 5:计算集成预测模型的预测值xt°。

|
(14) |
宝汉高速PH-4合同段白庙子隧道ZK131+495段围岩级别为Ⅴ级,岩性主要由强风化板岩和中风化板岩组成,围岩占比28%。隧道采用台阶法施工,由于下台阶开挖时间较晚,与上台阶的开挖时间无重叠部分,拱顶在隧道开挖初期沉降速率较大,故本文选取拱顶沉降监测数据和上台阶周边收敛变形监测数据作为建模样本(见表 2),运用上述理论进行建模预测。
| 日期 | 拱顶沉降变形/mm | 上台阶周边收敛变形/mm | 日期 | 拱顶沉降变形/mm | 上台阶周边收敛变形/mm | 日期 | 拱顶沉降变形/mm | 上台阶周边收敛变形/mm | ||
| 2016-4-19 | 0.84 | 1.04 | 2016-5-1 | 0.46 | 0.61 | 2016-5-12 | 0.12 | 0.08 | ||
| 2016-4-20 | 1.02 | 1.13 | 2016-5-2 | 0.71 | 0.63 | 2016-5-13 | 0.53 | 0.42 | ||
| 2016-4-21 | 0.55 | 0.72 | 2016-5-3 | 0.2 | 0.17 | 2016-5-14 | 0.12 | 0.25 | ||
| 2016-4-22 | 0.67 | 0.81 | 2016-5-4 | 0.31 | 0.35 | 2016-5-15 | 0.09 | 0.18 | ||
| 2016-4-23 | 0.39 | 0.55 | 2016-5-5 | 0.68 | 0.8 | 2016-5-16 | 0.25 | 0.21 | ||
| 2016-4-24 | 0.77 | 0.64 | 2016-5-6 | 0.16 | 0.24 | 2016-5-17 | 0.16 | 0.14 | ||
| 2016-4-25 | 0.47 | 0.52 | 2016-5-7 | 0.62 | 0.72 | 2016-5-18 | 0.32 | 0.3 | ||
| 2016-4-26 | 0.52 | 0.63 | 2016-5-8 | 0.57 | 0.64 | 2016-5-19 | 0.11 | 0.09 | ||
| 2016-4-27 | 0.49 | 0.44 | 2016-5-9 | 0.59 | 0.51 | 2016-5-20 | 0.08 | 0.16 | ||
| 2016-4-28 | 0.38 | 0.5 | 2016-5-10 | 0.20 | 0.11 | 2016-5-21 | 0.15 | 0.05 | ||
| 2016-4-29 | 0.41 | 0.47 | 2016-5-11 | 0.43 | 0.46 | 2016-5-22 | 0.07 | 0.13 | ||
| 2016-4-30 | 0.55 | 0.39 |
2.1 拱顶变形ARIMA模型预测
首先根据实测序列分别构建拱顶沉降预测模型、上台阶收敛预测模型,以拱顶沉降序列Yt的前28个数据作为建模样本,剩余6个数据作为预测检验样本。根据ACF,PACF图以及AIC等准则,经过反复试验可得模型的形式分别为ARIMA(1, 1, 1)模型,ARIMA(1, 1, 2)疏系数模型, 对模型进行残差序列检验,残差序列是白噪声序列,因此模型有效。
考虑到上台阶周边收敛变形与拱顶沉降变形之间的密切关系,将上台阶变形作为输入变量考虑进拱顶变形序列的模型中,进一步研究两者之间的关系。可以通过协相关图分析和确定回归模型。首先对输入输出序列做相关性分析,根据软件Eviews分析可知两组序列存在正相关,相关系数为0.876 168,属于高度相关,可以建立带输入变量的时序模型。对两者的协相关图分析,考虑模型采用ARIMA结构,以减少待估参数。经过分析计算,所建带输入变量的模型为:

|
(15) |
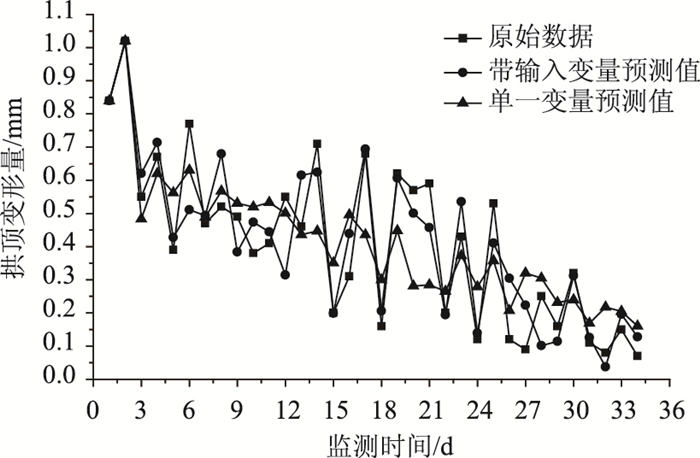
式中,Xt表示上台阶两侧收敛变形量; Yt表示拱顶沉降变形量。该模型的拱顶沉降预测结果见图 1。同时给出单一变量的时序模型预测值进行对比,可以看出带输入变量模型精度显著高于单一变量模型。
|
| 图 1 ARIMA模型预测值 Fig. 1 Predictive values by ARIMA model |
| |
2.2 GM(1, 2)模型预测
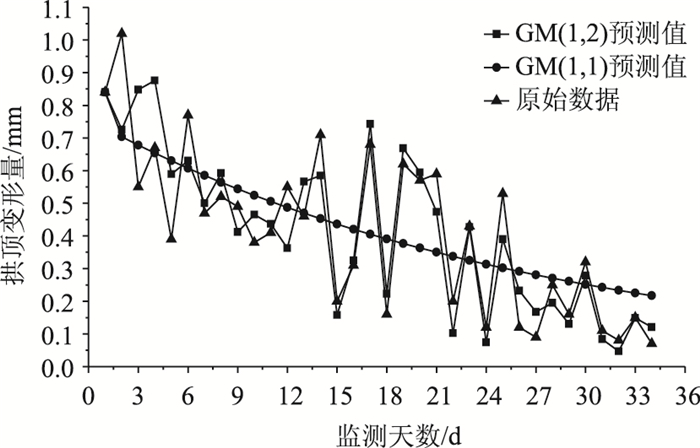
由GM(1, 2)建模理论, 利用前28个监测数据作为建模样本,后6个数据作为预测检验样本。根据式(3)至式(6),利用MATLAB编程计算可得a=0.961 7,b=0.892 7,预测结果见图 2,同时给出GM(1, 1)模型预测值作为对比,根据图 2可知GM(1, 2)模型预测精度远远高于GM(1, 1)模型,而GM(1, 1)模型则完全失效。
|
| 图 2 灰色模型预测值 Fig. 2 Prediction values by gray model |
| |
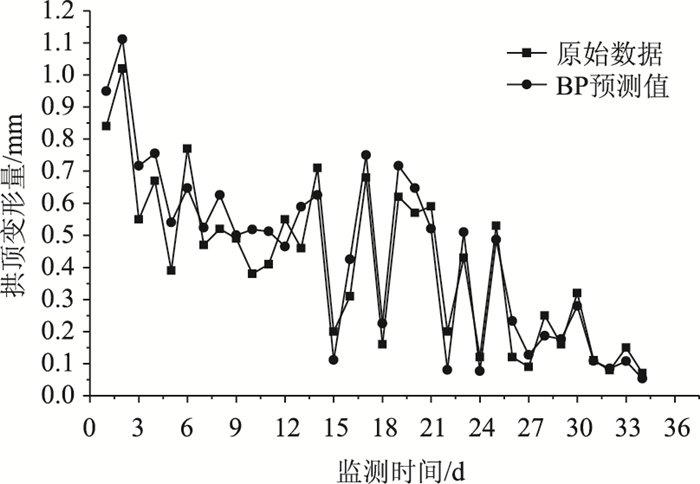
2.3 BP神经网络模型预测
理论上已经证明单隐层的BP神经网络可以逼近一个任意的连续非线性函数,故本研究采用单隐层的3层神经网络, 其中包括1个输入层神经元, 即上台阶收敛变形量;1个输出层神经元, 即拱顶沉降变形量;隐含层的神经元个数, 根据经验公式{m=log2n, 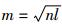
|
| 图 3 神经网络预测值 Fig. 3 Prediction values by neural network |
| |
2.4 综合集成预测
由上述预测结果可知时序模型、GM(1, 2)模型、BP模型的预测偏差的正负性不定,为了避免由于工程突发状况导致部分数据离散化程度加大而导致模型的预测精度降低,同时为了降低不同模型的固有缺陷造成的预测偏差,现利用集成策略将这3种模型综合考虑,从而使模型的预测值能更好地运用于实际工程中。现将拱顶沉降序列分为训练集和测试集, 数据分类同上。根据集成策略的相关公式来计算权重, 最终建立集成模型并预测后期的拱顶沉降量。模型的集成权重结果见表 3。
| 模型 | ARIMA模型 | GM(1, 2)模型 | BP模型 |
| 拱顶位移变形预测权重 | 0.234 8 | 0.377 0 | 0.388 2 |
根据文中给出的集成模型建模步骤对拱顶沉降变形进行集成预测,不同模型的预测结果见表 4。
| 时期 | 原始值 | ARIMA模型预测值 | GM(1, 2)模型预测值 | BP模型预测值 | 集成模型预测值 |
| 2016-5-17 | 0.16 | 0.114 1 | 0.130 0 | 0.176 3 | 0.142 3 |
| 2016-5-18 | 0.32 | 0.312 1 | 0.278 5 | 0.279 3 | 0.288 4 |
| 2016-5-19 | 0.11 | 0.126 1 | 0.083 5 | 0.108 1 | 0.104 7 |
| 2016-5-20 | 0.08 | 0.196 0 | 0.046 4 | 0.085 0 | 0.058 0 |
| 2016-5-21 | 0.15 | 0.037 6 | 0.148 5 | 0.107 7 | 0.147 3 |
| 2016-5-22 | 0.07 | 0.127 4 | 0.120 7 | 0.053 4 | 0.098 2 |
| RMSE | 0.030 0 | 0.034 2 | 0.025 9 | 0.018 3 | |
| 极差 | 0.112 4 | 0.050 7 | 0.042 3 | 0.031 6 | |
根据RMSE值与极差综合对比可知,集成模型的预测值更加稳定,离散程度最小,更能反映出拱顶沉降的变化趋势与日变形量;通过对集成模型预测值与原始值对比可知,其极差只有0.031 6,累计误差只有0.05 mm,考虑到地质条件的复杂性、施工方法等多方面因素,其极差与累计偏差都在可接受范围之内。该集成模型很好地避免了时序模型建模需要较多数据量、灰色模型不考虑系统内在机理、BP模型由于需要设置参数过多的局限性而带来的较大的预测偏差,表明该模型能较好地预测隧道拱顶沉降。
3 结论针对隧道在使用台阶法开挖过程中拱顶沉降变形的预测问题,本研究在构建以上3种预测模型时将上台阶周边收敛变形考虑在内,由图 1和图 2可知只考虑拱顶沉降的单变量模型只能反映出拱顶沉降的变化趋势,预测精度很差,其中只考虑拱顶沉降的单变量灰色模型则完全失效。最后利用熵权法和集成策略将带输入变量的3种单一模型进行加权集成,建立集成预测模型,由表 4可知本研究构建的集成模型的性能和预测精度都显著优于单一模型。
文中提出的集成预测模型建模方便快速,预测精度可满足工程需要,且建模前不用对数据做平滑等繁杂的处理,不用针对单一模型选择某种优化方法即可得到满意的结果。但是也存在以下不足之处:
第一,由于隧道拱顶变形速率在前期和后期存在明显的变化,故在建模时,3种模型很难对变形速率明显不同的地方均达到较高精度的拟合,从而对预测精度下降。
第二,由于工程中突发状况常使部分变形监测数据的离散程度较大,本研究建模时并未对这些特殊异常数据进行筛选处理,因此模型在存在异常数据的数据段的拟合程度相对较低,对预测精度产生影响。
| [1] |
郝哲, 罗敖, 刘斌. 隧道系统预测的多因素模型[J]. 岩土工程技术, 2004, 18(3): 116-121. HAO Zhe, LUO Ao, LIU Bin. Multifactor Forecast Model of Tunnel System[J]. Geotechnical Engineering Technique, 2004, 18(3): 116-121. |
| [2] |
齐甦, 周德军, 王立英, 等. 基于灰色-马尔可夫链的隧道围岩变形预测研究[J]. 现代隧道技术, 2013, 50(1): 80-86. QI Su, ZHOU De-jun, WANG Li-ying, et al. Deformation Prediction of Tunnel Surrounding Rock Based on the Grey-Markov Chain[J]. Modern Tunneling Technology, 2013, 50(1): 80-86. |
| [3] |
安永林, 黄戡, 彭立敏, 等. 强度折减法分析隧道整体稳定性[J]. 公路交通科技, 2011, 28(4): 91-95. AN Yong-lin, HUANG Kan, PENG Li-min, et al. Analysis of Tunnel Stability Based on Strength Reduction Method[J]. Journal of Highway and Transportation Research and Development, 2011, 28(4): 91-95. |
| [4] |
杨伟超, 彭立敏, 黄娟, 等. 非平稳时序分析法在隧道施工变形预测中的应用[J]. 郑州大学学报:工学版, 2008, 29(1): 132-135. YANG Wei-chao, PENG Li-min, HUANG Juan, et al. Deformation Prediction due to Tunnel Construction on Non-steady Time-series Analysis[J]. Journal of Zhengzhou University:Engineering Science Edition, 2008, 29(1): 132-135. |
| [5] |
孙闯, 张向东, 贾宝新. 基于收敛-约束法的隧道围岩安全性评价[J]. 公路交通科技, 2014, 31(3): 96-100. SUN Chuang, ZHANG Xiang-dong, JIA Bao-xin. Evaluation of Tunnel Surrounding Rock Safety Based on Convergence-constraint Method[J]. |
| [6] |
龙浩, 高睿, 孔德新, 等. 基于BP神经网络-马尔科夫链模型的隧道围岩位移预测[J]. 长江科学院院报, 2013, 30(3): 40-43. LONG Hao, GAO Rui, KONG De-xin, et al. Forecast of Tunnel's Surrounding Rock Displacement by BP Neural Network and Markov Chain[J]. Journal of Yangtze River Scientific Research Institute, 2013, 30(3): 40-43. |
| [7] |
汪寿阳, 余乐安, 黎建强. TEI@I方法论及其在外汇汇率预测中的应用[J]. 管理学报, 2007, 4(1): 21-27. WANG Shou-yang, YU Le-an, LI Jian-qiang. TEI@I Methodology and Its Application to Exchange Rates Prediction[J]. Chinese Journal of Management, 2007, 4(1): 21-27. |
| [8] |
汪远征, 徐雅静. 多元平稳时间序列ARIMAX模型的应用[J]. 统计与决策, 2007(18): 132-135. WANG Yuan-zheng, XU Ya-jing. Application of Multiple Stationary Time Series ARIMAX Model[J]. Statistics and Decision, 2007(18): 132-135. |
| [9] |
王黎明. 应用时间序列分析[M]. 上海: 复旦大学出版社, 2009, 220-226. WANG Li-ming. Analysis of Application Time Series[M]. Shanghai: Fudan University Press, 2009, 220-226. |
| [10] |
高文华, 朱建群, 黄自永, 等. 隧道围岩变形动态预测的灰色自适应模型及其参数智能辨识[J]. 公路交通科技, 2012, 29(1): 114-132. GAO Wen-hua, ZHU Jian-qun, HUANG Zi-yong, et al. Grey Self-adaptive Model of Dynamic Prediction of Surrounding Rock Deformation of Tunnel and Intelligent Identification of Parameters[J]. Journal of Highway and Transportation Research and Development, 2012, 29(1): 114-132. |
| [11] |
刘能铸. 基于灰色理论的隧道围岩稳定性预测分析[D]. 重庆: 重庆大学, 2007. LIU Neng-zhu. Prediction of Stability of Tunnel Surrounding Rock Based on Gray Theory[D]. Chongqing:Chongqing University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10611-2007182395.htm |
| [12] |
LIN K H, LIU B D. A Gray System Modeling Approach to the Prediction of Calibration Intervals[J]. IEEE Transactions on Instrumentation & Measurement, 2005, 54(1): 297-304. |
| [13] |
李建林, 李志强, 郑继东. 矿井涌水量灰色GM(1, 2)预测模型[J]. 河南理工大学学报:自然科学版, 2016, 35(3): 368-372. LI Jian-lin, LI Zhi-qiang, ZHENG Ji-dong. GM(1, 2) Model for Predicting Mine Discharge[J]. Journal of Henan Polytechnic University:Natural Science Edition, 2016, 35(3): 368-372. |
| [14] |
周国雄, 莫晓山. 基于灰色预测和BP的集气管压力集成预测方法[J]. 仪器仪表学报, 2011, 32(7): 1648-1654. ZHOU Guo-xiong, MO Xiao-shan. Integration Prediction of Gas Collector Pressure Based on Gray Forecasting and BP Neural Network[J]. Chinese Journal of Scientific Instrument, 2011, 32(7): 1648-1654. |
| [15] |
安永林, 彭立敏. BP与GM(1, 1)预测隧道涌水对比分析和实证[J]. 科技导报, 2008, 26(13): 71-74. AN Yong-lin, PENG Li-min. Forecast Water Gush in Tunnel Based BP and GM(1, 1):A Case Study[J]. Science and Technology Review, 2008, 26(13): 71-74. |
| [16] |
ZHAO Z Y, GONG Q M, ZHANG Y, et al. Prediction Model of Tunnel Boring Machine Performance by Ensemble Neural Networks[J]. Geomechanics and Geoengineering, 2007, 2(2): 123-128. |
| [17] |
陈华友. 熵值法及其在确定组合预测权系数中的应用[J]. 安徽大学学报:自然科学版, 2003, 27(4): 1-6. CHEN Hua-you. Entropy Method and Application to Determine Weights of Combination Forecasting[J]. Journal of Anhui University:Natural Science Edition, 2003, 27(4): 1-6. |
| [18] |
王春生, 吴敏, 曹卫华. 基于IGS和SVM的烧结返矿量智能集成预测模型[J]. 控制与决策, 2008, 23(4): 450-454. WANG Chun-sheng, WU Min, CAO Wei-hua. Intelligent Integrated Prediction Model for Quantity of Sintering Return Mines Based on IGS and SVM[J]. Control and Decision, 2008, 23(4): 450-454. |
 2017, Vol. 34
2017, Vol. 34
